Abstract
We investigate dissociation in flight of metastable molecular dications formed by ultrashort, intense laser pulses using the cold target recoil ion momentum spectroscopy technique. A method for retrieving the lifetime(s) of the transient metastable state(s) as well as the complete three-dimensional momenta of the dissociating fragments is presented. Specifically, we demonstrate and discuss this approach by focusing on dissociation in flight of the ethylene dication going to the deprotonation channel. Two lifetimes are found to be associated with this process, C2H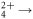 C2H3+ + H+:
C2H3+ + H+: 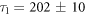 ns and
ns and 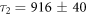 ns. For the corresponding channel in deuterated ethylene, lifetimes of
ns. For the corresponding channel in deuterated ethylene, lifetimes of 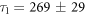 ns and
ns and  ns are obtained.
ns are obtained.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Many processes in molecules happen on fast timescales. For example, rotations and vibrations typically occur on picosecond and femtosecond timescales, respectively. Molecular bond rearrangement and fragmentation often proceed on similarly short timescales, as shown in [1–5] and many others. Hence, femtosecond laser pulses, possessing temporal durations shorter than these timescales, can be used to influence and shed light on molecular dynamics [6–9].
Not all processes in molecules, however, proceed so swiftly. Multiply charged molecular ions can exist in metastable states that lead to fragmentation happening on long timescales that range from picoseconds to even seconds [10–12]. The lifetimes of these transient systems are governed by the relevant potential energy landscape and the mechanisms responsible for decay, which can include tunneling, predissociation, and radiative decay to repulsive states. Investigating the formation, properties, and decay of these metastable molecular ions experimentally and theoretically has been a prominent field of research (see review papers [10–12] and [13–24], for example).
We study the decay dynamics of metastable molecules by employing coincidence three-dimensional (3D) momentum imaging, which provides the complete 3D momenta of the fragments and therefore their kinetic energy release (KER) and angular distributions. This information can in turn facilitate understanding of the dissociation mechanism(s), demonstrated for example in [17, 25, 26]. Hence, the 3D momentum imaging technique has been a powerful tool in studies of molecular fragmentation following ionization by ultrashort intense laser pulses, x-ray (or extreme ultraviolet) photons, or fast ion impact [27, 28], as long as the breakup is prompt. Prompt breakup happens on a sub-picosecond timescale, much shorter than the flight times of the fragments to the detector. The ionization processes in such experiments can readily form multiply charged metastable molecular ions, seen for example in [17, 22, 23, 29–34].
Importantly, in coincidence measurements, a metastable molecular ion may survive beyond the interaction region, traveling through the spectrometer for a non-negligible time before undergoing dissociation in flight. In this unimolecular fragmentation process, which is a subset of delayed dissociation, the survival time of a fragmenting metastable molecule, td, is a significant fraction of the time of flight (TOF) of intact metastable ions, tm. In the present experiments, td is on the order of hundreds of nanoseconds to a few microseconds. In general, the observable range of td may differ depending on the specific metastable system, as well as the conditions of the experiment.
One of the striking signatures of dissociation in flight in the coincidence time-of-flight (CTOF) spectrum is a long, curved stripe that extends from the prompt breakup region and terminates at the intact metastable ion time of flight. This signature has been noted in CTOF spectra from a myriad of studies [35–48].
Field and Eland developed a method to extract the lifetimes of metastable states decaying in flight by fitting Monte-Carlo simulated time-of-flight-difference distributions N( ) to the corresponding measured time-difference spectrum. Here, t1 and t2 are the times of flight of the first and second fragments, respectively. They have demonstrated their technique for a vast array of molecules [36]. Subsequent studies have implemented this method of lifetime retrieval for other metastable molecules [39, 41–44]. Recently, making some simplifying assumptions, Larimian et al [47] calculated td kinematically and retrieved the lifetime for deprotonation of the metastable ethylene dication. They also retrieved the momentum distribution of the fragments using Abel inversion [49] of the position image and discussed possible decay routes.
) to the corresponding measured time-difference spectrum. Here, t1 and t2 are the times of flight of the first and second fragments, respectively. They have demonstrated their technique for a vast array of molecules [36]. Subsequent studies have implemented this method of lifetime retrieval for other metastable molecules [39, 41–44]. Recently, making some simplifying assumptions, Larimian et al [47] calculated td kinematically and retrieved the lifetime for deprotonation of the metastable ethylene dication. They also retrieved the momentum distribution of the fragments using Abel inversion [49] of the position image and discussed possible decay routes.
Our aim in this work is to present a more direct approach for extracting information about dissociation in flight of metastable molecules from coincidence momentum imaging measurements, employing basic principles. This method takes advantage of the known symmetries regarding the fragmentation process and allows one to extract not only the lifetime(s) of the metastable molecule but also the momenta, KER, and angular distributions. This information can enable pinpointing of the likely metastable state(s) dissociating in flight, as well as their dissociation mechanisms. Furthermore, this technique is general and can be applied to many different systems that undergo dissociation in flight. While our method is versatile and can provide a wealth of information to deepen understanding of dissociation processes, the focus of this manuscript is the analysis method of retrieving this information from the measurement.
2. Experimental method
To demonstrate our approach, we examine the same dissociation-in-flight channel as Larimian et al [47]. Namely, we look at deprotonation of metastable ethylene dications, C2H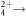 C2H3+ +H+ (as well as the deuterated equivalent), using the cold target recoil ion momentum spectroscopy (COLTRIMS) technique [27, 28]. Laser pulses with central wavelength of 790 nm, 23 fs duration (full width at half maximum (FWHM) in intensity), and peak intensity of about 3 × 1014 W cm−2 are used to doubly ionize the ethylene molecules, introduced as a supersonic jet. The pulse duration was measured using second harmonic frequency-resolved optical gating (SHG FROG) [50], and the intensity was evaluated using the kink in the photoelectron spectrum of neon associated with 2Up (where Up is the average quiver energy of the free electron), which represents the transition from direct to rescattered electrons. To determine the 2Up point, we measured the momenta of Ne+ recoil ions at low extraction field, following the method detailed in [51, 52].
C2H3+ +H+ (as well as the deuterated equivalent), using the cold target recoil ion momentum spectroscopy (COLTRIMS) technique [27, 28]. Laser pulses with central wavelength of 790 nm, 23 fs duration (full width at half maximum (FWHM) in intensity), and peak intensity of about 3 × 1014 W cm−2 are used to doubly ionize the ethylene molecules, introduced as a supersonic jet. The pulse duration was measured using second harmonic frequency-resolved optical gating (SHG FROG) [50], and the intensity was evaluated using the kink in the photoelectron spectrum of neon associated with 2Up (where Up is the average quiver energy of the free electron), which represents the transition from direct to rescattered electrons. To determine the 2Up point, we measured the momenta of Ne+ recoil ions at low extraction field, following the method detailed in [51, 52].
As shown in figure 1(a), we observe the well-known signature of dissociation in flight, a long stripe in the CTOF spectrum. In figure 1(b), we note another signature in a density plot of the ion yield as a function of the measured TOF and position, N(TOF, x), where two 'halos' extend from the light and heavy fragments to the small C2D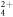 spot. Notably, in both the CTOF and N(TOF, x) spectra, the distributions of the two fragments converge to that of the intact metastable dication. Furthermore, as highlighted in figure 1(a), the predictions of Newton's equations of motion for dissociation in flight, which are marked by the open triangles, agree well with the measured data.
spot. Notably, in both the CTOF and N(TOF, x) spectra, the distributions of the two fragments converge to that of the intact metastable dication. Furthermore, as highlighted in figure 1(a), the predictions of Newton's equations of motion for dissociation in flight, which are marked by the open triangles, agree well with the measured data.
Figure 1. Signatures of dissociation in flight in coincidence spectra for laser-induced deprotonation of deuterated ethylene. (a) Coincidence time-of-flight (CTOF) spectrum. The long stripe that is marked by an arrow and extends from the prompt C2D3+ + D+ breakup region to the time of flight (TOF) of the metastable dication, tm, is a signature of dissociation in flight. The open triangles represent the predictions of Newton's equations of motion for dissociation in flight at different values of td, assuming  , where
, where 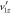 is the component of the dissociation velocity along the TOF axis. (b) Density plot of the ion yield as a function of TOF and x position, N(TOF, x). Highlighted by the dashed blue lines are two 'halos' that are signatures of dissociation in flight. One 'halo' extends from the light fragment, D+, and one extends from the heavy fragment, C2D3+. Both shrink in size and converge to the small C2D
is the component of the dissociation velocity along the TOF axis. (b) Density plot of the ion yield as a function of TOF and x position, N(TOF, x). Highlighted by the dashed blue lines are two 'halos' that are signatures of dissociation in flight. One 'halo' extends from the light fragment, D+, and one extends from the heavy fragment, C2D3+. Both shrink in size and converge to the small C2D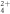 spot.
spot.
Download figure:
Standard image High-resolution image3. Analysis method and results
To accomplish our goal of directly extracting information about dissociation in flight of a metastable molecule from our measurements, we start from the kinematic equations. The coordinate system utilized is depicted in figure 2(a). We employ principles similar to those that have been applied for years to image collision- and laser-induced prompt molecular dissociation in CTOF measurements [27, 28]. The equations of motion become slightly different from those for prompt dissociation to account for the survival time of the dication, td. For two-body dissociation in flight of a generic metastable dication, AB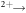
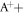 B+, we have the following equations in the x direction, which in our case is along the laser beam propagation and transverse to the spectrometer axis:
B+, we have the following equations in the x direction, which in our case is along the laser beam propagation and transverse to the spectrometer axis:
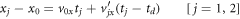
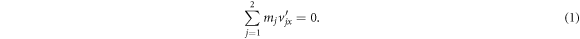
Here, xj is the measured position of fragment j, and x0 is the initial position of the metastable dication. v0x is the average initial x-component velocity of the dication in the laboratory frame (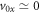 for a cold jet),
for a cold jet), 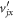 is the x-component dissociation velocity in the AB2+ center-of-mass frame, tj is fragment j's time of flight, and mj is its mass. Clearly, td is needed to properly calculate the transverse momenta of the fragments. Note that the y-component equations (transverse to the spectrometer axis and along the jet flow) are similar to the x equations, except that v0y, the supersonic jet velocity, is not negligible.
is the x-component dissociation velocity in the AB2+ center-of-mass frame, tj is fragment j's time of flight, and mj is its mass. Clearly, td is needed to properly calculate the transverse momenta of the fragments. Note that the y-component equations (transverse to the spectrometer axis and along the jet flow) are similar to the x equations, except that v0y, the supersonic jet velocity, is not negligible.
Figure 2. (a) A schematic view of the laser-molecule interaction region and coordinate system. (b) Diagram illustrating the measurement of dissociation in flight of doubly charged ethylene. This metastable dication dissociates at time td, and position and time information about the resulting H+ (or D+) and C2H3+ (or C2D3+) fragments is measured. (c) Cartoon demonstrating how 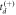 and
and 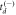 are related to the sign of
are related to the sign of 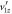 . (d) Computed time of flight as a function of td for C2D
. (d) Computed time of flight as a function of td for C2D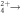 C2D3+ + D+ dissociation in flight, assuming
C2D3+ + D+ dissociation in flight, assuming 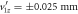 ns−1 (associated with typical kinetic energy release of 4 eV, as discussed later). On this plot, an example set of
ns−1 (associated with typical kinetic energy release of 4 eV, as discussed later). On this plot, an example set of  and
and 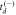 solutions is indicated by the blue and green vertical lines. Note that the difference between these delay times is small compared to tm. Also, it is readily seen that both situations,
solutions is indicated by the blue and green vertical lines. Note that the difference between these delay times is small compared to tm. Also, it is readily seen that both situations, 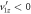 with
with 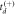 and
and 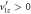 with
with 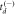 , lead to the same pair of t1 and t2 values, indicated by the dotted horizontal lines.
, lead to the same pair of t1 and t2 values, indicated by the dotted horizontal lines.
Download figure:
Standard image High-resolution imageAt this point, it is interesting to contrast momentum imaging of dissociation in flight to that of prompt breakup, for which 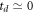 . In the case of prompt fragmentation, one can readily see that the transverse equations of motion are decoupled from motion along the z direction, which is parallel to the spectrometer axis. For the problem of dissociation in flight, however, this is not the case, as td leaves us with more unknowns than equations in the transverse directions. Thus, we need to determine td from the z-component kinematic equations first.
. In the case of prompt fragmentation, one can readily see that the transverse equations of motion are decoupled from motion along the z direction, which is parallel to the spectrometer axis. For the problem of dissociation in flight, however, this is not the case, as td leaves us with more unknowns than equations in the transverse directions. Thus, we need to determine td from the z-component kinematic equations first.
3.1. td and lifetime determination
How exactly can we retrieve td from the z-direction motion? First, we write the z-component equations of motion:
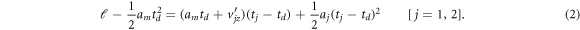
Here, ℓ is the ion flight distance, am is the AB2+ acceleration, 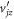 is the z-component dissociation velocity of the jth fragment in the AB2+ center-of-mass frame, and aj is its acceleration. We proceed to write the equations of motion in a more convenient dimensionless form. To that end, we multiply equation (2) by
is the z-component dissociation velocity of the jth fragment in the AB2+ center-of-mass frame, and aj is its acceleration. We proceed to write the equations of motion in a more convenient dimensionless form. To that end, we multiply equation (2) by 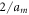 :
:
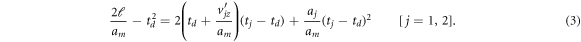
Noting that the AB2+ TOF is 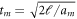 , we replace the first term on the left-hand side of equation (3) with tm2. Further, dividing both sides by tm2 leads us to dimensionless z-component equations of motion. We also write the equation for momentum conservation in the AB2+ center-of-mass frame:
, we replace the first term on the left-hand side of equation (3) with tm2. Further, dividing both sides by tm2 leads us to dimensionless z-component equations of motion. We also write the equation for momentum conservation in the AB2+ center-of-mass frame:
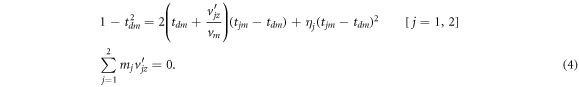
Here, we have defined 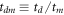 ,
, 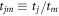 , and
, and 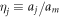 . Also, we have substituted in
. Also, we have substituted in 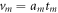 , the velocity of the dication.
, the velocity of the dication.
The equations above suggest that we can solve for tdm (and hence td), as we have three equations and three unknowns, tdm, 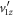 , and
, and 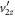 . Combining the above equations of motion and the equation for momentum conservation, we eliminate
. Combining the above equations of motion and the equation for momentum conservation, we eliminate  by substitution, resulting in an equation that can be solved for tdm. Several subsequent algebraic steps lead us to the following quadratic equation:
by substitution, resulting in an equation that can be solved for tdm. Several subsequent algebraic steps lead us to the following quadratic equation:

Here, 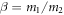 is the ratio of the mass of the light fragment to that of the heavy fragment.
is the ratio of the mass of the light fragment to that of the heavy fragment.
While the simplicity of our derivation and resulting equations makes the calculation of td and subsequent momentum imaging look quite straightforward, the problem is more convoluted than it initially seems. The quadratic equation for td has two solutions, which we denote as 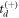 and
and 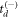 , where the superscripts correspond to the sign that is chosen in the quadratic formula.
, where the superscripts correspond to the sign that is chosen in the quadratic formula.
For the vast majority of events, it is not clear which solution is correct, as both are physical based on obvious criteria: td must be real and 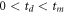 . The root of this complication, illustrated in figures 2(c) and (d), is the link between the sign of
. The root of this complication, illustrated in figures 2(c) and (d), is the link between the sign of 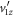 and the correct quadratic formula sign choice. Specifically,
and the correct quadratic formula sign choice. Specifically, 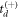 always corresponds to
always corresponds to 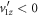 , meaning the H+ (or D+) is ejected away from the detector, and
, meaning the H+ (or D+) is ejected away from the detector, and 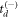 corresponds to
corresponds to 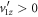 . Of course, in setting out to solve for td, one does not know a priori the sign of
. Of course, in setting out to solve for td, one does not know a priori the sign of 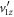 . Moreover, both situations—positive
. Moreover, both situations—positive  with delay time
with delay time 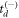 and negative
and negative 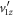 with
with 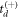 —lead to the same measured set of time-of-flight values
—lead to the same measured set of time-of-flight values 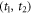 . This dilemma also thwarts retrieval of
. This dilemma also thwarts retrieval of 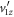 and the z-component momenta, for which one needs to properly evaluate td.
and the z-component momenta, for which one needs to properly evaluate td.
As a noteworthy aside, this dual-solution td retrieval problem belongs to an extensive family of inverse problems, in which one is trying to retrieve initial conditions from observable parameters. This is an important problem faced in a wide array of fields in science and mathematics, such as medical imaging, x-ray crystallography, optics, geology, acoustics, and many others [53–55]. Frequently, the solution to an inverse problem is not unique, as is the case for dissociation in flight.
To address the inverse problem at hand, we utilize symmetry concepts. For any given td, reflection symmetry of 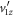 about 0 is expected, as the light fragment is equally likely to be ejected in either the forward or backward directions. Thus, one could select
about 0 is expected, as the light fragment is equally likely to be ejected in either the forward or backward directions. Thus, one could select 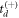 or
or 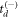 randomly with equal probability and fit an exponential decay function to the resultant N(td) distribution to get a lifetime τ.
randomly with equal probability and fit an exponential decay function to the resultant N(td) distribution to get a lifetime τ.
In the case of dissociation in flight, however, the symmetry of the overall 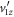 distribution should be broken to some degree due to the lifetime of the metastable molecule. That is, if τ is the lifetime of the dication, the ratio of the number of molecules that survive for times
distribution should be broken to some degree due to the lifetime of the metastable molecule. That is, if τ is the lifetime of the dication, the ratio of the number of molecules that survive for times  and
and 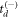 ,
, 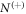 and
and 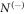 , respectively, is described by
, respectively, is described by
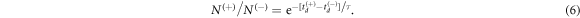
Thus, one could correct for the symmetry breaking using this factor. The extent of this correction is determined by the magnitude of 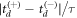 . Since
. Since 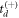 and
and  are typically not dramatically different compared to the lifetime τ, this correction is small.
are typically not dramatically different compared to the lifetime τ, this correction is small.
Thus, we use a self-consistent approach in which we start as suggested above, by choosing 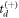 or
or 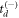 randomly with equal likelihood for each event. Recall that this choice is exact in the limit
randomly with equal likelihood for each event. Recall that this choice is exact in the limit 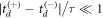 . An exponential decay function N(td)
. An exponential decay function N(td) 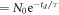 is then fitted to the resulting N(td) distribution to retrieve the lifetime. This lifetime allows computation of the aforementioned factor
is then fitted to the resulting N(td) distribution to retrieve the lifetime. This lifetime allows computation of the aforementioned factor 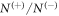 , given in equation (6), which is then used to weight the choice of
, given in equation (6), which is then used to weight the choice of  or
or  in the next iteration. The obtained N(td) distribution is again fit with an exponential decay function to retrieve a more accurate lifetime, again allowing calculation of a new weighting factor for the choice of
in the next iteration. The obtained N(td) distribution is again fit with an exponential decay function to retrieve a more accurate lifetime, again allowing calculation of a new weighting factor for the choice of 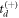 or
or 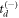 . This process is repeated until the lifetime τ converges. Note that for a given iteration, the choice of
. This process is repeated until the lifetime τ converges. Note that for a given iteration, the choice of 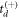 or
or  and the fitting procedure is repeated for multiple trials to account for the finite sample size of our data. Also, the lifetime τ used to compute the weighting factor for the subsequent iteration is the mean value of those obtained in the multiple trials. For more details about our iterative approach, visit appendix B.
and the fitting procedure is repeated for multiple trials to account for the finite sample size of our data. Also, the lifetime τ used to compute the weighting factor for the subsequent iteration is the mean value of those obtained in the multiple trials. For more details about our iterative approach, visit appendix B.
When this self-consistent method is applied to our data, we find good convergence within just a few iterations. We performed the analysis on the C2H4 and C2D4 data to explore the possibility of isotopic effects. Typical trials from the final iteration are shown in figures 3(a) and (b). Two-term exponential decay fits agree well with both measurements, suggesting that at least two metastable states are contributing to the observed dissociation in flight of ethylene dications. The final converged lifetimes for C2H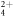 are
are 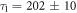 ns and
ns and 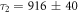 ns. For C2D
ns. For C2D , we obtain
, we obtain 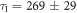 ns and
ns and 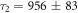 ns. The errors here represent the standard deviation of the trials in the last iteration.
ns. The errors here represent the standard deviation of the trials in the last iteration.
Figure 3.
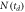 distributions obtained using the proposed self-consistent method for (a) C2H
distributions obtained using the proposed self-consistent method for (a) C2H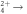 C2H3+ + H+ and (b) C2D
C2H3+ + H+ and (b) C2D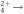 C2D3+ + D+. These both represent typical trials from the last iteration. Note that in both plots, the statistical error bars are smaller than the symbols. Two-term exponential decay fits, plotted in blue, agree nicely with the data. The gray dashed line shown in (a), which doesn't agree with the data, is a single-term exponential decay fit.
C2D3+ + D+. These both represent typical trials from the last iteration. Note that in both plots, the statistical error bars are smaller than the symbols. Two-term exponential decay fits, plotted in blue, agree nicely with the data. The gray dashed line shown in (a), which doesn't agree with the data, is a single-term exponential decay fit.
Download figure:
Standard image High-resolution imageNote that the weighting factor  has been modified to account for the two lifetimes,
has been modified to account for the two lifetimes, 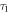 and
and  , and thus becomes
, and thus becomes
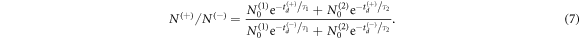
As mentioned, the two-term exponential fit indicates that at least two metastable states are responsible for the observed dissociation in flight. The single lifetime for C2H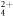 reported by Larimian et al, 498 ± 12 ns [47], lies between the two lifetimes that we have measured. This discrepancy could be due to a number of reasons, such as differences in the laser pulse parameters, the method used to compute td, or the td range chosen for the exponential decay fit. Note that when we perform a single exponential decay fit, shown in figure 3(a), we obtain a lifetime of 491 ± 19 ns, consistent with the previous measurement.
reported by Larimian et al, 498 ± 12 ns [47], lies between the two lifetimes that we have measured. This discrepancy could be due to a number of reasons, such as differences in the laser pulse parameters, the method used to compute td, or the td range chosen for the exponential decay fit. Note that when we perform a single exponential decay fit, shown in figure 3(a), we obtain a lifetime of 491 ± 19 ns, consistent with the previous measurement.
We also note that our measurements suggest a possible small isotopic effect in the shorter lifetime, 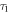 . The difference between the two shorter lifetimes is on the level of 2.2σ, while the longer lifetimes are the same within the measurement uncertainty. As dissociation in flight of ethylene dications is a low-rate channel, we expect that higher statistics data would make the presence or absence of an isotopic effect in the lifetimes more clear cut. Since we currently lack the good quality electronic structure information on these molecular ions needed to understand this isotopic effect and also to keep the focus on the method, we limit this discussion to highlighting the rich information afforded by our technique.
. The difference between the two shorter lifetimes is on the level of 2.2σ, while the longer lifetimes are the same within the measurement uncertainty. As dissociation in flight of ethylene dications is a low-rate channel, we expect that higher statistics data would make the presence or absence of an isotopic effect in the lifetimes more clear cut. Since we currently lack the good quality electronic structure information on these molecular ions needed to understand this isotopic effect and also to keep the focus on the method, we limit this discussion to highlighting the rich information afforded by our technique.
3.2. Momentum imaging
Having retrieved td and the lifetimes, we can proceed with performing momentum imaging, another aim of this work. While our solution of choosing 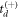 or
or 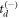 with some weighting works on a sample level and is thus a robust method for retrieving the lifetime(s), we note that for a large fraction of the individual events,
with some weighting works on a sample level and is thus a robust method for retrieving the lifetime(s), we note that for a large fraction of the individual events, 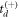 or
or 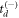 will be assigned incorrectly. Therefore, this method of computing td cannot be used for momentum imaging, as it is done on an event-by-event basis. As such, we need a single value of td for each event, even if it is approximate.
will be assigned incorrectly. Therefore, this method of computing td cannot be used for momentum imaging, as it is done on an event-by-event basis. As such, we need a single value of td for each event, even if it is approximate.
To approximate td, we neglect 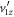 in equations (4), as the term containing this quantity is typically on the order of a few percent compared to the other terms, as further detailed in appendix C. Moreover, as shown in the same appendix, the error that this approximation introduces in the retrieved td and the transverse momenta is also estimated to be at most a few percent. Having neglected
in equations (4), as the term containing this quantity is typically on the order of a few percent compared to the other terms, as further detailed in appendix C. Moreover, as shown in the same appendix, the error that this approximation introduces in the retrieved td and the transverse momenta is also estimated to be at most a few percent. Having neglected 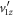 , the equation for td becomes linear and thus has a single solution for each event, given explicitly by
, the equation for td becomes linear and thus has a single solution for each event, given explicitly by
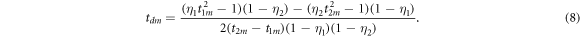
Employing this approximation of td, we have computed the transverse momentum of the D+ fragments from C2D , shown in figure 4. The distribution of the radial momentum,
, shown in figure 4. The distribution of the radial momentum,  , shown in figure 4(b), agrees well with the functional form for the projection of an isotropic distribution onto a plane [56]. To verify that the momentum distribution is isotropic, the complete 3D momentum distribution is needed. Therefore, the p1z component should also be measured.
, shown in figure 4(b), agrees well with the functional form for the projection of an isotropic distribution onto a plane [56]. To verify that the momentum distribution is isotropic, the complete 3D momentum distribution is needed. Therefore, the p1z component should also be measured.
Figure 4. (a) Retrieved transverse momentum distribution of the D+ fragments. In this measurement, the laser polarization is along the z (TOF) axis. As marked, φ is a rotation angle in the xy-plane that will be used to characterize the angular distribution (discussed further in the text). (b) Radial momentum distribution N(p1r) of the D+ fragments, where 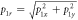 . The violet line indicates a fit to the data of the functional form for the projection of an isotropic distribution onto a plane, which is given explicitly on the figure. Here, A and B are fit parameters.
. The violet line indicates a fit to the data of the functional form for the projection of an isotropic distribution onto a plane, which is given explicitly on the figure. Here, A and B are fit parameters.
Download figure:
Standard image High-resolution imageIs there any way to retrieve the z-direction momentum? Recall our initial fundamental problem in evaluating 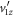 that is associated with the
that is associated with the 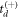 and
and 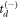 solutions. Now, we have gone even further and neglected
solutions. Now, we have gone even further and neglected 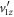 entirely, eliminating the possibility of recovering p1z directly from the measurement. It is important to note that the polarization is typically aligned along the spectrometer axis (z direction) in COLTRIMS measurements in order to reduce losses of fast fragments, which are usually ejected along the laser field. This choice leads to equivalent x and y momentum components due to the axial symmetry about the laser field and prevents the direct determination of p1z.
entirely, eliminating the possibility of recovering p1z directly from the measurement. It is important to note that the polarization is typically aligned along the spectrometer axis (z direction) in COLTRIMS measurements in order to reduce losses of fast fragments, which are usually ejected along the laser field. This choice leads to equivalent x and y momentum components due to the axial symmetry about the laser field and prevents the direct determination of p1z.
To retrieve the missing information, i.e., the p1z momentum component along the laser field, we take advantage of this axial symmetry and align the laser polarization along the y axis. Under these conditions, the measured p1y distribution is along the laser polarization, while p1x is transverse. Moreover, the 'lost' p1z distribution can be recovered from the measured p1x distribution by taking advantage of the axial symmetry about the laser polarization. Under ideal conditions, this measurement is sufficient to retrieve the complete 3D momentum distributions of the fragments. In many cases, however, imperfections like spatial non-uniformities in the detector response may bias the results.
To circumvent this issue and verify that the momentum distribution is isotropic, we performed two measurements with the polarization along the z and y directions, as illustrated in figures 5(a) and (b), respectively. Note that while the angular distributions drawn in this figure do not resemble the isotropic distribution we measure in the present experiment, they help to better convey the difference between the two measurement schemes.
Figure 5. (a) and (b) Schematic angular distributions. Note that these do not reflect our measured angular distributions, but they help better illustrate the concept of our two-measurement scheme. (a) First measurement: the laser polarization is aligned along the z direction (spectrometer axis). As 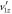 is neglected, momentum information parallel to the polarization is not accessible in this configuration. (b) Second measurement: the laser polarization is parallel to the y axis (jet direction), and thus, the momentum distribution along the laser polarization can now be retrieved. Additionally, exploiting the azimuthal symmetry about the laser polarization allows for retrieval of the pz distribution in this scheme, as N(p1z)
is neglected, momentum information parallel to the polarization is not accessible in this configuration. (b) Second measurement: the laser polarization is parallel to the y axis (jet direction), and thus, the momentum distribution along the laser polarization can now be retrieved. Additionally, exploiting the azimuthal symmetry about the laser polarization allows for retrieval of the pz distribution in this scheme, as N(p1z) 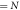 (p1x). (c) Ratio of the N(φ) distributions for the two measurement schemes.
(p1x). (c) Ratio of the N(φ) distributions for the two measurement schemes. 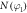 corresponds to the φ distribution measured with the laser polarization parallel to the time-of-flight axis, z, and
corresponds to the φ distribution measured with the laser polarization parallel to the time-of-flight axis, z, and 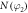 is measured after rotating the polarization to be along the jet direction, y. The dotted red line corresponds to the average value of this ratio.
is measured after rotating the polarization to be along the jet direction, y. The dotted red line corresponds to the average value of this ratio.
Download figure:
Standard image High-resolution imageIn the first measurement with the polarization along z, the momentum distribution along the polarization cannot be retrieved because 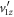 has been neglected. In the second measurement with the polarization along y, the momentum distribution parallel to the laser polarization can be retrieved directly, while the complete transverse momentum distribution can be recovered by using the axial symmetry about the laser field as discussed above.
has been neglected. In the second measurement with the polarization along y, the momentum distribution parallel to the laser polarization can be retrieved directly, while the complete transverse momentum distribution can be recovered by using the axial symmetry about the laser field as discussed above.
Let us define φ as a rotation angle in the xy-plane in both measurements. This angle is sketched on figure 4(a). We denote N(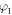 ) as the distribution obtained in the first measurement (polarization along z) and N(
) as the distribution obtained in the first measurement (polarization along z) and N(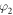 ) as the distribution found in the second measurement (polarization along y). Computing the ratio of these distributions yields the result shown in figure 5(c). Note that the position-dependent detection efficiency cancels out in this ratio, thus eliminating the impact of detector imperfections.
) as the distribution found in the second measurement (polarization along y). Computing the ratio of these distributions yields the result shown in figure 5(c). Note that the position-dependent detection efficiency cancels out in this ratio, thus eliminating the impact of detector imperfections.
The ratio shown in figure 5(c) is rather flat, directly demonstrating that dissociation in flight yields an isotropic momentum distribution. This distribution is likely the result of td being much longer than the rotational timescale of the molecule. Thus, information about the initial alignment of the molecule with respect to the laser polarization is lost, and the resulting distribution is isotropic.
3.3. Kinetic energy release
Finally, just as accessing the z-component momenta is problematic, so too is retrieving the KER on an event-by-event basis. To obtain a KER distribution, we utilize a method based on the onion peeling technique, which has been widely used to analyze photofragment images [57–60]. The transverse momentum distribution, which was obtained using the method described in the previous section, serves as our projected 'onion,' which we slice along the px direction. Some sample slices for dissociation in flight of C2D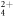 are shown in figure 6(a). As we carry out iterative onion peeling subtraction on the slices, the counts that are 'peeled' away are allocated into the appropriate KER bins to accumulate a distribution. For a given iteration being performed on a particular slice, the KER is found using the edges of the slice, as only events with the maximum KER reach this region. We employ this technique for measurements in which the laser polarization is along the y axis, even though the isotropic nature of the distribution would allow one to use data from either of the previously discussed measurement schemes. Further details about this KER retrieval method will be described in a forthcoming publication about the dissociation in flight of metastable carbon dioxide dications [61].
are shown in figure 6(a). As we carry out iterative onion peeling subtraction on the slices, the counts that are 'peeled' away are allocated into the appropriate KER bins to accumulate a distribution. For a given iteration being performed on a particular slice, the KER is found using the edges of the slice, as only events with the maximum KER reach this region. We employ this technique for measurements in which the laser polarization is along the y axis, even though the isotropic nature of the distribution would allow one to use data from either of the previously discussed measurement schemes. Further details about this KER retrieval method will be described in a forthcoming publication about the dissociation in flight of metastable carbon dioxide dications [61].
Figure 6. (a) A sample of the transverse momentum slices used in the 'sliced' onion peeling retrieval of the kinetic energy release (KER) distribution. (b) C2D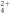 dissociation-in-flight KER spectrum retrieved using our 'sliced' onion peeling technique. (c) Comparison of experimentally measured and simulated
dissociation-in-flight KER spectrum retrieved using our 'sliced' onion peeling technique. (c) Comparison of experimentally measured and simulated 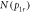 distributions. The open circles represent the experimental data, and the different lines correspond to simulated
distributions. The open circles represent the experimental data, and the different lines correspond to simulated 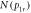 for different Gaussian KER distributions, with indicated centroids, KERc. The full width at half maximum (FWHM) of each of the KER distributions is 0.5 eV.
for different Gaussian KER distributions, with indicated centroids, KERc. The full width at half maximum (FWHM) of each of the KER distributions is 0.5 eV.
Download figure:
Standard image High-resolution imageThe KER distribution obtained using our 'sliced' onion peeling technique for dissociation in flight of C2D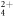 is presented in figure 6(b). We estimate the uncertainty in the obtained KER to be about 0.3 eV2
. The centroid of the KER, at about 4.2 eV, is in good agreement with that obtained by Larimian et al [47]. Finally, as an alternative method of retrieving the KER, we compare the measured
is presented in figure 6(b). We estimate the uncertainty in the obtained KER to be about 0.3 eV2
. The centroid of the KER, at about 4.2 eV, is in good agreement with that obtained by Larimian et al [47]. Finally, as an alternative method of retrieving the KER, we compare the measured 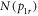 with several simulated
with several simulated 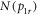 distributions corresponding to Gaussian KER distributions with different centroids and widths, as illustrated in figure 6(c). As can be seen, the simulated
distributions corresponding to Gaussian KER distributions with different centroids and widths, as illustrated in figure 6(c). As can be seen, the simulated 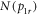 distribution with a KER centroid of 4.15 eV and a FWHM of 0.5 eV agrees well with the measured
distribution with a KER centroid of 4.15 eV and a FWHM of 0.5 eV agrees well with the measured 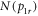 . Furthermore, this result supports that obtained using the 'sliced' onion peeling approach. As mentioned, the KER can supply a great deal of insight into dissociation pathways, e.g., [17, 25, 26]. This pursuit, however, is beyond the scope of this paper, which focuses on the method.
. Furthermore, this result supports that obtained using the 'sliced' onion peeling approach. As mentioned, the KER can supply a great deal of insight into dissociation pathways, e.g., [17, 25, 26]. This pursuit, however, is beyond the scope of this paper, which focuses on the method.
4. Summary and outlook
In summary, we have developed a method to study dissociation in flight of metastable molecular ions using coincidence momentum imaging measurements. Our approach, which supplies valuable information about the relevant metastable states, including the lifetime(s) and momentum distributions of the dissociating fragments, has been realized through the application and symmetries of the relevant kinematic equations.
Encountered hurdles such as the inverse problem of choosing 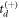 or
or 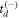 and the related problem of retrieving
and the related problem of retrieving 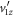 have been addressed by exploiting symmetries of the fragmentation. The readily expressed forward-backward symmetry breaking in the
have been addressed by exploiting symmetries of the fragmentation. The readily expressed forward-backward symmetry breaking in the 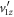 distribution was used in a self-consistent manner to obtain the N(td) distribution of the sample and hence the lifetimes of the metastable states dissociating in flight. This analysis allowed us to find two lifetimes in the deprotonation of metastable ethylene dications and a possible isotopic effect in the shorter lifetime.
distribution was used in a self-consistent manner to obtain the N(td) distribution of the sample and hence the lifetimes of the metastable states dissociating in flight. This analysis allowed us to find two lifetimes in the deprotonation of metastable ethylene dications and a possible isotopic effect in the shorter lifetime.
The necessity of a single td value for each event to obtain the momenta was fulfilled by neglecting 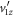 , an assumption which we have shown to be on solid ground, as it introduces minimal error in the calculation of td and the momenta. Furthermore, the azimuthal symmetry about the laser polarization was exploited to obtain all the components of the momentum rendered unretrievable by the td inverse problem.
, an assumption which we have shown to be on solid ground, as it introduces minimal error in the calculation of td and the momenta. Furthermore, the azimuthal symmetry about the laser polarization was exploited to obtain all the components of the momentum rendered unretrievable by the td inverse problem.
Finally, while we have demonstrated this method for the specific case of deprotonation of metastable ethylene dications formed by intense femtosecond laser pulses, this technique is applicable to coincidence measurements on a variety of metastable molecular systems dissociating in flight, which could also be formed via other means, such as x-ray photoabsorption or fast charged particle impact.
Acknowledgments
We gratefully acknowledge Kanaka Raju P and C W Fehrenbach for assistance with the laser beam. This work was supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy.
Appendix A.: Gating on the dissociation-in-flight coincidence stripe
The long, curved dissociation-in-flight stripe in the CTOF spectrum fairly closely follows a third-order polynomial dependence as a function of t1. To more effectively select true events while suppressing the contribution of random pairs (i.e., improve the signal to 'noise' ratio), we use the coefficients of a third-order polynomial fit to the curved coincidence stripe to straighten it and then apply a simple rectangular gate. More specifically, t⊥, the perpendicular distance from each (t1, t2) data point to the polynomial fit is calculated. A Gaussian function is fit to the  distribution, and a ±3σ gate is applied to the data, as shown in figure A1(a). Figure A1(b) shows the straightened stripe and gate around it. Note that for C2H4, the left and right gating bounds for t1 were chosen to be 825 ns and 2400 ns, respectively, and for C2D4, they were 1200 ns and 2400 ns, respectively. These data selection schemes allow one to avoid the prompt breakup region, as well as the area of the CTOF spectrum near the end of the dissociation-in-flight stripe, where 'noise' and other channels dominate.
distribution, and a ±3σ gate is applied to the data, as shown in figure A1(a). Figure A1(b) shows the straightened stripe and gate around it. Note that for C2H4, the left and right gating bounds for t1 were chosen to be 825 ns and 2400 ns, respectively, and for C2D4, they were 1200 ns and 2400 ns, respectively. These data selection schemes allow one to avoid the prompt breakup region, as well as the area of the CTOF spectrum near the end of the dissociation-in-flight stripe, where 'noise' and other channels dominate.
Figure A1. Illustration of the procedure used for selecting the CTOF stripe. (a) 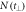 for C2H4, where t⊥ is the perpendicular distance of a measured (t1,t2) pair to a third-order polynomial fit to the CTOF stripe. Shown in red, a Gaussian function is fit to
for C2H4, where t⊥ is the perpendicular distance of a measured (t1,t2) pair to a third-order polynomial fit to the CTOF stripe. Shown in red, a Gaussian function is fit to 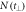 . As indicated by the purple dashed lines, a ±3σ gate about the centroid of this Gaussian is then set on the data. (b) Density plot of ion yield as a function of t1 and t⊥,
. As indicated by the purple dashed lines, a ±3σ gate about the centroid of this Gaussian is then set on the data. (b) Density plot of ion yield as a function of t1 and t⊥, 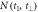 . In addition to the ±3σ gating, lower and upper bounds are chosen for t1 to minimize the contribution of noise and channels other than the dissociation-in-flight channel. The surviving data inside the gate (dashed purple box) is then used to retrieve the lifetimes and momenta.
. In addition to the ±3σ gating, lower and upper bounds are chosen for t1 to minimize the contribution of noise and channels other than the dissociation-in-flight channel. The surviving data inside the gate (dashed purple box) is then used to retrieve the lifetimes and momenta.
Download figure:
Standard image High-resolution imageAppendix B.: Dealing with limited statistics when determining lifetimes and convergence of the iterative method
Recall that due to the inverse problem related to the sign of 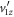 (and associated sign choice in the td equation), we employ an iterative procedure that starts with a choice of
(and associated sign choice in the td equation), we employ an iterative procedure that starts with a choice of 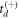 or
or 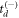 that is equally likely. Then, we use the values of τ in subsequent iterations to weight the choice of
that is equally likely. Then, we use the values of τ in subsequent iterations to weight the choice of  or
or 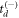 , using equation (7). As this method utilizes a random number generator to choose
, using equation (7). As this method utilizes a random number generator to choose 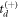 or
or 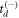 , it is imperative that the sample size be large enough to ensure true randomness.
, it is imperative that the sample size be large enough to ensure true randomness.
As we are applying this analysis to experimental data of a relatively weak channel for which statistics are limited, one may worry about the robustness of the proposed method that relies on random number generation. To address this issue, as mentioned in section 3.1, each iteration of the lifetime determination procedure consists of multiple trials. That is, for each iteration, the analysis is simply repeated multiple times (each time with a randomly selected seed). Each trial uses the same solution choice weighting scheme. An exponential decay function is fit to the resulting 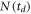 distributions to retrieve lifetimes for each trial. At the end of an iteration, the amplitudes
distributions to retrieve lifetimes for each trial. At the end of an iteration, the amplitudes  and
and 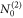 and lifetimes
and lifetimes 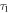 and
and 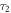 used to calculate the weighting factor in equation (7) are the average values from all the trials in that iteration.
used to calculate the weighting factor in equation (7) are the average values from all the trials in that iteration.
As mentioned, when applied to our ethylene data, the lifetimes and amplitudes converge within just a few iterations. Plots illustrating the convergence of these quantities are shown in figures B1(a)–(d). Note that in the first iteration, 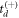 and
and 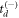 are selected with equal probability, and each iteration consists of 1000 trials.
are selected with equal probability, and each iteration consists of 1000 trials.
Figure B1. (a) and (b): Lifetimes 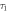 and
and  as a function of iteration for C2D4 data. The first iteration corresponds to
as a function of iteration for C2D4 data. The first iteration corresponds to 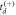 and
and 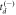 being chosen with equal likelihood. (c) and (d): Amplitudes
being chosen with equal likelihood. (c) and (d): Amplitudes 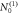 and
and 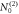 as a function of iteration for the same data. The error bars on these plots represent the error on the average for 1000 trials. The relative standard deviations on the lifetimes and the amplitudes,
as a function of iteration for the same data. The error bars on these plots represent the error on the average for 1000 trials. The relative standard deviations on the lifetimes and the amplitudes, 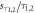 and
and  , respectively, are all of the order of 10%.
, respectively, are all of the order of 10%.
Download figure:
Standard image High-resolution imageAppendix C.: Approximation of td by neglecting 
To obtain a single value of td needed for evaluating the momentum of each event, an approximation is necessary. We start with the first expression in equations (4) and divide both sides by 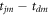 to obtain
to obtain
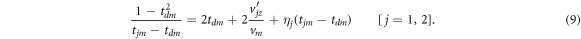
This equation is solved for tdm after neglecting the second term on the right-hand side that contains  . How valid is neglecting this term? To explore this question, we perform simulations using a few typical input random functional distributions, including a single-term exponential decay
. How valid is neglecting this term? To explore this question, we perform simulations using a few typical input random functional distributions, including a single-term exponential decay  distribution with
distribution with  ns, a Gaussian KER distribution centered at 4 eV with a 1 eV FWHM, and an isotropic angular distribution. Let us denote the terms on the right-hand side of equation (9) as '1st term,' '2nd term,' and '3rd term,' in left-to-right order. We evaluate the quantity R ≡∣2nd term∣/(1st term + 3rd term), shown in figure C1(a). For 99% of the events,
ns, a Gaussian KER distribution centered at 4 eV with a 1 eV FWHM, and an isotropic angular distribution. Let us denote the terms on the right-hand side of equation (9) as '1st term,' '2nd term,' and '3rd term,' in left-to-right order. We evaluate the quantity R ≡∣2nd term∣/(1st term + 3rd term), shown in figure C1(a). For 99% of the events, 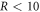 %. Furthermore, the error that neglecting the second term introduces into the recovered td and p1x, shown in figures C1(b) and (c), is also reasonably small. For td, about 77% of the simulated events lie below the 5% error level, and for p1x, about 98% of the events lie below the same error level.
%. Furthermore, the error that neglecting the second term introduces into the recovered td and p1x, shown in figures C1(b) and (c), is also reasonably small. For td, about 77% of the simulated events lie below the 5% error level, and for p1x, about 98% of the events lie below the same error level.
Figure C1. (a) N(R) for simulated events with Gaussian KER distribution centered at 4 eV with 1 eV FWHM, isotropic angular distribution and lifetime of 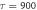 ns. (b) The td error from neglecting
ns. (b) The td error from neglecting  , where tdi corresponds to the exact td values, and td0 corresponds to the approximate td values obtained by neglecting
, where tdi corresponds to the exact td values, and td0 corresponds to the approximate td values obtained by neglecting 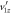 . (c) The px error introduced by neglecting
. (c) The px error introduced by neglecting 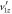 , where pxi corresponds to the exact momentum, and px0 corresponds to the values retrieved by neglecting
, where pxi corresponds to the exact momentum, and px0 corresponds to the values retrieved by neglecting 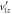 .
.
Download figure:
Standard image High-resolution imageSince the validity of neglecting 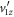 depends on the magnitude of
depends on the magnitude of  , and for our simulations we have assumed values of this quantity approximately matching the measured ones, it is reasonable to explore how large
, and for our simulations we have assumed values of this quantity approximately matching the measured ones, it is reasonable to explore how large 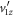 can be before the approximation breaks down. Thus, we performed simulations with a few larger KER values (and hence larger maximum values of
can be before the approximation breaks down. Thus, we performed simulations with a few larger KER values (and hence larger maximum values of 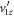 ). Even for a high KER of 20 eV (Gaussian distribution with 1 eV FWHM and the same lifetime and angular distribution as before), 99% of the simulated events have
). Even for a high KER of 20 eV (Gaussian distribution with 1 eV FWHM and the same lifetime and angular distribution as before), 99% of the simulated events have 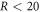 %, as shown in figure C2(a). Moreover, as shown in figures C2(b) and (c), 75% of the events have <20% error in the retrieved td, and about 98% of the events are below the same error level in p1x. Given this extreme example, we are thus assured that neglecting
%, as shown in figure C2(a). Moreover, as shown in figures C2(b) and (c), 75% of the events have <20% error in the retrieved td, and about 98% of the events are below the same error level in p1x. Given this extreme example, we are thus assured that neglecting 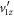 for momentum computation is a reasonable approximation for our case.
for momentum computation is a reasonable approximation for our case.
Figure C2. (a) N(R) for simulated events with Gaussian KER distribution centered at 20 eV with 1 eV FWHM, isotropic angular distribution and lifetime of 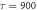 ns. (b) The td error from neglecting
ns. (b) The td error from neglecting 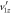 , where tdi corresponds to the exact td values fed into the simulation, and td0 corresponds to the approximate td values obtained by neglecting
, where tdi corresponds to the exact td values fed into the simulation, and td0 corresponds to the approximate td values obtained by neglecting 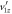 . (c) The px error introduced by neglecting
. (c) The px error introduced by neglecting  , where pxi corresponds to the exact momentum, and px0 corresponds to the values retrieved by neglecting
, where pxi corresponds to the exact momentum, and px0 corresponds to the values retrieved by neglecting  .
.
Download figure:
Standard image High-resolution imageIt is noteworthy that in general it is not merely the KER (and hence the maximum 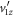 ) that is important for consideration but the ratio
) that is important for consideration but the ratio 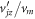 , as can be readily seen in equation (9). Recall that vm is the velocity of the dication. Therefore, in certain cases, it may also be desirable to increase the spectrometer voltage in the experiment to increase vm and thereby improve the validity of this approximation.
, as can be readily seen in equation (9). Recall that vm is the velocity of the dication. Therefore, in certain cases, it may also be desirable to increase the spectrometer voltage in the experiment to increase vm and thereby improve the validity of this approximation.
Appendix D.: Lifetime determination accuracy due to time-of-flight uncertainty
Due to the nature of our method for evaluating td, it is not straightforward to propagate errors in order to determine the uncertainty in the recovered lifetime(s). Here we demonstrate how simulations aid us in pinpointing important sources of error.
As measured TOF values are used to calculate td, a rather pertinent question is what effect the uncertainty in these quantities has on the retrieved lifetimes. Finite time resolution, number truncation by the time-to-digital converter (TDC) unit used (which has a 25 ps resolution), and uncertainty in the absolute time (i.e., the error associated with the exact time of the laser-molecule interaction) all influence the accuracy of the retrieved lifetime. While we have performed simulations to investigate each of these effects, for the sake of brevity, we use those exploring truncation to illustrate the impact that this type of uncertainty can have.
To examine the effects of truncation of the measured TOF values, we simulate events with the same parameters as in the previous appendix (4 eV KER centroid). Thus, each simulated event has an associated td and 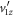 . The
. The ![$[j=1,2]$](https://content.cld.iop.org/journals/1367-2630/19/10/103006/revision2/njpaa81abieqn175.gif) equations in (4) are rearranged into quadratic expressions that can be solved for t1 and t2:
equations in (4) are rearranged into quadratic expressions that can be solved for t1 and t2:

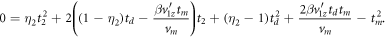
In solving for t1 and t2, we choose the positive root in the quadratic formula because choosing the negative root yields negative t1 and t2 values or 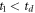 , which is unacceptable, in contrast to the td equation for which both roots can make physical sense. The values of t1 and t2 are truncated to varying levels of precision in ns, simulating the possible digitizer accuracy. Then a random fraction is added to the truncated number, as is done for the measured (digitized) data, to match the original number of digits. For example, if ti is a time-of-flight value truncated to n decimal place(s), the new TOF after adding the random fraction is
, which is unacceptable, in contrast to the td equation for which both roots can make physical sense. The values of t1 and t2 are truncated to varying levels of precision in ns, simulating the possible digitizer accuracy. Then a random fraction is added to the truncated number, as is done for the measured (digitized) data, to match the original number of digits. For example, if ti is a time-of-flight value truncated to n decimal place(s), the new TOF after adding the random fraction is 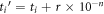 , where r is a random number between 0 and 1. The new values of t1 and t2 are then used to compute td and obtain a lifetime, which is then compared to the original input lifetime. A few examples of the effect of truncation on the recovered lifetime are shown in figures D1(a)–(c). As can be seen in the figure, as more of the true digits are initially truncated, the retrieved lifetime veers away from the original lifetime of 900 ns, and the range of
, where r is a random number between 0 and 1. The new values of t1 and t2 are then used to compute td and obtain a lifetime, which is then compared to the original input lifetime. A few examples of the effect of truncation on the recovered lifetime are shown in figures D1(a)–(c). As can be seen in the figure, as more of the true digits are initially truncated, the retrieved lifetime veers away from the original lifetime of 900 ns, and the range of 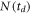 that can be used for fitting starts to deteriorate. As mentioned, similar tests were performed to examine the effects of finite resolution and absolute time uncertainty. These simulations yielded results comparable to the number truncation tests.
that can be used for fitting starts to deteriorate. As mentioned, similar tests were performed to examine the effects of finite resolution and absolute time uncertainty. These simulations yielded results comparable to the number truncation tests.
Figure D1.
 distributions and exponential decay fits obtained when the time-of-flight (TOF) values are truncated to an indicated number of decimal places (in ns) and random digits are appended to those numbers to match the original number of digits. (a) Truncation to 2 decimal places (b) truncation to 1 decimal place (c) truncation to an integer.
distributions and exponential decay fits obtained when the time-of-flight (TOF) values are truncated to an indicated number of decimal places (in ns) and random digits are appended to those numbers to match the original number of digits. (a) Truncation to 2 decimal places (b) truncation to 1 decimal place (c) truncation to an integer.
Download figure:
Standard image High-resolution imageWhile our simulations have proven instructive in identifying influential error sources such as those related to the measured time-of-flight values, note that the errors presented in the body of this manuscript reflect those evaluated by statistical means.
Footnotes
- 2
This error estimate was obtained by propagating the error in the transverse momentum (taken to be the bin size) through to the KER.















