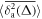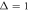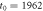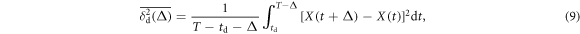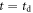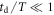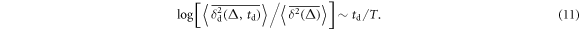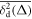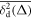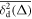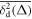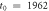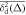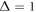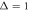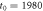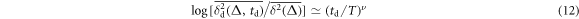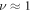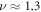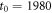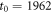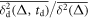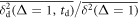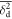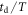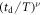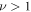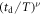Abstract
We introduce three strategies for the analysis of financial time series based on time averaged observables. These comprise the time averaged mean squared displacement (MSD) as well as the ageing and delay time methods for varying fractions of the financial time series. We explore these concepts via statistical analysis of historic time series for several Dow Jones Industrial indices for the period from the 1960s to 2015. Remarkably, we discover a simple universal law for the delay time averaged MSD. The observed features of the financial time series dynamics agree well with our analytical results for the time averaged measurables for geometric Brownian motion, underlying the famed Black–Scholes–Merton model. The concepts we promote here are shown to be useful for financial data analysis and enable one to unveil new universal features of stock market dynamics.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In 1900, Bachelier pioneered the concept that prices on financial markets are stochastic and may follow the laws of Brownian motion [1, 2]. Similar ideas for the mathematical description of option pricing were proposed by Bronzin in 1908 [3], a work which largely fell into oblivion until recently [4]. Later, in the 1960s, Mandelbrot [5, 6] and Fama [7] realised that the Gaussian distribution of price changes is often violated, and introduced Paretian and Lévy stable laws into financial mathematics [5, 8]. Another milestone in the stochastic modelling of financial markets is the famed Black–Scholes–Merton option pricing model [9–11], see also the classical textbooks on the mathematical analysis of markets [12–14].
The assessment of price variations for highly non-stationary [15–19] financial time series X(t) (figure 1) is nowadays typically rationalised mathematically via solutions of stochastic differential equations with multiplicative noise [20–27]. This approach is based on the key concept of volatility: the magnitude of market fluctuations increases with the value X(t). Numerous models for stock market price variation were developed to account for time-varying, clustered, and fluctuating volatility [12–14, 19, 26, 28–39]. In particular, the exponentially varying geometric Brownian motion (GBM) with its log-normal distribution, underlying the Black–Scholes–Merton model, is ubiquitously used in financial mathematics and econophysics [12, 14, 16, 40]. The GBM approach was generalised and extended for some alternative [24], specifically subdiffusive stochastic processes [41, 42], for power-law multiplicative noise [24–26, 43] (the square-root process [25, 44]), two-stock options [45], as well as fractional Brownian motion [46–48].
Figure 1. Historic stock price series for multiple Dow Jones indices. The initial values are normalised to unity. The colour scheme and the line types are defined in the legend, compare the labelling of the stocks in the main text.
Download figure:
Standard image High-resolution imageStatistical models of stock price variations often assume that the increments are Gaussian-distributed [14]. Extensive statistical analysis of financial data revealed, however, that the distribution of returns has a sharper maximum and fatter tails [8, 12, 19, 34]. To account for these features, random walk models based on, inter alia, truncated Lévy stable distributions [5, 8, 12, 36, 49] and jump-diffusion models [11, 13, 50] were proposed. Discrepancies between ensemble and time averaged measures were also discussed recently [18, 38, 51, 52]. Different market impacts onto price formation were considered as well [53]—in particular, one should mention here also market microstructure effects [54]. Despite decades of intense development and significant advances the quest for a universal mathematical model of stock price dynamics is still open.
Here we propose three concepts, complementary to the well established methods, for an advanced analysis of financial time series. Specifically, these are the time averaged mean squared displacement (MSD), perfectly suited for the analysis of a single time series, as well as the ageing and delay time methods. As we demonstrate from statistical analyses of real financial time series, these approaches are highly useful and reveal universal features of the market dynamics, which may be relevant for the further development of financial market models.
The central concept promoted here is based on time averaging. Most frequently, in theoretical approaches the MSD , defined as the ensemble average of over many realisations of the stochastic process X(t), is used to quantify the time evolution of the process. However, when dealing with a single or few but long time series X(t), the time averaged MSD [55]
is better suitable and more relevant for the analysis of time series of both stationary and non-stationary stochastic processes [55, 56]. For a given lag time Δ this quantity defines a sliding average over the entire time series, of length T. Hereafter, the overline denotes time averages and the angular brackets stand for averages over an ensemble of realisations of a process X(t). While the concept (1) is by now widely used for single-trajectory analysis in several areas of science, especially microscopic single particle tracking [55, 56], it is less common in mathematical finance [17, 18]. Our central focus here is to introduce this concept for the analysis of financial time series.
2. Analysis of financial time series
We here present the results of statistical analyses of financial time series based on the time averaged MSD (1) as well as the ageing and delay time methods defined below. The observed behaviour based on these analysis tools is demonstrated to agree well with analytical results for the famed GBM model, which is introduced in section 2.2. We study the daily values of multiple financial indices of different categories. All data were taken from and analysed via the Wolfram Mathematica 9 platform.
The data are categorised and abbreviated as follows. In the first category we study the Dow Jones Industrial Average (Mathematica ticker symbol DJI) group indices SP500: Standard and Poor's 500, GE: General Electric Comp, IBM: International Business Machines Corp, CAT: Caterpillar Inc, CVX: Chevron Corp, MCD: McDonald's Corp, BA: Boeing Comp, DIS: Walt Disney Comp, MMM: 3M Comp, PFE: Pfizer Inc, KO: Coca-Cola Comp, JNJ: Johnson and Johnson, PG: Procter and Gamble Comp, XOM: ExxonMobil Corp, WMT: Wal-Mart Stores, Inc, AXP: American Express Comp, DD: E. I. du Pont de Nemours and Comp, and MRK: Merck and Co Inc. In the next category we analyse some DAX indices at the Frankfurt Stock Exchange (Germany), with the tickers BMW: Bayerische Motoren Werke AG, DAI: DaimlerChrysler AG, DTE: Deutsche Telekom AG, LHA: Deutsche Lufthansa AG, VOW3: Volkswagen AG, DPW: Deutsche Post AG, RWE: RWE AG, SAP: SAP AG. Some high-tech tickers include T: AT&T Inc, INTC: Intel Corp, HPQ: Hewlett-Packard Comp, MSFT: Microsoft Corp. Finally, bank tickers comprise JPM: J. P. Morgan Chase and Co, BAC: Bank of America Corp, NYSE:BCS: Barclays PLC, NYSE:SAN: Santander-Chile Bank.
The raw data of the price variations of several high-capitalisation Dow Jones indices starting at are shown in figure 1. To improve the presentation we divided all prices by the corresponding initial value, such that all traces start at unit value. This is a legitimate procedure as for a GBM-like process the initial price X0 enters solely as a multiplicative factor (see below). Despite the common initial price, we observe large price fluctuations for different indices at later times, especially in the last decades. Roughly, an exponential increase is observed for all stocks.
2.1. Time averaged MSD
For sufficiently long time series the time averaged MSD (1) typically produces relatively smooth results as a function of lag time. This feature is immediately obvious from the plots of for data shown in figure 2. We emphasise that in the calculation of the time averaged MSD, for any given lag time Δ the entire time series is used and thus the initial values X0 always contribute to the magnitude of . The lag time increment is 10 days in figure 2, and we used the 'raw' time series in this analysis (no normalisation to X(t) values at the initial or final point is performed). Shorter lag times are computationally more expensive but would allow for a better resolution of the initial growth of . The spread of the computed magnitudes of at short lag times increases with T for growing stock market prices, as long as no market crises occur, as seen in figure 2.
Figure 2. Time averaged MSDs , equation (1), for varying trajectory lengths T (with time step of year). The Dow Jones indices analysed here are indicated by their tickers. In each panel, random colours are chosen for the traces. The lag time Δ is given in trading days, the data sets start in , the longest trace is years, and the shortest trace year. The expected linear asymptotes in the lag time are shown in each panel.
Download figure:
Standard image High-resolution imageWe observe a roughly linear growth at short lag times, in perfect accordance with the analytical result (6) for GBM derived below. This linear scaling stands in stark contrast to the exponential growth of the ensemble averaged MSD of GBM seen in equation (5) below. Such a fundamental discrepancy between the time and ensemble averaged MSD of the process X(t) is well known in the theory of stochastic processes and often referred to as weak ergodicity breaking [55, 56]. For financial time series the fact that allows the direct analysis of X(t) instead of its logarithm.
When the lag time approaches the length T of the time series, it is obvious from definition (1) that the statistic is worsening. This intrinsic property of time averages is reflected by the increasing fluctuations of seen in figure 2. Note that in the limit the time-ensemble averaged MSD, averaged over N independent trajectories of the same process, under identical starting conditions and parameters,
is equal to [55]. Note that the averaging over different trajectories in quantity (2) is necessary for our analytical calculations. In the analysis of the financial time series shown in the figures, single trajectory averages are considered throughout.
2.2. Geometric Brownian motion
Before continuing with our analysis of the actual stock market data, we briefly digress and provide a primer on GBM, a paradigm process employed in standard models for stock price dynamics. As we show this model reproduces the essential features observed in the market data.
GBM is defined in terms of the stochastic differential equation with multiplicative noise
Here is the price at time t, μ denotes a drift, and σ is the volatility (μ and σ are set constant below). The volatility is connected to the square root of the diffusivity [55]. The increments dW of the Wiener process are defined as white Gaussian noise with zero mean. The price evolution, starting with the initial value at t = 0, is obtained from equation (3) by use of Itô's lemma [12, 14] as
This process satisfies the log-normal distribution, emerging also in models of task success and income distribution [57]. The MSD shows the exponential growth
Due to this (much) faster growth compared to the linear increase of the MSD with t for Brownian motion, GBM is therefore a superdiffusive process [55].
To calculate the time averaged properties of interest, we resort to the average (2) over N independent realisations of X(t). We derive this quantity using the one and two point distribution functions of the Wiener process. For short lag times, , and in the absence of drift we find
As mentioned already, the non-equivalence of the ensemble and time averaged MSD, in the limit indicates weak ergodicity breaking, known for other non-stationary diffusion processes [55]. The time averaged MSD (6) scales linearly with the lag time Δ, in contrast to the exponential growth of , but grows exponentially with the trace length T, due to the highly non-stationary character of GBM.
2.3. Time averaged MSD analysis of financial data, continued
We now return to the discussion of the time averaged MSD of the different stocks. The time averaged MSD of the analysed financial time series, similar to equation (6) for the GBM process, is expected to be a growing function of the trajectory length T. Indeed, this behaviour is demonstrated in figure 2, in which we plot the time averaged MSD for varying trace length T for four different stock prices. This fact mirrors the accelerating nature of the stochastic process underlying the price variations.
What happens when the index value stagnates or drops substantially within a prolonged period of time, as can be seen in figure 1 following the 2008–2009 crisis? In this case the time averaged MSD evaluated for partial time series (different T values) encompassing this time window tend to cluster together. Consequently, the value of may saturate in this region, compare the original tick data in figure 1, the behaviour of versus lag time Δ in figure 2, and the explicit dependence on T shown in figure 3.
Figure 3. Initial values of the time averaged MSD versus trace length T, computed at the lag time of day for the indices from figure 1, plotted in log-linear scale. The data are normalised to the value of the shortest trace of year. The dashed exponential asymptote is a guide to the eye. The analysis starts at , and T is given in trading days (about 252 days per calendar year).
Download figure:
Standard image High-resolution imageEquation (6) predicts, to leading order, an exponential growth of the time-ensemble averaged MSD with the trace length T. As shown in figure 3, computed for day, the data indeed roughly follow an exponential increase with T. However, no universal dependence of the time averaged MSD as function of T could be found. Especially for those time windows encompassing prolonged drops or stalling of the index price, the ratio of the time averaged MSD for a trace length T to its value at does not grow rapidly but rather saturates, as can also be seen in figure 3. Thus, checking the dependence of on the trace length T may be used to unveil individual features of index price dynamics. In contrast to the strongly disparate and company-specific behaviour revealed in figure 3, universal features are found in the analysed index prices when employing the new concept of the delay time averaged MSD introduced below.
Figure 4 shows the data normalised to their end point. More specifically, this normalisation enhances the contribution of later parts of the time series, with typically larger prices. We find a considerable spread of individual traces for different companies, because each index can have different parameters such as the volatility value or the attitude of a given company leadership to maximise the short-term profit versus ensuring a long-time sustainability. Finite lifetimes of companies and their varying age at the start of the time series are likewise important. These factors individualise stock price variations for each company and complicate the evaluation of ensemble averaged quantities. In view of this the universality of stock prices observed in section 2.5 is even more remarkable.
Figure 4. Time averaged MSDs for some stock market indices, for which the prices are normalised to unity at the last point. The start of the data is at and years. Relation (6) is the dashed line.
Download figure:
Standard image High-resolution image2.4. Ageing analysis
Physically, the above dependence (6) of the time averaged MSD on the trace length T reflects the phenomenon of ageing, a characteristic property of non-stationary stochastic processes [55, 58]. For superdiffusive processes with an MSD growing faster than the linear growth in time of Brownian motion, the time averaged MSD exhibits an increase with T. This reflects the self-reinforcing volatility of the process, as seen for the exponentially fast growth in equation (6). In contrast, in subdiffusion the effective diffusivity of the process is a decaying function of time [55]. For instance, in processes with scale free waiting times the typical sojourn periods of the motion become increasingly long, on average, effecting the decay of the time averaged MSD with T [58].
Another way to analyse ageing processes is the following. If the time series X(t), starting at time t = 0, is evaluated only beginning with the so-called ageing time , the ageing time averaged MSD is defined as [58]
In this formal definition we shift the starting point for the analysis of the time series yet the length T of the analysed time interval remains fixed. Of course, larger values of ta limit the remaining number of data points available for this analysis, however, the ageing time averaged MSD provides important insights into the underlying stochastic process [55]. We note that the term ageing does not imply any relaxation to an ergodic state in the limit of long ageing times, as it does for subdiffusive processes (the limit of strong ageing). In superdiffusive processes such as GBM and, as shown here, for highly non-stationary financial data the term ageing delineates the process time dependent increase of the spread of the random variable X(t).
For GBM we find in the limit of short lag times, , and in absence of a drift, , that on average
The exponential growth with ta emerges as the process X(t) already experienced an acceleration of the price dynamics up to the ageing time ta, and thus the analysis starts with a higher volume. Note that in result (8) the argument of the exponential includes the volatility term of the GBM process.
To see whether such ageing effects can indeed be observed in real financial data we study the behaviour of the ageing time averaged MSD as function of the ageing time ta. The raw data variation of as function of the ageing time ta for a number of indices is shown in figure 5. Indices growing rapidly and continuously in value reveal pronounced ageing effects, and increases fast with ta. Similar to the observations above, when we varied the trace length T, partial clustering of the traces for varying ta is visible.
Figure 5. Ageing time averaged MSDs (7) for the trajectory length of T = 20 years, plotted for some Dow Jones indices, as indicated. The lag time step is days, the time series start at , and the longest ageing time is years.
Download figure:
Standard image High-resolution imageFigure 6 quantifies the behaviour of the logarithm of the ratio of the ageing time averaged MSD to the corresponding non-ageing value, plotted versus the ageing time ta. Although, again, a roughly exponential increase is evident and consistent with the prediction (8) for GBM, no data collapse onto a universal curve is observed. Even at short ageing times we find a substantial spread of the curves versus ta for different stock indices, as can be seen in figure 6. The non-universal behaviour is expected to be due to the fact that the volatility parameter varies between companies, as equation (8) predicts, and thus no data collapse in the growth of with the ageing time ta occurs. No averaging over different companies is performed for the ageing time averaged MSD to compute the mean value in figure 6 because the corresponding ensemble is not formed from trajectories with identical parameters. For instance, the volatility values and the effect of the ageing time ta for each stock market index can be markedly different.
Figure 6. Logarithm of the ratio of the ageing over the non-ageing time averaged MSDs computed at lag time of day, presented in log-log scale versus the ageing time ta. The longest ageing time is 33 years (ta is given in calendar years), the trace length is T = 20 years, and the analysis starts in , as in figure 5. The exponential dashed asymptote is equation (8) for the GBM model.
Download figure:
Standard image High-resolution image2.5. Delay time analysis: revealing universal features
What if we allow the length of the time series to vary in the above ageing analysis? Namely, what would the expected behaviour be for the quantity
in which we call td the delay time, and the trace X(t) is evaluated in the interval from until t = T. As long as the lag times Δ are short compared to the time span of the data, it can be shown that the mean delay time averaged MSD follows
For the ratio of the delay time averaged MSD (10) to the time averaged MSD (2) in the limit of short delay times and long traces we get the simple, parameter-free result,
The logarithm here cancels the leading exponential dependence of the delayed time averaged MSD on td in equation (10) and the final result (11) is independent on the index-specific volatility parameter σ. We emphasise that in this result it is crucial that the process X(t) has non-stationary increments. The behaviour of, say, a standard Brownian process would follow a different scaling law with the delay time. Can this universal behaviour predicted in equation (11) indeed be seen in real financial time series, on the single trajectory level?
Pronounced up and down trends in the price evolution of an index give rise to strong variations of the magnitudes, see figure 7. For longer td, the delay time averaged MSD includes a progressively shorter interval, causing a worsening statistic. Also, the magnitude of increases because windows with higher prices and larger price variations are being processed in the averaging (9). For longer delay times td—when later parts of the time series contribute stronger to the time averaged MSD—the magnitude of increases nearly linearly at short and moderate Δ, see figure 7. After a significant drop of stock index prices as a consequence of the 2008–2009 financial crisis, the variation of with the delay time td exhibits large fluctuations for the lag times values encompassing this period of the time series. Due to this, the growing trend of with the delay time may be reversed, see figure 7.
Figure 7. Delay time averaged MSDs (9) for varying td versus lag time Δ for the stock indices of figure 2. Shorter trajectories correspond to longer td, the longest delay time is 35 years, and the time series start in (in that case td = 0). The shortest traces are one year long. The linear asymptotic behaviour is shown by the dashed lines. Random colours for curves at different td values are used.
Download figure:
Standard image High-resolution imageFigure 8 shows the logarithm of the ratio of the delay time averaged MSD to the standard time averaged MSD, evaluated at unit lag time , as function of the delay time td. The universal behaviour (11) expected on average is followed very closely for each stock market time series. This universal behaviour—fulfilled for delay times td up to some 5–10 years—is the central result of this study. To our best knowledge, in terms of single time series this universal trend has not been reported before.
Figure 8. Logarithm of the ratio of the delay time averaged MSD to the time averaged MSD computed at day on double-logarithmic scale, plotted versus the delay time. The thick dashed line represents the universal law (11) for short td (given in calendar days). The asymptote (12) with is shown by the dashed line in the upper panel. The starting date for the analysis is (top) and (bottom panel). The number of available financial time series with earlier starting times is naturally smaller.
Download figure:
Standard image High-resolution imageAt longer delay times, we observe a distinct crossover to a somewhat steeper td-dependence in figure 8, consistent with a law of the form
with the scaling exponent . The observed behaviour features two relatively similar exponents: at short and intermediate delay times while for long delay times . The initial linear scaling is universal, compare top and bottom panels of figure 8 with starting dates 1980 and 1962, respectively. As shown by the thin dashed line in the upper panel of figure 8, the second regime with is more pronounced for the data starting , while it is less obvious for the data. For long delay times we however consistently observe a faster than exponential growth of the ratio . In particular, this disqualifies the predictions of GBM in this long delay time regime. Note that since the time averaged MSD initially grows approximately linearly with Δ, as one can see figures 2 and 7, the trends of figure 8 will also hold for other sufficiently short lag times.
Note that for some high tech companies and banks we did not observe a growth of with the delay time td (not shown). We believe that this is due to the very limited lengths of the time series available, starting in about 1987–1988. Therefore, effects of severe price drops during the 2008–2009 crisis dominate the magnitude of over the entire time range we examined, rendering the result (11) for the standard GBM inapplicable. For a number of German DAX companies, with time series available from 2001, the prediction (12) does not hold either (not shown).
3. Conclusions
Time averaging of observables of a stochastic process X(t) is a successful concept designed for the analysis of single or few, sufficiently long time series. It has been applied in various fields, in particular, in single particle tracking studies of microscopic objects [55, 56]. While for such microscopic particles, at least in principle, it is possible to record more than one trace under (almost) identical conditions, the situation is much more restricted for financial contexts. The market price evolution of a given company cannot be repeated several times under identical conditions. Thus, a statistical ensemble for averaging over a set of trajectories is inaccessible [17, 38]. Splitting up the time series into subparts is not an option due to the highly non-stationary character of the dynamics. The analysis in terms of time averaged observables is therefore the prime option.
Here we demonstrated that time averages indeed provide a useful toolbox for the analysis of financial data. Using the time averaged MSD, as well as the ageing and delay time methods, we showed that relevant features can be extracted from the analysis of financial time series. Good agreement of our data-driven observations with analytical predictions from the GBM model was observed, such as the linear lag time dependence of the time averaged MSD, contrasting the exponential growth for the ensemble averaged MSD. The ageing analysis combining the dependencies on the trace length T and the ageing time ta unveil peculiar features in a given time series such as prolonged stalling or even a decrease of the stock value.
Remarkably, the delay time analysis introduced here uncovered a universal behaviour for the analysed stock prices. For short and intermediate delay times td, the logarithm of the ratio of the delay time versus the regular time averaged MSD is a linear function of . At longer times, in our analysis beyond some 5–10 years, this logarithm approximately scales as a power-law with another scaling exponent, . This latter scaling behaviour is not captured with the standard GBM model, pointing at a need for improved theoretical approaches.
This study is to be viewed as a first step in applying time averaging, ageing, and delay time methods to the analysis of financial time series. Theoretically, modifications of the GBM model used here, to account for features such as the transition from the universal linear scaling to the scaling law for the delay time averaged MSD as well as the introduction of fluctuating or time-varying volatilities, are possible. The concept of 'diffusing diffusivities', which in some sense is similar to fluctuating volatilities, has been recently established in the physics literature [59–61]. How such concepts impact stochastic processes with multiplicative noise remains to be clarified, however, we expect a similarly rich behaviour with crossovers as observed for simple Brownian systems [59–61].
Deterministic time dependent volatilities may be adopted for the time averaging based description of unstable markets (at times of a financial crash), when the trading conditions change very rapidly [38]. Here, a stochastic process with a power-law volatility may be proposed: GBM with a volatility increasing with time can account for a faster than exponential price growth X(t) and explain a faster than linear trend (12) detected in the analysis of financial time series. Recently, ensemble averages of a similar modified GBM process with power-law and logarithmic volatilities were presented [53]. Also, models with value- and time-dependent diffusivity were empirically found to underlie the Euro–Dollar exchange rate dynamics [19, 62], compared to anomalous diffusion with space- and time-dependent diffusivity [55]. Combining such new theoretical approaches with time averaging may provide vital new impetus in the analysis of financial time series.
From a data analysis point of view, we were interested in the long-term trends for the time averaged MSD. Clearly, time series with one point a day hide possible intraday effects, such as intraday volatility patterns extracted from high-frequency data [18, 38, 63]. More observables from the time series should be taken into account, and the correlations between them remain to be rationalised. These include the auto-correlation function of price increments, the evaluation of volatility values [33] over different periods of time, the trading activity and volumes on the markets, a correction of the index price value due to inflation [34], crises, etc. These points, as well as the question how the dynamics observed herein is connected with heavy tailed spreads of financial volume [5, 8, 12, 36, 49] will be the focus of future work.
The area of mathematical finance is not the only domain where our time averaged MSD and ageing approaches may be useful. For instance, from a biological perspective the mathematical description of inherently highly stochastic disease outbreaks involves exponential processes similar to GBM. In epidemic spreading, an exponential increase in the number of diseased hosts is often postulated (up to the system size). The reader is referred to the optimal control models in epidemics spreading [64, 65], including density dependent growth and ageing. Finally, mathematical models of tumour spreading and the growth of bacterial colonies and cells [66] also employ exponential processes, providing additional ground for the application of the concepts outlined here.
Acknowledgments
DV was funded by a DAAD fellowship. EA was funded by a KoUP grant of the University of Potsdam and a MINERVA Short-Term Research Grant. RM and AVC acknowledge funding from the Deutsche Forschungsgemeinschaft, grant number ME 1535/6-1. We acknowledge the support of Deutsche Forschungsgemeinschaft and Open Access Fund of Potsdam University.





![$\mathrm{log}[X(t)]$](https://content.cld.iop.org/journals/1367-2630/19/6/063045/revision2/njpaa7199ieqn1.gif)
![$\mathrm{log}[X(t+{\rm{d}}{t})/X(t)]$](https://content.cld.iop.org/journals/1367-2630/19/6/063045/revision2/njpaa7199ieqn2.gif)
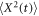
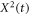
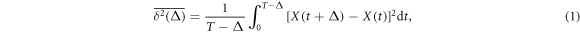

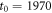

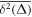
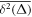
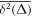


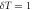

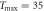

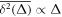


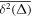
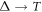

![$\langle {[X(t)-{X}_{0}]}^{2}\rangle $](https://content.cld.iop.org/journals/1367-2630/19/6/063045/revision2/njpaa7199ieqn21.gif)
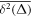

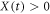

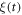
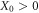
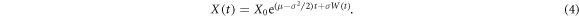
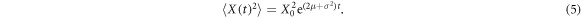
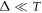
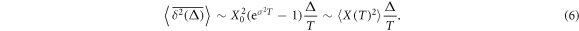
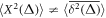
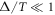
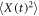
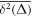
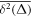
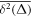
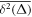

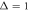
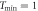
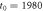
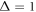
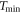

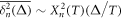
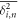

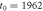
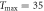
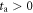
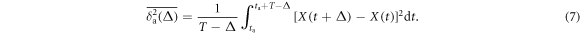
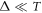

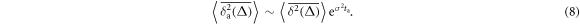
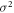
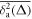
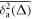
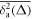

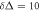
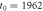
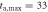
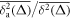
![$\mathrm{log}[\overline{{\delta }^{2}({\rm{\Delta }})}/\overline{{\delta }^{2}({\rm{\Delta }})}]$](https://content.cld.iop.org/journals/1367-2630/19/6/063045/revision2/njpaa7199ieqn56.gif)
![$\mathrm{log}[\overline{{\delta }_{{\rm{a}}}^{2}({\rm{\Delta }})}/\overline{{\delta }^{2}({\rm{\Delta }})}]$](https://content.cld.iop.org/journals/1367-2630/19/6/063045/revision2/njpaa7199ieqn57.gif)