Abstract
Controlled directional light propagation using optical nonlinearity has previously been proposed. Here, we propose a one-way optical device with linear elements controlled by synthetic magnetic fluxes. The device consists of two parity–time symmetric side-coupled resonators with balanced gain and loss. The gain and loss break the reflection symmetry and the magnetic fluxes break the transmission symmetry. Through tuning the magnetic fluxes, reflectionless full transmission in one direction and transmissionless full reflection in the opposite direction can be achieved. The device acts as a light-checking valve, preventing wave propagation in one direction. The proposed one-way transporter uses the nonreciprocity induced by non-Hermiticity and magnetic fluxes without applying nonlinearity. We anticipate that our findings will be useful for optical control and manipulation.
General Scientific Summary
Introduction and background. Light propagation is reciprocal in a linear system. The reciprocity of light is protected by time-reversal symmetry. For many years, directional light propagation has been a goal of research. A previous proposal used a series of nonlinear elements in which nonlinearity breaks the time-reversal symmetry and thus the reciprocity of light (Lepri S and Casati G 2011 Phys. Rev. Lett. 106 164101).
Main results. We propose a new method for realizing one-way light transport in a linear system. The non-Hermiticity and synthetic magnetic fluxes in the system break the light reciprocity. The system is an AB interferometer with a pair of side-coupled PT-symmetric resonators. We demonstrated that with the appropriate application of the magnetic fluxes, gain and loss, transmissionless fully reflected light incidence in one direction and reflectionless fully transmitted light incidence in the opposite direction can be realized (figure 1). Instead of using nonlinearity, the proposed method utilizes the emission and absorption of the gain and loss resonators to realize the unity amplitude for unidirectional propagation after scattering. The magnetic fluxes assist in achieving asymmetric transmission and destructive interference.
Wider implications. The proposal provides an effective method for one-way light transport without the application of nonlinearity. The findings provide an insight into the interplay between non-Hermiticity and magnetic fluxes. We anticipate that our results will be useful for the application of PT metamaterials.
Figure. Light-checking valve. Download figure:
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
General Scientific Summary
Introduction and background. Light propagation is reciprocal in a linear system. The reciprocity of light is protected by time-reversal symmetry. For many years, directional light propagation has been a goal of research. A previous proposal used a series of nonlinear elements in which nonlinearity breaks the time-reversal symmetry and thus the reciprocity of light (Lepri S and Casati G 2011 Phys. Rev. Lett. 106 164101).
Main results. We propose a new method for realizing one-way light transport in a linear system. The non-Hermiticity and synthetic magnetic fluxes in the system break the light reciprocity. The system is an AB interferometer with a pair of side-coupled PT-symmetric resonators. We demonstrated that with the appropriate application of the magnetic fluxes, gain and loss, transmissionless fully reflected light incidence in one direction and reflectionless fully transmitted light incidence in the opposite direction can be realized (figure 1). Instead of using nonlinearity, the proposed method utilizes the emission and absorption of the gain and loss resonators to realize the unity amplitude for unidirectional propagation after scattering. The magnetic fluxes assist in achieving asymmetric transmission and destructive interference.
Wider implications. The proposal provides an effective method for one-way light transport without the application of nonlinearity. The findings provide an insight into the interplay between non-Hermiticity and magnetic fluxes. We anticipate that our results will be useful for the application of PT metamaterials.
 Figure. Light-checking valve.
Figure. Light-checking valve.
1. Introduction
Light propagation in linear systems is reciprocal and the reciprocity of light is protected by time-reversal symmetry [1]. Directional light propagation has been a goal of research for many years. A photonic lattice with a series of nonlinear elements sandwiched in a linear medium was constructed to achieve one-way light transport in [2, 3]. By modulating couplings, two reflectionless potential wells with different depths and finite separation were proposed and solitons with approximately perfect unidirectional flow were found in [4, 5]. In these inspiring works, both nonlinearity and asymmetry were employed to achieve nonreciprocity. Nonreciprocity has realistic applications, such as optical diodes [4, 5]; a quantum switch was proposed in a strongly correlated system, where the interactions and asymmetry potentials play key roles [6, 7]. Utilizing topological protection is an alternative method for realizing one-way light transport. The advantage of this method is the robust resistance to disorders and imperfections of the edge modes [8–10]. In a two-dimensional photonic lattice, the unidirectional edge modes propagating along the edges are guided by the synthetic gauge field for photons. Employing an imaginary gauge field in the couplings has been proposed as a method for achieving robust one-way transport in a non-Hermitian system. The imaginary gauge field results in nonreciprocal photon tunneling, and leads to asymmetric amplification and attenuation of the counter-propagating waves. Light transport is robust, being insensitive to disorders and imperfections under a non-Hermitian delocalization [11, 12]. The light propagation in one direction is shape-preserving and accompanied by persistent amplification.
We propose a method for realizing unidirectional light transport in a linear non-Hermitian optical system with an enclosed synthetic magnetic field. This differs from one-way transport through optical nonlinearity in a Hermitian lattice and employs imaginary gauge fields in a non-Hermitian coupled optical resonator. The proposed one-way light transport is extremely nonreciprocal, exhibiting full transmission without reflection in one direction and full reflection without transmission in the other. An effective magnetic field for photons can be realized through various methods [13–15]. The optical path imbalance method applies a synthetic magnetic flux in a ring-shaped coupled resonator array [10]. The non-Hermiticity originates from the gain and loss of the side-coupled resonators. The role of gain and loss in optical structures has been intensively analyzed in the framework of parity–time ( ) symmetry both theoretically [16–21] and experimentally [22–27]. Novel phenomena have regularly been reported, for example, the spectral singularities in a
) symmetry both theoretically [16–21] and experimentally [22–27]. Novel phenomena have regularly been reported, for example, the spectral singularities in a  -symmetric system [28] and unidirectional reflectionless light propagation, in which the reflection was significantly suppressed in one direction [29]. Applying a side-coupled structure to a pair of balanced gain and loss resonators revealed unidirectional lasing induced by reflection divergence in one direction at Fano resonance [30].
-symmetric system [28] and unidirectional reflectionless light propagation, in which the reflection was significantly suppressed in one direction [29]. Applying a side-coupled structure to a pair of balanced gain and loss resonators revealed unidirectional lasing induced by reflection divergence in one direction at Fano resonance [30].  symmetry ensures symmetric transmission in
symmetry ensures symmetric transmission in  -symmetric non-Hermitian systems [31–35]. The orientation of
-symmetric non-Hermitian systems [31–35]. The orientation of  -symmetric structures causes symmetric transmission or symmetric reflection [36]. In
-symmetric structures causes symmetric transmission or symmetric reflection [36]. In  -symmetric microcavities, a gain-induced large nonlinearity can break the
-symmetric microcavities, a gain-induced large nonlinearity can break the  symmetry and produce an optical diode [37, 38]. We proposed achieving nonreciprocal transmission through a lossy element and synthetic magnetic flux, with the magnetic flux controlling asymmetric transmission with symmetric reflection [39, 40].
symmetry and produce an optical diode [37, 38]. We proposed achieving nonreciprocal transmission through a lossy element and synthetic magnetic flux, with the magnetic flux controlling asymmetric transmission with symmetric reflection [39, 40].
Here, we propose one-way light transport in a linear system that has a pair of balanced gain and loss resonators threaded by real magnetic fluxes. The system is a non-Hermitian double-flux Aharonov–Bohm (AB) interferometer. The reflection and transmission in the system are direction-dependent in the presence of nontrivial magnetic fluxes and resonator gain and loss. The coupled resonators are  -symmetric with identical frequencies and balanced gain and loss; however, the whole AB interferometer is non-
-symmetric with identical frequencies and balanced gain and loss; however, the whole AB interferometer is non- -symmetric under asymmetric magnetic fluxes. The interferometer exhibits reflectionless full transmission in one direction but transmissionless full reflection in the other direction, acting as a light-checking valve to prevent backflow at appropriate magnetic fluxes and resonator gain and loss settings. The proposed one-way transport uses wave emission and absorption at unidirectional spectral singularities without nonlinearity, or imaginary magnetic fields. The enclosed synthetic magnetic fluxes extend the application of
-symmetric under asymmetric magnetic fluxes. The interferometer exhibits reflectionless full transmission in one direction but transmissionless full reflection in the other direction, acting as a light-checking valve to prevent backflow at appropriate magnetic fluxes and resonator gain and loss settings. The proposed one-way transport uses wave emission and absorption at unidirectional spectral singularities without nonlinearity, or imaginary magnetic fields. The enclosed synthetic magnetic fluxes extend the application of  metamaterials for optical control and manipulation.
metamaterials for optical control and manipulation.
2. Modeling the AB interferometer
We examined a double-flux AB interferometer (figure 1(a)). The double-flux AB interferometer consists of a chain of passive resonators with the resonant frequency  uniformly coupled at strength J. Two resonators with gain or loss are coupled to the passive resonators in the middle of the chain resonator array. The coupled active and dissipative resonator frequencies with detunings
uniformly coupled at strength J. Two resonators with gain or loss are coupled to the passive resonators in the middle of the chain resonator array. The coupled active and dissipative resonator frequencies with detunings  are
are  the imaginary parts
the imaginary parts  represent the resonator gain and dissipation. They constitute two triangular coupled resonator loops. The synthetic magnetic flux in the left loop is introduced via an auxiliary resonator (figure 1(b)), which is coupled to resonators 0 and α. The auxiliary resonator induces a nonreciprocal effective coupling
represent the resonator gain and dissipation. They constitute two triangular coupled resonator loops. The synthetic magnetic flux in the left loop is introduced via an auxiliary resonator (figure 1(b)), which is coupled to resonators 0 and α. The auxiliary resonator induces a nonreciprocal effective coupling  between resonators 0 and α, where
between resonators 0 and α, where  is the optical path imbalance of the forward and backward directions between resonators 0 and α. Photons circling around the left loop experience an additional phase factor
is the optical path imbalance of the forward and backward directions between resonators 0 and α. Photons circling around the left loop experience an additional phase factor  thus, the effective magnetic flux introduced is
thus, the effective magnetic flux introduced is  . The effective magnetic flux
. The effective magnetic flux  is introduced in the right loop, where
is introduced in the right loop, where  is the optical path imbalance of the forward and backward directions between resonators 0 and β. In the side-coupled structure, photons at resonator −1 either tunnel to resonator 0 directly or travel through the intermediate resonator α; similarly, photons at resonator 0 either tunnel to resonator 1 directly or travel through the intermediate resonator β. Thus, the whole system is a double-flux AB interferometer enclosing two magnetic fluxes. The dynamics in the coupled resonator system are described by coupled mode theory [41]. According to coupled mode theory, the equations of motion for resonators
is the optical path imbalance of the forward and backward directions between resonators 0 and β. In the side-coupled structure, photons at resonator −1 either tunnel to resonator 0 directly or travel through the intermediate resonator α; similarly, photons at resonator 0 either tunnel to resonator 1 directly or travel through the intermediate resonator β. Thus, the whole system is a double-flux AB interferometer enclosing two magnetic fluxes. The dynamics in the coupled resonator system are described by coupled mode theory [41]. According to coupled mode theory, the equations of motion for resonators  or
or  are given by
are given by
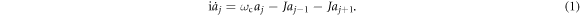
For resonator  , the equations of motion are provided by
, the equations of motion are provided by
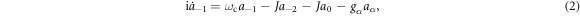
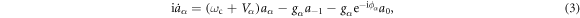
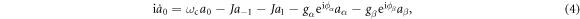
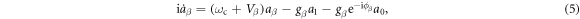
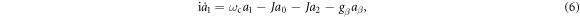
where the mode is  and the dispersion relation of the coupled resonators is
and the dispersion relation of the coupled resonators is  . The ring resonator supports two normal modes. We considered the clockwise mode without loss of generality. The magnetic fluxes introduced in the coupled resonator loops for the counter-clockwise mode are opposite to those for the clockwise mode (thus, any magnetic flux for clockwise mode Φ, is
. The ring resonator supports two normal modes. We considered the clockwise mode without loss of generality. The magnetic fluxes introduced in the coupled resonator loops for the counter-clockwise mode are opposite to those for the clockwise mode (thus, any magnetic flux for clockwise mode Φ, is  for the counter-clockwise mode, and vice versa). When
for the counter-clockwise mode, and vice versa). When  , the side-coupled resonators are
, the side-coupled resonators are  -symmetric; if
-symmetric; if  (
( ), the whole interferometer is also
), the whole interferometer is also  -symmetric, where parity operator (
-symmetric, where parity operator ( ) is defined as the mirror reflection with respect to resonator zero, i.e.
) is defined as the mirror reflection with respect to resonator zero, i.e.  ,
,  , and
, and  time-reversal operator (
time-reversal operator ( ) gives
) gives  . The scattering properties can be obtained from the steady-state solution of the equations of motion.
. The scattering properties can be obtained from the steady-state solution of the equations of motion.
Figure 1. (a) Schematic illustration of a non-Hermitian double-flux AB interferometer.  (red) and
(red) and  (green) represent two side-coupled resonators. Two magnetic fluxes are enclosed in the triangular loops. (b) Optical path imbalance between the coupling processes introduces the effective phase.
(green) represent two side-coupled resonators. Two magnetic fluxes are enclosed in the triangular loops. (b) Optical path imbalance between the coupling processes introduces the effective phase.
Download figure:
Standard image High-resolution imageControlling light propagation in the appropriate manner is essential for realizing one-way transport. In the following sections, we develop the directional propagation of light in this linear system. Notably, although the magnetic flux breaks the time-reversal symmetry, it cannot independently break the reciprocity of transmission or reflection with vanishing gain and loss, where Hermiticity protects the reciprocity of scattering. In addition, symmetry can protect the reciprocity of scattering.  or
or  symmetry leads to reciprocal transmission and reflection [40], and
symmetry leads to reciprocal transmission and reflection [40], and  symmetry leads to either reciprocal transmission or reflection [36]. To realize nonreciprocal transport, non-Hermitian gain and loss were introduced to break the Hermiticity. In this work, both gain/loss and magnetic fluxes were introduced to break
symmetry leads to either reciprocal transmission or reflection [36]. To realize nonreciprocal transport, non-Hermitian gain and loss were introduced to break the Hermiticity. In this work, both gain/loss and magnetic fluxes were introduced to break  and
and  symmetries; the asymmetric magnetic fluxes also break the
symmetries; the asymmetric magnetic fluxes also break the  symmetry of the whole interferometer in the balanced gain and loss. Both gain/loss and magnetic fluxes affect the interference and alter the scattering coefficients, and are employed to realize nonreciprocity and control the transmission and reflection of the interferometer.
symmetry of the whole interferometer in the balanced gain and loss. Both gain/loss and magnetic fluxes affect the interference and alter the scattering coefficients, and are employed to realize nonreciprocity and control the transmission and reflection of the interferometer.
3. Single-flux AB interferometer
3.1. Reciprocal reflectionless
To investigate asymmetric transmission, we first considered the simple case of a single-flux AB interferometer with only one side-coupled lossy resonator β (i.e.  ). The loss and magnetic flux enclosed in the side-coupled structure break the reciprocity of transmission and change the reflectance and transmittance. For
). The loss and magnetic flux enclosed in the side-coupled structure break the reciprocity of transmission and change the reflectance and transmittance. For  ,
,  and
and  , the right incidence has a perfect transmission when
, the right incidence has a perfect transmission when  . Affected by the magnetic flux, the superposition of the waves from the connection resonators (0 and 1) at the side-coupled resonator (β) is completely destructive. This indicates that the side-coupled resonator β is decoupled from the resonator chain array, i.e.
. Affected by the magnetic flux, the superposition of the waves from the connection resonators (0 and 1) at the side-coupled resonator (β) is completely destructive. This indicates that the side-coupled resonator β is decoupled from the resonator chain array, i.e.  . The side-coupled lossy resonator does not affect the right incidence, and left-going light waves propagate freely. However, for an incidence from the opposite direction (i.e. left incidence), the magnetic flux in the triangular loop results in a destructive interference at the output connection resonator (1), i.e.
. The side-coupled lossy resonator does not affect the right incidence, and left-going light waves propagate freely. However, for an incidence from the opposite direction (i.e. left incidence), the magnetic flux in the triangular loop results in a destructive interference at the output connection resonator (1), i.e.  . The incident light is absorbed by the side-coupled lossy resonator (β) without reflection. The appropriate loss and magnetic flux enclosed in the triangular loop induce reflectionless full absorption and full transmission in opposite incident directions; the reflections from both sides are all zero, i.e. the scattering is a unidirectional perfect absorption, in which
. The incident light is absorbed by the side-coupled lossy resonator (β) without reflection. The appropriate loss and magnetic flux enclosed in the triangular loop induce reflectionless full absorption and full transmission in opposite incident directions; the reflections from both sides are all zero, i.e. the scattering is a unidirectional perfect absorption, in which
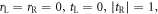
where  (
( ) denotes the reflection (transmission) coefficient for the left incidence and
) denotes the reflection (transmission) coefficient for the left incidence and  (
( ) denotes the reflection (transmission) coefficient for the right incidence. We call
) denotes the reflection (transmission) coefficient for the right incidence. We call  (
( ) and
) and  (
( ) the left reflection (transmission) and right reflection (transmission), respectively. Notably, the system in this situation is at a spectral singularity [40]. Correspondingly, unidirectional lasing occurs in a Hermitian conjugation system (i.e.
) the left reflection (transmission) and right reflection (transmission), respectively. Notably, the system in this situation is at a spectral singularity [40]. Correspondingly, unidirectional lasing occurs in a Hermitian conjugation system (i.e.  ,
,  and
and  ) [30]. The nonreciprocity in this situation is induced by the interplay between the non-Hermiticity and nontrivial magnetic flux. The magnetic flux and loss break the reciprocity of transmission but not the reciprocity of reflection. The reciprocal reflection coefficient is zero with an abrupt phase change π. The abrupt phase change π occurs in the nonreciprocal transmission coefficient in one incident direction with transmission zero; in the other incident direction, the transmission is unity and the phase changes smoothly. A direct method for breaking the reciprocity of reflection is to introduce another side-coupled resonator with gain (see figure 1(a)). Then, the reflection becomes asymmetric.
) [30]. The nonreciprocity in this situation is induced by the interplay between the non-Hermiticity and nontrivial magnetic flux. The magnetic flux and loss break the reciprocity of transmission but not the reciprocity of reflection. The reciprocal reflection coefficient is zero with an abrupt phase change π. The abrupt phase change π occurs in the nonreciprocal transmission coefficient in one incident direction with transmission zero; in the other incident direction, the transmission is unity and the phase changes smoothly. A direct method for breaking the reciprocity of reflection is to introduce another side-coupled resonator with gain (see figure 1(a)). Then, the reflection becomes asymmetric.
3.2. Unity scattering
Before proceeding to the double-flux AB interferometer, in the following analysis we demonstrate that unity left reflection and right transmission for opposite incident directions are possible in a single-flux AB interferometer, for example,  is possible. This is explained by solving the scattering coefficients in a single-flux AB interferometer. In contrast, we consider
is possible. This is explained by solving the scattering coefficients in a single-flux AB interferometer. In contrast, we consider  . The modal amplitudes in the equations of motion at steady-state satisfy
. The modal amplitudes in the equations of motion at steady-state satisfy
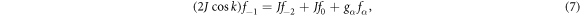
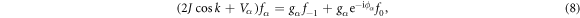
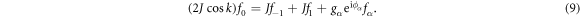
To analyze the scattering, we employ Jost solutions of the amplitude  for
for  , and
, and  for
for  for an incident wave with vector k. The reflection and transmission coefficients for the left incidence (D = 0) are defined as
for an incident wave with vector k. The reflection and transmission coefficients for the left incidence (D = 0) are defined as  ,
,  . Corresponding scattering coefficients for the right incidence (A = 0) are defined as
. Corresponding scattering coefficients for the right incidence (A = 0) are defined as  and
and  . By calculating the scattering coefficients, we obtained the conditions for
. By calculating the scattering coefficients, we obtained the conditions for  , which are
, which are  and
and  . Moreover, when the magnetic flux satisfies
. Moreover, when the magnetic flux satisfies  , unity left reflection and right transmission are simultaneously achieved (i.e.
, unity left reflection and right transmission are simultaneously achieved (i.e.  ). This indicates that the left-going (either the reflected left incidence or the transmitted right incidence) wave amplitudes after being scattered are unity.
). This indicates that the left-going (either the reflected left incidence or the transmitted right incidence) wave amplitudes after being scattered are unity.
4. Double-flux AB interferometer
4.1. Unidirectional transport
In the previous section, we first demonstrated a reciprocal reflectionless with nonreciprocal unity transmission, which realizes perfect absorption in one propagation direction after scattering. Then, we showed a wave scattering with unity amplitudes. When combining a unity scattering structure (with unity left-going after scattering, i.e.  ) on the left side of a reciprocal reflectionless structure (with unity right transmission after scattering, i.e.
) on the left side of a reciprocal reflectionless structure (with unity right transmission after scattering, i.e.  ), the right-going waves that are being scattered from the unity scattering structure are perfectly absorbed by the reciprocal reflectionless structure on the right side. Therefore, a unity left-going only wave is achieved after scattering (i.e.
), the right-going waves that are being scattered from the unity scattering structure are perfectly absorbed by the reciprocal reflectionless structure on the right side. Therefore, a unity left-going only wave is achieved after scattering (i.e.  ,
,  ). The physical processes are schematically illustrated in figure 2. For the left incidence shown in figure 2(a), the left reflection (blue solid arrow) is unity after being scattered at resonator α, the transmitted part (gray solid arrow) is perfectly absorbed (yellow and purple dashed arrow) at resonator β; the final outcome is a unity left reflection without left transmission (inside black box). For the right incidence shown in figure 2(b), the right reflection (yellow dashed arrow on the right) is zero, the transmitted part (blue solid arrow in the center) is unity after being scattered at resonator β. This transmitted part is scattered again at resonator α with unity right transmission (blue solid arrow on the left), the light reflected back (gray solid arrow) to the resonator β part is perfectly absorbed (yellow dashed arrow in the center and purple dashed arrow); the final outcome is a perfect right transmission without right refection (inside black box). Thus, the light transport is unidirectional, being left-going only after scattering and the amplitude is unity.
). The physical processes are schematically illustrated in figure 2. For the left incidence shown in figure 2(a), the left reflection (blue solid arrow) is unity after being scattered at resonator α, the transmitted part (gray solid arrow) is perfectly absorbed (yellow and purple dashed arrow) at resonator β; the final outcome is a unity left reflection without left transmission (inside black box). For the right incidence shown in figure 2(b), the right reflection (yellow dashed arrow on the right) is zero, the transmitted part (blue solid arrow in the center) is unity after being scattered at resonator β. This transmitted part is scattered again at resonator α with unity right transmission (blue solid arrow on the left), the light reflected back (gray solid arrow) to the resonator β part is perfectly absorbed (yellow dashed arrow in the center and purple dashed arrow); the final outcome is a perfect right transmission without right refection (inside black box). Thus, the light transport is unidirectional, being left-going only after scattering and the amplitude is unity.
Figure 2. Schematic illustration of one-way transport for perfect left reflection and right transmission.  ,
,  denote the resonator circles. The text under the arrows marks the representations. The physical processes are illustrated tat the top, and the outcomes are shown in the black box.
denote the resonator circles. The text under the arrows marks the representations. The physical processes are illustrated tat the top, and the outcomes are shown in the black box.
Download figure:
Standard image High-resolution imageBased on the analysis of the perfect absorption and directional propagation with unity amplitude, we demonstrated that achieving one-way transport with an appropriate interferometer structure and resonator parameters is possible in a double-flux AB interferometer. In this situation, the double-flux AB interferometer acts as an ideal light-checking valve; the phenomenon observed here is similar to that proposed by employing optical nonlinearity in asymmetric structures [2–5], however the system is linear in our proposal and the non-Hermiticity and magnetic flux controlled interference play key roles. Using asymmetric reflectionless potentials [4], an approximately unidirectional flow of solitons was found recently [5]; in this work, the reciprocal reflectionless in the designed unidirectional perfect absorption is also indispensable. Our proposed one-way device possesses perfectly full transmission and reflection for wave input in opposite directions under proper conditions. In other words, the scattering coefficients satisfy
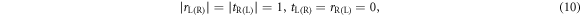
these imply a unidirectional flow of exactly 1. With respect to the scattering of combined double triangular loops in a resonator chain array, the loop-α on the left realizes a unity left reflection and a unity right transmission; the loop-β perfectly absorbs left incidence and perfectly transmits right incidence. The nonzero left transmission or right reflection being scattered from loop-α are both right-going waves, which are expected to be absorbed by loop-β on the right. For the left incidence, after being scattered by loop-α, the transmitted wave is absorbed by loop-β ( ) with a unity left reflection (
) with a unity left reflection ( ); for the right incidence, the wave reflected by loop-α is absorbed by loop-β with a unity right transmission (
); for the right incidence, the wave reflected by loop-α is absorbed by loop-β with a unity right transmission ( ). In this manner, the double-flux structure achieves both nonreciprocal transmission and reflection in an extreme case: the left incidence is perfectly reflected without transmission and the right incidence is perfectly transmitted without reflection (i.e. directional light propagation after scattering). Our one-way transport concept uses gain and loss to amplify and attenuate the incident wave. The magnetic flux is employed to facilitate the nonreciprocity and control scattering amplitudes. This unidirectional light transport is induced by the interplay between the non-Hermiticity and the nontrivial magnetic fluxes.
). In this manner, the double-flux structure achieves both nonreciprocal transmission and reflection in an extreme case: the left incidence is perfectly reflected without transmission and the right incidence is perfectly transmitted without reflection (i.e. directional light propagation after scattering). Our one-way transport concept uses gain and loss to amplify and attenuate the incident wave. The magnetic flux is employed to facilitate the nonreciprocity and control scattering amplitudes. This unidirectional light transport is induced by the interplay between the non-Hermiticity and the nontrivial magnetic fluxes.
The double-flux AB interferometer system is schematically illustrated in figure 1(a). To calculate the coefficients, the amplitudes of resonators 0, α, and β are set as f0,  , and
, and  . For the incident wave vector
. For the incident wave vector  , the magnetic fluxes act in a
, the magnetic fluxes act in a  period, in other words, a system with
period, in other words, a system with  ,
,  (
( ) results in the same scattering amplitudes as a system with
) results in the same scattering amplitudes as a system with  ,
,  . At
. At  , with respect to
, with respect to
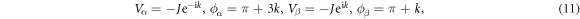
For the wave vector  , the solution from the equations of motion yields
, the solution from the equations of motion yields  , B = D. This yields a completely transmitted right incidence with the steady-state amplitudes
, B = D. This yields a completely transmitted right incidence with the steady-state amplitudes  and
and  . The left incidence at
. The left incidence at  leads to divergence of the amplitudes for the resonators f0,
leads to divergence of the amplitudes for the resonators f0,  , and
, and  .
.
For the wave vector  , the coefficients of the Jost solution satisfy
, the coefficients of the Jost solution satisfy  and C = 0, which is directly calculated from equations (2)–(6) at steady state. Therefore, the steady-state amplitudes of the double-flux AB interferometer have the following form
and C = 0, which is directly calculated from equations (2)–(6) at steady state. Therefore, the steady-state amplitudes of the double-flux AB interferometer have the following form
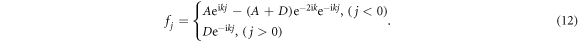
The amplitudes fj represent an arbitrary combination of completely reflected left input and completely transmitted right input. For coherent inputs from both sides with the same amplitude and a relative phase π (i.e.  ), the amplitude fj indicates a coherent perfect absorption (
), the amplitude fj indicates a coherent perfect absorption ( for
for  and
and  for
for  ) [24].
) [24].
For a left incidence of A = 1 and D = 0, the coefficient is  and C = 0. Thus, the reflection coefficient is
and C = 0. Thus, the reflection coefficient is  and the transmission coefficient is
and the transmission coefficient is  . These values indicate a completely reflected left incidence. The amplitudes at the center are
. These values indicate a completely reflected left incidence. The amplitudes at the center are  ,
,  , and
, and  . For a right incidence of A = 0 and D = 1, the coefficients are
. For a right incidence of A = 0 and D = 1, the coefficients are  and C = 0. The reflection coefficient is then
and C = 0. The reflection coefficient is then  and the transmission coefficients are
and the transmission coefficients are  these values indicate a fully transmitted right incidence. The wave dynamics correspond to a plane wave propagating from right to left. The synthetic magnetic fluxes lead to a cancellation of wave function at resonator f0; for right incidence, the amplitudes are
these values indicate a fully transmitted right incidence. The wave dynamics correspond to a plane wave propagating from right to left. The synthetic magnetic fluxes lead to a cancellation of wave function at resonator f0; for right incidence, the amplitudes are  ,
,  and
and  . Hence, perfect transmission in one direction and perfect reflection in the other direction appear (i.e.,
. Hence, perfect transmission in one direction and perfect reflection in the other direction appear (i.e.,  ). Only left-going waves are allowed after being scattered (figures 3(a)–(b) and (e)–(f)). The double-flux AB interferometer acts as a light-checking valve and unity one-way transport is achieved. An S-matrix can characterize the relationship between input and output. The S-matrix is in the form of
). Only left-going waves are allowed after being scattered (figures 3(a)–(b) and (e)–(f)). The double-flux AB interferometer acts as a light-checking valve and unity one-way transport is achieved. An S-matrix can characterize the relationship between input and output. The S-matrix is in the form of  and
and  . The parameter values of the magnetic fluxes and side-coupled resonators change the scattering coefficients. In the double-flux AB interferometer, exchanging the subscript of
. The parameter values of the magnetic fluxes and side-coupled resonators change the scattering coefficients. In the double-flux AB interferometer, exchanging the subscript of  in equation (11) (i.e. the system satisfies
in equation (11) (i.e. the system satisfies  ,
,  ,
,  ,
,  ), we obtain perfect right reflection without transmission and perfect left transmission without reflection (i.e.
), we obtain perfect right reflection without transmission and perfect left transmission without reflection (i.e.  ), which is an reverse case that allows right-going waves after being scattered (figures 3(c)–(d) and (g)–(h)).
), which is an reverse case that allows right-going waves after being scattered (figures 3(c)–(d) and (g)–(h)).
Figure 3. Time evolution profile for one-way transport. (a)–(d) show a wide Gaussian wave packet with w = 0.02, (e)–(h) show a narrow wave packet with  . The wave vector is
. The wave vector is  . The full left reflection and right transmission are simulated in a system with
. The full left reflection and right transmission are simulated in a system with  ,
,  ,
,  ,
,  in (a), (b), (e), and (f). The full left transmission and right reflection are simulated in a system with
in (a), (b), (e), and (f). The full left transmission and right reflection are simulated in a system with  ,
,  ,
,  ,
,  in (c), (d), (g), and (h).
in (c), (d), (g), and (h).
Download figure:
Standard image High-resolution imageThe perfect transmission and reflection in the double-flux AB interferometer are numerically simulated using Gaussian wave packets. Snapshots of the wave packet probability  for each resonator site in the dynamical process are shown in figure 3. Here, a Gaussian wave packet has the form of
for each resonator site in the dynamical process are shown in figure 3. Here, a Gaussian wave packet has the form of  , where
, where  is the center, and w controls the width of the wave packet in real space,
is the center, and w controls the width of the wave packet in real space,  is the renormalization constant, and + (−) corresponds to a right-going (left-going) wave traveling with a velocity of
is the renormalization constant, and + (−) corresponds to a right-going (left-going) wave traveling with a velocity of 
 ]. The time evolution is governed by the equations of motion. Regarding figure 3(a), total of 600 lead lengths were chosen. The Gaussian wave packet was initially centered at
]. The time evolution is governed by the equations of motion. Regarding figure 3(a), total of 600 lead lengths were chosen. The Gaussian wave packet was initially centered at  , traveling with a velocity of
, traveling with a velocity of  from left to right. The wave packet center reached the double-flux AB interferometer at the approximate time
from left to right. The wave packet center reached the double-flux AB interferometer at the approximate time  , and was then totally reflected. Regarding figure 3(b), the Gaussian wave packet was initially centered at
, and was then totally reflected. Regarding figure 3(b), the Gaussian wave packet was initially centered at  , traveling with a velocity of
, traveling with a velocity of  from right to left, the wave packet reached the double-flux AB interferometer at the approximate time
from right to left, the wave packet reached the double-flux AB interferometer at the approximate time  , then totally transmitted without reflection. The double-flux AB interferometer structure controls waves propagating to only the left. In figures 3(c) and (d), an reverse process was simulated. The situations depicted in figures 3(a)–(d) were performed again but using a narrow wave packet in figures 3(e)–(h), the unidirectional light transport appears approximately perfectly but is associated with discrete diffractions. When considering parameter deviations in the interferometer, unidirectional behavior still exists in the vicinity of the appropriate parameters, where all of the transmissions and reflections vary smoothly. For simultaneous 1% deviations on all of the magnetic fluxes, detunings, and gain/loss (i.e.
, then totally transmitted without reflection. The double-flux AB interferometer structure controls waves propagating to only the left. In figures 3(c) and (d), an reverse process was simulated. The situations depicted in figures 3(a)–(d) were performed again but using a narrow wave packet in figures 3(e)–(h), the unidirectional light transport appears approximately perfectly but is associated with discrete diffractions. When considering parameter deviations in the interferometer, unidirectional behavior still exists in the vicinity of the appropriate parameters, where all of the transmissions and reflections vary smoothly. For simultaneous 1% deviations on all of the magnetic fluxes, detunings, and gain/loss (i.e.  ,
,  ), the scattering coefficient derivations are below 3.7%, which decrease for deviations on fewer parameters.
), the scattering coefficient derivations are below 3.7%, which decrease for deviations on fewer parameters.
4.2. Unidirectional spectral singularity
Based on the theoretical analysis, the perfect left reflection and right transmission are a combination of unity left-going and perfectly absorbed right-going waves. Perfect absorption was implied by the zero probability at resonator 0 from the numerically simulated dynamical process. The one-way transport was a direct product of the unidirectional spectral singularities [40]. The double-flux AB interferometer light-checking valve uses the wave emission and absorption properties of the unidirectional spectral singularities in the non-Hermitian system [30]; this is facilitated by the magnetic fluxes and side-coupled gain and loss resonators. The wave function of the conjugation counterpart system yields divergent scattering coefficients. The Hermitian conjugation counterpart for the light-checking valve system is when parameters satisfy
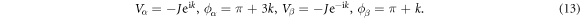
The solution of the amplitudes from the steady-state equations of motion yields  , and
, and  . Thus, the steady-state wave function is expressed as
. Thus, the steady-state wave function is expressed as
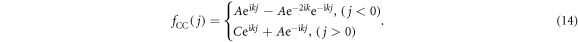
where  at A = 0 indicates unidirectional lasing induced by unidirectional spectral singularities [30]. In the Hermitian conjugation counterpart system in equation (13), the left transmission and right reflection coefficients diverge. However, the left reflection and right transmission remain finite. Input from any direction toward the AB interferometer center induces a right-going wave emission. Unidirectional lasing entails wave emission in one direction only, differing from the traditional lasing in two directions [30].
at A = 0 indicates unidirectional lasing induced by unidirectional spectral singularities [30]. In the Hermitian conjugation counterpart system in equation (13), the left transmission and right reflection coefficients diverge. However, the left reflection and right transmission remain finite. Input from any direction toward the AB interferometer center induces a right-going wave emission. Unidirectional lasing entails wave emission in one direction only, differing from the traditional lasing in two directions [30].
4.3. Discussion
Perfect unidirectional absorption is critical for the realization of the proposed light-checking valve. When maintaining the parameters of loop-β satisfies a unidirectional perfect absorption condition (for instance,  ,
,  , and
, and  ), the left incident wave at loop-β is perfectly absorbed and the right incident wave at loop-β transmits without reflection. This leads to right-going waves vanishing after being scattered (i.e.
), the left incident wave at loop-β is perfectly absorbed and the right incident wave at loop-β transmits without reflection. This leads to right-going waves vanishing after being scattered (i.e.  ); with respect to the left-going waves, the coefficients
); with respect to the left-going waves, the coefficients  and
and  for the double-flux AB interferometer change according to the magnetic flux
for the double-flux AB interferometer change according to the magnetic flux  and the resonator parameters of loop-α. An exceptional case for loop-β at unidirectional perfect absorption conditions is when the left incidence toward loop-β is a persistent emission wave (i.e. lasing from loop-α). The cooperation of wave emission from loop-α and wave absorption by loop-β leads to a finite transmission instead perfect absorption.
and the resonator parameters of loop-α. An exceptional case for loop-β at unidirectional perfect absorption conditions is when the left incidence toward loop-β is a persistent emission wave (i.e. lasing from loop-α). The cooperation of wave emission from loop-α and wave absorption by loop-β leads to a finite transmission instead perfect absorption.
We analyzed triangular loop-α with  ,
,  and observed that the two resonators are not
and observed that the two resonators are not  -symmetric at
-symmetric at  . When the spectral singularities of the two triangular structures are coincident, the scattering coefficients for the left-going waves are
. When the spectral singularities of the two triangular structures are coincident, the scattering coefficients for the left-going waves are  , except when
, except when  and
and  . We investigated the scattering coefficients of the left-going waves after being scattered as functions of γ and
. We investigated the scattering coefficients of the left-going waves after being scattered as functions of γ and  . In figure 4(a),
. In figure 4(a),  represents resonator α with gain, the left reflection and right transmission vary as γ, and both reach unity at
represents resonator α with gain, the left reflection and right transmission vary as γ, and both reach unity at  . This indicates that the side-coupled resonators α and β are
. This indicates that the side-coupled resonators α and β are  -symmetric in this situation, although the unbalanced asymmetric fluxes break the
-symmetric in this situation, although the unbalanced asymmetric fluxes break the  symmetry of the interferometer and the reciprocity of transmission.
symmetry of the interferometer and the reciprocity of transmission.
Figure 4. The left reflection and right transmission. (a)  , (b)
, (b)  . Contour plots of (c)
. Contour plots of (c)  and (d)
and (d)  as functions of
as functions of  and
and  . The system parameters are
. The system parameters are  ,
,  ,
,  , the wave vector is
, the wave vector is  . Correspondingly,
. Correspondingly,  and
and  except for
except for  at
at  and
and  .
.
Download figure:
Standard image High-resolution imageIn figure 4(b), the left reflection is unity, remaining unchanged; the right transmission diverges at  (black cross in figure 4(d)); at
(black cross in figure 4(d)); at  (empty diamond in figure 4(c)) not only are the side-coupled resonators α and β
(empty diamond in figure 4(c)) not only are the side-coupled resonators α and β  -symmetric but also the interferometer is with respect to resonator 0.
-symmetric but also the interferometer is with respect to resonator 0.  symmetry leads to the coincidence of the unidirectional lasing from loop-α and unidirectional perfect absorbing in loop-β. In this case, loop-β cannot fully absorb the lasing emitted from its
symmetry leads to the coincidence of the unidirectional lasing from loop-α and unidirectional perfect absorbing in loop-β. In this case, loop-β cannot fully absorb the lasing emitted from its  -symmetric counterpart loop-α, resulting in a finite transmission after loop-β absorbed the persistent wave emitted from loop-α toward it (
-symmetric counterpart loop-α, resulting in a finite transmission after loop-β absorbed the persistent wave emitted from loop-α toward it ( ); however, this leaves
); however, this leaves  , which evidenced the wave emission. The
, which evidenced the wave emission. The  symmetry leads to a reciprocal unity transmission with unidirectional reflectionless (
symmetry leads to a reciprocal unity transmission with unidirectional reflectionless ( ,
,  ).
).
The dynamical processes for  at
at  are special and relate to the spectral singularities. In figure 4(c), the reflectionlessness of the left incidence is controlled by the enclosed magnetic flux
are special and relate to the spectral singularities. In figure 4(c), the reflectionlessness of the left incidence is controlled by the enclosed magnetic flux  . At
. At  , the left incidence is reflectionless (
, the left incidence is reflectionless ( ) except when
) except when  (
( ). At
). At  , the left incidence is fully reflected (
, the left incidence is fully reflected ( ) for any
) for any  . In figure 4(d), the right transmission is unity at
. In figure 4(d), the right transmission is unity at  the right transmission diverges at
the right transmission diverges at  and
and  (marked by a black cross), and corresponding right reflection is zero, these indicate unidirectional lasing. The right transmission vanishes at
(marked by a black cross), and corresponding right reflection is zero, these indicate unidirectional lasing. The right transmission vanishes at  and
and  , where the incidence waves from any direction are perfectly absorbed without reflection; the double-flux AB interferometer acts as a reciprocal perfect absorber. At
, where the incidence waves from any direction are perfectly absorbed without reflection; the double-flux AB interferometer acts as a reciprocal perfect absorber. At  and
and  , the double-flux AB interferometer acts as a unidirectional perfect absorber.
, the double-flux AB interferometer acts as a unidirectional perfect absorber.
Figure 4 depicts the left-going wave amplitudes (left reflected and right transmitted) under the influence of magnetic flux in loop-α, and the detuning and gain/loss of resonator α. In a non-Hermitian system, the magnetic flux as an independent parameter can be used to realize and control the asymmetric scattering, benefiting from the fact that the magnetic flux simultaneously breaks  and
and  symmetries. There are several advantages to the proposed double-flux AB interferometer. First, the system is linear and the physics behind it is clear and simple. Second, the designed one-way behavior is perfect unidirectional. Although the realization of exact balance of gain and loss (i.e.
symmetries. There are several advantages to the proposed double-flux AB interferometer. First, the system is linear and the physics behind it is clear and simple. Second, the designed one-way behavior is perfect unidirectional. Although the realization of exact balance of gain and loss (i.e.  symmetric side-coupled resonators) is a disadvantage, the control parameters are only two side-coupled resonators rather than involving a wide region. Third, the appearance of nonunitary, nonreciprocal properties and the spectral singularities bring extraordinary dynamical behaviors; rich scattering phenomena exist in the interferometer system. Notably, applying effective magnetic flux in a coupled waveguide system is possible [39] and the proposed one-way transport is also applicable in optical waveguides.
symmetric side-coupled resonators) is a disadvantage, the control parameters are only two side-coupled resonators rather than involving a wide region. Third, the appearance of nonunitary, nonreciprocal properties and the spectral singularities bring extraordinary dynamical behaviors; rich scattering phenomena exist in the interferometer system. Notably, applying effective magnetic flux in a coupled waveguide system is possible [39] and the proposed one-way transport is also applicable in optical waveguides.
5. Conclusions
We propose a method for realizing one-way light transport in a linear optical system. We employed a double-flux AB interferometer consisting of two resonators with  -symmetric gain, loss and detuning, that was side-coupled to a uniform resonator chain array. The side-coupled resonators form two closed loops, in which synthetic magnetic fluxes are enclosed. The magnetic fluxes combine with the resonator gain and loss to break the reciprocity of the scattering, leading to nonreciprocal reflection and transmission. At appropriate values, directional light transmission with unity amplitude is possible. Thus, the AB interferometer can function as a light-checking valve, fully reflecting without incident light transmission in one direction, and fully transmitting without incident light reflection in the opposite direction. This incredible phenomenon occurs at the system spectral singularities. Our findings are based on linear elements, and provide a method for realizing one-way transport through the appropriate use of amplification, attenuation and synthetic magnetic flux. The unidirectionality is universal in the presence of magnetic fluxes and is non-Hermitian. We anticipate that these results will be useful in the design of optical devices for control and manipulation.
-symmetric gain, loss and detuning, that was side-coupled to a uniform resonator chain array. The side-coupled resonators form two closed loops, in which synthetic magnetic fluxes are enclosed. The magnetic fluxes combine with the resonator gain and loss to break the reciprocity of the scattering, leading to nonreciprocal reflection and transmission. At appropriate values, directional light transmission with unity amplitude is possible. Thus, the AB interferometer can function as a light-checking valve, fully reflecting without incident light transmission in one direction, and fully transmitting without incident light reflection in the opposite direction. This incredible phenomenon occurs at the system spectral singularities. Our findings are based on linear elements, and provide a method for realizing one-way transport through the appropriate use of amplification, attenuation and synthetic magnetic flux. The unidirectionality is universal in the presence of magnetic fluxes and is non-Hermitian. We anticipate that these results will be useful in the design of optical devices for control and manipulation.
Acknowledgments
We acknowledge the support of the National Natural Science Foundation of China (Grant Nos. 11605094 and 11374163), the Tianjin Natural Science Foundation (Grant No. 16JCYBJC40800), and the Baiqing plan foundation of Nankai University (Grant No. ZB15006104).









