Abstract
Broadband quantum memories, used as temporal multiplexers, are a key component in photonic quantum information processing, as they make repeat-until-success strategies scalable. We demonstrate a prototype system, operating on-demand, by interfacing a warm vapour, high time-bandwidth-product Raman memory with a travelling wave spontaneous parametric down-conversion source. We store single photons and observe a clear influence of the input photon statistics on the retrieved light, which we find currently to be limited by noise. We develop a theoretical model that identifies four-wave mixing as the sole important noise source and point towards practical solutions for noise-free operation.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Photonics is a promising platform for quantum technologies [1]. However, photon sources [2] and two-photon gates [3] currently only operate probabilistically. Large-scale photonic processing will therefore be prohibitively inefficient without a multiplexing strategy to actively select successful events. For this reason, spatial [4, 5], spectral [6] and temporal [7, 8] multiplexing are being investigated. For temporal multiplexing, quantum memories, which are capable to store and retrieve single photons on-demand, are an efficient solution. In particular, on-demand recall of the stored light can be used to temporally synchronize different outputs of heralded probabilistic events. Such temporal multiplexing enables scalable photonic architectures using repeat-until-success strategies [8–10]. A key figure of merit for this task is the time-bandwidth-product 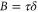 , where τ is the memory lifetime and δ is the memory acceptance bandwidth. B corresponds to the maximum number of possible processor steps that can occur within the memory lifetime. Dramatic enhancements in the scaling of photonic networks become possible with
, where τ is the memory lifetime and δ is the memory acceptance bandwidth. B corresponds to the maximum number of possible processor steps that can occur within the memory lifetime. Dramatic enhancements in the scaling of photonic networks become possible with  [8]. The very long storage times [11–13] and large time-bandwidth products [14, 15] obtainable by optical storage in atoms make these systems prime candidates for temporal synchronization devices. Notably, besides atomic systems, broadband signal storage has also been achieved in solid-state systems. Examples for these are off-resonant Raman storage [8] in diamond [16, 17] and in cryogenic rare-earth ion doped crystals [18], using atomic-frequency-comb (AFC) echoes with preprogrammed storage times. The recently demonstrated spin-wave storage in AFC [19–22] could also offer a route to temporal multiplexing.
[8]. The very long storage times [11–13] and large time-bandwidth products [14, 15] obtainable by optical storage in atoms make these systems prime candidates for temporal synchronization devices. Notably, besides atomic systems, broadband signal storage has also been achieved in solid-state systems. Examples for these are off-resonant Raman storage [8] in diamond [16, 17] and in cryogenic rare-earth ion doped crystals [18], using atomic-frequency-comb (AFC) echoes with preprogrammed storage times. The recently demonstrated spin-wave storage in AFC [19–22] could also offer a route to temporal multiplexing.
The first step towards memory-based synchronization of single-photon generation is the storage of single photons. This has been demonstrated by spin-wave storage in cold atomic ensembles [23–26], single atoms [27, 28], and by pre-programmed AFC echoes in cryogenic rare-earth ion doped crystals [18, 29–31]. Storage [32, 33] and retrieval [34] of non-classical light in the room-temperature regime has been achieved with narrow bandwidths on the order of a few MHz. However, a quantum memory suitable for large-scale temporal multiplexing is still elusive. Key desiderata are broad acceptance bandwidths, on-demand storage and retrieval, as well as room-temperature operation with low noise. The ability to store multiple temporal modes in a single device [35, 36] is also appealing, if multiple memories could not be operated in parallel [37]. Notably, when we mention temporal multiplexing in this work we refer to temporal synchronization using a single-mode memory [8], not time-mode-multiplexing within a multimode memory; see supplementary material (stacks.iop.org/njp/17/043006/mmedia) for a more detailed discussion.
In this paper we report the storage of GHz-bandwidth heralded single photons, generated by spontaneous parametric down-conversion (SPDC), in a warm caesium (Cs) vapour Raman memory, for which  [14, 38]. On-demand memory operation, which is crucial for synchronization tasks, is implemented by triggering the memory on the detection of a herald photon. The performance of our system is characterized by measuring the autocorrelation of the fields transmitted through, and retrieved from the memory. We present a simple theoretical model which describes the system dynamics and identify four-wave mixing (FWM) as the sole significant noise source. Suppressing this noise process will make it possible to use the presented technology to construct large-scale photonic networks.
[14, 38]. On-demand memory operation, which is crucial for synchronization tasks, is implemented by triggering the memory on the detection of a herald photon. The performance of our system is characterized by measuring the autocorrelation of the fields transmitted through, and retrieved from the memory. We present a simple theoretical model which describes the system dynamics and identify four-wave mixing (FWM) as the sole significant noise source. Suppressing this noise process will make it possible to use the presented technology to construct large-scale photonic networks.
2. Experimental setup
Our memory is based on transient Raman absorption in a Cs vapour cell at  [14, 38, 40–42] (figure 1 and appendix
[14, 38, 40–42] (figure 1 and appendix  GHz, set by the control pulse bandwidth, allows it to be directly interfaced with a traveling-wave SPDC source without the need to enhance the spectral brightness by an optical cavity [43]. Our source is based on type-II SPDC in a periodically-poled potassium-titanyl-phosphate waveguide (figure 1 (a)). The single-pass waveguide is pumped by a pulse of approximately 260 ps duration at a wavelength of 426 nm. SPDC produces photons in pairs, thus we herald the presence of a signal photon to be stored in the memory by detecting its partner idler photon (
GHz, set by the control pulse bandwidth, allows it to be directly interfaced with a traveling-wave SPDC source without the need to enhance the spectral brightness by an optical cavity [43]. Our source is based on type-II SPDC in a periodically-poled potassium-titanyl-phosphate waveguide (figure 1 (a)). The single-pass waveguide is pumped by a pulse of approximately 260 ps duration at a wavelength of 426 nm. SPDC produces photons in pairs, thus we herald the presence of a signal photon to be stored in the memory by detecting its partner idler photon ( in figure 1(a)). Optimization of the SPDC spatial mode (figures 1 (b)–(d)) and signal path transmission yields a heralding efficiency of
in figure 1(a)). Optimization of the SPDC spatial mode (figures 1 (b)–(d)) and signal path transmission yields a heralding efficiency of  , which is the probability that a single photon is sent into the memory given a herald detection event (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia). As shown in figure 1, we operate the memory in feed-forward configuration (see supplementary material), whereby herald photon triggers the control field that operates the memory. Control pulses are prepared by pulse picking with a Pockels cell. Spectrally filtering the idler projects the signal photon's marginal spectrum into Raman resonance with the control [44, 45]. The heralded signal photons have a full-width-half-maximum bandwidth of ∼1.8 GHz. Conditioning on herald detection ensures that storage and retrieval are only attempted when a spectrally matched photon is sent into the memory. To benchmark the storage of heralded single photons we also store coherent states with average photon numbers similar to
, which is the probability that a single photon is sent into the memory given a herald detection event (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia). As shown in figure 1, we operate the memory in feed-forward configuration (see supplementary material), whereby herald photon triggers the control field that operates the memory. Control pulses are prepared by pulse picking with a Pockels cell. Spectrally filtering the idler projects the signal photon's marginal spectrum into Raman resonance with the control [44, 45]. The heralded signal photons have a full-width-half-maximum bandwidth of ∼1.8 GHz. Conditioning on herald detection ensures that storage and retrieval are only attempted when a spectrally matched photon is sent into the memory. To benchmark the storage of heralded single photons we also store coherent states with average photon numbers similar to  . These are generated by phase modulation of a weak control beam pick-off [14, 38, 41]. Behind the Cs cell, the control field is separated from the signal by polarization and spectral filtering. The signal is then split 50:50 on a beam splitter and directed to a pair of photon-counting detectors (
. These are generated by phase modulation of a weak control beam pick-off [14, 38, 41]. Behind the Cs cell, the control field is separated from the signal by polarization and spectral filtering. The signal is then split 50:50 on a beam splitter and directed to a pair of photon-counting detectors (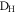 ,
, 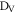 in figure 1 (a)). See supplementary material available at stacks.iop.org/njp/17/043006/mmedia for details.
in figure 1 (a)). See supplementary material available at stacks.iop.org/njp/17/043006/mmedia for details.
Figure 1. (a): experimental setup (main text (see supplementary material)): HWP: half-wave plate, SHG: second-harmonic generation, DM: dichroic mirror, PBS: polarizing beam splitter, PC: Pockels cell, EOM: electro-optic modulator, COH: coherent-state input signal, SPCM: single-photon counting module. (b): PPKTP waveguide chip input face. (c): waveguides of 4–2 μm width (left to right). (d): EM-CCD image showing the spatial mode of the SPDC photons from the 3 μm waveguide used in the experiment. (e): Raman memory scheme (appendix  ). During storage the signal is read in by exciting a spin-wave coherence [38–40] between the initial state
). During storage the signal is read in by exciting a spin-wave coherence [38–40] between the initial state 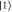 and the storage state
and the storage state 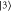 , which are seperated by the ground state hyperfine splitting ΔS. Read-out, by reapplication of the control, transfers the atoms back to the initial state
, which are seperated by the ground state hyperfine splitting ΔS. Read-out, by reapplication of the control, transfers the atoms back to the initial state 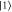 and releases the signal. (f): FWM noise process (main text, appendix
and releases the signal. (f): FWM noise process (main text, appendix 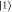 , driving spontaneous anti-Stokes scattering, which produces spurious atomic excitations that are retrieved as noise. (g): feed-forward timing diagram (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia): Herald detection triggers the Pockels cell to pick a pair of control pulses from the Ti:Sa output. Appropriate time delays, introduced by a digital delay generator (Stanford Research Systems DG535), ensure control and signal pulses enter the memory simultaneously.
, driving spontaneous anti-Stokes scattering, which produces spurious atomic excitations that are retrieved as noise. (g): feed-forward timing diagram (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia): Herald detection triggers the Pockels cell to pick a pair of control pulses from the Ti:Sa output. Appropriate time delays, introduced by a digital delay generator (Stanford Research Systems DG535), ensure control and signal pulses enter the memory simultaneously.
Download figure:
Standard image High-resolution image3. Mean field measurements
The memory efficiency and noise are determined by measuring the arrival time histograms of signal photons transmitted through and retrieved from the memory. As shown in figure 2, the performance is similar for both signal types, with a total memory efficiency 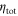 of 29% for coherent states and 21% for heralded single photons, limited by the control pulse energy, mode-matching between signal and control, and optical pumping (see supplementary material (stacks.iop.org/njp/17/043006/mmedia)). In addition to the signal, there is noise present in the read-in and the read-out time bins. It is visible as a pulse emitted from the memory when only the control field is applied. These noise pulses contain on average
of 29% for coherent states and 21% for heralded single photons, limited by the control pulse energy, mode-matching between signal and control, and optical pumping (see supplementary material (stacks.iop.org/njp/17/043006/mmedia)). In addition to the signal, there is noise present in the read-in and the read-out time bins. It is visible as a pulse emitted from the memory when only the control field is applied. These noise pulses contain on average 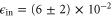 photons per read-in and
photons per read-in and 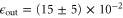 photons per read-out control cycle. The noise originates from FWM, which is a two-step process: first, the control generates spurious spin-wave excitations by spontaneous anti-Stokes scattering (figure 1(f), appendix
photons per read-out control cycle. The noise originates from FWM, which is a two-step process: first, the control generates spurious spin-wave excitations by spontaneous anti-Stokes scattering (figure 1(f), appendix 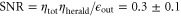 . It should be noted that, with FWM present, the SNR, measured with the signal present and removed, may not be a faithful measure of memory performance due to a small amount of FWM gain during the memory operation. We have analysed this in the supplementary material, using a worse case model (stacks.iop.org/njp/17/043006/mmedia) and found only a small perturbation to the SNR presented here. Notably, the sub-unity heralding efficiency
. It should be noted that, with FWM present, the SNR, measured with the signal present and removed, may not be a faithful measure of memory performance due to a small amount of FWM gain during the memory operation. We have analysed this in the supplementary material, using a worse case model (stacks.iop.org/njp/17/043006/mmedia) and found only a small perturbation to the SNR presented here. Notably, the sub-unity heralding efficiency  sets tight tolerances on the unconditional noise floor of the memory. For future implementations it is thus vital to understand the effects of noise on the properties of stored single photons.
sets tight tolerances on the unconditional noise floor of the memory. For future implementations it is thus vital to understand the effects of noise on the properties of stored single photons.
Figure 2. Temporal intensity profiles demonstrating memory. Storage for 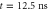 of (a) single-photon input signals, and (b) weak coherent states, with approximately equal input photon numbers per pulse of
of (a) single-photon input signals, and (b) weak coherent states, with approximately equal input photon numbers per pulse of 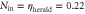 and
and 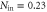 , respectively. Green traces show the input signal field transmitted through the memory when the control is blocked, i.e. the memory is off (signal only). Red lines show the noise emitted by the memory in both time bins, when the input signal is blocked (control only). Blue lines represent the pulses when the memory is on, i.e. control field and input signal are applied together (signal + control). This includes signal, transmitted through or recalled from the memory, along with any added noise. Subtracting the noise from this trace in the read-out bin gives the effective retrieved signal (lilac). Its direct comparison with the input signal (signal only) yields the memory efficiency (see supplementary material).
, respectively. Green traces show the input signal field transmitted through the memory when the control is blocked, i.e. the memory is off (signal only). Red lines show the noise emitted by the memory in both time bins, when the input signal is blocked (control only). Blue lines represent the pulses when the memory is on, i.e. control field and input signal are applied together (signal + control). This includes signal, transmitted through or recalled from the memory, along with any added noise. Subtracting the noise from this trace in the read-out bin gives the effective retrieved signal (lilac). Its direct comparison with the input signal (signal only) yields the memory efficiency (see supplementary material).
Download figure:
Standard image High-resolution image4. Photon statistics measurements
We characterize these effects by measuring the 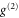 autocorrelation of all field combinations shown in figure 2 for both time bins. From the detector count statistics, the normalized autocorrelation [44], conditional on herald detection, is given by
autocorrelation of all field combinations shown in figure 2 for both time bins. From the detector count statistics, the normalized autocorrelation [44], conditional on herald detection, is given by 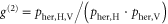 (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia). Here,
(see supplementary material available at stacks.iop.org/njp/17/043006/mmedia). Here, 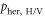 is the probability that the heralding detector (
is the probability that the heralding detector (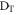 ) and one of the signal detectors (
) and one of the signal detectors (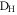 or
or 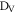 ) detect a photon in coincidence.
) detect a photon in coincidence. 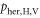 is the probability for a coincidence event between all three detectors (
is the probability for a coincidence event between all three detectors (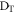 ,
, 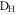 and
and  ). Blocking the control, we measure
). Blocking the control, we measure 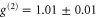 for coherent-state inputs (average over all input photon numbers
for coherent-state inputs (average over all input photon numbers 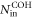 ) and
) and 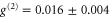 for heralded single photons, which are close to the ideal values of 1 and 0. When the input signal is blocked, we measure
for heralded single photons, which are close to the ideal values of 1 and 0. When the input signal is blocked, we measure 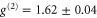 and
and  for the noise in the input and output time bins, respectively. With normal memory operation, i.e. signal and control applied, the photon statistics are modified by the accompanying FWM process. The
for the noise in the input and output time bins, respectively. With normal memory operation, i.e. signal and control applied, the photon statistics are modified by the accompanying FWM process. The 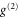 of the transmitted and retrieved signals increase, yielding the results displayed in figure 3. In the input time bin, transmitted coherent-state signals converge towards the ideal
of the transmitted and retrieved signals increase, yielding the results displayed in figure 3. In the input time bin, transmitted coherent-state signals converge towards the ideal 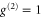 for larger input photon numbers of
for larger input photon numbers of 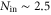 , as the amount of signal increases compared to the fixed amount of noise. Heralded single photons show
, as the amount of signal increases compared to the fixed amount of noise. Heralded single photons show 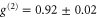 , slightly below the classicality boundary. Looking at the memory read-out (figure 3(b)), we find that coherent states with an input photon number of
, slightly below the classicality boundary. Looking at the memory read-out (figure 3(b)), we find that coherent states with an input photon number of 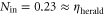 have
have 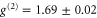 and are thus indistinguishable from the noise. Importantly, heralded single photons however show
and are thus indistinguishable from the noise. Importantly, heralded single photons however show 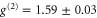 . This is a drop in
. This is a drop in  by more than three standard deviations compared to coherent states and noise (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia). The lower
by more than three standard deviations compared to coherent states and noise (see supplementary material available at stacks.iop.org/njp/17/043006/mmedia). The lower 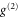 for heralded single photons reveals the influence of the non-classical SPDC input photon statistics in the memory read-out.
for heralded single photons reveals the influence of the non-classical SPDC input photon statistics in the memory read-out.
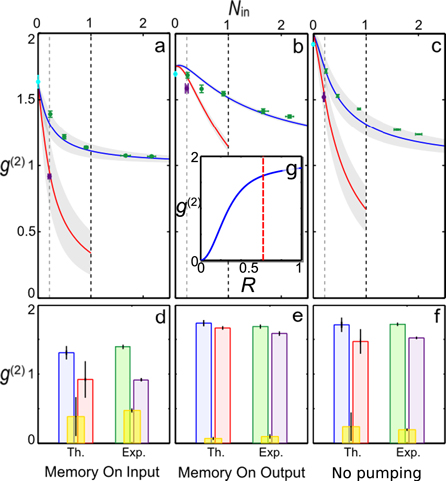
Figure 3. Photon statistics measurements showing 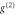 for increasing average photon number per pulse, Nin, of the input signal in three cases. (a): not-stored signal transmitted through the memory ('memory on input'), (b): signal retrieved from the memory ('memory on output'), (c): signal transmitted through the memory without optical pumping, i.e. without storage and retrieval ('no pumping'). Green points are coherent-state input signal data; purple datapoints represent heralded single-photon input (
for increasing average photon number per pulse, Nin, of the input signal in three cases. (a): not-stored signal transmitted through the memory ('memory on input'), (b): signal retrieved from the memory ('memory on output'), (c): signal transmitted through the memory without optical pumping, i.e. without storage and retrieval ('no pumping'). Green points are coherent-state input signal data; purple datapoints represent heralded single-photon input ( ), cyan points are FWM noise. Error bars derive from Poissonian counting statistics (see supplementary material). Blue and red lines show the theoretical predictions obtained from our coherent g2 model (see main text and appendix
), cyan points are FWM noise. Error bars derive from Poissonian counting statistics (see supplementary material). Blue and red lines show the theoretical predictions obtained from our coherent g2 model (see main text and appendix 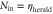 and
and 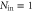 (perfect heralding efficiency), respectively. The bar plots (d)–(f) compare model prediction (Th.) with measurement (Exp.) for
(perfect heralding efficiency), respectively. The bar plots (d)–(f) compare model prediction (Th.) with measurement (Exp.) for  , with equal colour coding. Yellow bars denote the
, with equal colour coding. Yellow bars denote the 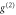 -differences between coherent-state and heralded single-photon inputs. In all three cases, the experimentally observed drop in
-differences between coherent-state and heralded single-photon inputs. In all three cases, the experimentally observed drop in 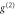 between coherent-state and heralded single photon inputs is well predicted by the model. (g): theoretical prediction for the
between coherent-state and heralded single photon inputs is well predicted by the model. (g): theoretical prediction for the  autocorrelation of the retrieved field after storing a single photon, as the ratio
autocorrelation of the retrieved field after storing a single photon, as the ratio 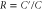 between anti-Stokes coupling C' and Stokes coupling C is varied (appendix
between anti-Stokes coupling C' and Stokes coupling C is varied (appendix
Download figure:
Standard image High-resolution imageTo investigate the observed photon statistics we compare two models: first a model based on incoherent addition of signal and noise [46]. It treats both as independent fields with different 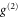 values, whose mixing ratio is determined by the SNR (see appendix
values, whose mixing ratio is determined by the SNR (see appendix 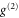 and fails to describe the data (see appendix
and fails to describe the data (see appendix 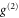 difference between single photons and coherent states. Having the same good agreement for both signal types also displays how well the SPDC source can be mode matched to the Raman memory. Importantly, this result means that the FWM process has a much greater influence on the photon statistics than naively expected from the SNR. To benchmark memory performance, one consequently needs to investigate the photon statistics and the influence of noise thereon in addition to the SNR. However, since the
difference between single photons and coherent states. Having the same good agreement for both signal types also displays how well the SPDC source can be mode matched to the Raman memory. Importantly, this result means that the FWM process has a much greater influence on the photon statistics than naively expected from the SNR. To benchmark memory performance, one consequently needs to investigate the photon statistics and the influence of noise thereon in addition to the SNR. However, since the 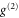 increase originates solely from FWM, eliminating it would result in the noise free case [40] with full photon statistics conservation (see appendix
increase originates solely from FWM, eliminating it would result in the noise free case [40] with full photon statistics conservation (see appendix
Luckily, FWM is not intrinsic to the memory interaction. The correlation between Stokes and anti-Stokes emission in FWM allows one to reduce Stokes noise by suppressing the anti-Stokes scattering. This enables noise reduction, while leaving the Raman memory unaffected. In principle, FWM can be suppressed by terminating the control field coupling to the initial atomic ground state via polarization selection rules. Yet, this approach is ineffective in alkali vapours far from resonance [47]. As FWM has phase-matching constraints similar to SPDC [48], an alternative could be to introduce dispersion between the Stokes and anti-Stokes frequencies, or to use a storage medium with larger Stokes shifts [17]. For alkali vapours, the approach of choice is to reduce the density of states at the anti-Stokes frequency by placing the memory inside a low-finesse cavity or photonic-bandgap structure [42]. As shown in figure 3(g), a FWM suppression by a factor of ∼2.5, readily achievable with the aforementioned techniques, would preserve the nonclassical signature of retrieved heralded single photons (see also appendix
5. Conclusion
In conclusion, we have, for the first time, interfaced sub-ns heralded single-photons with a warm atomic vapour memory in a practical configuration suitable for temporal multiplexing; a key goal for photonics quantum information science. Using this new device we have investigated the storage and retrieval of broadband heralded single photons in the memory. We have demonstrated that FWM is the only, ultimately important, noise source in EIT- and Raman-type memories. Its influence on the photon statistics is more severe than naively expected, but possible to mitigate.
Acknowledgments
We thank A Lvovsky, E Poem and C Kupchak for helpful discussions on FWM in Raman systems. We acknowledge Nathan Langford for early contributions to the design of the source, Michał Karpiński for assistance with the source optimization. We thank Justin Spring for assistance with the FPGA. This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC; EP/J000051/1 and Programme Grant EP/K034480/1), the Quantum Interfaces, Sensors, and Communication based on Entanglement Integrating Project (EU IP Q-ESSENCE; 248095), the Air Force Office of Scientific Research: European Office of Aerospace Research & Development (AFOSR EOARD; FA8655-09-1-3020), EU IP SIQS (600645), the Royal Society (to J.N.), EU ITN FASTQUAST (to P.S.M.), and EU Marie-Curie Fellowships (PIIF-GA- 2011-300820 to X.-M.J.; PIEF-GA-2012-331859 to W.S.K.; PIIF-GA-2013-629229 to D.J.S.). I.A.W. acknowledges an ERC Advanced Grant (MOQUACINO).
Appendix A.: The Raman memory protocol
As shown in figures 1 (a) and (e) of the main text, storage of a signal field, which is blue-detuned by 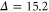 GHz from the Cs
GHz from the Cs 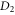 -line, is triggered by a co-propagating, orthogonally polarized control pulse tuned into two-photon resonance with the ground-state hyperfine transition (
-line, is triggered by a co-propagating, orthogonally polarized control pulse tuned into two-photon resonance with the ground-state hyperfine transition (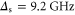 hyperfine ground state splitting). Signal storage transfers Cs atoms, initially prepared in the
hyperfine ground state splitting). Signal storage transfers Cs atoms, initially prepared in the 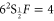 hyperfine ground state (
hyperfine ground state (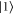 ) by optical pumping with a counter-propagating resonant diode laser, to the
) by optical pumping with a counter-propagating resonant diode laser, to the 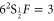 hyperfine ground state (
hyperfine ground state (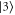 ), exciting a spin-wave coherence between both states [38–40]. Re-application of the control field drives the reverse process, producing a read-out signal and returning the atoms to
), exciting a spin-wave coherence between both states [38–40]. Re-application of the control field drives the reverse process, producing a read-out signal and returning the atoms to 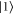 .
.
Appendix B.: Modelling the  autocorrelation measurements
autocorrelation measurements
B.1. Coherent  model
model
Figure 3 in the main text shows our measurements of the 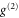 field autocorrelations alongside the predictions of a theoretical model that includes the effects of FWM seeded by spontaneous anti-Stokes scattering. The agreement is extremely good, which suggests that FWM is the only significant source of noise in the memory. Here we briefly outline the theoretical model, which is based on [14, 17], and is in fact identical to [49]. We consider one-dimensional propagation along the z-axis, normalized so that z runs from 0 to 1, of Stokes (signal) and anti-Stokes fields S, A through an ensemble of three-level Λ-type atoms (see figures 1 (e), (f)) in the presence of a control pulse with time-dependent Rabi frequency
field autocorrelations alongside the predictions of a theoretical model that includes the effects of FWM seeded by spontaneous anti-Stokes scattering. The agreement is extremely good, which suggests that FWM is the only significant source of noise in the memory. Here we briefly outline the theoretical model, which is based on [14, 17], and is in fact identical to [49]. We consider one-dimensional propagation along the z-axis, normalized so that z runs from 0 to 1, of Stokes (signal) and anti-Stokes fields S, A through an ensemble of three-level Λ-type atoms (see figures 1 (e), (f)) in the presence of a control pulse with time-dependent Rabi frequency 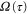 , where
, where  is the local time, at time t, in a frame propagating with the pulse at velocity c. After adiabatic elimination of the excited state
is the local time, at time t, in a frame propagating with the pulse at velocity c. After adiabatic elimination of the excited state  [50, 51], the Maxwell–Bloch equations describing the Raman interaction of the fields with the ground state coherence are given by
[50, 51], the Maxwell–Bloch equations describing the Raman interaction of the fields with the ground state coherence are given by
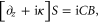
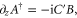
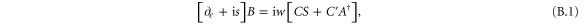
where 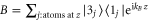 is the annihilation operator for spin wave excitations with wavevector
is the annihilation operator for spin wave excitations with wavevector 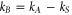 , with
, with 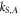 the Stokes, anti-Stokes wavevectors. The effective time
the Stokes, anti-Stokes wavevectors. The effective time 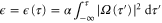 , with α such that
, with α such that 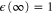 , parameterizes the adiabatic following of the control pulse [40]. With this coordinate transformation, the dynamic Stark shift is
, parameterizes the adiabatic following of the control pulse [40]. With this coordinate transformation, the dynamic Stark shift is 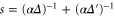 , where
, where 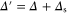 is the anti-Stokes detuning (figure 1 (e)). The dimensionless coupling constant C is given by
is the anti-Stokes detuning (figure 1 (e)). The dimensionless coupling constant C is given by  , where d is the resonant optical depth and γ the homogeneous linewidth of the excited state [38, 51]. C' is identical to C, except that Δ is replaced by
, where d is the resonant optical depth and γ the homogeneous linewidth of the excited state [38, 51]. C' is identical to C, except that Δ is replaced by 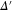 . Both are inversely proportional to the respective detuning of the channel they couple to (Stokes or anti-Stokes).
. Both are inversely proportional to the respective detuning of the channel they couple to (Stokes or anti-Stokes).  corresponds to a vanishing anti-Stokes coupling which represents the noiseless case [40]. The population inversion is
corresponds to a vanishing anti-Stokes coupling which represents the noiseless case [40]. The population inversion is  , where
, where 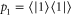 and
and 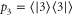 are the initial occupation probabilities of the ground states
are the initial occupation probabilities of the ground states 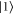 ,
, 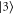 , respectively. Finally, we have defined the FWM phase mismatch
, respectively. Finally, we have defined the FWM phase mismatch  , where
, where 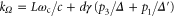 is the wavevector of the control with frequency
is the wavevector of the control with frequency 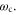 We also have
We also have ![${{k}_{S}}=L{{\omega }_{S}}/c+d\gamma [{{p}_{1}}/\Delta +{{p}_{3}}/(\Delta -{{\Delta }_{{\rm s}}})]$](https://content.cld.iop.org/journals/1367-2630/17/4/043006/revision1/njp511105ieqn93.gif) , and
, and ![${{k}_{A}}=L{{\omega }_{A}}/c+d\gamma [{{p}_{3}}/\Delta ^{\prime} +{{p}_{1}}/(\Delta +2{{\Delta }_{{\rm s}}})]$](https://content.cld.iop.org/journals/1367-2630/17/4/043006/revision1/njp511105ieqn94.gif) . Here the length L of the cell appears, to account for the normalization of the z-coordinate. These expressions are simply derived by considering the refractive index for each field, due to off-resonant interaction with the atomic transitions. Note that on Raman resonance we have
. Here the length L of the cell appears, to account for the normalization of the z-coordinate. These expressions are simply derived by considering the refractive index for each field, due to off-resonant interaction with the atomic transitions. Note that on Raman resonance we have 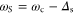 and
and 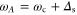 . Our experiments were done with a 7.5 cm Cs cell held at 70 °C, giving a resonant optical depth
. Our experiments were done with a 7.5 cm Cs cell held at 70 °C, giving a resonant optical depth 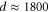 . We focus 10 nJ control pulses with duration
. We focus 10 nJ control pulses with duration  ps into the cell with a waist ∼300 μm, giving a peak Rabi frequency
ps into the cell with a waist ∼300 μm, giving a peak Rabi frequency  GHz, so that
GHz, so that 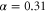 ns. We operate blue-detuned from resonance with the D2 line, whereby the detuning is
ns. We operate blue-detuned from resonance with the D2 line, whereby the detuning is 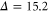 GHz and the Stokes shift in Cs is
GHz and the Stokes shift in Cs is 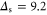 GHz. Finally, the homogeneous linewidth is
GHz. Finally, the homogeneous linewidth is 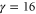 MHz, so that we have C = 0.82. When the memory is operated normally, the atoms are optically pumped into the ground state
MHz, so that we have C = 0.82. When the memory is operated normally, the atoms are optically pumped into the ground state 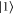 , and we set
, and we set 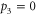 (w = 1). For the case where the optical pumping beam is blocked, the atoms thermalize and we set
(w = 1). For the case where the optical pumping beam is blocked, the atoms thermalize and we set 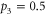 (w = 0).
(w = 0).
The system of coupled partial differential operator equations (B.1) is linear, and the solutions can therefore be written as a linear mapping from initial input to final output fields via the system's Green's functions Gjk. For example, the signal field transmitted through the memory during the storage interaction is

where 'vac' and 'therm' denote initial vacuum and thermal states for the anti-Stokes and spin-wave fields. The signal field retrieved from the memory after a storage time T is given by a similar expression,
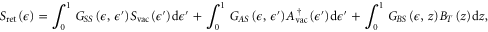
where to a good approximation in our experiment we may neglect decoherence and set 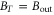 , since T = 12.5 ns, while the memory lifetime is
, since T = 12.5 ns, while the memory lifetime is  μs [14]. Here, the spin-wave at the end of the storage interaction is given by
μs [14]. Here, the spin-wave at the end of the storage interaction is given by
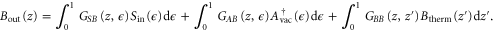
The  autocorrelation for a short-pulsed time-dependent field measured by slow detectors is given by
autocorrelation for a short-pulsed time-dependent field measured by slow detectors is given by
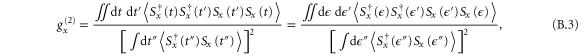
where the label 'x' is either 'ret' or 'trans'. Since the initial field operators satisfy bosonic commutation relations (or in the case of ![$\langle [{{B}_{{\rm in}}}(z),B_{{\rm in}}^{\dagger }(z^{\prime} )]\rangle =w\delta (z-z^{\prime} )$](https://content.cld.iop.org/journals/1367-2630/17/4/043006/revision1/njp511105ieqn110.gif) , boson-like) and their expectation values on the initial state of the atomic-optical system are known, the expectation values of normally ordered products of the output field operators can be computed from products of the Green's functions [14, 49], enabling the calculation of the
, boson-like) and their expectation values on the initial state of the atomic-optical system are known, the expectation values of normally ordered products of the output field operators can be computed from products of the Green's functions [14, 49], enabling the calculation of the 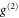 . The Green's functions can be found analytically [49], although for convenience we use a previously-developed numerical code. Full details will be given elsewhere. However here we note that the
. The Green's functions can be found analytically [49], although for convenience we use a previously-developed numerical code. Full details will be given elsewhere. However here we note that the 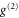 predicted by this calculation depends on the statistics of the input field, and on its brightness, through taking expectation values involving the field operator Sin in equation (B.2).
predicted by this calculation depends on the statistics of the input field, and on its brightness, through taking expectation values involving the field operator Sin in equation (B.2).
B.2. Monte-Carlo error propagation
We use a Monte-Carlo approach to generate the shaded error regions around the theoretical predictions plotted in figure 3 in the main text, and in figure B1 above. We computed the theory predictions 1000 times, with each input parameter drawn from a Gaussian distribution with a standard deviation set by its experimental uncertainty. For each value of Nin, the standard deviations of the predictions are then used to set the vertical width of the error regions in the plots. The errors δ on the various input parameters are estimated as follows:  ,
, 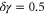 MHz,
MHz, 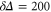 MHz,
MHz,  ps and
ps and 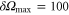 MHz.
MHz.
B.3. Effect of reduced anti-Stokes scattering
The undesired effects of FWM can be reduced by suppressing the strength of anti-Stokes scattering. To explore this theoretically, we consider the storage and retrieval of single photons with a range of values for the ratio of coupling strengths 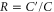 . As shown in figure 3(g), suppressing the anti-Stokes coupling by a factor of 2.5 is sufficient to observe non-classical statistics in the memory output time bin. If a suppression of 30 could be achieved, the output statistics would be as non-classical as those of the input, i.e. the noise would be dominated by the source, rather than the memory.
. As shown in figure 3(g), suppressing the anti-Stokes coupling by a factor of 2.5 is sufficient to observe non-classical statistics in the memory output time bin. If a suppression of 30 could be achieved, the output statistics would be as non-classical as those of the input, i.e. the noise would be dominated by the source, rather than the memory.
B.4. Incoherent  model
model
We alternatively model the combined photon statistics  as a superposition between FWM noise
as a superposition between FWM noise  and the input signal
and the input signal 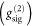 , whereby both fields are imagined to be combined on a beam-splitter. The expected value for
, whereby both fields are imagined to be combined on a beam-splitter. The expected value for 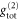 is derived following the argumentation presented in [46], yielding
is derived following the argumentation presented in [46], yielding

It depends on the number of signal photons, Nsig, and noise photons, Nnoise, per pulse contributing to the mixture. If the memory is on, Nsig represents the transmitted fraction of the signal, 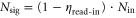 , in the read-in time bin and the retrieved fraction of the signal,
, in the read-in time bin and the retrieved fraction of the signal, 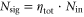 , in the read-out time bin. Nin is the respective input photon number,
, in the read-out time bin. Nin is the respective input photon number,  is the memory read-in efficiency and
is the memory read-in efficiency and 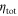 is the total memory efficiency (storage and retrieval). Figure B1
shows the results of equation (B.4) alongside the experimental data and the coherent
is the total memory efficiency (storage and retrieval). Figure B1
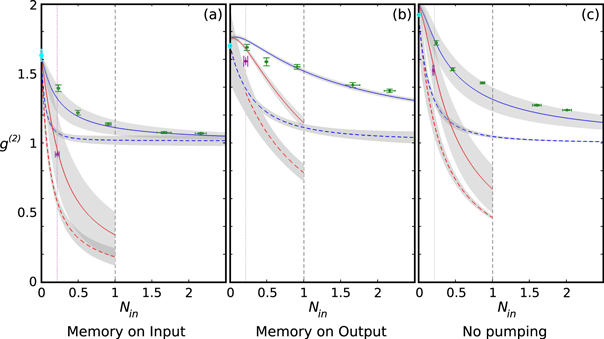
shows the results of equation (B.4) alongside the experimental data and the coherent  -model predictions. Clearly the incoherent model predictions significantly underestimate the measured
-model predictions. Clearly the incoherent model predictions significantly underestimate the measured  data in all three cases.
data in all three cases.
Figure B1. Photon statistics measurements.  -values expected from the incoherent model in equation (B.4) (dashed lines) versus the experimental data (points) and the coherent
-values expected from the incoherent model in equation (B.4) (dashed lines) versus the experimental data (points) and the coherent 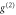 model prediction (solid lines), for (a) the fields transmitted through the memory at storage, (b) the fields retrieved from the memory at read-out, and (c) the fields transmitted through the memory when the optical pumping beam is blocked. Grey shaded regions denote errors derive from the experimentally measured errors on the variables in equation (B.4) and from propagating uncertainties in the experimental parameters through the coherent g2 model with a Monte-Carlo simulation. The remaining colour coding is equal to figure 3.
model prediction (solid lines), for (a) the fields transmitted through the memory at storage, (b) the fields retrieved from the memory at read-out, and (c) the fields transmitted through the memory when the optical pumping beam is blocked. Grey shaded regions denote errors derive from the experimentally measured errors on the variables in equation (B.4) and from propagating uncertainties in the experimental parameters through the coherent g2 model with a Monte-Carlo simulation. The remaining colour coding is equal to figure 3.
Download figure:
Standard image High-resolution imageNotably, if the photon statistics for the input signal during memory storage was not conserved, it would not be justified to use the input signal's 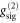 in equation (B.4) for calculating
in equation (B.4) for calculating 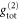 of the memory output. Instead, a modified
of the memory output. Instead, a modified 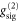 would be required, which is not directly accessible experimentally. This potential flaw is circumvented by also measuring
would be required, which is not directly accessible experimentally. This potential flaw is circumvented by also measuring 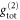 with the optical pumping switched off (figures 3(c) and B1(c)). Since there is no Raman storage, no modification of
with the optical pumping switched off (figures 3(c) and B1(c)). Since there is no Raman storage, no modification of 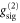 occurs. Moreover, Nsig corresponds directly to the input photon number
occurs. Moreover, Nsig corresponds directly to the input photon number 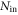 , without additional memory efficiency factors. Yet, equation(B.4) also fails to describe this situation, despite the fact that all variables are known by direct measurement. Hence we can reject this model and its associated implication. Consequently, both light fields cannot be considered as individual entities; i.e. describing the system requires to take the full dynamics between the Cs atoms and the input light fields into account.
, without additional memory efficiency factors. Yet, equation(B.4) also fails to describe this situation, despite the fact that all variables are known by direct measurement. Hence we can reject this model and its associated implication. Consequently, both light fields cannot be considered as individual entities; i.e. describing the system requires to take the full dynamics between the Cs atoms and the input light fields into account.