Abstract
A recent work (Björk and Shabbir 2014 New J. Phys. 16 013006) claims that nonmonotonic structures found in the many-particle quantum-to-classical transition (Ra et al 2013 Proc. Natl Acad. Sci. USA 110 1227–31; Tichy et al 2011 Phys. Rev. A 83 062111) are not exclusive to the many-body domain, but they also appear for single-photon as well as for semi-classical systems. We show that these situations, however, do not incorporate any quantum-to-classical transition, which makes the claims unsustainable.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recently, reference [1] reported on the nonmonotonic dependence of projection probabilities of quantum states, observed for a single-photon state and semiclassical states. Based on this observation, reference [1] argues that the nonmonotonic change of many-particle event probabilities observed in [2, 3] is 'not unnatural' and 'not a manifestation of a quantum-to-classical transition'. Here, we show that the situation considered in reference [1] is qualitatively different from the scenario in [2, 3], such that the conclusions of reference [1] cannot be sustained.
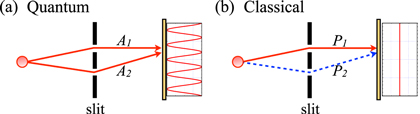
Let us first rigorously establish the quantum-to-classical transition considered in [2, 3]. In the quantum realm, event probabilities are determined by the sum of complex probability amplitudes of all processes leading to the event in question, figure 1(a): the probability amplitudes are added, and the absolute value of the sum is squared. In the classical realm, event probabilities are obtained by adding the probabilities of all disjoint processes leading to the event, see figure 1(b). Within the quantum regime, due to the interference of probability amplitudes, event probabilities oscillate as a function of the relative phases between the amplitudes. Such phase-dependence is absent in the classical realm.
Figure 1. The double-slit experiment with a single particle. In (a), interference is observed, which requires a quantum description: probability amplitudes A1 and A2 are added. On the contrary, in (b), no interference is observed, and a classical description is sufficient: probabilities P1 and P2 are added.
Download figure:
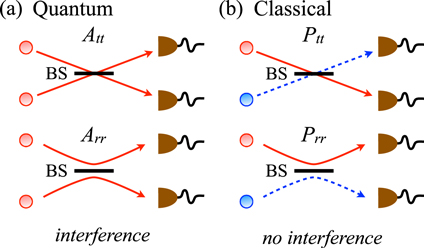
Standard image High-resolution imageThe situation sketched in figure 1 applies to both single- and many-particle interference. For example, in the two-particle experiment sketched in figure 2, two-particle amplitudes (Att and Arr) of two indistinguishable particles need to be added to infer the quantum mechanical coincidence event probability, while the sum of the probabilities Ptt and Prr matches the event probability in the classical realm. Similar to single-particle interference, many-particle interference can also exhibit phase-dependent oscillations when the relative phases between many-particle amplitudes are varied [3–5].
Figure 2. The Hong–Ou–Mandel experiment using a 50:50 beamsplitter (BS). Two-particle paths of both photons transmitted (upper panels) and both photons reflected (lower panels) (a) interfere in the quantum realm, but (b) they do not in the classical realm. Therefore, probability amplitudes Att and Arr are added in the former, but probabilities Ptt and Prr are added in the latter.
Download figure:
Standard image High-resolution imageThe transition to the classical regime is induced by lifting the indistinguishability of the processes that contribute to an event [6–8]. In particular, the detection of any distinctive property of such process (whether controlled by the experimentalist or uncontrolled by the environment) provides which-way information, hence renders different processes distinguishable, and leads to a reduced (if not completely suppressed) ability to interfere [9]. For a single particle that can take two slits to fall onto a screen, the observation of the path of the particle leads to the breakdown of the interference pattern; in close analogy, the path delay between identical particles controls the indistinguishability of the interfering processes (i.e. of the many-particle paths) [10]. We emphasize that, during such transition, acquiring which-path information does not change the amplitude of either path, but it solely affects the degree to which probabilities, instead of probability amplitudes, are added.
Intuitively, one may expect that the total event probability can always be written as

where α ![$\in \;[0;1]$](https://content.cld.iop.org/journals/1367-2630/16/11/118003/revision1/njp503948ieqn1.gif) suitably quantifies the degree of interference and mediates the transition from the event probability in quantum realm
suitably quantifies the degree of interference and mediates the transition from the event probability in quantum realm 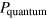 to that in classical realm
to that in classical realm 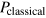 . Any dependence on the relative phase or other parameters is implicit in
. Any dependence on the relative phase or other parameters is implicit in 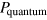 . This relation remains valid for one- or two-particle interference, in which only fully quantum and fully classical terms arise. Therefore, every observable that is monitored during the transition between the quantum and classical behavior of one or two particles features a monotonic dependence on the degree of coherence α. However, [2, 3] report that multi-particle event probabilities can be nonmonotonic, which rules out a generalization of the intuitive description inherent to equation (1). Instead of a purely classical and a purely quantum contribution, the probability for an N-particle event needs to be written as
. This relation remains valid for one- or two-particle interference, in which only fully quantum and fully classical terms arise. Therefore, every observable that is monitored during the transition between the quantum and classical behavior of one or two particles features a monotonic dependence on the degree of coherence α. However, [2, 3] report that multi-particle event probabilities can be nonmonotonic, which rules out a generalization of the intuitive description inherent to equation (1). Instead of a purely classical and a purely quantum contribution, the probability for an N-particle event needs to be written as

where d is the number of particles that interfere, and 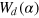 and Pd are the corresponding weight and the associated event probability, respectively. The case d = 0 can be identified with the classical, d = N with the quantum realm. Since the probabilities Pd do not obey any ordering (in general, neither
and Pd are the corresponding weight and the associated event probability, respectively. The case d = 0 can be identified with the classical, d = N with the quantum realm. Since the probabilities Pd do not obey any ordering (in general, neither 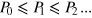 , nor
, nor 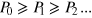 ), the event probability described by equation (2) is, in general, more involved than one described by equation (1). In particular, it can be nonmonotonic in α.
), the event probability described by equation (2) is, in general, more involved than one described by equation (1). In particular, it can be nonmonotonic in α.
An exception of this general behavior is described in [2]: A bunched final event with all particles in one mode can be reached by one many-particle path only, leaving no place for any phase-dependent interference. The enhancement of such events purely relies on bosonic bunching, and not on the interference of different physical processes. Since no amplitudes with different phases appear, greater indistinguishability always leads to an enhancement of such events and to 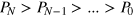 , which implies a monotonic transition. Most importantly, this enhancement does not 'fortuitously turn [..] out to be monotonic' as stated in reference [1], but the absence of different many-particle paths forces every transition to a bunched final state of the form
, which implies a monotonic transition. Most importantly, this enhancement does not 'fortuitously turn [..] out to be monotonic' as stated in reference [1], but the absence of different many-particle paths forces every transition to a bunched final state of the form 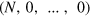 to be monotonic.
to be monotonic.
In contrast to the hitherto established scenario, the examples put forward in reference [1] do not mediate a quantum-to-classical transition. The transition given in reference [1] interpolates from a pure state to another pure state, without loss of interference capability at any stage. Let us take equation (8) in reference [1] as an example,
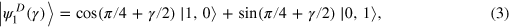
where 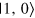 (
(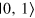 ) denotes a horizontally (vertically) polarized single-photon state, and γ changes from 0 to
) denotes a horizontally (vertically) polarized single-photon state, and γ changes from 0 to 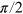 , inducing a transition of the state from
, inducing a transition of the state from 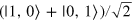 to
to 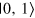 . The state is projected onto
. The state is projected onto 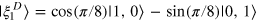 , resulting in the projection probability
, resulting in the projection probability 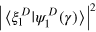 , which is nonmonotonic as a function of γ. However, this transition cannot be identified as a quantum-to-classical transition by any means; it neither includes a transition to a mixed state nor does it involve any which-path information that degrades interference capability. The nonmonotonicity exhibited by the other examples in reference [1] (figures 3 and 5 therein) has the same origin, none of these examples is related to the quantum-to-classical transition.
, which is nonmonotonic as a function of γ. However, this transition cannot be identified as a quantum-to-classical transition by any means; it neither includes a transition to a mixed state nor does it involve any which-path information that degrades interference capability. The nonmonotonicity exhibited by the other examples in reference [1] (figures 3 and 5 therein) has the same origin, none of these examples is related to the quantum-to-classical transition.
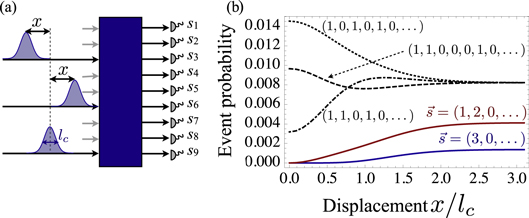
Figure 3. Nonmonotonicity in three-fermion interference. (a) Fermions of coherence length lc are prepared in the state 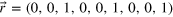 , i.e. only the third, the sixth, and the last input modes are populated. The particles are delayed by a displacement x with respect to each other and scatter off a 9-mode Fourier-multiport, for which every single-particle probability is
, i.e. only the third, the sixth, and the last input modes are populated. The particles are delayed by a displacement x with respect to each other and scatter off a 9-mode Fourier-multiport, for which every single-particle probability is 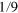 [13]. The number of particles in each output mode, represented as
[13]. The number of particles in each output mode, represented as 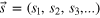 , is measured. (b) Probabilities for different final events. For
, is measured. (b) Probabilities for different final events. For 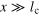 , the particles can be treated as distinguishable, and the event probabilities can be obtained by combinatorics, i.e.
, the particles can be treated as distinguishable, and the event probabilities can be obtained by combinatorics, i.e. 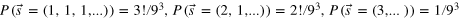 . When the displacement is reduced, the quantum realm is attained. The event probabilities for
. When the displacement is reduced, the quantum realm is attained. The event probabilities for 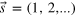 (red solid) and
(red solid) and 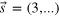 (blue solid) decay monotonically with increasing interference capability and eventually vanish for x = 0. The events allowed by the Pauli principle (black dashed, dotted and dash-dotted lines) can evolve in a nonmonotonic fashion, in close analogy to the effects observed in [2]. The event probabilities are computed in direct analogy to the methods developed in [2, 3], taking into account the anti-commutativity of fermionic creation operators.
(blue solid) decay monotonically with increasing interference capability and eventually vanish for x = 0. The events allowed by the Pauli principle (black dashed, dotted and dash-dotted lines) can evolve in a nonmonotonic fashion, in close analogy to the effects observed in [2]. The event probabilities are computed in direct analogy to the methods developed in [2, 3], taking into account the anti-commutativity of fermionic creation operators.
Download figure:
Standard image High-resolution imageIn reference [1], γ is claimed to vary 'distinguishability', but that 'distinguishability' is used in a different sense compared with the generally accepted usage. Distinguishability is generally used to indicate the distinguishability of different processes (e.g. different paths of particles), i.e. distinguishability degrades interference [9–12]. On the other hand, the 'distinguishability' in reference [1] affects the overlap of the state 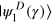 with an unbiased (in terms of its basis
with an unbiased (in terms of its basis 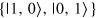 ) state
) state 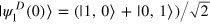 , i.e. it governs the magnitude of
, i.e. it governs the magnitude of 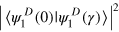 . Therefore, while general distinguishability adjusts the degree to which probabilities instead of probability amplitudes are added, the 'distinguishability' in reference [1] changes the very probabilities themselves: in equation (3), γ defines the probability to populate the horizontal and the vertical modes. Formally, γ varies the predictability [9], i.e. the capability to predict in which mode the particle resides, rather than the degree of interference between different modes. As a result, the 'distinguishability' in reference [1] does not mediate the quantum-to-classical transition. If the degree of interference is varied, a monotonic rather than a nonmonotonic probability transition emerges, evident from equation (14) of reference [1].
. Therefore, while general distinguishability adjusts the degree to which probabilities instead of probability amplitudes are added, the 'distinguishability' in reference [1] changes the very probabilities themselves: in equation (3), γ defines the probability to populate the horizontal and the vertical modes. Formally, γ varies the predictability [9], i.e. the capability to predict in which mode the particle resides, rather than the degree of interference between different modes. As a result, the 'distinguishability' in reference [1] does not mediate the quantum-to-classical transition. If the degree of interference is varied, a monotonic rather than a nonmonotonic probability transition emerges, evident from equation (14) of reference [1].
In contrast to the statements regarding fermions in reference [1], many fermions can interfere collectively in a non-trivial way beyond Pauli exclusion effects: As soon as the number of available modes is larger than the number of particles, fermions can collectively interfere just as bosons do [4, 13]. In particular, many-fermion interference is governed by the very same principles as many-boson interference [13]. As a consequence, many-fermion signals can exhibit nonmonotonic features just like many-boson signals, as evident from figure 3, which shows the probabilities of exemplary events for three interfering fermions of varying distinguishability in a 9-mode Fourier-multiport. The experimental observation of such fermionic nonmonotonicity is admittedly challenging, but recent developments in the simulation of fermions via entangled photons [14] or the interference of electrons [12] feed the hope that such experiments become feasible in future.
In conclusion, we have shown that the criticism in reference [1] on [2, 3] is inappropriate. In the first place, references [2, 3] do not claim that a nonmonotonically evolving probability should always be regarded as a signature for the quantum-to-classical transition. Instead, references [2, 3] report that, in the multi-particle quantum-to-classical transition, probabilities are typically nonmonotonic, which we generalized here for fermions in figure 3. The examples presented in reference [1] cannot be regarded as quantum-to-classical transitions by any means, and the nonmonotonic probabilities in reference [1] are not rooted in the quantum-to-classical transition, but in a unitary evolution of pure quantum states.
Acknowledgments
We thank Gunnar Björk and Saroosh Shabbir for usuful discussions. This work was supported in part by the National Research Foundation of Korea (grant no. 2013R1A2A1A01006029 and 2011-0021452). H-TL acknowledges support from the National Junior Research Fellowship (grant no. 2012–000642). AB acknowledges partial support through the COST Action MP1006 'Fundamental Problems in Quantum Physics', and by DFG. MCT would like to thank the Danish Council for Independent Research.