Abstract
Quantum phase transitions (QPTs) describe when a many-body quantum system displays non-analytic behavior associated with a discontinuous change in a property of the ground state as a parameter is varied. The QPT in prototypical Dicke model is difficult to reach experimentally as the spin–field coupling strength must be quite large. In this work we describe a new model—the off-resonant Tavis–Cummings model where we drive the common mode, and discover a new type of QPT at quite low coupling strengths which are comparable with the geometric mean of the atomic and field detunings  . Through analytic methods we demonstrate this QPT for both finite and infinite numbers of spins and show that |〈Jx(Jz)〉|/(N/2) ∼ |λ/λc − 1|γx(γz) and 〈a†a〉/N ∼ |λ/λc − 1|γa for λ ⩾ λc, with critical exponents γx ≈ 1/2, γz ≈ 1 and γa ≈ 1. We show that this QPT can be immediately observed by laboratory cavity-QED setups such as Bose–Einstein condensate in optical cavity and superconducting circuit-QED as well as a line of trapped ultracold ions.
. Through analytic methods we demonstrate this QPT for both finite and infinite numbers of spins and show that |〈Jx(Jz)〉|/(N/2) ∼ |λ/λc − 1|γx(γz) and 〈a†a〉/N ∼ |λ/λc − 1|γa for λ ⩾ λc, with critical exponents γx ≈ 1/2, γz ≈ 1 and γa ≈ 1. We show that this QPT can be immediately observed by laboratory cavity-QED setups such as Bose–Einstein condensate in optical cavity and superconducting circuit-QED as well as a line of trapped ultracold ions.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The quantum emulation/simulation of many-body collective effects offers the possibility of using quantum simulators to gain new insights into numerous fascinating phenomena in nature. One of the most intriguing of these is the quantum phase transition (QPT), where the ground state of a many-body interacting quantum state displays non-analytic behavior as some parameter is varied [1]. Recently, there has been a lot of work done toward developing quantum simulators [2–7], and observing QPTs [8–11], but the latter goal is made very challenging as the coupling strengths required to exhibit traditional examples of QPTs, such as the Dicke model [12], are typically very large. So far only a few setups, e.g. superconducting circuit-QED and cavity-QED with Bose–Einstein condensates (BECs) have the strength of coupling to begin to explore the Dicke phase transition. It is therefore highly desirable to find other examples of QPTs which occur at lower coupling strengths, and, if possible, via a full analytic solution. Below we will demonstrate such a new class of QPTs using the driven Tavis–Cummings (TC) model and describe how it can be realized in a variety of setups.
The TC model describes the collective interaction of many spins with a single-mode bosonic field under the rotating wave approximation [13]. Although it seems a straightforward extension of the Jaynes–Cummings (JC) model [14], the TC model exhibits a wide variety of interesting phenomena such as spin squeezing and multi-photon transitions [15, 16] and has been widely employed to study many-body quantum systems, e.g. in multi-atom cavity-QED or quantum dots (many nuclear spins coupled to a common electronic wave function) [17], in trapped-ion systems [18], in coupled cavity-QED systems ('solid light') [19] and in superconducting systems [20]. QPTs are special phenomena associated with many-body quantum systems with the most famous examples being the Dicke model [12, 21–24], and the spin–boson model [25–27]. More precisely, a QPT is associated with a significant change in the ground state of a quantum system at zero temperature with a change in some system parameter [1]. In the strong coupling case of the Dicke model, the QPT occurs around the critical point  of the spin–field coupling with ωa/c the resonance frequencies of the two-level atoms/cavity. The undriven TC model also has a phase transition at the same critical coupling as the Dicke model [28], but reaching such large coupling strengths is very challenging experimentally. We show below that a new QPT appears in the TC model at much weaker couplings if detunings and driving are introduced.
of the spin–field coupling with ωa/c the resonance frequencies of the two-level atoms/cavity. The undriven TC model also has a phase transition at the same critical coupling as the Dicke model [28], but reaching such large coupling strengths is very challenging experimentally. We show below that a new QPT appears in the TC model at much weaker couplings if detunings and driving are introduced.
2. The driven Tavis–Cummings model and the solution
The case of the driven on-resonance TC model was initially investigated semiclassically to explore a QPT in an array of trapped ions [29] (here Δa = Δc = 0, vanishing detunings of the atomic/cavity with respect to the frequency of the driving field). To see why we expect a drastic change in the driven case one can return to the JC model and recall that the ladder of splittings,  (with g the light–matter coupling), suffers a uniform narrowing when the mode (or atoms) is driven with a strength
(with g the light–matter coupling), suffers a uniform narrowing when the mode (or atoms) is driven with a strength  , giving
, giving ![$\Delta E_n\rightarrow \Delta E_n\times [1-(2{\cal E}/g)^2]^{3/4}$](https://content.cld.iop.org/journals/1367-2630/15/12/123032/revision1/nj484892ieqn5.gif) [30, 31], and this effect is just evident in recent circuit-QED experiments (figure 3(b) of [32]). As the driving strength increases then at the value
[30, 31], and this effect is just evident in recent circuit-QED experiments (figure 3(b) of [32]). As the driving strength increases then at the value  , the nonlinear character of JC model vanishes and the system undergoes a drastic change in behavior. Different from [29], we study the off-resonant TC model under a linear driving of either the field or spins. Our analysis is not applicable when the detunings vanish but in the detuned case we find the onset of a QPT when the spin–boson coupling strength reaches
, the nonlinear character of JC model vanishes and the system undergoes a drastic change in behavior. Different from [29], we study the off-resonant TC model under a linear driving of either the field or spins. Our analysis is not applicable when the detunings vanish but in the detuned case we find the onset of a QPT when the spin–boson coupling strength reaches  with Δa (Δc) being the detunings between the driving field and atomic (cavity) transition frequencies ωa(ωc). We solve this model fully quantum mechanically, and present a QPT occurring with different numbers of spins, different driving frequencies and strengths. In [29] the scaled ground-state moment |〈Jx〉| behaves in a discontinuous way around the critical point. In our fully quantum mechanical treatment we can extend this analysis to explore the underlying physics behind our QPT, such as the avoided-crossings with the ground state in the system's eigenspectrum or changes in a symmetry or near symmetry in the ground state due to introduction of the driving.
with Δa (Δc) being the detunings between the driving field and atomic (cavity) transition frequencies ωa(ωc). We solve this model fully quantum mechanically, and present a QPT occurring with different numbers of spins, different driving frequencies and strengths. In [29] the scaled ground-state moment |〈Jx〉| behaves in a discontinuous way around the critical point. In our fully quantum mechanical treatment we can extend this analysis to explore the underlying physics behind our QPT, such as the avoided-crossings with the ground state in the system's eigenspectrum or changes in a symmetry or near symmetry in the ground state due to introduction of the driving.
We consider a driven TC model in units of ℏ = 1,  where ωa (ωc) is the resonance frequencies of the identical spins (bosonic field mode), the latter with raising (lowering) operators a† (a), σ±,j,σz,j are the jth spin Pauli operators, λ is the coupling strength between the spins and the bosonic field and Ω(ω) is the strength (frequency) of the driving applied to the bosonic field. In the driving field's rotating frame the Hamiltonian is
where ωa (ωc) is the resonance frequencies of the identical spins (bosonic field mode), the latter with raising (lowering) operators a† (a), σ±,j,σz,j are the jth spin Pauli operators, λ is the coupling strength between the spins and the bosonic field and Ω(ω) is the strength (frequency) of the driving applied to the bosonic field. In the driving field's rotating frame the Hamiltonian is
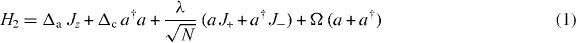
with detunings Δa = ωa − ω, Δc = ωc − ω and collective spin operators  (a = z,+,−). If Δa = Δc = 0, equation (1) is reduced to the resonance case considered in [29]. Our fully quantum mechanical treatment is based on the displaced Fock state method [33], where we obtain a precise approximation to the eigenstates of equation (1) based on an expansion in terms of displaced Fock states. We will investigate the QPT via the moments {〈Jx〉, 〈Jz〉}/(N/2) by varying the coupling, the driving, the detunings and the number of the spins.
(a = z,+,−). If Δa = Δc = 0, equation (1) is reduced to the resonance case considered in [29]. Our fully quantum mechanical treatment is based on the displaced Fock state method [33], where we obtain a precise approximation to the eigenstates of equation (1) based on an expansion in terms of displaced Fock states. We will investigate the QPT via the moments {〈Jx〉, 〈Jz〉}/(N/2) by varying the coupling, the driving, the detunings and the number of the spins.
To solve equation (1), we absorb the linear driving term by moving to a displaced frame generated by A = D†(α) a D(α) where D(α) = eαa† − α*a is a displacement operator with α = Ω/Δc. In this frame H2 becomes
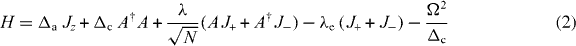
with the effective driving  . From equations (1) and (2) the two situations of either driving the field or the spins are unitarily identical. We note however, due to the presence of Δc in the denominator of α, equation (2) cannot represent the resonant case studied previously in [29]. We now make the following ansatz for the eigenstates of H as
. From equations (1) and (2) the two situations of either driving the field or the spins are unitarily identical. We note however, due to the presence of Δc in the denominator of α, equation (2) cannot represent the resonant case studied previously in [29]. We now make the following ansatz for the eigenstates of H as  , where
, where  [33], are displaced Fock states where |0〉A is the vacuum state of A, and the collective spin states satisfy Jz|j,m〉 = m|j,m〉,
[33], are displaced Fock states where |0〉A is the vacuum state of A, and the collective spin states satisfy Jz|j,m〉 = m|j,m〉,  , with
, with  m = −j, −j + 1, ..., j − 1, j. Using these properties we examine the time-independent Schrödinger equation to obtain the following recurrence relation for Cn,m which only converges when E is an eigenenergy of H:
m = −j, −j + 1, ..., j − 1, j. Using these properties we examine the time-independent Schrödinger equation to obtain the following recurrence relation for Cn,m which only converges when E is an eigenenergy of H:
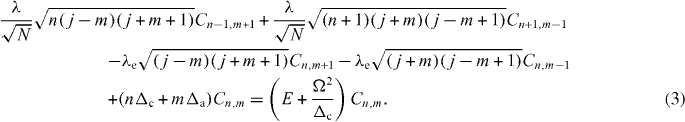
We numerically solve equation (3), for the values of E that yield convergent solutions for Cn,m, truncating the displaced Fock basis to be 0 ⩽ n ⩽ n*, where n* is determined by |〈Jz(n*)〉 − 〈Jz(n* + 10)〉|/(N/2) < 10−8 and 〈a†a(n*)〉 − 〈a†a(n* + 10)〉|/N < 10−8.
3. Properties of the ground state
We first study the ground state properties when one varies the coupling and the driving strengths {λ,Ω}, for a fixed number of spins, N = 8, and set the two detunings to be Δa/Δc = 1 (for other values of Δa/Δc there are changes in the results but without changes in physical essence for the problem under consideration). As shown in figure 1, the moments {〈Jx〉,〈Jz〉}/(N/2) display sharp changes around the critical point λ/λc = 1, when the driving is weak (solid curves), which shows the trend toward a QPT in the thermodynamic limit. It is very similar to the normal-superradiant phase transition in the Dicke model [34–36]. Below the critical coupling (the normal phase), the ground state of the Dicke model has vacuum in the cavity and the atoms all in the ground state. When excited into a superradiant state in this normal phase one obtains a collective, or polariton, state where the atomic excitation is hybridized with the optical excitation. However this is an excited state of the coupled system in the normal phase. If the matter–field coupling is larger than the critical coupling (superradiant phase), then the ground state (which was previously only of atomic character), now becomes a polaritonic hybrid atomic-field excitation which is stable. Despite some differences from the Dicke model (discussed later), we may also call the phases below and above λc in our driven detuned TC system as the normal phase and the superradiant phase, respectively. Before we go to the thermodynamic limit, we plot out the lowest few eigenenergies of the model in figure 2, and observe that the critical point λc in figure 1 corresponds to an avoided-crossing with the ground state. Moreover, in the case of weak driving, the moments 〈Jx〉 and 〈Jz〉 exhibit, respectively, multiple-peak and staircase like behavior. To understand this result, we solve equation (3) for Ω = 0 in the supplementary material (available from stacks.iop.org/NJP/15/123032/mmedia), with a large truncation Ntr and find a digital staircase change in the moment 〈Jz〉, where the step height reduces for larger λ/λc > 1, while we observe 〈Jx〉 to be always zero. This behavior is intimately related to a symmetry and associated conserved quantity whose value in the ground state changes by an integer amount which we discuss later below.
Figure 1. The scaled moments as functions of λ/λc with (a) 〈Jx〉/(N/2) and (b) 〈Jz〉/(N/2), where λc is the critical point for the QPT. The parameters are N = 8, Δa/Δc = 1, for Ω/λc = 100 (purple dashed-dotted), 10−1 (green dashed), 10−2 (red solid) and 10−3 (blue solid). The peaks (blue—weak driving) in (a) and the stairs in (b) from the left to right correspond to approximately integer increases in the almost conserved quantity L.
Download figure:
Standard image High-resolution imageFigure 2. Energy spectra for the two lowest eigenstates and the fidelity susceptibility SF as functions of λ/λc with (a) Ω/λc = 10−2 and (b) Ω/λc = 10−3 for E0 (blue line), E1 (green line) and SF (red line). The eigenenergies are calculated numerically by equation (3).
Download figure:
Standard image High-resolution imageIt is known that there are level crossings of the ground state with excited states in the standard TC model, which bring about changes in a conserved quantity. In our case, for equation (1) without the driving term (denoted by H'), we observe that the level operator L = a†a + Jz + N/2 is conserved and satisfies [H',L] = 0. In addition, in the undriven TC model the parity Π ≡ eiπL is also conserved. The eigenstates of H' are thereby eigenstates of the parity Π and level operator L. The parity operator Π has two eigenvalues ±1, depending on whether the eigenvalue of the level operator is even or odd. As shown in the supplementary material (available from stacks.iop.org/NJP/15/123032/mmedia), the ground state of the system H' can be of either even or odd parity, depending on the coupling strength λ, and the parity of the ground state changes abruptly at each consecutive level crossing. As a result, in the absence of driving, the ground-state moment 〈Jx〉 should be always zero because the operator Jx only induces the transition between different parity states, whereas 〈Jz〉 remains non-zero since the operator Jz does not change the parity of the ground-state wavefunction. With the introduction of the driving, however, the level crossings turn into level avoided-crossings, as shown in figure 2, which also means that both the parity and the level constant as exact conserved quantities break down, e.g. [H,Π] ≠ 0. This is different from in the Dicke model, in which the parity is conserved in the normal phase. This point is also reflected by the fidelity susceptibility [37] defined as ![$S_{\mathrm { F}}(\lambda )=\sum _{n\neq 0} \frac {|\langle \phi _{n}(\lambda )|H_{\lambda }|\phi _{0}(\lambda )\rangle |^{2}}{[E_{n}(\lambda )-E_{0}({\lambda })]^{2}},$](https://content.cld.iop.org/journals/1367-2630/15/12/123032/revision1/nj484892ieqn15.gif) where we rewrite equation (2) as H = H" + λHλ by resorting the terms related to λ as Hλ, |ϕk〉 and Ek are kth eigenstates and the corresponding eigenenergy of H. So SF presents the response of fidelity to a small change in the spin–field interaction [37], connected quantitatively to the case of level avoided-crossing. In the case when there is a level avoided-crossing then one can find the discontinuous change of SF in the ground state properties is related to the QPT features we observe [38]. We see in figure 2 that the first peak of SF actually corresponds to the critical point λc in figure 1.
where we rewrite equation (2) as H = H" + λHλ by resorting the terms related to λ as Hλ, |ϕk〉 and Ek are kth eigenstates and the corresponding eigenenergy of H. So SF presents the response of fidelity to a small change in the spin–field interaction [37], connected quantitatively to the case of level avoided-crossing. In the case when there is a level avoided-crossing then one can find the discontinuous change of SF in the ground state properties is related to the QPT features we observe [38]. We see in figure 2 that the first peak of SF actually corresponds to the critical point λc in figure 1.
4. Quantum phase transition toward thermodynamical limit
Strictly speaking, QPT happens only in the thermodynamic limit. So to show a strict QPT we should extend our study to infinite numbers of spins. By fixing the driving strength and the ratio between the two detunings, we have calculated the variation of the moments with respect to the coupling for different numbers of spins. As shown in figure 3, with increasing numbers of spins N, the cusp-like behavior becomes more and more evident around the critical point. When λ/λc < 1, the moments {〈Jx〉,〈Jz〉}/(N/2) stay almost at their minimum values (0 and −1) when N → ∞. But for λ/λc > 1, the moments arise quickly. The limiting case of N → ∞ is calculated analytically in the thermodynamic limit (see the supplementary material), and here we observe a sharp cusp in the moments, i.e. a QPT around the critical point λc and find that the moments have the behaviors {〈Jx〉,〈Jz〉}/(N/2) ∼ {|λ/λc − 1|γx,|λ/λc − 1|γz} for λ ⩾ λc, with γx = 1/2 and γz = 1. In addition, the QPT can also be observed in other order parameters, such as the mean number of excitations in the bosonic mode. We find in figure 3(c) 〈a†a〉/(N) ∼ |λ/λc − 1|γa for λ ⩾ λc with γa = 1.
Figure 3. The scaled moments and the bosonic number as functions of λ/λc, with (a) for 〈Jx〉/(N/2), (b) for 〈Jz〉/(N/2) and (c) for 〈a†a〉/N, where we consider N = 21 (blue solid), 22 (purple dashed-dotted), 23 (green dot), 24 (red dashed) and ∞ (black solid: analytic). Other parameters are chosen as Ω/λc = 10−1 and Δa/Δc = 1.
Download figure:
Standard image High-resolution imageAs demonstrated above, the critical point λ/λc = 1, corresponds strictly to the first level avoided-crossing with the ground state. The physics behind the level avoided-crossing relates to the breaking of parity and level constants. With the introduction of the driving, we may consider the modified level operator L' = A†A + Jz + N/2 and the parity operator Π' = eiπL' , both of which now do not commute with H. The cusp-like behaviors occur at very small values of Ω, implying the QPT occurs when Ω changes from vanishing to non-vanishing. In the case of finite numbers of spins, as we increase Ω, the trend toward a QPT (as evidenced by the collective spin moments), disappears gradually (see the dashed and dashed-dotted curves in figure 1). To check this point more carefully we consider the change of the driving from negative to positive, which is achieved by altering the phase of the driving from π to zero. As plotted in figure 4, if λ/λc is small e.g. 10−3 or 10−1, {〈Jx〉,〈Jz〉}/(N/2) = {0,−1}, and remain almost unchanged as the driving strength is increased. For larger couplings, e.g λ/λc ∼ 1,2, a sharp (non-analytic) change takes place around Ω = 0, signaling the presence of QPTs. Since the ground state of the TC model with Ω = 0 is of even or odd parity, these sharp changes from −|Ω| to 0 and then to |Ω| characterize regions where the parity/level operators are bad/good/bad quantum numbers for the model. On the other hand, the curves in figure 4 present the QPTs from another angle to show the normal (superradiant) phase for λ < λc (λ > λc).
Figure 4. The scaled moments as functions of Ω/λc, with (a) for 〈Jx〉/(N/2) and (b) for 〈Jz〉/(N/2), where we consider the cases λ/λc = 10−3 (blue solid), 10−1 (red dot), 1 (green solid) and 2 (purple solid). We take N = 2 and Δa/Δc = 1 as an example. Similar curves for N > 2 and for other values of Δa/Δc.
Download figure:
Standard image High-resolution imageTo clarify, to observe the QPT for an intermediate spin–field coupling, we list below the essential conditions on the characteristic parameters:
- (i)
 ;
; - (ii)0 < Ω ≪ λ;
- (iii)N ⩾ 2,
where condition (i) is the restriction on the driving frequency ω, (ii) conditions the driving strength Ω and (iii) describes the least number of the spins which can demonstrate the effect. Larger numbers of spins provide a clearer demonstration of the cusp-like variation in the QPT. We mention again that the QPT originates from the parity breaking due to the introduction of driving and condition (ii) ensures that the spin–field coupling plays the dominant role in the process of the QPT.
5. Experimental feasibility
The QPT outlined above can be immediately realized experimentally in cavity-QED systems, such as a BEC confined in an optical cavity [8, 9, 39], and using an array of qubits in circuit-QED [20, 40]. The Dicke QPT has been observed experimentally in a system containing a BEC with 105 57Rb atoms coupled to an optical Fabry–Perot cavity [8]. By tuning down the spin–field coupling (so that the Dicke model is reduced to the TC model), and applying a driving on the cavity mode, we may observe the QPT studied in the present letter by detecting the leaking photons from the cavity using a heterodyne detection. The identical and homogeneous spin–field coupling is due to the BEC being deeply within the Lamb–Dicke regime and the scaling depends on the number of atoms in the BEC.
On the other hand, the undriven TC model has been demonstrated experimentally in position-fixed, superconducting, transmon qubits coupled to a transmission line resonator [20]. With driving applied on the mode of the resonator, our QPT can be observed from the transmission spectrum. Since the qubits are static and fully controlled, near identical spin–light coupling is possible.
Moreover, equation (1) can be also simulated by a line of trapped ultracold ions under laser irradiation at the first red-sideband and by either driving (slightly detuned) the center of mass motion or the collective internal states. A string of N-ions (40Ca+) under the irradiation of 729 nm laser and cooled down to the vibrational ground state can be deeply within the Lamb–Dicke regime with Lamb–Dicke parameter  . We have noticed that good entanglement involving eight 40Ca+ ions with uniform coupling has been experimentally demonstrated [41, 42]. As a result, the QPT in our case can be observed from 〈Jz(x)〉 by changing the phase of the driving or by varying the strengths of the coupling.
. We have noticed that good entanglement involving eight 40Ca+ ions with uniform coupling has been experimentally demonstrated [41, 42]. As a result, the QPT in our case can be observed from 〈Jz(x)〉 by changing the phase of the driving or by varying the strengths of the coupling.
6. Conclusion
In a real light–matter interaction, there should be an A2 term in addition to the conventionally considered JC or Rabi coupling. Although it is much smaller than the JC or Rabi coupling term, the A2 term can forbid the QPT in the Dicke model due to the restriction from the Thomas–Reiche–Kuhn (TRK) sum rule, which is called a 'no-go' theorem [43–45]. This no-go theorem can be circumvented in non-equilibrium situations such as our driven system and the sideband-driven system of [11]. This extra small quadratic term Hdiamag = κ(a + a†)2, forbids a QPT in the case when Ω = 0 (no driving), but for strong diving this term reduces to a small shift in Δc in equation (1), following the rotating wave approximation and a QPT is allowed as the TRK sum rule is no longer violated. Furthermore, we have excluded decoherence from our considerations above, implying that evidence for the QPT should be acquired much faster than the decay rates of the physical system. This requirement has been satisfied with currently available technology [8, 20, 41, 42]. On the other hand, although decoherence always exists in the realistic system, if the decoherence is not strong, we may treat the detrimental influence as a perturbation within a master equation. As noted in [45], in the case of a driven system then the master equation in the rotating frame can lead to weak excitation of the system which can be neglected if the system–bath coupling is much smaller than the strength of the drive. The QPT demonstrated above will still occur but will be modified by the small decoherence effects. The detailed discussion of environmental influence on the QPT is interesting, but beyond the scope of this work.
In summary, we have made a fully quantum mechanical treatment for the driven TC model using the displaced Fock state technique. We have shown that a QPT occurs when the driving is detuned from both the atoms and common mode and that the QPT occurs near the first avoided crossing of the system's ground state which are associated with the breaking of the parity and level symmetries in the ground state. Although we have only considered the ideal case, our treatment and the main results still hold under some realistic conditions, such as weak atomic spontaneous emission and weak cavity dissipation. But our treatment does not work if there is a magnetic field gradient or a position-dependent coupling, and our main results will largely change for strong decay cases. Anyway, the phenomena studied above can be demonstrated in various systems using current laboratory techniques.
Acknowledgments
This work was supported by National Fundamental Research Program of China (grant numbers 2012CB922102 and 2013CB921803), National Natural Science Foundation of China (grant numbers 11274352, 11147153, 11274351 and 11004226) and the ARC Centre of Excellence in Engineered Quantum Systems CE110001013.







