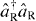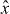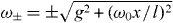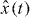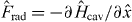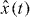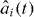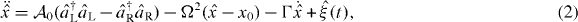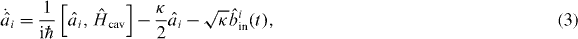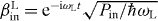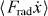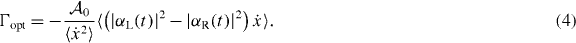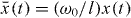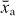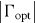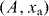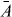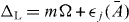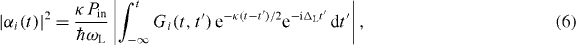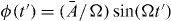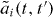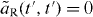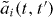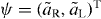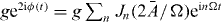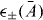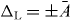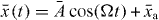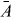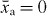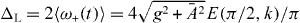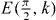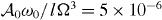The effect of Landau–Zener dynamics on phonon lasing

The exploration of nanomechanical objects and their interaction with light constitutes the rapidly evolving field of optomechanics (see [1, 2] for recent reviews). The key element of any optomechanical system is a laser-driven optical mode whose resonance frequency shifts in response to the displacement of a mechanical object. The photon dynamics conversely acts back on the mechanics in terms of a radiation pressure force. These dynamical back-action effects, mediated by the light field, can cool or amplify mechanical motion, and even drive the system into a regime of self-induced mechanical oscillations [3–10] akin to lasing. This regime (called 'phonon lasing', 'parametric instability' or 'self-induced oscillations') constitutes the most basic nonlinear effect in optomechanical systems. Thus, its exploration is of considerable importance for several reasons. Not only is it important to map out the instabilities of any optomechanical system, but it has also been shown that the nonlinear dynamics can be exploited for applications and fundamental research. For example, it may improve the measurement sensitivity for small forces [7], and in the deep quantum regime the nonlinear dynamics can generate nonclassical mechanical quantum states [11]. In addition, nonlinear dynamics in optomechanical systems may also be exploited for synchronization of mechanical oscillations [12–14].

An exciting new recent development has introduced optomechanical setups with multiple coupled optical and vibrational modes. For example, two optical and one mechanical mode (the system to be investigated in the present manuscript) have by now been coupled in several different experimental setups: (i) inside an optical cavity with a membrane in the middle [15–17], (ii) in the case of two microtoroids [18] and (iii) in a microsphere with whispering gallery modes [19]. These systems allow one to realize sophisticated measurement schemes such as quantum-nondemolition measurements of phonon number [16, 17] or enhanced position readout [20], novel cooling schemes like 'Brillouin cooling' with scattering between the two optical modes [19] and they can also show phonon lasing behaviour [18]. In addition, the two-mode setup to be investigated here could be used to mechanically drive nontrivial coherent photon dynamics between the two modes [21, 22], or to enhance quantum nonlinearities and thus observe nonlinear effects even on the level of single photons and phonons [23, 24].

Other novel multimode setups feature two mechanical modes coupled to a single optical mode, where optomechanical synchronization of mechanical self-induced oscillations has been studied recently [13, 14]. It is to be expected that the near future will see a largely increasing variety of optomechanical multimode setups, not least due to the powerful platform of optomechanical crystals [25–29], where optical and vibrational defect modes in photonic/phononic crystal structures may get coupled. These and similar setups [30, 31] have stimulated prospects of integrated optomechanical circuits. Ultimately, this could lead to optomechanical arrays, i.e. arrangements of many such coupled modes. These are currently inspiring a range of theoretical proposals, such as slow light [32], quantum information processing [33], synchronization of mechanical oscillations in arrays [12] and various versions of quantum many-body physics of photons and phonons [34–36].

Given the impact of nonlinear dynamics on applications of optomechanical systems, as well as the recent surge in multimode optomechanical platforms, it seems timely to ask about the simplest of all nonlinear optomechanical effects (i.e. self-induced oscillations) in the context of multimode setups. This will be the subject of the present paper.

As pointed out above, phonon lasing for an optomechanical setup involving a tunable optical two-mode system has already been demonstrated experimentally [18]. Hence, implementing a nanomechanical analogue of a laser (as originally envisioned in a slightly different setting [37]) has finally been achieved. Here, we develop the fully nonlinear theory of phonon lasing (self-induced mechanical oscillations) in such multimode optomechanical setups. 'Nonlinear' here implies that we are able to treat not only the onset of oscillations in the small amplitude regime, but cover the highly nonlinear dynamics at arbitrary amplitudes. In particular, we will point out that the mechanical oscillations may induce Landau–Zener (LZ) physics with respect to the optical two-level system, and that this has a strong effect on the dynamical back-action. The resulting phenomena drastically change the nonlinear attractor diagram, i.e. the relation between the mechanical lasing amplitudes and the experimentally tunable parameters. Changes in the attractor diagram could become important for applications like more sensitive measurements [7]. In addition, the rather complex attractor diagram can be used for a more detailed characterization of the system than would be possible in the purely linear regime.

Our analysis will exploit the insights we have gained in our previous study of the dynamics of the light field in such a system [21]. In that study, we assumed some prescribed mechanical oscillations and found the resulting LZ physics for the driven optical two-level system. It is, however, far from clear what the impact of this would be on the nonlinear dynamics, when back-action is included and light and mechanics evolve as a coupled system. That is what we will explore here.

We will refer to an existing optomechanical setup, i.e. a membrane in the middle of an optical cavity [15, 17], where our predictions could be verified experimentally. In particular, we will argue that the more recent version of the experiment [17], with its smaller splitting in the optical two-level system, would readily give rise to the phenomena to be predicted here.

However, most of our analysis and discussion are in fact applicable to the quite generic situation where self-induced oscillations are pumped by a parametrically coupled, driven two-level system. Our findings thus are also relevant for nanomechanical structures or microwave modes whose oscillations are amplified by coupling to, e.g. current-driven double quantum dot setups, superconducting single-electron transistors, or Cooper-pair boxes [38].

We consider the system depicted in figure 1(a). A dielectric membrane is placed in the middle between two high-finesse mirrors [15]. Transmission through the membrane couples the optical modes of the left and right half of the cavity, respectively. Focusing on two nearly degenerate modes, the Hamiltonian of the cavity reads

$$\begin{equation} \skew3\hat{H}_{\rm cav} = \hbar\omega_{0}\left[1-\frac{\skew3\hat{x}}{l}\right]\skew3\hat{a}_{\rm L}^{\dagger}\skew3\hat{a}_{\rm L}+\hbar\omega_{0}\left[1+\frac{\skew3\hat{x}}{l}\right]\skew3\hat{a}_{\rm R}^{\dagger}\skew3\hat{a}_{\rm R} +\hbar g\left(\skew3\hat{a}_{\rm L}^{\dagger}\skew3\hat{a}_{\rm R}+\skew3\hat{a}_{\rm R}^{\dagger}\skew3\hat{a}_{\rm L}\right). \end{equation} \tag{ 1 }$$

Here, $\hat {a}_{\mathrm { L}}^{\dagger }\hat {a}_{\mathrm { L}}$ ($\hat {a}_{\mathrm { R}}^{\dagger }\hat {a}_{\mathrm { R}}$) is the photon number operator of the left (right) cavity mode, ω₀ is the modes' frequency for x = 0 (where the two modes are degenerate) and 2l is the length of the full cavity. The membrane's displacement $\hat {x}$ linearly changes the modes' bare frequencies, while the optical coupling g leads to an avoided crossing for the system's two optical resonances, $\omega _{\pm }=\pm \sqrt {g^{2}+(\omega _{0}x/l)^{2}}$ (figure 1(b)). Thus, mechanical oscillations $\hat {x}(t)$ periodically sweep the system along the hyperbola branches ω_±.

Zoom In Zoom Out Reset image size

We focus on the experimentally accessible, nonadiabatic regime [17, 21] where fast periodic sweeping through the avoided crossing results in consecutive LZ transitions [39, 40]. For a photon inserted into the left mode, the first transition splits the photon state into a coherent superposition, the two contributions gather different phases and interfere the next time the system traverses the avoided crossing (figure 1(c)). For a two-state system, the resulting interference patterns are known as Landau–Zener–Stueckelberg (LZS) oscillations [41]. These have been demonstrated in many setups, ranging from atomic systems [42–44] to quantum dots and superconducting qubits [45–48]. In all of these situations, LZS effects are produced by a fixed external periodic driving. In contrast, here we address the case where LZS oscillations act back on the mechanism that drives them (i.e. the mechanical motion), via the radiation pressure force. We will see that LZS interference strongly influences this back-action force and thereby drastically affects the mechanical self-oscillations that occur when this force overcomes the internal friction (figure 1(d)). More generally, the following discussion thus illustrates the effect of LZS dynamics on back-action induced instabilities.

Given the radiation pressure force $\hat {F}_{\mathrm { rad}}=-\partial \hat {H}_{\mathrm { cav}}/\partial \hat {x}$, the coupled equations of motion for the displacement $\hat {x}(t)$ and $\hat {a}_{i}(t)$ (i = L,R), read

$$\begin{equation} \skew3\ddot{\skew3\hat{x}}=\mathcal{A}_{0}(\skew3\hat{a}_{\rm L}^{\dagger}\skew3\hat{a}_{\rm L}-\skew3\hat{a}_{\rm R}^{\dagger}\skew3\hat{a}_{\rm R})-\Omega^{2}(\skew3\hat{x}-x_{0})-\Gamma\dot{\skew3\hat{x}}+\skew3\hat{\xi}(t), \end{equation} \tag{ 2 }$$

$$\begin{equation} \dot{\skew3\hat{a}}_{i}=\frac{1}{\mathrm{i}\hbar}\left[\skew3\hat{a}_{i},\skew3\hat{H}_{\rm cav}\right]-\frac{\kappa}{2}\skew3\hat{a}_{i}-\sqrt{\kappa}\skew3\hat{b}_{\rm in}^{i}(t), \end{equation} \tag{ 3 }$$

where we used input–output theory for the light fields and set $\mathcal {A}_{0}=\hbar \omega _{0}/lm$. The membrane has a mechanical frequency Ω, an intrinsic damping rate Γ and a rest position x₀. Photons decay at a rate κ out of the cavity. We assume the left mode $\hat {a}_{\mathrm { L}}$ to be driven by a laser at frequency ω_L; the input fields $\hat {b}_{\mathrm { in}}^{i}(t)$ contain this contribution. In the following, we will consider purely classical (large-amplitude) nonlinear dynamics and replace the operators $\hat {a}_{i}(t)$ by the coherent light amplitudes α_i(t). The classical input fields then read β^R_in = 0, $\beta _{\mathrm { in}}^{\mathrm {L}}={\mathrm { e}}^{-{\mathrm { i}}\omega _{\mathrm { L}}t}\sqrt {P_{\mathrm { in}}/\hbar \omega _{\mathrm { L}}}$ where P_in is the laser input power and the mechanical Langevin force will be neglected (ξ ≈ 0). For convenience, we define the laser detuning Δ_L = ω_L − ω₀.

The radiation pressure force gives rise to a time-averaged net mechanical power input $\langle F_{\mathrm { rad}}\dot {x}\rangle$. In analogy to the intrinsic friction Γ, see equation (2), we can define $\langle F_{\mathrm { rad}}\dot {x}\rangle =-m\Gamma _{\mathrm { opt}}\langle \dot {x}^{2}\rangle$ such that we obtain an effective optomechanical damping rate

$$\begin{equation} \Gamma_{\rm opt}=-\frac{\mathcal{A}_{0}}{\langle\dot{x}^{2}\rangle}\langle\left(\left|\alpha_{\rm L}(t)\right|^{2}-\left|\alpha_{\rm R}(t)\right|^{2}\right)\dot{x}\rangle. \end{equation} \tag{ 4 }$$

For Γ_opt > 0 (Γ_opt < 0) the light-field interaction damps (anti-damps) the mechanics. For given oscillations x(t) = A cos(Ωt) + x_a, Γ_opt can be calculated via the periodic light field dynamics α_L(t), α_R(t) that is found by solving equation (3); see also equation (6) further below. Note that our Γ_opt is amplitude-dependent, and the usual linearized case [16, 49] is recovered for A → 0. In the following we will express displacement in terms of frequency, $\bar {x}(t)=(\omega _{0}/l)x(t)$ (see equation (1)); likewise for $\bar {A}$, $\bar {x}_{\mathrm {a}}$.

Figure 2(a) shows results for Γ_opt in this setup, at moderate amplitudes A. Optomechanical damping and amplification is largest if the optical modes' frequency difference is in resonance with the mechanical frequency Ω [10, 18]. In this case, photon transfer from the laser-driven left mode into the right one involves absorption (or emission) of a phonon, that yields strong mechanical amplification (or cooling), see figures 2(b) and (c). For finite amplitudes, we observe an Autler–Townes (AT) splitting [50] that scales as $2g\bar {A}/\Omega$ [21]. Given Γ_opt, we now turn to discuss back-action driven mechanical self-oscillations (phonon lasing) of the membrane.

Zoom In Zoom Out Reset image size

For suitable laser input powers, the radiation pressure force only weakly affects the mechanics over one oscillation period and the mechanics approximately performs sinusoidal oscillations at its unperturbed eigenfrequency Ω; x(t) = A cos(Ωt) + x_a. The possible attractors of the dynamics $\left (A,x_{\mathrm {a}}\right )$ have to meet two conditions [7, 8]. Firstly, the time-averaged total force must vanish: $\langle \ddot {x}\rangle =0$. Secondly, the overall mechanical power input due to radiation pressure must equal the power loss due to friction, $\langle \ddot {x}\dot {x}\rangle =0$. From equation (2), the power balance $\langle \ddot {x}\dot {x}\rangle =0$ is equivalent to

$$\begin{equation} \Gamma_{\rm opt}(A,x_{\mathrm{a}})=-\Gamma. \end{equation} \tag{ 5 }$$

The force balance $\langle \ddot {x}\rangle =0$ yields $\langle F_{\mathrm { rad}}(t)\rangle =m\Omega ^{2}\left (x_{\mathrm {a}}-x_{0}\right )$, i.e. the radiation pressure force displaces the membrane's average position x_a from its rest position x₀. In general, one solves the force balance to find x_a = x_a(A,x₀) and uses this to calculate Γ_opt(A,x_a) [7, 8]. For high quality mechanics (Ω/Γ ≫ 1), the power balance (equation (5)) is met for weak radiation pressure forces where x_a ≃ x₀. For clarity, we will focus on this case. Otherwise, attractor diagrams get deformed slightly [7].

Figure 3(a) displays the effective optomechanical damping Γ_opt depending on laser-detuning Δ_L and amplitude A. The structure of this diagram is drastically different from the standard case with one optical mode [7, 8]. There are 'ridges' of high Γ_opt which display an oscillatory shape (clarified in the inset).

Zoom In Zoom Out Reset image size

A physical understanding of figure 3 can be found from the general structure of the light field dynamics that enters the optomechanical damping, equation (4). For given mechanical oscillations x(t) = Acos(Ωt) + x_a, the formal solution to equation (3) can be expressed as

$$\begin{equation} \left|\alpha_{i}(t)\right|^{2}=\frac{\kappa P_{\rm in}}{\hbar\omega_{\rm L}}\left|\int_{-\infty}^{t}G_{i}(t,t')\,{\rm e}^{-\kappa(t-t')/2}{\rm e}^{-{\rm i}\Delta_{\rm L}t'}\,{\rm d}t'\right|, \end{equation} \tag{ 6 }$$

where the Green's function G_i(t,t') describes the amplitude for a photon entering the left mode at time t' and to be found in the left or right one (i = L,R) at time t. From equation (3) G_i(t,t') is found to be $G_{i}(t,t')=\tilde {a}_{i}(t,t'){\mathrm { e}}^{-{\rm i }\phi (t')}$ where $\phi (t')=(\bar {A}/\Omega )\sin (\Omega t')$ and $\tilde {a}_{i}(t,t')$ is a solution to

$$\begin{equation} \mathrm{i}\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{@{}c@{}} \tilde{a}_{\rm R}\\ \tilde{a}_{\rm L}\end{array}\right)=\left(\begin{array}{@{}cc@{}} \bar{x}_{\mathrm{a}} & g{\rm e}^{+2\mathrm{i}\phi(t)}\\ g{\rm e}^{-2\mathrm{i}\phi(t)} & -\bar{x}_{\mathrm{a}}\end{array}\right)\left(\begin{array}{@{}c@{}} \tilde{a}_{\rm R}\\ \tilde{a}_{\rm L}\end{array}\right) \end{equation} \tag{ 7 }$$

with t ⩾ t' and initial condition $\tilde {a}_{\mathrm { R}}(t',t')=0$, $\tilde {a}_{\mathrm { L}}(t',t')=1$. Thus, the internal photon dynamics between the two modes $\tilde {a}_{i}(t,t')$ is expressed in terms of a two-level system with a time-dependent coupling ge^2iϕ(t). With $\psi =(\tilde {a}_{\mathrm { R}},\tilde {a}_{\mathrm { L}})^{\mathrm {T}}$, equation (7) is the Schrödinger equation including a time-periodic Hamiltonian, H(t + T) = H(T). In this case it is appropriate to consider the time-evolution operator for one period, ψ(t' + T) = U(T)ψ(t'), and its two eigenvalues, the so-called Floquet eigenvalues _±: $U(T)\chi _{\pm }=\exp (-{\mathrm { i}}\epsilon _{\pm }T)\chi _{\pm }$. U(T) is obtained by integrating equation (7).

Using Floquet theory [51], we find the general structure of the Green's function $G_{i}(t,t')=\sum _{j,n,n'}C_{i}^{n,n',j}{\rm {e} }^{-{\mathrm { i}}\Omega (nt-n't')}{\mathrm {e}}^{-{\mathrm {i}}\epsilon _{j}(t-t')}$, where C^n,n',j_i are time-independent coefficients. Then, via equation (6) we obtain pronounced resonances in Γ_opt located at $\Delta _{\mathrm { L}}=m\Omega +\epsilon _{\pm }(\bar {A})$, corresponding to the ridges in figure 3. The interference between consecutive LZ transitions renormalizes the coupling between modes in terms of Bessel functions J_n: $g{\mathrm {e}}^{2\mathrm {i}\phi (t)}=g\sum _{n}J_{n}(2\bar {A}/\Omega ){\rm e}^{\mathrm {i}n\Omega t}$ (equation (7)). This results in an oscillatory modulation of the Floquet eigenvalues $\epsilon _{\pm }(\bar {A})$. At certain amplitudes, these vanish due to total destructive interference, see figure 3(a). The oscillatory shape of the ridges in Γ_opt then directly determines the attractor diagram for the self-induced oscillations, via the power balance equation (5), see figure 3(b).

Regarding the global structure of figure 3(a), Γ_opt tends to be large near $\Delta _{\mathrm { L}}=\pm \bar {A}$ (dashed lines). This is because then the left mode gets into resonance with the laser at the motion's turning point. For larger amplitudes, we recover the predictions for the standard optomechanical setup [7] (checkerboard in figure 3(a)).

So far, we discussed dynamical back-action effects for parameters where the mechanical frequency is larger than the optical splitting, Ω > 2g (figures 2 and 3). In general, the parameter space can be subdivided as shown in figure 4(a). Multimode dynamics that goes beyond the standard scenario [7, 8] can only be observed if the photon lifetime inside the cavity is larger than the timescale for photons to tunnel between modes, 2g > κ (colored region, figure 4(a)). Otherwise, photons inserted into the left mode decay before the second mode affects the dynamics and we recover the standard results [7, 8]. Within the new region (colored in figure 4(a)), the most interesting regime is where mechanical sidebands can in fact be resolved, i.e. κ < Ω.

Zoom In Zoom Out Reset image size

Above, we had focussed on the sector 2g < Ω within this regime. Now figure 4(b) displays Γ_opt in the opposite sector where 2g > Ω. This is important, as experimental setups will presumably first detect the effects described here in that regime (see our discussion on experimental parameters below).

When 2g > Ω, several mechanical sidebands lie within the avoided crossing. With respect to self-induced mechanical oscillations, these sidebands and their interaction yield an intricate web of multistable attractors, see figure 4(c).

Provided the setup is sideband-resolved (i.e. κ < Ω), then one can imagine that during one cycle of oscillation the optical field accumulates a phase that is the time-integral over the (changing) instantaneous optical frequency ω₊(t). Since κ < Ω, the driving laser field will actually see an effective optical frequency which is the time-average of ω₊(t). This picture immediately suggests that the intracavity power (and all effects on the nonlinear dynamics) will be largest when the laser is in resonance with that time-averaged frequency. Therefore, the global asymptotics of these resonant structures (green lines in the attractor diagram, figure 4(c)) can be found from the condition: $\Delta _{\mathrm { L}}=2\langle \omega _{+}(t)\rangle =4\sqrt {g^{2}+\bar {A}^{2}}E(\pi /2,k)/\pi$, where $k=\sqrt {\bar {A}^{2}/\left (g^{2}+\bar {A}^{2}\right )}$ and $E(\frac {\pi }{2},k)$ turns out to be the complete elliptic integral of the second kind.

Apart from these asymptotes, the attractor diagram in that regime is dominated by sidebands which are removed from these asymptotic lines by integer multiples of Ω, corresponding to multi-phonon absorption/emission.

We now turn to a brief discussion of the required experimental parameters. Since we are interested in nonadiabatic dynamics of the light field, the splitting g should not be too large. In the original membrane-in-the-middle setup [15], the splitting was proportional to the transmission amplitude for photons to pass through the membrane. There, due to a membrane reflectivity in the range of about 1/2, the splitting was comparable to the free spectral range of the optical cavity, i.e. roughly 2g ∼ 2π × 2 GHz. This would still be far larger than the membrane oscillation frequency of about Ω ∼ 2π × 100 kHz, making it difficult to observe the effects discussed here. In addition, at these levels of reflectivity, the two-mode approximation used here would not be very good, and the optical spectrum should rather be treated with a cos-type dependence on the membrane position.

However, a more recent version [17] of that setup features far smaller splittings. This is due to the fact that now another effect is exploited to couple two optical modes: the modes in question are now cavity modes of different transverse mode profile, and the photon tunnel coupling between them is due to slight asymmetries of the membrane alignment. Thus, the coupling strength g is no longer tied to the membrane reflectivity. Indeed, splittings down to 2g/2π ∼ 0.2 MHz have been reported, 10 000 times smaller than what was available in the original setup. Decreases in g are required to increase the curvature of the optical dispersion (∂²ω₊/∂x² in our notation) and thereby increase the quadratic coupling (desired for future applications such as single-phonon or phonon shot noise measurements). Thus, future setups will tend to operate in such a regime. This is the parameter regime that we need for our approach to be applicable and for the predictions here to become relevant. Note that for us it is only necessary for g to be comparable to Ω (say, within an order of magnitude), not necessarily much smaller. This is demonstrated especially in figure 4. In addition, future applications may increase the mechanical frequency by either turning to a smaller membrane or to higher-order mechanical flexural modes of the membrane, which sometimes have better damping properties as well. This would also go into the direction of g ∼ Ω. In fact, the discussion of future setups in [17] envisions having Ω ∼ 2π × 1 MHz.

The finesse of the cavity is sufficient also in the more recent version of the experiment, i.e. κ is small enough to resolve the splitting g. In addition, future experiments on the applications mentioned above will also require the sideband-resolved regime κ < Ω, such that this can be assumed to be attained. We conclude that future investigations of phonon lasing in such a setup will be able to show the features predicted here, as all requirements will be met.

The ansatz adopted here, i.e. of sinusoidal mechanical motion, will break down at very large laser powers, when the system can become chaotic (which has also been seen in standard optomechanical setups [52]). We have checked by direct numerical simulations of the original equations of motion (see equations (2) and (3)) that, for the typical parameters of the experiments using this kind of setup, this occurs at far larger powers than the ones discussed here. In our dimensionless units, these powers are about P_in/ℏω₀Ω ∼ 10⁴ for g/Ω = 0.2, κ/Ω = 0.1, Γ/Ω = 0.01 and $\mathcal {A}_{0}\omega _{0}/l\Omega ^{3}=5\times 10^{-6}$.

To conclude, we have investigated self-induced mechanical oscillations (phonon lasing) in a multimode optomechanical system. The mechanical motion drives Stueckelberg oscillations in the light field of two coupled optical modes, and this drastically modifies the attractor diagram. The additional influence of quantum (and thermal) noise could be analyzed along the lines of [7, 8]. Our example, which can be realized in present optomechanical setups, illustrates the potential of LZ physics to appreciably alter lasing behavior.

FM acknowledges support by the DFG (Emmy-Noether program,NIM), as well as DARPA ORCHID, ITN cQOM, and an ERC Starting Grant. HZW was supported by the China Scholarship Council and the National Natural Science Foundation of China under grant numbers 11247283 and 11305037.