Abstract
We study the effective dipole–dipole interactions in ultracold quantum gases on optical lattices as a function of asymmetry in confinement along the principal axes of the lattice. In particular, we study the matrix elements of the dipole–dipole interaction in the basis of lowest band Wannier functions which serve as a set of low-energy states for many-body physics on the lattice. We demonstrate that, for shallow lattices in quasi-reduced dimensional scenarios, the effective interaction between dipoles in an optical lattice is non-algebraic in the inter-particle separation at short to medium distance on the lattice scale and has a long-range power-law tail, in contrast to the pure power-law behavior of the dipole–dipole interaction in free space. The modifications to the free-space interaction can be sizable; we identify differences of up to 36% from the free-space interaction at the nearest-neighbor distance in quasi-one-dimensional arrangements. The interaction difference depends essentially on asymmetry in confinement, due to the d-wave anisotropy of the dipole–dipole interaction. Our results do not depend on statistics, applying to both dipolar Bose–Einstein condensates and degenerate Fermi gases. Using matrix product state simulations, we demonstrate that use of the correct lattice dipolar interaction leads to significant deviations from many-body predictions using the free-space interaction. Our results are relevant to up and coming experiments with ultracold heteronuclear molecules, Rydberg atoms and strongly magnetic atoms in optical lattices.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recent experimental progress in cooling heteronuclear polar molecules with large electric dipole moments [1–11], Rydberg atoms [12] and atoms with large magnetic dipole moments, in particular chromium [13], erbium [14] and dysprosium [15, 16], has sparked interest in the properties of ultracold dipolar gases. While in many ultracold atomic systems interactions are short-range and well-modeled by a contact pseudopotential, the interactions in dipolar gases have a long-range and anisotropic character in free space, decaying as 1/r3 with the separation r between particles. These features of the dipole–dipole interaction have lead to a variety of intriguing theoretical proposals such as exotic pairing and bound states in ladder geometries [17, 18] and the realization of quantum liquid crystal states of matter [19–21]. Even for atoms with relatively weak dipole moments, such as rubidium, dipole–dipole interactions can play a significant role [22, 23]. In this paper, we show that the effective dipolar interaction in a lattice can deviate significantly from its free-space form. In particular, we find a non-algebraic decay at moderate separations which becomes algebraic for large separations. Corrections of order 36–48% arise for interactions at the nearest-neighbor distance in moderately confined quasi-low-dimensional scenarios.
A key component of our analysis is the presence of a continuous, periodic potential, which for ultracold atomic and molecular gases is provided by an optical lattice. As first discovered by Kohn [24], Wannier functions, the most localized set of orthogonal single-particle states with the symmetries of the lattice, generally feature an exponential decay. We find that the effective dipolar interaction in an optical lattice depends essentially on the exponential tails of the Wannier functions rather than only on their widths. Hence, approximating the Wannier functions with localized functions which match only the mean width will fail to accurately capture the effective interaction in an optical lattice.
An additional essential ingredient for our findings is an asymmetry in the degree of confinement along the principal axes of the lattice due to the anisotropic character of the dipole–dipole interaction. In this work, we characterize confinement using the curvature of a lattice site minimum. Our work builds on a wealth of confinement-induced phenomena in ultracold quantum gases, such as confinement-induced resonances [25–28], the fermionization of a one-dimensional (1D) Bose gas [29] and the Berezinskii–Kosterlitz–Thouless transition in a quasi-two-dimensional (2D) Bose gas [30, 31]. We stress, however, that our work does not deal with dipolar confinement-induced resonances such as those studied in [32], but rather on the modification of the effective interaction in an optical lattice due to the localization properties of the single-particle basis. In dipolar gases, the effects of confinement have been studied in harmonic traps [33–35], and within the Gross–Pitaevskii approximation in a triple-well potential [36] and a 1D lattice [37]. For the harmonic oscillator, it has been shown that strong confinement along the axis of a field orienting the dipoles leads to purely repulsive interactions in the weakly confined plane. Additionally, because of the anisotropic character of the dipole–dipole interaction, the stability of a dipolar Bose–Einstein condensate (BEC) displays a strong dependence on anisotropy in external confinement, and stable solutions can even take surprising forms such as the 'red blood cell' dipolar BEC [38]. Similarly, anisotropic lattice confinement has surprising differences from preconceptions based on uniform isotropic systems. Dipolar interactions in confined geometries appear in many other branches of physics, such as in ferromagnetic nanostructures [39], where the dipole–dipole interaction plays a key role in the dispersion relation for spin waves in ferromagnetic films [40] and wires [41].
An important application of our results is in deriving many-body models to describe the low-energy physics of dipolar gases on lattices. Previous derivations, for example [42–46], assume that the interaction between localized lattice states has the same functional form as in the continuum. Since this amounts to replacing the localized single-particle probability distributions with delta functions, we will call this the delta function approximation (DFA). Performing matrix product state (MPS) simulations [47] on infinite 1D lattices, we demonstrate that the DFA can lead to significant errors in the determination of the phase diagram.
This paper is organized as follows. In section 2 we review the theory of Wannier functions and their use in deriving effective many-body lattice models for strongly correlated systems. In particular, we provide a quantitative analysis of the decay properties of Wannier functions as well as properties of their squares interpreted as probability distributions. Section 3 provides numerical results for the effective dipole–dipole interactions in the presence of an optical lattice and discusses the effects of confinement. In section 4 we study the phase diagram of hard-core bosons in one dimension with infinite-size MPS techniques to exemplify the impact of the confinement-induced modification of dipole–dipole interactions on many-body physics. Finally, in section 5, we conclude. In appendix A we discuss numerical methods for evaluating matrix elements of nonlocal potentials in a basis of Wannier functions, and in appendix B, we provide an explicit evaluation of the dipole–dipole interaction in a cylindrically symmetric harmonic trap for a comparison with the results in an optical lattice.
2. Optical lattices, Wannier functions and Hubbard models
The theory of quantum mechanical objects in a continuous periodic potential is well established [48]. Here, we present a review of the basic facts in order to set notation, and also provide some explicit computations for the optical lattice potential equation (1) which do not appear elsewhere in the literature, to the best of our knowledge.
We consider that our system is subject to the separable simple cubic potential

where a is the lattice spacing. The typical energy scale derived from a is the recoil energy ER = ℏ2π2/2ma2. A potential of the form equation (1) is produced for ultracold gases by an optical lattice consisting of three sets of counter-propagating laser beams. The interaction of an optical potential which is far detuned from any atomic or molecular resonances may be described by the ac Stark shift [49]

where  is the optical field and
is the optical field and 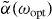 is the dynamical polarizability tensor of the object evaluated at the optical frequency ωopt. The quantities Vx, Vy and Vz in equation (1), which we will refer to as the lattice heights along the x, y and z directions, may be tuned by increasing the intensity of the optical field. Throughout this paper, we will use the notation
is the dynamical polarizability tensor of the object evaluated at the optical frequency ωopt. The quantities Vx, Vy and Vz in equation (1), which we will refer to as the lattice heights along the x, y and z directions, may be tuned by increasing the intensity of the optical field. Throughout this paper, we will use the notation 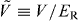 to denote the dimensionless ratio of a lattice height to the recoil energy. The assumption of a separable potential such as equation (1) applies when the polarizability tensor is a scalar, as occurs naturally for alkali atoms. When the dynamical polarizability contains non-scalar components, internal states of, e.g., a rotating molecule can be coupled together for certain polarizations of the optical potential [50]. The theory given in this paper can be extended to this case, but the analysis is more complex. For clarity of exposition, we will focus on the separable case, equation (1).
to denote the dimensionless ratio of a lattice height to the recoil energy. The assumption of a separable potential such as equation (1) applies when the polarizability tensor is a scalar, as occurs naturally for alkali atoms. When the dynamical polarizability contains non-scalar components, internal states of, e.g., a rotating molecule can be coupled together for certain polarizations of the optical potential [50]. The theory given in this paper can be extended to this case, but the analysis is more complex. For clarity of exposition, we will focus on the separable case, equation (1).
For particles subject to a periodic lattice potential, the energy eigenfunctions are Bloch functions ψnk(r) characterized by a quasi-momentum index k in the first Brillouin zone (BZ) and a band index n. Bloch functions are the simultaneous eigenfunctions of the single-particle Hamiltonian and the lattice translation operators, and so represent the analogues of plane waves in free space when the translational symmetry is a discrete, rather than continuous, group. As such, Bloch functions are delocalized objects, and so are often not an appropriate basis for expanding a many-body Hamiltonian with strong local interactions. A more appropriate basis for describing strong interactions in lattices is provided by Wannier functions, which are the quasi-momentum Fourier transforms of the Bloch functions
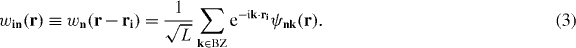
Here L is the total number of unit cells in a lattice with periodic boundary conditions and ri denotes the coordinate of lattice site i. For simplicity, we will restrict our attention to the lowest band in most cases. When the band index n is not specified, lowest band Wannier functions are assumed. The extension of our results to multi-band situations [51] is straightforward. Additionally, our methods also extend readily to other bases, for example, localized bases which take into account strong contact interactions [52–55].
2.1. Properties of Wannier functions
It was shown in a seminal work by Kohn [24] that the phases on the Bloch functions can be chosen such that the Wannier functions are exponentially decaying away from their centers for 1D centro-symmetric lattice potentials in a sense to be discussed in the next paragraph. The Wannier functions with this choice of phases are called maximally localized Wannier functions, and are used throughout this paper. The exponential decay of Wannier functions has been extended to general 1D lattice potentials [56], non-degenerate bands in arbitrary dimensions [57] and general 2D and three-dimensional (3D) insulators with vanishing Chern number [58]. Hence, the exponential localization of Wannier functions, which will play an important role in our results, is a general property which does not require fine tuning or a specific lattice structure.
Because the potential we consider, equation (1), is separable, the Bloch solutions of the 3D single-particle Schrödinger equation are products of the Bloch solutions of the 1D Hamiltonian

The linearity of the transformation equation (3) implies that the 3D Wannier functions of equation (1) are hence products of 1D Wannier functions obtained by quasi-momentum Fourier transform of the 1D Bloch eigenfunctions of equation (4),

Thus, we can use the results of Kohn [24] to discuss the properties of the 1D Wannier functions  . In particular, the Wannier functions decay exponentially as
. In particular, the Wannier functions decay exponentially as 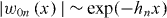 in the sense that
in the sense that

The parameter hn is the distance to the nearest branch point from the real axis in the complex quasi-momentum plane. The decay length hn can be determined numerically by locating crossings in the band structure computed with quasi-momentum k = kn + iκ, 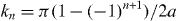 and κ real. At the point k where bands n and n + 1 cross, hn = κ. The results of this analysis for the lowest two bands of the 1D potential equation (4) are shown in figure 1(a). He and Vanderbilt [59] pointed out that equation (6) is consistent with an exponential decay multiplied by an algebraic factor. They then demonstrated that the precise asymptotic behavior of maximally localized, orthogonal Wannier functions in 1D is
and κ real. At the point k where bands n and n + 1 cross, hn = κ. The results of this analysis for the lowest two bands of the 1D potential equation (4) are shown in figure 1(a). He and Vanderbilt [59] pointed out that equation (6) is consistent with an exponential decay multiplied by an algebraic factor. They then demonstrated that the precise asymptotic behavior of maximally localized, orthogonal Wannier functions in 1D is

for a lattice consisting of periodically repeating Gaussian wells. By performing numerical fits with the obtained hn from figure 1(a), we find that this same algebraic factor appears in the Wannier functions of the potential equation (4), and the power of the algebraic correction does not appear to depend on the lattice height or the band index. The resulting fits to the Wannier functions, together with the numerically computed Wannier functions, are shown in figure 1(b). Figure 1 provides a rigorous definition of the decay of the Wannier functions we consider in this paper as a function of the height of the optical lattice potential.
Figure 1. (a) Exponential decay constant hn of the 1D Wannier function as a function of the lattice height  for the lowest two bands. Deeper lattices localize the Wannier functions more effectively. (b) Decay of the Wannier functions of the first two bands (points) together with their fits to the asymptotic exponential form equation (7)(solid lines), V =10ER.
for the lowest two bands. Deeper lattices localize the Wannier functions more effectively. (b) Decay of the Wannier functions of the first two bands (points) together with their fits to the asymptotic exponential form equation (7)(solid lines), V =10ER.
Download figure:
Standard image High-resolution image2.2. Approximation of Wannier functions by Harmonic oscillator functions
It is difficult to obtain quantitative analytical predictions from Wannier functions due to their complicated form. Hence, approximations to the true Wannier functions are often made for analytical convenience. The most common such approximation is to replace a single site of the optical lattice by a harmonic well with the same local curvature. We shall call this the harmonic oscillator approximation (HOA). The curvature-matching condition amounts to  , where ℓν is the harmonic oscillator length along Cartesian direction ν. The 1D ground state wave function, which is taken to approximate the 1D lowest band Wannier function, is
, where ℓν is the harmonic oscillator length along Cartesian direction ν. The 1D ground state wave function, which is taken to approximate the 1D lowest band Wannier function, is

There are several important differences between the HOA equation (8) and the true Wannier function. Firstly, equation (8) is everywhere positive, while Wannier functions, even for the lowest band, always have nodes in order to maintain orthogonality between lattice sites. Thus, the HOA poorly captures quantities like tunneling, which involve overlaps of derivatives of Wannier functions. Also, equation (8) decays much more rapidly than the true Wannier functions, as a Gaussian rather than an exponential. Hence, the HOA will consistently underestimate the overlap of Wannier functions at different sites. Thirdly, the HOA equation (8) is more peaked around its center value than the true Wannier function, and so quantities computed on-site are overestimated by the HOA. Finally, the true Wannier functions have all of the lattice symmetries, while the HOA displays the symmetries of an ellipsoid for the simple cubic lattice. The difference in symmetries is especially important when discussing interaction-induced diagonal tunneling [27, 28].
We can make the comparison between Wannier functions and the HOA more quantitative by considering the moments of their associated single-particle probability distributions. We define the pth 1D moments as
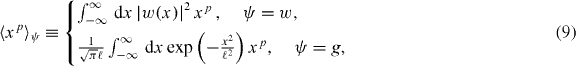
where ψ = w and g stand for Wannier and Gaussian, respectively. The second moment gives an estimate for the width of the distribution. It is convenient to define the kurtosis κψ ≡ (〈x4〉ψ/〈x2〉2ψ) − 3, which is a measure of the peakedness of a distribution as well as the heaviness of its tails [60]. We show the second and fourth moments of the true Wannier functions and the HOA in figure 2. The width of the lowest band Wannier function is well captured by the HOA for deep lattices with  , although the HOA always has a smaller second moment than the true Wannier function. The harmonic oscillator always has a vanishing kurtosis, κg = 0, as is known for Gaussian distributions. In contrast, the Wannier functions have an always positive kurtosis which is very sizable for shallow lattices and approaches zero for deeper lattices. For example, we observed κw = 10 for
, although the HOA always has a smaller second moment than the true Wannier function. The harmonic oscillator always has a vanishing kurtosis, κg = 0, as is known for Gaussian distributions. In contrast, the Wannier functions have an always positive kurtosis which is very sizable for shallow lattices and approaches zero for deeper lattices. For example, we observed κw = 10 for 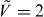 and κw = 0.12 for
and κw = 0.12 for  . This difference in the kurtosis quantifies the essential difference between the decay of the Wannier functions and the HOA.
. This difference in the kurtosis quantifies the essential difference between the decay of the Wannier functions and the HOA.
Figure 2. The second (solid lines) and fourth (dashed lines) moments of the lowest band Wannier function (red) and the HOA, equation (8), (blue) as a function of the lattice height. While the HOA captures the mean width of the Wannier functions for deep lattices, the heavy tails of the Wannier functions cause large deviations in the fourth moments, especially in shallow lattices.
Download figure:
Standard image High-resolution image2.3. Derivation of Hubbard models for dipolar particles
With the identification of the lowest band Wannier functions as the appropriate single-particle basis for describing strongly interacting particles in a lattice, we derive a many-body lattice model using the well-known procedure [61, 62] of expanding the field operator 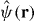 in the basis of Wannier functions and substituting this expansion into the second-quantized expression for the interaction Hamiltonian
in the basis of Wannier functions and substituting this expansion into the second-quantized expression for the interaction Hamiltonian
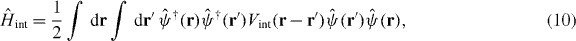
where  is the two-particle interaction potential. The expansion of equation (10) in Wannier functions yields
is the two-particle interaction potential. The expansion of equation (10) in Wannier functions yields

where 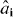 destroys a particle in a lowest band Wannier state centered at site i and
destroys a particle in a lowest band Wannier state centered at site i and
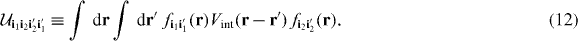
Here, fii'(r) ≡ w⋆i(r)wi'(r) is a product of Wannier functions. The matrix elements 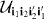 , which we will call Hubbard parameters, describe the interactions between particles localized in lowest band Wannier states.
, which we will call Hubbard parameters, describe the interactions between particles localized in lowest band Wannier states.
The interaction we consider is the dipole–dipole interaction, commonly given as

where  is the dipole operator, r is the relative position of the interacting particles,
is the dipole operator, r is the relative position of the interacting particles,  and er is a unit vector in the direction of r. It is convenient to instead recast the dipole–dipole potential as the contraction of two spherical tensors as [63]
and er is a unit vector in the direction of r. It is convenient to instead recast the dipole–dipole potential as the contraction of two spherical tensors as [63]
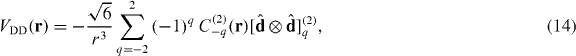
where 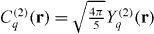 is an unnormalized spherical harmonic in the spherical coordinates of r and
is an unnormalized spherical harmonic in the spherical coordinates of r and
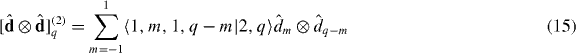
is the irreducible tensor product of two dipole operators with 〈j1m2j2m2|jm〉 a Clebsch–Gordan coefficient. The operators

are the spherical decompositions of the vector operator  . The interaction Hamiltonian may be written in terms of coupling constants UDD,q and geometrical factors
. The interaction Hamiltonian may be written in terms of coupling constants UDD,q and geometrical factors  as
as

where

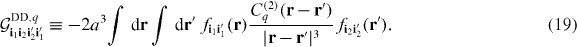
All of the information about the size of the dipole moment and the lattice spacing are contained in the coupling constants equation (18). On the other hand, the geometrical integrals equation (19) contain the information about the effects of lattice confinement on the effective interaction through the Wannier function products 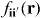 . It is these geometrical factors which we are interested in studying in the present paper.
. It is these geometrical factors which we are interested in studying in the present paper.
While our methods can be applied to all components q of the dipole–dipole interaction, for simplicity we focus on the terms in equation (17) with q = 0. These terms do not change the projection of the total angular momentum along a space-fixed quantization axis. The q = 0 components are the only terms relevant for ultracold 1Σ molecules in an optical lattice and oriented in a strong dc electric field, as states with dipole-allowed transitions are separated by energy splittings large compared to the characteristic dipole–dipole interaction energy [45, 64]. Also, these are the most relevant processes for magnetic dipoles in an optical lattice with a strong magnetic field to prevent dipolar relaxation and spontaneous demagnetization [65–67], or a quantum simulation of magnetic dipoles using symmetric top molecules in a strong electric field [68]. In this case, we have
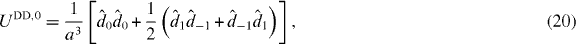
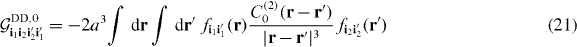
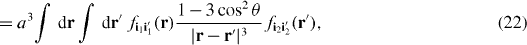
where θ is the polar angle of the relative coordinate (r − r'). The commonly used DFA [42–46] replaces  , such that
, such that

where θi1i2 is the polar angle of the relative vector between lattice sites i1 and i2 with positions ri1 and ri2, respectively.
The terms in equation (17) may be viewed as scattering processes in which particles in the lowest band at lattice sites i1' and i2' move to lattice sites i1 and i2, respectively, in the course of an interaction. The largest magnitude terms in equation (17) are those in which i1 = i1' and i2 = i2', which we will call direct interactions using the scattering process analogy. The direct terms arise as density–density interactions in the interaction Hamiltonian, proportional to 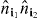 . Another class of terms which are proportional to
. Another class of terms which are proportional to 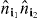 are the exchange interactions, in which i1 = i2' and i2 = i1' with i1' ≠ i2'. All other processes involve changing the position of a Wannier state from its initial position. Examples of such processes are assisted tunneling [46] and pair hopping [27, 69], both of which can introduce new quantum phases in shallow lattices [69]. However, assisted tunneling, pair hopping and exchange terms are all suppressed by factors related to the exponential decay of the Wannier functions, see figure 1, and the behavior of these Hubbard parameters with lattice confinement is qualitatively similar. Because the focus of this work is on the qualitative behavior of the Hubbard parameters with the lattice confinement, we will restrict our attention to the direct and exchange terms with the understanding that the behavior of assisted tunneling and pair hopping is similar to that of the exchange term. It should be noted that our methods apply to any Hubbard parameter. Hence, keeping only the direct and exchange interactions and taking into account the statistics of the particles, the expansion equation (11) may be written for the dipole–dipole interaction as
are the exchange interactions, in which i1 = i2' and i2 = i1' with i1' ≠ i2'. All other processes involve changing the position of a Wannier state from its initial position. Examples of such processes are assisted tunneling [46] and pair hopping [27, 69], both of which can introduce new quantum phases in shallow lattices [69]. However, assisted tunneling, pair hopping and exchange terms are all suppressed by factors related to the exponential decay of the Wannier functions, see figure 1, and the behavior of these Hubbard parameters with lattice confinement is qualitatively similar. Because the focus of this work is on the qualitative behavior of the Hubbard parameters with the lattice confinement, we will restrict our attention to the direct and exchange terms with the understanding that the behavior of assisted tunneling and pair hopping is similar to that of the exchange term. It should be noted that our methods apply to any Hubbard parameter. Hence, keeping only the direct and exchange interactions and taking into account the statistics of the particles, the expansion equation (11) may be written for the dipole–dipole interaction as
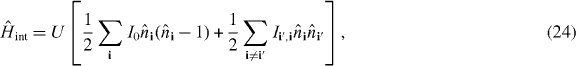
where we have defined U ≡ UDD,0 and

The plus (minus) sign on the exchange term in equation (25) refers to bosons (fermions). Results for the effective interactions, equation (25), computed using the methods of appendix A, are presented in the next section.
3. Effective dipole–dipole interactions
With respect to the length scale of the lattice constant a, the short range physics is given by the interactions I0 which occur within a unit cell. A point of comparison for the on-site dipolar interaction I0 is provided by the dimensionless interaction energy 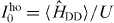 of two bosonic particles in the ground state of a harmonic trap, where the harmonic trap is chosen to match the local curvature of a lattice site as detailed in section 2.2. In the case where the oscillator lengths in the xy plane are equal, ℓx = ℓy = ℓ⊥, we have that
of two bosonic particles in the ground state of a harmonic trap, where the harmonic trap is chosen to match the local curvature of a lattice site as detailed in section 2.2. In the case where the oscillator lengths in the xy plane are equal, ℓx = ℓy = ℓ⊥, we have that
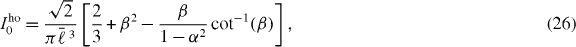
where  is the geometric mean oscillator length in units of a, α ≡ ℓz/ℓ⊥ measures the confinement asymmetry and β ≡ α(1 − α2)−1/2. Notably, the interaction energy Iho0 vanishes for isotropic confinement, α = 1. For α < 1, corresponding to stronger confinement along the quantization axis, contributions from
is the geometric mean oscillator length in units of a, α ≡ ℓz/ℓ⊥ measures the confinement asymmetry and β ≡ α(1 − α2)−1/2. Notably, the interaction energy Iho0 vanishes for isotropic confinement, α = 1. For α < 1, corresponding to stronger confinement along the quantization axis, contributions from 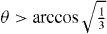 , where the dipole–dipole potential is negative, are suppressed. Hence, Iho0 is positive for α < 1. In contrast, for α > 1 where confinement is weakest along the quantization axis, Iho0 is negative. These qualitative features are shared by the true effective interaction using Wannier functions, as is shown in appendix B. Of particular interest is that the on-site dipole–dipole interaction vanishes when the lattice heights are equal,
, where the dipole–dipole potential is negative, are suppressed. Hence, Iho0 is positive for α < 1. In contrast, for α > 1 where confinement is weakest along the quantization axis, Iho0 is negative. These qualitative features are shared by the true effective interaction using Wannier functions, as is shown in appendix B. Of particular interest is that the on-site dipole–dipole interaction vanishes when the lattice heights are equal,  . Also, as noted in section 2.2, the HOA energy Iho0 is always greater than the on-site energy computed using Wannier functions.
. Also, as noted in section 2.2, the HOA energy Iho0 is always greater than the on-site energy computed using Wannier functions.
For the moderate- to long-range interactions Ii',i, let us define Ij ≡ Ii+j,i with j along the x direction. The parameters Ij correspond to effective dipole–dipole interactions separated by a distance of j lattice spacings along a principal axis. The DFA predicts that the exchange contribution vanishes and the direct term contributes a factor of j−3 such that Ij = j−3. Hence, there are two possible sources of deviation from the DFA. The first source is a non-vanishing contribution from the exchange term. The second source is a deviation of the direct term from j−3. The exchange term is non-vanishing due to overlap between Wannier functions on different sites, and so decreases with increasing lattice height as the exponential localization factor h1 increases, see figure 1. We can expect that the exchange processes will be negligible in magnitude even at the nearest-neighbor distance when 2h1a > 1, as then the Wannier functions are well-localized within a unit cell. From figure 1, this gives an estimation of  . In contrast to the modification of the effective interaction by the exchange term, modification of the effective interaction due to the direct term relies essentially on asymmetry in 3D confinement. This can be understood in analogy with the effective short-range interaction discussed in the last paragraph, and is a consequence of the fact that the dipole–dipole interaction has relative d-wave symmetry.
. In contrast to the modification of the effective interaction by the exchange term, modification of the effective interaction due to the direct term relies essentially on asymmetry in 3D confinement. This can be understood in analogy with the effective short-range interaction discussed in the last paragraph, and is a consequence of the fact that the dipole–dipole interaction has relative d-wave symmetry.
To demonstrate the effects of asymmetric lattice confinement, we evaluate the parameters Ij for two quasi-low dimensional scenarios. In the quasi-2D scenario, we take the z direction to be tightly confined with a lattice height 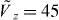 and the lattice heights along the x and y directions to be equal,
and the lattice heights along the x and y directions to be equal, 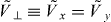 . In the quasi-1D scenario we take both the z and y lattices to be tightly confining with
. In the quasi-1D scenario we take both the z and y lattices to be tightly confining with 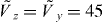 , and call the x lattice height
, and call the x lattice height  . These quasi-dimensional reductions are quite moderate and are commonplace in current experiments [70, 71]. The confinement-induced modifications of effective dipole–dipole interactions with respect to the DFA in the quasi-1D and quasi-2D scenarios are shown in figure 3. Here, the modifications to the direct term are shown as
. These quasi-dimensional reductions are quite moderate and are commonplace in current experiments [70, 71]. The confinement-induced modifications of effective dipole–dipole interactions with respect to the DFA in the quasi-1D and quasi-2D scenarios are shown in figure 3. Here, the modifications to the direct term are shown as 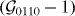 , which is the deviation from the DFA prediction of 1 at the nearest-neighbor distance. The exchange term is identically zero in the DFA, and so any non-vanishing value for the exchange term represents a deviation from the DFA. The red curves are the numerical computation with Wannier functions, and the blue curves use the HOA. We note that the exchange contributions, shown with dashed lines, are drastically underestimated by the HOA, as expected, since the HOA has Gaussian rather than exponential tails, and the exchange term depends on overlap between these tails. The modifications of the direct term shown with solid lines display qualitatively similar features between the true solution and the HOA. In particular, both show vanishing modifications of the direct term when there is no asymmetry in confinement,
, which is the deviation from the DFA prediction of 1 at the nearest-neighbor distance. The exchange term is identically zero in the DFA, and so any non-vanishing value for the exchange term represents a deviation from the DFA. The red curves are the numerical computation with Wannier functions, and the blue curves use the HOA. We note that the exchange contributions, shown with dashed lines, are drastically underestimated by the HOA, as expected, since the HOA has Gaussian rather than exponential tails, and the exchange term depends on overlap between these tails. The modifications of the direct term shown with solid lines display qualitatively similar features between the true solution and the HOA. In particular, both show vanishing modifications of the direct term when there is no asymmetry in confinement, 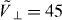 . However, the HOA underestimates the modifications of the direct term, quite significantly for shallow quasi-low-dimensional confinement.
. However, the HOA underestimates the modifications of the direct term, quite significantly for shallow quasi-low-dimensional confinement.
Figure 3. Panels (a) and (b) show the modifications of effective dipole–dipole interactions from their delta function approximation (DFA) values at the nearest-neighbor distance in quasi-1D and quasi-2D, respectively, as a function of confinement asymmetry. The shown values are the dimensionless integrals equation (19), but may also be interpreted as the confinement-induced interaction in units of UDD,0 from equation (17). The solid lines are the deviations from the DFA prediction for the direct term, and the dashed lines are the exchange term. Note that the exchange term identically vanishes in the DFA. The red curves are the values computed with actual Wannier functions, and the blue curves use the HOA.
Download figure:
Standard image High-resolution imageIn figure 3, we showed the behavior of the confinement-induced modifications of the effective dipole–dipole interactions with confinement asymmetry at the nearest-neighbor distance. These modifications also depend on the distance between sites in the lattice, and this dependence has a length scale set by the confinement. In order to get a complete picture of the dependence of confinement effects on both distance between sites and confinement asymmetry we fit the numerically obtained data for Ij to the form

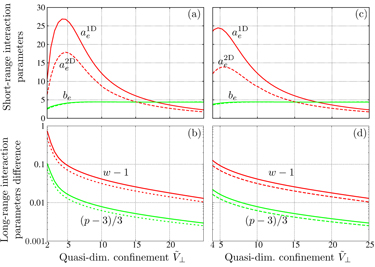
for j∈[1,7], i.e. out to seven sites. The DFA predicts no exponential, ae = 0 or be → ∞ and w = 1 and p = 3 for the long-range contribution. The factor w gives a renormalization of the algebraic part of the effective dipole–dipole potential which can be easily accounted for. The fit parameters for our data generated using the numerical methods of appendix A are shown in figure 4. Here the solid (dashed) lines refer to the quasi-1D (quasi-2D) scenarios. The top panels are the short-range parameters ae and be in equation (27), with panel (a) (panel (c)) pertaining to bosons (fermions). The bottom panels are the per cent differences of the long-range parameters w and p in equation (27) with respect to the DFA predictions, w − 1 and (p − 3)/3. Here, panel (b) (panel (d)) pertains to bosons (fermions). We note that for quasi-low dimensional confinement 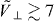 , the predictions for bosons and fermions are the same to a few per cent. This implies that the exchange contribution in equation (25) plays no role for deep lattices, where deep lattices corresponds to
, the predictions for bosons and fermions are the same to a few per cent. This implies that the exchange contribution in equation (25) plays no role for deep lattices, where deep lattices corresponds to 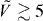 in accordance with our expectations.
in accordance with our expectations.
Figure 4. In all panels the solid (dashed) lines denote the best fit parameters to equation (27) in the quasi-1D (quasi-2D) scenarios as a function of the quasi-low dimensional lattice height 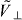 . Panels (a)–(b) pertain to bosons and panels (c)–(d) to fermions. The top panels are the exponential weight ae (red) and the decay constant be (green). The bottom panels are differences of long-range weight w (red) and power p (green) with respect to the DFA. Confinement effects are strongest for large confinement asymmetry, shallow quasi-dimensional confinement and small separation between lattice sites.
. Panels (a)–(b) pertain to bosons and panels (c)–(d) to fermions. The top panels are the exponential weight ae (red) and the decay constant be (green). The bottom panels are differences of long-range weight w (red) and power p (green) with respect to the DFA. Confinement effects are strongest for large confinement asymmetry, shallow quasi-dimensional confinement and small separation between lattice sites.
Download figure:
Standard image High-resolution imageWe chose the ansatz equation (27) from several fit functions because it had the lowest fitting error and it provides a characteristic length scale ac ∼ a/be of the confinement-induced modifications. However, we do not propose that the form of equation (27) is exact. We also stress that the exponential constant be has no a priori relation to the exponential decay constant hn of the Wannier functions. Across a wide range of quasi-low dimensional confinement, ac ∼ 0.2a, and so the moderate range over which confinement modifies interactions is a few lattice sites. While the fact that ac < a means that the modifications of dipole–dipole interactions are quite short range, these modifications can be sizable even out to the second neighbor distance when the coefficient of the short range modification, ae, is large, see figures 4(a), (c) and 5(b). It should also be noted that the confinement-induced modifications of the effective interactions will also have a nontrivial angular dependence due to the fact that Wannier functions are not spherically symmetric, but rather have the symmetries of the lattice. We leave investigations of the nontrivial angular dependence for future work.
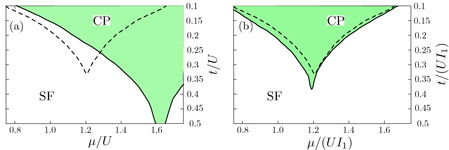
Figure 5. Bordered regions represent iMPS predictions of the superfluid (SF) to crystalline phase (CP) transition. Panel (a) displays the phase diagram with U set to the unit of energy. The region bounded by dashed lines uses the DFA, and has significant deviation from the green region with a solid boundary which uses the numerically determined effective dipole–dipole interaction. The green region will be the phase boundary measured in experiment. Panel (b) is the same phase diagram with the unit of energy set to the nearest-neighbor interaction energy UI1. The effect of the confinement-modified interaction is not a simple rescaling of axes, as seen by the differences between the two bordered regions.
Download figure:
Standard image High-resolution image4. Many-body physics
To illustrate the implications of our findings for many-body physics, we study a model of quasi-1D hard-core bosons with long-range dipolar interactions [64]

Here, the nearest-neighbor tunneling amplitude is t, 〈i,j〉 denotes nearest-neighbor pairs i and j and μ is the chemical potential. We compute the phase diagram of equation (28) for two realizations of Ij using the infinite size variational ground state search algorithm for MPSs (iMPS) [72]. In one realization, we use the DFA result, Ij = j−3. In the second realization, Ij is the effective interaction in an optical lattice computed with Wannier functions, equation (25). We take the lattice heights to be 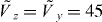 ,
, 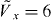 , which fixes the tunneling energy t and ensures that assisted tunneling terms are small. The large confinement asymmetry enforces the hard-core constraint through a large on-site interaction, see appendix B5. Due to the hard-core constraint, the dominant interactions which transfer particles to higher bands occur at the nearest-neighbor distance. Due to the fact that Wannier functions for different bands are orthogonal, the interaction matrix elements of these processes are small and we find that the effect of transitions to higher bands is ≲ 6 times smaller than the effects considered in this paper. We also stress that band excitations at the nearest-neighbor distance and beyond rely crucially on the finite widths of the Wannier functions, and so a quantitative estimate of these processes requires the methods developed in this paper. The coefficient U can be tuned for ultracold polar molecules by an applied dc electric field. One can determine the strength of the interaction U = UDD,0 knowing only the expected dipole moment and the lattice constant from single-particle physics. Since our goal is to demonstrate deviations of many-body predictions using the true effective dipole–dipole interactions from the DFA, we will scale the phase diagram to U, as this is the nearest-neighbor interaction energy predicted by the DFA.
, which fixes the tunneling energy t and ensures that assisted tunneling terms are small. The large confinement asymmetry enforces the hard-core constraint through a large on-site interaction, see appendix B5. Due to the hard-core constraint, the dominant interactions which transfer particles to higher bands occur at the nearest-neighbor distance. Due to the fact that Wannier functions for different bands are orthogonal, the interaction matrix elements of these processes are small and we find that the effect of transitions to higher bands is ≲ 6 times smaller than the effects considered in this paper. We also stress that band excitations at the nearest-neighbor distance and beyond rely crucially on the finite widths of the Wannier functions, and so a quantitative estimate of these processes requires the methods developed in this paper. The coefficient U can be tuned for ultracold polar molecules by an applied dc electric field. One can determine the strength of the interaction U = UDD,0 knowing only the expected dipole moment and the lattice constant from single-particle physics. Since our goal is to demonstrate deviations of many-body predictions using the true effective dipole–dipole interactions from the DFA, we will scale the phase diagram to U, as this is the nearest-neighbor interaction energy predicted by the DFA.
The iMPS method assumes that the many-body ground state has translational invariance under shifts by q sites, and represents the wave function of the q-site unit cell as a MPS [47] with entanglement cutoff χ. One minimizes the energy functional of the unit cell variationally in the parameters of the matrix product, using a sweeping procedure across sites in the unit cell reminiscent of the density-matrix renormalization group (DMRG) procedure for finite lattices [75]. Alternating with unit cell minimization is an updating of the effective environment of the unit cell using the most current parameters of the unit cell. The procedure is halted when the two-norm distance between the unit cell in successive optimizations drops below a desired tolerance. Long-range interactions are facilitated within iMPS by using matrix product operators and fitting the interaction Ij to a sum of exponentials [76–78]. The advantage of the iMPS method for the problem at hand is its ability to handle strong long-range interactions without the significant boundary effects that plague DMRG-type procedures on finite lattices. All results given here have been checked for convergence in the entanglement cutoff χ and the unit cell length q.
The phase diagrams of equation (28) for the DFA and lattice-modified dipolar interactions are shown in figure 5. The bordered areas represent predicted regions of crystalline phase (CP) with density ρ = 1/2 and a non-vanishing single-particle gap. The remainder of the plots are a gapless superfluid phase. In the CP, the density correlation function 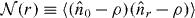 behaves as
behaves as 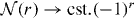 as r → ∞ and the single-particle density matrix
as r → ∞ and the single-particle density matrix 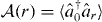 is exponentially decaying with r. In panel (a), the area bounded with dashed lines represents the region of CP computed using the DFA in the parameters μ/U and μ/U. The green area bordered with solid lines represents the CP boundaries computed with the actual lattice dipolar interaction. The region predicted by the DFA is shifted both in chemical potential and tunneling by approximately I1 − 1 ≈ 36%. However, the difference between the DFA and the true solution is not a simple rescaling of the axes. This is shown in panel (b), which rescales the chemical potential and tunneling to the nearest-neighbor interaction energy, μ/(UI1) and t/(UI1). The fact that a difference between the DFA and the true interaction persists even when the phase diagram is rescaled to the nearest-neighbor interaction energy demonstrates that the modifications of the dipole–dipole potential are significant beyond the nearest-neighbor distance due to either strong short-range interactions or significant modification of the long-range algebraic tail, see equation (27) and figure 4. The accuracy of the DFA will increase with increasing lattice depth and lesser confinement imbalance. Similar changes in the phase diagram will occur for the 2D case, with shifts of about 48% for the parameters of [43]. For soft-core particles which also possess local, isotropic interactions, the modified dipolar interaction will be relevant to the convexity of the interaction potential and hence to the formation of supersolid phases [79].
is exponentially decaying with r. In panel (a), the area bounded with dashed lines represents the region of CP computed using the DFA in the parameters μ/U and μ/U. The green area bordered with solid lines represents the CP boundaries computed with the actual lattice dipolar interaction. The region predicted by the DFA is shifted both in chemical potential and tunneling by approximately I1 − 1 ≈ 36%. However, the difference between the DFA and the true solution is not a simple rescaling of the axes. This is shown in panel (b), which rescales the chemical potential and tunneling to the nearest-neighbor interaction energy, μ/(UI1) and t/(UI1). The fact that a difference between the DFA and the true interaction persists even when the phase diagram is rescaled to the nearest-neighbor interaction energy demonstrates that the modifications of the dipole–dipole potential are significant beyond the nearest-neighbor distance due to either strong short-range interactions or significant modification of the long-range algebraic tail, see equation (27) and figure 4. The accuracy of the DFA will increase with increasing lattice depth and lesser confinement imbalance. Similar changes in the phase diagram will occur for the 2D case, with shifts of about 48% for the parameters of [43]. For soft-core particles which also possess local, isotropic interactions, the modified dipolar interaction will be relevant to the convexity of the interaction potential and hence to the formation of supersolid phases [79].
5. Conclusions
In conclusion, we have shown that the dipole–dipole interaction can be strongly modified by imperfect localization of particles in an unequally confined lattice, as found in many experiments in ultracold quantum gases. In particular, we demonstrated that the effective dipole–dipole interactions in optical lattices, given by the matrix elements of the dipole–dipole interaction in a basis of lowest band Wannier functions, can be significantly modified from the free-space form of the dipole–dipole interaction. The modifications of the dipole–dipole interaction arise both from interactions in the exchange channel, controlled by the overlap between Wannier functions at different sites, and interactions in the direct channel. The latter interactions depend crucially on the asymmetry in lattice confinement due to the d-wave symmetry of the dipole–dipole interaction. We compared our results to results obtained by approximating Wannier functions as localized Gaussians. Interactions in the direct channel are qualitatively reproduced by this approximation, though estimates of the magnitude can be off by significant factors. Interactions in the exchange channel are quantitatively very poor in the exchange channel, underestimating interactions by orders of magnitude. Based on numerical results, we put forward a simple characterization of the modified interaction as being exponential at moderate separations of a few lattice sites and power-law for large separations. Using iMPS simulations, we showed that the modified interaction can significantly alter the predictions of many-body systems, including the determination of phase diagrams.
Acknowledgments
We acknowledge useful discussions with Mahadevan Ganesh, Kenji Maeda and Zhigang Wu. This research was supported in part by the National Science Foundation under Grants PHY-1207881 and NSF PHY11-25915, by AFOSR grant number FA9550-11-1-0224, by the Heidelberg center for Quantum Dynamics and by the Alexander von Humboldt Foundation. We also acknowledge the Golden Energy Computing Organization at the Colorado School of Mines for the use of resources acquired with financial assistance from the National Science Foundation and the National Renewable Energy Laboratories. We would like to thank the KITP for hospitality.
Appendix A.: Numerical procedures to compute Hubbard parameters
In this section, we discuss numerical techniques for computing geometrical integrals such as equation (19) which determine the effective interaction between particles localized in lowest band Wannier states. Such integrals may be written in the general form
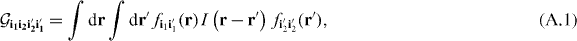
where 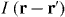 is the dimensionless two-particle potential. The first method employs the convolution theorem to express the integration over the primed coordinates in equation (A.1) as a function of the unprimed coordinates with high accuracy. The remaining 3D integral is then performed with standard numerical quadrature. We will call this method the real-space method. In the second method, we compute the interaction matrix elements of the dipole–dipole interaction potential in the basis of lowest band Bloch functions. The matrix elements in the Wannier basis are then obtained by quasi-momentum Fourier transform. We will refer to this latter method as the Bloch expansion method. Both methods exhibit steep scaling with the linear domain size L which prohibits studies of very large systems. In order to ensure well-converged results, we restricted our analysis to a separation of at most seven lattice sites, see section 3.
is the dimensionless two-particle potential. The first method employs the convolution theorem to express the integration over the primed coordinates in equation (A.1) as a function of the unprimed coordinates with high accuracy. The remaining 3D integral is then performed with standard numerical quadrature. We will call this method the real-space method. In the second method, we compute the interaction matrix elements of the dipole–dipole interaction potential in the basis of lowest band Bloch functions. The matrix elements in the Wannier basis are then obtained by quasi-momentum Fourier transform. We will refer to this latter method as the Bloch expansion method. Both methods exhibit steep scaling with the linear domain size L which prohibits studies of very large systems. In order to ensure well-converged results, we restricted our analysis to a separation of at most seven lattice sites, see section 3.
A.1. Real-space method
In the real-space method, we begin with equation (A.1) and apply the convolution theorem to find
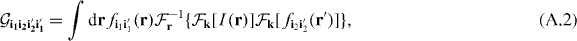
where ![$\mathcal {F}_{\mathbf {k}}[g(\mathbf {r})]$](https://content.cld.iop.org/journals/1367-2630/15/12/123005/revision1/nj474403ieqn45.gif) denotes the Fourier transform of the function g(r) as a function of k and likewise for the inverse transform
denotes the Fourier transform of the function g(r) as a function of k and likewise for the inverse transform 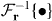 . For example, the Fourier transform of the spatial part of the dipole–dipole potential is
. For example, the Fourier transform of the spatial part of the dipole–dipole potential is ![$\mathcal {F}_{\mathbf {k}}[{C^{(2)}_q(\mathbf {r})}/{r^3}]=- {4\pi }C^{(2)}_q(\mathbf {k})/3$](https://content.cld.iop.org/journals/1367-2630/15/12/123005/revision1/nj474403ieqn47.gif) , 6 and the Fourier transform of the delta-function potential is a constant. Hence, the evaluation of the Hubbard parameter may be computed by 3D Fourier transforms followed by a 3D integration in real-space rather than by a six-dimensional real-space integral. To perform these procedures numerically, we consider each Cartesian dimension to be a symmetric finite interval S = [ − L/2,L/2] with periodic boundary conditions, and discretize each interval with ng grid points. The grid spacing in the discrete Fourier conjugate domain is 2π/L and the extent of the domain in Fourier space is controlled by πng/L, the inverse real-space step size. The transformation from a function to its discrete Fourier conjugate is performed by the fast Fourier transform algorithm in
, 6 and the Fourier transform of the delta-function potential is a constant. Hence, the evaluation of the Hubbard parameter may be computed by 3D Fourier transforms followed by a 3D integration in real-space rather than by a six-dimensional real-space integral. To perform these procedures numerically, we consider each Cartesian dimension to be a symmetric finite interval S = [ − L/2,L/2] with periodic boundary conditions, and discretize each interval with ng grid points. The grid spacing in the discrete Fourier conjugate domain is 2π/L and the extent of the domain in Fourier space is controlled by πng/L, the inverse real-space step size. The transformation from a function to its discrete Fourier conjugate is performed by the fast Fourier transform algorithm in  time [80]. Because the Wannier functions on a finite domain are periodic and band-limited, their discrete and continuous Fourier transforms are related by a scaling constant provided we sample the entire domain at a frequency of at least twice their largest frequency component [80]. As is known for spectral methods, convergence of the Fourier space calculation in equation (A.2) is exponential in L provided that ng/L is large enough to capture the full support of the function in Fourier space. Defining g to be the support of the lowest band Wannier function in the discrete Fourier space, the choice ng = 2gL + 1 ensures that the function is fully captured in Fourier space. The support of a Wannier function in Fourier space can be determined by using Parseval's theorem on finite Fourier subintervals to determine that the norm is unity to a desired tolerance. For typical g ∼ 5 − 7, the real-space integration in equation (A.2) is of acceptable precision using a high-order Simpson integrator [81].
time [80]. Because the Wannier functions on a finite domain are periodic and band-limited, their discrete and continuous Fourier transforms are related by a scaling constant provided we sample the entire domain at a frequency of at least twice their largest frequency component [80]. As is known for spectral methods, convergence of the Fourier space calculation in equation (A.2) is exponential in L provided that ng/L is large enough to capture the full support of the function in Fourier space. Defining g to be the support of the lowest band Wannier function in the discrete Fourier space, the choice ng = 2gL + 1 ensures that the function is fully captured in Fourier space. The support of a Wannier function in Fourier space can be determined by using Parseval's theorem on finite Fourier subintervals to determine that the norm is unity to a desired tolerance. For typical g ∼ 5 − 7, the real-space integration in equation (A.2) is of acceptable precision using a high-order Simpson integrator [81].
There are two dominant sources of error in the real-space method. The first error is due to the discretization of the real-space domain and the associated discretization error of the numerical quadrature. This error may be controlled by increasing g. The second source of error is spurious interactions due to periodic boundary conditions. While these interactions vanish as the domain becomes infinite, convergence may be slow due to, e.g. the power-law decay of the dipole–dipole interaction at long range. Hence, we have instead used a finite-size scaling analysis to extrapolate our results to the limit of an infinite lattice. The main limitation on the system sizes that we can reach using the real-space method is a memory requirement which scales as 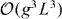 due to the non-separability of the dipole–dipole potential.
due to the non-separability of the dipole–dipole potential.
A.2. Bloch expansion method
In the Bloch expansion method, we study the matrix elements of the interaction potential in the basis of lowest band Bloch functions 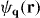 ,
,
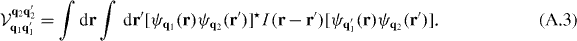
The geometric integral equation (A.1) is then given by
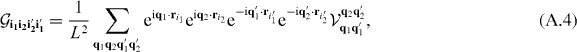
see equation (3). Using the fact that the interaction potential depends only on the relative coordinate, we find

where R is any Bravais lattice vector and Q ≡ q1' + q2' − q1 − q2 modulo 2π. This implies that there are only N3 independent non-vanishing matrix elements in equation (A.3) for a lattice with N unit cells, as opposed to the N4 possible configurations of the four quasi-momenta. As in the main text, we will study the case of the simple cubic lattice in which the Bloch functions separate along principal axes,

The separability of the Bloch functions allows us to write the integral equation (A.3) in the form
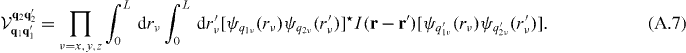
Changing integration variables to 2ξν ≡ rν + rν', 2ην ≡ rν − rν' with Jacobian 2 along each Cartesian direction and expanding the 1D Bloch functions as

with L the number of lattice sites along each Cartesian direction, we find
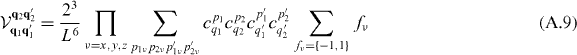
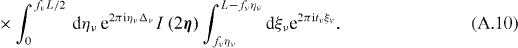
Here, ℓ is a finite Fourier cutoff used in numerics and we have defined
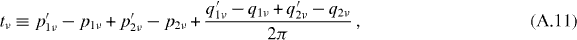

The integrals over ξν are
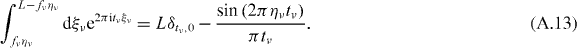
We will keep only the term proportional to the Kronecker delta, as this is the dominant contribution for large lattices. This approximation becomes exact in the limit of an infinite lattice, L → ∞, as has been shown for the delta-function potential in [28]. For simplicity, we now also require that the interaction potential is invariant under inversion by any Cartesian coordinate. This is true for the q = 0 component of the dipole–dipole interaction, as well as for the delta function potential. However, the method directly extends to more general interactions. With these two conditions, we find in the limit as L → ∞,
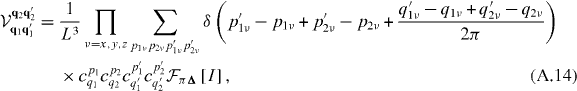
where ![$\mathcal {F}_{\mathbf {k}}[I]$](https://content.cld.iop.org/journals/1367-2630/15/12/123005/revision1/nj474403ieqn51.gif) is again the Fourier transform of I as a function of k and
is again the Fourier transform of I as a function of k and 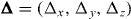 .
.
The Bloch expansion method has the advantage of not introducing any discretization error, and also requires significantly less memory when the lattice is separable. However, the computational scaling of this method is  as opposed to
as opposed to  for the real-space method. The Bloch expansion method suffers from spurious interactions due to periodic boundary conditions, just as in the real-space method. We find that both methods agree when we extrapolate to the limit L → ∞, and allow us to put a conservative bound of 1% on our estimated error. Additionally, we have benchmarked both methods with the case of a delta-function potential, where both analytical and numerically exact results are available.
for the real-space method. The Bloch expansion method suffers from spurious interactions due to periodic boundary conditions, just as in the real-space method. We find that both methods agree when we extrapolate to the limit L → ∞, and allow us to put a conservative bound of 1% on our estimated error. Additionally, we have benchmarked both methods with the case of a delta-function potential, where both analytical and numerically exact results are available.
Appendix B.: Dipole–dipole interaction energy of the anisotropic harmonic oscillator
In this appendix we derive the dipolar interaction energy of two particles in the ground state of an anisotropic harmonic oscillator, equation (26) of the main text, and compare the results with the on-site interaction energy in an optical lattice. As in the main text, we use the quasi-2D geometry ℓx = ℓy ≡ ℓ⊥ and choose the harmonic oscillator lengths to match the local curvature of a lattice site minimum via

The ground state wave function may be written in cylindrical coordinates as

where ρ2 = x2 + y2. Using the convolution theorem, we can write the dimensionless dipolar interaction energy as

where
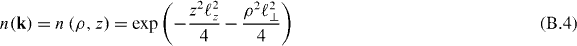
is the Fourier transform of the density and θ is the angle between k and the z-axis. Performing the integration in equation (B.3) over z and ϕ yields
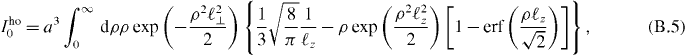
with  the error function. Integrating over ρ yields
the error function. Integrating over ρ yields
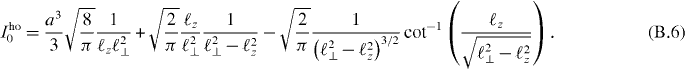
Inserting the definitions from the main text,  , α ≡ ℓz/ℓ⊥ and β ≡ α(1 − α2)−1/2, we find
, α ≡ ℓz/ℓ⊥ and β ≡ α(1 − α2)−1/2, we find
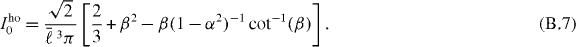
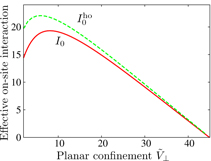
A comparison between the function equation (B.7) with the oscillator lengths chosen as in equation (B.1) and the result computed via Wannier functions as explained in appendix A is given in figure B.1. We find that the on-site interaction energy in the harmonic oscillator is always larger than the corresponding energy in an optical lattice, often by 10%. Additionally, the on-site interaction is large for small to moderate V∥, enforcing the hard-core constraint used in the many-body study in the main text.
Figure B.1. The on-site dipolar interactions in a quasi-2D lattice, I0 (red solid line), and the dipolar interaction energy of a cylindrically symmetric harmonic oscillator with the same local curvature as the lattice site, Iho0 (green dashed line), have similar qualitative behavior with respect to confinement asymmetry. In particular, both vanish as the confinement becomes isotropic,  , and are significant for large confinement asymmetry.
, and are significant for large confinement asymmetry.
Download figure:
Standard image High-resolution imageFootnotes
- 5
- 6
The Fourier transform of the dipole–dipole potential is ill-defined at k = 0, but our results do not depend on this value.