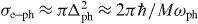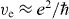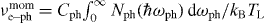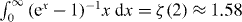Ultrafast electronic relaxation in superheated bismuth

In ultra-short laser–matter interaction the electrons absorb the energy during the pulse leaving the lattice cold for a period necessary for the energy transfer. The optical, transport and relaxation properties of a swiftly excited solid are all time- and temperature-dependent and mutually inter-related by fundamental kinetics laws. Studying the relaxation processes provides key understanding for the lattice transformations and micro-processing of materials with short pulse lasers, formation of new material by laser induced micro-explosion and non-equilibrium phenomena in astrophysics.

The electron energy, E_e = C_e (T_e )n_e T_e , increases due to energy absorption from the laser field, 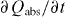${{\partial Q_{{\rm{abs}}} }/ {\partial t}}$, and decreases through the electron–phonon interaction, 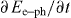${{\partial E_{{\rm{e}}\kern-1pt-\kern-1pt{\rm{ph}}} } / {\partial t}}$, and losses through electronic heat conduction κ:

$$\begin{equation} \frac{{\partial E_{\rm e} }}{{\partial t}} = \frac{{\partial Q_{{\rm{abs}}} }}{{\partial t}} - \frac{{\partial E_{{\rm e}\kern-1pt-\kern-1pt{\rm{ph}}} }}{{\partial t}} - \nabla \kappa \nabla T_{\rm e} . \end{equation} \noindent \tag{ 1 }$$

The energy transfer from the swiftly heated electrons to cold phonons has been first considered in [1]. The temperature exchange term was derived from kinetic equation under assumption that electrons and phonons possess the equilibrium distribution functions with different temperatures, T_e ≫ (T_L;ℏ ω_ph). In this case the temperature relaxation term takes the form 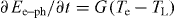${{\partial E_{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}} } / {\partial t}} = G(T_{\rm e}- T_{\rm{L}} )$, similar to that obtained by Landau for the electron–ion exchange in plasma [2, 3]. The energy coupling coefficient, G = C_e (T_e ) n_e ν_e-ph^en (T_L ) , is product of electronic heat capacity, 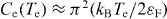$C_{\rm e} (T_{\rm e} ) \approx \pi ^2 ({{k_{\rm{B}} T_{\rm e} } / {2\varepsilon _{\rm{F}} }})$, electron density n_e, and electron–phonon energy exchange rate ν_e-ph^en . The energy conservation law couples the equations for the electron and lattice temperatures, 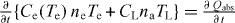$\frac{\partial }{{\partial t}}\{ {C_{\rm e} (T_{\rm e} )\,n_{\rm e} T_{\rm e}+ C_{\rm{L}} n_{\rm{a}} T_{\rm{L}} } \} = \frac{{\partial {\kern 1pt} Q_{{\rm{abs}}} }}{{\partial {\kern 1pt} t}}$, thus producing the familiar set of two-temperature equations. These equations have been broadly used with the temperature relaxation set constant [4]. We note that all three terms in the energy equation (1) are inherently linked to each other. Indeed, the absorbed energy density rate expresses via the gradient of the Pointing vector. After the averaging over the field period and applying the boundary conditions it transforms to the form ${{\partial Q_{{\rm{abs}}} } / {\partial t}} = {{2AI}\!/ {l_{\rm{s}} }}$, where the Fresnel absorption coefficient A and the absorption length l_s both are functions of dielectric permittivity [5, 6]. I(t) is laser intensity.

The transfer of momentum and energy in a single act of electron–phonon scattering is small. The energy equilibration between species in such interaction is considered as diffusion along the energy axis. The energy exchange rate in this case appears to be proportional to the momentum rate [7]. The momentum exchange rate averaged by a distribution function is proportional to the lattice temperature [8–10]. Thus, the energy exchange rate, ν_e-ph^en , should be temperature-dependent function. Landau used this approach to establish a link between the energy and momentum exchange rates for electron–ion interaction in plasma at T_e ≫ T_i [2, 3]. Note, that momentum exchange rate is an explicit function of the real and imaginary part of dielectric permeability. The heat conduction coefficient is an explicit function of the momentum exchange rate through the diffusivity, 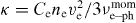$\kappa= {{C_{\rm e} n_{\rm e} v_{\rm e}^2 } / {3\nu _{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} }}$. Thus, all three terms in equation (1) are inter-related and temperature dependent. Setting any one of the parameters in a chain of inherently linked time and temperature dependent characteristics of excited matter constant creates inconsistency between the optical, transport and relaxation coefficients. This inconsistency produced many controversies in the interpretation of laser–matter interaction experiments performed in similar experimental conditions [11–19].

In this paper we link the electron–phonon momentum and energy exchange rates with the help of kinetic equation transformed in agreement with Landau's guidelines [2, 3], and obtain the explicit temperature dependence for both rates. Then we recover the temperature-dependent electron–phonon collision rate from the measurements of dielectric function in equilibrium and show that theory presented here complies with experiments. We apply the temperature dependent optical, transport and relaxation coefficients to interpret the results of ultrashort laser excitation of Bi with single pump and double probe, and with double pump and single probe experiments. We demonstrate that the obtained temperature dependence complies well with the transient dielectric function recovered from ultra-short laser excited Bi. Finally, the energy relaxation coefficient is established as a function of temperature and laser fluence. Presented analysis of experiments on excitation of Bi by ultra-short lasers using temperature-dependent relaxation rates shows that all observed phase transformations occur after electron and lattice temperature equilibration.

2.1. Electron–phonon energy exchange rates

Energy loss of energetic electrons to the cold lattice [1] expresses via the Boltzmann–Peierls–Bloch collision integral I_e-ph(ε_e-ph) taken over all electron and phonon states under the assumption that the medium is isotropic [1, 5]:

$$\begin{equation} \frac{{\partial E_{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}} }}{{\partial t}} = \frac{3}{2}\int_0^{\varepsilon _{\rm{F}} + k_{\rm{B}} T_{\rm e} } {I_{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}} \left( {\varepsilon _{\rm e} } \right)\,n_{\rm e} \left( {\frac{{\varepsilon _{\rm e} }}{{\varepsilon _{\rm{F}} }}} \right)^{3/2} } {\rm{d}}\varepsilon _{\rm e} . \end{equation} \tag{ 2 }$$

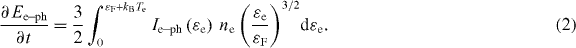
Separating integration by electronic states and phonon states in different terms reduces equation (2) to the familiar form: 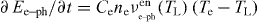${{\partial {\kern 1pt} E_{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}} } / {\partial t}} = C_{\rm e} n_{\rm e} \nu _{_{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}} }^{{\rm{en}}} (T_{\rm{L}} )\,(T_{\rm e}- T_{\rm{L}} )$; where the energy relaxation rate is explicitly introduced as

$$\begin{equation} \nu _{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{en}}} \left( {T_{\rm{L}} } \right) = \int_0^\infty {\frac{{3(\hbar \omega _{{\rm{ph}}} )^2 }}{{2\varepsilon _{\rm{F}} k_{\rm{B}} T_{\rm{L}} }}N_{{\rm{ph}}} n_{\rm{e}} w\left( k \right){{{\rm{d}}^3 k}/{\left( {2\pi } \right)^3 }}} . \end{equation} \noindent \tag{ 3 }$$

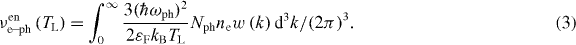
In agreement with the Landau's approach [2, 3] we replace the probability of the electron–phonon scattering per unit time with the elastic collision rate, 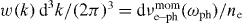${{w(k)\,{\rm{d}}^3 k}/{(2\pi )^3 }} = {\rm{d}}{{\nu _{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} (\omega _{{\rm{ph}}} )}/{n_{\rm e} }}$. Therefore integration over quasi-momentum space is replaced by the integration over all collision events. It is also assumed that the number density of electrons and the Fermi energy are both constant. Then, the energy exchange rate reduces to the following:

$$\begin{equation} \nu _{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{en}}} \left( {T_{\rm{L}} } \right) = \int {\frac{{N_{{\rm{ph}}} (\hbar \omega _{{\rm{ph}}} )^2 }}{{\varepsilon _{\rm{F}} k_{\rm{B}} T_{\rm{L}} }}{\rm{d}}\nu _{{\rm e} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} } \left( {\omega _{{\rm{ph}}} } \right), \end{equation} \noindent \tag{ 4 }$$

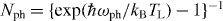where $N_{{\rm{ph}}}= \{ \exp ({{\hbar \omega _{{\rm{ph}}} } / {k_{\rm{B}} T_{\rm{L}} }}) - 1\} ^{ - 1}$ is the Bose–Einstein distribution for phonons. The microscopic momentum exchange rate is proportional to the phonon frequency, ν_e-ph^mom = C_ph ω_ph .¹ Averaging by the phonon distribution function one obtains the well-known linear dependence, 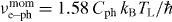$\nu _{{\rm{e}}\kern-1pt-\kern-1pt{\rm{ph}}}^{{\rm{mom}}}= 1.58\,C_{{\rm{ph}}}\,{{k_{\rm{B}} T_{\rm{L}} } / \hbar }$;² we are omitting the averaging sign for simplicity. Integrating equation (4) one obtains the explicit link between the momentum and energy exchange rates:

$$\begin{equation} \nu _{{\rm{e}}\kern-1pt-\kern-1pt{\rm{ph}}}^{{\rm{en}}} \left( {T_{\rm{L}} } \right) = \frac{{2.28k_{\rm{B}} T_{\rm{L}} }}{{\varepsilon _{\rm{F}} }}\nu _{{\rm{e}}\kern-1pt-\kern-1pt{\rm{ph}}}^{{\rm{mom}}} \left( {T_{\rm{L}} } \right). \end{equation} \noindent \tag{ 5 }$$

The rates in the above formulae are the functions, as a first order approximation, only of the lattice temperature, in condition ε_F > T_e ≫  (T_L;ℏ ω ph ) . The dependence on the electron temperature appears in the second order term proportional to 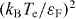$({{k_{\rm{B}} T_{\rm{e}} } / {\varepsilon _{\rm{F}} }})^2$ [5]. In the temperature range where the above model holds (k_B T_e <  0.1ε _F ) this correction is negligible. Now one can retrieve all three inter-connected coefficients in equation (1) responsible for heating and relaxation directly from the experiments.

2.2. Link between momentum exchange rate and dielectric function

The real and imaginary parts of dielectric function of bismuth were measured in equilibrium in temperature range 294–773 K by optical ellipsometry at 800 nm [20–22] (see figure 1(a)), and analysed in [23]. The measured values at room temperature coincide well to those in the reference books [24]. It was found long ago that dielectric permittivity of Bi at room temperature (>293 K) and higher obeys well the Drude function [21, 22]. In this case the collision frequency, 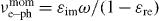$\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}}= {{\varepsilon _{{\rm{im}}} \omega } / {(1 - \varepsilon _{{\rm{re}}} )}}$, and the electron plasma frequency ω_pe, ${{\omega _{{\rm{pe}}}^2 }/ {\omega ^2 }} = \left( {1 - \varepsilon _{{\rm{re}}} } \right)\{ 1 + ({{\varepsilon _{{\rm{im}}} } / {1 - \varepsilon _{{\rm{re}}} }})^2 \}$, both are the unique functions of the real and imaginary parts of the permittivity. 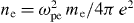Moreover, under the assumption that the electron mass is the same as for a free particle, the number density of electrons in the conduction zone, $n_{\rm{e}}= \omega _{{\rm{pe}}}^2 \,{{m_{\rm{e}} } / {4\pi \,e^2 }}$, the Fermi energy, 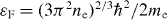$\varepsilon _{\rm{F}}= (3\pi ^2 n_{\rm{e}} )^{{2 / 3}} {{\hbar ^2 }/{2m_{\rm{e}}}}$, and electronic heat capacity can be directly recovered from the experiments as a function of temperature. The momentum exchange rate and the Fermi velocity govern electronic heat conduction in the conditions k_BT_e ≪ ε_F.

Zoom In Zoom Out Reset image size

Temperature dependence of the electron–phonon momentum exchange rate based on the ellipsometry measurements of dielectric function at 775 nm is presented in figure 1(a). The linear dependence of momentum exchange rate on temperature is well justified for a solid metal. The frequency of atomic vibrations in liquid has similar behaviour 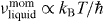$\nu _{{\rm{liquid}}}^{{\rm{mom}}}\propto {{k_{\rm{B}} T}\!/ \hbar }$, however, the proportionality coefficients might be different. Bismuth is a semimetal at T < T_room with a complicated structure of the Fermi surface (small band gap and overlap are intermittent in the quasi-momentum space). The difference between the energy of dielectric and metallic phases is small owing to a small band gap (∼0.015 eV at 10 K). This structure is completely destroyed by a rising pressure, or by increase in temperature, as elucidated by Abrikosov [25] in the 1960s. The real part of dielectric function of Bi at 800 nm and at room temperature is negative [24]: $\varepsilon _{{\rm{re}}}^{{\rm{Bi}}} = -{\rm{16}}.{\rm{25}}$, thus Bi in these conditions behaves as a good metal. It should be mentioned that the density of liquid Bi is higher than that for solid as it is characteristic for open structure crystals. However, it is still unclear if the solid–liquid phase transition is of the first or of the second order. Thus, a jump in the temperature dependence of some parameters at the melting point cannot be excluded [26].

We should note here that thermal diffusivity of metals directly relates to the collision rate: $D = {{v_{\rm{F}}^2 } / {3\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} }}$. However, the diffusivity values D = (2.9–2.1) cm² s⁻¹ recovered from the ellipsometry measurements of the dielectric function at 775 nm at room temperature and above [20–22, 24] are in sharp discrepancy to the bulk value of 0.067 cm² s⁻¹ from the reference books measured by calorimetric methods (see, e.g., [27]), indicating metallic behaviour of Bi in optical spectral range. One possible explanation of the discrepancy in the heat conduction is that the processes of the electronic heat conduction in the bulk are different from those on the surface exposed to the high-frequency laser field.

2.3. Electron–phonon relaxation

Now we shall use the energy exchange rate linked to the momentum rate for recovering the temperature relaxation coefficient from experiments. The experimental dependence of the momentum rate is close to the linear law in solid as well as in liquid state, $\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} ( {T_{\rm{L}} } ) \approx ( {{T / {T_{{\rm{room}}} }}})\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} \left( {T_{{\rm{room}}} } \right)$ in agreement with other equilibrium data and the theory [8–10]. The energy exchange increases slower, $\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{en}}} \left( {T_{\rm{L}} } \right) \approx \left( {{T / {T_{{\rm{room}}} }}} \right)^{1.33}\! 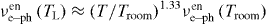\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{en}}} \left( {T_{{\rm{room}}} } \right)$, due to experimentally observed temperature dependence of the Fermi energy and electron number density, which are assumed constant in theory—see figure 2(a). The temperature relaxation time at room temperature appears to be very short, ∼43 fs, and it decreases to ∼11 fs at 773 K.

Zoom In Zoom Out Reset image size

However, there is a natural upper limit for the collision rate. Indeed, the mean free path for collisions, l_mfp = v_e /ν_e-ph^mom, cannot be less than the inter-atomic distance [9, 28]³. Thus, the upper limit for the collision rate is set by the condition v_e/r_a ⩾ ν_e-ph^mom. For Bi this limit equals to ∼10¹⁶ s⁻¹ (r_a = 2.04 × 10^–8 cm; v_e,max ∼ 1.9 × 10⁸ cm s⁻¹). The momentum exchange rate reaches maximum at the temperature $T_{\nu _{\max } }\approx T_{{\rm{room}}} [{{v_{\rm{e}} } / {r_{\rm{a}} \nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}} (T_{{\rm{room}}} )}}]$. For Bi this temperature equals to ∼1400 K. Note that Bi in equilibrium remains in a liquid state within a temperature span of 1292 K (the melting point is ∼545 K, the boiling point is ∼1837 K) [24, 27]. It is worth noting that the fundamental upper limit for the collision rate is also set by the atomic frequency $\omega _{{\rm{at}}} :{\rm{ }}\nu _{{\rm{e}} \kern-1pt-\kern-1pt {\rm{ph}}}^{{\rm{mom}}}\leqslant \omega _{{\rm{at}}}= {{m_{\rm{e}} e^4 } / {\hbar ^3 }}$. 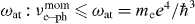With temperature growth well above the limit, the collision rate remains at the maximum level until ionization becomes essential. Then, contribution of electron–ion collisions, ν_ei^mom∝T_e ^{- 3/2} , leads to the decreasing of the average effective rate with increase of temperature. It occurs when the temperature approaches several eV, comparable to the ionization potential [5, 9].

The temperature relaxation coefficient retrieved from experiments grows slower, 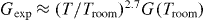$G_{\exp }\approx ({T / {T_{{\rm{room}}} }})^{2.7} G(T_{{\rm{room}}} )$, than predicted by theory, 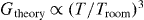$G_{{\rm{theory}}}\propto ({T / {T_{{\rm{room}}} }})^3$, because the electron number density and the Fermi energy both appear to be temperature dependent. For Bi at room temperature G(T_room) = 4.17 × 10¹¹ W cm⁻³ K⁻¹ is of the same order of magnitude as for other metals [29, 30]. Saturation of G is expected at the maximum temperature estimated above, G_max ∼ 1.27 × 10¹³ W cm⁻³ K⁻¹. At elevated temperature and at significant ionization level the electron–ion relaxation coefficient along with collision rates decreases with temperature, G_ion∝T_e^{- 3/2} .

Femtosecond laser–solid interactions create non-equilibrium transient states of matter where, along with the electron–lattice equilibration, other relaxation processes take place. Probing Bi, excited by a single pump, by two simultaneous optical probes allows measuring both real and imaginary parts of dielectric function with sub-picosecond time resolution and therefore to obtain a deeper insight into the time history of material restructuring [14–18].

Bismuth crystal was excited by 50 fs, 775 nm, 6.9 mJ cm⁻² pump pulse and probed by two synchronized optical pulses set to reflect at two different angles, 19.5° and 34.5°. The reflectivity changes were measured with an accuracy of 10⁻⁵ [14, 15]. The pump beam was p-polarized whereas the two probes arriving at different angles on the sample surface were s-polarized. The time-dependent real and imaginary parts of the dielectric function were retrieved from numerical solution of two equations for two reflection coefficients expressed by the Fresnel formulae (see figure 3).

Zoom In Zoom Out Reset image size

The absorbed energy density delivered by a 6.9 mJ cm⁻² pump pulse equals to 1.24 kJ cm⁻³ that is 2.5 times larger the equilibrium enthalpy of Bi melting [27]. That means that the maximum temperature at the end of the 50 fs pulse is around 1360 K (2.5 × T_m) and thus, as follows from the temperature dependent relaxation rates established above, the electron and lattice temperatures are equilibrated well before the end of the pulse. For this reason, it is legitimate to use the extrapolation of the temperature dependence of the dielectric function in equilibrium for interpretation of optical properties under fast excitation. The imaginary part of the dielectric function reaches maximum, (ε_im)_max = 37 at the end of the 50 fs laser pulse (figure 3). Using extrapolation of the equilibrium data, 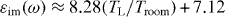$\varepsilon _{{\rm{im}}} (\omega ) \approx 8.28({{T_{\rm{L}} } / {T_{{\rm{room}}} }}) + 7.12$, one finds that the maximum of the imaginary part is reached at 1060 K. The maximum temperature can be also recovered independently from the energy conservation, T_L,max = 1328 K.⁴ All three temperature estimates give qualitatively similar results indicating that the temperature dependence predicted by the theory above and supported by equilibrium experiments describes the experiments with 50 fs laser excitation of bismuth rather well. Moreover, the equilibrium thermal diffusion of D = (2.9–2.1) cm² s⁻¹ is in a good agreement with the non-equilibrium data from fs-laser excited bismuth, D = 2.3 cm² s⁻¹, from [13] giving the cooling time 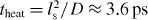$t_{{\rm{heat}}} = l_{\rm{s}}^2 /D \approx {\rm{3}}.{\rm{6}}\,{\rm{ps}}$. However, one can see that dielectric function drops faster then it is predicted by the heat conduction either for solid or liquid indicating on unusual structural changes. Indeed, after 15 ps the excited Bi attains a quasi-stationary phase state different from a solid and a liquid state, which lasts up to ∼4 ns before returning to the initial conditions [17]. The transient state at temperature apparently close to the room temperature remains less metallic than melted bismuth.

Double-pump experiments with a time delay between the pumping pulses also support the conclusion on fast cooling followed from the equilibrium heating and from the double probe experiments [17]. The experiments were performed in order to excite and then to probe the transient state, where the second pump pulse arrived 25 ps after the first pump. The time-dependent reflectivity functions of the probe after the first and second pump were almost identical, apart from a small shift in oscillation frequency indicating 20–40 K increase of lattice temperature [17]. Fast cooling time of 3.6 ps suggests that during 25 ps after the first pump the excited Bi is cooled down almost to the room temperature, but remains in the transient phase state. High superheating in equilibrium would indicate complete melting. However it is well known that a perfect, defects-free crystal can be strongly superheated without melting even in equilibrium conditions [31, 32]. It is also known that thermal disordering and thermal point defects contribute almost equally to the entropy catastrophe value, which signifies the ultimate limit for crystal stability [31, 32]. The limit entropy value for metals is ∼6k_B–7k_B. The entropy rise due to isochoric superheating alone in considered case, 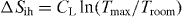$\Delta S_{{\rm{ih}}}= C_{\rm{L}} \ln ({{T_{\max } } / {T_{{\rm{room}}} }})$, is less than a half of the catastrophe value. It is established recently that the time for formation of thermal defects' density required for the order–disorder transition induced by fast heating is a strong function of superheating, 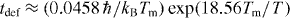$t_{{\rm{def}}}\approx \left( {{{0.0458\,\hbar }/ {k_{\rm{B}} T_{\rm{m}} }}} \right)\exp ( {{{18.56T_{\rm{m}} }/ T}})$ [5, 33]. At the maximum temperature in the above experiments this time is around a picosecond, it rapidly increases with cooling. Therefore, fast cooling prevents formation of thermal defects necessary for melting.

Several inter-related conclusions follow from the presented analysis. Firstly, the electron–lattice temperature equilibration occurs much faster that it was anticipated before due to strong temperature dependence of the momentum and energy exchange rates. This is common for all good metals, including bismuth at 800 nm, where ε_re = –16.25 [26]. In ultrafast laser excited Bi at the deposited energy density 2.5 times higher the melting enthalpy, the electron–lattice temperature equilibration occurs well before the end of a 50 fs pulse. Secondly, the swiftly heated Bi crystal is not disordered due to the fast cooling and due to insufficient time for the thermal point defects formation necessary for the completion of disordering. Thirdly, during the fast cooling process the excited crystal surpass the energy minimum corresponded to a solid in equilibrium, and transforms into a transient phase state with optical properties distinct from those for the solid, or liquid, or a mixture of the solid and liquid states.

The direct proportion of electron–phonon momentum exchange rate (or, phonon frequency averaged over the whole spectrum) on lattice temperature is quite general and holds for both metals and dielectrics [8]. Our theoretical contribution is the introduction of this dependence, in agreement with the Landau's guidelines, into the general kinetic equation for electron–phonon interaction in any metal, which immediately leads to the temperature dependence of the energy exchange rate.

Availability of both equilibrium and non-equilibrium data for Bi allows to demonstrate that a strong temperature dependence of the electron–phonon relaxation rates implies much shorter energy relaxation time. Currently, and to our surprise, there are no published experimental data reporting on the temperature dependence of the dielectric function in the optical spectral range in equilibrium and non-equilibrium conditions for common metals such as Al, Au, Cu and Ag. If available, such data would allow us to examine, and probably to confirm, how far our findings can be generalized beyond the case of Bi discussed here.

We are grateful to D Boschetto and T Garl for numerous fruitful discussions and for providing experimental data on ellipsometry measurements of temperature dependent dielectric function in equilibrium conditions from T Garl's PhD thesis [20]. We would like to thank one of the referees for his/her friendly and helpful comments, which allowed us to improve the manuscript. This work was supported under Australian Research Council's Discovery Projects funding scheme (project numbers DP0988054 and DP120102980), and by a travel grant from the Australian Academy of Science (2010).