Abstract
In the absence of charges, Maxwell's equations are highly symmetrical. In particular, they place the electric and magnetic fields on equal footing. In light of this electric–magnetic symmetry, we introduce a variational description of the free electromagnetic field that is based upon the acknowledgement of both electric and magnetic potentials. We use our description, together with Noether's theorem, to demonstrate that electric–magnetic symmetry is, in essence, an expression of the conservation of optical helicity. The symmetry associated with the conservation of Lipkin's zilches is also identified. We conclude by considering, with care, the subtle separation of the rotation and boost angular momenta of the field into their 'spin' and 'orbital' contributions.
Export citation and abstract BibTeX RIS
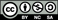
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY Introduction and background. It is a familiar fact that freely propagating light possesses conserved mechanical properties: energy, linear momentum, rotation angular momentum and boost angular momentum. Less familiar, perhaps, is the fact that freely propagating light possesses other conserved properties, many of which are highly obscure and are, at present, not entirely understood. Of course, light is an electromagnetic phenomenon. Noether's theorem tells us that the conserved properties of freely propagating light in particular are, in fact, intimately associated with various symmetries of Maxwell's equations (as written in the absence of charges) which govern the electric and magnetic fields. Our paper is concerned with such associations.
Main results. Our investigation is centred upon the observation, due to Heaviside and Larmor, that Maxwell's equations place the electric and magnetic fields on equal footing. We demonstrate that this electric–magnetic symmetry is associated with the conservation of the helicity of light: the helicity of a photon is the value taken by the component of the photon's intrinsic spin in the direction of propagation. We also consider other symmetries, including those associated with the conservation of the zilches of light which have recently been the focus of much attention within the context of chiroptical phenomena. We conclude our investigation with a careful examination of the separation of the rotation and boost angular momenta of light into their spin and orbital parts. See the representative figure below.
Wider implications. Our results, being concerned with Maxwell's equations themselves, are of relevance to all types of freely propagating light.
 Figure. (a) The effect of our (infinitesimal) boost spin symmetry transformation upon a linearly polarised plane wave. The amplitude of the wave is increased. (b) The effect of our boost orbital symmetry transformation upon the same wave. The wavelength of the wave is blue-shifted. Note that the separate transformations depicted in (a) and (b), when taken together, yield a complete boost of the wave in the direction of propagation.
Figure. (a) The effect of our (infinitesimal) boost spin symmetry transformation upon a linearly polarised plane wave. The amplitude of the wave is increased. (b) The effect of our boost orbital symmetry transformation upon the same wave. The wavelength of the wave is blue-shifted. Note that the separate transformations depicted in (a) and (b), when taken together, yield a complete boost of the wave in the direction of propagation.
1. Introduction
In the absence of charges, Maxwell's equations are highly symmetrical. In particular, they place the electric and magnetic fields on equal footing, an observation due to Heaviside [1] and Larmor [2]. We speak accordingly of electric–magnetic symmetry.
In her well-known (first) theorem, Noether [3] established a fundamental connection between symmetries and conservation laws [4]. Much has been written about the application of Noether's theorem for the free electromagnetic field. However, there remains a great deal that is not understood.
In the present paper, we approach this subject from the perspective of electric–magnetic symmetry. We begin by reviewing the standard variational description of the field in section 2. This description is based upon the use of the familiar magnetic potential and does not obviously treat the electric and magnetic fields themselves as equals. Although this apparent asymmetry does not present any fundamental difficulties, it does lead us to enquire as to the position held by the notion of electric–magnetic symmetry in the variational description of the field. This question encourages us, in section 3, to introduce our electric–magnetic variational description of the field: a simple extension of the standard one to include, in addition to the magnetic potential, an analogous electric potential. The form that we recognize for the electric–magnetic action of the field differs from those considered by Zwanziger [5], Schwinger [6] and Drummond [7, 8]. Our treatment of the eight components of the magnetic and electric potentials as independent generalized coordinates during the variational procedure yields, with the understanding of a subsidiary condition, the complete set of eight Maxwell equations explicitly. In contrast, Schwinger [6] and Drummond [7, 8] treat various components of the potentials and the field itself as quantities to be subjected to independent variations. We obtain a form of Noether's theorem for our electric–magnetic Lagrangian density in section 4 and examine our formalism in section 5, where we observe that all symmetries of Maxwell's equations are also strict symmetries of our electric–magnetic Lagrangian density, a pleasing correspondence that does not exist between symmetries of Maxwell's equations and strict symmetries of the standard Lagrangian density. Our investigation is opened in section 6 where we demonstrate, in particular, that the electric–magnetic symmetry inherent in Maxwell's equations is associated with the conservation of optical helicity. Furthermore, we identify the obscure symmetry that is associated with the conservation of Lipkin's zilches. Section 7 is centered upon a careful consideration of the separation of the rotation and boost angular momenta of the field into their 'spin' and 'orbital' contributions. We close our investigation in section 8 with a discussion of our findings.
Acknowledgement of both magnetic and electric potentials has led Drummond [7, 8] and Anco and The [9] to undertake related investigations. Naturally, we recognize some overlap between our observations. Just prior to submitting the present paper for publication, it came to our attention that our electric–magnetic variational description of the field has also been recognized recently by Bliokh et al [10]. They too have used it as the basis for a Noether investigation and have obtained some of the results presented here.
We work with Cartesian coordinates in Minkowski spacetime, using a system of units in which the speed of light c = 1. Greek indices α,β, etc may assume the values 0 and 1,2,3, corresponding, respectively, to time, t, and spatial coordinates, x,y,z. Latin indices i,j, etc may assume the values 1,2,3. When an index appears twice in a term, summation over its allowed values is to be understood. The metric ηαβ = diag(+1,−1,−1,−1) is employed.
2. The standard Lagrangian density
The electric field, E, and the magnetic flux density, B, are related to the charge density, ρ, and the current density, J, by Maxwell's equations:




It has long been known that these equations can be obtained from a variational principle. We begin by reviewing this procedure.
The electromagnetic field is a continuous entity and is, therefore, described by a Lagrangian density, 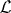 . The Lagrangian, L, is the integral over all space of the Lagrangian density:
. The Lagrangian, L, is the integral over all space of the Lagrangian density:

In turn, the action, S, is the integral over some time interval of the Lagrangian [11]:

Perhaps the most commonly used Lagrangian density in electromagnetic theory is
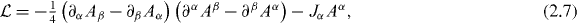
where 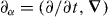 is the partial derivative four-vector, Aα = (Φ,A) is the magnetic potential four-vector and Jα = (ρ,J) is the current four-vector [12]. The first term in (2.7) describes the field whilst the second term describes the interaction of the field with charges, the motion of which we assume to be given [13, 14]. The components of the magnetic potential, Aα, are taken to be the generalized coordinates of the field, their first derivatives constituting generalized velocities. Applying Hamilton's principle [15–17] to the action (2.6), without varying Jα, we then obtain four Euler–Lagrange equations [11–14, 18]:
is the partial derivative four-vector, Aα = (Φ,A) is the magnetic potential four-vector and Jα = (ρ,J) is the current four-vector [12]. The first term in (2.7) describes the field whilst the second term describes the interaction of the field with charges, the motion of which we assume to be given [13, 14]. The components of the magnetic potential, Aα, are taken to be the generalized coordinates of the field, their first derivatives constituting generalized velocities. Applying Hamilton's principle [15–17] to the action (2.6), without varying Jα, we then obtain four Euler–Lagrange equations [11–14, 18]:

Explicit calculation using (2.7) reveals that (2.8) is

where Fαβ is the field tensor, expressible in matrix form as

and we have identified Fαβ = ∂αAβ − ∂βAα as usual. For α = 0, (2.9) is Gauss's law (2.1) and for α = 1,2,3, (2.9) yields the components of the Ampère–Maxwell law (2.4). Note that the standard Lagrangian density (2.7) has, through application of Hamilton's principle, only provided us explicitly with four of the eight Maxwell equations. However, the remaining four Maxwell equations are

where Gαβ =  αβμνFμν/2 is the dual field pseudotensor, with
αβμνFμν/2 is the dual field pseudotensor, with  0123 = + 1 the usual Levi–Civita pseudotensor [14]. In matrix form
0123 = + 1 the usual Levi–Civita pseudotensor [14]. In matrix form

For α = 0, (2.11) is Gauss's law for magnetism (2.2) and for α = 1,2,3, (2.11) yields the components of the Faraday–Lenz law (2.3). These are satisfied automatically by virtue of our definition of the field in terms of the magnetic potential: Fαβ = ∂αAβ − ∂βAα.
We refer to (2.7) as the standard Lagrangian density. It is due to Schwarzschild [19].
3. The electric–magnetic Lagrangian density
For the remainder of the present paper, we assume an absence of charges, in which case Maxwell's equations (2.1)–(2.4) are




It is well-known that these equations retain their form under a duality rotation:

for any Lorentz pseudoscalar angle θ [13]. This symmetry, due to Heaviside [1] and Larmor [2], embodies the fact that the electric and magnetic fields stand on equal footing in the absence of charges.
As Jα = 0, it is possible to introduce, in addition to the familiar magnetic potential four-vector, Aα = (Φ,A), an analogous electric potential four-pseudovector, Cα = (Θ,C), [20] such that

provided, of course, that
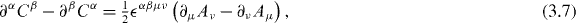
as Gαβ =  αβμνFμν/2. The potentials, Aα and Cα, enjoy independent gauge freedoms.
αβμνFμν/2. The potentials, Aα and Cα, enjoy independent gauge freedoms.
It should be noted that the complete set of Maxwell equations (3.1)–(3.4) are satisfied automatically when one acknowledges, in a consistent manner, the simultaneous existence of both magnetic and electric potentials: Aα and Cα. Indeed, it follows from (3.6) and (3.7) that

which is the complete set of Maxwell equations, as given by (2.9) and (2.11) with Jα = 0. We return to this observation below and in section 5.
The present paper was motivated by a desire to understand the implications of electric–magnetic symmetry within the context of Noether's theorem. Surprisingly, however, we find that the standard Lagrangian density:
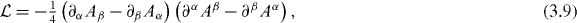
as obtained from (2.7) with Jα = 0, does not retain its form under a duality rotation, which is invoked in all gauges by taking

This is, perhaps, a reflection of the fact that (3.9) is defined solely in terms of the magnetic potential, Aα. In light of electric–magnetic symmetry, it seems natural to add half of (3.9) to half of the analogous electric form, obtaining the quantity
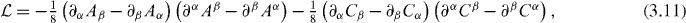
which is invariant in form under the transformation (3.10). We might then consider the eight components of the potentials, Aα and Cα, to be the generalized coordinates of the field, their first derivatives constituting generalized velocities. There is, however, a subtle but important point that must be appreciated here, one that stems from the problem of overdetermination. If we identify Aα and Cα in (3.11) as the potentials a priori, we find that (3.11) vanishes, by virtue of (3.7). To proceed, suppose initially that we attach no physical interpretation to the four-vector Aα and the four-pseudovector Cα in (3.11) (except, of course, that their dimensions are such that (3.11) in turn has the dimensions of an energy per unit volume) and consider them to be independent of each other. Applying Hamilton's principle to the action associated with (3.11), we then obtain eight Euler–Lagrange equations:

which govern the independent evolutions of Aα and Cα. If we now assume and understand the subsidiary condition (3.7) to be satisfied we can interpret Aα and Cα as our potentials, identifying the electric and magnetic fields in the usual manner (3.6), as (3.7) is then Gαβ =  αβμνFμν/2. With this understanding, we recognize the Euler–Lagrange equations (3.12) as being the complete set of Maxwell equations (3.8). It is interesting to contrast this with the fact that the standard Lagrangian density (3.9) only provides us with four of the eight Maxwell equations explicitly, the remaining four holding implicitly.
αβμνFμν/2. With this understanding, we recognize the Euler–Lagrange equations (3.12) as being the complete set of Maxwell equations (3.8). It is interesting to contrast this with the fact that the standard Lagrangian density (3.9) only provides us with four of the eight Maxwell equations explicitly, the remaining four holding implicitly.
We refer to (3.11) as the electric–magnetic Lagrangian density. Like the standard Lagrangian density (3.9), our electric–magnetic Lagrangian density (3.11) possesses a form that is insensitive to gauge transformations. It is a Lorentz scalar with the dimensions of an energy per unit volume, as required. Furthermore, the so-called kinetic terms (∂A/∂t)2/4 and (∂C/∂t)2/4 appear with positive signs, as they should [14, 18]. We find that the Hamiltonian associated with our electric–magnetic Lagrangian density (3.11) is

which is the desired form [7, 8].
As discussed in section 1, our electric–magnetic Lagrangian density (3.11) has also been recognized recently by Bliokh et al [10] who have used it as the basis of a Noether investigation. The form (3.11) has also been considered briefly by Rañada [21] in a different context.
4. Noether's theorem
Noether's theorem established a fundamental connection between symmetries and conservation laws [3, 4]. In this section, we derive a form of Noether's theorem for our electric–magnetic Lagrangian density (3.11).
We consider ourselves to be in an inertial frame of reference and perform an active transformation of the potentials (which initially satisfy the Euler–Lagrange equations (3.12) as well as the subsidiary condition (3.7)) as

where, at present, we make no assumptions about the four-vector ΔAα and the four-pseudovector ΔCα, except that they are infinitesimal and possess suitable dimensions. We return to this point in section 5. Considering  , a standard calculus result gives us an expression for the change,
, a standard calculus result gives us an expression for the change,  , induced in our electric–magnetic Lagrangian density (3.11) by the transformation (4.1):
, induced in our electric–magnetic Lagrangian density (3.11) by the transformation (4.1):
where, in going from the first line to the second line, we have taken advantage of the fact that the transformation (4.1) is active so that ∂β' = ∂β and  [12, 18]. Likewise,
[12, 18]. Likewise,  . In the final line, the terms in braces vanish by virtue of (3.8), leaving us with
. In the final line, the terms in braces vanish by virtue of (3.8), leaving us with

If the transformation (4.1) constitutes a symmetry of our electric–magnetic Lagrangian density (3.11), leaving it invariant in form ( ), we immediately extract its associated local conservation law from (4.3). This is the form of Noether's theorem that we adopt initially.
), we immediately extract its associated local conservation law from (4.3). This is the form of Noether's theorem that we adopt initially.
5. An important subtlety
Before proceeding, we must highlight an important subtlety inherent in our formalism. For arbitrary independent choices of ΔAα and ΔCα, the transformation (4.1) is, in general, meaningless. If we were to identify Aα' and Cα' as transformed 'potentials', we would then find that the transformed 'field' itself is not uniquely defined. Different results would be obtained, for example, depending on whether the transformed 'field' were calculated, in the usual manner, using Aα' or using Cα'. This stems from the problem of overdetermination. Clearly, ΔAα and ΔCα cannot be chosen independently if we intend on staying faithful to the electromagnetic field. In fact, we demand that ΔAα and ΔCα be related such that Aα' and Cα' satisfy
in which case we can identify Aα' and Cα' as transformed potentials, identifying the transformed field itself, uniquely, in the usual manner:

as (5.1) is then Gαβ' =  αβμνFμν'/2. We observe further, that all such transformations constitute symmetries of Maxwell's equations, which are themselves satisfied automatically when the field is defined consistently in terms of both magnetic and electric potentials, as explained in section 3. In particular, Maxwell's equations
αβμνFμν'/2. We observe further, that all such transformations constitute symmetries of Maxwell's equations, which are themselves satisfied automatically when the field is defined consistently in terms of both magnetic and electric potentials, as explained in section 3. In particular, Maxwell's equations

for the transformed field follow from the identifications (5.2) and the fact that Gαβ' =  αβμνFμν'/2: (5.1). Hence, finding a meaningful transformation (4.1) of the potentials: one that satisfies (5.1), yielding a unique transformation of the field, is equivalent to finding a symmetry of Maxwell's equations.
αβμνFμν'/2: (5.1). Hence, finding a meaningful transformation (4.1) of the potentials: one that satisfies (5.1), yielding a unique transformation of the field, is equivalent to finding a symmetry of Maxwell's equations.
Consider a seemingly unrelated question: what conditions must the transformation (4.1) satisfy in order that it constitutes a symmetry of our electric–magnetic Lagrangian density (3.11)? Substituting the transformation (4.1) into our electric–magnetic Lagrangian density (3.11) explicitly, we find that the latter transforms such that
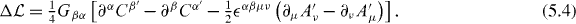
Evidently, we will have a symmetry ( ) and an associated conservation law (4.3) if and only if the transformed potentials, Aα' and Cα', satisfy (5.1). Hence, a meaningful transformation (4.1) of the potentials constitutes, simultaneously, a symmetry of Maxwell's equations themselves and our electric–magnetic Lagrangian density (3.11), a pleasing correspondence. All transformations (4.1) that we consider will be of this nature.
) and an associated conservation law (4.3) if and only if the transformed potentials, Aα' and Cα', satisfy (5.1). Hence, a meaningful transformation (4.1) of the potentials constitutes, simultaneously, a symmetry of Maxwell's equations themselves and our electric–magnetic Lagrangian density (3.11), a pleasing correspondence. All transformations (4.1) that we consider will be of this nature.
It is interesting to note that there is no such correspondence between symmetries of Maxwell's equations and strict symmetries (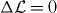 ) of the standard Lagrangian density (3.9). In their recent work, Bliokh et al [10] have claimed that the standard Lagrangian density (3.9) implies a lack of optical helicity conservation because it does not retain its form (
) of the standard Lagrangian density (3.9). In their recent work, Bliokh et al [10] have claimed that the standard Lagrangian density (3.9) implies a lack of optical helicity conservation because it does not retain its form ( ) under a duality rotation (see below). In fact, one can deduce the conservation of optical helicity using the standard Lagrangian density and Noether's theorem, as demonstrated in the appendix. We suggest that our electric–magnetic description be viewed as an alternative to the standard description, rather than a replacement.
) under a duality rotation (see below). In fact, one can deduce the conservation of optical helicity using the standard Lagrangian density and Noether's theorem, as demonstrated in the appendix. We suggest that our electric–magnetic description be viewed as an alternative to the standard description, rather than a replacement.
6. Local symmetries and their associated conserved quantities
6.1. Duality rotations and the optical helicity
The invariance in form of Maxwell's equations (3.1)–(3.4) under a duality rotation (3.5) is the embodiment of electric–magnetic symmetry and was, perhaps, the first symmetry observed in electromagnetic theory [1, 2, 13]. We begin our investigation here.
From (3.10), the infinitesimal transformation

where θ is an infinitesimal Lorentz pseudoscalar angle, yields, in all gauges:

which is the infinitesimal form of a duality rotation (3.5). From (6.1) and our form (4.3) of Noether's theorem, with 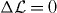 , we obtain
, we obtain

As θ ≠ 0, the conservation law

follows immediately from (6.3). Although the conservation law (6.4) holds in all gauges, the density, h0, of the conserved quantity is itself not gauge invariant. When we integrate h0 over all space, however, we obtain the quantity
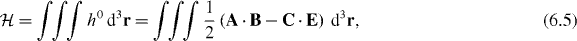
which is both conserved (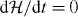 , assuming that the field falls off suitably as |r| → ∞) and gauge invariant. The latter property follows from the fact that the integral over all space of the dot product of a transverse and a longitudinal field vanishes [11]. Thus, it is only the transverse, gauge invariant [11] pieces, A⊥ and C⊥, of the vector and pseudovector potentials that contribute to (6.5) such that
, assuming that the field falls off suitably as |r| → ∞) and gauge invariant. The latter property follows from the fact that the integral over all space of the dot product of a transverse and a longitudinal field vanishes [11]. Thus, it is only the transverse, gauge invariant [11] pieces, A⊥ and C⊥, of the vector and pseudovector potentials that contribute to (6.5) such that

We recognize (6.6) as the optical helicity [22, 23]. It is equivalent to the 'screw-action' introduced by Candlin [24]. The association of duality rotations (3.5) with the optical helicity (6.6) was recognized by Calkin [25] (see also [7–9, 22, 23, 26–33]). The optical helicity (6.6) is a Lorentz pseudoscalar with the dimensions of an angular momentum and is, as its name suggests, the total photon helicity of the field [22, 23]. For a plane wave, a duality rotation (3.5) simply rotates the electric and magnetic field vectors about the direction of propagation [22, 23]. It seems natural that such a symmetry transformation should be associated with the conservation of the optical helicity (6.6).
Interestingly, this is not the end of our story. Consider the infinitesimal transformation

where we interpret the infinitesimal Lorentz scalar ϕ as an angle. Just as (6.2) is, for a plane wave, an infinitesimal rotation of the electric and magnetic field vectors about the direction of propagation through an angle θ, (6.7) is an infinitesimal boost of the electric and magnetic field vectors in the direction of propagation with rapidity ϕ, leaving the spacetime distribution of the wave unchanged (this interpretation also holds for the finite form of (6.7)). Thus, (6.2) and (6.7) are 'partners'. Noether's theorem leads us to associate (6.7) with the conservation law
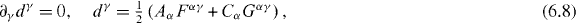
which holds in all gauges. The density, d0, of the conserved quantity has the dimensions of a boost angular momentum per unit volume, in line with our interpretation of (6.7). Although the density, d0, is gauge dependent, we can obtain a gauge invariant quantity by integrating over all space:

This quantity is, however, trivial, as

In going from the second line to the third line, we have used Gauss's theorem to convert the final term into a surface integral which vanishes, assuming that the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials fall off suitably as |r| → ∞. Related observations have been made by Fushchich and Nikitin [34, 35], Drummond [7, 8] and Anco and The [9].
The idea that symmetries exist in pairs, only one member of which is associated with a non-trivial conserved quantity, appears to hold with generality, as we shall see in what follows.
6.2. Conformal symmetries and Bessel-Hagen's tensors
Bessel-Hagen [36] was the first to apply Noether's theorem in electromagnetic theory. Equipped with the standard Lagrangian density (3.9), he obtained the conservation laws associated with the 15 parameter group of conformal symmetries. We now consider these symmetries and, as a check on our present approach, confirm that our electric–magnetic Lagrangian density (3.11) leads us to the same conservation laws obtained by Bessel-Hagen.
An infinitesimal conformal transformation of the field is invoked, in all gauges, by transforming the potentials as

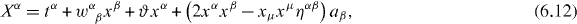
with xα = (t,r) the position four-vector. The infinitesimal components of tα and wαβ = −wβα define a translation in spacetime and a rotation and boost, respectively. Such transformations constitute the Poincaré group [12, 39]. In addition, ϑ and the components of aα, also infinitesimal, define a scale transformation and a so-called special conformal transformation, respectively. The physical significance of such transformations, due to Bateman [40, 41] and Cunningham [42], is, it seems, not entirely understood (see e.g. [39, 43–45]). Their independence from the transformations of the Poincaré group has been questioned by Fushchich and Nikitin [34]. Note that the transformation (6.11) is an active one, like all transformations in the present paper. In this active form, tα, wαβ = −wβα, ϑ and aα are tensors, with suitable dimensions, so that Xα is itself a four-vector [46]. Plybon has claimed that the 15 conformal symmetry transformations are the only ones that assume the form of (6.11), referred to by him as being 'geometric' [46].
From (6.11) and our form of Noether's theorem (4.3), we deduce, following some simple manipulations, that

As tα,wαβ = −wβα,ϑ and aα are independent, we obtain from (6.12) and (6.13), a total of 15 conservation laws:
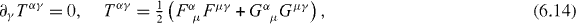
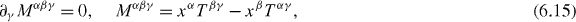

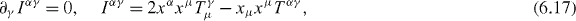
corresponding to spacetime translations, rotations and boosts, scale transformations and special conformal transformations, respectively [47]. Our results (6.14)–(6.17) are essentially the ones advocated by Bessel-Hagen [36], as desired.
As is well-known, (6.14) expresses the conservation of energy and linear momentum, whilst (6.15) expresses the conservation of rotation and boost angular momenta, to which we return in section 7. Of the remaining conservation laws, (6.16) and (6.17), Bessel-Hagen commented that 'the future will show if they have any physical significance' [36, 48]. It appears that their physical significance is still not understood, a point noted by Rohrlich [39] and Fulton et al [43], by Plybon [38] and, more recently, by Ibragimov [48]. The independence of the conservation law (6.17) from the others has been questioned by Plybon [38].
In passing, we remark that the conserved quantity with density D0 has the dimensions of a boost angular momentum. For a single plane wave, the conservation law (6.16) can be interpreted as a statement of the familiar dispersion relation, ω = |k|. This relation connects a time (the period of the wave) with a (wave)length which is somewhat appropriate given that the invariance of Maxwell's equations (3.1)–(3.4) under a scale transformation (which, importantly, invokes a dilation or contraction of temporal and spatial properties of the field in equal measure) is itself a reflection of the fact that all periods and wavelengths of light are equally welcome, provided, of course, that they are related such that ω = |k|.
An infinitesimal conformal symmetry transformation, as invoked by (6.11), possesses a (non-geometric) partner that is invoked, in all gauges, by transforming the potentials as
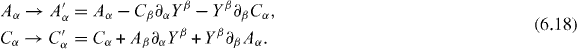
The four-pseudovector Yα is
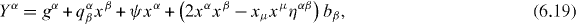
where the components of the pseudotensors gα, qαβ = −qβα, ψ and bα are infinitesimal and have suitable dimensions. This symmetry has also been recognized by Krivskii and Simulik [49, 50] and Anco and The [9]. Through Noether's theorem, we find that (6.18) is associated with trivial conserved quantities, as noted by Anco and The [9].
6.3. The zilch symmetry and Lipkin's zilch tensor
In 1964, Lipkin [51] introduced a rank-three pseudotensor which describes a set of nine independent conserved quantities, referred to collectively as the 'zilch' of the field. Considering a monochromatic plane wave, he demonstrated that the components of his pseudotensor are dependent upon the wave's sense of circular polarization, suggesting a connection with the helicity of the photon. Lipkin also observed, however, that his zilches do not have the dimensions of an angular momentum, but rather, that of a force, displaying a highly unusual frequency dependence. The situation was clarified shortly afterwards by Candlin [24], who effectively introduced the optical helicity (6.6) itself and conjectured that Lipkin's zilches are simply members of an infinite hierarchy of higher-order extensions of the optical helicity (6.6). Related generalizations of Lipkin's discovery were also made by Morgan [52], O'Connell and Tompkins [53], and Kibble [54].
Despite these facts, the zilches have recently been reintroduced into the literature by Tang, Cohen and Yang [55, 56]. In particular, they have referred to Lipkin's 00-zilch density as the 'optical chirality', advocating it as a measure of the chirality of the field, an interpretation that has been utilized to predict and describe the results of experiments [55–60]. Considering a strictly monochromatic field, Bliokh and Nori [61] recognized, much as Lipkin himself did, that the 00-zilch and the 0i-zilches are, in the chosen frame of reference, proportional to, but not equal to, the helicity of the field and the components of the spin of the field, respectively. The proportionality factor is the square of the associated angular frequency. Such proportionalities were also observed by Andrews and Coles [62–64].
We have recently demonstrated elsewhere [22, 23] that Lipkin's zilches are indeed members of an infinite hierarchy of extensions of the optical helicity (6.6) and related quantities, as Candlin suggested [24]. For a strictly monochromatic field in a given frame of reference, the apparent similarity that exists between, for example, the optical helicity (6.6) and Lipkin's 00-zilch can be traced to a remarkable self-similarity inherent in Maxwell's equations (3.1)–(3.4) [22]. We return to this observation below.
For a general polychromatic field, there are no proportionalities like the ones seen by Bliokh and Nori [61] and Coles and Andrews [62–64]. Thus, there is no sense in which the optical helicity (6.6) and related quantities are 'equivalent' to Lipkin's zilches [22, 23]. It is the optical helicity (6.6) in particular, which has the dimensions of an angular momentum and is the conserved Lorentz pseudoscalar associated with a duality rotation (6.2), that provides a physically meaningful description of photon helicity. Other quantities such as Lipkin's 00-zilch lack both the dimensions and the Lorentz transformation properties that are required in this context.
We can further highlight the fact that Lipkin's zilches do not describe the angular momentum of the field by identifying their associated symmetry. The infinitesimal transformation

where the components of the pseudotensor ζαβ = ζβα are infinitesimal and have the dimensions of a squared length (not an angle!), yields

in all gauges. The infinitesimal transformation (6.21) resembles an infinitesimal duality rotation (6.2), but differs crucially through the appearance of second derivatives and is not a rotation of any kind. This obscure symmetry is, in fact, the one associated with Lipkin's zilches. From (6.20) and our form (4.3) of Noether's theorem, acknowledging the independence of the ζαβ = ζβα, we obtain, as claimed, the conservation law:

where Zαβγ is the form of Lipkin's zilch pseudotensor recognized by Morgan [52] and Kibble [54].
The symmetries associated with the individual zilches have been identified variously by Calkin [25] and Przanowski et al [31]. Frequent incorrect identifications of the symmetries associated with Lipkin's zilches [48–50, 65] can be traced to the use of 'Lagrangians' that do not have the dimensions of an energy.
The infinitesimal zilch symmetry transformation (6.21) possesses a partner which is

where the components of the tensor ζμν = ζνμ are infinitesimal and have the dimensions of a squared length. Through Noether's theorem, we find that this symmetry is associated with trivial conserved quantities which have also emerged in the work of Fradkin [66].
6.4. Some simple generalizations
We now demonstrate that the field possesses an infinite number of local symmetries and associated tensor and pseudotensor conservation laws.
We have seen that the infinitesimal symmetry transformations:


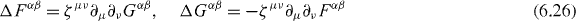
are associated with the helicity four-pseudovector (6.4) (of rank-one), a trivial pseudotensor (of rank-two) and the zilch pseudotensor (6.22) (of rank-three), respectively. In addition, we have observed a complimentary structure in that the infinitesimal symmetry transformations:


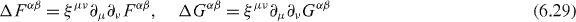
are associated with a trivial four-vector (6.8) (of rank-one), the energy momentum tensor, Tαβ (6.14) (of rank-two) and a trivial tensor (of rank-three), respectively.
These observations are readily generalized. The infinitesimal transformation

constitutes a symmetry for any number of derivatives provided, of course, that the components of the pseudotensor  , which are infinitesimal, possess suitable dimensions. Without loss of generality, we take
, which are infinitesimal, possess suitable dimensions. Without loss of generality, we take  to be symmetric in all of its indices. This, (6.30), is the generalization of (6.24)–(6.26). Through Noether's theorem, we find that the conservation laws associated with (6.30), for one or more derivatives, can be expressed as
to be symmetric in all of its indices. This, (6.30), is the generalization of (6.24)–(6.26). Through Noether's theorem, we find that the conservation laws associated with (6.30), for one or more derivatives, can be expressed as
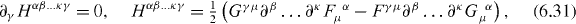
where we have assumed that the components of the symmetric pseudotensor  are otherwise independent. The existence of this infinite hierarchy of pseudotensor conservation laws was observed by Morgan [52] (although the helicity four-pseudovector (6.4), which lies 'lowest' amongst these pseudotensors, being of rank-one, escaped Morgan's attention). We have now tied them to their associated symmetries (6.30).
are otherwise independent. The existence of this infinite hierarchy of pseudotensor conservation laws was observed by Morgan [52] (although the helicity four-pseudovector (6.4), which lies 'lowest' amongst these pseudotensors, being of rank-one, escaped Morgan's attention). We have now tied them to their associated symmetries (6.30).
In a similar vein, the infinitesimal transformation

constitutes a symmetry for any number of derivatives provided that the components of the tensor 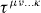 , which are infinitesimal, possess suitable dimensions. Without loss of generality, we take
, which are infinitesimal, possess suitable dimensions. Without loss of generality, we take 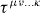 to be symmetric in all of its indices. Through Noether's theorem, we find that the conservation laws associated with (6.32), for one or more derivatives, can be expressed as
to be symmetric in all of its indices. Through Noether's theorem, we find that the conservation laws associated with (6.32), for one or more derivatives, can be expressed as

where we have assumed that the components of the symmetric tensor  are otherwise independent. The existence of this infinite hierarchy of tensor conservation laws was also observed by Morgan [52] (although the trivial four-vector (6.8), which lies 'lowest' amongst these tensors, being of rank-one, also escaped Morgan's attention). We have now tied them to their associated symmetries (6.32).
are otherwise independent. The existence of this infinite hierarchy of tensor conservation laws was also observed by Morgan [52] (although the trivial four-vector (6.8), which lies 'lowest' amongst these tensors, being of rank-one, also escaped Morgan's attention). We have now tied them to their associated symmetries (6.32).
It seems that the pseudotensors (6.31) and tensors (6.33) of even and odd rank, respectively, describe trivial conserved quantities whilst those of odd and even rank, respectively, describe conserved quantities that are dependent upon the difference and sum, respectively, of photon numbers of opposite circular polarization. Thus, we identify a kind of 'alternation' as we ascend rank. This pattern, whose first three 'layers' are


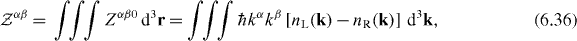
appears to extend indefinitely and is, in fact, the pattern the existence of which was conjectured by Candlin [24]. Here, 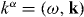 is the wave four-vector [13] whilst nL(k) and nR(k) are, respectively, the classical limits of the photon numbers of the left- and right-handed circular polarizations associated with the wavevector k [11]. The pieces of this pattern that are dependent upon the difference in photon numbers of opposite circular polarization in particular have recently been examined within the framework of quantum electrodynamics by Coles and Andrews [67].
is the wave four-vector [13] whilst nL(k) and nR(k) are, respectively, the classical limits of the photon numbers of the left- and right-handed circular polarizations associated with the wavevector k [11]. The pieces of this pattern that are dependent upon the difference in photon numbers of opposite circular polarization in particular have recently been examined within the framework of quantum electrodynamics by Coles and Andrews [67].
The simple picture that we have painted is enlivened by the existence of an infinite number of conserved tensors and pseudotensors that depend explicitly upon time and position. Consider, for example, the conserved tensors (6.15)–(6.17) which are constructed from the energy momentum tensor, Tαγ, and the position four-vector, xα. Conserved pseudotensors can also be constructed from the zilch tensor, Zαβγ, and the position four-vector xα, a fact that has been observed by Krivskii and Simulik [49]. In general, such quantities are obscure and we shall not consider them in any detail here.
6.5. A comment on interpretation
Amongst the tensor and pseudotensor conservation laws considered above, which are infinite in number, there are but a small handful, of low rank, that describe conserved quantities that possess familiar dimensions. In particular, we can readily appreciate the physical significance of the optical helicity (6.6) as well as the energy momentum tensor (6.14) and the angular momentum tensor (6.15).
We should also comment, however, on those higher-order tensor and pseudotensor conservation laws, amongst them most of (6.31) and (6.33), that describe conserved quantities with unfamiliar dimensions. We suggest that these conserved quantities describe properties of various derivatives of the electric and magnetic fields. To illustrate the idea, suppose that we define, in terms of various first derivatives of the electric and magnetic fields, a pseudovector  and a vector
and a vector 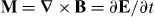 . We then find that these obey the equations:
. We then find that these obey the equations:

which are identical in form to Maxwell's equations (3.1)–(3.4) themselves. Furthermore, we find that various second derivatives of the electric and magnetic fields also obey a set of Maxwell-like equations. In fact, such patterns recur indefinitely as we consider derivatives of ever-increasing order [7, 8, 22]. Superficially, at least, it seems that it is this self-similarity that is being reflected in the existence of the infinite hierarchies of conserved quantities considered above. For example, we have explained elsewhere [22] that Lipkin's 00-zilch (as obtained from (6.36) with αβ = 00) is to G and M what the optical helicity (6.34) is to the electric and magnetic fields, E and B, themselves. That the Lorentz transformation properties of Lipkin's 00-zilch (6.36) differ from those of the optical helicity (6.34) is, perhaps, a reflection of the fact that the Lorentz transformation properties of G and M differ from those of the electric and magnetic fields, E and B. Indeed, the equations (6.37) can be expressed as

and may be seen to follow from the general observation that all contractions of the tensor 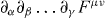 and the pseudotensor
and the pseudotensor 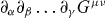 vanish, irrespective of the number of derivatives present.
vanish, irrespective of the number of derivatives present.
7. Non-local symmetries and their associated conserved quantities
7.1. The electric–magnetic Lagrangian and Noether's theorem
In the present section we devote ourselves to our chosen frame of reference. Some of the quantities that we are about to meet make explicit reference to the transverse, gauge invariant [11] pieces, A⊥ and C⊥, of the vector and pseudovector potentials. These pieces can be expressed as non-local functions of the electric and magnetic fields [68]. It seems appropriate, therefore, for us to consider our electric–magnetic Lagrangian, L, rather than our electric–magnetic Lagrangian density,  , in what follows. Integrating our result (4.3) over all space gives us the change, ΔL, induced in our electric–magnetic Lagrangian by the transformation (4.1):
, in what follows. Integrating our result (4.3) over all space gives us the change, ΔL, induced in our electric–magnetic Lagrangian by the transformation (4.1):
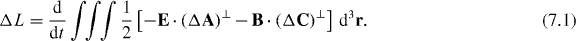
Note that this result (7.1) has been obtained with generality, making no gauge assumptions. Evidently, however, our electric–magnetic Lagrangian is sensitive only to the transverse pieces, (ΔA)⊥ and (ΔC)⊥, of the changes in the vector and pseudovector potentials and is not sensitive to changes in the scalar and pseudoscalar potentials. This is a reflection of both its gauge invariant form and the fact that the time derivatives of A0 and C0 do not make an appearance in our electric–magnetic Lagrangian density (3.11), so that the scalar and pseudoscalar potentials are themselves not true dynamical variables [11, 18].
As explained in section 5, all meaningful transformations (4.1) of the potentials constitute, automatically, symmetries of both Maxwell's equations and our electric–magnetic Lagrangian. Their associated global conservation laws are obtained from (7.1) with ΔL = 0. This is the form of Noether's theorem that we adopt in the present section. In light of the observations discussed in the preceding paragraph, we focus our attention upon transformations of the transverse, gauge invariant [11] pieces, A⊥ and C⊥, of the vector and pseudovector potentials, making no transformations of their longitudinal pieces or the scalar and pseudoscalar potentials.
7.2. Rotation and boost angular momenta of the field
An infinitesimal rotation of the field about the origin is invoked by taking [69, 70]:
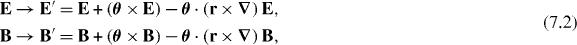
where the orientation and magnitude of the infinitesimal pseudovector θ define an axis and an angle of rotation about that axis, respectively. The first contributions to (7.2) rotate the electric and magnetic field vectors whilst the second contributions rotate the spatial distribution of the field. Of course, (7.2), the form of which may be deduced readily from (6.11), is a local transformation that leaves Maxwell's equations (3.1)–(3.4) invariant in form. The (rotation) angular momentum

of the field is the conserved quantity associated with this symmetry. Indeed, the conservation law

follows from the space-like components of the tensor equation (6.15).
An infinitesimal boost of the field 'about' the origin is invoked by taking [70]

where the orientation and magnitude of the infinitesimal vector ϕ define the direction of the boost and its rapidity, respectively. The first contributions to (7.5) mix the electric and magnetic field vectors whilst the second contributions 'rotate' the spacetime distribution of the field in a hyperbolic manner [12, 14]. The local transformation (7.5), the form of which may be deduced readily from (6.11), also leaves Maxwell's equations (3.1)–(3.4) invariant in form. The boost angular momentum
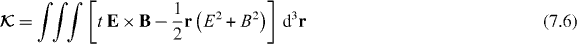
of the field is the conserved quantity associated with this symmetry. Indeed, the conservation law

follows from the mixed components of the tensor equation (6.15) and is essentially a statement of the uniform motion of the field's centre of energy [13, 14, 39].
Although the boost angular momentum (7.6) of the field is, perhaps, less familiar than the angular momentum (7.3) of the field, it is important to note that relativity places these quantities on equal footing as, taken together, they form an antisymmetric rank-two tensor [70]. This fact is inherent in (6.15). Let us now look more closely at these properties of the field in our chosen frame of reference. We begin with the more familiar angular momentum (7.3) of the field before turning to the boost angular momentum (7.6) of the field.
In optics, the idea is well-established that light can possess both 'spin' and 'orbital' angular momenta [71]. The spin angular momentum is intrinsic and is associated with polarization [72] whilst the orbital angular momentum is extrinsic in general and is associated with the spatial distribution of the field. Helical phase fronts, in particular, give rise to an orbital contribution [73] that has been the subject of much research in recent years [74]. Regarding the description of these properties of light in electromagnetic theory, it is also well-established that the angular momentum (7.3) of the field can be recast, using integration by parts, as the sum of a conserved spin-like contribution,  , and a conserved orbital-like contribution,
, and a conserved orbital-like contribution, 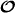 [11, 69, 70, 75]:
[11, 69, 70, 75]:

The spin-like contribution in (7.8) is

This gauge invariant and intrinsic quantity, which we refer to as the optical spin, displays a critical dependence upon the polarization of light. We have recently suggested elsewhere [22, 23] that the optical spin (7.9) is most meaningfully thought of as a quantity that describes photon helicity, in addition to the optical helicity (6.6) itself of course. Indeed, the integrand of the optical spin (7.9), which may be thought of as the spin density of the field, is also the helicity flux density, as given by the spatial components of the helicity four-pseudovector (6.4) in the Coulomb gauge. Note that the components of the optical spin are not equivalent, in any sense, to Lipkin's 0i-zilches [51] which are to G and M in (6.37) what the components of the optical spin are to the electric and magnetic fields, E and B, themselves [22, 23]. The remaining orbital-like contribution in (7.8) is
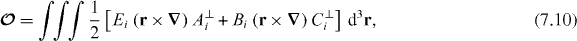
and is both gauge invariant and extrinsic.
At first glance, it is tempting, perhaps, to associate the conservation of the optical spin (7.9) with the rotation of the electric and magnetic field vectors in (7.2) and the conservation of the orbital-like contribution (7.10) with the rotation of the spatial distribution of the field in (7.2). In fact, these pieces of (7.2), when considered separately, do not constitute symmetries of Maxwell's equations (3.1)–(3.4). In particular, they do not respect the transversality of the field [69]. Such (incorrect) identifications have led to suggestions that the optical spin (7.9) and the orbital-like contribution (7.10) are not separately meaningful [11, 39, 76].
This situation was clarified by Van Enk and Nienhuis [77, 78] who established that the optical spin (7.9) and the orbital-like contribution (7.10) are separately meaningful, but noted that neither is a 'true' angular momentum, as the components of their quantized forms do not satisfy the usual angular momentum commutation relations. More recently, it has been demonstrated [69] that the infinitesimal transformation associated with the optical spin (7.9) is, in fact

which does leave Maxwell's equations (3.1)–(3.4) invariant in form [22, 69]. Physically, the spin symmetry transformation (7.11) differs from the first contributions in (7.2) in that it is the closest approximation to an infinitesimal rotation of the electric and magnetic field vectors, in the sense defined by the infinitesimal pseudovector θ, leaving the spatial distribution of the field unchanged, that is consistent with the requirement of transversality [69, 77, 78]. In a similar vein, it has been demonstrated that the infinitesimal transformation associated with the orbital-like contribution (7.10) is

which also leaves Maxwell's equations (3.1)–(3.4) invariant in form. Physically, the orbital symmetry transformation (7.12) differs from the second contributions in (7.2) in that it is the closest approximation to an infinitesimal rotation of the spatial distribution of the field about the origin, in the sense defined by the infinitesimal pseudovector θ, leaving the orientations of the electric and magnetic field vectors unchanged, that is consistent with the requirement of transversality [69]. Note that both (7.11) and (7.12) constitute non-local symmetries in that the transverse pieces indicated are obtainable, in general, through the evaluation of integrals that extend over all space [11, 69]. Let us now approach such ideas using Noether's theorem. As may be confirmed simply by taking its time derivative, the infinitesimal transformation

of the transverse pieces of the vector and pseudovector potentials gives rise to (7.11). Following some simple manipulations, observing the independence of the components of θ, we deduce from (7.13) and our form (7.1) of Noether's theorem, that

justifying the association of the spin symmetry transformation (7.11) with the conservation of the optical spin (7.9), as expected. An analogous derivation allows us to deduce, from (7.12) that

justifying the association of the orbital symmetry transformation (7.12) with the conservation of the orbital-like contribution (7.10).
Although the components of their quantized forms do not satisfy the usual angular momentum commutation relations [77, 78], we can suggest that the optical spin (7.9) and the orbital-like contribution (7.10) are angular momenta in the more liberal sense that they are pseudovectors with the dimensions of an angular momentum, the conservation of which is associated with the transversality maintaining rotations (7.11) and (7.12), respectively. A similar mentality is applicable, perhaps, to the optical helicity (6.6) which, despite the fact that it is a Lorentz pseudoscalar and not a pseudovector, is a quantity with the dimensions of an angular momentum, the conservation of which is associated with duality rotations (6.2).
We now turn our attention to the boost angular momentum (7.6) of the field. The question has been posed recently [70]: is it possible to divide the boost angular momentum (7.6) of the field into conserved 'spin' and 'orbital' contributions which, if only by analogy with the angular momentum (7.3) of the field, we might separately associate with the mixing of electric and magnetic field vectors and with the hyperbolic rotation of the spacetime distribution of the field exhibited in the first and second contributions, respectively, to (7.5)? It has been shown [70] that (7.6) can be recast, using integration by parts, as

The first contribution to (7.16),
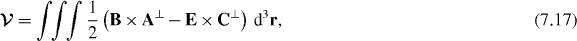
is gauge invariant and does not make explicit reference to t or r. The second contribution to (7.16),
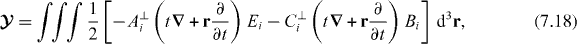
is gauge invariant and does make explicit reference to t and r. It seems natural, perhaps, to identify (7.17) and (7.18) as the spin and orbital contributions, respectively, to the boost angular momentum (7.6) of the field.
We can now examine the separation (7.16) using Noether's theorem. As may be confirmed simply by taking its time derivative, the infinitesimal transformation

of the transverse pieces of the vector and pseudovector potentials invokes the infinitesimal transformation:

of the electric and magnetic fields which leaves Maxwell's equations (3.1)–(3.4) invariant in form. Let us identify (7.20) as our boost spin symmetry transformation. Comparing it with (7.5), we see that (7.20) is the closest approximation to an infinitesimal mixing of the electric and magnetic field vectors, in the sense defined by the infinitesimal vector ϕ, leaving the spacetime distribution of the field unchanged, that is consistent with the requirement of transversality. In a similar vein, we identify the infinitesimal transformation:
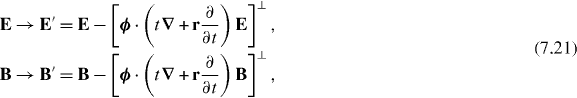
which leaves Maxwell's equations (3.1)–(3.4) invariant in form, as our boost orbital symmetry transformation. Comparing it with (7.5), we see that (7.21) is the closest approximation to an infinitesimal hyperbolic rotation of the spacetime distribution of the field about the origin, in the sense defined by the infinitesimal vector ϕ, without mixing the electric and magnetic field vectors, that is consistent with the requirement of transversality. The effects of the symmetry transformations (7.20) and (7.21) on a linearly polarized plane wave are depicted in figures 1 and 2, respectively.
Figure 1. The effect of the boost spin symmetry transformation (7.20) on a linearly polarized plane wave, with ϕ parallel to the direction of propagation. The amplitude of the wave is increased, leaving the spacetime distribution of the wave unchanged. For the sake of clarity, the magnitude of this transformation has been exaggerated and the magnetic field of the wave has been omitted.
Download figure:
Standard imageFigure 2. The effect of the boost orbital symmetry transformation (7.21) on a linearly polarized plane wave, with ϕ parallel to the direction of propagation. The spacetime distribution of the wave is modified such that the wavelength of the wave is blue-shifted, leaving the amplitude of the wave unchanged. For the sake of clarity, the magnitude of this transformation has been exaggerated and the magnetic field of the wave has been omitted.
Download figure:
Standard imageFollowing some simple manipulations, observing the independence of the components of ϕ, we deduce from (7.19) and our form (7.1) of Noether's theorem, that

which, pleasingly, expresses the conservation of our candidate (7.17) for the spin contribution to the boost angular momentum (7.6) of the field. As was noted originally [70], however, this candidate (7.17) is a vanishing quantity ( ). It appears, therefore, that the separation of the boost angular momentum (7.6) of the field into separately conserved spin and orbital contributions ultimately fails in that our candidate (7.18) for the orbital contribution constitutes the entirety of the boost angular momentum (7.6) of the field (
). It appears, therefore, that the separation of the boost angular momentum (7.6) of the field into separately conserved spin and orbital contributions ultimately fails in that our candidate (7.18) for the orbital contribution constitutes the entirety of the boost angular momentum (7.6) of the field (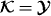 ).
).
The boost spin symmetry transformation (7.20) that we have identified is the natural partner of the spin symmetry transformation (7.11). The vanishing of our candidate (7.17) for the spin contribution to the boost angular momentum (7.6) of the field thus falls in line with our general observations regarding such symmetry pairs. For completeness, we note that the partner symmetries of (7.12) and (7.21) are seemingly obscure and are associated with trivial conserved quantities.
7.3. Other non-local symmetries and their associated conserved quantities
We have seen that the optical spin (7.9) and the orbital-like contribution (7.10), which have the dimensions of an angular momentum, are associated with non-local symmetry transformations, as necessitated by the requirement of transversality. Other conserved quantities that possess familiar dimensions and are associated with non-local symmetries also exist, for example the ij-infra-zilches which we have considered elsewhere [22].
We recognize, in fact, that there are an infinite number of non-local symmetries and associated conserved quantities. Unlike, for example, the optical spin (7.9), the orbital-like contribution (7.10) and the ij-infra-zilches [22], however, the majority of these conserved quantities have unfamiliar dimensions. To illustrate this claim, we present the infinitesimal transformation:

where α is an infinitesimal scalar with the dimensions of an inverse length. Note that (7.23) is a non-local transformation in the sense that the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials are expressible as non-local integral functions of the electric and magnetic fields, E and B [68], as noted earlier. That (7.23) constitutes a symmetry follows from the fact that the transverse pieces of the vector and pseudovector potentials obey the equations:

which are identical in form to Maxwell's equations (3.1)–(3.4) themselves. Such self-similarity recurs indefinitely as we delve into the realms of various integrals of the electric and magnetic fields and is quite analogous to the self-similarity seen as we consider various derivatives of the electric and magnetic fields (compare (7.24) with (6.37)) [22]. In light of this structure, one can readily deduce the existence of an infinite hierarchy of non-local symmetries, as claimed. Through Noether's theorem, we find that (7.23), for example, is associated with the conservation law:

A comparison of (7.24) and (7.25) with (3.1)–(3.4) and (3.13), respectively, leads us to identify the conserved quantity,  , above, which has unfamiliar dimensions, as the 'energy' of the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials, in much the same way that Lipkin's 00-zilch (6.36) is the 'helicity' of G and M in (6.37), for example. This particular conserved quantity (7.25) has also been recognized by Drummond [7, 8]. We emphasize that (7.25) is but one of an infinite number of conserved quantities with unfamiliar dimensions that are associated with non-local symmetries and appear to describe properties of various integrals of the electric and magnetic fields.
, above, which has unfamiliar dimensions, as the 'energy' of the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials, in much the same way that Lipkin's 00-zilch (6.36) is the 'helicity' of G and M in (6.37), for example. This particular conserved quantity (7.25) has also been recognized by Drummond [7, 8]. We emphasize that (7.25) is but one of an infinite number of conserved quantities with unfamiliar dimensions that are associated with non-local symmetries and appear to describe properties of various integrals of the electric and magnetic fields.
As with local symmetries, it seems that non-local symmetries exist in pairs, only one member of which is associated with a non-trivial conserved quantity. Through Noether's theorem, we find that the partner symmetry of (7.23), for example, is associated with a trivial conserved quantity. The existence of various non-local symmetries has also been recognized by Fushchich and Nikitin [34, 35].
In proof, an anonymous referee highlighted the fact that the time derivative of the 'energy', 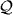 , (7.25) of the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials is essentially equal to the trivial quantity,
, (7.25) of the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials is essentially equal to the trivial quantity, 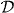 , that we met earlier (6.9), in that
, that we met earlier (6.9), in that 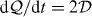 . Thus, the vanishing (6.10) of the latter quantity (
. Thus, the vanishing (6.10) of the latter quantity (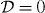 ) can be viewed as a statement of the conservation law
) can be viewed as a statement of the conservation law 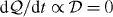 deduced above (7.25). Such observations are readily generalized. In particular, we find, following the discussion above, that the (conserved) 'linear momentum' of the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials is
deduced above (7.25). Such observations are readily generalized. In particular, we find, following the discussion above, that the (conserved) 'linear momentum' of the transverse pieces, A⊥ and C⊥, of the vector and pseudovector potentials is

Note that the form of the integrand in (7.26) is analogous to Poynting's vector, E × B [13, 79]. We observe that the time derivative of (7.26) is essentially equal to our candidate, 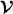 , for the spin contribution (7.17) to the boost angular momentum (7.6) of the field in that
, for the spin contribution (7.17) to the boost angular momentum (7.6) of the field in that  . It appears, therefore, that the vanishing of our candidate (
. It appears, therefore, that the vanishing of our candidate (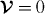 ) can be viewed as a statement of the conservation law
) can be viewed as a statement of the conservation law 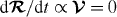 .
.
8. Discussion
In light of electric–magnetic symmetry, we have introduced a variational description of the free electromagnetic field that is based upon the acknowledgement of both electric and magnetic potentials. We have used our formalism within the context of Noether's theorem to investigate symmetries and their associated conserved quantities.
It seems that the field only possesses a handful of conserved quantities with familiar dimensions, simple Lorentz transformation properties and readily appreciable physical significance. In particular, our investigation has uncovered the optical helicity (6.6) as that Lorentz pseudoscalar whose conservation is associated with the (non-geometric) symmetry that is the invariance of Maxwell's equations (3.1)–(3.4) under a duality rotation (3.5) [1, 2, 13]. Furthermore, the fact is familiar that the energy momentum tensor (6.14) and the angular momentum tensor (6.15) are associated with (geometric) Poincaré transformations. Accordingly, these tensors possess generalizations in the presence of charges such that energy, linear momentum, angular momentum and boost angular momentum are absolutely conserved quantities in electromagnetic theory [11, 13]. The optical helicity, in contrast, is a property of freely propagating electromagnetic waves and is not conserved in general.
Other gauge invariant conserved quantities with familiar dimensions and appreciable physical significance are also readily recognized in a given frame of reference. The optical spin (7.9) and the orbital-like (7.10) contribution to the angular momentum (7.3) of the field are familiar examples. Indeed, we have recently advocated the optical spin (7.9) and the ij-infra-zilches elsewhere as being conserved quantities with the dimensions of an angular momentum which, in a given frame of reference, exist in addition to the optical helicity (6.6), providing a larger description of photon helicity [22, 23]. It seems, however that such quantities are not related between reference frames in a simple manner. To shed light on this, it may be instructive to examine, with care, their associated non-local symmetry transformations as they appear in different frames of reference. This may also lead to deeper insights regarding the apparent inability to separate the boost angular momentum (7.6) of the field into spin and orbital contributions and, for that matter, our general observation that symmetries exist in pairs, only one member of which is associated with a non-trivial conserved quantity.
Regarding the infinite hierarchies of conserved quantities with increasingly unfamiliar dimensions (amongst them, Lipkin's zilches [51]), we have suggested that their existence is a reflection of the self-similarity inherent in (6.37) and (7.24), for example, and that they describe properties of various derivatives and integrals of the electric and magnetic fields [22].
Acknowledgments
We thank Alison Yao for helpful discussions and comments as well as two anonymous referees who read our manuscript with care and provided valuable suggestions. This work was supported by the Carnegie Trust for the Universities of Scotland, the UK Engineering and Physical Sciences Research Council (EPSRC), the Royal Society, the Wolfson Foundation and the Leverhulme Trust.
Appendix.: Regarding the standard Lagrangian density
Consider the standard Lagrangian density (3.9). Assuming an active transformation of the magnetic potential

where the four-vector ΔAα is infinitesimal and possesses suitable dimensions, a derivation analogous to the one presented in section 4 yields the result

An infinitesimal duality rotation (6.2) is invoked, in any gauge, by taking ΔAα = θCα, where θ is an infinitesimal Lorentz pseudoscalar angle. Explicit calculation then reveals that  . Thus, as noted in section 3, an infinitesimal duality rotation does not leave the standard Lagrangian density (3.9) invariant in form, despite the fact that it constitutes a symmetry of Maxwell's equations (3.1)–(3.4) themselves. Nevertheless, we have, from (A.2)
. Thus, as noted in section 3, an infinitesimal duality rotation does not leave the standard Lagrangian density (3.9) invariant in form, despite the fact that it constitutes a symmetry of Maxwell's equations (3.1)–(3.4) themselves. Nevertheless, we have, from (A.2)

which is

As θ ≠ 0, it follows from (A.4) that

where hγ is the helicity four-pseudovector (6.4), as desired. This is at odds with the recent claim that the standard Lagrangian density (3.9) implies an absence of optical helicity conservation [10].
Use of the standard Lagrangian density (3.9) does not lead to any fundamental difficulties when applying Noether's theorem, although the manipulations required to arrive at the desired results can be rather involved. In contrast, all symmetries of Maxwell's equations (3.1)–(3.4) are automatically symmetries of our electric–magnetic Lagrangian density (3.11), as explained in section 5.




