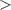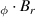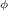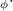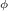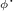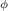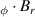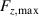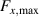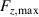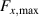Identifying the current penetration depth in high-Tc superconducting bulks through levitation force measurements

Justin Brooks; Luke Porteous; James G Storey; Rodney Badcock

doi:10.1088/1361-6668/adad4c

1. Introduction

Superconducting magnetic bearings (SMBs) have garnered significant attention in recent years due to their unique properties and potential applications. Unlike conventional bearings, SMBs utilize the phenomenon of superconducting levitation, which results from the Meissner effect and flux pinning properties of type-II superconductors [1]. These characteristics eliminate frictional loss and wear, making SMBs ideal for applications which may require low maintenance, and long operational lifespans.

The phenomenology of superconducting levitation lies in the ability of type-II superconductors to expel magnetic fields from their interior through the Meissner effect, while simultaneously allowing magnetic flux to penetrate through in the form of quantized vortices. These vortices within the superconducting material exhibit flux pinning, where the vortices are fixed in a lattice structure. The pinning of these vortices can produce restoring forces if the source of the external magnetic field is perturbed, enabling SMBs to support loads and maintain their position without additional feedback control.

There are numerous potential applications for SMBs, such as flywheel energy storage systems [2–4], maglev trains [5, 6], high speed motors [7, 8], and cryogenic fuel pumps [9–11]. In flywheel energy storage systems, SMBs can significantly reduce energy losses due to friction, thereby improving overall efficiency. Maglev trains benefit from the reduced mechanical resistance and increased speed potential offered by SMBs. Using electric motors, high speed rotating machines can be designed with RPM $\gt$ 100 000, all in frictionless conditions. This may be of use in centrifugal cryogenic fuel pumps for example where passive cooling can be extracted from the cryogenic fluid. However, SMB's are limited by their poor lateral stiffness [12, 13] compared to conventional bearings.

Several bearing configurations have been investigated, including axial thrust bearings, Halbach arrays [14, 15], multi-surface bearings [16–18], shaped HTS and permanent magnets (PMs) [19, 20], bulks with artificial holes [21], mixed-µ [22, 23], Evershed bearings [1, 24], and various combinations of stacked coated conductor bearings [25–31]. Dynamically controlled bearings have also been demonstrated using a combination of HTS coils and flux pumps [32, 33].

In this work, the focus is on the impact of adjusting the thickness of type-II superconducting bulks on the generated levitation forces in the simplest thrust bearing configuration, consisting of a PM and a single HTS bulk. By polishing away layers of the superconducting bulk, an understanding of how the depth at which currents are generated within the material influences the overall levitation force is developed. This investigation is further conducted as a function of temperature, providing insights into the temperature dependence of levitation forces and the superconducting properties of the bulk material.

Through systematic levitation force measurements and numerical modelling, our study seeks to elucidate the relationship between bulk thickness, current distribution, and levitation performance. Understanding these parameters is crucial for optimising the design and functionality of SMBs in various applications. These findings have the potential to inform future developments in superconducting technologies, enhancing their applicability and efficiency across a broad spectrum of fields.

2. Methods

The following section contains information on the studied superconducting bulk, the experimental setup, the measurement procedures, and the numerical methods used to interpret the experimental data.

2.1. Bulk materials

The superconducting bulk investigated in this report is a single-direction melt growth (SDMG) GdBCO bulk prepared by CAN superconductors [34]. The SDMG bulk is made by preparing a bulk precursor pellet which is placed on top of a seed plate. The seed plate is a single grain bulk grown using top seeded melt growth. In the SDMG growth process, the SDMG bulk is grown exclusively parallel to the c-axis. This process eliminates the sector boundaries present in top-seeded melt growth bulks, improving the homogeneity of the grown crystal [35, 36]. The SDMG bulk studied is cylindrical with an initial thickness of 4.5 mm and a radius of 17.5 mm. The bulk thickness is adjusted using a reticulating diamond wire saw and polishing using a fine grit sandpaper on a granite slab. The bulk is always polished on the face farthest from the PM (non-seed face), leaving the seed face unchanged.

2.2. Experimental methods

This section describes the equipment used to measure the levitation force between the SDMG bulk and a PM. The PM is a cylindrical N52-grade NdFeB magnet with a radius and thickness of 10 mm. The PM is bonded to a flat plate, the position of which is controlled by two linear stages. These linear stages allow the PM to move along the z-axis and x-axis. These correspond to travel in directions perpendicular and parallel to the broad face of the SDMG bulk respectively. The PM is connected to a 3-axis GLOCE GPB161 load cell which can measure the respective components of the levitation force between the SDMG bulk and the PM. The positioning of the linear stages is monitored using two linear variable differential transformers (LVDTs).

The experiment takes place inside of a vacuum chamber with the bulk housed in a recessed aluminium plate which is mounted directly onto a cold head. Between the bulk and the aluminium plate there is an aluminium spacer. The spacers are necessary to maintain a fixed minimum z-axis separation between the bulk and PM as the bulk thickness is reduced. Four resistors are mounted symmetrically around the edges of the aluminium plate which are used to adjust the temperature of the bulk. A PT100 thermocouple is bonded to the aluminium plate to monitor/control the temperature using PID control with a Cryocon 26 temperature controller.

The force sensors, the LVDTs and the PT100 are connected to a NI-DAQ 9205. The measurement and hardware is controlled using custom LabVIEW software. An image of the experimental setup including the SDMG bulk, the PM and the above mentioned sensors, alongside the motion of the PM during zero-field cooled (ZFC) and field-cooled experiments, is shown in figure 1.

Figure 1. Refer to the following caption and surrounding text. — **Figure 1.** Photo of the HTS bulk in the recessed aluminium plate and the PM, and a diagram describing the different measurement routines and the motion of the PM relative to the superconducting disc.
Download figure:
Standard image High-resolution image

Three measurement routines are used. These are:

(i)
ZFC where the PM is initially 49 mm away from the SDMG bulk along the z-axis. The bulk is cooled to the desired temperature with the temperature left to stabilise for approximately 30 minutes. The PM then travels towards the bulk while simultaneously measuring the levitation forces between the two objects. The PM travels until there is 2 mm between the PM and SDMG bulk faces. The PM remains static and the relaxation of the levitation force is measured for several minutes.
(ii)
FC z-axis motion measurements where the initial z-axis separation between the SDMG bulk and the PM faces is 2 mm. The SDMG bulk is then cooled to the desired temperature and the temperature left to stabilise over 30 minutes. The PM z-axis separation is repeatedly moved between z = 2 and 49 mm while measuring the levitation forces to capture hysteresis effects.
(iii)
FC x-axis motion measurements where the z-axis separation between the SDMG bulk and the PM is 2 mm. The SDMG is then cooled to the desired temperature and left to stabilise for 30 minutes. The PM is repeatedly moved between x = ± 6 mm to capture hysteresis effects.

In each of these measurements, the PM and the SDMG bulk are co-axially aligned and the PM travels at 1 mm · s⁻¹. After a measurement is completed, the temperature is raised to 120 K to purge any trapped currents and flux before beginning the subsequent measurement.

3. Finite element methods

Finite element models were used to interrogate the experimental results. The finite element model utilises both the H-formulation and the A-formulation, implemented in COMSOL Multiphysics [37]. The model is axi-symmetric and is comprised of two separate studies. First, a stationary study produces the magnetic field from the PM in a large air-domain using the A-formulation. The magnetic field is determined entirely by its geometry and the assignment of a remnant flux density value, chosen to be 1.27 T. The second study is time dependent where the superconductor is modelled inside of a small rectangular domain with an air gap of 1 mm using the H-formulation. The sum of the PM field modelled in the first part and the self-field due to currents circulating in the bulk is applied as a boundary condition on the surrounding rectangular domain. The self-field components are calculated using the Biot–Savart law.

Figure 2 shows the finite element domains and the meshing density in the two studies used to model the levitation force between the HTS bulk and PM. Figures 2(a) and (b) are used in study one. Figure 2(a) shows a magnified view of the PM, highlighted in blue. Figure 2(b) shows the entire surrounding air domain. Figure 2(c) shows the complete domain used in study two. The HTS region is highlighted in blue. The red dashed line indicates the boundary where the sum of the PM and self-field from the HTS is applied. The rotationally symmetric axis is the left hand side vertical edge of each domain.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.** Image of the finite element model domains and mesh density.
Download figure:
Standard image High-resolution image

With appropriate choices for the time dependent values of the boundary conditions, ZFC and FC z-axis motion experimental conditions can be simulated. The PM vertical speed is set at 1 mm · s⁻¹ and moves in a continuous manner. The FC x-axis motion experiment can not be recreated using an axi-symmetric model. The superconductor is modelled using the conventional power-law constitutive relationship, relating the resistivity of the superconductor to the local components of the electric field E, current density J, and the critical current density J_c(B,θ) given by

$\begin{align} \boldsymbol{E} = \rho \boldsymbol{J}\end{align} \tag{ 1 }$

$\begin{align} \rho = \frac{E_0}{J_c{\left(B,\theta\right)}} \left| \frac{J_\phi}{J_c{\left(B,\theta\right)}}\right| ^{n{\left(B,\theta\right)}}\end{align} \tag{ 2 }$

with levitation force exerted on the PM extracted using

$\begin{align} \textbf{F} = \int \textbf{J} \times \textbf{B} \mathrm{d}V\end{align} \tag{ 3 }$

where the integral is performed over the volume of the HTS bulk.

The J_c(B,θ) and n(B,θ) values input into the finite element model are obtained using the SuperCurrent facility at Paihau-Robinson Research Institute [38]. Using this system, a transport current is passed through a bar cut from the SDMG superconducting bulk while the bar is positioned inside a split-pair HTS magnet capable of generating up to 8 T. The superconducting bar is then rotated, collecting I_c(B,θ) and n(B,θ) data at temperatures relevant to the experimental programme. This process was carried out once all levitation measurements had been collected as the process of cutting the bulk into bars destroys the sample. The bars were cut from a 0.5 mm thick layer taken from the seed-face. J_c(B,θ) is extracted by assuming I_c is uniformly distributed over the cross-section of the bar used in the SuperCurrent system. The measured I_c(B,θ) and n(B,θ) data is shown in appendix. The bulk is assumed to be at a constant temperature during simulation. This is justified as the ratio J ${\,}_{\phi}$ /J_c(B,θ) never exceeds 1. A full description of the process used to prepare the bulks and collect the data is given in [39].

4. Results

This section presents levitation force measurements conducted under both ZFC and FC conditions, accompanied by corresponding finite element models. These results provide insight into how variations in bulk thickness and temperature affect the penetration depth of currents, magnetic fields, and the resulting levitation forces.

4.1. ZFC: experimental results and finite element models

The ZFC measurements provide an initial understanding of how bulk thickness and temperature influence the levitation force. Figure 3 shows the levitation force for the uncut bulk (seed and non-seed faces) and a 2.5 mm thin disk cut from the larger bulk. The levitation force for the 2.5 mm disc is nearly identical to the seed face data. The non-seed face exhibited a slightly lower maximum force by 6%, suggesting some minor variation in current distribution between the faces.

Figure 3. Refer to the following caption and surrounding text. — **Figure 3.** Comparison between levitation forces generated between a PM and the top and bottom faces of the bulk, as well as from a 2.5 mm thick slice of the bulk with the interior face towards the PM under zero-field cooling conditions at 77 K.
Download figure:
Standard image High-resolution image

Figure 4 compares the experimental and finite element model results for levitation forces at four bulk thicknesses (d = 2.5 mm, 1.8 mm, 1 mm, and 0.5 mm) and four temperatures (T = 77 K, 85 K, 88 K, and 90 K). The inset within each figure shows the time-dependent levitation force decay when the PM reaches it is closest position and ceases movement. The oscillations within each decay set are due to the vibrations of the cold-head.

Figure 4. Refer to the following caption and surrounding text. — **Figure 4.** Vertical levitation force, F_z vs z-separation measurements and finite element modelling results for various thickness bulks and temperatures under zero-field cooling conditions. Insets show the time dependence, including the force decay.
Download figure:
Standard image High-resolution image

The experimental data (blue solid lines) and model results (orange dashed lines) agree well for the thicker samples (2.5 mm and 1.8 mm) across all temperatures. At 77 K, the maximum levitation force remains almost unchanged for thicknesses greater than 1 mm, indicating that the currents and magnetic fields responsible for levitation are confined to a region within the first millimetre of the bulk. Once the thickness drops below 1 mm, the levitation force decreases significantly, reflecting a redistribution of the current as the bulk becomes too thin to support significant shielding currents without full penetration. This also coincides with a deviation from the steady increase predicted by the finite element model. As we will see in the following section, this deviation occurs when the the external magnetic field fully penetrates the bulk through its thickness, followed by a change in the distribution of induced eddy currents. As the bulk temperature increases, this deviation from the steady increase occurs at higher magnet positions as the bulk becomes fully penetrated at higher magnet positions.

At higher temperatures (88 K and 90 K), the levitation force decreases sharply across all thicknesses, with the thinnest bulk (0.5 mm) showing the largest drop. In these cases, the model tends to overestimate the levitation force, particularly for the 0.5 mm bulk, suggesting that the model does not fully account for the increased current penetration or the reduced J_c values at elevated temperatures. One possible reason for this may be the presence of pores or cracks within the bulk which become increasingly relevant as the bulk thickness is reduced. In [34], pores as large as 100 µm are observed in cross-sections of SDMG bulks. Pores this size may cause a significant disruption in the flow of eddy currents.

Figure 5 shows the calculated distribution of the azimuthal current density, J_φ (column 1), radial magnetic field, B_r (column 2), and the levitation force given by their product, J ${\,}_{\phi} \cdot$ B_r (column 3) within the bulk. Shown are the calculated values at two temperatures (T = 77 K, 85 K) for all the thicknesses considered experimentally, when the PM is at the moment of closest approach, ie 2 mm above the bulk. At 77 K, the thicker bulks (2.5 mm and 1.8 mm) show minimal current penetration into the interior, with currents concentrated around the bulk faces closest to the PM at r ≈ 10 mm, near the edge of the PM. This aligns with the observation that the levitation force remains relatively unchanged for thicknesses greater than 1 mm. For thinner bulks (1 mm and 0.5 mm), current penetration becomes more uniform, which correlates with the reduction in levitation forces for these samples.

Figure 5. Refer to the following caption and surrounding text. — **Figure 5.** Finite element results showing the local variables J ${\,}_{\phi}$ , B_r, and J ${\,}_{\phi} \cdot B_r$ , within the superconducting bulk during ZFC conditions and when the PM is 2 mm away from the bulk. Shown are the results for T = 77 K (top four rows) and T = 85 K (bottom four rows) and for all the thicknesses considered experimentally.
Download figure:
Standard image High-resolution image

**Figure 5.** Finite element results showing the local variables J ${\,}_{\phi}$ , B_r, and J ${\,}_{\phi} \cdot B_r$ , within the superconducting bulk during ZFC conditions and when the PM is 2 mm away from the bulk. Shown are the results for T = 77 K (top four rows) and T = 85 K (bottom four rows) and for all the thicknesses considered experimentally.
Download figure:
Standard image High-resolution image

At higher temperatures (85 K and above), the current penetration becomes more pronounced in the thinner bulks. The plots show a reduction in the magnitude of J ${\,}_{\phi}$ and deeper penetration of both the current and magnetic field, which explains the significant reduction in levitation forces at these temperatures. The product J ${\,}_{\phi} \cdot$ B_r, which is proportional to the levitation force, is concentrated on the bulk face nearest the PM in thicker samples but is more uniformly distributed in thinner bulks, further explaining the reduced levitation forces measured experimentally at higher temperatures.

While the finite element model qualitatively captures these trends, it overestimates the levitation force for thinner bulks, especially at higher temperatures (88 K and 90 K). This discrepancy could be due to a mismatch between the set temperature during the I_c(B, θ) measurements and the temperature recorded on the aluminium plate during levitation force measurements, variations in temperature or J_c through the bulk, damage to the bulk during the polishing process, or the presence of porous features within the bulk which become increasingly relevant as the bulk thickness is reduced. Nevertheless, the model does reproduce the general behaviour observed experimentally, especially for thicker bulks and lower temperatures, where the current remains confined to a surface layer.

4.2. Field cooling: z-axis motion experimental results and finite element models

The FC measurements provide further insight into the behaviour of the superconductor under conditions where a magnetic field is present during the cooling process. These measurements are crucial for understanding how hysteresis and temperature affect the levitation force in superconducting bulks of varying thicknesses.

Figure 6 shows the vertical levitation force profiles for different bulk thicknesses at temperatures ranging from 77 K to 90 K. At 77 K, the hysteresis curves for the 2.5 mm and 1.8 mm bulks are nearly identical, supporting the findings from the ZFC measurements, where reducing the thickness below 2.5 mm had minimal effect on the current distribution at lower temperatures. However, once the thickness is reduced to 1 mm, a slight broadening of the hysteresis curves is observed, along with an increase in levitation force at the closest z-axis separation between the bulk and the PM. This trend becomes more pronounced for the 0.5 mm bulk, which exhibits the largest hysteresis and highest levitation force at closest approach.

Figure 6. Refer to the following caption and surrounding text. — **Figure 6.** Vertical levitation force, *F_z*, vs z-separation measurements and finite element modelling results for various thickness bulks and temperatures under field cooling conditions. The arrows indicate the direction of travel of the PM.
Download figure:
Standard image High-resolution image

As the temperature increases, these behaviours change. By 88 K, the levitation force for bulks thinner than 1 mm begins to decrease significantly, with the 90 K data showing a sharper decline. This reduction in levitation force can be attributed to a combination of lower J_c values due to the increased temperature and the reduced superconducting volume in the thinner samples, limiting their ability to generate substantial levitation forces.

The finite element model captures the essential characteristics of the field-cooled experiments, despite some discrepancies in the predicted levitation forces at higher temperatures and for the thinnest samples. Figure 7 illustrates the calculated azimuthal current density (J ${\,}_{\phi}$ ), the radial magnetic field (B_r), and the levitation force given by J ${\,}_{\phi} \cdot$ B_r, for key moments during the FC z-axis motion experiments at 77 K. For thicker bulks, the current and magnetic field penetration remains shallow, leading to narrower hysteresis curves. As the bulk thickness decreases, current penetration becomes more complete, resulting in stronger repulsive forces at closer z-axis separations.

Figure 7. Refer to the following caption and surrounding text. — **Figure 7.** Finite element results showing the local variables J ${\,}_{\phi}$ , B_r, and J ${\,}_{\phi} \cdot B_r$ , within the superconducting bulk during FC conditions and while the PM is moving along the z-axis. Shown are the results for T = 77 K when the z-separation is 2 mm after the PM has moved from its initial position, (top four rows) and 49 mm, having returned to its initial position(bottom four rows) and for all the thicknesses considered experimentally.
Download figure:
Standard image High-resolution image

**Figure 7.** Finite element results showing the local variables J ${\,}_{\phi}$ , B_r, and J ${\,}_{\phi} \cdot B_r$ , within the superconducting bulk during FC conditions and while the PM is moving along the z-axis. Shown are the results for T = 77 K when the z-separation is 2 mm after the PM has moved from its initial position, (top four rows) and 49 mm, having returned to its initial position(bottom four rows) and for all the thicknesses considered experimentally.
Download figure:
Standard image High-resolution image

One notable result is that, for the thinnest bulk (0.5 mm), the maximum levitation force at 77 K reaches 16.7 N, compared to only 1.8 N for the 2.5 mm bulk. This significant increase in levitation force can be linked to the complete penetration of currents through the thinner bulk. In the thicker samples, there are regions where the current induced by the initial motion of the PM away from the bulk are positive (blue) and located nearer to the bulk face furthest from the PM. When the magnet is brought back into close proximity, the newly induced currents (red) do not penetrate deeply enough to erase these screening currents. Given that the radial magnetic field has the same polarity through the bulk at this moment, the currents at the surface closest to the PM act to repel the PM while the deeper situated currents have an attractive force.

In the thinner samples, the sample is fully penetrated as the PM descends. The induced currents and magnetic fields, completely erase those trapped when the PM is initially moved away. When this occurs, the FC levitation force profiles overlap those obtained in ZFC conditions. This is observed in both the finite element results and the experimental results. There is a slight discrepancy between the ZFC and FC data for the 0.5 mm thickness wafer where the peak FC levitation force exceeds the ZFC data. This is attributed to variations in thermal anchoring to the cooling plate and therefore variations in the temperature.

The overall trends observed in the experimental data, such as the increasing levitation force for thinner bulks at low temperatures and the sharp decline in levitation force at elevated temperatures, are qualitatively reproduced by the finite element model. However, the model tends to overestimate the levitation force for thinner samples, especially at higher temperatures, for the same reasons discussed in the ZFC section.

4.3. Field cooling: x-axis motion experimental results

Figure 8 presents the lateral levitation force profiles for different bulk thicknesses at temperatures ranging from 77 K to 90 K. Note that the 77 K, 1.8 mm thick experiment was not run, and this was not noticed until after the bulk was polished, thus the measurement is missing.

Figure 8. Refer to the following caption and surrounding text. — **Figure 8.** Lateral levitation force, *F_x*, vs x-position measurements and finite element modelling results for various thickness bulks and temperatures under field cooling conditions. The arrows indicate the direction of travel of the PM.
Download figure:
Standard image High-resolution image

Unlike the z-axis motion experiments, the maximum lateral levitation force steadily decreases as the sample thickness is reduced or the temperature raised. The area of the hysteresis loops also have a peak at a particular thickness value, dependent on the temperature. The area of the hysteresis loops peaks at bulk thicknesses of 0.5 mm, 1.5 mm, 1.8 mm, and 2.5 mm as the temperature increases from 77 K to 85 K, 88 K, and 90 K, respectively. Increases in the hysteresis loop area indicates a corresponding increase in damping effects of dynamic motion, however, provides little resistance to slow movements under constant loading.

At temperatures of 88 K and above, for samples thinner than 2.5 mm, the hysteresis profiles flatten for displacements larger than a few mm, and the peak lateral force becomes position independent. This flattening of the hysteresis curve suggests that that the vortex lattice within the bulk has melted [40, 41], resulting in a steady viscous drag force, rather than providing any significant restoring force. This also results in a significant shift in the equilibrium position of the PM. For the thinnest samples at the highest temperatures, the area of the hysteresis loop starts to decrease, suggesting that the bulk is fully saturated, thus the removal of material simply reduces the overall hysteresis.

4.4. Comparison of the maximum measured levitation forces

To better illustrate the trends observed in the FC measurements, we compare the maximum measured axial and lateral levitation forces, $F_{z,\mathrm{max}}$ and $F_{x,\mathrm{max}}$ , as a function of bulk thickness for different temperatures in figure 9.

Figure 9. Refer to the following caption and surrounding text. — **Figure 9.** Comparison of the maximum measured forces, $F_{z,\mathrm{max}}$ and $F_{x,\mathrm{max}}$ , as a function of sample thickness and temperatures for field-cooled experiments..
Download figure:
Standard image High-resolution image

Figure 9(a) presents the measured $F_{z,\mathrm{max}}$ during FC z-axis motion experiments. Each temperature curve exhibits a peak force value at a specific bulk thickness. Given the sparseness of the data however, the precise peak position cannot be determined. The peaks occur after the magnetic field penetrates through the thickness of the bulk and additional induced currents occupy the bulk centre and edge regions. This redistribution of current coincides with the deviation from steady increase observed in the ZFC measurements and finite element modelling. Thus, we may use these force peaks as a proxy to identify the thickness when the bulk is fully penetrated, noting that they will slightly underestimate the true value. Before full penetration, radial magnetic fields are trapped on the face farthest from the PM, providing attractive forces. However, once the bulk is fully penetrated, these opposite polarity fields are erased, increasing the repulsive force. If the bulk thickness is reduced further, the maximum repulsive force decreases as there is less bulk material and subsequently less current available to levitate the PM.

The position of the peak shifts toward thicker samples as temperature increases, reflecting the temperature dependence of the critical current density, J_c. At higher temperatures, J_c decreases, resulting in deeper field penetration and requiring thicker bulks to maintain partial shielding.

Neither the 77 K nor the 90 K data resolves the peak. For 77 K, the maximum levitation force appears to continue increasing as bulk thickness decreases, implying that the peak may occur below the thinnest sample tested (0.5 mm). For 90 K, the data suggests that the peak may occur at a thicker sample than those tested. Peaks for intermediate temperatures are observed at approximately 1 mm for 85 K and 1.8 mm for 88 K.

Figure 9(b) shows the measured $F_{x,\mathrm{max}}$ during FC x-axis motion experiments. In contrast to the axial force data, no peak is observed in the lateral forces. Instead, the maximum force consistently increases as the bulk thickness increases, across all tested temperatures. This trend highlights that lateral stiffness depends primarily on the available superconducting volume, with thicker samples providing greater restoring forces due to their ability to sustain larger shielding currents. These results results are consistent with data presented in [21] where similar measurements were performed for large thickness bulks (1–18 mm) at 77 K.

5. Conclusion

This study demonstrates the critical influence of temperature and bulk thickness on the levitation forces generated between a GdBCO SDMG bulk and an NdFeB PM. In ZFC conditions at a fixed temperature, the axial levitation force increases as a function of bulk thickness up until a critical thickness. Beyond this thickness, any additional bulk volume is not penetrated by the approaching PM, and thus does not contribute any levitation force. This critical thickness increases as a function of temperature due to lower J_c values and the resultant decrease in shielding capacity. The critical thickness values were found to range from 1 mm to 2.5 mm between 77 and 88 K.

The situation is somewhat different in field cooling conditions. The initial field cooling traps magnetic field and current deeper into the bulk than is possible in ZFC. This magnetic field and current are responsible for an attractive force between the PM and the bulk. Finite element models indicate that when the PM is moved, the eddy currents and fields vary over the same thickness as is observed in the ZFC, ie the deeper magnetic field and current is frozen in. If the bulk thickness is reduced, the frozen in magnetic field and current is lost, increasing the repulsive force between the magnet and superconductor, and subsequently shifts the magnet equilibrium position further away. If the bulk thickness is such that the induced eddy currents saturate the bulk, the bulk is returned to a ZFC state. In doing so, the repulsive force between the magnet and bulk is maximised, at the expense of stabilising attractive forces from currents and fields trapped in the bulk interior or on the alternate face.

While the finite element models did not perfectly match the experimental results, they qualitatively captured key trends and serve as valuable design tools for optimising bearing performance.

Acknowledgements

We acknowledge helpful instruction on the force-decay measurements from Dr Mohammad Siamaki.

This work was supported by the New Zealand Ministry of Business, Innovation and Employment (MBIE) Advanced Energy technology Platform (AETP) Program High power electric motors for large scale transport under Contract RTVU2004.

Data availability statement

All data that support the findings of this study are included within the article (and any supplementary files).

Appendix: J_c(B,θ) data

Figure 10 shows the measured J_c(B,θ) data on the SDMG bulks as measured in the SuperCurrent facility at Robinson Research institute at T = 77, 85, and 90 K. The calculated maximum internal magnetic field is approximately 1 Tesla.

Figure 10. Refer to the following caption and surrounding text. — **Figure 10.** Experimentally measured I_c(B,θ) (column 1) and n(B,θ) (column 2) data obtained on bars cut from the SDMG bulk over 180^∘ and in fields up to 2 Tesla.
Download figure:
Standard image High-resolution image

Identifying the current penetration depth in high-Tc superconducting bulks through levitation force measurements

Author notes

Notes

Article metrics

Submit

Share this article

Dates

Abstract