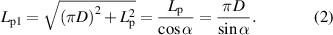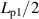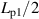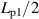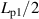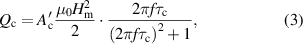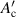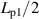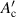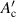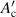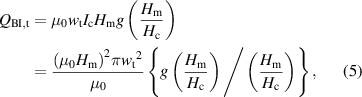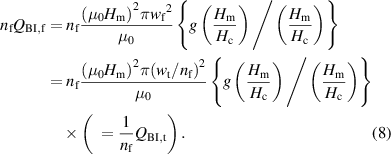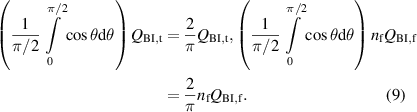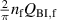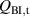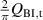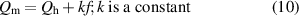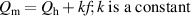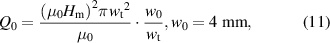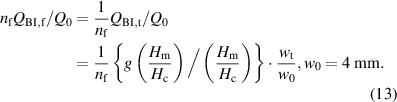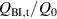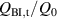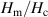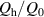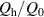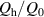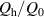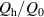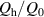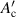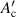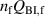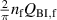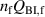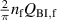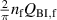Abstract
We wound copper-plated multifilament coated conductors spirally on a round core to decouple filaments electromagnetically under ac transverse magnetic fields and measured their magnetisation losses. Although the coated conductors were plated with copper, which connects all filaments electrically and allows current sharing among them, the spiral geometry decoupled filaments similar to the twist geometry, and the magnetisation loss was reduced effectively by the multifilament structure. The measured magnetisation loss of a 4 mm wide, 10-filament coated conductor with a 20 μm thick copper wound spirally on a 3 mm core was only 7% of that of the same 10-filament coated conductor with a straight shape under an ac transverse magnetic field with an amplitude and frequency of 100 mT and 65.44 Hz, respectively. We separated the measured magnetisation losses into hysteresis and coupling losses and discussed the influence of filament width, copper thickness, and core diameter on both losses. We compared the hysteresis losses with the analytical values given by Brandt and Indenbom and compared the coupling losses with the values calculated using a general expression of coupling loss with the coupling time constants and geometry factors.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Small magnetisation losses under ac transverse magnetic fields and protection as well as stability against normal transition are keys to the various power applications of coils wound with coated conductors. In principle, by striating the wide superconductor layer of a coated conductor to form narrower filaments, magnetisation loss can be reduced [1–17], and insulating the filaments electrically from one another might be ideal for this purpose.
However, note that filaments must be electrically connected to one another at both terminals of a conductor in a real coil in order to feed a current. In such a case, we must transpose filaments to decouple against an ac transverse magnetic field and, then, to reduce the magnetisation loss. Šouc et al wound multifilament coated conductors spirally on a round core to transpose filaments and demonstrated significant reduction in magnetisation loss [18]. However, the lack of a stabilisation layer, such as copper, is a concern in similar multifilament coated conductors to the ones shown in figure 1(a). Copper plating is a popular approach to improve the stability of coated conductors and to help their protection. Several groups have applied this approach to multifilament coated conductors [13–15]. Most of them did not connect filaments electrically using copper, as shown in figure 1(b), to avoid electromagnetic coupling among filaments, which affects magnetisation loss reduction by the multifilament structure. Vojenčiak et al striated the superconductor layers of coated conductors through their copper layers using a laser to form filaments, fabricated conductor on round core (CORC®) cables using such coated conductors, and demonstrated magnetisation loss reduction compared to reference cables fabricated using monofilament coated conductors [14]. Similar experiments were reported by Li et al [19] and Goo et al [20]. All of these previous studies used multifilament coated conductors with a copper stabilising layer that does not electrically connect filaments, as shown in figure 1(b).
Figure 1. Multifilament coated conductors with and without a copper stabilising layer: (a) without copper stabilising layer, (b) with copper stabilising layer on each filament, which does not connect filaments electrically, and (c) copper stabilising layer covers entire group of filaments, which connects all filaments electrically.
Download figure:
Standard image High-resolution imageMeanwhile, electrical connection among filaments through copper is preferable for stability and protection, because it enables the detour of current to avoid the local normal section (an intrinsic defect or a normal-transiting part) of a filament. Such a current detour is known as current sharing. Note that a local defect in a filament can block the current in the filament, which is insulated from the others. If there is one local defect in each narrow insulated filament in a long multifilament coated conductor, the conductor cannot carry any current. If we plate the entire group of filaments with copper, as shown in figure 1(c), the copper connects all filaments electrically and allows current sharing [15–17]. In this paper, we call this type of conductor a copper-plated multifilament (or striated) coated conductor. The drawback of this type of conductor is the electromagnetic coupling of filaments under ac transverse magnetic fields by the coupling current flowing through the copper, which could increase the magnetisation loss [15]. To reduce the magnetisation loss effectively, the coupling time constant, which is the decay time constant of the coupling current, must be much shorter than the characteristic time of the magnetic field change. The coupling time constants are quite large even in low-Tc superconductor (LTS) wires unless they are not twisted, but we can twist round metallic LTS wires to reduce their coupling time constants. We previously conducted proof-of-concept experiments on the reduction of coupling time constants of copper-plated multifilament coated conductors using spiral geometry, that is, CORC-like geometry. In the experiments, we wound coated conductors with a 100 μm thick substrate loosely on round cores with relatively large diameters (10–20 mm) [21]. The spiral geometry successfully played a role equivalent to that of the twist geometry in reducing the coupling time constants.
Up-to-date CORC® wires are wound on cores with a diameter of 2.5 mm [22, 23], and the symmetric tape round (STAR) wires are wound on even smaller cores [24, 25]. If we wind a copper-plated multifilament coated conductor spirally on a core with such a small diameter with a sufficiently short pitch, we can reduce its coupling time constant significantly, as explained in section 2 [26–28]. Based on this consideration, we have proposed the concept of a spiral copper-plated striated coated-conductor cable (SCSC cable) (also called as 'double SC' cable), as shown in figure 2, in which we wind copper-plated striated (multifilament) coated conductors spirally on a round core [26, 27] 4 . The copper improves the stability and helps the protection whereas the spiral geometry decouples filaments against ac transverse magnetic fields, thus effectively reducing magnetisation losses. The configuration of the superconducting elements (thin strips twisted around a core) in the SCSC cable is almost identical to the filament configuration in classical LTS wires. Consideration on ac losses and reduction strategies (finer filaments, shorter twist pitches, and higher transverse resistivity) are therefore similar.
Figure 2. Schematic view of the SCSC cable.
Download figure:
Standard image High-resolution imageA drawback of the SCSC cables is the reduction in engineering and winding pack current density. However, it should be noted that reasonably high engineering current densities were reported for the CORC® wires [22, 23] and the STAR wires [24, 25] whose spiral structures are same as those of the SCSC cables.
The objective of this study is to demonstrate the magnetisation-loss reduction of copper-plated multifilament coated conductors subjected to ac transverse magnetic fields using the spiral geometry. Note that we reduced the core diameter to 3 mm to decrease the coupling time constant. We also aim to clarify the details of the coupling and hysteretic loss characteristics of copper-plated multifilament coated conductors wound spirally on round cores (hereafter, spiral copper-plated multifilament coated conductors), such as the influence of their filament width, copper thickness, and core diameter. To achieve these objectives, we prepared copper-plated multifilament coated conductors with a 30 μm thick substrate, wound them spirally on round cores with diameters of 3 and 5 mm, and measured their magnetisation losses.
The remainder of this paper is organised as follows. First, we explain the effect of spiral geometry on decoupling filaments in a copper-plated multifilament coated conductor in section 2. Section 3 describes the specifications of the coated conductors and their spiral geometries, and section 4 describes the experimental method. Section 5 presents and discusses the results. We compare the magnetisation losses of straight and spiral samples made with copper-plated multifilament and monofilament coated conductors. Then, we separate the measured magnetisation loss into frequency-independent and frequency-dependent components and examine their detailed characteristics. The former component primarily corresponds to hysteresis loss, whereas the latter component includes coupling and eddy current losses. Finally, section 6 presents our conclusions.
2. Spiral geometry of copper-plated multifilament coated conductor to decouple filaments
A method that is equivalent to twisting in LTS wires to reduce coupling time constants [29, 30] is required to reduce magnetisation losses effectively in practical long copper-plated multifilament coated conductors.
Figure 3(a) shows a schematic side view of the coupling currents in a spiral copper-plated multifilament coated conductor. D and Lp denote the diameter and pitch of the spiral coated conductor, respectively:
Figure 3. Schematic view of coupling currents in a spiral copper-plated multifilament coated conductor: (a) side view and (b) the coated conductor unwound and put on a flat plane.
Download figure:
Standard image High-resolution imagewhere α is the angle between the coated conductor and the core axis. As shown in this figure, when the spiral copper-plated multifilament coated conductor is subjected to an ac transverse magnetic field, the coupling current is confined to every half spiral pitch, because the orientation of the tape (coated conductor) faces against the magnetic field is inverted every half spiral pitch. In figure 3(b), we unwind the spiral copper-plated multifilament coated conductor and put it on a flat plane. In terms of coupling currents, figure 3(b) is equivalent to figure 3(a), where Lp1 denotes the length of the section of the coated conductor corresponding to a single spiral pitch Lp:
Because the length of the coupling current Lc is restricted to as shown in figure 3(b), the coupling time constant, which is proportional to the square of its length in principle, is proportional to the square of . Whereas the coupling current expands to the entire length Lt in a straight copper-plated multifilament coated conductor, as shown in figure 4(a), it is confined to each half pitch and is independent of Lt in a spiral copper-plated multifilament coated conductor, as shown in figure 4(b). This is the principle by which the spiral geometry reduces the coupling time constant and decouples filaments [21].
Figure 4. Coupling currents in copper-plated multifilament coated conductors: (a) straight coated conductor, in which coupling current expands to its entire length Lt and (b) spiral coated conductor, in which coupling current is confined to each half pitch and is independent of Lt.
Download figure:
Standard image High-resolution image3. Coated conductors used in experiments and spiral geometries
Furukawa Electric Co., Ltd. and SuperPower Inc. fabricated the coated conductors used in the experiments. A schematic cross section is shown in figure 5. Their 30 μm thick HASTELLOY® substrate allows us to wind them on core with small diameters. The superconductor layer with a silver protective layer was striated by a laser to form filaments, covered with an additional silver layer, and subsequently plated with copper. The striations between the superconductor filaments were filled with copper. The superconductor filaments were connected electrically by the copper filled in the striations between them and by the copper covering them. We prepared variations of multifilament coated conductors and reference monofilament coated conductors, whose detailed specifications are listed in table 1. Comparing the critical currents of the monofilament coated conductors (B2-a2, B3-a1, and B3-a2) with multifilament coated conductors (the others), we find that the losses of critical currents by striation are at an acceptable level.
Figure 5. Schematic cross section of copper-plated multifilament coated conductor.
Download figure:
Standard image High-resolution imageTable 1. Specifications of coated conductors used in experiments.
| Coated conductor type | Conductor width (wt) | Substrate thickness (tsub) | Number of filaments (nf) | Filament width (wf) a | Copper thickness per side (tCu) b | Critical current (Ic) c |
|---|---|---|---|---|---|---|
| B2-a2 | 4 mm | 30 μm | 1 | 4 mm | 20 μm | 176.7 A |
| B2-b1 | 4 mm | 30 μm | 5 | 0.8 mm | 40 μm | 173.3 A |
| B2-b2 | 4 mm | 30 μm | 5 | 0.8 mm | 20 μm | 171.1 A |
| B2-b3 | 4 mm | 30 μm | 5 | 0.8 mm | 10 μm | 165.9, 166.4 A |
| B2-c1 | 4 mm | 30 μm | 10 | 0.4 mm | 40 μm | Not available |
| B2-c2 | 4 mm | 30 μm | 10 | 0.4 mm | 20 μm | 154.0 A |
| B3-a1 | 2 mm | 30 μm | 1 | 2 mm | 40 μm | 67.8 A |
| B3-a2 | 2 mm | 30 μm | 1 | 2 mm | 20 μm | 69.1 A |
| B3-b1 | 2 mm | 30 μm | 3 | 0.67 mm | 40 μm | 35.4 A |
| B3-b2 | 2 mm | 30 μm | 3 | 0.67 mm | 20 μm | 40.2 A |
| B3-c1 | 2 mm | 30 μm | 5 | 0.4 mm | 40 μm | 33.8 A |
a wf is given as wt divided by nf. bCopper covers the entire periphery of each coated conductor. cThese values were measured at 77 K at SuperPower Inc. The separation of the voltage taps is 3.1 m, and the criterion of the critical current is 100 μV m−1.
We wound each coated conductor listed in table 1 spirally on a round glass fibre-reinforced plastic core with a diameter Dc of 3 or 5 mm, so that the superconductor layer and the substrate of the coated conductor face inside and outside, respectively. This orientation is favourable for preventing critical current degradation, as reported for CORC wires [23], which use coated conductors with the same substrate thickness (30 μm) and a core diameter of 2.5 mm. We measured the critical current of a monofilament coated conductor wound spirally on 3 mm core with α of 55° and confirmed that the critical current was not degraded by the winding. Because the number of layers is one, we assume that D in equations (1) and (2) is equal to Dc. The specifications of the spiral copper-plated coated conductors for magnetisation loss measurements are listed in table 2 together with those of the reference straight copper-plated coated conductors. The pictures of spiral copper-plated multifilament coated conductors are shown in figure 6.
Figure 6. Pictures of spiral copper-plated multifilament coated conductors: (a) one 4 mm wide coated conductor wound spirally on a 3 mm core and (b) two 4 mm wide coated conductors wound spirally on a 5 mm core.
Download figure:
Standard image High-resolution imageTable 2. Specifications of spiral copper-plated coated conductors and reference straight copper-plated coated conductors for magnetisation loss measurements.
| Coated conductor type | Conductor (tape) length (lt) | Core diameter (Dc) | Spiral angle (α) | Spiral pitch (Lp) | Conductor (tape) length corresponding to Lp/2 (Lp1/2) | Number of conductors (tape) (nt) | Critical current (Ic) a |
|---|---|---|---|---|---|---|---|
| Spiral copper-plated coated conductor | |||||||
| B2-a2 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 1 | 173.4 A |
| B2-b1 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 1 | 167.4 A |
| B2-b2 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 1 | 158.4 A |
| B2-b3 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 1 | 161.5 A |
| B2-c1 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 1 | 140.6 A |
| B2-c2 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 1 | 168.6 A |
| B3-a1 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 2 | 67.6, 67.9 A |
| B3-a2 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 2 | 72.3, 70.3 A |
| B3-b1 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 2 | 42.1, 42.7 A |
| B3-b2 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 2 | 59.6, 55.7 A |
| B3-c1 | 174 mm | 3 mm | 55° | 6.60 mm | 5.75 mm | 2 | 39.3, 38.2 A |
| B2-a2 | 174 mm | 5 mm | 55° | 11.0 mm | 9.59 mm | 2 | 176.7, 176.1 A |
| B2-b1 | 174 mm | 5 mm | 55° | 11.0 mm | 9.59 mm | 2 | 167.2, 161.6 A |
| B2-b2 | 174 mm | 5 mm | 55° | 11.0 mm | 9.59 mm | 2 | 159.5, 160.9 A |
| B2-b3 | 174 mm | 5 mm | 55° | 11.0 mm | 9.59 mm | 2 | 173.4, 170.1 A |
| B2-c1 | 174 mm | 5 mm | 55° | 11.0 mm | 9.59 mm | 2 | 137.6, 140.4 A |
| B2-c2 | 174 mm | 5 mm | 55° | 11.0 mm | 9.59 mm | 2 | 162.6, 157.4 A |
| Straight copper-plated coated conductor | |||||||
| B2-a2 | 150 mm | N/A | N/A | N/A | N/A | N/A | 176.7 A b |
| B2-b2 | 150 mm | N/A | N/A | N/A | N/A | N/A | 171.1 A b |
| B2-c2 | 150 mm | N/A | N/A | N/A | N/A | N/A | 138.9 A |
aThese values were measured at 77 K for each coated conductor unless otherwise noted. The critical current of each spiral coated conductor was measured before winding spirally. The criterion of the critical current is 100 μV m−1. bThese values were measured at 77 K at SuperPower Inc. The separation of the voltage taps is 3.1 m, and the criterion of the critical current is 100 μV m−1.
4. Experimental method
We measured the magnetisation losses Qm of the samples cooled in liquid nitrogen (77 K) using our ac loss measurement systems, the schematic of which is shown in figure 7 [16, 31, 32]. Note that we describe magnetisation loss using the energy dissipated in the unit length of a coated conductor per cycle of magnetic field change, whose unit is J m−1. AC transverse magnetic fields with sinusoidal waveforms were applied to a sample using a copper magnet, and the magnetisation losses were measured using a pickup coil [31]. The empty compensation coil, whose geometry is identical to that of the pickup coil, was connected in series to the pickup coil to suppress the inductive voltage component. We conducted two types of experiments using two ac loss measurement systems with different operational conditions.
Figure 7. Schematic view of ac loss measurement system, with which we measured magnetisation losses at 77 K [16, 31, 32].
Download figure:
Standard image High-resolution imageIn most of the experiments reported in this paper, the amplitude of the applied magnetic field μ0 Hm was varied from 1 to 100 mT, but its frequency f was discrete (13.38, 26.62, 65.44, and 112.5 Hz), because capacitors were used to compensate for the large inductive voltage of the magnet.
In another experiment, μ0 Hm was fixed at 0.15 mT, and f was varied continuously up to 20 kHz. In such a low-field region, the hysteresis loss Qh, which is proportional to Hm 3, is negligible, and the coupling loss Qc is dominant. In general, the coupling loss per cycle of the sinusoidal field change is expressed as follows:
where and τc are a geometry factor determined by the conductor geometry and the coupling time constant, respectively [29, 30, 33]. Note that the unit of is m2, because the unit of Qc is J m−1. If Qc is plotted against f, it reaches its peak at the frequency fc:
In this study, we refer to this as the characteristic frequency. Filaments decouple electromagnetically at frequencies that are sufficiently low compared to the characteristic frequency fc. By fitting equation (3) to the measured Qm–f plot of a sample, which is approximately Qc–f plot, we can determine both τc and Ac' of the sample using the least-squares method.
5. Results and discussion
5.1. Effect of spiral geometry on the reduction of magnetisation losses in copper-plated multifilament coated conductors
In this subsection, we compare the magnetisation losses of straight and spiral copper-plated multifilament and monofilament coated conductors.
Before comparing their magnetisation losses directly, we compare their coupling time constants τc, which we determined experimentally. As an example, we plot the measured magnetisation losses Qm against frequency f for the spiral 10-filament coated conductor B2-c2 (Dc = 3 mm) in figure 8 where μ0 Hm was fixed at 0.15 mT. From such a plot for each sample, we determined the coupling time constant τc and the geometry factor for the sample using the method explained in section 4. Table 3 lists τc, fc, and of the spiral and straight 5-filament coated conductors B2-b2 and 10-filament coated conductors B2-c2. As listed in tables 2 and 3, the conductor length Lt of the straight coated conductors was 150 mm, and that of the spiral coated conductors was 174 mm. The experimentally determined coupling time constants τc of the spiral copper-plated multifilament coated conductors are much smaller than those of straight copper-plated multifilament coated conductors, even though Lt of the spiral conductors is larger than that of the straight conductors. In straight copper-plated multifilament coated conductors, Lt determines their coupling time constants, which are proportional to the square of Lt [16]. Meanwhile, in spiral copper-plated multifilament coated conductors, (=5.75 and 9.59 mm when D = 3 and 5 mm, respectively) determines their coupling time constants, which are much shorter than Lt (=174 mm) and independent of Lt.
Figure 8. Measured magnetisation losses Qm plotted against frequency f for the 10-filament coated conductor B2-c2 (Dc = 3 mm).
Download figure:
Standard image High-resolution imageTable 3. Coupling time constant τc, characteristic frequency fc (=1/2πτc), and geometry factor of straight and spiral copper-plated multifilament coated conductors.
| Straight | Spiral | ||
|---|---|---|---|
| Conductor (tape) length lt | 150 mm | 174 mm | |
| Core diameter Dc | N/A | 3 mm | |
| Spiral angle α | N/A | 55° | |
| B2-b2 | Conductor width wt = 4 mm, number of filaments nf = 5, copper thickness per side tCu = 20 μm | ||
| Coupling time constant τc | 20.1 ms | 47.3 μs | |
| Characteristic frequency fc | 7.91 Hz | 3.36 kHz | |
| Geometry factor | 6.45 × 10−5 m2 | 2.80 × 10−5 m2 | |
| B2-c2 | Conductor width wt = 4 mm, number of filaments nf = 10, copper thickness per side tCu = 20 μm | ||
| Coupling time constant τc | 15.4 ms | 34.6 μs | |
| Characteristic frequency fc | 10.3 Hz | 4.60 kHz | |
| Geometry factor | 7.94 × 10−5 m2 | 3.19 × 10−5 m2 | |
In figure 9, we compare the magnetisation losses of various straight and spiral copper-plated coated conductors (monofilament B2-a2, 5-filament B2-b2, and 10-filament B2-c2, all with 20 μm thick copper) subjected to an ac transverse magnetic field whose amplitude μ0 Hm is 100 mT and frequency f is 65.44 Hz. Looking at the magnetisation losses of the straight coated conductors, the magnetisation losses of the monofilament coated conductor (B2-a2, with nf = 1) and multifilament coated conductors (B2-b2 with nf = 5, and B2-c2 with nf = 10) are almost the same. Filaments coupled electromagnetically in the straight B2-b2 and the straight B2-c2 at 65.44 Hz, which was remarkably larger than their fc (7.91 and 10.3 Hz, respectively). Because coupled filaments behaved as a monofilament, the magnetisation losses of the straight B2-b2 and the straight B2-c2 at 65.44 Hz were at the same level as that of the monofilament coated conductor B2-a2. In practical applications, coated conductors are much longer than 150 mm, and magnetisation losses cannot be reduced using straight copper-plated multifilament coated conductors. On the contrary, when comparing spiral coated conductors, the magnetisation loss decreases with increasing number of filaments nf, that is, with decreasing filament width wf. The magnetisation loss of the spiral 10-filament coated conductor B2-c2 is approximately 15% of that of the spiral monofilament coated conductor B2-a2. This must be due to a small τc of the spiral B2-c2: the corresponding fc, 4.60 kHz, is much higher than the frequency of the applied magnetic field, 65.44 Hz. The reason for Qm of the spiral monofilament coated conductor B2-a2 being smaller than Qm of the corresponding straight monofilament coated conductor B2-a2 could be the rotation of the tape face against the magnetic field in the spiral case. Because the magnetisation loss of a coated conductor is dominated by the applied magnetic field component normal to the tape face [34, 35], the rotation of the tape face in a spiral coated conductor could reduce the magnetisation loss. Finally, note that the magnetisation loss of the spiral 10-filament coated conductor B2-c2 is only 7% of that of the straight 10-filament coated conductor B2-c2 as well as that of the straight monofilament coated conductor B2-a2. This magnetisation loss reduction could be effective in longer multifilament coated conductors, because their coupling time constants are determined by the spiral pitch and independent of the overall length.
Figure 9. Magnetisation losses of various straight and spiral copper-plated coated conductors subjected to an ac transverse magnetic field whose amplitude μ0 Hm is 100 mT and frequency f is 65.44 Hz. nf denotes number of filaments, Dc denotes core diameter, and Lt denotes the length of the coated conductor, respectively. Coupling time constants of the spiral multifilament coated conductors whose number of filaments nf are 5 and 10 are 47.3 and 34.6 μs, respectively, whereas those of the straight multifilament coated conductors whose number of filaments nf are 5 and 10 are 20.1 and 15.4 ms, respectively.
Download figure:
Standard image High-resolution image5.2. Magnetisation losses of a typical spiral copper-plated multifilament coated conductor and separating into hysteresis losses and frequency-dependent loss components
Figure 10 shows the measured magnetisation losses Qm of the spiral 10-filament coated conductor B2-c2 (Dc = 3 mm), which are plotted against field amplitude μ0 Hm. Here, we provide several analytical values for hysteretic magnetisation loss. The hysteresis loss in the coupled-filaments coated conductor is given as the hysteresis loss in a superconductor strip (or the monofilament coated conductor) with the same width and the same critical current [36]:
Figure 10. Measured magnetisation losses Qm of the spiral 10-filament coated conductor B2-c2 (Dc = 3 mm) plotted against field amplitude μ0 Hm, together with analytical values of Brandt and Indenbom given by equations (5)–(9).
Download figure:
Standard image High-resolution imagewhere,
wt is the width of the coated conductor, and Ic is the critical current of the coated conductor. Assuming that the filament width wf and the critical current of each filament are wt/nf and Ic/nf, respectively, the hysteresis loss in the decoupled-filaments coated conductor is given as:
Considering the rotation of the tape face in a spiral coated conductor mentioned in section 5.1, QBI,t and nf QBI,f can be reduced as follows:
These analytical values are plotted in figure 10. When μ0 Hm is high (higher than 20 mT, for example), the measured magnetisation losses Qm are almost independent of frequency and are dominated by hysteresis losses. In this high field region, the measured Qm almost follows and , rather than and even at f = 112.5 Hz. These experimental results clearly show that spiral geometry can decouple filaments and reduce magnetisation losses. When μ0 Hm is low (lower than 20 mT, for example), frequency-dependent coupling and/or eddy current losses may increase the measured Qm.
In figure 11, we plot the measured magnetisation losses Qm of the spiral 10-filament coated conductor B2-c2 (Dc = 3 mm) against frequency f (symbols at 13.38, 26.62, 65.44, and 112.5 Hz) where μ0 Hm = 5, 10, 20, 50, and 100 mT. The measured Qm apparently shows frequency dependence. By fitting equation (10) to the measured Qm–f plot shown in figure 11 to determine the values of Qh and k, we can separate the measured magnetisation loss into frequency-independent and frequency-dependent components:
Figure 11. Measured magnetisation losses Qm of the spiral 10-filament coated conductor B2-c2 (Dc = 3 mm) plotted against frequency f (symbols at 13.38, 26.62, 65.44, and 112.5 Hz) where μ0 Hm = 5, 10, 20, 50, and 100 mT, together with fitted curves by equation (10): .
Download figure:
Standard image High-resolution imagewhere Qh is the frequency-independent component, which is indeed the hysteresis loss, and kf is the frequency-dependent component, which contains the coupling loss and eddy current loss. In the following, kf is denoted as Qm–Qh. The curves in figure 11 are given by equation (10), with Qh and k determined by the fitting.
5.3. Hysteresis loss characteristics
Here, we compare the hysteresis losses Qh of various spiral copper-plated multifilament coated conductors listed in table 2. As shown in table 2, the critical currents of the samples were not always the same. To eliminate the influence of the difference in the critical currents, Qh is normalised by the following Q0:
and, then, of the coated conductors with various critical currents are compared with one another. Ideally, the hysteresis loss per unit length in two pieces of decoupled 2 mm wide superconductor strip is half of that in one piece of 4 mm wide superconductor strip. The factor is included to represent this relationship. Consequently, the normalised analytical values QBI,t and nf QBI,f are given as follows:
Using this normalisation, when we plot or against , the plots for conductors with different critical currents but with identical geometries agree with each other. The normalised hysteresis loss of two pieces of coated conductor whose width wt is 2 mm becomes half of of one piece of coated conductor whose width wt is 4 mm. The normalised hysteresis loss of the nf-filament coated conductor is reduced to 1/nf times that of the monofilament coated conductor .
In figure 12, we plot the normalised hysteresis losses of various spiral copper-plated coated conductors and analytical values against the normalised magnetic field , where we fix the coated conductor width wt at 4 mm and vary the filament width wf (number of filaments nf) and the copper thickness tCu. Dc is 3 mm in figure 12(a) and 5 mm in figure 12(b). Here, we focus on a high-field region, which is interesting from the viewpoint of practical applications. When , normalised measured hysteresis losses nearly follow the normalised , and of a coated conductor whose wf is 0.4 mm are about half the of a coated conductor whose wf is 0.8 mm. These results show the effect of decreasing the filament width to reduce hysteresis loss. Note that is almost independent of the copper thickness tCu: of coated conductors with an identical wf but with different tCu are almost at the same level.
Figure 12. Normalised hysteresis losses of various spiral copper-plated coated conductors and analytical values plotted against normalised magnetic field where is omitted in labels in the figures to save space: (a) Dc = 3 mm and (b) Dc = 5 mm.
Download figure:
Standard image High-resolution imageIn figure 13, we plot the normalised hysteresis losses of spiral copper-plated coated conductors with various wt, wf (nf), tCu, and Dc against filament width wf. is almost proportional to the filament width.
Figure 13. Normalised hysteresis losses of spiral copper-plated coated conductors with various wt, wf (nf), tCu, and Dc plotted against filament width wf.
Download figure:
Standard image High-resolution image5.4. Characteristics of frequency-dependent loss components
Next, we examine the frequency-dependent loss components. Figure 14 shows the frequency-dependent loss components Qm–Qh of various spiral copper-plated multifilament coated conductors plotted against frequency f when μ0 Hm = 50 mT. Dc is 3 mm in figure 14(a) and 5 mm in figure 14(b). The symbols represent the experimentally determined Qm–Qh, and the lines associated with the symbols are given by kf in equation (10), with k determined by fitting to the measured Qm. The proportionality of Qm–Qh to f is reasonable, because Qm–Qh consists of the coupling loss Qc and eddy current loss Qe, both of which are proportional to frequency f when f is much smaller than fc. In the figure, we also plot the eddy current loss Qe,num, which was calculated numerically for spiral copper strips whose geometries are the same as those of the spiral-coated conductors. We calculated the eddy current losses in a spiral copper tape with a thickness and resistivity of 20 μm and 2 × 10−9 Ωm, respectively. Then, we multiplied by two to obtain Qe,num, because both sides of a tape-shaped coated conductor are plated with copper. The calculated eddy current loss Qe,num is substantially smaller than the experimentally determined Qm–Qh, and it is acceptable to assume that Qm–Qh is dominated by the coupling loss Qc.
Figure 14. Frequency-dependent loss components Qm–Qh of various spiral copper-plated multifilament coated conductors plotted against frequency f when μ0 Hm = 50 mT where symbols representing experimentally determined Qm–Qh, and the lines associated with the symbols representing kf in equation (10), with k determined by fitting to the measured Qm: (a) Dc = 3 mm and (b) Dc = 5 mm.
Download figure:
Standard image High-resolution imageIn figure 15, Qm–Qh is plotted against the copper thickness tCu. It is natural that Qm–Qh increases with increasing copper thickness tCu, because the copper thickness tCu naturally increases the coupling loss and eddy current loss. The dependence of Qm–Qh (dominated by coupling loss Qc) on the copper thickness tCu and our previous study on coupling time constants [21] suggest that copper resistivity dominates the transverse resistance. Therefore, it should be noted that coupling time constant and, then, coupling loss may increase with decreasing temperature because of the temperature dependence of the resistivity of copper. We have to consider this temperature dependence of coupling time constant (characteristic frequency) when we operate the coil using the SCSC cable at a low temperature such as 4.2 K.
Figure 15. Frequency-dependent loss component Qm–Qh plotted against copper thickness tCu.
Download figure:
Standard image High-resolution imageIn figure 16, we plot Qm–Qh against core diameter Dc. The coupling time constant τc [21] and geometry factor decrease with decreasing core diameter Dc, as listed in table 3. Considering equation (3), it is understandable that Qm–Qh, which is dominated by the coupling loss Qc, also decreases with decreasing core diameter Dc. The crosses in the figure show the coupling losses Qc of the spiral 10-filament coated conductor B2-c2 (tCu = 20 μm) calculated using equation (3) together with τc and listed in table 3. Their dependence on the core diameter Dc qualitatively agrees with that of the measured values.
Figure 16. Frequency-dependent loss component Qm–Qh plotted against core diameter Dc, together with Qc of the spiral 10-filament coated conductor B2-c2 (tCu = 20 μm) calculated by using equation (3) together with τc and listed in table 3.
Download figure:
Standard image High-resolution image5.5. Comparison between hysteresis loss and frequency-dependent loss component
First, in figure 17(a), we compare the hysteresis loss Qh and the frequency-dependent loss component Qm–Qh of the spiral 10-filament coated conductor B2-c2 (Dc = 3 mm), which are plotted with symbols against field amplitude μ0 Hm. In this spiral coated conductor with a 3 mm core, the hysteresis loss is larger than the frequency-dependent loss component, which is dominated by the coupling loss. In the figure, the dash–dot–dash line represents given by equation (8), the broken line represents given by equation (9), and the solid line represents Qc calculated using equation (3) together with τc and ; listed in table 3. The experimentally determined Qh agrees well with the hysteresis loss of the decoupled-filaments multifilament coated conductor considering the rotation of the tape face against the field direction. The experimentally determined Qm–Qh agrees well with the coupling loss Qc calculated using equation (3) together with τc and listed in table 3.
Figure 17. Hysteresis loss Qh and frequency-dependent loss component Qm–Qh of the spiral 10-filament coated conductors B2-c2 (tCu = 20 μm) plotted with symbols against field amplitude μ0 Hm, together with dash–dot–dash line representing given by equation (8), broken line representing given by equation (9), and solid line representing Qc calculated by using equation (3) and τc and listed in table 3: (a) Dc = 3 mm and (b) Dc = 5 mm.
Download figure:
Standard image High-resolution imageFigure 17(b) shows similar plots for the spiral 10-filament coated conductor B2-c2 (Dc = 5 mm). In this conductor, the hysteresis loss and the frequency-dependent loss component are at almost the same level. The larger core diameter could increase the coupling loss. In this figure, again, the hysteresis loss agrees well with calculated using equation (9), whereas the frequency-dependent loss component is approximately two-thirds of Qc calculated using equation (3) together with τc and listed in table 3. This error may be attributable to various uncertainties in the measurements as well as to fitting.
The experimental results suggest that we can estimate the hysteresis loss and coupling loss of an SCSC cable using equations (9) and (3) together with experimentally determined τc and . When using these equations to estimate the entire magnetisation loss of an SCSC cable, we must consider the following points:
- The hysteresis loss and coupling loss of the equations show different dependences on the amplitude and frequency of the applied magnetic field. Therefore, considering the expected amplitude and frequency of the applied magnetic field, we must identify which loss component is dominant when designing a copper-plated multifilament coated conductor.
- In addition to the geometry of a coated conductor, its critical current density and its transverse resistance between filaments influence its hysteresis loss and its coupling loss, respectively. In contrast, the critical current density and transverse resistance do not influence the coupling loss and hysteresis loss, respectively.
6. Conclusions
When a spiral copper-plated multifilament coated conductor, whose filaments are connected electrically by the copper layer, is subjected to an ac transverse magnetic field, its spiral geometry decouples filaments electromagnetically and effectively reduces its magnetisation loss. When a 4 mm wide, 10-filament coated conductor with 20 μm thick copper was wound spirally on a core whose diameter was 3 mm, the coupling time constant was 34.6 μs. Its magnetisation loss was only 7% of that of the same 10-filament coated conductor with a straight shape when they were subjected to an ac transverse magnetic field whose amplitude and frequency were 100 mT and 65.44 Hz, respectively. Because the coupling time constant is determined by the spiral pitch and is independent of the overall length of the coated conductor, the magnetisation loss reduction using spiral geometry is effective in long coated conductors in practical applications as well. The measured magnetisation loss of a spiral copper-plated multifilament coated conductor can be separated into a hysteresis loss and frequency-dependent loss component, which is mainly attributable to the coupling loss. The former can be reduced by decreasing the filament width, whereas the latter can be reduced by decreasing the copper thickness and core diameter. When designing a low-loss spiral copper-plated multifilament coated conductor such as the SCSC cable, we must identify which loss component is dominant, considering the operational conditions and the critical current density, which influences the hysteresis loss, and then we must choose proper conductor parameters such as filament width and copper thickness. Although their low engineering current density is a drawback of spiral coated conductors such as the SCSC cables and the CORC® wires, it can be increased by winding coated conductors with thinner substrate or those like STAR wires on cores with smaller diameters. Because the smallest filament width in this study (400 μm) is still much larger than the filament diameters of LTS wires, the ac loss could be much larger than LTS wires. However, the SCSC cables are still useful, because coated conductors have much larger temperature margins than those of LTS wires and can be operated at higher temperatures at which cooling systems are more efficient.
Acknowledgment
This work was supported by JST-Mirai Program Grant Number JPMJMI19E1, Japan.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Footnotes
- 4
Some authors called such cables CORC cables consisting of multifilament coated conductors. We avoid calling our cable CORC cable, because CORC® is a trademark. In this paper, we use spiral multifilament coated conductor as a common terminology, whereas we call our cable consisting of copper-plated multifilament coated conductor SCSC cable.