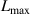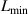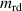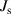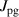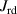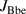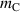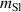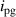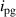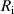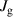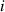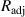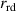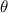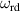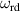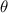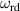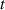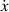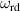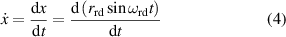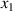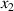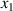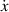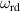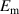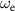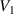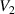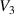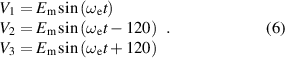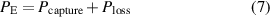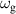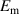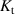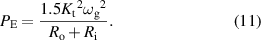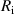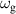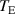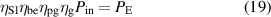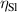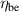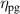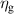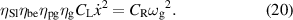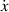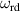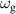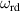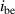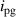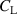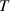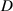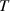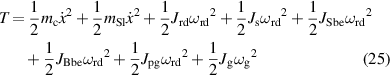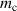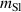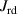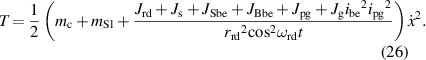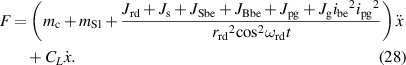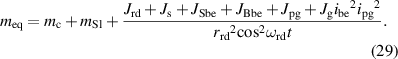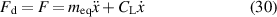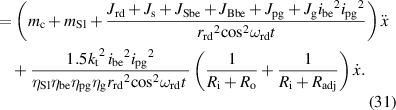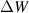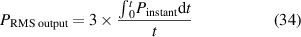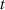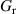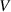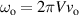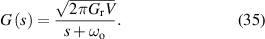Abstract
In recent years, the increasing adoption of electric buses (EBs) worldwide has contributed significantly to reducing environmental pollution. Nevertheless, the most challenging obstacle hindering the efficiency of EBs is their power supply. In this study, a multi-purpose variable damping energy regenerative damper (VD-ERD) using a double coaxial slotted link motion conversion mechanism was proposed for health monitoring of the EBs suspension system, tunning the damping during the operation on different road conditions while providing electric energy for self-powered sensors in EBs. The VD-ERD consists of two identical generators; one is connected to optimal constant resistance for maximum energy harvesting, and the other is linked to adjustable resistance for fine-tuning the damping. Consequently, both generators connect to a rectifier and storage circuits. Furthermore, VD-ERD was developed in MATLAB/Simulink to evaluate its performance in damping and energy harvesting in different road excitations. The VD-ERD achieved an 11.59 W peak and 1.84 W RMS power at 50 km h−1 on an ISO class A road and a 36.38 W peak and 6.34 W RMS power on an ISO class B road. In addition, the experimental finding indicated that controlling the external resistance is capable of tuning the damping. Simultaneously, the prototype achieved a peak power output of 10.29 W at 12 mm and 3 Hz. Furthermore, the voltage signals received from the generators were analyzed using a deep learning model to monitor the condition of the suspension system in four different modes, namely slow, medium, fast, and failure; the result shows 99.37% training accuracy. Feasibility analysis and performance testing showed that VD-ERD provides sufficient power to 10 sensors, indicating that it can power the self-powered and self-sensing devices of EBs.
1. Introduction
Nowadays, one of the most pressing issues worldwide is diminishing oil reserves and escalating air pollution. The transportation sector ranks as the second-largest contributor to CO2 emissions as it consumes 27% of the world's energy, such as diesel, petrol, jet fuel, etc [1]. These are also the motivation behind the Sustainable Global Goals of the UN especially Goal 7 [2]. Therefore, meeting transportation energy needs strongly advocates exploring sustainable, low CO2 emission energy sources [3]. In recent years, the increasing adoption of electric vehicles (EVs) globally has contributed significantly to reducing pollution and lowering energy consumption [1]. Many countries, including the USA, China, Japan, and others, implemented policies to promote the adoption of EVs in the automotive industry and enhance transportation energy efficiency [4]. Recently, China has developed and adopted an innovative type of electric buses (EBs) known as autonomous rail rapid transit (ART) to meet the growing need for efficient urban transportation solutions [5]. ART is an urban transit system that combines the advantages of train and bus. It operates on regular city streets without traditional railway tracks [6]. In addition, the ART is equipped with many sensors that are responsible for safety operations [7]. However, the limited range of ART is caused by the low battery capacity; this also affects the sensors powered by the battery, as their operating time is limited due to the lower battery capacity [6]. Researchers suggested two significant techniques to address these issues [6]. The first technique focuses on the external aspects of ARTs, such as implementing faster and more practical charging technology, developing battery management tactics, and selecting the best locations for charging stations [8]. The second technique is more concerned with energy harvesting technology, such as vibration energy [9], brake energy [10], solar energy [11], wind energy [12], and piezoelectric materials [13]. However, this technology contributed significantly to self-powered self-sensing devices to operate without external power sources enhancing sustainability and efficiency [14, 15]. In recent years, attention has been focused on the alternatives mentioned above, particularly energy harvesting based on regenerative suspension systems [16]. The researcher proposed the energy regenerative damper (ERD) to harvest wasted energy in the suspension system while providing ride comfort [17]. However, based on the published literature, ERDs can be classified into three main groups: electromagnetic design, hydraulic design, and mechanical design [18].
The first group is electromagnetic design; this type of ERD is divided into two types according to the method of energy production [19]. Linear electromagnetic regenerative damper (LERD) this type incorporates a linear electromagnetic generator inside the system, producing electrical power through the relative linear motion between magnets and coils [20]. The other is a rotary electromagnetic regenerative damper (RERD), this type requires a motion conversion mechanism to convert the vibration into one-way rotation. Lafarge et al [20] developed LERD for vehicle suspension; during the experiment, it achieved around 10 W at 1 m s−1. Another study [21] designed a LERD that recovered kinetic energy, yielding an average power of 124 W at a speed of 0.157 m s−1 under real road conditions. In addition [22], introduced a self-powered system, integrating a magnetorheological damper and a linear generator to counter increased unsprung mass in in-wheel motor EVs, leading to a 17.05% reduction in body acceleration. Abdelkareem et al [23] designed an RERD for application in truck suspension, which can capture an average power of 0.33 W, 1.33 W, 5.24 W, and 21.3 W under different ISO road classes.
The second group is a hydraulic energy regenerative damper (HERD). The process of controlling and converting the suspension vibration involves a hydraulic system with a piston and cylinder, which forces hydraulic fluid to rotate the generator [24]. Zou et al [25] designed a novel HERD; the findings of this study demonstrated that under real excitation, RMS power reaches 107.94 W. In addition [26], developed a HERD to replace conventional vehicle suspension dampers. Findings show the damping coefficient ranges from 32 to 91 kN.s m−1, covering the typical heavy-duty vehicle damping range of 25–50 kN.s m−1. Furthermore [27], proposed HERD recovers vibration energy from vehicle suspensions due to road roughness. Results showed HERD meets the necessary damping characteristics and power requirements for heavy vehicles. As well, Qin et al [28] designed a HERD with damping coefficients varying from 3608 to 9913 N.s m−1 and a mean power of 82 W recorded at 2 Hz and 20 mm.
The third group involves mechanical design, garnering research interest due to its capacity to enhance dynamic performance and extract energy efficiently [16]. Abdelrahman et al [29] developed an ERD with a scotch yoke mechanism to power low-wattage devices in EBs, achieving a mean power output of 6.591 W and an average efficiency of 39.37% at 7.5 mm and 2.5 Hz. The authors in [30] designed an ERD for in-wheel motors with two generators to enhance output power. Laboratory tests showed an efficiency of 62% and a power output of 380 W. Moreover [31], developed ERD using two helical racks, with an efficiency of 65.02% recorded at 7 mm and 2.5 Hz. Also [32], designed an ERD with two parallel racks and a pinion mechanism for EV suspension, achieving 4.302 W mean power and 44.24% efficiency at 7 mm and 2.5 Hz in lab tests. Furthermore [33], created a novel ERD based on a barrel cam follower module to recover vibration energy, achieving a maximum efficiency of 51.4% and power output of 3.85 W at 2 Hz and 7.5 mm. In addition, Wang et al [34] suggested ERD based on twin ball screws, demonstrated energy of 3.701 W and mean efficiency of 51.1% at 1 Hz and 3 mm, while the range extended by 1 mile while EVs driving on road class B at 60 km h−1 speed. Another study [35] designed an ERD with a ball-screw module, reducing vehicle chassis acceleration by 11.12% and harvesting 13.3 W of power at 40 mph on paved roads. Also, Bowen et al [36] developed an ERD achieving 105 W mean power and 60% efficiency at vehicle speeds of 20–30 km h−1. Maravandi and Moallem [37] designed ERD based on a two-leg mechanism, the experiment showed a 1720 N.s m−1 damping coefficient, attained by controlling the external load with conversion and mechanical efficiencies of 84% and 71%, respectively. Additionally [38], proposed an ERD utilizing an algebraic screw mechanism. Experiment results showed 0.54 W output power achieved at excitation inputs of 5.6 Hz and 2.5 mm.
Recent studies [1, 29, 39, 40] show that LERD and HERD suffer from low harvesting efficiency and high manufacturing costs. Furthermore, the previous design reported in the literature consists of a single generator considered for energy harvesting and tuning the damping. However, when a single generator is connected to a tunable resistance, this can lead to a limited damping range, and most of the electrical energy will be wasted through the tunable resistance. On the other hand, different motion monitoring, identity recognition, and detection of running status enabled by deep learning have recently attracted the attention of many researchers [41]. Fang et al [41] designed an energy self-consistent system (ESCS) utilizing a triboelectric nanosensor, along with a Long-Short Term Memory (LSTM), to monitor freight train operations. Test results demonstrated an ESCS detection accuracy of 96.6%. Kong et al [42] proposed a self-powered and self-sensing system incorporating negative energy harvesting for smart healthcare. This system utilizes LSTM deep learning to detect the angle and direction of knee joint rotation. However, this technology has contributed significantly to smart transportation systems, which increase the safety and convenience of human life [43]. Therefore, analyzing voltage signals recorded from the generator of the proposed variable damping energy regenerative damper (VD-ERD) using deep learning can provide valuable insights into the performance and health of the suspension system. Figure 1 shows the applications of self-powered sensors and self-sensing devices in smart transportation.
Figure 1. Typical applications of self-powered sensors and self-sensing devices in intelligent transportation.
Download figure:
Standard image High-resolution imageIn this paper, a multi-purpose VD-ERD using a double coaxial slotted link conversion mechanism was proposed for (i) tunning the damping during the operation based on the road condition, (ii) providing electric energy for self-powered sensors, (iii) the health of the suspension system enabled by deep learning. However, the VD-ERD consists of two identical generators; one generator is connected with optimal constant resistance for maximum energy harvesting, and the other generator is linked with adjustable resistance for fine-tuning the damping generated by the proposed VD-ERD. Consequently, both generators connect to a rectifier circuit to charge the batter. Additionally, the suggested VD-ERD holds significant practical implications, including (i) minimizing environmental emissions, (ii) enhancing the power supply of ART, and (iii) providing power to self-sensing devices in ART. Moreover, the bibliometric analysis was performed to find the research gap using VOSviewer based on data from 2005 to 2023 from Web of Science, as depicted in figure 2. It demonstrates that numerous scholars suggested ERD to harvest wasted energy due to road roughness, as shown in figure 2(b). However, the term 'design' is the most explored when weighed against alternative co-occurring keywords, as shown in figure 2(c), and combining research of energy harvesting from suspension systems related to 'design enhancement' is the least explored research topic.
Figure 2. Bibliometric analysis: (a) ERD research domain and (b) connections in the research area of ERDs.
Download figure:
Standard image High-resolution imageThe structure of this article is organized as follows. Section 2 addresses the design of the suggested VD-ERD and the operation principle. Section 3 follows with a description of the kinematics studies and modeling of the proposed VD-ERD. The details of the simulation are covered in section 4. Consequently, experimental validation is addressed in section 5. The results and discussion are presented in section 6. Section 7 addresses the conclusion and recommendations for future studies.
2. Design of the proposed VD-ERD
The proposed VD-ERD employs a double coaxial slotted link mechanism to control the vibration and capture wasted kinetic energy in ART suspension systems. Unlike available vibration conversion mechanisms such as ball screw [34, 35], rack and pinion [30–32], crank [9], and barrel cam-follower [33], double coaxial slotted link motion conversion mechanisms offer distinct advantages. Firstly, low friction losses, high conversion efficiency, lower production costs, and easier to design and construct [44]. Furthermore, it balances a compact design, reducing operational downtime and maintenance expenses. Meanwhile, it offers smooth, reliable motion, decreased friction, and less backlash [29, 45]. Figure 3 illustrates the schematic diagram of the design and working principle of the proposed VD-ERD. However, the design of the suggested VD-ERD comprises five modules, as shown in figure 3: (i) a suspension vibration input module, (ii) a transmission mechanism module, (iii) a generator module, and (iv) energy harvesting, and damping control module, and (vi) deep learning model. Additionally, table 1 shows the design parameters of the suggested VD-ERD.
Figure 3. The flow chart of the operation principle of the proposed VD-ERD.
Download figure:
Standard image High-resolution imageTable 1. Design parameters of the suggested VD-ERD.
| Symbol | Value | Description |
|---|---|---|
| 0.4 m | Extension length | |
| 0.35 m | Compression length | |
| Stroke | 0.05 m | Stroke |
| 0.6 kg | Mass of the two rotational discs | |
| 3.108 × 10−6 kg m2 | The inertia of the input shaft | |
| 1.6 × 10−3 kg m2 | The inertia of the planetary gearbox | |
| 2.487 × 10−6 kg m2 | Inertia of the rotational disc | |
| 9.4555 × 10−6 kg m2 | The inertia of the small bevel gear | |
| 2.4463 × 10−6 kg m2 | The inertia of a big bevel-gear | |
| 0.04 m | Rotational discs radius | |
| 3.94 kg | Upper cylinder mass | |
| 0.72 kg | Mass of the two slotted link flowers | |
| 2:1 | Bevel gear transmission ratio | |
| 6:1 | Planetary gearbox transmission ratio |
2.1. Suspension vibration input module
The suspension vibration input module comprises a lower cylinder linked with a middle cylinder through the base of VD-ERD and an upper cylinder connected with two coaxial slotted link flowers, the right rotational disc, the left rotational disc, the right one-way bearing B, the left one-way bearing A and input shaft. However, the lower cylinder of the proposed VD-ERD is assembled in the vehicle body, and the upper cylinder is connected to the chassis, as described in figure 4. While the ART travels on uneven roads, the roughness induces vibrations into the proposed VD-ERD, resulting in vibration movement between the lower and middle cylinders. Therefore, the upper cylinder with the two coaxial slotted link flowers can absorb the vibration and move up and down. Research indicates that suspension vibration can be caused by various variables, including road roughness, acceleration, and deceleration, but the primary cause of suspension vibration excitation is road roughness [32].
Figure 4. Installation diagram of the proposed VD-ERD.
Download figure:
Standard image High-resolution image2.2. Transmission mechanism module
The function of the transmission mechanism module in the proposed VD-ERD is to control and convert the vibration motion that occurs between the cylinders of the proposed system to unidirectional rotational motion. However, the transmission mechanism module is assembled between the upper and lower generator bases, as described in figure 5(a). The most significant parts of the transmission mechanism are the two coaxial slotted link flowers, the right and left rotational disc, the right one-way bearing B, the left one-way bearing A, the bevel gears set, overrunning clutch, and input shaft as depicted in figure 5(b). The suspension will vibrate while the ART travels on the road due to the roughness profile. Therefore, the upper and middle cylinders of the proposed VD-ERD will move up and down. Consequently, the right and left slotted link flowers will move upwards and downwards to rotate the right and left rotational discs. As displayed in figure 5(c), during the downward movement, the double-slotted link flowers will move downwards to rotate the right and left rotational disc intermitted rotation. Therefore, the left one-way bearing (A) will engage in the left-hand rotational disc to transform this intermitted movement to unidirectional rotation to rotate the input shaft unidirectionally, simultaneously the right one-way bearing (B) will disengage in the right-hand rotational disc. Figure 5(c) shows the details of the motion during the downward movement. Consequently, as depicted in figure 5(d), the double-slotted link flowers will move upward to rotate the right and left rotational disc intermitted rotation during the upward movement. Therefore, the right one-way bearing (B) will engage in the right rotational disc to transform this intermitted movement to unidirectional rotation to rotate the input shaft unidirectionally, as occurs in a downward movement. In contrast, the left one-way bearing (A) will disengage in the left-hand rotational disc. Subsequently, figure 5(d) shows the details of the motion during the upward movement. As a result, the input shaft will rotate continuously in one direction during both strokes. On the other hand, the bevel gear set with a gear ratio of 2:1 was used to transform this motion into two identical brushless DC motors. The left-hand large bevel gear is connected to the input shaft through a key, and the right-hand large bevel gear is linked to the input shaft through an overrunning clutch. The function of the overrunning clutch is to keep the motion in one direction on both generators.
Figure 5. Transmission mechanism module: (a) a sectional view of the VD-ERD, (b) the details parts of the motion transmission module, (c) downward movement, and (d) upward movement.
Download figure:
Standard image High-resolution image2.3. Generator module
The two identical brushless generator models 57BL04 with minimal rotor inertia and a high energy conversion rate enclosed with a gear head with a gear ratio of 6:1 were selected, as depicted in figure 6(a). The generator's specification parameters are presented in table 2. However, one of these generators is assembled in the upper base while the other generator is assembled on the lower base of the suggested VD-ERD. Both generators are assembled concentrically with the bevel gear, which rotates at the same speed based on the vibration in the suspension system. Figure 6(b) shows the simulation circuit of the generator.
Figure 6. (a) Generator's prototype; (b) simulation circuit for the three-phase generator.
Download figure:
Standard image High-resolution imageTable 2. The generator's specification parameters.
| Parameters | Value |
|---|---|
| Voltage source | 24 V |
| Generator model | Brushless 57BL04 |
| Rated speed | 3000 rpm |
| Torque rating | 0.22 N m |
| Power | 69 W |
| Torque constant | 0.062 N.m A−1 |
| The induced voltage | 6.5 V/KRPM |
| Internal resistance | 2 Ω |
| The inertia of the generator | 0.183 × 10−4 Kg m2 |
| Gearbox gear ratio | 6:1 |
| Weight | 0.67 Kg |
| Length | 73.8 mm |
2.4. Electric circuit for damping control and energy harvesting
The goal of the proposed VD-ERD is to vary the damping coefficient when the ART travels on the road according to road conditions to give the passengers a comfortable ride, enhanced stability, and improved handling while providing electrical energy. Figure 7 shows the diagram of the electric circuit for energy harvesting and tuning the damping. However, as depicted in figure 7, the three phases of the upper generator G1 connect with optimal resistance to harvest energy as much as possible, which equals the internal resistance of the generator. In addition, G1 is connected to a rectifier and a voltage stabilization circuit that uses LM317 to maintain a stable voltage. After that, this produces energy stored in the supercapacitors, which are used as a battery. Consequently, the lower generator G2 is connected with an adjustable resistance the control system regulates this variable resistance value for tuning the damping coefficient based on the road condition. To maximize vibration energy harvesting, G2 is also connected to a rectifier and voltage stabilization circuit incorporating LM317 for voltage stability.
Figure 7. Schematic diagram of the energy harvesting and damping control circuit.
Download figure:
Standard image High-resolution image3. Modeling and analysis
3.1. The dynamic and kinematics analysis of the proposed VD-ERD
The dynamic and kinematics analysis of a double coaxial slotted link conversion mechanism is discussed in this section as follows [29, 37]. As depicted in figure 8, when proposed VD-ERD subjected to excitation input the double-slotted link mechanism causes rotational discs to rotate at an angular velocity of . Here, and denote the radius and rotational angle, respectively. When the ART travels on uneven roads, the roughness induces vibrations into the proposed VD-ERD, resulting in vibration movement between the lower and upper cylinders. Therefore, during the upward and downward movement, the double-slotted link flowers will move upward and downward, causing displacement , and rotate the rotational disc intermitted rotation from an initial position on (a) to position (b) at the rotational speed as shown in figure 8. Hence, the mathematical relationship between and can be determined as follows:
Figure 8. The dynamic schematic model of the suggested VD-ERD.
Download figure:
Standard image High-resolution imageSubstitute by t:
Take the first derivative of equation (2) with respect to time to determine the linear velocity of the slotted link mechanism as a function in :
In the double coaxial slotted link conversion mechanism, one should take into consideration limitations between the rotational speed of the rotational discs and the translational motion of the slotted link flower to avoid locking into a maximum angle. However, after considering the limited space in the suspension system and manufacturing limits, it was measured and calculated the effective translation motion of the slotted link flower and the maximum rotation angle of the rotational disc of the proposed VD-ERD are 40 mm and 90°, respectively. According to published research [37, 46, 47], the maximum stroke of the conventional damper for a typical road would be 15 mm. Hence, a double coaxial slotted link conversion mechanism is proposed to transform the 33 mm of maximum translational motion at 55.6° of the rotation angle with a maximum radius of 40 mm, giving displacement variation of = 15 mm to = 33 mm with a static operating point at = 22.5 mm, as depicted in figure 9.
Figure 9. A nonlinear and linear relationship between the translation motion of a double-slotted link flowers and rotational speed of the rotational discs .
Download figure:
Standard image High-resolution image3.2. Analysis of the generator model
The main function of the suggested VD-ERD is to provide a damping force, and the major portion of damping is produced by the generator linked to energy harvesting and damping control circuits. The three-phase generator links to the energy storage module with adjustable resistances, modulating the damping of the generators, as shown in figure 6(b). The amplitude of the induced voltage is , the angular frequency is , and the voltages induced in each phase , , and can be calculated as follows [37]:
The following equation can be used to get the instantaneous power:
Substituting equation (6) into equation (8) and simplifying:
The relationship between the generator's rotational speed and is described as follows:
The torque constant of the generator is denoted as , and by adding equations (10) to (9):
the constant optimal external resistance and the internal resistance of the generators. The mathematical relation between and torque of the shaft is expressed as follows:
where denote the rotating damping of the generator linked to the energy storage model. Let us take the power balancing between mechanical and electrical:
Using equation (12) in equation (13) results in:
However, the rotating damping of the generator can be determined by contrasting equations (11) and (14) as follows:
Equation (15) shows the damping provided by G1, which is connected with constant external load. However, in the proposed VD-ERD, two identical generators were used; one is connected with constant optimal resistance, and the other is connected with adjustable resistance for fine-tuning damping, as shown in figure 7. Therefore, in this case, the generator connected with constant resistance will give us constant damping, and another generator connected with controlling resistance will provide us with variable damping according to the road condition. Hence, equation (15) will be modified and simplified as follows:
where, represent the adjustable external resistance, which can be controlled by the control system.
3.3. The linear damping model
The input power to the proposed VD-ERD can be defined following those suggested by [37]:
The input power is divided into representing the power lost due to friction in the transmission mechanism, gearhead, and generators, and , denoting the power produced by the generator thus,
where, represents the efficiency of the slotted link mechanism, denotes the efficiency of the bevel gears, is the efficiency of the gearhead and stands for the efficiency of the generators. Substituting equations (14) and (17) into equation (19):
The mathematical relationship between and is given by:
The relationship between and is given by:
where represent the gear ratio of the bevel gears and represent the transmission ratio of the planetary gearbox, substituting equations (16), (21) and (22) into equation (20), and the equation can be streamlined and rearranged to determine :
3.4. Dynamics of the proposed VD-ERD under input excitations
The Lagrangian formulation can represent the excitation force of the proposed VD-ERD under various vibration inputs as follows.
here, represents displacement, denotes the excitation force, and and signify the energies associated with kinetic and damping effects, respectively. The kinetic energy is defined as follows.
here, and denotes the mass of the upper cylinder and double-slotted link mechanism, respectively. Additionally, , , , , and stand for the rotary inertia of the rotational disc, input shaft, small bevel gear, big bevel gear, gearhead, and generator
Inserting equations (21) and (22) into equation (25) simplifying the equation:
The damping effect is given by:
Replacing equations (26) and (27) in equation (24):
To determine the equivalent mass of VD-ERD, the following formula can be applied:
Following Newton's third law:
4. Simulation modeling
The simulation is conducted to predict the performance of the suggested VD-ERD for tuning damping and energy harvesting. However, the simulation was performed using MATLAB/Simulink based on the derived governing equation discussed in section 3. Nevertheless, the simulation force-displacement loop for different external loads of G2 under different vibration amplitudes from 4 to 12 mm (with interval 2 mm), and frequencies vary from 1.5 to 3 Hz (with interval 0.5 Hz) was calculated by generating MATLAB code using equation (31) as displayed in figures 11(a)–(e). Furthermore, the damping coefficient of the proposed VD-ERD can be calculated and plotted by generating MATLAB code based on the equation (23), as shown in figure 11(f). Furthermore, VD-ERD was developed in MATLAB/Simulink, as depicted in figure 10, and the simulation was conducted with sinusoidal excitation to evaluate the performance of the proposed VD-ERD in terms of energy harvesting. However, the simulation model of the VD-ERD consists of the base, a double coaxial slotted link flower, two rotational discs, an input shaft, a bevel gears set, two unidirectional clutches, two identical brushless DC motors with gearheads, and Wye-shape external resistive load. In the proposed model, the sinusoidal excitation signal is converted into a physical signal to stimulate the slotted link conversion mechanism. The power output data are obtained from the transmission mechanism module and generator modules, respectively, as shown in figures 13(a)–(d). The parameters used in the simulation are given in tables 1 and table 2, and efficiencies of the gearhead, bevel gear, and generators are considered 90%, 85%, and 90%, respectively [33]. While the slotted link conversion mechanism's efficiency was estimated as 85%. The simulation has been performed for maximum energy harvesting by connecting both generators with optimal resistance, which is 2 Ω at different excitation inputs. However, as shown in figures 11(a)–(e), the damping force loop behavior of the VD-ERD is observed to be symmetric during both the rebound and compression strokes, indicating its potential to enhance ride comfort in ART.
Figure 10. Schematic diagram of MATLAB/Simulink model of the proposed VD-ERD.
Download figure:
Standard image High-resolution imageFigure 11. Simulation results of the force-displacement loop when G1 is connected with constant optimal resistance while G2 is linked with adjustable external resistances under 12 mm and: (a)1.5 Hz, (b) 2 Hz, (c) 2.5 Hz, (d) 3 Hz. 4 mm, and (e) 1.5 Hz; (f) damping coefficient at different external resistances.
Download figure:
Standard image High-resolution imageAdditionally, as external resistance increases, the damping force decreases at a constant amplitude of 12 mm and different frequencies, as depicted in figures 11(a)–(d), and at a constant amplitude of 4 mm and 1.5 Hz, as illustrated in figure 11(e). Meanwhile, damping increases with decreased extremal resistance, showcasing the VD-ERD's capability to adjust damping based on different road conditions. Furthermore, the magnitude of the damping coefficient decreased as external resistance increased, as depicted in figure 11(f). The area enclosed in the loop in figures 11(a)–(e) represents the work from which input power can be calculated as work done per unit of time. The upper half cycle of the force-displacement loop corresponds to the power required during the rebound of the VD-ERD, while the lower half cycle represents the power required during compression. However, when analyzing damping characteristics and energy dissipation, it is essential to consider the force-displacement behavior of the VD-ERD, which exhibits a symmetric shape.
On the other hand, the voltage from the VD-ERD is based on the simulation model shown in figure 12 at different excitation inputs, while the VD-ERD is linked with optimal Wye shape external resistance of 2 Ω the voltage increases as the frequency rises under different excitation amplitudes as shown in figures 12(a)–(d). Moreover, figure 12(e) shows the three-phase voltage of VD-ERD, while figure 12(f) depicts the shape of the voltage. Figures 13(a)–(d) show the simulation instantaneous power, while figures 13(e) and (f) depict the RMS power under different excitation inputs. However, the instantaneous and RMS power increases as amplitude and frequency increase.
Figure 12. Simulation results of the voltage under different excitation amplitudes and frequencies of: (a) 1.5 Hz, (b) 2 Hz, (c) 2.5 Hz, and (d) 3 Hz; (e) voltage output from three phases; (f) voltage output shape at 12 mm, 3 Hz, and 2 Ω respectively.
Download figure:
Standard image High-resolution imageFigure 13. Simulation results of the instantaneous power under different excitation amplitudes and frequencies of: (a) 1.5 Hz, (b) 2 Hz, (c) 2.5 Hz, and (d) 3 Hz; (e) output power at different amplitudes and (f) output power at different frequencies.
Download figure:
Standard image High-resolution image5. Experimental validation
A full-scale prototype was manufactured, as described in figure 14(a), to evaluate the performance of energy harvesting and damping tunability of the VD-ERD. The experiment was conducted using a Mechanical Test and Sensing System (MTS), as shown in figure 14(b). First, to install the prototype in the MTS, as shown in figure 14(d), on both ends of the VD-ERD, the eyelets were removed and changed with two shaft holder compact flanges, and the outer case of the motion conversion module was removed to show the motion during the experiments. Secondly, one end of the prototype was fixed with a force sensor for real-time recording of damping force, while the other end was connected to the MTS actuator, generating sinusoidal excitation. After that, a Wye-shape constant optimal external resistance 2 Ω is linked to the G1 as an external resistance, as indicated in figure 14(d). Simultaneously, a Wye-shaped tunable resistance is connected to G2 as a variable external load to tunning damping based on the road condition. Experiments have been performed by different resistances connected to G2, which are (1 Ω, 2 Ω, 3 Ω, and 4 Ω) at different excitation frequencies of (1.5 Hz, 2 Hz, 2.5 Hz, and 3 Hz) and different amplitudes of (4 mm, 6 mm, 8 mm, 10 mm, and 12 mm). However, this tunable resistance can be controlled by a control system. Moreover, as shown in figure 14(b), damping force data is recorded in the operating system of MTS on a computer after being recognized by the MTS. Additionally, the UTD2102CEX-EDU digital oscilloscope is used to store the voltage output from both generators, as depicted in figure 14(e).
Figure 14. MTS testing setup: (a) A full-scale prototype of the VD-ERD, (b) MTS hydraulic test bench components, (c) prototype installation on MTS, (d) prototype components and its installation on MTS, and (e) oscilloscope.
Download figure:
Standard image High-resolution image6. Results and discussion
6.1. Damping performance of the proposed VD-ERD
This section discusses and validates the damping performance of the suggested VD-ERD based on the damping force generated by the suggested system and the linear damping coefficient at different excitation inputs and different external resistances.
6.1.1. Force displacement loop of the proposed VD-ERD.
The force-displacement loops of the proposed VD-ERD for various external resistances on G2, under an amplitude of 12 mm and different excitation frequencies, are shown in figures 15(a)–(d). Furthermore, figure 15(e) shows the force-displacement loops under 4 mm and 1.5 Hz. It is observed that adjusting the external resistance on G2 can tune the damping force provided by the suggested VD-ERD. Specifically, as the external resistance increases, the damping force decreases, and conversely, as the external resistance decreases, the damping force increases.
Figure 15. Damping performance of proposed VD-ERD when G1 is connected with constant optimal resistance while G2 is linked with adjustable external resistances, under12 mm and: (a)1.5 Hz, (b) 2 Hz, (c) 2.5 Hz, (d) 3 Hz, 4 mm, and (e) 3 Hz; simulation validation at different frequencies: (f)1.5 Hz, (g) 2 Hz, (h) 2.5 Hz and (i) 3 Hz.
Download figure:
Standard image High-resolution imageOn the other hand, the simulation results were validated in figures 15(f)–(i). This validation was conducted under similar simulation excitation conditions. The experimental results correlate well with the simulation results, demonstrating a good agreement with allowable error revealed under similar conditions. For further evaluation, the experiment was carried out with an open circuit to analyze the impact of electrical damping, as illustrated in figures 15(a)–(e). It appears that the damping force is low in this scenario. When both generators are connected to an open circuit, the electrical damping of the generators reduces to zero.
6.1.2. Linear damping coefficient.
The linear damping coefficient was calculated when a Wye-shaped tunable resistance connected to G2 at different frequencies and optimal constant resistance connected with G1 as follows [37]:
where is the mechanical work done by the VD-ERD, which is the area enclosed by each loop in figure 15, is the excitation amplitude in (m), and is the excitation frequency in (rad s−1). However, the linear damping coefficient can be calculated by applying equation (32) in each force-displacement loop in figures 15(a)–(e). Table 3 shows the damping coefficient values at the excitation amplitude of 4 mm with different frequencies and resistances applied on G2. However, at 4 mm excitation amplitude, the maximum value is 1348.53 N.s m−1, which was achieved in 1 Ω, and the damping coefficient decreases significantly with an increase in the external resistance and increases the frequency till 650.75 N.s m−1 at an open circuit as depicted in figure 16(a). In addition, at 6 mm excitation amplitude, the maximum value of the damping coefficient is 1112.5 N.s m−1, which was achieved in 1 Ω, and the damping coefficient decreases significantly with an increase in the external adjustable resistance and increases the frequency to 479.47 N.s m−1 at an open circuit as depicted in figure 16(b).
Figure 16. Damping coefficient with different frequencies and different external resistors connected with G2 at amplitudes of: (a) 4 mm, (b) 6 mm, (c) 8 mm, (d) 10 mm, and (e) 12 mm. In this figure, G1 is connected with constant optimal resistance.
Download figure:
Standard image High-resolution imageTable 3. Damping coefficients at 4 mm amplitude with different frequencies and different external resistances.
| External resistance Ω | 4 mm and 1.5 Hz | 4 mm and 2 Hz | 4 mm and 2.5 Hz | 4 mm and 3 Hz |
|---|---|---|---|---|
| 1 Ω | 1348.53 | 1318.44 | 1255.15 | 1141.84 |
| 2 Ω | 1310.75 | 1122.33 | 972.31 | 870.91 |
| 3 Ω | 1290.16 | 922.78 | 869.11 | 753.76 |
| 4 Ω | 1270.97 | 875.39 | 765.77 | 656.98 |
| Open circuit | 1223.81 | 811.54 | 720.71 | 650.75 |
Furthermore, the same effect happens at excitation inputs of 8 mm, 10 mm, and 12 mm, as shown in figures 16(c)–(e). Therefore, varying the external load values significantly alters the damping; as shown in figure 16, a lower external load value extracts more mechanical work, resulting in larger damping coefficients. Conversely, the damping coefficient decreases with higher amplitudes and frequencies, as shown in figure 16(f). For further validation of the damping performance of the proposed VD-ERD, the simulation damping coefficient was compared to the experimental damping coefficient, as shown in figure 17(a). This comparison was conducted under excitation inputs of 4 mm amplitude and 3 Hz frequency. The experimental results correlate well with the simulation results, demonstrating a good agreement with allowable error revealed under similar conditions.
Figure 17. (a) Damping performance validation; (b) the output power and damping coefficient variation with different external resistors at excitation input of 4 mm, 3 Hz.
Download figure:
Standard image High-resolution image6.2. Output voltage of the proposed VD-ERD
For maximum and optimal energy harvesting of the proposed VD-ERD, both generators are connected with optimal resistance, which is 2 Ω, as shown in figure 17(b). However, the excitation input has a greater influence on the output voltage, and the voltage rises as the frequency increases at constant excitation amplitudes, as indicated in figures 18(a)–(d). Also, the voltage increases while amplitude rises at a constant frequency, as shown in figures 18(a)–(d). In addition, the experiment results validated the simulation results, which are very close with a minor error, as shown in figures 18(e) and (f).
Figure 18. Output voltage under different excitation amplitudes and frequencies of: (a) 1.5 Hz, (b) 2 Hz, (c) 2.5 Hz, (d) 3 Hz; simulation validation at 12 mm, 3 Hz, and: (e) 2 Ω, (f) 4 Ω.
Download figure:
Standard image High-resolution image6.3. Output power of the proposed VD-ERD
Using the voltage and optimal resistance values, the instantaneous output power can be obtained as follows,
However, the excitation input has a greater influence on the instantaneous power, which will increase as the frequency increases at a constant amplitude and an optimal resistance load of 2 Ω, as displayed in figures 19(a)–(d). Meanwhile, instantaneous power increases while amplitude rises at a constant frequency, as shown in figures 19(a)–(d). Moreover, the RMS output power was calculated as follows:
Figure 19. Instantaneous power under different excitation amplitudes and frequencies of: (a) 1.5 Hz, (b) 2 Hz, (c) 2.5 Hz, (d) 3 Hz; Simulation validation at: (e) different amplitudes and (f) different frequencies.
Download figure:
Standard image High-resolution imagewhere represents the period of sinusoidal excitation. As described in figures 19(e) and (f), the RMS output power increased significantly with both amplitude and frequency, and the maximum RMS power achieved was 10.29 W at 12 mm and 3 Hz. Also, as shown in figures 19(e) and (f), the simulation power output was validated at different amplitudes and frequencies, showing minor errors.
To validate the energy harvesting potential of VD-ERD and approximate real road surface excitation more closely. MATLAB/Simulink is employed to simulate real random road excitation due to limitations on the real practical test. Theoretically, random road profiles can be implemented based on road roughness grades classified by ISO 8608 [47]. Nevertheless, equation (35) presents the time domain displacement of the uneven road, depicted by a white noise signal that passes through a first-order filter. represent road-roughness coefficient classified by ISO 8608, represents the vehicle speed, , a value between 0.001 and 0.02 cycle m−1 is used to limit the displacement, and equals the unity. However, random road profile excitation was conducted, considering ART driving on class A and class B ISO 8608 roads at a driving speed of 50 km h−1
Figure 20(a) shows the road profile of road class A, and figures 20(b) and (c) show the single-phase voltage and single-phase power output achieved in class A, respectively. While figure 20(d) shows the road profile of road class B, figures 20(e) and (f) show the single-phase voltage and single-phase power output achieved in class B, respectively. However, the suggested VD-ERD achieved peak and RMS output power of 11.59 W and 1.84 W, respectively, when ART electric bus driving in ISO class A at a speed of 50 km h−1. In contrast, 36.38 W and 6.34 W peak and RMS power output were achieved when the ART driving on an ISO class B road at a speed of 50 km h−1. However, the power consumption of general sensors is in the range of microwatts to milliwatts. Therefore, this generated power can power most of the sensors installed in ART.
Figure 20. Performance of the VD-ERD under real road conditions: (a) road class A input, (b) single phase voltage and (c) single phase power; (d) road class B input, (e) single phase voltage, and (f) single phase power.
Download figure:
Standard image High-resolution image6.4. Deep learning for the health of the suspension system
Analyzing voltage signals from VD-ERD using deep learning can provide valuable insights into the performance and health of the suspension system. However, the main role of the deep learning module is to recognize and analyze the received voltage signal from the generator to determine the motion state of the suspension system. The deep learning module is located in the remote computer. Furthermore, the deep learning module receives the voltage signal after capture from the generator using the UTD2102CEX-EDU digital oscilloscope during various excitation conditions, which are 1.5 Hz, 2 Hz, 2.5 Hz, and 3 Hz frequencies and 4 mm, 6 mm, 8 mm, and 10 mm amplitudes. Figure 21(a) shows the data handling process, where the computer receives the voltage signal from the generator. The data is neatly arranged into 2 columns. Starting from the leftmost side, the slices are sliced at a specified length each time. One step is to separate between two slices until all data is sliced. The disorganized slices were divided into 15% validation, 15% test, and 70% training set. To extend training set samples and prevent overfitting, window smoothing was performed to augment the setup sample. The training model is shown in figure 21(b), which is a 4-classified Gate Recurrent Unit (GRU) model. GRU is a special type of Recurrent Neural Network (RNN) that is also optimized based on LSTM. Compared to LSTM, GRU has fewer parameters and is, therefore, less computationally expensive. GRU is designed to help solve the problem of gradient vanishing in traditional RNN by allowing the model to retain or forget information from previous time steps selectively.
Figure 21. Deep learning model: (a) the data handling process and (b) training model.
Download figure:
Standard image High-resolution imageThe four states of the vehicle's suspension are assumed and listed as examples based on the frequency provided by the MTS bench test: slow, medium, fast, and failure. A two-channel captures the voltage signals, and the deep learning module accepts the signals and outputs the recognition results. To select the optimal slice size, train and test from 10 to 200; to select the optimal step size, train and test from 2 to 10. Finally, the best resultant slice length of 50 was selected, and a step size of 4 was demonstrated. Furthermore, to avoid overfitting, each training iteration was conducted 200 times. Figure 22(a) shows voltage signals received by the deep learning module. The signals were categorized into four categories, namely slow, medium, fast, and failure. However, this frequency in the real vehicle's suspension system results when vehicles travel at various speeds over different road conditions. This study uses 1.5 Hz, 2 Hz, and 2.5 Hz to simulate vehicles traveling at low, medium, and high speeds. In addition, 3 Hz is used to simulate the situation where the suspension system of the vehicle has a problem. However, the suspension system of vehicles has problems due to high-frequency vibration. The four different suspension speeds were simulated by feeding four different excitation frequencies into the proposed VD-ERD. Intercept the output voltage signal simultaneously for comparison, as shown in figure 22(a). The distinctive features make it easy for GRU to acquire and identify features accurately. Figure 22(c) shows the validation accuracy and missing images, and figure 22(b) shows the training accuracy and missing, respectively. Additionally, the confusion matrix image is described in figure 22(d), and the accuracy of the model is 99.37%, as depicted in figure 22(b).
Figure 22. (a) Voltage signals received by deep learning module: (b)training accuracy and loss for motion recognition, (b)validation accuracy and loss for motion recognition, (c) confusion matrix.
Download figure:
Standard image High-resolution image6.5. Experimental results of power supply
To further confirm that the electrical energy produced by the proposed VD-ERD can be used to power different sensors in ART. Firstly, the charging experiment was conducted as follows: the prototype of the suggested VD-ERD was installed in the MTS as indicated in figures 23(a) and (b); after that, the output of the G1 was connected to the rectifier, and then linked with voltage regulator and supercapacitors. Also, the oscilloscope is connected to a supercapacitor to record and monitor the voltage output. In addition, the excitation amplitude is set at 10 mm and the frequency at 2 Hz. Different supercapacitors are used during the experiments, as displayed in figure 23(c) 2 F, (d) 3.3 F, and (e) 5 F capacitance. However, during the experiment, the VD-ERD can recharge a 5 F capacitor from 0 V to 3.5 V in 4 s, as depicted in figure 23(h).
Figure 23. (a) Charging experiment, (b) sensors experiment, (c) 2 F capacitor, (d) 3.3 F capacitor, (e) 5 F capacitor, (f) lighting up 80 LED lights, (g) tests of power supply for 10 different sensors and (h) transient voltage of supercapacitor.
Download figure:
Standard image High-resolution imageFurthermore, the lighting experiment was conducted as follows: the three phases of the G1 of the VD-ERD are connected to the rectifier, and after that, the voltage regulator is linked to 80 LEDs, as indicated in figure 23(f). As a result, the proposed VD-ERD successfully lit all LEDs. For further analysis, the G1 of the proposed VD-ERD is connected to 10 different types of sensors simultaneously to validate its ability to power sensors in ART, as illustrated in figure 23(b).
6.6. Feasibility study and application of the proposed VD-ERD
In recent years, developing and implementing self-powered self-sensing systems has become the main objective of developing smart transportation to ensure optimal safety and sustainable EVs [48]. However, the ART has many self-sensing devices, including the RADAR sensor, microphone, video camera, rear camera, inertial sensor, A/C sensor, ultrasonic sensor, GPS, pressure sensor, and infrared sensor. Therefore, in this section, the feasibility study is presented to verify the capability of the VD-ERD to supply power to a self-sensing device for ART. Figure 24(f) illustrates the composition of a typical self-sensing device for ART, while table 4 presents the required power of the self-sensing devices used in ART. While figures 24(a)–(c) show ART driving in different road types. However, the output power of the proposed VD-ERD per one regenerative damper is 10.29 W, achieved at 12 mm and 3 Hz. As a result, when the proposed VD-ERD is implemented in the suspension system instead of the traditional hydraulic damper of an ART, it can generate approximately 41.16 W of electricity from four VD-ERDs. Additionally, future work includes installing the prototype of the VD-ERD in the suspension system of ART and performing field experiments. Figure 24(d) displays the installation and real practical test of the VD-ERD in the CRRC SRIG RAIL TRANSIT Co, Ltd, facilitating continuous optimization and evaluation of the damping performance and power generation of the proposed VD-ERD.
Figure 24. Application of the proposed VD-ERD in the ART while ART driving on different ISO 8608 roads: (a) class A, (b) class B, and (c) class c; (d) installation of the VD-ERD in ART factory, (e) damping control and energy harvesting circuit, (f) self-powered sensors and (g) analyzing voltage signals in the deep learning model.
Download figure:
Standard image High-resolution imageTable 4. Energy usage for the self-powered sensors employed in the ART. Reproduced from [48]. CC BY 4.0.
| Name | Power required (W) | Quantity | Power required (W) | Proposed system harvested power (W) |
|---|---|---|---|---|
| RADAR sensor | 0.0025 | 20 | 0.05 | — |
| Pressure sensor | 0.48 | 10 | 4.8 | — |
| GPS | 1–3 | 1 | 3 | — |
| Video camera | 3.5 | 2 | 7 | — |
| Microphone | 0.4 | 3 | 1.2 | — |
| A/C sensor | 0.014 | 20 | 0.28 | — |
| Rear camera | 0.0025 | 20 | 0.05 | — |
| Ultrasonic sensor | 7 | 2 | 14 | — |
| Inertial sensor | 0.12 | 5 | 0.6 | — |
| Infrared sensor | 0.12 | 5 | 0.6 | — |
| Total power required (W) | — | — | 31.85 W | 41.16 W |
Moreover, the findings of the suggested VD-ERD were compared with the previous ERD reported in the literature for energy harvesting and damping performance, as shown in table 5. However, the proposed VD-ERD has demonstrated a good damping performance compared with those studies ranging from 100 N.s m−1 to 1500 N.s m−1, showing the capability of the suggested VD-ERD for tunning the damping coefficient during the operation based on the road condition. Simultaneously, harvest and capture the wasted kinetic energy in the suspension system to supply power to self-powered sensors of ART for sustainable and smart EBs.
Table 5. Comparative studies of energy harvesting and damping performance of the proposed VD-ERD with published literature.
| References | Motion conversation model | Energy harvesting performance at different excitation inputs | Damping performance | ||
|---|---|---|---|---|---|
| Frequency (Hz) | Amplitude (mm) | Power (W) | Damping coefficient range N.s m−1 | ||
| Li et al [9] | Crank mechanism | 3 | 12.5 | 4.8 | 3132.16 |
| Li et al [31] | Two helical racks with opposite threads | 2.5 | 7 | 4.25 | 1839.27 |
| Zhang et al [32] | Rack and Pinion | 2.5 | 7.5 | 4.3 | 1511.8 |
| Ali et al [33] | Barrel cam-follower | 2 | 7.5 | 3.85 | 500–3500 |
| Wang et al [34] | Twin-Ball Screw | 2 | 6 | 3.7 | 5000–10 580 |
| Liu et al [35] | Ball-screw mechanism | 4 | 2 | 11.52 | 4430–15 420 |
| Bowen L et al [36] | Using cable transmission | — | — | 105 | 220–2720 |
| Maravandi et al [37] | Two-leg mechanism | 3 | 10 | 0.54 | 1720 |
| Sabzehgar et al [38] | Algebraic screw linkage | 5.6 | 2.5 | 0.54 | 97–237 |
| Li et al [49] | Rack and Pinion | 4 | 5 | 25.6 | — |
| Li et al [46] | Rack and Pinion | 0.5 | 30 | 12 | 1800–5000 |
| Proposed Design (VD-ERD) | Double coaxial slotted link conversion mechanism | 3 | 12 | 10.29 | 100–1500 |
7. Conclusion
This paper designed and tested a multi-purpose VD-ERD using a double coaxial slotted link motion conversion module to monitor the health of the suspension system, tunning the damping coefficient during the operation based on the road condition while providing electric energy to supply power to self-powered sensors of ART for sustainable, and smart EBs. The proposed VD-ERD consists of two identical generators; one generator is connected with optimal constant resistance for maximum energy harvesting, and the other generator is connected with adjustable resistance for fine-tuning the damping coefficient. Both generators connect to a rectifying circuit and charge the battery. An analytical model was developed to evaluate the damping performance of the suggested VD-ERD by controlling the external resistance, and simulation was performed using MATLAB. A force-displacement loop is generated under different sinusoidal excitation with different amplitudes and frequencies by controlling the external resistance to assess the performance of the suggested VD-ERD regarding the damping coefficient.
Furthermore, VD-ERD was developed in MATLAB/Simulink, and the simulation was conducted with sinusoidal excitation to evaluate the performance of the proposed VD-ERD in terms of output voltage and power. Moreover, to validate the potential energy of VD-ERD in real road conditions, random road profile excitation was conducted, considering ART driving on class A and class B ISO 8608 roads at a driving speed of 50 km h−1. Consequently, a full-scale prototype was manufactured and assessed by an experimental investigation using MTS to validate the simulation results under similar parameters. Furthermore, the voltage signals received from the generators of the proposed VD-ERD were analyzed on a deep learning model, which can provide valuable insights into the performance and health of the suspension system in four different modes, namely slow, medium, fast, and failure. Additionally, a feasibility analysis and power supply experiment were performed to evaluate the ability of the suggested system to supply power to self-powered sensors of ART. The key findings of the current study are:
- (i)The experimental results validated the simulation results with minor errors, indicating that controlling the external resistance of VD-ERD can tune the damping coefficient. Simultaneously, harvest the wasted energy in the suspension system of ART.
- (ii)Minor errors were found while comparing and matching the force-displacement loops based on simulation and experimental studies. Moreover, the damping force loop behavior of the VD-ERD is observed to be symmetric during both the rebound and compression strokes, indicating its potential to enhance ride comfort in ART. In addition, the experiment damping coefficient at various external resistances was determined and found to be nearly identical to the simulation damping coefficient under similar conditions.
- (iii)The suggested VD-ERD achieved peak and RMS output power of 11.59 W and 1.84 W, respectively, when ART electric bus driving on ISO class A road at 50 km h−1. In contrast, 36.38 W and 6.34 W peak and RMS power output were achieved when the ART electric bus driving on an ISO class B road at 50 km h−1.
- (iv)During the lab test, the prototype of the proposed VD-ERD achieved a peak power output of 10.29 W at sinusoidal excitation of 12 mm and 3 Hz amplitude and frequency, respectively.
- (v)In addition, when the external resistance is adjusted within the range of (1–4) Ω, with different frequencies and amplitude, the damping coefficient changes from (100 to 1500) N.s m−1, which proves the proposed VD-ERD capable of tuning the damping coefficient based on the road condition.
- (vi)Furthermore, the voltage signals received from the generators were analyzed using a deep learning model, and the result shows 99.37% training accuracy for monitoring the health of suspension systems.
- (vii)The proposed VD-ERD sufficiently powers the RADAR sensor, microphone, video camera, GPS, rear camera, inertial sensor, ultrasonic sensor, pressure sensor, and infrared sensor.
8. Limitations and future research
- (i)Due to limitations on practical experimental conditions and equipment, future work includes installing the prototype of the VD-ERD in a suspension of ART and conducting field experiments. However, this will assess energy harvesting capabilities and the dynamics of VD-ERD, considering ride comfort and stability. Figure 24(d) displays the installation and real practical test environment of the VD-ERD in the CRRC SRIG RAIL TRANSIT Co, Ltd, facilitating continuous optimization and evaluation of the damping performance and power generation of the proposed VD-ERD.
Acknowledgments
This work was supported by the National Natural Foundation of China under Grant No. 51975490 and by the Science and Technology Projects of Sichuan under Grants Nos. 23QYCX0280 and 2022NSFSC0461; and by the Science and Technology Projects of Yibin under Grant Nos. 2021ZYCG017, 2023SJXQYBKJJH005, Nos. SWJTU2021020001 and SWJTU2021020002, and by the Science and Technology Projects of Chengdu under Grant No. 2021YF0800138GX.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.