Abstract
Defects in crosslinked networks have a negative effect on mechanical and functional properties. In this study, an epoxy resin diglycidyl ether of bisphenol A crosslinked by a hardener 4,4-diaminodiphenyl methane with various cyclic topologies was simulated to find correlations between the mechanical/shape memory properties (i.e. glassy/rubbery elastic modulus, shape recovery ratio, and recovery stress) and cyclic topologies (i.e. number of total loops, number of defective loops (DLs), etc). The effect of cyclic topology on shape memory properties was more significant than its effect on mechanical properties, altering recovery stress by more than 25% on average. After analyzing several topological fingerprints such as total number of loops, number of DLs, and number of higher order loops, we found that the effect of cyclic topology on the mechanical/shape memory properties of the systems can be best understood by the fraction of hardeners reacted with four distinct epoxy molecules (tetra-distinctly-reacted (TDR) hardeners). By increasing the number of TDR hardeners, the network is closer to ideal, resulting in an increase in the number of higher order loops and a reduction in the number of DLs, which in turn leads to an increase in rubbery elastic modulus and shape recovery ratio to a lesser degree, but a substantial increase in recovery stress. These results suggest that utilization of experimental techniques such as semibatch monomer addition, which leads to a more expanded and defect-free network, can result in a simultaneous increase in both shape recovery ratio and recovery stress in thermoset shape memory polymers (TSMPs). Moreover, topology alteration can be used to synthesize TSMPs with improved recovery stress without significantly increasing their stiffness.
Export citation and abstract BibTeX RIS
1. Introduction
Polymer networks exhibit extraordinary mechanical properties [1, 2], and thus, have been used for the synthesis of selective membranes [3–8], elastomers and superabsorbers [9–11], and a variety of biological materials such as tissues, scaffolds, and extracellular matrices [12–21]. Shape memory polymers (SMPs), a subset of polymer networks, are stimuli-responsive materials capable of recovering from a temporary, deformed shape back to an original, memorized shape under the effect of various stimuli such as temperature, light, magnetic field, moisture, pH, or electrical current. SMPs exist as either thermoplastic or thermoset polymers depending on their crosslinked networks. Thermoset shape memory polymers (TSMPs) are a network of percolating chemical covalent bonds [22]. Their shape recovery capabilities, as well as their exceptional thermal stability and creep and chemical resistance [23], make them great candidates for use in the manufacturing of novel materials such as aerospace structures [24, 25], actuators [26–28], sealant [29], proppants [30, 31], biodegradable sutures [32], stents [33–35], and many others.
The temporary shape in SMPs can be induced through the 'hot programming' process, which consists of three stages: pre-straining at a temperature sufficiently greater than the glass transition temperature ( ), followed by constrained cooling of the material to a temperature below the
), followed by constrained cooling of the material to a temperature below the  , and lastly by removing the applied load and fixing a temporary shape. When heated above the
, and lastly by removing the applied load and fixing a temporary shape. When heated above the  , the material returns to its original shape. The stress the material exerts during the recovery process is known as the recovery stress. The fraction of the temporary shape recovered to the original shape is known as the recovery ratio [36]. Upon releasing the constraints at the end of the programming event, the chains are aligned with reduced entropy; upon reheating, the chains revert to their favored coil-shaped state, thus recovering the lost entropy and restoring the original shape [23, 36]. In some cases, energy can also be stored enthalpically per bond length change and bond angle change [37, 38].
, the material returns to its original shape. The stress the material exerts during the recovery process is known as the recovery stress. The fraction of the temporary shape recovered to the original shape is known as the recovery ratio [36]. Upon releasing the constraints at the end of the programming event, the chains are aligned with reduced entropy; upon reheating, the chains revert to their favored coil-shaped state, thus recovering the lost entropy and restoring the original shape [23, 36]. In some cases, energy can also be stored enthalpically per bond length change and bond angle change [37, 38].
Shape recovery properties (i.e. recovery stress and shape recovery ratio) are important performance-determining properties of SMPs. The current generation of TSMPs suffers from low recovery stress [38], which limits the application of these materials due to the inability of the material to support the weight of larger sample sizes [39]. Thus, finding means by which one can improve these properties in existing TSMPs has been a priority for researchers in this field. Additionally, attempts have been made to enhance the properties of SMPs through reinforcing them with carbon nanotubes [40–42], particulates [43, 44], and fibers [25, 45, 46]. While these approaches can lead to an improvement in recovery stress, they have major drawbacks such as partial or near total loss of shape memory. Thus, more robust approaches are needed to improve both the recovery stress and shape recovery of existing TSMPs.
The effects of cyclic topology on the mechanical properties of polymer networks have been studied before, suggesting that the presence of primary loops [47–49] (which are elastically inactive [50–52]) as well as secondary loops [53–55] adversely affect the mechanical properties (i.e. elastic and storage moduli) of these networks [56–60]. TSMPs are a subclass of polymer networks, and yet, the effects of cyclic topology on their mechanical, and more importantly, shape memory properties and ultimately, the possibility of enhancing their shape memory properties through manipulation of their topological properties, have not been explored.
In this work, we aim to investigate the effects of cyclic topology on the shape memory properties of TSMPs by studying many systems that are similar to epoxy-hardener pair and crosslinking density but of different cyclic topologies. Given the large number of systems required to conduct such a study, we opt to utilize a coarse-grained (CG) model to reduce the total computational time required to carry out this study. The CG model of diglycidyl ether of bisphenol A (DGEBA) as the epoxy monomer and 4,4-diaminodiphenyl methane (DDM) as the hardener, proposed by Duan et al [61] was chosen. The advantage of this particular model over other CG models for various epoxy-hardener pairs in the literature persists in its capability to capture properties of the material at different temperatures. Almost all other CG models in the literature are only viable at a fixed temperature. Such a feature of the model is essential in calculations of shape memory properties because the shape fixity and shape recovery are temperature dependent.
The rest of the paper is organized as follows: we first introduce the details of the model and the simulations employed, followed by the results of our simulations and the statistically significant correlation among those properties and various topological properties of our systems. Finally, we discuss the physical interpretation and significance of those significant correlations. We close this work by summarizing our findings, suggesting its application in the synthesis of TSMPs, and proposing prospects for future studies.
2. Methodology
2.1. Model
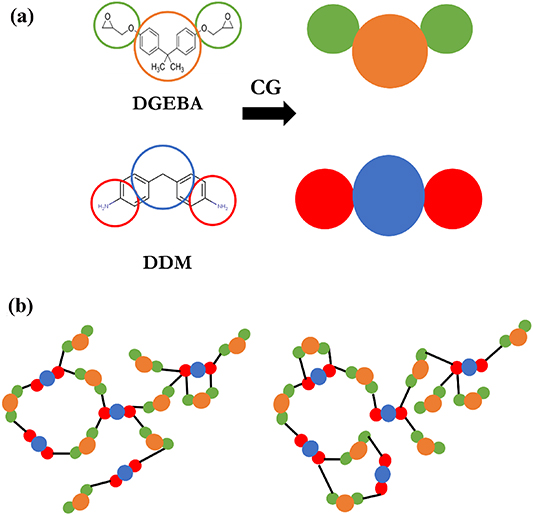
The CG model used for the DGEBA-DDM pair, which is taken from [61], reduces each of the epoxy/hardener molecules into three super atoms (figure 1(a)). Harmonic forms are used for bond stretching and bending to approximate the bonded potential, and the non-bonded interactions are defined by the 12–6 Lennard–Jones (LJ) potential. The force field parameters including the mass of super atoms, bond and angle stiffness, equilibrium bond lengths and angles, and the LJ interactions parameters, i.e. the radial distance corresponding to zero inter-particle potential ( ) and potential well depth (
) and potential well depth ( ) were obtained from the same work [61]. The efficacy of this model in reproducing the results of the more-accurate all-atom models (especially density and elastic modulus) was demonstrated in the original work. More complex CG forcefields can be created [62], or even the more accurate Brenner potential [63] can be used, but for the purpose of studying the effect of topology, a relatively simple form is appropriate.
) were obtained from the same work [61]. The efficacy of this model in reproducing the results of the more-accurate all-atom models (especially density and elastic modulus) was demonstrated in the original work. More complex CG forcefields can be created [62], or even the more accurate Brenner potential [63] can be used, but for the purpose of studying the effect of topology, a relatively simple form is appropriate.
Figure 1. Plot of (a) the epoxy (DGEBA) and hardener (DDM) molecules and their representative coarse-grained model, and (b) schematic of two structures with similar crosslinking density but different cyclic topology.
Download figure:
Standard image High-resolution image2.2. Simulation details
All the simulations were conducted using the LAMMPS software package [64], in the absence of solvent, in either the constant number of atoms, pressure, and temperature (NPT) or the constant number of atoms, volume, and temperature (NVT) ensemble. A timestep of  was used in the simulations, unless specified otherwise. Nose–Hoover thermostats and barostat [65, 66] were utilized with damping constants for temperature and pressure control equating 100 times and 1000 times the timestep, respectively. In all the simulations, the periodic boundary conditions were imposed on the cubic simulation boxes in all three directions.
was used in the simulations, unless specified otherwise. Nose–Hoover thermostats and barostat [65, 66] were utilized with damping constants for temperature and pressure control equating 100 times and 1000 times the timestep, respectively. In all the simulations, the periodic boundary conditions were imposed on the cubic simulation boxes in all three directions.
2.3. Crosslinking procedure
Initial simulation boxes were prepared by using the Polymatic software [67] to randomly place  hardener molecules and
hardener molecules and  epoxy molecules in a cubic simulation box. The simulations were initialized at a temperature of
epoxy molecules in a cubic simulation box. The simulations were initialized at a temperature of  . After energy minimization, the initial equilibration was performed for a duration of
. After energy minimization, the initial equilibration was performed for a duration of  steps in the NPT ensemble at a temperature of
steps in the NPT ensemble at a temperature of  and pressure of
and pressure of  , with a timestep of
, with a timestep of  . The polymer rearrangement in the rubbery state occurs over timescales in orders of seconds, while the timescales accessible to MD simulations are on the order of nanoseconds. Therefore, to avoid having to run extremely long equilibrium simulations, the initialization step of the simulations is conducted at temperatures much higher than the glass transition temperature to speed up the relaxation process. At the end of the relaxation procedure, the simulation box side length reached ∼78 Å.
. The polymer rearrangement in the rubbery state occurs over timescales in orders of seconds, while the timescales accessible to MD simulations are on the order of nanoseconds. Therefore, to avoid having to run extremely long equilibrium simulations, the initialization step of the simulations is conducted at temperatures much higher than the glass transition temperature to speed up the relaxation process. At the end of the relaxation procedure, the simulation box side length reached ∼78 Å.
To create the systems with a fixed topology and a target crosslinking density (i.e. the ratio of the number of bonds between epoxy and hardener molecules to the total number of possible bonds between them) of  , the crosslinking procedure was conducted in NVT ensemble using 'fix bond/create' option in LAMMPS, with a timestep of
, the crosslinking procedure was conducted in NVT ensemble using 'fix bond/create' option in LAMMPS, with a timestep of  , a bond formation minimum distance (i.e. the distance indicating how close a pair of epoxy-hardener sites need to be in order to form a bond) of 7 Å for a total duration of
, a bond formation minimum distance (i.e. the distance indicating how close a pair of epoxy-hardener sites need to be in order to form a bond) of 7 Å for a total duration of  steps, and an attempt to create bonds executed every 1000 steps. The reaction procedure was stopped once the system achieved a crosslinking density of
steps, and an attempt to create bonds executed every 1000 steps. The reaction procedure was stopped once the system achieved a crosslinking density of  . About 25 systems with the same topology were produced and equilibrated. These 25 systems were made by equilibrating one system with 25 different initial velocities.
. About 25 systems with the same topology were produced and equilibrated. These 25 systems were made by equilibrating one system with 25 different initial velocities.
To create the systems with random topologies, the same procedure was conducted but with a bond formation minimum distance of 50 Å to create a system with almost  crosslinking density. Afterward, this system was used to generate
crosslinking density. Afterward, this system was used to generate  systems with different topologies by removing several epoxy-hardener bonds from the initial system to reduce the overall crosslinking density to
systems with different topologies by removing several epoxy-hardener bonds from the initial system to reduce the overall crosslinking density to  . By repeating this process 100 times, these 100 systems with different topologies were created. All these simulations were conducted with a timestep of
. By repeating this process 100 times, these 100 systems with different topologies were created. All these simulations were conducted with a timestep of  . Given the large bond formation minimum distance used in this approach, the systems contained long bonds. These rather long bonds were equilibrated in a stepwise manner: Initially, the bond stiffness and equilibrium distances were set to a low (0.5 kcal mol−1 Å−3) and a high (20 Å) value, respectively. At each stage, the bond stiffness was increased, the bond equilibrium distance was reduced, and the systems were equilibrated for a duration of
. Given the large bond formation minimum distance used in this approach, the systems contained long bonds. These rather long bonds were equilibrated in a stepwise manner: Initially, the bond stiffness and equilibrium distances were set to a low (0.5 kcal mol−1 Å−3) and a high (20 Å) value, respectively. At each stage, the bond stiffness was increased, the bond equilibrium distance was reduced, and the systems were equilibrated for a duration of  steps. The procedure was conducted for a total of
steps. The procedure was conducted for a total of  stages.
stages.
2.4. Cooling
After the crosslinking procedure and bond relaxation were completed, the reacted systems were energy minimized and equilibrated for an additional  steps in the NPT ensemble at a temperature of
steps in the NPT ensemble at a temperature of  and pressure of
and pressure of  . Then, the systems were cooled down with an effective cooling rate of
. Then, the systems were cooled down with an effective cooling rate of  to a temperature of
to a temperature of  in a stepwise manner: In each step, the temperature was reduced by
in a stepwise manner: In each step, the temperature was reduced by  , and the system was equilibrated in NPT ensemble at the current temperature and a pressure of
, and the system was equilibrated in NPT ensemble at the current temperature and a pressure of  , for a duration of
, for a duration of  steps. At the end of each step, a data file was saved as a starting point for the system at that temperature. It should be mentioned that this cooling rate is not experimentally achievable, but such a rate is common in MD simulations since the simulations can only capture a few nanoseconds of the system evolution [37, 68]. This rate probably overestimates the absolute shape memory properties [37], but allows for comparison between the effects of topologies which is the main focus of this work.
steps. At the end of each step, a data file was saved as a starting point for the system at that temperature. It should be mentioned that this cooling rate is not experimentally achievable, but such a rate is common in MD simulations since the simulations can only capture a few nanoseconds of the system evolution [37, 68]. This rate probably overestimates the absolute shape memory properties [37], but allows for comparison between the effects of topologies which is the main focus of this work.
2.5. Elastic modulus
To determine the elastic modulus, the temperatures  and
and  (
( above or below the system
above or below the system  [61]), were selected for calculating the glassy and rubbery elastic modulus, respectively. At each temperature, the system was first energy minimized. A linear deformation totaling 3% was imposed over ten different steps of 0.3% each. Each step included a linear deformation of
[61]), were selected for calculating the glassy and rubbery elastic modulus, respectively. At each temperature, the system was first energy minimized. A linear deformation totaling 3% was imposed over ten different steps of 0.3% each. Each step included a linear deformation of  was imposed over a very short period (
was imposed over a very short period ( steps), followed by an equilibration period of 200 000 steps. The stress in the system was obtained during the second half of the equilibration process and averaged over that period. Six total simulations were conducted for both stretching (positive deformation) and compression (negative deformation) and in all three orthogonal directions independently. Both the glassy elastic modulus (
steps), followed by an equilibration period of 200 000 steps. The stress in the system was obtained during the second half of the equilibration process and averaged over that period. Six total simulations were conducted for both stretching (positive deformation) and compression (negative deformation) and in all three orthogonal directions independently. Both the glassy elastic modulus ( ) and rubbery elastic modulus (
) and rubbery elastic modulus ( ) were then calculated as the slope of the stress vs. strain curve at the corresponding temperatures.
) were then calculated as the slope of the stress vs. strain curve at the corresponding temperatures.
3. Programming
To determine the recovery stress and recovery ratio, the systems were first energy minimized at  and then, similar to the procedure used for the calculation of elastic modulus, a linear deformation of
and then, similar to the procedure used for the calculation of elastic modulus, a linear deformation of  (compression) was imposed on them for a very short duration (ten steps) and the systems were held at fixed deformation for
(compression) was imposed on them for a very short duration (ten steps) and the systems were held at fixed deformation for  steps. This procedure was repeated
steps. This procedure was repeated  more times to reach an overall
more times to reach an overall  compression, followed by a relaxation period with fixed deformation for a duration of
compression, followed by a relaxation period with fixed deformation for a duration of  steps. The programming stress (
steps. The programming stress ( ) was calculated as the average of the stress in the system during the second half of this relaxation stage. Afterward, the systems were cooled to a temperature of
) was calculated as the average of the stress in the system during the second half of this relaxation stage. Afterward, the systems were cooled to a temperature of  with fixed deformation over a period of
with fixed deformation over a period of  steps, followed by a relaxation period at the same temperature for a duration of
steps, followed by a relaxation period at the same temperature for a duration of  steps, during which the systems were allowed to fully relax, and experienced a small elastic spring-back by load removal. Afterward, the systems were heated up back to a temperature of
steps, during which the systems were allowed to fully relax, and experienced a small elastic spring-back by load removal. Afterward, the systems were heated up back to a temperature of  with fixed deformation over a duration of
with fixed deformation over a duration of  steps, followed by a relaxation period at the same temperature and with a fixed deformation. During this stage, the stress data was collected, and the recovery stress (
steps, followed by a relaxation period at the same temperature and with a fixed deformation. During this stage, the stress data was collected, and the recovery stress ( ) was calculated as the average of stress data over the second half of this period. At the final stage (i.e. the shape recovery stage), the system temperature was raised to
) was calculated as the average of stress data over the second half of this period. At the final stage (i.e. the shape recovery stage), the system temperature was raised to  , the stress was removed, and the system was allowed to recover from its temporary shape for a duration of 54 000 000 steps. The recovery ratio (
, the stress was removed, and the system was allowed to recover from its temporary shape for a duration of 54 000 000 steps. The recovery ratio ( ) was calculated as
) was calculated as  , with
, with  being the initial strain at the beginning of the shape recovery stage and
being the initial strain at the beginning of the shape recovery stage and  being the strain as a function of time during the recovery stage. The final recovery ratio (
being the strain as a function of time during the recovery stage. The final recovery ratio ( ) is calculated as the time-averaged
) is calculated as the time-averaged  over the last 2000 000 steps of the shape recovery stage. The temperature at this stage was raised beyond the starting programming temperature (i.e.
over the last 2000 000 steps of the shape recovery stage. The temperature at this stage was raised beyond the starting programming temperature (i.e.  instead of
instead of  ) to essentially observed a more substantial shape recovery process. At 440 K, the systems experienced very small shape recovery (
) to essentially observed a more substantial shape recovery process. At 440 K, the systems experienced very small shape recovery ( ) due to the small timescales used in the simulations. The programming procedure was applied in all 3 orthogonal directions independently, and the results were averaged.
) due to the small timescales used in the simulations. The programming procedure was applied in all 3 orthogonal directions independently, and the results were averaged.
4. Results and discussions
The results for  ,
,  ,
,  ,
,  and
and  for both sets of systems (those with random topologies and those with a fixed topology) are plotted in figure S1, and a summary of the mean, standard deviation, and standard error for the aforementioned properties on both sets of systems are presented in table 1. Moreover, to verify whether the means of the properties of the systems with random topologies are affected by the topological properties and not just the uncertainties associated with the MD simulations, the validity of the null hypothesis with regards to the mean of the results for the two sets of systems was evaluated. The resulting p-values are presented in table 1.
for both sets of systems (those with random topologies and those with a fixed topology) are plotted in figure S1, and a summary of the mean, standard deviation, and standard error for the aforementioned properties on both sets of systems are presented in table 1. Moreover, to verify whether the means of the properties of the systems with random topologies are affected by the topological properties and not just the uncertainties associated with the MD simulations, the validity of the null hypothesis with regards to the mean of the results for the two sets of systems was evaluated. The resulting p-values are presented in table 1.
Table 1. Mean ( ), standard deviation (
), standard deviation ( ), and standard error (
), and standard error ( ) of glassy elastic modulus (
) of glassy elastic modulus ( ), rubbery elastic modulus (
), rubbery elastic modulus ( ), shape recovery ratio (
), shape recovery ratio ( ) and recovery stress (
) and recovery stress ( ) for systems with random topologies and those with a fixed topology. Results with statistical significance are highlighted in red.
) for systems with random topologies and those with a fixed topology. Results with statistical significance are highlighted in red.
| Property |
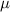 (fixed) (fixed) |
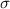 (fixed) (fixed) |
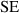 (fixed) (fixed) |
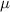 (random) (random) |
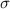 (random) (random) |
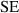 (random) (random) |
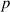
|
|---|---|---|---|---|---|---|---|
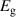
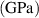
| 3.123 | 0.196 | 0.039 | 3.109 | 0.207 | 0.020 | 0.757 |
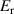
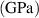
| 1.300 | 0.131 | 0.026 | 1.430 | 0.150 | 0.015066 | 0.0001 |
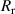
| 0.681 | 0.089 | 0.017 | 0.631 | 0.067 | 0.006723 | 0.014 |
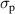
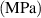
| 132.2723 | 14.07687 | 2.815373 | 176.8977 | 20.22058 | 2.022058 | 0 |
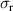
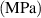
| 27.800 | 2.852 | 0.570 | 35.131 | 4.335 | 0.433 | 0 |
As observed in table 1, the  ,
,  ,
,  and
and  are indeed affected by more than just the statistical uncertainties associated with the MD simulations.
are indeed affected by more than just the statistical uncertainties associated with the MD simulations.  is unaffected by the topology in a statistically significant manner because the material properties are not determined by the longer-range topological structures, but by the short-range local interactions. The difference in average
is unaffected by the topology in a statistically significant manner because the material properties are not determined by the longer-range topological structures, but by the short-range local interactions. The difference in average  and
and  is not only statistically significant (
is not only statistically significant ( is less than
is less than  and
and  , respectively) but differs by 33% and 26%, respectively, between the two populations. Furthermore, the range of the recovery stress data (i.e. the difference between the maximum and the minimum) for the systems with a fixed topology is
, respectively) but differs by 33% and 26%, respectively, between the two populations. Furthermore, the range of the recovery stress data (i.e. the difference between the maximum and the minimum) for the systems with a fixed topology is  , compared to
, compared to  for the systems with random topologies. A recent study by some of us demonstrated that the range of recovery stress data for a set of systems with various epoxy-hardener pairs can be as high as
for the systems with random topologies. A recent study by some of us demonstrated that the range of recovery stress data for a set of systems with various epoxy-hardener pairs can be as high as  [68]. Thus, while the effect of topology on the mechanical/shape memory properties of TSMPs might not be as strong as the effect of chemical composition, manipulation of the topological properties of the system seems to be a viable method for improving mechanical/shape memory properties of these materials.
[68]. Thus, while the effect of topology on the mechanical/shape memory properties of TSMPs might not be as strong as the effect of chemical composition, manipulation of the topological properties of the system seems to be a viable method for improving mechanical/shape memory properties of these materials.
To establish a correlation between the shape memory and topological properties, we considered three 'fingerprints' of the topology involving loops. In our analysis, a loop is defined as a collection of atoms where if one starts tracing the bonds beginning at any atom in the collection, the tracing would end at that same atom. Thus, the number of loops ( ) is the number of such collections in a system, the size of the loop (
) is the number of such collections in a system, the size of the loop ( ) is the number of atoms in any such collection, and the mass of the loops (
) is the number of atoms in any such collection, and the mass of the loops ( ) is the sum of masses of all atoms in any such collection. Based on these definitions, the three topological fingerprints are: the number of loops (
) is the sum of masses of all atoms in any such collection. Based on these definitions, the three topological fingerprints are: the number of loops ( ), the average size of the loops (
), the average size of the loops ( ), defined as
), defined as  , and the weight-averaged size of the loops (
, and the weight-averaged size of the loops ( ), defined as
), defined as  with
with  and
and  being the mass and the size of the ith loop, respectively.
being the mass and the size of the ith loop, respectively.  and
and  can be thought of as the number and weight average molecular weight of the loops, respectively. The Pearson correlation coefficient (
can be thought of as the number and weight average molecular weight of the loops, respectively. The Pearson correlation coefficient ( ) between the mechanical and shape memory properties and the aforementioned fingerprints, as well as the p-values for each correlation, is presented in table 2.
) between the mechanical and shape memory properties and the aforementioned fingerprints, as well as the p-values for each correlation, is presented in table 2.
Table 2. Pearson correlation coefficient and its corresponding p-value among the topological fingerprints: number of loops ( ), average size of the loops (
), average size of the loops ( ) and weight-averaged size of the loops (
) and weight-averaged size of the loops ( ), and the mechanical and shape memory properties of the systems with random topologies: glassy elastic modulus (
), and the mechanical and shape memory properties of the systems with random topologies: glassy elastic modulus ( ), rubbery elastic modulus (
), rubbery elastic modulus ( ), shape recovery ratio (
), shape recovery ratio ( ) and recovery stress (
) and recovery stress ( ). Results with statistical significance are highlighted in red.
). Results with statistical significance are highlighted in red.
| Property |
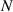
|
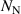
|
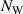
| |||
|---|---|---|---|---|---|---|

|
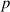
|

|
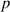
|

|
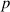
| |
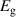
| 0.055 | 0.585 | 0.006 | 0.950 | 0.007 | 0.941 |

| 0.131 | 0.194 | 0.068 | 0.496 | 0.069 | 0.492 |

| 0.199 | 0.046 | 0.143 | 0.153 | 0.145 | 0.150 |
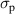
| 0.190 | 0.057 | 0.131 | 0.193 | 0.132 | 0.191 |

| 0.259 | 0.009 | 0.075 | 0.453 | 0.077 | 0.446 |
The results presented in table 2 indicate a statistically significant positive correlation between the number of loops and the programming stress, recovery stress, and shape recovery ratio. However, we do not observe any statistically significant correlations involving the rubbery elastic modulus. Yet, the effect of topology on the rubbery elastic modulus is evident from table 1. Thus, the topological fingerprints need to be further refined to capture the effect of topology on the rubbery elastic modulus.
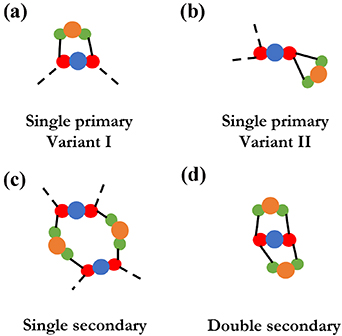
As mentioned earlier, previous studies on the effect of cyclic topology on the mechanical properties of the polymer networks suggest that 'defective' loops (figure 2) [57] adversely affect the elastic modulus of polymer networks [47–57]. Primary DLs contain one hardener molecule that is reacted to the same epoxy molecule thus forming a single loop (figures 2(a) and (b)). These loops are described as elastically inactive and act as the endpoints of the network (figures 2(a) and (b)), which harm the network properties by inhibiting network growth and taking away epoxy molecules that could otherwise participate in network perfection. Secondary DLs (figures 2(c) and (d)) contain two hardener molecules that reacted with either one or two epoxy molecules, thus forming either a single or a double loop. While the single secondary loops can be a part of the network, the double secondary loops (figure 2(d)) do not participate in the network at all. Furthermore, their adverse effect on the storage modulus of the polymer networks has been demonstrated previously [58, 59]. Interestingly, the recovery stress and shape recovery ratio appear to have a stronger correlation with N than the rubbery elastic modulus does.
Figure 2. Schematics of primary and secondary loop types formed in the systems of interest in this work.
Download figure:
Standard image High-resolution imageBased on this information, we opted to examine the correlation between the cyclic topology and shape memory properties of the TSMPs in the context of those studies. Given that the TSMPs are a subset of polymer networks, it is expected to see the adverse effect of the DLs on the properties of the TSMPs. However, given that the shape memory properties are positively correlated with the total number of loops, it seems that non-defective loops (NDLs) have a positive effect on those properties. Thus, we split the total number of loops into two separate fingerprints: the number of DLs and the number of NDLs, which is the total number of loops subtracted by the number of DLs. In other words, NDLs are any loops that are not a DL. Given that we saw a positive correlation between both the shape recovery ratio as well as the recovery stress and the total number of loops, we expect the DLs to have adverse effects on the aforementioned properties, and we would also expect NDLs to have a positive effect on those properties.
DLs are identified as loops with a specific size: 6 for single primary-variant I loops (figure 2(a)), 4 for single primary-variant II (figure 2(b)), 12 for single secondary loops (figure 2(c)), and 8 for double secondary loops (figure 2(d)). It should be noted that double secondary loops count as three DLs: one secondary loop (with a size of  instead of
instead of  , since the hardener's non-reactive atom (blue particle in figure 2(d)) does not participate in the formation of the larger loop) and two primary loops (single-variant I). Then, we calculated the correlation coefficient between the mechanical and shape memory properties and the two loop subsets (table 3).
, since the hardener's non-reactive atom (blue particle in figure 2(d)) does not participate in the formation of the larger loop) and two primary loops (single-variant I). Then, we calculated the correlation coefficient between the mechanical and shape memory properties and the two loop subsets (table 3).
Table 3. Pearson correlation coefficient and its corresponding p-value among the topological fingerprints: number of non-defective loops (NDLs) as well as the number of defective loops (DLs) and the mechanical and shape memory properties of the systems with random topologies: glassy elastic modulus ( ), rubbery elastic modulus (
), rubbery elastic modulus ( ), shape recovery ratio (
), shape recovery ratio ( ) and recovery stress (
) and recovery stress ( ). Results with statistical significance are highlighted in red.
). Results with statistical significance are highlighted in red.
| Property | Number of NDLs | Number of DLs | ||
|---|---|---|---|---|

|
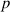
|

|
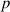
| |
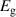
| 0.048 | 0.632 | 0.108 | 0.284 |
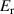
| 0.137 | 0.173 | −0.125 | 0.214 |
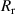
| 0.201 | 0.044 | −0.062 | 0.537 |

| 0.199 | 0.045 | −0.170 | 0.091 |
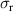
| 0.269 | 0.006 | −0.197 | 0.0491 |
Out of the ten possible correlations, five of them are statistically significant: positive correlations between the number of higher order loops and the programming stress, recovery stress, and the shape recovery ratio, and a negative correlation between the number of DLs and the programming stress and recovery stress. Thus, our assumption that the NDLs would have a positive effect on the properties of the TSMPs is proven to be valid. However, it should be mentioned that no statistically significant correlations were found between either the NDLs or DLs and the rubbery elastic modulus.
As evident from table 1, topology has a significant effect on the programming and recovery stress, while its effect on the rubbery elastic modulus is less pronounced. Both programming and recovery stress are measured at relatively higher levels of deformation (i.e. 50% compression), while the rubbery elastic modulus is measured at a lower level of deformation (i.e. overall, 3% compression/stretching). Therefore, it seems that topology impacts the properties of TSMPs at larger deformation. Furthermore, the fact that the number of DLs in our systems with random topologies is relatively small (only  ), coupled with the fact that the effect of topology is more substantial at higher deformation levels, can explain why these current fingerprints are still unable to capture the effect of topology on the rubbery elastic modulus. Moreover, in our analysis, NDLs consist of many loops of different orders. Characterizing the effects of loops of any individual order is a cumbersome task, given that not all systems are going to contain loops of every order. Thus, it is crucial to find a more generalized context to justify the observed effects of NDLs on the properties of TSMPs.
), coupled with the fact that the effect of topology is more substantial at higher deformation levels, can explain why these current fingerprints are still unable to capture the effect of topology on the rubbery elastic modulus. Moreover, in our analysis, NDLs consist of many loops of different orders. Characterizing the effects of loops of any individual order is a cumbersome task, given that not all systems are going to contain loops of every order. Thus, it is crucial to find a more generalized context to justify the observed effects of NDLs on the properties of TSMPs.
To do this, we considered a perfect network. DL are deviations from such a network. NDLs would then be associated with a more perfect network, the exact distribution of which depends on the distribution of DL. An increase in the number of NDLs would thus be expected to correlate with a more perfect network and thus correlate positively with both shape recovery ratio and recovery stress as found above.
The building blocks of a perfect network are defined as the hardener molecules that have bonded with as many distinct epoxy molecules as possible. In the case of the system of interest in this study, the number of unique epoxy molecules that can bond to a single hardener molecule is 4 (figure 3(b)). We name these specific hardener molecules TDR and introduce a new fingerprint: TDR fraction, which is the ratio of the number of TDR hardener molecules to the total number of hardener molecules present in the system. The correlation between the number of NDLs and DLs and the TDR fractions is presented in figure 4.
Figure 3. Schematic of (a) a complete, defect-free network and (b) tetra-distinctly-reacted (TDR) hardener molecules.
Download figure:
Standard image High-resolution imageFigure 4. Plot of (a) the number of non-defective loops (NDLs) vs the fraction of tetra-distinctly-reacted (TDR) hardener molecules, and (b) the number of defective loops (DLs) vs. TDR fraction. The Pearson correlation coefficient ( ) and its corresponding p-value (
) and its corresponding p-value ( ) are presented in blue on the top-left corner of each plot.
) are presented in blue on the top-left corner of each plot.
Download figure:
Standard image High-resolution imageAs evident from figure 4, the number of NDLs is positively correlated with the TDR fraction, and the number of DLs is negatively correlated with the TDR fraction. The correlations are relatively strong in both cases. Thus, it is elucidated that the number of NDLs and DLs are a measure of network perfection and how it is affected by the defects; the mechanical and shape memory properties of the system are indeed determined by the degree of network perfection and TDR fraction. To showcase this, the correlation between these properties and the TDR fraction is analyzed and those correlations with statistical significance are presented in figure 5.
Figure 5. Plot of (a) shape recovery ratio ( ) vs the fraction of tetra-distinctly-reacted (TDR) hardener molecules, (b) recovery stress (
) vs the fraction of tetra-distinctly-reacted (TDR) hardener molecules, (b) recovery stress ( ) vs. TDR fraction, and (c) rubbery elastic modulus (
) vs. TDR fraction, and (c) rubbery elastic modulus ( ) vs. TDR fraction. The Pearson correlation coefficient (
) vs. TDR fraction. The Pearson correlation coefficient ( ) and its corresponding p-value (
) and its corresponding p-value ( ) are presented in blue on the top-left corner of each plot.
) are presented in blue on the top-left corner of each plot.
Download figure:
Standard image High-resolution imageIt can be observed in figure 5 that not only the recovery stress and recovery ratio are positively correlated with the TDR fraction, but also the rubbery elastic modulus, as implied in the previous studies of the relationship between mechanical properties and cyclic topology in polymer networks. Interestingly, the correlation between the TDR fraction and the shape memory properties is stronger than that between the elastic rubbery modulus and the TDR fraction. It is also important to note that the correlation coefficient between the programming stress and the TDR fraction is  , with a p-value of
, with a p-value of  . We have strictly defined a statistically significant correlation as one with
. We have strictly defined a statistically significant correlation as one with  . However, that should not negate the strong effect of the topology on the programming stress as well.
. However, that should not negate the strong effect of the topology on the programming stress as well.
Although our study focuses on only a single pair of hardener-epoxy, the fundamental result—that the enhancement of network perfection during the synthesis of TSMPs will increase desirable mechanical/shape memory properties of those materials—applies to this whole class of materials. Techniques such as semibatch monomer addition [69] could improve the network connectivity by increasing the TDR fraction in the system and ultimately result in the availability of more building blocks for the formation of a perfect network. Furthermore, modifying the number of functional groups on the hardener molecules could increase the probability of the formation of TDR hardener molecules. Finally, while increasing the overall crosslinking density of the system would enhance the network perfection, it would also increase the risk of defect formation in the system. Thus, attempts at increasing the overall crosslinking density should be complemented with methods that would increase the TDR fraction, during their synthesis. Implementing such techniques would lead to an overall decrease of defects in the system and thus, an improvement in shape memory properties, specifically the recovery stress. Moreover, such an approach can lead to an improvement in both recovery stress and shape recovery ratio, unlike other methods such as fiber/particulate reinforcement of TSMPs mentioned earlier.
5. Conclusions
Using molecular dynamics simulations and a CG model, the effect of cyclic topology on the mechanical and shape memory properties of a TSMP, DGEBA-DDM, was investigated. Hundred structures of the TSMP of interest with random topologies and 25 structures of the same system with a fixed topology were prepared. The statistical significance of the differences between the mean of mechanical properties (glassy and rubbery elastic modulus) as well as shape memory properties (recovery stress and shape recovery ratio) between the two groups of systems were evaluated by calculating the p-values. The differences in the rubbery elastic modulus, shape recovery ratio, and recovery stress between the two sets of systems were found to be statistically significant ( ) and resulted in variations greater than 33% and 25% in programming stress and recovery stress, respectively, while the variation in rubbery elastic modulus was only about 10%. This indicates that topology and network perfection are important indicators of shape memory performance. Moreover, the effect of topology seems to be more substantial at higher levels of deformation.
) and resulted in variations greater than 33% and 25% in programming stress and recovery stress, respectively, while the variation in rubbery elastic modulus was only about 10%. This indicates that topology and network perfection are important indicators of shape memory performance. Moreover, the effect of topology seems to be more substantial at higher levels of deformation.
Inspired by the existing studies in the literature regarding the effect of loops and more specifically, DLs on the mechanical properties of the polymer networks, the correlations between the mechanical/shape memory properties of the systems and the number of loops as well as their average size and weight-averaged size, the number of DLs and the number of higher order loops were examined. Although it was found that the shape recovery ratio and recovery stress are positively correlated with the number of NDLs, and the recovery stress is negatively correlated with the number of DLs, no statistically significant correlations were found between any of the aforementioned topological fingerprints and the rubbery elastic modulus. Given that the number of higher order loops and the number of DLs can be seen as measures of how a real network is closer to or deviates from a perfect network, it was then investigated whether the properties of the systems are correlated with any other features that are representative of the network completeness. Upon examining the correlation between the properties of the systems and the fraction of the hardener molecules that are reacted to four different epoxy molecules (TDR molecules, or TDRs), it was found that the rubbery elastic modulus, shape recovery ratio, and the recovery stress are all positively correlated with said fraction, and these correlations are stronger than those found with the number of DL or the number of NDLs. TDR is thus a proper measure of network perfection and a better descriptor for mechanical/shape memory properties, setting up a goal for new design and processing methods of thermoset shape memory epoxies.
The elucidation of the correlation between the mechanical as well as shape memory properties of TSMPs and the fraction of hardener molecules that have reacted with the maximum number of distinct epoxy molecules have very interesting implications in terms of the synthesis of TSMPs with improved properties, especially shape memory properties. Techniques such as semibatch monomer addition or conceptually similar methods can lead to an improvement in both shape recovery ratio and recovery stress, as opposed to other methods such as fabric/particulate reinforcement of the TSMPs, which sometimes lead to a loss of shape memory altogether. Moreover, topology alteration can also be explored to produce TSMPs with improved shape memory properties and not necessarily a higher stiffness, enabling even more control over the synthesis of these materials for more specialized applications. Exploring the impact of the number of functional sites per hardener molecule and the role of crosslinking density on the degree of network perfection will be the focus of future studies.
Acknowledgments
This work is funded by the US National Science Foundation under Grant No. OIA-1946231 and the Louisiana Board of Regents for the Louisiana Materials Design Alliance (LAMDA). All the simulations were conducted using the high-performance computing resources provided by the Louisiana Optical Network Infrastructure (LONI). Pouria Nourian would like to thank Behnam Taghavi Fard for discussions regarding the statistical analysis of the results.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.