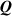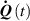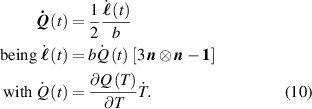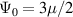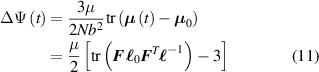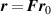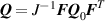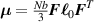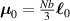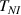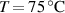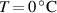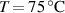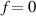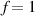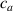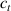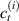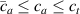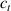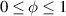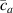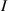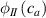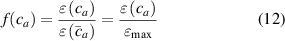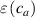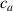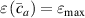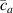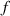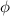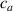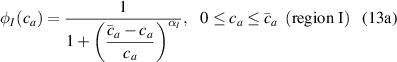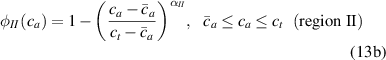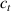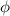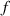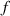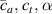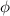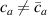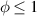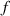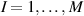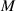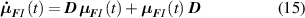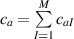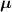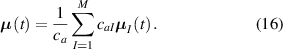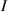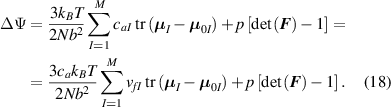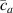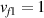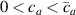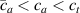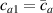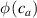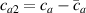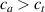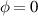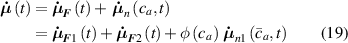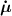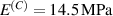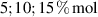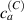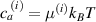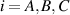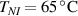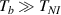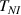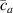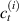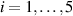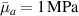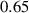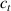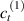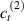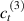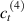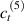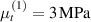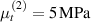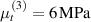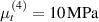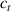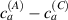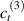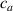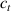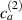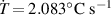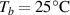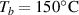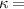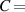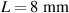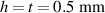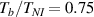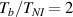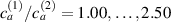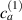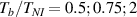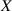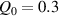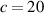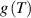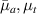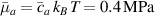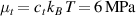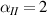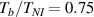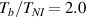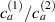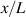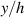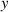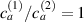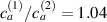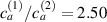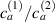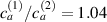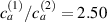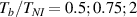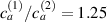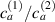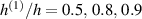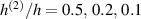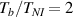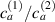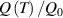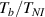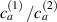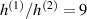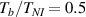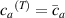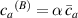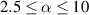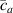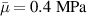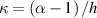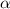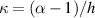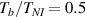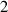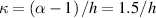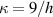Abstract
Liquid crystal elastomers (LCEs) exhibit some remarkable physical properties, such as the reversible large mechanical deformation induced by proper environmental stimuli of different nature, such as the thermal stimulus, allowing their use as soft actuators. The unique features displayed by LCE are originated from their anisotropic microstructure characterized by the preferential orientation of the mesogen molecules embedded in the polymer network. An open issue in the design of LCEs is how to control their actuation effectiveness: the amount of mesogens molecules, how they are linked to the network, the nematic order degree, the cross-link density are some controllable parameters whose spatial distribution, in general, cannot be tuned except for the last one. In this paper, we develop a theoretical micromechanical-based framework to model and explore the effect of the network cross-link density on the mechanical actuation of LCE elements. In this context, the light-induced polymerization (photopolymerization) for obtaining the elastomers' cross-linked network is of particular interest, being suitable for precisely tuning the cross-link density distribution within the material. This technology enables to obtain a molecular-scale architected LCEs, allowing the optimal design of the obtainable actuation. The possibility to properly set the cross-link density arrangement within the smart structural element (LCE microstructure design and optimization), represents an intriguing way to create molecular-scale engineered LCE elements having a material microstructure encoding the desired actuation capabilities.
1. Introduction
The increasing demand for smart and responsive devices in advanced applications, has stimulated the interest in the development of new materials that are nowadays constantly being developed for obtaining new performances and new functionalities. A common feature shown by all smart materials is their responsiveness to proper environmental inputs, which can range within a broad family of stimuli such as those of chemical, physical and mechanical nature [1–7]. Smart materials have, to some extent, several similarities to living systems: in order to optimize the function they are devoted to, they adapt their physical, chemical properties or geometrical shape in response to environmental stimuli.
Different types of smart responsive materials, characterized by different mechanical properties and response mechanisms, have been developed so far. Polymer-based materials have been often considered for the development of responsive devices because of the low cost and light weight, good processability, good corrosion resistance, high level of biocompatibility, ease of inserting particular molecules within their network [8], and because their mechanical properties are suitable to mimic biological tissues and living organisms [9, 10]. Among the most intriguing applications of responsive polymers, it is worth mentioning their use as artificial muscles, in industrial manufacturing, for health and micro-electromechanical systems, for the development of drug delivery systems, sensors, actuators, to mention a few [11–13].
Among the smart polymers, it worth recalling those capable of a reversible mechanical deformation induced by an electrical potential, such as dielectric elastomers (DEs) [14] and ionic polymer–metal composites (IPMC) [15].
Within the huge family of smart materials, a group of polymers—embedding at the same time properties of both liquid crystals and elastomers—usually referred to as liquid crystal elastomers (LCEs), is of particular interest. They are characterized by a peculiar microstructural anisotropy providing the capability of responding to external stimuli with a large mechanical reversible deformation, similar to that observed in soft living systems [16].
Differently by DEs and IPMCs, LCEs are particularly suitable in applications requiring the device, capable of reversibly responding to environmental stimuli such as heat and light, to be unthetered.
They contain mesogens units whose preferential spatial alignment provides a self-organization nature to the material; the stimuli-induced change of the orientational order of the network's chains structure can be readily exploited to induce self-deformation in the material.
Due to the anisotropic nature of the spatial arrangement of the rod-like molecules contained in LCEs in the nematic state, LCEs exhibit a liquid crystalline structure: the mesogenic units—whose organization has a certain preferential orientation—remain individually mobile and thus flow past each other.
LCEs have been recognized to be particularly useful and promising materials because of their multiple properties, such as high deformability, elastic response, good strength, durability, light weight, significant reversible actuation, etc.
The self-organization, typical of liquid crystals, and the deformation capabilities of elastomers, are the key elements allowing large and reversible dimensional change, taking place, in response to environmental stimuli, accompanied by a noticeable force density and mechanical strength [17–19].
When the material is in the nematic phase, the mesogen units are preferentially aligned in one specific direction, namely the nematic director; if mesogens are topologically connected—via their incorporation into a cross-linked polymer network—a distortion of the polymer network, usually detectable at the macroscale, takes place because of the liquid crystalline nematic-isotropic phase transition. Such a reversible anisotropic-isotropic transition can be induced by various stimuli such as non-mesogenic solvents, heating, or, in some cases, ultraviolet (UV) light. During phase transition, a monodomain nematic LCE material will contract along the director and expand in the direction perpendicular to it. It is worth recalling that during the phase change uniaxial deformations up to 300% have been observed in experiments [20]; these large deformation values make LCEs suitable to be applied in artificial muscle technologies and in the production of soft actuators, soft robots and compliant responsive devices.
The nature of the mesogen molecules, the degree of cross-link, the way the mesogen units are connected to the polymer network (side-chain or main-chain), are all factors affecting the responsiveness, whose intensity is quantified by the length change and the mechanical force shown by the material.
A customized LCE actuation can be obtained by properly arranging the nematic orientation within the material domain and/or playing with the cross-link density of the material itself, for example through the use of modern 3D printing technologies [21–25].
By considering the light-induced polymerization in elastomers synthesis (such as in the so-called additive manufacturing stereolithography (SLA) technology), the possibility to design molecular-scale architected LCE elements showing specific actuation capabilities, becomes easily feasible. A desired cross-link density distribution can be obtained by adjusting the light intensity (typically a UV light is adopted) as well as the exposure time.
Various models have been proposed for modeling LCE materials; in [26] the Helmholtz free energy and a Rayleigh dissipation energetic term have been used to model the shape change of LCEs under light stimulus. Similarly, in [27] the order tensor—originally introduced for nematic fluids [28]—has been extended for modelling LCEs. Mechanical models describing the mechanics of particular structural elements (such as plates, membranes, etc) have been also proposed [29], while phenomenological approaches, typically based on the implementation in finite element (FE) models of the experimentally determined deformation–temperature relationship, have been proposed for modeling shape morphing of LCE [30]. Despite existing approaches provide a suitable description of the nematic-isotropic transition-dependent deformation of LCEs, they usually do not take into account how the cross-link density affects the actuation capability of LCEs.
In the present paper, starting from the well-known molecular theory of rubber elasticity developed by Warner and Terentjev for LCEs [31–34], we propose a physics-based model capable of considering the effect of the chains cross-link density on the actuation capability of LCE materials through its effect on the chain distribution tensor, a quantity strictly related to the step length tensor.
In this paper, based on experimental evidences, we investigate the mechanical response of LCEs by accounting for the role played by the cross-link density distribution within the material. Another relevant parameter affecting the actuation effectiveness of LCEs, is represented by the so-called order parameter, quantifying the degree of mesogens alignment; however, as shown by several experimental observations, a simple way of tuning the actuation in LCEs (especially in the so-called main chain LCEs), is through the cross-link density of their underneath chain network [35]. Starting from a micromechanical-based theory, we investigate the role played by the cross-link density on the actuation capability of LCE elements showing a thermal-induced nematic-isotropic transition. The developed theoretical model, implemented in an FE framework, has been used to study the actuation shown by various LCE elements and to reproduce experimental data.
2. Micromechanical model of LCEs
2.1. Mechanics of a polymer network
The microstructure of an elastomeric material consists of an amorphous arrangement of entangled chains joined at discrete points to form a network; the mechanics of this class of materials can be conveniently modelled by adopting a statistical-based approach describing the spatial chain arrangement [36–40].
Because of the disordered arrangement of the chains, the physical state of the network is well described by the entropic energy rather than by the standard deformation energy, the latter being typical of solids with an ordered microstructure such as crystalline ones. According to the freely-jointed chain model, a polymer chain is usually assumed to be made of rigid (Khun's) segments (monomers) of equal length , arranged in the 3D space according to the so-called random-walk theory [39]. The maximum disorder degree of the network usually takes place in the stress-free state of the material; upon stretching, the chains are forced to elongate in the load direction and, because of the increasing order taking place during the deformation, the entropic energy decreases. The above-mentioned assumption referred to the conformation of a single chain, entails a limit for its maximum extension because of the rigidity of the constituting monomer segments; as a consequence, the maximum length of a stretched chain cannot overcome its contour length , and the corresponding maximum stretch becomes equal to . It has also been observed that the so-called end-to-end vector , identifying the relative position of the two chain's extremities, represents a suitable parameter identifying the chain's physical state [39].
By harnessing this concept, the statistical description of the chain arrangement provides a suitable tool for describing the physical state of the polymer. Let us now introduce the function describing the chain end-to-end vector distribution in the stress-free state of the material:
where represents the chain density (number of cross-linked chains per unit volume) while is the normalized distribution function, usually assumed to be the 3D Gaussian characterized by mean value and standard deviation . According to the above definition, the integration of the function over the chain space (spanning all the possible chain lengths and orientations) must provide the number of chains per unit volume, , where the integral takes into account only the 'mechanically active' chains, i.e. those fully connected to the network that are able to contribute to the load carrying mechanism induced by an applied deformation. It is worth mentioning that the chain concentration is strictly related to the shear modulus of the material through the well-known expression: , where and are the Boltzmann constant and the absolute temperature, respectively [39].
A simplifying assumption, often made in rubber elasticity, is the so-called affine deformation hypothesis: at the microscopic scale, the polymer chains deform as the material does at the continuum level. Hereafter, we are going to adopt such as assumption in the development of our theory. As a consequence, the energy density of the polymer is provided by the following integral, , where the term represents the deformation energy per single chain, usually expressed as a function of the end-to-end vector distance ; according to the Gaussian statistics, the deformation energy per single chain is expressed as , while, according to the more realistic Langevin assumption, the chain energy is given by , being the inverse of the Langevin function (with ) which provides unlimited values when the chain length tends to its contour length, i.e. when ) [36].
At a generic time , the configuration of the network is fully known through the corresponding distribution function which, starting from the initial chain configuration quantified by the distribution function , evolves because of the applied mechanical deformation and/or in a LCE, due to the self deformation induced by the change of the nematic order [32, 41].
Figure 1 sketches how the distribution function or equivalently its dimensionless counterpart changes because of the change of the mesogens preferential orientation induced by cooling down or heating up the material.
Figure 1. Scheme of the distribution function at a generic material point of a liquid crystal elastomer at a temperature above (a) and below (b) the transition temperature . The distribution function , whose values are schematically represented by the intensity of the background green colour, is isotropic in the first state (random orientation of the mesogens) and anisotropic in the other (nematic state with mesogens preferentially aligned along the -direction).
Download figure:
Standard image High-resolution imageThe current elastic energy density of a deformed network, evaluated with respect to its initial (stress-free) state, is expressed as:
where is the deformation gradient tensor, is the second order identity tensor, and is the displacement field, while is the hydrostatic pressure playing the role of a multiplier constraint required to fulfill the incompressibility condition (hereafter always assumed) expressed by .
By introducing the distribution tensor , quantifying the number of chains with a given end-to-end distance and orientation in the 3D chain space [42], the previous energy density can be rewritten as follows:
where is the distribution tensor in the initial stress-free state, while refers to the current deformed configuration.
In a standard polymer whose chain network has not any preferential direction, the chain orientations are distributed isotropically in the stress-free state and, by adopting the Gaussian statistics for the chain's energy, the distribution tensor assumes the simple expression .
It is worth mentioning that the distribution tensor can be thought as an extension of the so-called structure's tensor [43]. By harnessing the expression of the power density of the material:
the Cauchy stress tensor at the time can be easily identified to be expressed as [42]:
In equation (4), is the symmetric part of the velocity gradient tensor , namely =, being , while the symbol: indicates the double contraction operator. In the case both damage (i.e. chain loss) and self-healing (i.e. chain gain) mechanisms do not take place, remains constant all along the whole mechanical deformation process. The evolution in time of the distribution function rate , required to evaluate (4), can be determined from the chain density conservation relationship , stating that the time derivative of the chain concentration is zero (the number of chains in the volume is constant in time), i.e. [42].
2.2. Mechanics of a liquid crystal elastomer
Various models, based on the description of molecular force interaction, aimed at describing the behavior of liquid crystals have been proposed in the literature [41, 44].
The universally-recognized physics-based theory of Warner, Terentjev et al has had the merit to extend the classical rubber elasticity to nematic elastomers by accounting for the molecular anisotropy induced by the coupling of the mesogens reorientation to the elastomer network [31, 33, 34]. The physical state of a nematic elastomer is usually described by the director field, whose change, occurring even if the elasticity of the network partially hinders the mesogen reorientation, triggers the appearance of a spontaneous deformation.
Hereafter, by harnessing the statistical description of the network arrangement through the use of the above-mentioned distribution tensor, the mechanics of LCEs is developed based on the classical molecular rubber elasticity [31–34].
Differently from classical polymers having a random isotropic distribution of the chains orientation in the stress-free state (in such a case the distribution tensor is characterized by a spherical symmetry and has three identical eigenvalues, ), polymers polymerized in the nematic state have the network's chains preferentially aligned with the nematic order of the mesogens. This implies that the distribution function is non-isotropic, and a general expression for , to be used in place of equation (1), is the following [32]:
being the step-length tensor of the chain distribution; it quantifies the anisotropy of the polymer chains at the time of cross-linking and is expressed through the effective initial step lengths and , measured parallel and perpendicular to the director , respectively (figure 2(a)). In the nematic state it happens to be , while in a perfectly isotropic state the step length tensor reduces to and the averaged square of the end-to-end distance becomes [33, 39].
Figure 2. (a) Preferential orientation of mesogen molecules about the director , in the figure assumed to be nearly aligned with the axis. (b) Nematic-isotropic transition in LCE induced by a temperature increase crossing the transition temperature (from left to right).
Download figure:
Standard image High-resolution imageAt the time of cross-linking we assume the state of the polymer is stress-free; it can be easily shown that, in this case, the distribution tensor is related to the step-length tensor by the following simple relation: [45].
In its principal directions' frame of reference the distribution tensor can be expressed as , being a second order rotation tensor and the versor of the principal direction, while () are the three eigenvalues of . When the principal directions are superposed to the frame of reference's axes, assumes the simple diagonal form .
It is worth mentioning that, when the principal directions of the distribution tensor are aligned with the coordinate axes, the eigenvalues () are related to the standard deviation of the end-to-end distance components measured along the axes, namely , i.e. when the mesogen units are preferentially aligned along the 3rd Cartesian axis: and
In the frame of reference's principal directions, the distribution tensor can be graphically represented by an ellipsoid whose axes are the principal directions. A mechanical deformation, as well as the order imposed by the nematic mesogens, have the effect of inducing the elongation of such an ellipsoid in a preferential direction (i.e. that of the stretch or that of the nematic director) and, because of the material incompressibility constraint, a contraction in the perpendicular directions arises.
The so-called order parameter at the time , —expressing the dispersion of the angle formed by the mesogen units with respect the their average direction identified by the director (figure 2(a))—is defined as , and the corresponding distribution tensor becomes . In particular, when the order parameter (whose possible values range in the interval ) is equal to , the nematic order of the mesogens is perfect, and they are ideally aligned along a well defined direction, while when they are randomly oriented such as in a standard isotropic arrangement of polymeric chains. When , the mesogens are characterized by an intermediate degree of alignment, where the degree of the orientation dispersion increases as . Finally, the value of the nematic order parameter indicates that all the rod molecules lay on the plane.
When the case of a temperature-driven order change is concerned, i.e. , the distribution tensor describing the chain distribution in space becomes itself a function of the temperature. The above-defined distribution tensor can be related to the so-called nematic order tensor (also called the de Gennes order tensor [32, 46]), through the relation:
As mentioned in the introduction, the nematic order of LCEs is strictly related to the temperature of the material: for the order parameter is , being the value of the nematic order at the time of cross-linking assumed to occur in the nematic state, while if then , i.e. the chain configuration tends to become isotropic.
The nematic order-temperature dependence is influenced by the physical-chemical properties of the mesogens and by the cross-link density, and can be determined from experimental tests [47]. Typically, LCEs are responsive to a temperature change because the initial order of the mesogen units is progressively destroied when the material is heated above the so-called nematic-isotropic transition temperature . This process is fully reversible and provides a noticeable actuation force [32]. In the present study, we assume the nematic order parameter to be related to the temperature change by the relationship: , with , being a material-dependent parameter. The function quantifies the way the transition of the order parameter, from (nematic state) to the isotropic one , occurs as the temperature increases beyond the transition temperature (figure 2(b)).
The precise tuning of such a transition function is important if the nematic-isotropic transient response has to be determined, while it is not so relevant if only the final self-deformation arising because of the temperature change is sought.
Dealing with LCE materials, in general it must be considered that the distribution tensor evolves and changes in time because of: (a) the applied mechanical deformation, and (b) the spontaneous deformation induced by the nematic-isotropic transition triggered by an external stimulus. The evolution of the distribution tensor can thus be expressed through its time rate splitted into the following contributions:
where the term indicates the stress distribution tensor rate induced by the mechanical deformation, while is the rate associated with the change of the nematic order. Explicitly, the above rates can be evaluated as follows [7, 45]:
where the notations , indicate that the quantity is evaluated at constant nematic order and at constant deformation, respectively, while is the spin tensor [27]. The distribution tensor at the current time instant can be evaluated by integrating the above-defined rates over the time interval as .
By assuming that the order parameter is related to the environmental temperature while the principal directions of do not change, the rate of the nematic order tensor is expressed by
By considering a generic deformation, quantified by the deformation gradient taking place while the material undergoes a nematic order change due to a temperature variation, the energy density increment (evaluated with respect to the initial stress-free state for which ), is [45]:
where the affine deformation hypothesis, mathematically expressed by , has been adopted; equation (11) provides an extension of the deformation energy of the classical rubber elasticity theory [39]. Since the order tensor in the spatial configuration is related to that in the reference domain through [32] , the distribution tensor in the current (deformed) configuration is related to the initial step length tensor as follows: , being .
3. Effect of the degree of polymerization on the mechanics of LCEs
The possibility to realize programmable actuation by means of LCE elements, whose responsiveness is tuned by controlling their degree of cross-linking, has become nowadays easily feasible through a proper setting of the photo-cross-linking parameters (such as the UV light intensity and exposure time) and has been recently demonstrated [35]. As a matter of fact, on one side tuning the cross-link density of the LCE matrix allows changing the phase transition temperature and on the other side affects the deformation capability and the stiffness of the material. The role played by the cross-link density on the self deformation capabilities of LCEs, represents an issue which depends on a variety of factors such as the type of mesogens, the value of the order parameter reached during the polymerization, the nature of cross-links, the polymer chemistry, etc [35, 48, 49].
The formation of cross-links between the polymer chains prevents them from flowing past each other, making the material a solid rather than a liquid melt; however, a sufficiently low value of the polymerization degree still allows the thermal motion of the polymer chains but does not hinder the formation of the liquid crystal order [50], and permits a certain self-deformation capability. On the other hand, for a given nematic-transition temperature and an initial order parameter, a too high cross-link density may reduce the thermal-induced motion of the polymer chains and thus could hinder the deformation capacity of LCE material.
The understanding of the cross-link-related mechanical response of LCEs, allows designing the underneath network—leading to a so-called micro-scale architected material—aimed at obtaining a desired functionality in terms of mechanical response (degree and pattern of deformation) obtainable from the device being developed.
As a matter of fact, it has been experimentally shown that the deformation capabilities of LCE, as well as other relevant physical properties, are affected by the degree of cross-linking (chain density) of the network. LCE samples with different cross-link densities have been investigated in [48]; LCE samples have been pre-stretched in the isotropic state () and then—passing through the transition temperature—cooled-down to to get an elongation of the sample, followed by re-heating to to induce contraction [48]. Despite the well-known nematic-isotropic reversibility, hysteresis of the actuation heating-cooling loops was observed; irrespectively of the applied tension, the maximum actuation strain decreased as the cross-link density increased, leading to some issues in designing LCE actuators.
[48] Depending on the LCE's outcome we are interested in—deformation capability or force actuation— according to [48] two different aspects arise: (a) the actuation can be increased by decreasing the cross-link density (i.e. lower cross-link densities enable higher deformation capabilities); (b) correspondingly, the actuation force reduces because decreasing the cross-link density entails a the reduction of the stiffness of the material.
It has been demonstrated that an increase of the amount of an acrylate-based cross-linker in the solution, provides an increase of the nematic-isotropic transition temperature, as well as a reduction of the strain induced in the material when thermally-stimulated [51].
The effect of using two types of cross-linking agents at different concentrations, with the purpose of optimizing the output strain and the transition temperature, has been studied and exploited to tune the physical properties of the LCE matrix [52]. LCE films made of a combination of a nematogen units (C411U8) with a cross-linker (TAC-4) at various percentages have shown an increase of the elastic modulus of about 4 times by tripling the amount of TAC-4 cross-linker; moreover, increasing the TAC-4 cross-linker led to a decrease of the transition temperature and of the strain of the sample in thermoelastic experiments [52].
On the other hand, by increasing the cross-linker concentration in LCE samples, a greater deformation has been obtained [53]; according to the Authors, this happens because a high value of the cross-linker entails a higher value of the order parameter due to the formation of stronger bonds between the polymer chains with a consequent better alignment of the mesogens [53].
A better deformation capability of main-chain (i.e. LCEs having the mesogen units bonded within the chains) with respect to side-chain LCEs has been observed as reported in [54].
In the present study, we are interested in modeling the actuation response of LCE elements by varying the cross-link density of the network; in particular, the reduction of the actuation with increasing the cross-link density will be considered. To this end, let us consider the actuation of a LCE element (quantified in terms of the deformation or the rotation shown by an element undergoing a temperature change crossing the transition temperature ) as the measure of the self-deformation effectiveness; in the following, we indicate with such a deformation degree, where indicates no actuation and indicates the maximum possible actuation.
By changing the cross-link density of the elastomer from zero up to the maximum value (for which the actuation does not take place because of the too strong constraint exerted by the highly cross-linked chains of the polymer), the degree of actuation under the same stimulus changes because of the effect of the cross-link density. We assume that the maximum actuation takes place when the elastomer has the optimal cross-link density . For cross-link densities lower than the actuation increases as increases (region in figure 3 [53]), while if the actuation decreases (region II in figure 3). In order to compare the actuations provided by LCEs with different cross-link densities, a reference cross-link density is adopted for sake of expressing the generic cross-link density in dimensionless form. In figure 3 such a behaviour is illustrated for different LCEs (), each one characterized by its own optimal () and maximum () cross-link densities. It can be observed that for (region II) the actuation effectiveness, measured through the LCE chain mobility (see below), decreases until the maximum cross-link density suitable for the actuation to occur, , is attained. The decreasing of the chain mobility, quantified through the parameter , is a material-dependent parameter, so the various curves indicate different cross-link density dependences of the LCEs actuation effectiveness. For sake of representing the curves related to different materials in the same graph, in figure 3 the same value of the optimal chain concentration has been assumed for all the cases. It is worth mentioning that no experimental data have been found to quantitatively describe the cross-link actuation dependence occurring in region . However, the increase of actuation due to the increase of cross-link density taking place in such a region is reasonably related to the corresponding variation of the polymer chains mobility [50].
Figure 3. Effect of the cross-link density on the actuation effectiveness of LCEs. Data from [35, 52] have been considered and elaborated to be graphically represented in the same graph. The best fitting of the experimental data through the function is also reported.
Download figure:
Standard image High-resolution imageFrom the above discussion, it appears that creating a specific distribution patterns within a LCE element—such as the cross-link density, the mesogen orientation and the corresponding gradient, the actuation temperature, etc.—offers the possibility to extend the design space of LCE elements, allowing to tune and adjust the actuation capabilities arising when the nematic to isotropic transition takes place [21, 55].
This possibility is nowadays offered by modern additive manufacturing (AM) technologies, enabling to get a precise microscale structure arrangement of the material; to this end, it is worth recalling the so-called Direct Ink Writing [55, 56] or the photopolymerization (SLA) technologies, among others [57, 58].
4. Micromechanics of a partially cross-linked network
Because of the increasing constraint degree induced by increasing the cross-link density existing between the network chains, it is reasonable to assume that the effectiveness of the mesogens in driving the polymer's network from the anisotropic to the isotropic state could be limited. In other words, we assume that a fraction of the elastomer containing the mesogen units is effective in inducing the self-deformation, while the remaining is not; from a micromechanical perspective, this can be seen as the case of a polymer characterized by a multiple network structure, i.e. a cross-linked network displaying the phase transition of the mesogen units, and another one not showing such a transition.
According to figure 3, the effectiveness of the mesogen units, quantified in terms of the actuation strain, can be expressed as:
where is the deformation, relevant to the problem in turn, taking place for the actual cross-link density , while is the corresponding maximum deformation obtained for the optimal cross-link density of the elastomer. The scalar function can be considered as a macroscopic measure of the mesogens effectiveness in inducing the deformation of the network. On the other hand, from a microscopic viewpoint, according to the experimental observations it is reasonable to express the mesogen self-deformation effectiveness to be related to the cross-link density through the expressions:
where we recall that is the degree of cross-link at which the actuation vanishes, and (or ) is a material's parameter required for tuning the model (figure 3). In other words, starting from (correspondig to a purely liquid monomer for which no actuation takes place because the chains are not cross-linked and thus can flow freely past each other) up to , the actuation increases because the interconnections between the chains enable the mesogen units to orient the chains (equation (13a )). This aspect has been justified in [50], and is expected to be confirmed by experimental data. On the other hand, it is worth mentioning that all the examples illustrated in section 5 refer only to region II where experimental data are available (see figure 3).
By further increasing beyond the optimal density up to (corresponding to no actuation), the self-deformation shown by LCE decreases because of the progressive reduction of the chains mobility induced by the increased constraint degree existing in the network (equation (13b ). By assuming to be proportional to , we can use the macroscopic deformation effectiveness, quantified by the scalar , to estimate the parameters appearing in the function . This assumption comes from the chains alignment driven by the mesogens: the degree of order-disorder of the network is reasonably proportional to the amount of mesogen units linked to the polymer chains, i.e. to the cross link density or, in other words, to the mesogen molecules joined to the network. When the optimal chain concentration exists, the network displays the maximum self deformation, being all the mesogens effective in modifying the chains orientation arrangement. When the actual chain density exists in the network, only the fraction of the mesogens is effective in the deformation, whose intensity is now times lower than that of the optimal cross link condition (see equation (12)).
These aspects can be easily accounted for through the concept of multiple networks; in order to generalize this hypothesis, let us assume that the polymer is made of a series of non-interacting entangled networks, each one associated with its own chain concentration .
Under these hypothesis, in the stress-free state the network statistics is provided by distribution functions and by the corresponding distribution tensors:
whose evolution due to deformation is expressed as:
while the total chain concentration is given by and the overall distribution tensor , representing the entire multiple network, is expressed as:
By assuming that the polymer has a mass density independent of the chain's cross-link density, i.e. the number of chains per unit volume does not depent on the number of cross-links per unit volume and all the networks are chemically identical, the chain concentration can be used to express the volume fraction of the network in the multiple network, i.e.
Since we assume that the networks are non interacting with each other, the elastic energy stored in the material can be additively decomposed as:
The new expression of the Cauchy stress tensor follows directly from equation (5), where the distribution tensor for multiple networks has to be used.
In the case of LCEs in which the cross-link density effect has to be accounted for, we can adopt the concept of multiple network for quantifying the nematic-isotropic driven deformation of the network.
According to equation (13a ), the mesogens effectiveness in the actuation is maximum when the cross-link density is ; correspondingly, in such a case the network can be reasonably assumed to be made of a single network containing the mesogen molecules, i.e. . On the other hand, when (region I) or (region II) the effectiveness of the obtainable actuation is lower, and the network can be assumed to be made of a double network (only from the mesogen orientation-induced deformation point of view): by focusing on region II, the effective network can be assumed to have concentration whose effectiveness has to be weighted by the parameter , while the second one, with concentration , is assumed to have no self-deformation effectiveness on the material. The splitting of the network in two sub-networks has been introduced only for quantifying the deformation effectiveness related to the actual cross-link density, while it is not required—despite formally correct—to account for the mechanical deformation. Of course, when the self-deformation effectiveness of the LCE vanishes, i.e. .
According to the above assumption, the sub-network 1 can be assumed to produce the maximum possible actuation, while the network 2 has no effect on the deformation due to the nematic-isotropic transition hindered by either the excessively low (region I) or by the too high (region II) cross-link density, respectively.
Thus, in order to account for the cross-link density effect on the self-deformation capabilities of LCEs, equation (8) has to be updated as follows (figure 4):
Figure 4. Scheme of the double network assumption adopted for modelling the effect of the cross-link density on the self-deformation capability of LCEs. The rate of the distribution tensor depends on the mechanical deformation () and on the nematic-isotropic transition due to the first network only ().
Download figure:
Standard image High-resolution imagewhere the contribution of the second network to the nematic-isotropic-driven deformation, has been neglected being unable to produce any actuation, i.e. .
The above-described micromechanical approach, properly implemented into an FE framework (see [45] for more details), is hereafter employed to simulate the actuation corresponding to the self-deformation shown by LCE elements under a temperature change.
5. Numerical simulations and discussion
5.1. Simulation of an experimental test
In this section, we compare the results provided by the present micromechanical model with an experimental case reported in [52]. The uniaxial contraction of an element made of a single LCE layer synthesized by using different cross-linker contents, observed during a thermoelastic experiment by heating the material above the , is studied. We analyze three different LCE strips whose matrix has been prepared by combining nematogen units (C411U8) with a cross-linker (TAC-4) at three different percentages, leading to different values of the material's Young's modulus; according to [52], it has been assumed to be , and corresponding to content of T-4 cross-linker, respectively.
From the above mentioned Young's modulus values, the corresponding chain concentrations , and have been evaluated through the standard rubber elasticity relationship (see section 2.1) with , figure 5. In the numerical model, we simulate a LCE monodomain strip, with initial order parameter , having the mesogen units aligned with the element's longitudinal axis in order to provide a contraction of the sample when heated above the transition temperature ; the parameter governing the phase transition has been assumed to be . Since we consider the maximum actuation achievable after the nematic-isotropic transition has occurred (i.e. at ), the exact value and its dependence on the cross-linker content, as emphasized in [52], is neglected.
Figure 5. Actuation strain (contraction) vs chain concentration for a fixed optimal cross-link density () and different maximum chain concentrations (, ). Comparison with the experimental data from [52] is reported.
Download figure:
Standard image High-resolution imageWe assume the material, whose optimal cross-link density corresponding to the optimal shear modulus is assumed, to be in region II (see figure 3), while the parameter in equation (13b) is assumed to be . Since the value of the maximum cross-link density hindering the self-deformation is not known, for each of the three investigated materials we consider five different values of such a cross-link density, namely , , , and (see figure 5); the above listed quantities have been determined through the above-mentioned cross-link density-shear modulus relationship, by assuming the following values of the shear modulus , , , and . The results of the numerical simulations are reported in figure 5 where the experimental data are also shown; it appears that, if the value of decreases, the contraction deformation reduces in the considered range of cross-link densities, . It can be observed that the maximum cross-link density is the one that best fits the experimental results.
It is important to emphasize that when is greater than the mesogen effectiveness disappears and no deformation takes place in the material; this is the case of the material characterized by the smallest , namely , whose response is represented by empty triangles in figure 5: the bottom right portion of the curve goes to zero because the cross-link density in such a region overcomes the maximum cross-link density of the material.
5.2. Bi-layer LCE beam with different chain concentrations
In this section we simulate numerically the self-deformation shown by a bi-layer plate made of two superposed LC layers with identical thickness, each one with its own cross-link concentration, in the lower layer and in the upper layer.
By applying a temperature rate , the temperature of the bottom surface of the lower layer is made to increased from the room temperature up to .
The temperature evolution within the element is determined by solving the heat conduction problem by adopting the thermal conductivity and the specific heat to be 0.8 W mK−1 and 1050 J Kg−1 K−1, respectively, while the sizes of the bi-layer cantilever beam, restrained along the edge marked with ① in figure 6, are , (figure 6).
Figure 6. Deformed shapes of the LCE bi-layer element (middle line) at two different temperatures (, a; , b) of the bottom surface. Different bottom to top layer cross-link density ratios are assumed. Two cross-link densities of the lower layer corresponding to a soft (A) and very soft material (B) are considered.
Download figure:
Standard image High-resolution imageIn order to exclude further deformations not related to the phase change of the LCE, the thermal expansion of the material is assumed to be negligible in the temperature range considered.
Unless differently stated, for all the LCE parts we assume the nematic-isotropic transition temperature to occur at , while the parameters describing the transition from the initial nematic (the mesogens are assumed to be initially aligned with the direction) to the final isotropic state are assumed to be and (see the expression for the function , section 2.2). The chain concentrations of the double network, expressed through the corresponding shear moduli , are as follows: , while the exponent in equation (13a ) has been adopted to be .
In figure 6, the deformed pattern of the middle line of the bi-layer element is shown for two dimensionless temperatures of the bottom surface, namely (figure 6(a)) and (figure 6(b)) by varying the relative cross-link density, , of the composing layers. In this figure, as well as in the following ones, geometrical quantities are plotted by using the dimensionless coordinates and , where and represent the current coordinates evaluated in the deformed configurationt (see the adopted frame of reference in figure 6(b)). The greater the difference of the cross-link density of the two layers, the larger the bending actuation shown by the element; when the element shows a simple contraction without any bending actuation. In figure 7, the deformed shapes of the LCE element and the corresponding values of the relative order parameter field, , for (left column) and (right column) are displayed.
Figure 7. Deformed shapes of the bi-layer LCE element and corresponding dimensionless order parameter fields, obtained by adopting different cross-link density ratios (bottom to top value ratio) of the two constituting layers, for three different temperatures of the bottom surface. Specifically, the results refer to (a)–(c) and (d)–(f) for the three considered temperatures, respectively, namely . The undeformed configurations are reported in grey colour.
Download figure:
Standard image High-resolution image5.3. Bi-layer LCE beam with different layers' thickness
In this section, we consider the actuation shown by a bi-layer LCE element (the same boundary conditions assumed in the previous example are considered) whose constituent layers have different thicknesses and different chain concentrations.
The bottom to top cross-link density ratio is assumed to be equal to and , while the layer's relative thickness ratio is assumed to be equal to (figure 8). It can be appreciated that the bending actuation increases when the layers' thickness tends to be identical, while a large thickness ratio is not effective in producing actuation.
Figure 8. Deformed shapes of the middle line of the LCE bi-layer element for two different bottom to top chain concentration ratios (1.25, (a); 2.5, (b)) and various layer thickness ratios, () when the temperature of the bottom surface of the element equal to .
Download figure:
Standard image High-resolution imageIn the limit case of a very large value of the ratio, the deformed shape tends to that of a single layer, as previously shown in figure 6 (simple contraction).
As was observed in the previous parametric example, due to the small size of the element, for a fixed relative thickness ratio a higher chain concentration ratio enables a larger bending actuation (see figures 8(a) and (b)).
Finally, in figure 9 the deformed shapes of the element for two thickness ratios are displayed; the colour quantifies the relative order parameter corresponding to the dimensionless temperature assigned at the bottom of the elemen. It is worth noticing that, due to the small size of the element, the temperature field is almost constant within the domain so the order parameter is uniform throughout the beam.
Figure 9. Deformed shapes of the LCE bi-layer element with different layer thickness ratios (equal to 2 and 4) and different cross-link density ratios ; the corresponding dimensionless order parameter field is displayed. The two cases with (left column, (a)–(c)) and (right column, (d)–(f)) are shown for three different relative temperatures of the bottom edge of the element, , . The undeformed configurations are reported in grey colour.
Download figure:
Standard image High-resolution image5.4. LCE beam with graded cross-link density
The actuation of a cantilever beam having a graded distribution of the cross-link density, is considered in this section. The main parameters involved in the simulations are the same used in the previous examples; however, the beam is now assumed to have a fixed cross-link density at its top edge, , while the cross-link density varies linearly through the thickness of the element (-direction), up to the maximum value reached at the bottom edge where it assumes the value (), being the cross-link density corresponding to the shear modulus . The cross-link density gradient parameter is thus defined as . The mesogen units are assumed to be initially aligned with the -direction, while the initial order parameter has been assumed to be equal to (figure 10).
Figure 10. Functionally graded beam with chain concentration gradient used for tuning the shape morphing. The dimensionless chain concentration varies linearly from at the top edge up to the maximum value at the bottom edge (a). Deformed pattern of the middle line of the LCE for different values of the parameter at (b). Deformed shapes of the graded LCE element with different chain concentration gradients , for two different temperatures of the bottom edge of the element, , . The undeformed configurations are reported in grey colour (c).
Download figure:
Standard image High-resolution imageGreater chain density gradients produce more pronounced self-deformation actuation, with an increase of the actuation amplitude up to four times by amplifying the cross-link density gradient parameter from up to .
It can be appreciated that creating a graded cross-link density distribution across the thickness—nowadays easily obtainable by modern 3D printing technologies—can be used to encode the element's morphing response into the material's microstructure.
6. Conclusions
Liquid crystalline elastomers are intriguing polymers for making elements showing a large reversible self-deformation. Their morphing capabilities, originated by the nematic to isotropic transition taking place in their molecular network, occurs when they are properly triggered by environmental stimuli. In LCEs, the amount of the deformation arising when the nematic-isotropic transition takes place (as occurs in temperature responsive LCEs when the transition temperature is overcome) strongly depends on the kind of the mesogen molecules, the way they are connected to the polymer network (side-chain or main-chain), and on the degree of cross-link.
In particular, we have considered the influence of the cross-link density, a property that can be nowadays easily controlled by using AM technologies, on the actuation capabilities of LCEs. In the liquid state, corresponding to a purely monomer melt, LCE units are reciprocally disconnected and no self-deformation capability is possible. By increasing the chain density, the actuation effectiveness increases until an optimal cross-link density, for which the actuation is maximum, is reached. By further increasing the cross-link density, the actuation decreases until a maximum cross-link density, at which no self-deformation is possible because of the excessive constraints existing among the network chains.
A theoretical micromechanical-based approach for the simulation of LCE elements by accounting for the role played by the cross-link density, has been proposed and implemented into a FE computational framework. It has been shown that tuning the cross-link density, allows obtaining a molecular-scale architected material, capable of providing tunable deformation functionalities according to the application of interest. This way of encoding the responsiveness by operating at the molecular level, is of particular interest in small scale applications; this is made possible, for instance, by the advanced photopolymerization technique, widely used in AM production of polymers; thanks to its simplicity and high resolution, the dimensional scale limitations of other production approaches can be easily overcome.
Acknowledgments
The authors gratefully acknowledge the support from European Union's Horizon 2020 research and innovation program (H2020-WIDESPREAD-2018, SIRAMM, GA 857124), under Grant Agreement No 857124.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflict of interest
There are no conflicts to declare.





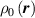
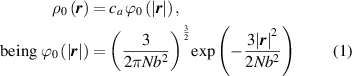
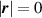
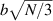
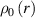
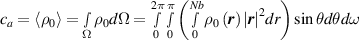
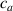
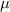
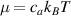
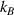
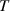
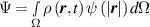
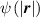
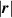
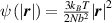
![$\psi \left( {\left| {\boldsymbol{{r}}} \right|} \right) = N{k_B}T\left( {\beta {\mathcal L^{ - 1}}\left( \beta \right) + \ln \frac{{{\mathcal L^{ - 1}}\left( \beta \right)}}{{\sinh \left[ {{\mathcal L^{ - 1}}\left( \beta \right)} \right]}}} \right)$](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn22.gif)
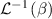
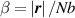
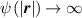

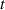
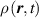
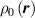
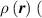
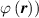

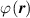
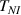
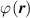


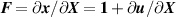

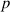
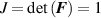
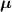
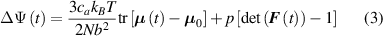
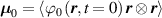
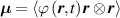
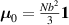
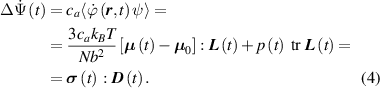

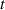
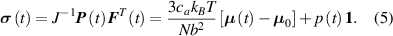
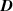
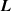
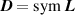
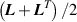
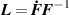
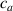
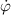
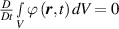
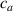


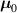
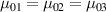
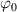
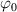
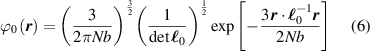
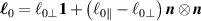
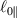

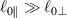
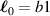
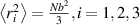


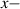
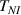
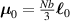
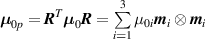
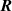
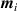
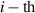
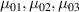
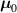
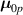
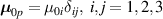
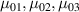
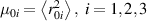
![${\mu _{01}} = \left\langle {r_{01}^2\left( t \right)} \right\rangle = \frac{{N{b^2}}}{3}\left[ {1 - Q\left( t \right)} \right],{\text{ }}{\mu _{02}} = \left\langle {r_{02}^2\left( t \right)} \right\rangle = \frac{{N{b^2}}}{3}$](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn83.gif)
![$\left[ {1 - Q\left( t \right)} \right]$](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn84.gif)
![$ {\mu _{03}} = \langle r_{03}^2\left( t \right)\rangle = \frac{{N{b^2}}}{3}\left[ {1 + 2Q\left( t \right)} \right].$](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn85.gif)

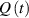
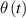

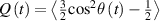
![${\boldsymbol{{\mu }}}\left( t \right) = \frac{{Nb}}{3}{\boldsymbol{{\ell }}} \left( t \right) = \frac{{Nb}}{3}b\left[ {\left( {1 - Q\left( t \right)} \right){\mathbf{1}} + 3Q\left( t \right){ }{\boldsymbol{{n}}} \otimes {\boldsymbol{{n}}}} \right]$](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn91.gif)
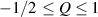
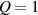
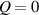
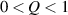

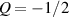
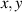
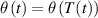
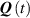
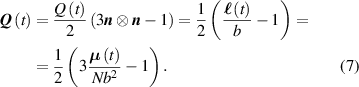
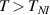

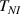

![$g\left( T \right) = {\left[ {1 + \exp \frac{{T - {T_{NI}}}}{c}} \right]^{ - 1}}$](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn108.gif)

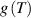
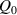

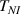
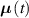
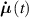
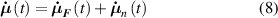
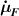
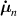
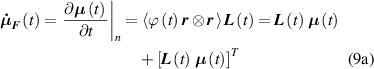

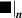
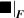

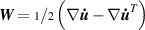
![${\boldsymbol{{\mu }}}\left( t \right) = {\boldsymbol{{\mu }}}\left( 0 \right) + \mathop \smallint \limits_0^t \left[ {{{{\boldsymbol{{\dot \mu }}}}_{\boldsymbol{{F}}}}\left( \tau \right) + {{{\boldsymbol{{\dot \mu }}}}_n}\left( \tau \right)} \right]d\tau $](https://content.cld.iop.org/journals/0964-1726/31/1/015012/revision2/smsac34bfieqn124.gif)