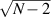Abstract
Molecular nanomagnets (MNMs), molecules containing interacting spins, have been a playground for quantum mechanics. They are characterized by many accessible low-energy levels that can be exploited to store and process quantum information. This naturally opens the possibility of using them as qudits, thus enlarging the tools of quantum logic with respect to qubit-based architectures. These additional degrees of freedom recently prompted the proposal for encoding qubits with embedded quantum error correction (QEC) in single molecules. QEC is the holy grail of quantum computing and this qudit approach could circumvent the large overhead of physical qubits typical of standard multi-qubit codes. Another important strength of the molecular approach is the extremely high degree of control achieved in preparing complex supramolecular structures where individual qudits are linked preserving their individual properties and coherence. This is particularly relevant for building quantum simulators, controllable systems able to mimic the dynamics of other quantum objects. The use of MNMs for quantum information processing is a rapidly evolving field which still requires to be fully experimentally explored. The key issues to be settled are related to scaling up the number of qudits/qubits and their individual addressing. Several promising possibilities are being intensively explored, ranging from the use of single-molecule transistors or superconducting devices to optical readout techniques. Moreover, new tools from chemistry could be also at hand, like the chiral-induced spin selectivity. In this paper, we will review the present status of this interdisciplinary research field, discuss the open challenges and envisioned solution paths which could finally unleash the very large potential of molecular spins for quantum technologies.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr Piers Coleman
1. Introduction
The huge amount of information appearing on our digital devices (such as weather forecasts or prediction of traffic flow) is often the result of very complex calculations, performed in large super-computing centers. Capabilities of these machines are currently pushed to their limit. By performing many calculations in parallel on the same processor, quantum computers (QCs) could solve nowadays intractable problems, with a potentially disruptive impact on society and economy. Among these are optimization problems, the management of huge amounts of data and their protection from unwanted access, and the development of plans for secure and super-dense communication [1]. By simulating other nano-systems, QCs would also allow one to design novel materials and medicines or to understand microscopical processes.
After more than 20 years of intense research, the actual realization of QCs still faces significant challenges. Even the most advanced platforms, based for instance on superconducting transmon qubits or trapped ions [2–4], are still noisy, intermediate scale quantum devices (NISQs). Thanks to recent hardware improvements and calibrations, transmon-based architectures have reached scales beyond 100 qubits with non-trivial circuit depths, enabling the execution of larger problems exploiting error mitigation techniques [5, 6]. However, they are not presently able to actually implement quantum error correction (QEC) and fault-tolerant computation, which represent crucial milestones to achieve a real quantum advantage. The roadblock is represented by the enormous overhead of physical resources implied by standard multi-qubit codes, in which a single logical unit must be encoded into a large collection of physical qubits, whose control easily becomes unattainable. This motivates the investigation of different kinds of architectures that have not yet reached this degree of development but that could offer a different perspective, and competitive advantages, towards the ambitious goal of a general purpose QC. In this respect, molecular spin systems and in particular molecular nanomagnets (MNMs) offer peculiar features which make them particularly promising [7, 8].
Indeed, it was immediately clear since their discovery that many MNMs are multi-level quantum systems, thus potentially offering many well characterized and coherent degrees of freedom which could be exploited for quantum information processing (QIP) [9]. A second crucial difference from established technologies is the possibility of engineering the energy spectrum and eigenvectors of MNMs, thanks to joint efforts of theoretical physicists and synthetic chemists [8, 10–13]. This molecular design can provide many low-energy levels potentially protected from decoherence. On the one hand, these can be exploited to design QIP schemes in presence of permanent qubit–qubit interactions [14–16] and to develop algorithms going beyond the binary logic, where standard two-level elementary unit of quantum logic (qubits) are replaced by d > 2 quantum systems called qudits. The latter approach could significantly simplify algorithms and thus lead to important advantages in the current NISQ era. Moreover, d > 2 quantum systems can host error-protected logical units, where QEC is embedded within single objects. The possibility of building a quantum processor with elementary physical units, the molecules, that encode error resilient logical qubits represents a potential advantage as compared to multi-qubit encodings [8]. Indeed, it reduces the number of resources needed to carry out any particular computation and it considerably simplifies the practical implementation of QEC, by eliminating nonlocal operations.
Below, we overview the crucial steps already accomplished in the synthesis and control of molecular spin qubits and qudits, together with different proposals for encoding and processing information in an efficient way, i.e. in a scalable fashion potentially accommodating switchable couplings and/or protection from decoherence. Quantum simulation experiments can already be realized [17] on properly designed diluted molecular crystals, thus demonstrating the feasibility of the molecular approach for quantum computing.
Nonetheless, unleashing the full power of quantum technologies requires to reach the single-molecule level both in the implementation of qubit gates and especially in the readout of the the molecular spin states. This represents nowadays the most important challenge for the field and could take benefit from the easiness to transfer individual MNMs onto a solid state device, as already demonstrated [18, 19]. Strategies to get through this bottleneck are discussed in the second part of the manuscript. Some of them are based on adapting to the realm of single molecules methods that are successfully employed with other solid state qubits, such as spins in semiconductors and superconducting circuits. These include the application of molecular electronics techniques to convert spin states into current states, the realization of optically active spin states, mimicking those found in NV centers in diamond, and the design of circuit quantum electrodynamics devices able to concentrate a photon magnetic field in nanoscopic regions. A final perspective alternative benefits from the exploitation of the novel chiral-induced spin selectivity (CISS) effect [20].
These experimental issues must be interfaced with theoretical efforts mainly devoted to the development of a blueprint for a molecular spin quantum processor where quantum information can be initialized, processed and readout [21] thus achieving DiVincenzo criteria [22].
The manuscript is organized as follows: we first (section 2) overview the most important features of paradigmatic MNMs which make them a playground for quantum mechanics, highlighting their behavior as multi-level systems. After providing in section 3 a quick introduction to QIP basic ingredients, we review in section 4 theoretical proposals and experimental implementations of molecular qubits and quantum gates. In particular, we introduce the change of perspective offered by the qudit approach, which fully exploits the richness of the molecular spectrum. This lays the foundations for designing QEC algorithms embedded in single molecular units (section 5) and increase the potential of MNMs as quantum simulators (section 6). Then, sections 7 and 8 address the most important challenges, represented by single-molecule control and readout and scaling up the architecture. Finally, we briefly summarize in section 9 the current state-of-play to build a molecular spin quantum processor, discussing both the achieved milestones and the perspective strategies to accomplish the missing steps.
2. Molecular nanomagnets, a playground for quantum mechanics
Spins represent archetypical quantum systems, not only for their purely non-classical nature, but also for being the simplest objects where quantum mechanics can be framed and exemplified. They are inherently described by a finite vector space and a finite number of independent observables. As a result, they can embody and display many fundamental phenomena in the conceptually cleanest and easiest framework. This is especially the case when two or more spins interact with one another according to some Hamiltonian, thus forming extended quantum objects with a larger vector space, a larger number of observables and a variety of possible physical properties.
Among finite spin clusters, MNMs lead the way [7, 23, 24]. These are molecules containing a small number of 3d or 4f metal ions (between one and a few dozens), surrounded by organic ligands. Ligands act as a spacer, screening the magnetic core from the environment, thus preserving to a large extent the few-spins character of its quantum states.
MNMs can exist in a multiplicity of macroscopic forms. The most common one is a crystal, with the molecules self-assembling into a regular three-dimensional lattice, thus forming a bulk material of identical and nearly non-interacting magnetic units. While organic ligands effectively suppress exchange-type couplings between adjacent molecules, the magnetostatic coupling between their dipole moments persists as a small residual interaction. Its effects are marginal down to sub-Kelvin regimes, unless the total spin of the core is large ('giant' spin, see below). The resulting large dipolar couplings can yield collective effects like dipolar-ordered structures [25–28] or dipolar-assisted quantum tunneling [29–31]. However, for quantum-information applications dipolar interactions can be harmful even for a small total spin of the core, as they delocalize the information encoded in a single core into the bulk on a relatively short timescale. In some cases, it is possible to synthesize a non-magnetic analogue of the MNM, where magnetic metal ions in the core are replaced by metal ions without unpaired electrons. A crystalline solid solution is then grown, with few magnetic molecules diluted into a lattice of nonmagnetic molecules, thus decreasing the average dipolar interaction strength.
Besides being assembled into crystals, MNMs can be deposited onto surfaces, exploiting either physisorption or chemisorption [32, 33]. For the latter, the organic ligands are chemically engineered to produce an effective anchor bridge, or the surface is functionalized with a group binding with the molecule. Thanks to a large degree of screening of the core, it is often possible to preserve its magnetic properties after the grafting [34, 35]. Grafted MNMs can be individually addressed by using tips, thus opening interesting perspectives for quantum-information applications [36, 37].
MNMs are also often produced in the form of frozen solutions. This approach requires dissolving the nanomagnets in a suitable solvent and then cooling the mixture to a temperature below its freezing point. The MNMs are thus immobilized within the frozen matrix. Similarly to crystalline solid solutions, the frozen solution preserves the individual properties of the molecules while diluting them in a solid environment. However, achieving perfectly identical orientations for all MNMs can be challenging, due to the inherent stochastic nature of thermal motion. The use of external magnetic fields during the freezing process can aid the alignment, especially if the dipole moment of the core is large.
The ultimate goal for molecular magnetism is to control and read out the spins of single molecules. Inspired by results obtained on defect spins is semiconductors [38, 39], some seminal experimental results have already been achieved [40–44]. For instance, a nuclear spin qubit transistor has been realized, consisting of a single TbPc2 molecule directly forming a bridge between source and drain metallic nanoelectrodes opened by electromigration [40, 43, 44]. Although most molecules are insulating, organic ligands can serve as an auxiliary resource. For instance, the Pc ligands in the TbPc2 MNM (bis-(phthalocyaninnato) Terbium(III)) carry delocalized π-electrons that were used in [42] as for readout of a single molecule.
The magnetic cores of MNMs differ little across the various possible environments, and their magnetic Hamiltonian and resulting spin dynamics are often essentially unchanged. Yet, on long timescales the dynamics will depend to some extent on the specific environment, either because of coherent evolution driven by intermolecular dipolar couplings, or because incoherent processes depend on the type of heat bath the environment supplies. For example, magnetic relaxation times depend on the density of states of environmental phonons and on their coupling to the spins, and both can change in passing from the bulk of a molecular crystal to a host surface used for grafting (see below).
The chief advantage of MNMs with respect to other nanoscale magnetic systems, such as conventional magnetic nanoparticles, solid-state defect spins (e.g. NV-centers in diamond or P donor electron spins in Si) [38, 45, 46], artificially assembled magnetic nanostructures (e.g. spins in quantum dots [47, 48] or atoms deposited on surfaces [49, 50]), is the precise bottom-up assembly of the cluster, which enables to chemically engineer the spin Hamiltonian and the resulting properties. This spin Hamiltonian includes anisotropic single-spin terms and two-spin couplings of various types. Parameters defining this Hamiltonian display a typical hierarchy which depends solely on the type of magnetic ions involved (e.g. 3d vs 4f). For 3d ions isotropic superexchange is usually largely dominating over anisotropic, anti-symmetric, or quadrupolar couplings, whereas for 4f ions the single-ion anisotropy (crystal electric field) is the largest term, and superexchange two-ion terms are often negligible due to the small radius of the 4f shell. The dominant two-ion coupling is then the classical dipolar interaction. It should be stressed that most quantum-information protocols using MNMs are designed to fit the hierarchy of Hamiltonian parameters, and do not require specific or fine-tuned values. For a specific MNM, these parameters can be estimated using first-principles calculations [51–61], and precisely determined from fit to experiments. The latter include macroscopic measurements (e.g. heat capacity, magnetometry) as well as spectroscopic ones (inelastic neutron scattering, EPR) [62–72]. Parameters for the incoherent dynamics can be extracted from AC-susceptibility measurements, magnetometry, NMR and µSR [73–77].
These aspects were apparent when the first polynuclear MNMs were synthesized in the early 1990s [79]. In these clusters, at low temperatures and energies, the spins of 3d-block ions are exchange-locked to one another into a single 'giant' total-spin S, sitting in an effective anisotropic potential. Its nearly uniaxial form, with the resulting double-well arrangement of the 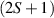 states, makes the cluster a bistable molecular magnet (SMM, single-molecule magnet), which might be used to encode a nanoscale classical bit of information [63, 72, 74, 79]. This startling perspective was a major motivation for research in the field. Nonetheless, SMMs turned out to be possibly even more interesting for the fundamental questions they allow one to address. Being the molecular counterpart of a single-domain ferromagnet, they are unique in displaying spectacular quantum effects in their hysteresis cycles and associated relaxation dynamics.
states, makes the cluster a bistable molecular magnet (SMM, single-molecule magnet), which might be used to encode a nanoscale classical bit of information [63, 72, 74, 79]. This startling perspective was a major motivation for research in the field. Nonetheless, SMMs turned out to be possibly even more interesting for the fundamental questions they allow one to address. Being the molecular counterpart of a single-domain ferromagnet, they are unique in displaying spectacular quantum effects in their hysteresis cycles and associated relaxation dynamics.
In conventional bulk ferromagnets and in magnetic nanoparticles the dynamics is entirely classical, being driven by the movement of domain walls, or by rotation of the magnetization in a single domain through classical barrier-climbing. Conversely, in SMMs quantum barrier-tunneling activated by non-axial anisotropy terms fastens the classical dynamics at resonance conditions, and it can be clearly singled out, tuned and studied through a number of macroscopic measurements [80–83]. In particular, steps in the hysteresis loop are detected when the external magnetic field B sets a resonance between states on opposite sides of the barrier. These multiple steps represent a clear manifestation of the multi-level quantum behavior of this class of materials and are shown in figure 1 for Mn12 [78], which can be considered together with Fe8 [63] as the fore-father of SMMs. The control of tunneling probabilities by means of transverse magnetic fields has given the opportunity to explore quantum interference between different tunneling paths [81], to stabilize quantum superpositions of spin up and spin down states [84] and to study the thermodynamic limits for the energy cost of erasing a magnetic memory [85].
Figure 1. Quantum tunneling of the magnetization in a Landau–Zener experiment on [Mn12]2− single-molecule magnet (a) [78], characterized by a S = 10 ground multiplet split by the easy-axis anisotropy into 21 levels arranged into a typical double-well potential. (b) Hysteresis loop, displaying steps at resonance conditions between states on opposite sides of the barrier (c), due to quantum tunneling induced by non-axial anisotropy terms in the spin Hamiltonian. At zero field (B = 0) relaxation occurs within the ground doublet 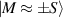 . Zeeman interaction then lowers/raises energy levels on the two sides of the barrier, thus subsequently blocking and re-activating tunneling between different pairs of states, as schematically shown in (c) for the lowest energy levels. (b) Reprinted (figure) with permission from [78], Copyright (2005) by the American Physical Society.
. Zeeman interaction then lowers/raises energy levels on the two sides of the barrier, thus subsequently blocking and re-activating tunneling between different pairs of states, as schematically shown in (c) for the lowest energy levels. (b) Reprinted (figure) with permission from [78], Copyright (2005) by the American Physical Society.
Download figure:
Standard image High-resolution imageIn the course of time several variants of SMMs have been produced, and single-lanthanide-ion molecules have now turned out to largely outperform polynuclear d-ion clusters in terms of blocking temperatures [74, 86, 87]. That this should be the case was not obvious a priori. While the large spin–orbit coupling of lanthanides may produce high uniaxial anisotropy barriers in appropriate ligands environments, it can also increase the strength of off-axis anisotropy terms, potentially yielding large tunneling efficiency and large magnetoelastic coupling.
Besides SMMs, over the years numerous different types of MNMs have been synthesized, differing in the pattern of spin values and exchange constants, and which can be model systems to investigate a variety of issues in magnetism. For example, there are molecular counterparts of antiferro- or ferri-magnets [64, 65, 88–91] frustrated magnets [92–95], toroidal magnets [96–99] or also ferroelectric materials [100]. In general, just as it happens for SMMs, the nanometric size enhances quantum effects, which are often overwhelming and can produce a phenomenology not present in the bulk. For instance, in antiferromagnetic rings the pair of classical two-sublattice Néel arrangements are strongly destabilized by quantum-fluctuations even at zero temperature, to the point that not even a tunneling picture similar of that of SMMs usually holds [90, 101, 102]. If the geometry of antiferromagnetic exchange constants leads to magnetic frustration [103, 104], distinct classically equivalent spin-configurations can coalesce quantum-mechanically into a single nondegenerate ground state, with the spins resonating among the different classical states [105]. In toroidal MNMs, quantum tunneling between classically degenerate configurations can occur [106]. In antiferro-type MNMs anticrossings induced by a varying applied field can emerge at the macroscopic level in striking oscillations of the magnetic torque, due to mixing between different total-spin states [89, 107, 108].
Quantum effects shape the dynamics of MNMs over many timescales. The shortest relevant ones are usually characterized by high degree of coherence and are associated with spectral gaps of the cluster Hamiltonian, roughly of the order of meVs. The associated two-times spin correlations portray the intricate dynamics of the quantum fluctuations which usually characterizes this regime and which can be captured by inelastic-neutron-scattering techniques [109, 110].
For longer timescales, the quantum spin dynamics is perturbed and eventually overwhelmed by the effects of coupling to environmental degrees of freedom. Vibrations play a major role, as they yield loss of coherence, but also relaxation of the state populations to thermal equilibrium. MNMs have provided model realizations for some fundamental phenomena associated with the coupling of spin and mechanical degrees of freedom, such as the quantum Einstein–De Haas effect [111], and contributed to expand the understanding of spin-phonon interactions by means of effective models and even ab initio simulations. The coupling to spins occurs through the modulation of the different spin-Hamiltonian parameters (anisotropy, exchange, or even hyperfine interactions). Various different phonon types (acoustical or optical) and processes (direct, Orbach, Raman) can play a role, their relative importance depending on the specific MNM, on the structure of the phonons, and on the temperature range [7, 60, 61, 74, 77, 112–116]. The rate of direct and Orbach processes strongly depends on the structure of the molecular energy spectrum. In particular, direct transitions between two states are associated with resonant phonon absorption/emission and can be suppressed if the number of electrons is odd and the two states form a Kramers doublet [117]. In this case, these processes would violate time-reversal invariance. Orbach processes are exponentially suppressed at low-enough temperatures, whereas Raman processes are only suppressed as a power-law. With respect to the simple spin-1/2 case, where relaxation is mono-exponential with a single timescale (T1), in MNMs the many-levels spectrum usually yields multi-exponential relaxation over several characteristic times. Their relative importance depends on external parameters (temperature, magnetic field) and on the observable whose relaxation is monitored [75]. The longest timescales have been observed for the easy-axis magnetization in SMMs (hours or days at low-enough temperatures), whereas for other cases (e.g. intra-barrier relaxation in SMMs, or for generic MNMs) relaxation times are not macroscopic.
At low temperatures phonon processes become less important, and only environmental nuclear spins (typically those of surrounding H ions) persist as a source of pure decoherence, without producing relaxation [118–120]. The timescale over which such decoherence occurs is that of the nuclear spin dynamics (associated with dipolar interactions). Careful design of the cluster environment can increase the cluster decoherence time up to several hundreds of microseconds [121], as discussed in section 4.1.
The spin dynamics of MNMs can be controlled from outside through magnetic EPR pulses or pulse-sequences, which couple to the total magnetization of the cluster. The size of the relevant matrix-elements determine the speed of the control, which is in the range of ten nanoseconds for the simplest operations, like flipping a total-spin 1/2. In spite of the many-level spectrum, it is usually possible to address specific levels with high fidelity [122–126], save for cases in which leakage occurs between levels that are not well-resolved as compared to the pulse spectral-width, which is unusual considering the attainable pulse durations and can be strongly limited by pulse-shaping techniques [127]. With respect to a single spin-1/2, the richer Hamiltonian of MNMs also opens the possibility to use electric fields as a manipulation tool, for which shorter manipulation times can be envisaged. In addition, in a scenario where the fields are created by tips, electric fields are preferable as strong electric fields can be created in small regions, and can be rapidly modulated by applying voltage pulses. The main difficulty lies in small size of the coupling to an electric field, as by parity conservation the underlying atomic states are only coupled to electric-field derivatives, and not to the field itself. However, spin-electric coupling can effectively arise through the electric tunability of some of the spin-Hamiltonian parameters [50, 128, 129], as described in section 4.1. Still not much explored is the possibility to optically control MNMs, in particular for initialization and readout of the state (see section 8), in the line of what is done for solid-state defects. This possibility has been demonstrated in MNMs with a single spin center [130].
Besides being interesting as individual quantum objects, MNMs can be linked together through supramolecular chemistry [131], forming dimers, trimers [12, 132, 133] or very complex polymers clusters [134] which further enrich the range of possible physical effects and applications. The inter-cluster magnetic coupling is usually weak, thus the internal structure of single-molecule states is barely affected when collective supramolecular states are formed. The coupling can generate inter-cluster entanglement [110, 135], and can be exploited to design schemes for the implementation of two-qubit gates in quantum-information applications [16], as discussed in section 4.3.
In short, MNMs and their supramolecular complexes provide a large variety of possible spin Hamiltonians and associated quantum effects, which are of interest for both fundamental reasons and possible applications. In particular, their tunable multi-level structure, and the relatively good resilience of their spin-dynamics to decoherence, with foreseeable margins of improvements, has made them promising (multi-level) units to encode and process quantum information.
3. Quantum information in a nutshell
Hereafter, we introduce some basic concepts of QIP, while we refer to the appendices for more technical details that are recalled throughout the paper.
In perfect analogy with classical computation, the great majority of QIP schemes is based on encoding information in elementary binary units called quantum bits or qubits. In principle, these can be realized on any quantum system providing at least two easily accessible levels, which can be prepared by the experimenter in a generic state of the form

This represents the superposition of the two orthogonal states 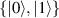 forming the computational basis.
forming the computational basis.
Logic operations (gates) on a register of N qubits constituting the quantum hardware are represented by unitary operators. Arbitrary N-qubit unitaries can be implemented, provided the capability to realize generic single-qubit gates and at least one two-qubit entangling operation between each qubit pair. The algebra of a two-level qubit is described by the Pauli matrices σα
, 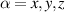 , or by the corresponding spin operators
, or by the corresponding spin operators 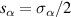 . This means that any unitary on the qubit can be expressed in terms of Pauli matrices, and in particular in terms of rotations of arbitrary angles about two non parallel axes of the Bloch sphere [1]. These single-qubit unitaries are given by
. This means that any unitary on the qubit can be expressed in terms of Pauli matrices, and in particular in terms of rotations of arbitrary angles about two non parallel axes of the Bloch sphere [1]. These single-qubit unitaries are given by
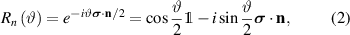
where ϑ is the rotation angle, 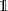 is the identity matrix and n is the rotation axis versor. Decomposition of arbitrary single-qubit gates based on a discrete set of operations also exist, but they are usually complex. Hence, it is preferable to rely on continuous rotations, given the easiness to control the duration of electromagnetic pulses used to set the rotation angle in molecular spins.
is the identity matrix and n is the rotation axis versor. Decomposition of arbitrary single-qubit gates based on a discrete set of operations also exist, but they are usually complex. Hence, it is preferable to rely on continuous rotations, given the easiness to control the duration of electromagnetic pulses used to set the rotation angle in molecular spins.
To complete a universal gate-set on a multi-qubit register, two-qubit entangling gates are also needed. Important two-qubit gates are the controlled operations, in which a given rotation is applied to the target qubit only if the control qubit is in 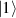 . Among these, the most common are the controlled-NOT (cX or cNOT) and the controlled-ϕ (cϕ), corresponding to a conditioned flip (σx
) or phase [
. Among these, the most common are the controlled-NOT (cX or cNOT) and the controlled-ϕ (cϕ), corresponding to a conditioned flip (σx
) or phase [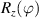 ] gate on the target qubit. Other important two-qubit gates can be obtained from the time evolution of a two-spin Hamiltonian of the form
] gate on the target qubit. Other important two-qubit gates can be obtained from the time evolution of a two-spin Hamiltonian of the form 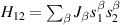 . This leads for instance to the the so-called iSWAP
. This leads for instance to the the so-called iSWAP gate (see appendix
gate (see appendix 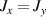 and
and 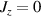 , which choosing the proper time evolution (or, equivalently, setting
, which choosing the proper time evolution (or, equivalently, setting 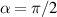 ) reduces to the maximally entangling
) reduces to the maximally entangling 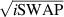 gate.
gate.
Although the combination of single-qubit rotations and one kind of entangling gate is universal, we also mention the three-qubit Toffoli or controlled-controlled-NOT (ccNOT) gate. This yields a flip of the third qubit if and only if both of the other two are in state 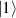 .
.
To achieve a reliable computation, quantum gates must be implemented in a controlled and precise way, before decoherence has significantly corrupted the quantum state. As a figure of merit of the qubit coherence, one could consider the ratio η between the coherence time T2 and the time required for an elementary operation, such as a 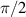 pulse
pulse  –10 ns [136]. It roughly represents the number of gates which can be reliably implemented on the quantum hardware. Below we discuss the values of η which can be reached by the different kinds of molecular spin qubits. Single-qubit rotations are usually achieved by exploiting (resonant) magnetic pulses addressing specific transitions, while two qubit gates can be implemented along different lines, relying either on specific control pulses or on free Hamiltonian evolution. The most important proposals and experimental realizations of these tasks are described in section 4 at the intra-molecular level and in section 7 with inter-molecular gates mediated by superconducting resonators. The accuracy in the implementation of quantum gates is quantified in numerical simulations by computing the state fidelity (as defined in appendix
–10 ns [136]. It roughly represents the number of gates which can be reliably implemented on the quantum hardware. Below we discuss the values of η which can be reached by the different kinds of molecular spin qubits. Single-qubit rotations are usually achieved by exploiting (resonant) magnetic pulses addressing specific transitions, while two qubit gates can be implemented along different lines, relying either on specific control pulses or on free Hamiltonian evolution. The most important proposals and experimental realizations of these tasks are described in section 4 at the intra-molecular level and in section 7 with inter-molecular gates mediated by superconducting resonators. The accuracy in the implementation of quantum gates is quantified in numerical simulations by computing the state fidelity (as defined in appendix
The actual implementation of a QC also requires initialization of the register in a known state and readout of the final output of the computation [22]. These issues, related to single-molecules addressing, are discussed in the second part of the paper, together with scalability of the device to a sizable number of qubits (sections 7 and 8). In the next section, we first focus on building one- and multi-qubit structures, manipulate and protect them from errors and in particular from decoherence. Indeed, by assuming to work at low enough temperatures to achieve thermal initialization, this is the only relevant error for MNMs, and will be the subject of most of the strategies described below to improve the performance of the molecular hardware. Conversely, we will neglect relaxation effects, usually occurring on a much longer timescale [137–139], as already discussed in section 2.
4. Molecular qubits/qudits: gates, decoherence, multi-qubit structures
Thanks to their quantum behavior and properties, MNMs are valid and competitive candidates to realize spin-based qubits for Quantum Technologies. The first envisaged molecular qubits were clusters comprising a finite number of exchanged-coupled paramagnetic ions [9, 140, 141]. Indeed, it was immediately clear that the unparalleled degree of chemical control mentioned in section 2 could be combined with the possibility of designing the multi-level energy spectrum for specific applications. In particular, the additional states can be exploited in the design of gates [14, 142], for decoherence-protected encodings [143] or for implementing qudit-based algorithms [9]. These characteristics, combined with the possibility of coherently driving their spin dynamics [118, 123, 144], allowed MNMs to enter the QC game.
Below, we first overview the most important classes of molecular spin qubits, along with their strong and weak points, related to coherence and manipulation tools. We then move to describe permanently-coupled multi-qubit structures, experimentally demonstrated two-qubit gates and proposed schemes to effectively turn on and off their mutual interaction. Finally, we broaden our point of view to the real extra-gear of MNMs, i.e. the capability to efficiently support a multi-level (qudit) logic.
4.1. Building qubits with MNMs
The Cr7Ni ring [145], with its 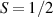 ground state, has been one of the most studied molecular qubits (see table 1(i)). The seven Cr3+ (
ground state, has been one of the most studied molecular qubits (see table 1(i)). The seven Cr3+ (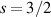 ) and the Ni2+ (s = 1) ions are at the vertices of a regular octagon and their spins are antiferromagnetically coupled, yielding a
) and the Ni2+ (s = 1) ions are at the vertices of a regular octagon and their spins are antiferromagnetically coupled, yielding a  ground state with very little mixing with higher S states (at low magnetic fields). The ground doublet of Cr7Ni was thus shown to be suitable for the encoding of the
ground state with very little mixing with higher S states (at low magnetic fields). The ground doublet of Cr7Ni was thus shown to be suitable for the encoding of the 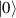 and
and 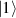 logical states of a qubit [122]. In addition, the energy gap to the first excited multiplet (
logical states of a qubit [122]. In addition, the energy gap to the first excited multiplet (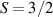 ) is around 13 K, ensuring a small leakage to non-computational levels during single-qubit rotations. In addition, the properties of antiferromagnetic rings can be tailored for the realization of different QC architectures, from changing the ligands in order to facilitate their linking into multi-qubit structures [67] (see section 4.2), to tuning their anisotropy [57] and hence matrix elements of specific transitions. Moreover, Cr7Ni molecules can be successfully deposited on surfaces preserving their magnetic properties [35, 146–150]. This is crucial for the realization of molecular quantum processors, since single molecules organized on a surface in a chip-like architecture would provide notable advantages in the individual addressing of qubits and eventual wiring into other nanodevices.
) is around 13 K, ensuring a small leakage to non-computational levels during single-qubit rotations. In addition, the properties of antiferromagnetic rings can be tailored for the realization of different QC architectures, from changing the ligands in order to facilitate their linking into multi-qubit structures [67] (see section 4.2), to tuning their anisotropy [57] and hence matrix elements of specific transitions. Moreover, Cr7Ni molecules can be successfully deposited on surfaces preserving their magnetic properties [35, 146–150]. This is crucial for the realization of molecular quantum processors, since single molecules organized on a surface in a chip-like architecture would provide notable advantages in the individual addressing of qubits and eventual wiring into other nanodevices.
Table 1. Most important classes of molecular spin qubits and related features/achievements. (first row, second column) Reprinted with permission from [121]. Copyright (2015) American Chemical Society. Further permission related to the material excerpted should be directed to the ACS. (first row, fourth column) Reproduced with permission from [126]. CC BY-NC 3.0. (second row, first column) Reprinted (figure) with permission from [161], Copyright (2019) by the American Physical Society. (second row, third column) Reproduced from [163]. CC BY 4.0. (second row, fourth column) Reproduced from [165]. CC BY 4.0. (third row, first column) Reproduced from [16]. CC BY 4.0. (third row, fourth column) Reproduced with permission from [166]. CC BY-NC 3.0. (fourth row, first column) Reproduced from [155]. CC BY 4.0. (fourth row, third column) Reproduced with permission from [167]. CC BY-NC 3.0. (fifth row, first column) Reprinted (figure) with permission from [133], Copyright (2008) by the American Physical Society. (fifth row, third column) Reproduced from [160]. CC BY 4.0. (sixth row, first column) Reproduced from [156]. CC BY 4.0. (sixth row, second column) Reproduced with permission from [169]. CC BY-NC 3.0. (sixth row, third column) Reproduced with permission from [133]. CC BY-NC 3.0. (sixth row, fourth column) Reprinted (adapted) with permission from [125]. Copyright (2018) American Chemical Society.
| (i) Multi-spin clusters | (ii) Monomers (3d) | (iii) Ln qubits | (iv) Nuclear spins | |
|---|---|---|---|---|
| Very long T2 |

|

| ||
| [121, 158, 159] | [126] | |||
| Electric control |
|

|

| |
| [160–162] | [129, 163] | [43, 164, 165] | ||
| Auxiliary states |

|
| ||
| [14, 16, 122, 156] | [166] | |||
| Engineering |
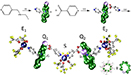
|
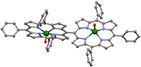
|
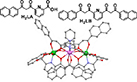
| |
| [12, 155] | [132, 167] | [133] | ||
| Noise-protected encoding |

|
| ||
| [128, 157, 160] | [163, 168] | |||
| Embedded quantum-error correction |

|
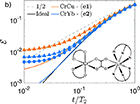
|
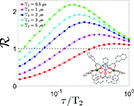
|

|
| [156] | [169] | [133] | [125, 126, 170] |
Antiferromagnetic rings also satisfy another crucial prerequisite for the deployment of MNMs in QC. Indeed, coherence times T2 of the order of a few µs were already measured in 2007 on Cr7Ni [118]. To further improve T2 when measured in crystals, Cr7Ni qubits can be diluted in a matrix of non-magnetic analogues (i.e. isostructural molecules where the magnetic ions are replaced by equivalent diamagnetic ones, like Ga7Zn for Cr7Ni) [151], thus reducing harmful inter-molecular interactions. In this regime, decoherence at low temperature mostly originates from the hyperfine interaction of each qubit with the surrounding nuclear spins [119]. A further improvement of the Cr7Ni coherence time (up to T2
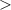 15 µs) was obtained by chemical engineering of the nuclear-spin environment of the magnetic ions [152, 153]. By combining these synthetic techniques significant values of
15 µs) was obtained by chemical engineering of the nuclear-spin environment of the magnetic ions [152, 153]. By combining these synthetic techniques significant values of 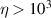 (i.e. the number of elementary operations which can be implemented within the coherence time) can be reached. All in all, Cr7Ni and its fellow rings are still important building blocks for molecule-based QIP [154, 155]. A final comment on multi-spin molecules is in order. By a proper design of the molecular spin Hamiltonian and of the hierarchy and structure of the spin–spin couplings, it is possible to identify a regime in which decoherence does not increase with the number of levels, as discussed in sections 4.4 and 5 below [156, 157].
(i.e. the number of elementary operations which can be implemented within the coherence time) can be reached. All in all, Cr7Ni and its fellow rings are still important building blocks for molecule-based QIP [154, 155]. A final comment on multi-spin molecules is in order. By a proper design of the molecular spin Hamiltonian and of the hierarchy and structure of the spin–spin couplings, it is possible to identify a regime in which decoherence does not increase with the number of levels, as discussed in sections 4.4 and 5 below [156, 157].
A decisive step forward to increase T2 was achieved in [159] by shifting the attention from multi-spin clusters to much simpler complexes containing a single metal ion (see table 1(ii)). This strategy allowed reaching T2 values as large as 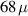 s at 7 K in a (PPh4)2[Cu(mnt)2] molecule, at the price of renouncing to the additional degrees of freedom typical of multi-spin clusters. Moreover, by shifting non-computational excited states from
s at 7 K in a (PPh4)2[Cu(mnt)2] molecule, at the price of renouncing to the additional degrees of freedom typical of multi-spin clusters. Moreover, by shifting non-computational excited states from 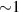 meV (as in Cr7Ni) to the eV range, phonon-induced relaxation is strongly suppressed, resulting in coherence times as large as 0.6 µs at room temperature [159]. Record T2 values, outperforming those observed in solid-state qubits, were observed in a V-based system, ((d20-Ph4P)2[V(C8S8)3]), reaching ~ 1 ms at 10 K after a proper chemical tuning of the nuclear spin content in both ligands and solvents [121]. By combining this T2 with the capabilities of the highest-power available EPR spectrometer [136],
meV (as in Cr7Ni) to the eV range, phonon-induced relaxation is strongly suppressed, resulting in coherence times as large as 0.6 µs at room temperature [159]. Record T2 values, outperforming those observed in solid-state qubits, were observed in a V-based system, ((d20-Ph4P)2[V(C8S8)3]), reaching ~ 1 ms at 10 K after a proper chemical tuning of the nuclear spin content in both ligands and solvents [121]. By combining this T2 with the capabilities of the highest-power available EPR spectrometer [136], 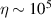 can be reached.
can be reached.
Performances at room temperature, however, are strongly limited in this system by the rapid decrease of the spin- lattice relaxation time T1, on increasing temperature. Replacing the V-ion with a 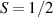 vanadyl moiety (VO2+) has been decisive in this sense, with VOPc (Pc = phthalocyanine) displaying very long T1 = 2.4 s, thanks to its stable coordination geometry [139]. In addition, pulsed EPR spectroscopy experiments on VOPc revealed quantum coherence up to room temperature with an almost constant
vanadyl moiety (VO2+) has been decisive in this sense, with VOPc (Pc = phthalocyanine) displaying very long T1 = 2.4 s, thanks to its stable coordination geometry [139]. In addition, pulsed EPR spectroscopy experiments on VOPc revealed quantum coherence up to room temperature with an almost constant 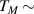 1 µs [158]. These results were also accompanied by the observation of Rabi oscillations, demonstrating the possibility to coherently manipulate the VOPc molecular spin qubit up to room temperature. This and all the results that followed [171, 172], have established VO-based complexes as the new paradigm for temperature-resistant molecular spin qubits. Among these, VO(TPP) (TPP = tetraphenylporphyrinate) is one of the most promising molecular qubit [173]. It can be arranged in dimeric species where the two electronic spins are distinguishable and exchange-coupled to implement quantum gates [167]. The incoherent spin dynamics of VO-based systems was also extensively studied from both an experimental and theoretical point of view [113, 114, 174–176], shedding new light on the role of phonons and on spin-phonon couplings in molecular spin relaxation and decoherence. Last but not least, square- pyramidal vanadyl complexes can also be deposited on surfaces, obtaining monolayers of ordered arrays of intact molecules, retaining their paramagnetic nature [177] and can also be embedded into superconducting coplanar resonators [18, 178, 179], paving the way for the integration of molecular spin ensembles into microwave quantum architectures.
1 µs [158]. These results were also accompanied by the observation of Rabi oscillations, demonstrating the possibility to coherently manipulate the VOPc molecular spin qubit up to room temperature. This and all the results that followed [171, 172], have established VO-based complexes as the new paradigm for temperature-resistant molecular spin qubits. Among these, VO(TPP) (TPP = tetraphenylporphyrinate) is one of the most promising molecular qubit [173]. It can be arranged in dimeric species where the two electronic spins are distinguishable and exchange-coupled to implement quantum gates [167]. The incoherent spin dynamics of VO-based systems was also extensively studied from both an experimental and theoretical point of view [113, 114, 174–176], shedding new light on the role of phonons and on spin-phonon couplings in molecular spin relaxation and decoherence. Last but not least, square- pyramidal vanadyl complexes can also be deposited on surfaces, obtaining monolayers of ordered arrays of intact molecules, retaining their paramagnetic nature [177] and can also be embedded into superconducting coplanar resonators [18, 178, 179], paving the way for the integration of molecular spin ensembles into microwave quantum architectures.
Interesting systems are also monomers containing a single spin S transition-metal ion like Fe3+, as they provide  -levels qudits which can be coherently manipulated by microwave drives [180]. For instance, coherence times of a few µs at 5 K were shown for [Cr3+C2O4)3]3− spin 3/2 and [Fe3+C2O4)3]3−
-levels qudits which can be coherently manipulated by microwave drives [180]. For instance, coherence times of a few µs at 5 K were shown for [Cr3+C2O4)3]3− spin 3/2 and [Fe3+C2O4)3]3−
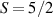 complexes [137, 180].
complexes [137, 180].
Concurrently with these progresses obtained with 3d-based complexes, MNMs containing single lanthanide (Ln) ions have been also largely studied (table 1(iii)). The original idea behind the investigation of these molecules was to exploit the large magnetic anisotropy of Ln ions to increase the energy barrier of SMMs. Indeed, after the discovery of a SMM behavior of double-decker Pc complexes containing a single Tb or Dy ion [181] in the early 2000s, a lot of efforts were devoted to the theoretical design and the synthesis of Ln SMMs with increasingly high blocking temperatures [74, 86, 87, 182–192]. At the same time, Ln-based mononuclear complexes have also offered new alternatives for realizing molecular qubits and qudits [11]. For instance, rare-earth polyoxometalates (POM) have been considered as promising qubit candidates with competitive coherence times [13, 168, 193–196]. The simplest situation is given by Kramers ions, with a ground doublet that naturally encodes a qubit whose frequency can be tuned by external magnetic fields. The case of non-Kramers ions, with an integer angular momentum 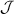 , exemplifies a more subtle crystal-field engineering. Transverse magnetic anisotropy terms induce avoided level crossings between states with opposite angular momentum projections
, exemplifies a more subtle crystal-field engineering. Transverse magnetic anisotropy terms induce avoided level crossings between states with opposite angular momentum projections 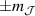 at specific magnetic fields . The gap at these spin clock transitions can be maximized by adequately choosing the lanthanide ion and its local coordination (e.g. a Ho3+ with a
at specific magnetic fields . The gap at these spin clock transitions can be maximized by adequately choosing the lanthanide ion and its local coordination (e.g. a Ho3+ with a 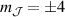 ground state in a fourth fold symmetric coordination, as it is the case with HoW10 [168, 194, 197]). The qubit states are then encoded into symmetric and anti-symmetric superpositions of
ground state in a fourth fold symmetric coordination, as it is the case with HoW10 [168, 194, 197]). The qubit states are then encoded into symmetric and anti-symmetric superpositions of 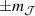 states resulting in a qubit which is practically insensitive to magnetic noise, as it was shown for HoW10 [168], where a maximum in T2 was observed at the avoided-crossing magnetic field. Other examples confirming that coherence times increase sharply near each clock transition have been found in 3d-metal-based compounds [198, 199], where the anticrossing gap can be tuned via the chemical design of the molecular structure [163, 200].
states resulting in a qubit which is practically insensitive to magnetic noise, as it was shown for HoW10 [168], where a maximum in T2 was observed at the avoided-crossing magnetic field. Other examples confirming that coherence times increase sharply near each clock transition have been found in 3d-metal-based compounds [198, 199], where the anticrossing gap can be tuned via the chemical design of the molecular structure [163, 200].
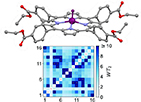
Nuclear spins of magnetic ions are also a valuable addition to their electronic counterparts in encoding qubits or qudits (see table 1(iv)). As discussed below, nuclear spins in transition metal or Ln ions can provide a significant number of states for qudit-based algorithms. They are in general more isolated from the environment and this yields both a higher protection from decoherence and longer manipulation times. Nevertheless, in contrast to organic radicals usually employed in NMR quantum computation [201, 202], nuclear spins exploited for QIP in MNMs are coupled to the electronic spins by a large hyperfine interaction (A). This is especially true for Ln-complexes, but also for transition metals. Such a sizable 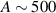 –800 MHz on the one hand increases the splitting between the ground and excited states (thus enabling initialization by cooling below
–800 MHz on the one hand increases the splitting between the ground and excited states (thus enabling initialization by cooling below 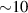 mK). On the other hand, it makes nuclear spin manipulations by radio-frequency pulses much faster than in organic radicals and it distinguishes different energy gaps even in nuclei with small intrinsic quadrupole. In particular, it is usually possible to identify a regime at intermediate magnetic fields (0.2–0.3 T) where the electronic and nuclear spin wavefunctions are practically factorized, but (i) the Rabi frequency of nuclear spin oscillations is enhanced by several orders of magnitude compared to the case with A = 0 [125]; (ii) an effective quadrupole interaction allows one to distinguish all nuclear transitions and address each of them separately by resonant drives [126]. In this context, Yb(trensal) provided the first example of coupled electronic qubit-nuclear qudit system for the implementation of QEC algorithms [125, 203] (details in section 5). Another important example is given by 51V in VO(TPP), which embeds a nuclear spin 7/2 coupled to the electronic spin 1/2. This yields electronuclear spin states for the encoding of a qudit (see section 4.4 below), whose coherent manipulations was demonstrated via pulsed EPR and broadband NMR experiments [126, 166].
mK). On the other hand, it makes nuclear spin manipulations by radio-frequency pulses much faster than in organic radicals and it distinguishes different energy gaps even in nuclei with small intrinsic quadrupole. In particular, it is usually possible to identify a regime at intermediate magnetic fields (0.2–0.3 T) where the electronic and nuclear spin wavefunctions are practically factorized, but (i) the Rabi frequency of nuclear spin oscillations is enhanced by several orders of magnitude compared to the case with A = 0 [125]; (ii) an effective quadrupole interaction allows one to distinguish all nuclear transitions and address each of them separately by resonant drives [126]. In this context, Yb(trensal) provided the first example of coupled electronic qubit-nuclear qudit system for the implementation of QEC algorithms [125, 203] (details in section 5). Another important example is given by 51V in VO(TPP), which embeds a nuclear spin 7/2 coupled to the electronic spin 1/2. This yields electronuclear spin states for the encoding of a qudit (see section 4.4 below), whose coherent manipulations was demonstrated via pulsed EPR and broadband NMR experiments [126, 166].
The most traditional way to control the state of MNMs employs oscillating external magnetic fields, but their local application at the single-molecule level within short timescales, as required for QC, still represents a major challenge. For this reason, the electric control of molecular spin qubits has also been envisaged. Contrary to magnetic fields, electric fields involve no flowing currents (thus no dissipation) and can be confined by nanoscopic gates, which allows for enhancing the field intensity while achieving a high degree of integration. Yet, their coupling to electron spins is typically rather weak. To overcome this intrinsic hurdle, antiferromagnetically-coupled triangular molecules were proposed. Indeed, the exchanged-coupled magnetic ions interact with external electric fields through chirality of their spin structure and thus the spin-electric coupling is possible even in the absence of spin-orbit interaction [128, 160]. Moreover, the peculiar encoding of the qubits into the chirality degree of freedom makes them intrinsically protected from decoherence driven by the interaction with neighboring nuclear spins [128]. We mention here, in turn, a different proposal of a decoherence-protected encoding of logical qubit states, based on toroidal magnetic states [97], as those found in Dy3 [204, 205] and Dy6 systems [98].
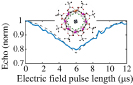
The first experimental demonstrations of molecular spin control by means of electric fields were achieved some years later, along different proposals. A crucial milestone is represented by the electric-field modulation of the hyperfine interaction between a nuclear spin 3/2 and an Tb qubit (the so-called hyperfine Stark effect). Experiments were performed on a single TbPc2 [43, 164] molecule arranged in a single-molecule transistor setup, presented in section 8. The Authors found a modification of the nuclear Rabi frequency induced by application of an electric field which periodically modulates A when the system is subject to microwave pulses, thus demonstrating an electrically-driven magnetic resonance. A remarkable dephasing time 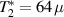 s was also reported, measured by Ramsey interferometry on the individual nuclear qudit.
s was also reported, measured by Ramsey interferometry on the individual nuclear qudit.
Another approach was pursued in [162] to study MnPhOMe helices, by applying an oscillating electric field during a continuous-wave EPR experiment. A magnetoelectric effect was observed and attributed to a modulation of the exchange interaction induced by the electric field. Conversely, electric field pulses were embedded in EPR Hahn-echo sequences to investigate spin-electric properties of AF rings and of the triangular molecule Cu3 [161]. In particular, an electric field pulse is applied just after the 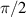 pulse. As a consequence, during free precession the spin accumulates an additional phase which depends linearly on the electric field via the spin-electric coupling constant (SEC). Hence, the method allows one to investigate the magnitude of the SEC, finding
pulse. As a consequence, during free precession the spin accumulates an additional phase which depends linearly on the electric field via the spin-electric coupling constant (SEC). Hence, the method allows one to investigate the magnitude of the SEC, finding  rad (V m−1)−1 in both Cr7Mn and Cu3. To increase this value, the attention was shifted to Ln complexes, in line with the aforementioned choice of TbPc2 [43]. To this end, the method was applied to the POM HoW10 [129], finding a significantly larger SEC of 11.4 Hz (V m−1)−1. This value is close to that obtained on Mn2+ impurities in ZnO [206], where the electric field was used to modulate the zero-field splitting anisotropy of spin 5/2 ions. The key ingredients to reach a sizable spin-electric coupling are identified to be an electrically polarizable and soft environment for the spin, together with spin energy levels strongly sensitive to distortions. The strategy applied to HoW10 would allow one to reach Rabi frequencies larger than
rad (V m−1)−1 in both Cr7Mn and Cu3. To increase this value, the attention was shifted to Ln complexes, in line with the aforementioned choice of TbPc2 [43]. To this end, the method was applied to the POM HoW10 [129], finding a significantly larger SEC of 11.4 Hz (V m−1)−1. This value is close to that obtained on Mn2+ impurities in ZnO [206], where the electric field was used to modulate the zero-field splitting anisotropy of spin 5/2 ions. The key ingredients to reach a sizable spin-electric coupling are identified to be an electrically polarizable and soft environment for the spin, together with spin energy levels strongly sensitive to distortions. The strategy applied to HoW10 would allow one to reach Rabi frequencies larger than 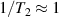 MHz by using an electric field of 1 mV nm−1, as available in nanogaps. Further steps would be required to reach control capabilities comparable to magnetic drives. One possibility is also to design exchange-coupled multi spin molecules with sizable electric dipole, thus enabling to tune the exchange coupling by electric fields [207].
MHz by using an electric field of 1 mV nm−1, as available in nanogaps. Further steps would be required to reach control capabilities comparable to magnetic drives. One possibility is also to design exchange-coupled multi spin molecules with sizable electric dipole, thus enabling to tune the exchange coupling by electric fields [207].
4.2. Multi-qubit structures
Chemistry can also be exploited to expand the computational space, moving from single to multiple qubits encoded in single molecules. A quite intuitive option of this 'scaling up by molecular design' path is to create molecular structures hosting several weakly coupled and addressable magnetic centers [208]. Examples include molecular dimers and trimers of lanthanide ions [133, 209, 210], as well as supramolecular structures able to bind several well-known molecular qubits, such as Cr7Ni, and, in some cases, combine them with other complexes having an effective 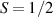 [12, 16, 134, 211, 212].
[12, 16, 134, 211, 212].
In 2009, it was shown that AF rings like Cr7Ni can be chemically and magnetically linked to each other through an interposed paramagnetic ion [12]. This work paved the way for the synthesis of different weakly-coupled supramolecular dimers, where the coherence of the individual units is also preserved [16, 154, 213]. In [12] the Authors also demonstrated that it is possible to generate maximally entangled states in these 'trimers' with simple microwave pulse sequences. Starting from this result, many supramolecular compounds containing linked antiferromagnetic rings were synthesized and investigated. Being entanglement an essential resource for QIP, dimers of weakly-coupled MNMs were also exploited as a playground for experimentally investigating entangled states. Initially, entanglement between molecular subunits was experimentally demonstrated by exploiting susceptibility as an entaglement witness or by fitting trial model Hamiltonians to electron paramagnetic resonance data [135]. More recently, a dimer of Cr7Ni rings has been used as a benchmark to develop and test a method exploiting 4-dimensional inelastic neutron scattering to detect and quantify entanglement [110] in these supramolecular compounds.
A relevant question is how to implement in molecular systems the single and two-qubit gates required to perform universal operations. The possibility of introducing switchable spin–spin interactions will be discussed in the following sub-section. Here, we consider the situation in which the spin centers are permanently coupled. If, as it is often the case, the inter-qubit couplings are stronger than the Rabi frequencies 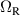 of each qubit, the operations rely on the ability of addressing resonant transitions between different spin states by their resonant frequencies. It can be shown that this implies a certain asymmetry between each of the spin centers in the molecule to make different energy gaps distinguishable, anticipating the more general case of spin qudits discussed further below. Let's consider the spin Hamiltonian of two interacting (pseudo-)
of each qubit, the operations rely on the ability of addressing resonant transitions between different spin states by their resonant frequencies. It can be shown that this implies a certain asymmetry between each of the spin centers in the molecule to make different energy gaps distinguishable, anticipating the more general case of spin qudits discussed further below. Let's consider the spin Hamiltonian of two interacting (pseudo-) 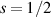 spins
spins
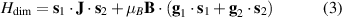
coupled by an exchange interaction tensor J and with different gyromagnetic tensors 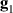 and g2. The latter property makes both spin qubits separately addressable through their different resonance frequencies under any finite magnetic field. Because of their mutual coupling, the energy associated with flipping each spin also depends on the state of the other, which provides the necessary ingredient to implement conditional operations. These two conditions result in a fully 'anharmonic' energy level scheme, as shown in figure 2(a). Then, two-qubit gates can be realized by single shot resonant electromagnetic pulses. For instance, a pulse tuned at the
and g2. The latter property makes both spin qubits separately addressable through their different resonance frequencies under any finite magnetic field. Because of their mutual coupling, the energy associated with flipping each spin also depends on the state of the other, which provides the necessary ingredient to implement conditional operations. These two conditions result in a fully 'anharmonic' energy level scheme, as shown in figure 2(a). Then, two-qubit gates can be realized by single shot resonant electromagnetic pulses. For instance, a pulse tuned at the 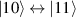 transition of a molecular spin dimer implements the prototypical cNOT gate.
transition of a molecular spin dimer implements the prototypical cNOT gate.
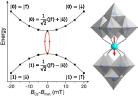
Figure 2. Two-qubit gates with permanently coupled spin qubits. (a) Scheme of spin levels of the [CeEr] molecular dimer whose structure is shown in (b). The very different magnetic moments of the two ions, combined with their weak mutual coupling gives rise to 4 non equidistant levels. This allows performing two-qubit CNOT or SWAP gates via single shot pulses resonant with the corresponding spin transitions. Spin echo measurements (c) performed on a frozen solution of these molecules show that all relevant transitions can be coherently driven, and provide a spin coherence time 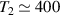 ns. Panel (d) shows a color map of the speed W of operations that link any two logic states via a sequence of allowed resonant transitions (marked as yellow crosses). The fact that
ns. Panel (d) shows a color map of the speed W of operations that link any two logic states via a sequence of allowed resonant transitions (marked as yellow crosses). The fact that 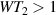 for any of them shows that [CeEr] can encode a two-qubit universal processor. (b), (c) Reprinted with permission from [210]. Copyright (2014) American Chemical Society. Further permission related to the material excerpted should be directed to the ACS.
for any of them shows that [CeEr] can encode a two-qubit universal processor. (b), (c) Reprinted with permission from [210]. Copyright (2014) American Chemical Society. Further permission related to the material excerpted should be directed to the ACS.
Download figure:
Standard image High-resolution imageThis scheme was proposed on an asymmetric Tb2 [209] and CeEr [210] dimers (see figure 2(b)), where a Hamiltonian of the type of equation (3) was used. The necessary magnetic assymmetry was achieved via the different coordinations of the two Tb3+ ions and by the heteronuclear composition, respectively. The transition involved in the cNOT gate was spectroscopically resolved by continuous-wave and the associated decoherence time T2 was measured by pulsed EPR experiments (figure 2(c)). Resolving such a transition (i.e. the excitation of the target spin depending on the state of the control) demonstrates the existence of a sizable coupling between the two distinguishable qubits. An analogous time-resolved experiment was implemented on a two-qubit assembly consisting of two NO radicals in a TEMPO molecule [214], made inequivalent by the differently-oriented g tensors. A coherent oscillation of the target qubit state (corresponding to a cNOT gate) was observed on a time-scale of about 200 µs. However, the implementation of single qubit rotations becomes more involved with permanently coupled qubits.
Spin-correlated radical pairs obtained from photodriven electron transfer from a molecular donor to an acceptor were also studied as potential two-qubit units [215]. These can be faithfully initialized in an entangled singlet state 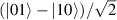 even at room temperature and then manipulated by microwave pulses to implement one and two-qubit gates. Donor–acceptor entanglement can also be transferred to a third spin [216, 217] and controlled by charge recombination, thus in fact implementing a quantum teleportation protocol [218]. Using a chiral bridge to link donor and acceptor could result in a local spin polarization which can be exploited for initialization and readout of single molecules, as explained in section 8.
even at room temperature and then manipulated by microwave pulses to implement one and two-qubit gates. Donor–acceptor entanglement can also be transferred to a third spin [216, 217] and controlled by charge recombination, thus in fact implementing a quantum teleportation protocol [218]. Using a chiral bridge to link donor and acceptor could result in a local spin polarization which can be exploited for initialization and readout of single molecules, as explained in section 8.
Showing that the system affords universal operations in the Hilbert space spanned by the two qubits reduces to demonstrating that the set of allowed resonant transitions can generate a complete set of operations, i.e. that any state can be generated via a sequence of such transitions [219]. Figure 2(d) shows such a 'universality plot' of the rates of operations 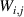 , with
, with 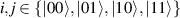 , linking any two basis states. The fact that
, linking any two basis states. The fact that 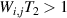 for any
for any 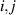 shows that the molecular system is universal and provides a quantitative method to benchmark the performances of different molecules [8, 166, 196, 220].
shows that the molecular system is universal and provides a quantitative method to benchmark the performances of different molecules [8, 166, 196, 220].
An alternative scheme applies when the intramolecular spin–spin couplings J are very weak, i.e. when 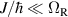 . Along the lines of nuclear magnetic resonance (NMR) quantum computing, it is then possible to let the system evolve freely into an entagled state [124, 221]. This approach was demonstrated on a family of Cr7Ni supramolecular dimers [124] by applying double electron-electron resonance techniques to detect the evolution of a proper initial state on a timescale
. Along the lines of nuclear magnetic resonance (NMR) quantum computing, it is then possible to let the system evolve freely into an entagled state [124, 221]. This approach was demonstrated on a family of Cr7Ni supramolecular dimers [124] by applying double electron-electron resonance techniques to detect the evolution of a proper initial state on a timescale 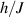 . Later on, a similar method, combining single qubit rotations and free evolution of the coupled system, was proposed for implementing two-qubit gates between Cr7Mn dimers, encoding clock-transitions qubits [221].
. Later on, a similar method, combining single qubit rotations and free evolution of the coupled system, was proposed for implementing two-qubit gates between Cr7Mn dimers, encoding clock-transitions qubits [221].
A serious drawback of these methods is that the permanent qubit–qubit interaction strongly limits scalability of the architecture. As it has been mentioned above, rotations of each qubit might require a large number of frequencies, depending on the state of other qubits in the qubit register. Moreover, in the second scheme the inability of turning off the inter-qubit coupling leads to an unwanted spontaneous evolution of the system, which should be corrected for a reliable computation.
4.3. Switchable qubit–qubit couplings within the same molecule
Molecular multi-qubit structures introduced in the previous section present permanent spin–spin interactions, which cannot be reversibly removed on the time scale of qubit gates. Hence, alternative strategies must be found to switch on and off such mutual qubit–qubit interactions in an effective way. We overview the most important proposals in this direction in figure 3, based on using suitable driving fields and on exploiting non-computational states which can be easily obtained in MNMs, thanks to the high degree of chemical control.
Figure 3. Different schemes to implement an effectively switchable qubit–qubit interaction between molecular spins. First column: switch off; second column: switch on (implemented gate indicated in between); third column: main features (black), pros (green) and cons (red) of each scheme. (a) ABAB chain of spins 1/2 isosceles triangles, where excitation of the state of the basis from singlet to triplet effectively turns on the A-B coupling. (b)–(d) Cr7Ni logical qubits with interposed switch units represented by (b) anti-ferromagnetic spin dimers, (c) single spins 1/2, controlled by microwave pulses, (d) redox-active complexes where a single-electron can be reversibly added or removed. (e) HoW10 clock-transition qubits coupled by dipole-dipole interaction, which is ineffective as long as states 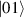 and
and 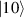 are non degenerate (as with an applied electric field E). The gap is removed by turning E off, thus activating a iSWAP
are non degenerate (as with an applied electric field E). The gap is removed by turning E off, thus activating a iSWAP gate. A similar tuning of single-qubit transition frequency can be achieved by applying a longitudinal microwave field. (f) Photon-mediated resonant interaction between molecular qubits within coplanar wave-guide resonators, exploiting and auxiliary level
gate. A similar tuning of single-qubit transition frequency can be achieved by applying a longitudinal microwave field. (f) Photon-mediated resonant interaction between molecular qubits within coplanar wave-guide resonators, exploiting and auxiliary level  and the tunability of the resonator frequency (by a SQUID) to bring it into resonance with specific transitions, thus implementing a cϕ gate after two subsequent photon emissions and absorptions [21].
and the tunability of the resonator frequency (by a SQUID) to bring it into resonance with specific transitions, thus implementing a cϕ gate after two subsequent photon emissions and absorptions [21].
Download figure:
Standard image High-resolution imageSchemes reported in panels (a)–(c) employ global microwave pulses acting on the whole qubit register as the only manipulation tool. This removes the challenge of addressing single-molecules (discussed in section 8), but also brings along some limitations if the target is a universal QC (see below). Conversely, it represents a promising scheme for quantum simulation of a large class of model Hamiltonians (see section 6). In scheme (a), qubits are encoded into multi-spin MNMs, exploiting the richness of their spectrum as a resource for computation. In a first proposal [122], a chain of Cr7Ni qubits with properly tuned inter-molecular couplings was shown to behave as a non-interacting register as long as each ring is in the computational subspace. Conversely, an effective finite coupling between pairs of neighboring qubits is obtained by temporarily exciting one of them to a specific state. However, in order to perfectly switch off the interaction within the computational subspace, a fine tuning of the inter-qubit couplings at the synthetic level is required 6 . Such a limitation is overcome by encoding qubits into anti-ferromagnetic isosceles triangles, as reported in figure 3(a). In that case, each qubit is described by the spin Hamiltonian
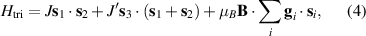
with  the isotropic exchange interactions between spins si
and
the isotropic exchange interactions between spins si
and  the respective gyromagnetic tensors. Hamiltonian
the respective gyromagnetic tensors. Hamiltonian  is diagonal in the total spin basis
is diagonal in the total spin basis 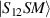 (
(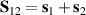 ,
, 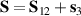 ) and the energy spectrum results in two low-energy doublets
) and the energy spectrum results in two low-energy doublets  and
and 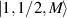 split by
split by 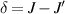 and a higher energy
and a higher energy 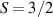 . The two doublets characterized by
. The two doublets characterized by  are used as the computational and auxiliary states, respectively. The former are exploited to encode logical states
are used as the computational and auxiliary states, respectively. The former are exploited to encode logical states 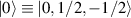 and
and 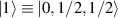 , the latter to implement two qubit gates in a switchable manner. In particular, let us consider (figure 3(a)) a pair of neighboring triangular units, made distinguishable by slightly different parameters in Htri
(e.g.
, the latter to implement two qubit gates in a switchable manner. In particular, let us consider (figure 3(a)) a pair of neighboring triangular units, made distinguishable by slightly different parameters in Htri
(e.g. 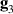 ), and coupled by
), and coupled by 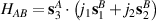 , with
, with 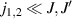 . As long as both A and B triangles are in the computational subspace (
. As long as both A and B triangles are in the computational subspace (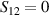 ), the effective AB interaction is off and single-qubit gates can be implemented by microwave pulses resonant with the
), the effective AB interaction is off and single-qubit gates can be implemented by microwave pulses resonant with the 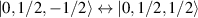 transition on either A or B qubits in the reigister. The interaction is activated by bringing B triangle to the auxiliary state with
transition on either A or B qubits in the reigister. The interaction is activated by bringing B triangle to the auxiliary state with 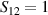 . This transition is allowed, but generally slower compared to single-qubit ones, because the corresponding matrix element
. This transition is allowed, but generally slower compared to single-qubit ones, because the corresponding matrix element 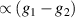 , which for transition metals is typically
, which for transition metals is typically 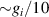 . A (semi)resonant 2π pulse (corresponding to excitation and de-excitation) from the computational to the auxiliary subspaces conditioned by the state
. A (semi)resonant 2π pulse (corresponding to excitation and de-excitation) from the computational to the auxiliary subspaces conditioned by the state  (
(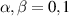 ) of the AB pair implements a cϕ gate, as detailed in appendix
) of the AB pair implements a cϕ gate, as detailed in appendix 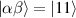 (i.e. for a specific M of both qubits in the computational and auxiliary states). The simplest implementations of these triangular qubits are represented by spin 1/2 ions such as V4+ or Cu2+ [222]. A drawback of these systems are possible (dipolar) interactions between vertices of different triangles, which can be reduced by replacing the single vertex spin with a larger molecule with a spin 1/2 ground state [14].
(i.e. for a specific M of both qubits in the computational and auxiliary states). The simplest implementations of these triangular qubits are represented by spin 1/2 ions such as V4+ or Cu2+ [222]. A drawback of these systems are possible (dipolar) interactions between vertices of different triangles, which can be reduced by replacing the single vertex spin with a larger molecule with a spin 1/2 ground state [14].
An alternative scheme (illustrated by figure 3(b)) was put forward in [15], where the switch of the interaction between neighbouring logical qubits was a separated antiferromagnetic unit with S = 0 ground state. Both logical qubits and switches are arranged in an alternating ABAB pattern, i.e. A/B qubits as well as A-B/B-A switches are spectroscopically distinguishable and hence can be separately addressed by global magnetic pulses. If we consider, for instance, Cr7Ni qubits, such a selectivity can be obtained by tilting their respective orientations and exploiting the anisotropy of their g tensors. The simplest implementation of the switch unit is represented by a dimer of spins 1/2 coupled by antiferromagnetic interaction and characterized by different (or differently oriented) g tensors. As in scheme (a), this latter ingredient allows the excitation of the switch unit from the S = 0 ground state to a S = 1 excited one, thus dynamically turning on the effective coupling between neighboring qubits and implementing a controlled-phase gate among them, as discussed above. This proposal could be realized for instance by linking two non-parallel Cr7Ni rings through a Cu2 dimer with significantly different g on the two ions and a not too large exchange coupling. An even simpler implementation is represented by using a single spin (such as an effective spin 1/2) as a switch of the effective qubit–qubit coupling (see figure 3(c)). To this end, several compounds were synthesized in the following years [132, 211, 223]. The idea to dynamically turn on and off the qubit–qubit coupling is the following. By working in a sizable magnetic field, such that the qubit-switch coupling is much smaller than the difference of Zeeman energies between qubits and switch, the state of the qubits and of the switch are factorized. In the idle configuration, the switch is frozen into its ground state and hence its coupling to the qubits only renormalizes the magnetic field on the qubits. However, the excitation energy of the switch depends on the states of both qubits to first order via the (longitudinal component of the) qubit-switch exchange interaction. Hence, an excitation of the switch by a semi-resonant pulse only for a specific state of the qubit pair (e.g. when the two qubits are in  ) can be exploited to implement a cϕ gate, as explained before. The same scheme can also be adapted to an electro-nuclear spin system [132], where electronic spin provide a fast effective switch, while logical qubits are encoded in hyperfine-coupled nuclear spins. Although simpler to be synthesized compared to scheme (b), the approach of figure 3(c) allows one to switch on and off the effective qubit–qubit coupling only to first order. Indeed, the transverse component of the qubit-switch exchange interaction induces a second-order effective coupling between the two qubits, arising from mixing with excited states of the switch. Such an unwanted time evolution can be partially suppressed by using a pair of inequivalent qubits [16]. However, it limits scalability of the platform [16] compared to proposals (a), (b), were the interaction was completely turned off in the idle phase.
) can be exploited to implement a cϕ gate, as explained before. The same scheme can also be adapted to an electro-nuclear spin system [132], where electronic spin provide a fast effective switch, while logical qubits are encoded in hyperfine-coupled nuclear spins. Although simpler to be synthesized compared to scheme (b), the approach of figure 3(c) allows one to switch on and off the effective qubit–qubit coupling only to first order. Indeed, the transverse component of the qubit-switch exchange interaction induces a second-order effective coupling between the two qubits, arising from mixing with excited states of the switch. Such an unwanted time evolution can be partially suppressed by using a pair of inequivalent qubits [16]. However, it limits scalability of the platform [16] compared to proposals (a), (b), were the interaction was completely turned off in the idle phase.
Remarkably, schemes (a)–(c) on a chain of ABAB qubits allow one to implement gates in the absence of local qubit control [122], by exploiting non-computational qubit states to embed an auxiliary control-unit [224], which marks specific sites along the chain and can be moved by SWAP gates. This approach makes the proposed ABAB linear register universal, but it also implies a sizeable number of SWAP gates which could make the resulting computation very long.
Another proposal, differing both in the manipulation tool and in the nature of the switch, is illustrated by figure 3(d). It is based on using a scanning tunneling microscope (STM) tip to locally control the state of a redox-active unit interposed between pairs of molecular qubits. The latter can be brought back and forth from a reduced (s = 0) to an oxidized (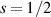 ) state by quickly adding/removing an electron via the STM tip, thus turning on/off the inter-qubit interaction. An implementation of this scheme on a pair of VO2+ qubits, connected to a central switch consisting of mixed valence [PMo12O40] Keggin unit, was proposed in [225]. In the on state, the three-spin Hamiltonian is of the form
) state by quickly adding/removing an electron via the STM tip, thus turning on/off the inter-qubit interaction. An implementation of this scheme on a pair of VO2+ qubits, connected to a central switch consisting of mixed valence [PMo12O40] Keggin unit, was proposed in [225]. In the on state, the three-spin Hamiltonian is of the form
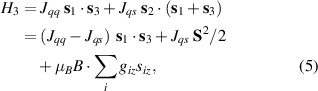
where 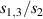 are the qubits/switch spins, Jqq
and Jqs
are the qubit–qubit and qubit-switch exchange interactions and it is fixed B = 0. An entangling gate such as the
are the qubits/switch spins, Jqq
and Jqs
are the qubit–qubit and qubit-switch exchange interactions and it is fixed B = 0. An entangling gate such as the 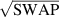 between s1 and s3 is here obtained by exploiting the free evolution induced by Hamiltonian (5). To achieve this, one then needs to cancel the evolution due to the term proportional to
between s1 and s3 is here obtained by exploiting the free evolution induced by Hamiltonian (5). To achieve this, one then needs to cancel the evolution due to the term proportional to 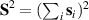 , which can be achieved for particular sets of parameters of H3 after specific time intervals. However, high fidelity for the
, which can be achieved for particular sets of parameters of H3 after specific time intervals. However, high fidelity for the 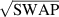 gate is guaranteed only for fixed
gate is guaranteed only for fixed 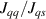 ratios.
ratios.
A more flexible scheme, implementing the equivalent iSWAP gate, was proposed in [16, 212], and applied to a three spin system with a redox-active unit (either a Co
gate, was proposed in [16, 212], and applied to a three spin system with a redox-active unit (either a Co Co2+ or a Ru
Co2+ or a Ru Co
Co Ru
Ru Co2+) linking two Cr7Ni qubits. The scheme works in an applied magnetic field (along z in the following) and requires the two qubits to have the same Zeeman energy, but different from that of the oxidized switch. In particular, if
Co2+) linking two Cr7Ni qubits. The scheme works in an applied magnetic field (along z in the following) and requires the two qubits to have the same Zeeman energy, but different from that of the oxidized switch. In particular, if 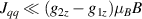 , one can derive an effective qubit–qubit Hamiltonian of the form
, one can derive an effective qubit–qubit Hamiltonian of the form
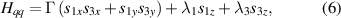
by restricting to the subspace in which the switch is practically frozen into its 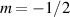 state. Here
state. Here 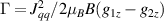 ,
, 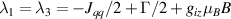 . Apart from single qubit Rz
rotations, free evolution induced by Hqq
implements the iSWAP
. Apart from single qubit Rz
rotations, free evolution induced by Hqq
implements the iSWAP gate, as described in section 3.C. Simulations performed on Cr7Ni–Co–Cr7Ni and Cr7Ni–Ru2Co–Cr7Ni complexes, including experimentally measured values of T2, demonstrate that both single- and two-qubit gates can be implemented with high fidelity along these lines. Here we are neglecting small direct dipolar interactions between s1 and s3, which would worsen the performance of the scheme, by introducing an always on coupling which would require proper schemes to be corrected.
gate, as described in section 3.C. Simulations performed on Cr7Ni–Co–Cr7Ni and Cr7Ni–Ru2Co–Cr7Ni complexes, including experimentally measured values of T2, demonstrate that both single- and two-qubit gates can be implemented with high fidelity along these lines. Here we are neglecting small direct dipolar interactions between s1 and s3, which would worsen the performance of the scheme, by introducing an always on coupling which would require proper schemes to be corrected.
A iSWAP -like gate can be implemented on any qubit pair with a mutual XY interaction (see appendix
-like gate can be implemented on any qubit pair with a mutual XY interaction (see appendix  and
and 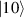 are degenerate (i.e.
are degenerate (i.e. 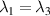 in (6)). Otherwise, if
in (6)). Otherwise, if  , the qubit–qubit coupling is ineffective. Nevertheless, there exist several possibilities to tune single-qubit energies and hence activate an interaction which implements the iSWAP
, the qubit–qubit coupling is ineffective. Nevertheless, there exist several possibilities to tune single-qubit energies and hence activate an interaction which implements the iSWAP gate, as sketched for instance in figure 3(e). A first option is based on applying longitudinal microwave pulses to the qubit pair, with
gate, as sketched for instance in figure 3(e). A first option is based on applying longitudinal microwave pulses to the qubit pair, with 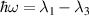 , as suggested in [154]. This longitudinal pulse perturbatively compensates the difference between single-qubit transition energies, thus implementing an iSWAP
, as suggested in [154]. This longitudinal pulse perturbatively compensates the difference between single-qubit transition energies, thus implementing an iSWAP evolution. However, this gate occurs on a rather long time-scale, because the effective inter-qubit interaction is re-scaled (for spins 1/2) by a factor
evolution. However, this gate occurs on a rather long time-scale, because the effective inter-qubit interaction is re-scaled (for spins 1/2) by a factor 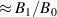 , where B1 is the amplitude of the oscillating field.
, where B1 is the amplitude of the oscillating field.
An alternative recent proposal exploits an electric field to tune single-qubit energies between pairs of HoW10 CT qubits coupled by a weak dipole-dipole interaction [226]. By properly choosing the applied magnetic field, one can identify an experimental configuration (close to the clock transition) which guarantees protection from decoherence, while also activating a dipolar coupling (which would instead vanish exactly at the CT). As sketched in figure 3(e), in presence of an electric field E states 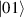 and
and 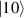 are split and each of the two qubits can be selectively addressed by microwave pulses; by turning E temporarily off
are split and each of the two qubits can be selectively addressed by microwave pulses; by turning E temporarily off 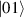 and
and 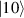 become degenerate and therefore a iSWAP
become degenerate and therefore a iSWAP gate is implemented via the free evolution induced by the dipolar coupling. The proposal requires a diluted crystal of qubits and a precise dipolar interaction between two neighboring HoW10, thus making scalability challenging. However, pulse sequences can be designed to only affect the desired kind of molecular pairs, leaving isolated molecules (and, to a lesser extent, also other pairs) unaffected [226]. The implementation of two qubit gates with both these methods based on varying the static Hamiltonian is rather slow. In addition, in the absence of a switch, the always on spin–spin coupling will induce a non-trivial evolution of the register, making, e.g. rotation of each qubit dependent on the state of those coupled to it.
gate is implemented via the free evolution induced by the dipolar coupling. The proposal requires a diluted crystal of qubits and a precise dipolar interaction between two neighboring HoW10, thus making scalability challenging. However, pulse sequences can be designed to only affect the desired kind of molecular pairs, leaving isolated molecules (and, to a lesser extent, also other pairs) unaffected [226]. The implementation of two qubit gates with both these methods based on varying the static Hamiltonian is rather slow. In addition, in the absence of a switch, the always on spin–spin coupling will induce a non-trivial evolution of the register, making, e.g. rotation of each qubit dependent on the state of those coupled to it.
All in all, the list of proposals presented above are promising, but have either met difficulties at the synthetic stage (a), (b) or present serious issues to scalability (d,e). Proposal (c) lies in between, since it can be applied to existing compounds, but can only be scaled up to a limited extent (up to 5–10 qubits) [16]. As discussed in detail in section 7, the real way to scale up a molecular spin quantum processor is by placing one or a few molecules (such as a short register of kind (c)) within superconducting resonators [227] and achieving the strong coupling between an individual molecule and a single photon. Recent progresses in this direction, combining top-down and bottom-up approaches in the design of both molecules and circuits [228], make this ambitious target reachable in the near future. Along these lines, schemes to implement two-qubit gates between a pair of molecules, whose interaction is mediated by the virtual or real exchange of photons (figure 3(f)), have been already put forward and are described in section 7.
4.4. From qubits to qudits
Besides the design of peculiar QIP schemes, the capability to combine magnetic ions into complex structures brings along the most important tool of MNMs for quantum computation: a multi-level spectrum where both coherence and matrix elements can be engineered to a large extent. This allows one to move from a binary to a qudit logic, thus increasing the computational power of the architecture. The qudit approach expands the tools of quantum logic compared to qubit-based platforms by introducing a larger range of quantum states and computational opportunities. Qudits represent quantum information using systems with d > 2 levels. While qubits can exist in a superposition of just two states, a qudit can exist in a superposition of up to d states. This larger state space allows for the representation of more information in a single quantum unit and can provide more efficient execution of some specific applications, such as quantum simulation of field theories [229], nuclear [230], fermionic and bosonic models [231] and especially QEC (discussed in sections 5 and 6). Qudits also allow for the encoding of multiple qubits within a single unit. This can lead to more efficient quantum simulation algorithms, where part of the interaction terms, usually implemented by two-qubit gates, is represented as simpler single-qudit operations. For other quantum algorithms, the use of qudits yields a logarithmic advantage in the number of logical units along with more efficient decompositions [232, 233], which are not impressive for a perspective fault-tolerant machine but can be important in the NISQ era. There are then approaches to quantum computing besides the quantum circuit model, such as the one-way (measurement-based) and adiabatic paradigms, which might also benefit from qudit encoding [232]. Qudits can also be advantageous for quantum communication protocols, such as quantum key distribution [234] and for quantum sensing applications [235]. Working with qudits also presents challenges, including a possible increase of vulnerability to noise and decoherence, due to the larger computational space. Qubit-based architectures have been more extensively developed and researched, and transitioning to qudit-based ones requires addressing these challenges and developing new tailored techniques and algorithms. We show below that the specific features of MNMs can be exploited to address these issues.
The first proposal for exploiting a MNM as a qudit dates back to 2001 [9], when Grover's search algorithm was adapted to the 21 energy levels of the ground S = 10 multiplet of Fe8 or Mn12 SMM (figure 1(a)), split by a nearly axial anisotropy and Zeeman interaction. A scheme to implement the algorithm exploiting multi-frequency EPR pulses was designed, based on complex multi-photon processes occurring at high-order perturbation theory. Later on, a simpler sequence of radiofrequency pulses with proper amplitudes, phases and frequencies was proposed using a generalized rotating frame representation for smaller nuclear spin qudits [236] with nuclear spin I ranging from 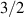 to
to 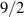 . This scheme was then experimentally applied to three of the four levels of a TbPc2 nuclear
. This scheme was then experimentally applied to three of the four levels of a TbPc2 nuclear 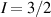 qudit [44] in a single-molecule transistor setup (figure 4(a)). A first pulse sequence was employed to prepare the system in a superposition of the qudit states with equal weights, implementing in fact a qudit-Hadamard gate Hd
. A second pulse sequence is subsequently used to enhance the amplitude of the searched state, by setting the duration of the pulses to obtain the proper time-evolution in the generalized rotating frame, as shown in figure 4(a).
qudit [44] in a single-molecule transistor setup (figure 4(a)). A first pulse sequence was employed to prepare the system in a superposition of the qudit states with equal weights, implementing in fact a qudit-Hadamard gate Hd
. A second pulse sequence is subsequently used to enhance the amplitude of the searched state, by setting the duration of the pulses to obtain the proper time-evolution in the generalized rotating frame, as shown in figure 4(a).
Figure 4. Examples of different molecular spin qudits: (a) TbPc2
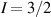 nuclear spin qudit, readout by gate voltages in a single-molecule transistor setup (top right). The molecule is characterized by 4 energy levels (left) with energy gaps made different by quadrupole interaction and is manipulated by properly detuned radio-frequency pulses, to enhance population of one of the levels and hence implement Grover's search algorithm (bottom right). (b) 173Yb(trensal)
nuclear spin qudit, readout by gate voltages in a single-molecule transistor setup (top right). The molecule is characterized by 4 energy levels (left) with energy gaps made different by quadrupole interaction and is manipulated by properly detuned radio-frequency pulses, to enhance population of one of the levels and hence implement Grover's search algorithm (bottom right). (b) 173Yb(trensal) 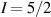 nuclear spin qudit and (c) GdW30
nuclear spin qudit and (c) GdW30
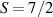 electronic spin qudit, manipulated by radiofrequency and microwave resonant pulses, respectively. Each pulse addresses a transition between
electronic spin qudit, manipulated by radiofrequency and microwave resonant pulses, respectively. Each pulse addresses a transition between  states, used to implement either single-qudit operations or multi-qubit gates if the d levels of the qudit are used to encode multiple qubits. (d) Hypothetical multi-spin molecule (left) with antiferromagnetic competing interactions, whose spectrum can be designed to allow pod connectivity (i.e. all the computational energy levels in black connected to the auxiuliary red state). This simplifies the implementation of single-qudit unitaries such as the Hadamard gate Hd
, with respect to a giant spin molecule. Right: error
states, used to implement either single-qudit operations or multi-qubit gates if the d levels of the qudit are used to encode multiple qubits. (d) Hypothetical multi-spin molecule (left) with antiferromagnetic competing interactions, whose spectrum can be designed to allow pod connectivity (i.e. all the computational energy levels in black connected to the auxiuliary red state). This simplifies the implementation of single-qudit unitaries such as the Hadamard gate Hd
, with respect to a giant spin molecule. Right: error  in the implementation of Hd
on giant spin (blue lines, S1, S2, S3) or competing interaction (green, C1, C2, C3) molecules with the same number of levels, ranging from 4 (S1, C1) to 6 (S2, C2) and 8 (S3, C3). Inset: corresponding ratio
in the implementation of Hd
on giant spin (blue lines, S1, S2, S3) or competing interaction (green, C1, C2, C3) molecules with the same number of levels, ranging from 4 (S1, C1) to 6 (S2, C2) and 8 (S3, C3). Inset: corresponding ratio  between errors for S and C systems. (a) Reprinted (figure) with permission from [44], Copyright (2017) by the American Physical Society. Reprinted with permission from [164]. Copyright (2017) American Chemical Society. (b) Reprinted with permission from [125]. Copyright (2018) American Chemical Society. (c) Reprinted (figure) with permission from [196], Copyright (2017) by the American Physical Society. (d) Reproduced from [157]. CC BY 4.0.
between errors for S and C systems. (a) Reprinted (figure) with permission from [44], Copyright (2017) by the American Physical Society. Reprinted with permission from [164]. Copyright (2017) American Chemical Society. (b) Reprinted with permission from [125]. Copyright (2018) American Chemical Society. (c) Reprinted (figure) with permission from [196], Copyright (2017) by the American Physical Society. (d) Reproduced from [157]. CC BY 4.0.
Download figure:
Standard image High-resolution imageNuclear spins 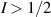 represent indeed the simplest realization of a qudit [125, 126, 166, 237]. These can be controlled by resonant radiofrequency pulses in a broadband NMR setup [125, 126] either at intermediate fields, where the electronic and nuclear spin wavefunctions are practically factorized, or at low field, where electronic and nuclear spins are entangled and behave as a unique
represent indeed the simplest realization of a qudit [125, 126, 166, 237]. These can be controlled by resonant radiofrequency pulses in a broadband NMR setup [125, 126] either at intermediate fields, where the electronic and nuclear spin wavefunctions are practically factorized, or at low field, where electronic and nuclear spins are entangled and behave as a unique 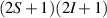 -level electro-nuclear qudit [166]. The capability to implement universal qudit unitaries in times significantly shorter than T2 on an entangled electro-nuclear qudit was demonstrated in [166] on a 51VO(TPP) molecule, consisting of a nuclear spin 7/2 coupled to an electronic spin 1/2 and thus providing a 16-level qudit (equivalent to 4 qubits). The proof uses the same method introduced in section 4.2, by showing that any pair of logical states could be connected by an arbitrary gate before losing coherence [219, 238]. An example of Rabi oscillations between a pair of
-level electro-nuclear qudit [166]. The capability to implement universal qudit unitaries in times significantly shorter than T2 on an entangled electro-nuclear qudit was demonstrated in [166] on a 51VO(TPP) molecule, consisting of a nuclear spin 7/2 coupled to an electronic spin 1/2 and thus providing a 16-level qudit (equivalent to 4 qubits). The proof uses the same method introduced in section 4.2, by showing that any pair of logical states could be connected by an arbitrary gate before losing coherence [219, 238]. An example of Rabi oscillations between a pair of 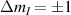 levels is shown in figure 4(b) for 173Yb(trensal)
levels is shown in figure 4(b) for 173Yb(trensal) 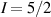 qudit, coupled by a strong hyperfine interaction to an effective electronic qubit [125]. Such a strong coupling enables nuclear spin manipulations (dependent on the electronic spin state) 3 orders of magnitude faster than for a bare nuclear spin with A = 0, even in presence of a moderate magnetic field (
qudit, coupled by a strong hyperfine interaction to an effective electronic qubit [125]. Such a strong coupling enables nuclear spin manipulations (dependent on the electronic spin state) 3 orders of magnitude faster than for a bare nuclear spin with A = 0, even in presence of a moderate magnetic field (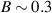 T) which yields a small electro-nuclear mixing [125].
T) which yields a small electro-nuclear mixing [125].
Similarly, single 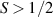 compounds such as transition metal
compounds such as transition metal 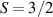 or
or 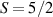 complexes [180] or giant-spin systems originating from the interaction of multiple spins can be used to encode a qudit. The simplest existing examples are transition metal single-ion complexes [137] or Gd3+ compounds [196] (figure 4(c)), for which Rabi oscillations between neighboring
complexes [180] or giant-spin systems originating from the interaction of multiple spins can be used to encode a qudit. The simplest existing examples are transition metal single-ion complexes [137] or Gd3+ compounds [196] (figure 4(c)), for which Rabi oscillations between neighboring 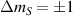 levels were already achieved experimentally by resonant microwave pulses. The 8 levels of the
levels were already achieved experimentally by resonant microwave pulses. The 8 levels of the 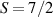 Gd qudit were exploited in [196] to encode the state of three qubits. Within such an encoding, a single resonant pulse addressing the
Gd qudit were exploited in [196] to encode the state of three qubits. Within such an encoding, a single resonant pulse addressing the 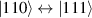 transition can be used to implement the important three qubit Toffoli gate.
transition can be used to implement the important three qubit Toffoli gate.
In order to reach even larger Hilbert spaces, the idea of exploiting internal spin states can be combined with the ability of coupling several magnetic centers within the same molecular or supramolecular entity that was described in section 4.2. Examples are an asymmetric Gd2 dimer, with up to 64 electronic spin levels [220] and Tb2Pc3 molecules, hosting two mutually coupled nuclear spin qudits [239]. Yet, these experiments also illustrate some inherent limitations to scaling up quantum resources within each molecule. Increasing the qudit dimension eventually introduces a spin level crowding and unwanted degeneracies between spin transitions that limit manipulation and readout to a subset of all spin states.
A further drawback of using a giant-spin as a qudit is the increase of the effect of decoherence with the system size. Indeed, as detailed in section 5, coherence between pairs of 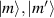 states decays with a rate
states decays with a rate 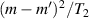 , thus making superpositions of several
, thus making superpositions of several 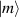 states particularly error-prone. To overcome this limitation, multi-spin clusters with anti-ferromagnetic competing interactions have been recently proposed [157]. Remarkably, these systems were shown to be protected from decoherence and in particular from its increase with the number of levels used for the qudit encoding (see section 5). A hypothetical molecule belonging to this class of systems is shown in figure 4(d), with a bi-pyramidal structure analogous to that of the existing Ni7 cluster [93]. Besides protection from decoherence, the system Hamiltonian was engineered to increase the connectivity between the energy levels (by slight symmetry distortions and/or anisotropic terms in the spin Hamiltonian), thus enabling efficient decomposition of single-qudit unitaries such as the generalized Hadamard (Hd
) gate. For instance, it is possible to allow transitions between each of the energy levels belonging to the computational subspace (black lines in figure 4(d)) and an auxiliary state (red). Both suppression of decoherence and increase of inter-level connectivity can be obtained by satisfying general requirements on the hierarchy of the spin–spin couplings in the Hamiltonian, thus making the synthesis of these optimal systems within the capabilities of coordination Chemistry. The error reduction compared to a giant spin molecule with the same number of levels in the implementation of the paradigmatic Hd
gate (corresponding to the quantum Fourier transform on a qudit) is shown in the right part of figure 4(d). The final gain (ratio between the two errors) increases with the system size and reaches values of
states particularly error-prone. To overcome this limitation, multi-spin clusters with anti-ferromagnetic competing interactions have been recently proposed [157]. Remarkably, these systems were shown to be protected from decoherence and in particular from its increase with the number of levels used for the qudit encoding (see section 5). A hypothetical molecule belonging to this class of systems is shown in figure 4(d), with a bi-pyramidal structure analogous to that of the existing Ni7 cluster [93]. Besides protection from decoherence, the system Hamiltonian was engineered to increase the connectivity between the energy levels (by slight symmetry distortions and/or anisotropic terms in the spin Hamiltonian), thus enabling efficient decomposition of single-qudit unitaries such as the generalized Hadamard (Hd
) gate. For instance, it is possible to allow transitions between each of the energy levels belonging to the computational subspace (black lines in figure 4(d)) and an auxiliary state (red). Both suppression of decoherence and increase of inter-level connectivity can be obtained by satisfying general requirements on the hierarchy of the spin–spin couplings in the Hamiltonian, thus making the synthesis of these optimal systems within the capabilities of coordination Chemistry. The error reduction compared to a giant spin molecule with the same number of levels in the implementation of the paradigmatic Hd
gate (corresponding to the quantum Fourier transform on a qudit) is shown in the right part of figure 4(d). The final gain (ratio between the two errors) increases with the system size and reaches values of  for an 8-level qudit. We note that here leakage effects are neglected. Nevertheless, these are strongly system specific and can be largely limited by using quantum optimal control techniques, as demonstrated in [127] on a Gd 8-level qudit.
for an 8-level qudit. We note that here leakage effects are neglected. Nevertheless, these are strongly system specific and can be largely limited by using quantum optimal control techniques, as demonstrated in [127] on a Gd 8-level qudit.
5. Embedding quantum error correction in single molecules
In section 4.1, we have listed several approaches to protect molecular spin systems from the leading sources of error, thus somewhat enhancing their effective coherence. These include the synthesis of engineered molecules with enhanced T2 and T1, smart qubit encodings [119, 157], post-processing error-mitigation techniques [5, 240–242], as well as the design of proper pulse sequences [127] or tailored experimental conditions (such as those occurring at specific avoided-crossing fields for atomic-clock transitions [168]).
However, building a scalable QC capable of implementing arbitrary complex algorithms requires a qualitative change of perspective. For instance, in order to factor a 2000-bit number using Shor's algorithm one would need about 4000 logical units, each characterized by errors below 10−14–10−15 [243]. Quantum error-correction (QEC) provides a route towards this ambitious goal. Basically, implementing QEC means using a Hilbert space with dimension d > 2 to encode a single qubit of information, as outlined in figure 5. Indeed, the final state of a quantum system can always be expressed in terms of a dynamical map 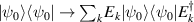 (see appendix
(see appendix 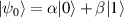 . This means that, after noise has acted, the system is brought into a mixture of states
. This means that, after noise has acted, the system is brought into a mixture of states 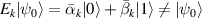 , i.e. each error Ek
has corrupted the information by distorting the original coefficients α and β (figure 5(a)). Conversely, the presence of additional degrees of freedom (more than two levels) provides the possibility to identify and correct a proper set of errors (figure 5(b)). Indeed, suitable encodings can map the system eigenstates into proper superpositions (code words or logical states)
, i.e. each error Ek
has corrupted the information by distorting the original coefficients α and β (figure 5(a)). Conversely, the presence of additional degrees of freedom (more than two levels) provides the possibility to identify and correct a proper set of errors (figure 5(b)). Indeed, suitable encodings can map the system eigenstates into proper superpositions (code words or logical states)  and
and  such that errors bring the encoded logical state
such that errors bring the encoded logical state  rigidly into an error state
rigidly into an error state 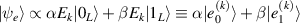 without corrupting the information stored into the coefficients α and β (figure 5(c)). The conditions, depicted in figures 5(b) and (c), which suitable code words must fulfill to allow error detection and correction were formalized by Knill and Laflamme [244]. The set of errors
without corrupting the information stored into the coefficients α and β (figure 5(c)). The conditions, depicted in figures 5(b) and (c), which suitable code words must fulfill to allow error detection and correction were formalized by Knill and Laflamme [244]. The set of errors 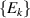 are correctable if:
are correctable if:
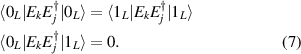
Note that the second Knill–Laflamme condition (KLc) requires that different errors bring different code words to orthogonal states. However, states 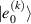 and
and  need not to be orthogonal to
need not to be orthogonal to  , although this is often the case.
, although this is often the case.
Figure 5. (a) A two-level system can be used to represent the state of a qubit 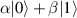 . However, errors corrupt the quantum superposition. (b) Additional levels (easily available in molecular spins such as a 4-dimensional
. However, errors corrupt the quantum superposition. (b) Additional levels (easily available in molecular spins such as a 4-dimensional  ) can be exploited to embed QEC and protect quantum information. Indeed, by proper electromagnetic pulses (i.e implementing unitary gates) one can encode the logical
) can be exploited to embed QEC and protect quantum information. Indeed, by proper electromagnetic pulses (i.e implementing unitary gates) one can encode the logical  and
and 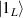 into combinations of eigenstates protected from leading errors, which bring these encoded
into combinations of eigenstates protected from leading errors, which bring these encoded 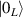 and
and 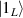 rigidly into error states in which the superposition is preserved (c). Then, a suitable detection step (d) projects the state of the system into orthogonal subspaces, corresponding here to error (left) or no-error (right). In the former case, proper correction pulses are then used to restore the original state, thus correcting the detected error.
rigidly into error states in which the superposition is preserved (c). Then, a suitable detection step (d) projects the state of the system into orthogonal subspaces, corresponding here to error (left) or no-error (right). In the former case, proper correction pulses are then used to restore the original state, thus correcting the detected error.
Download figure:
Standard image High-resolution imageThe most common way of enlarging the Hilbert space to accommodate 'protected qubits' is the so-called block-encoding, i.e. one qubit of information is mapped onto the state of a group of several (or many) physical qubits. For instance, in the three-qubit code a logical qubit (LQ) is encoded into three physical qubits [1], according to 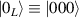 and
and 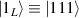 . Each correctable error is represented by the identity or by a flip of one of the three physical qubits, i.e.
. Each correctable error is represented by the identity or by a flip of one of the three physical qubits, i.e.  (
(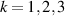 ). This leads to the following equalities:
). This leads to the following equalities:
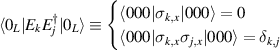

and
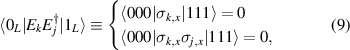
thus fulfilling KLc. An alternative possibility (discussed in section 5.2 below), which better fits the capabilities of molecular spin qubits, is to follow the qudit encoding and exploit many levels within a single object to define a LQ. As stressed below, embedding a LQ within a single qudit would have a disruptive technological impact by dramatically reducing the number of objects to be manipulated for the desired error suppression.
In both encodings, error correction then requires to project the state of the system into two-dimensional subspaces corresponding to different errors Ek
, thus in fact discretizing errors [1]. This must be done by means of a proper measurement scheme which does not collapse the stored information. For instance, we consider in figure 5
qudit encoding in a 4-dimensional  . Here the detection step projects the state of the system after a possible error either into the logical state
. Here the detection step projects the state of the system after a possible error either into the logical state  , or into the orthogonal state
, or into the orthogonal state  . In the former case (right), no correction is required. In the latter (left), a unitary operation (depicted as an electro-magnetic pulse) corrects the state by restoring
. In the former case (right), no correction is required. In the latter (left), a unitary operation (depicted as an electro-magnetic pulse) corrects the state by restoring  .
.
To conclude this general introduction to QEC a final remark is in order. The theoretical framework of block-encoding techniques was largely developed, with a particularly important result. If the error probability on each physical qubit (p) is below a certain threshold and for proper implementations, the resulting error on the LQ (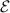 ) can be suppressed further and further by increasing the number of qubits in the LQ. This can be achieved either by concatenating coding techniques or by topological encodings such as the surface code [243, 245, 246], the latter showing an exponential gain with a linear increase of physical qubits [245]. Nevertheless, even with this favorable scaling, each of the resulting logical units consists of a collection of at least
) can be suppressed further and further by increasing the number of qubits in the LQ. This can be achieved either by concatenating coding techniques or by topological encodings such as the surface code [243, 245, 246], the latter showing an exponential gain with a linear increase of physical qubits [245]. Nevertheless, even with this favorable scaling, each of the resulting logical units consists of a collection of at least 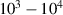 qubits (each with
qubits (each with 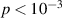 ) to reach the aforementioned bound on
) to reach the aforementioned bound on  for the implementation of the Shor's code. This clearly makes the actual implementation of QEC based on physical redundancy still a very important barrier to be overcome, even for the currently most advanced QC platforms [247, 248]. The orthogonal approach of embedding a LQ into a single multi-level quantum system could provide a sort of tunneling through this barrier, with a huge reduction in the number of objects to be controlled. Clearly, achieving this requires to fulfill requirements in the structure of the qudit eigenstates which is not common to all architectures. Nevertheless, a highly engineerable structure of the molecular eigenstates is a peculiar feature of MNMs which can be exploited to fit our targets. Below we show how the combined design of molecule and of qudit code can yield an impressive correcting power.
for the implementation of the Shor's code. This clearly makes the actual implementation of QEC based on physical redundancy still a very important barrier to be overcome, even for the currently most advanced QC platforms [247, 248]. The orthogonal approach of embedding a LQ into a single multi-level quantum system could provide a sort of tunneling through this barrier, with a huge reduction in the number of objects to be controlled. Clearly, achieving this requires to fulfill requirements in the structure of the qudit eigenstates which is not common to all architectures. Nevertheless, a highly engineerable structure of the molecular eigenstates is a peculiar feature of MNMs which can be exploited to fit our targets. Below we show how the combined design of molecule and of qudit code can yield an impressive correcting power.
5.1. Block-encoding within individual molecules
The most straightforward approach is to translate the block-encoding onto a molecule containing several weakly-interacting spins 1/2 (each representing a physical qubit), in the spirit of pioneering works on NMR QC [249–252]. A first proposal to implement the three-qubit code was put forward in [253], based on using 159Tb3+ or 63Cu2+ trimers. However, a crucial point is that a QEC code must target the leading errors affecting the physical hardware and this must be reflected by a proper correspondence between the errors which occur on the hardware and those managed by the code (this is obviously important also for the qudit approach). For instance, the simplest (three-qubit) block-code is designed to correct independent errors on any of the physical qubits, while correlated errors are not managed. Therefore, its implementation requires a platform consisting of weakly interacting spins 1/2, such that two-qubit errors on the real hardware are very unlikely.
Moreover, in the specific case of MNMs, the leading error at low temperatures is represented by pure dephasing, induced by the interaction between the central spins and the surrounding nuclear spin bath. Hence, on our molecular hardware we must focus on encodings designed to fight pure dephasing, such as the phase-flip version of the three qubit code. Although it is not a full quantum code (it only corrects a specific biased noise), it is tailored to protect from the most important error in this class of systems. Protection is achieved by introducing the code words  and
and 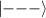 [with
[with 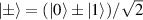 ] for the logical states
] for the logical states 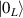 and
and  , respectively. A phase flip error on any of the three qubits (i.e. a Kraus operator
, respectively. A phase flip error on any of the three qubits (i.e. a Kraus operator 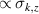 ) induces the transformation
) induces the transformation 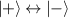 , thus bringing
, thus bringing 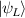 to an orthogonal (erred) state which can be detected by the code and corrected by a final Toffoli (ccNOT) gate on the target spin.
to an orthogonal (erred) state which can be detected by the code and corrected by a final Toffoli (ccNOT) gate on the target spin.
Realization of this code on a properly synthesized rare-earth trimer of weakly-interacting effective spins 1/2 (Er-Ce-Er) was proposed in [133]. The molecule was shown to be promising for such an implementation (see figure 6) thanks to the small coupling between different spins combined with largely different and anisotropic g tensors. As a consequence, the system eigenstates are practically factorized and represent a suitable basis for the code.
Figure 6. (a) Quantum circuit for the 3-qubit phase-flip QEC code. Starting from a generic superposition 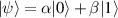 encoded into the spin of the central (Ce) ion
encoded into the spin of the central (Ce) ion  , two cNOT gates controlled by the Ce spin onto the two target Er spins bring to the encoded superposition
, two cNOT gates controlled by the Ce spin onto the two target Er spins bring to the encoded superposition 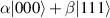 , which is then transformed into
, which is then transformed into 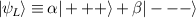 by three simultaneous
by three simultaneous 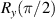 rotations on the three qubits. The system is then subject to dephasing for a memory time τ and decoded (blue-shaded area). Finally, a Toffoli (ccNOT) gate is used to correct the state of the central (Ce) qubit. (b) Molecular structure of ErCeEr. (c) Energy level diagram as a function of the external applied field, with logical states indicated on the right. All transitions are spectroscopically resolved, thanks to the spin–spin interactions. Double arrows represent pulses to implement each gate. For instance, a cNOT with the second qubit as control and the third as target corresponds to the two simultaneous pulses
rotations on the three qubits. The system is then subject to dephasing for a memory time τ and decoded (blue-shaded area). Finally, a Toffoli (ccNOT) gate is used to correct the state of the central (Ce) qubit. (b) Molecular structure of ErCeEr. (c) Energy level diagram as a function of the external applied field, with logical states indicated on the right. All transitions are spectroscopically resolved, thanks to the spin–spin interactions. Double arrows represent pulses to implement each gate. For instance, a cNOT with the second qubit as control and the third as target corresponds to the two simultaneous pulses  and
and  . A ccNOT gate in which the second qubit is the target is instead obtained by a single pulse, resonant with
. A ccNOT gate in which the second qubit is the target is instead obtained by a single pulse, resonant with 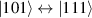 transition. Reproduced with permission from [133]. CC BY-NC 3.0.
transition. Reproduced with permission from [133]. CC BY-NC 3.0.
Download figure:
Standard image High-resolution imageThe sequence of operations is outlined in figure 6(a), with the central (Ce) ion representing the logical qubit in which information is initially stored and the two lateral Er ions acting as ancillae. Gates were applied to the well-characterized Er-Ce-Er system (reported in panel (b)), by simulating the time evolution of the system under the sequence of resonant pulses implementing them. An example of these microwave pulses is shown in figure 6(c). Despite the code is designed to correct only errors occurring during the memory time τ (in which the system evolves freely), simulations were performed by including pure dephasing during the whole sequence. This yields an uncorrectable error which limits the performance of the code and that makes it rather strongly dependent on T2. Nevertheless, the break-even point compared to an uncorrected spin 1/2 with the same T2 was already crossed for 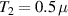 s.
s.
5.2. Molecular spin qudits as protected logical units
Hereafter, we consider the alternative qudit encoding. This formal approach (in which a single qudit encodes a qubit protected from a given error set) was first proposed on abstract [254, 255] or bosonic [256, 257] multi-level systems. It is particularly appropriate for MNMs, because it allows one to combine the design of targeted codes with that of the hardware Hamiltonian, in order to maximize protection of the system from unwanted errors.
A first simple application of these ideas was put forward in [125], where the 173Yb(trensal) complex (figure 4(b)) was considered, consisting of a nuclear spin 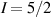 coupled to an electronic (effective) spin 1/2. The system was characterized by broad-band NMR measurements and the nuclear spin coherence was probed by Hahn-echo and Carr–Purcell–Meibum–Gill rf-pulse sequences. In a static field of
coupled to an electronic (effective) spin 1/2. The system was characterized by broad-band NMR measurements and the nuclear spin coherence was probed by Hahn-echo and Carr–Purcell–Meibum–Gill rf-pulse sequences. In a static field of 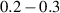 T, the eigenstates are practically factorized
T, the eigenstates are practically factorized 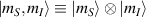 states with well defined electronic and nuclear spin projections along the magnetic field
states with well defined electronic and nuclear spin projections along the magnetic field  ,
, 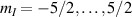 . All the electronic and nuclear spin transitions are well resolved thanks to the sizeable quadrupole and hyperfine interactions. Hence, the d = 6 (nuclear) qudit space with
. All the electronic and nuclear spin transitions are well resolved thanks to the sizeable quadrupole and hyperfine interactions. Hence, the d = 6 (nuclear) qudit space with 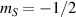 was exploited to encode a qubit protected from a generic amplitude shift error
was exploited to encode a qubit protected from a generic amplitude shift error 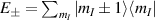 . This brings the logical state
. This brings the logical state 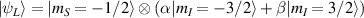 into one of the orthogonal error words
into one of the orthogonal error words 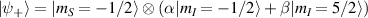 or
or 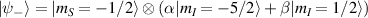 , corresponding to a
, corresponding to a 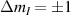 error. Note that these error words preserve the original superposition without overlap with
error. Note that these error words preserve the original superposition without overlap with 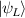 , thus enabling error detection according to KLc. This is achieved by two selective microwave pulses inducing a conditional excitation of the electronic spin only for two specific states of the nuclear qudit. For instance, two pulses resonant with
, thus enabling error detection according to KLc. This is achieved by two selective microwave pulses inducing a conditional excitation of the electronic spin only for two specific states of the nuclear qudit. For instance, two pulses resonant with 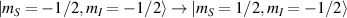 and
and 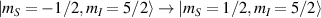 transitions bring
transitions bring 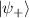 to
to 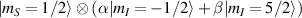 . Hence, the electronic spin is flipped if
. Hence, the electronic spin is flipped if 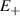 error has happened . Therefore, the occurrence of
error has happened . Therefore, the occurrence of 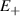 can be detected by a measurements of the electronic spin only (without projecting the nuclear spin component). In a superconducting resonator architecture (see below), this could be achieved by a two-tone dispersive measurement setup [120, 258], in which a two-frequency photon drive is used to excite the resonator and the measurement is done by a broadband high-efficiency photon detector that is only sensitive to the amplitude of the output field. Finally, depending on the measurement outcome, a simple recovery procedure is applied, i.e. if the electronic spin is measured to be in
can be detected by a measurements of the electronic spin only (without projecting the nuclear spin component). In a superconducting resonator architecture (see below), this could be achieved by a two-tone dispersive measurement setup [120, 258], in which a two-frequency photon drive is used to excite the resonator and the measurement is done by a broadband high-efficiency photon detector that is only sensitive to the amplitude of the output field. Finally, depending on the measurement outcome, a simple recovery procedure is applied, i.e. if the electronic spin is measured to be in  , it is de-excited and then two radio-frequency pulses are employed to transform back
, it is de-excited and then two radio-frequency pulses are employed to transform back  into
into 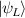 .
.
This error model constitutes a useful playground to clarify the basic principles of qudit-based QEC. However, it does not model the main errors occurring in real molecular spin systems. To this aim, specific encodings to fight pure dephasing [120, 156, 170] were designed. Two of them are shown in figure 7, targeted to different molecular systems. On the left panels (a,b), we consider a spin S (either a single ion or the total spin ground state of a molecule with ferromagnetic exchange interactions), while on the right (panels c,d) a set of spins coupled by competing anti-ferromagnetic interactions. In both cases, dephasing of the spin system at low temperature originates from the coupling between the system spins and the surrounding nuclear spin bath. Conversely, phonon-mediated relaxation and dephasing processes can be neglected at low temperature, as long as the energy gaps are sufficiently smaller than the Debye energy (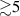 meV) [159, 171, 172]. Then, the incoherent dynamics of the spin systems can be modeled by a Lindbald master equation (see appendix
meV) [159, 171, 172]. Then, the incoherent dynamics of the spin systems can be modeled by a Lindbald master equation (see appendix  eigenstates (
eigenstates ( ), this takes the form
), this takes the form
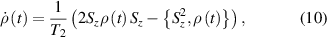
where 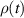 is the density operator of the qudit. By performing a perturbative expansion for small
is the density operator of the qudit. By performing a perturbative expansion for small 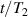 of the solution of equation (10)
of the solution of equation (10) 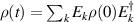 , one can write an analytical expression for the error operators [170]:
, one can write an analytical expression for the error operators [170]:
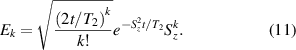
Starting from this expansion for the error-operators, it is then possible to find code words satisfying KLc
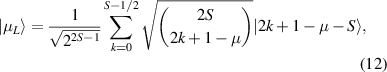
with 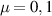 and half-integer S. We note that
and half-integer S. We note that 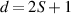 levels are enough to correct
levels are enough to correct 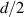 errors Ek
, i.e. dephasing up to order
errors Ek
, i.e. dephasing up to order 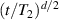 and the corresponding powers of Sz
. The structure of these spin-binomial code words is reported in figure 7(a) as a bar plot. The smallest qudit dimension d enabling a minimal correction is d = 4, corresponding to a
and the corresponding powers of Sz
. The structure of these spin-binomial code words is reported in figure 7(a) as a bar plot. The smallest qudit dimension d enabling a minimal correction is d = 4, corresponding to a 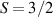 system. In that case the code words are given by
system. In that case the code words are given by 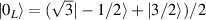 ,
,  and the lowest order Sz
error brings them to the orthogonal error words
and the lowest order Sz
error brings them to the orthogonal error words  ,
, 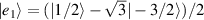 , which are therefore clearly distinguishable and make the Sz
error detectable by the code. In general, the correcting power can be quantified by considering the error
, which are therefore clearly distinguishable and make the Sz
error detectable by the code. In general, the correcting power can be quantified by considering the error 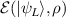 on an initial state
on an initial state  subject only to pure dephasing for a memory time t and then to a cycle of error correction, ending up in the mixed state ρ. Results are plotted in figure 7(b) for spins up to 9/2 (d = 10) and evidence an increased correcting power by increasing S and hence the number of levels in the encoding.
subject only to pure dephasing for a memory time t and then to a cycle of error correction, ending up in the mixed state ρ. Results are plotted in figure 7(b) for spins up to 9/2 (d = 10) and evidence an increased correcting power by increasing S and hence the number of levels in the encoding.
Figure 7. (a), (c) Composition of the code words in terms of the spin Hamiltonian eigenstates for a multi-spin cluster with ferromagnetic (a) or anti-ferromagnetic competing exchange interactions (c). The structure of the two molecules (six spins 1/2 and a spin 3/2 in the middle) and their spin arrangement are sketched in the insets. The low-energy spectrum of system (a) is equivalent to a single spin  ion. (b), (d) Corresponding error after a memory time t (in units of the coherence time T2) and an ideal implementation of the QEC sequence, starting from the error-prone state
ion. (b), (d) Corresponding error after a memory time t (in units of the coherence time T2) and an ideal implementation of the QEC sequence, starting from the error-prone state 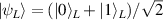 and exploiting an increasing number of eigenstates for the encoding. Inset of panel (b): Comparison between
and exploiting an increasing number of eigenstates for the encoding. Inset of panel (b): Comparison between 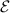 in the two systems at
in the two systems at 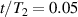 . Reproduced from [156]. CC BY 4.0.
. Reproduced from [156]. CC BY 4.0.
Download figure:
Standard image High-resolution imageMany different ways can be identified to increase the number of levels in a single molecular spin qudit by combining spins via synthetic Chemistry methods. As mentioned in section 4.4, multi-spin clusters with a proper hierarchy of spin–spin interactions can yield to particularly advantageous choices. We illustrate this below by deriving the key ingredients driving decoherence in a molecule containing several interacting spins sj . Within the same approximations used for (10), the Lindblad equation becomes:
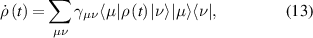
with 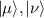 the eigenstates of the system. This leads to a decay of the coherences
the eigenstates of the system. This leads to a decay of the coherences 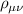 with a rate
with a rate
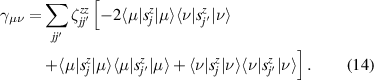
where 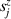 are local spin operators, we are assuming for simplicity axial symmetry, and coefficients
are local spin operators, we are assuming for simplicity axial symmetry, and coefficients 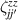 contain the dipolar couplings between the spins of the system and nuclear spin bath operators [156]. Starting from this expression, we can now design strategies to improve the capabilities of the code. In the case of a spin S,
contain the dipolar couplings between the spins of the system and nuclear spin bath operators [156]. Starting from this expression, we can now design strategies to improve the capabilities of the code. In the case of a spin S, 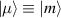 ,
, 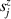 can be summed to give Sz
and equation (13) reduces to (10), with
can be summed to give Sz
and equation (13) reduces to (10), with 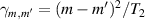 . Hence, decoherence is much faster for superpositions of states with large
. Hence, decoherence is much faster for superpositions of states with large 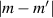 , enhancing its impact as S increases. This limits the performance of the spin-binomial code words for large S, as shown in figure 7(b).
, enhancing its impact as S increases. This limits the performance of the spin-binomial code words for large S, as shown in figure 7(b).
In order to suppress decoherence and its increase with the qudit size, we focus on the expression for 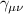 . We note that, apart from the system specific coefficients
. We note that, apart from the system specific coefficients 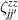 depending on the nuclear spin bath and on its coupling to the system, decoherence is ruled by differences of expectation values of
depending on the nuclear spin bath and on its coupling to the system, decoherence is ruled by differences of expectation values of  on different eigenstates. To enhance the capabilities of the code, one needs
on different eigenstates. To enhance the capabilities of the code, one needs 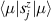 and its variation between different eigenstates
and its variation between different eigenstates 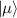 to be as small as possible. As already stated in section 4.4, a general class of molecules showing this property is represented by half-integer spins coupled by antiferromagnetic competing interactions, giving rise to several total spin
to be as small as possible. As already stated in section 4.4, a general class of molecules showing this property is represented by half-integer spins coupled by antiferromagnetic competing interactions, giving rise to several total spin 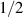 multiplets in the lowest part of the spectrum. As demonstrated in [156] for the illustrative hypothetical system sketched in the inset of figure 7(c), these low energy multiplets can be used to numerically find optimized code words involving an increasing number of levels. Compared to an analogous system with ferromagnetic couplings (characterized by a ground
multiplets in the lowest part of the spectrum. As demonstrated in [156] for the illustrative hypothetical system sketched in the inset of figure 7(c), these low energy multiplets can be used to numerically find optimized code words involving an increasing number of levels. Compared to an analogous system with ferromagnetic couplings (characterized by a ground 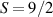 multiplet) this molecular qudit shows an exceedingly better performance, with a 5-order of magnitude reduction of the final error, as shown in figure 7(d) and in the inset of panel (b). From that it also emerges that the error suppression is almost exponential in the qudit size
d and rather small values of d already bring errors below 10−10. This result certifies the impact that the qudit approach to QEC, combined with molecular design, could have on quantum computing.
multiplet) this molecular qudit shows an exceedingly better performance, with a 5-order of magnitude reduction of the final error, as shown in figure 7(d) and in the inset of panel (b). From that it also emerges that the error suppression is almost exponential in the qudit size
d and rather small values of d already bring errors below 10−10. This result certifies the impact that the qudit approach to QEC, combined with molecular design, could have on quantum computing.
The Lindbald description of the bath dynamics provided so far is useful to highlight the essential ingredients of the system spin Hamiltonian which rule decoherence, but it also involves several approximations. It neglects, in particular, any memory effect in the bath. A more realistic (although much more computationally demanding) description of the many-body bath dynamics can be obtained by means of the cluster-correlation expansion, as done in [120] to describe decoherence of a single spin S ion in a nuclear spin bath. With a real molecule at hand (i.e. knowing the position of the nuclear spins), this technique allows for a precise quantitative prediction of the coherence decay of the spin system (usually not exponential as given by the Lindblad approximation) and then for the derivation of code words tailored for that specific noise. Remarkably, apart from some quantitative changes, conclusions for QEC on a spin S ion are not significantly modified by this more accurate description of the bath [120].
Several simple existing molecular systems can already embed QEC within the scheme outlined in this section. They consist of a nuclear spin I > 1 coupled by hyperfine interaction to an electronic spin 1/2 used as ancilla, along the lines described above. Besides Yb(trensal) [125], it is worth mentioning V-based compounds (VO(TPP) and VCp2Cl2) hosting a nuclear spin 7/2 together with an electronic spin with remarkable coherence. These systems have been characterized by combined NMR [126, 259] and EPR studies [259] both in terms of spin Hamiltonian parameters and of electronic and nuclear coherence times. As already noted in section 4.1, the sizeable hyperfine interaction (yielding well distinguished gaps and fast manipulations of the qudit), combined with the remarkable coherence times, make VO(TPP) a promising nuclear qudit [126], where transitions between specific pairs of levels can be driven by resonant radio-frequency pulses (see figure 8).
Figure 8. Coherent manipulation of 51V nuclear qudit in VO(TPP) molecule by NMR (a) Energy level diagram as a function of the static magnetic field B0. (b) Simulation of the sequence of pulses used to encode a qubit protected from dephasing in four levels of the nuclear qudit and (c) measured Rabi oscillations between the levels involved in such encoding. Inset: molecular structure of VO(TPP). Reproduced with permission from [126]. CC BY-NC 3.0.
Download figure:
Standard image High-resolution imageExamples of electronic spin systems promising for implementing this code are given by Gd3+ (electronic spin 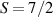 ) monomers [196] or dimers [220] or by transition metal dimers, as proposed, e.g. in [169]. Another possibility, offered by the flexibility of chemistry, is to improve the performance of a processing molecular qubit by adding a magnetic ion with a nuclear spin qudit acting as a quantum memory with QEC. This was proposed in [154] on a Cr7Ni-Cu compound, where 63Cu ion provides a nuclear spin
) monomers [196] or dimers [220] or by transition metal dimers, as proposed, e.g. in [169]. Another possibility, offered by the flexibility of chemistry, is to improve the performance of a processing molecular qubit by adding a magnetic ion with a nuclear spin qudit acting as a quantum memory with QEC. This was proposed in [154] on a Cr7Ni-Cu compound, where 63Cu ion provides a nuclear spin 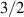 coupled to an electronic ancilla, used both for error detection and for swapping information to the Cr7Ni processor by virtual excitations.
coupled to an electronic ancilla, used both for error detection and for swapping information to the Cr7Ni processor by virtual excitations.
5.3. Towards a fault-tolerant quantum processor
The scheme proposed above is for protecting a quantum memory from its most important noise source. This represents the first step in the QEC framework, but it does not take into account errors occurring during the detection steps or during logical operations between encoded states.
In addition, thus far we have considered a code correcting only a biased noise acting on the system (pure dephasing) when this is left idle. However, this error can be transformed into other not correctable ones by unitary operations such as the detection/correction step or logical gates between encoded states. For instance, the result of decoherence acting during a correction procedure is a plateau in the error  that would appear at short
that would appear at short 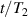 in figures 7(b) and (d), thus limiting the corrective power of the code [156, 170]. This effect can be reduced by engineering the pulses in order to reduce their duration without increasing leakage to neighboring levels (an effect usually induced by fast, spectroscopically broad, pulses). For instance, one could employ derivative removal by adiabatic gate (DRAG) methods as in [169, 260, 261] or optimal quantum control techniques [127], which, in turn, also suppress possible leakage during manipulations. However, a residual relevant not-correctable error will always be present unless one designs bias-preserving schemes for error correction and implementation of logical gates. This was proposed in other qudit-based architectures [262, 263] and recently also on a molecule-based setup [264, 265]. In [265] a general Fault-Tolerant scheme against pure dephasing errors is introduced, which allows for the implementation of error correction and of a universal set of quantum gates without error propagation. As a result, the QEC advantage increases almost exponentially with the qudit size (as in figure 7(d)), even during the implementation of stabilizers for error-correction and of a universal set of logical gates.
in figures 7(b) and (d), thus limiting the corrective power of the code [156, 170]. This effect can be reduced by engineering the pulses in order to reduce their duration without increasing leakage to neighboring levels (an effect usually induced by fast, spectroscopically broad, pulses). For instance, one could employ derivative removal by adiabatic gate (DRAG) methods as in [169, 260, 261] or optimal quantum control techniques [127], which, in turn, also suppress possible leakage during manipulations. However, a residual relevant not-correctable error will always be present unless one designs bias-preserving schemes for error correction and implementation of logical gates. This was proposed in other qudit-based architectures [262, 263] and recently also on a molecule-based setup [264, 265]. In [265] a general Fault-Tolerant scheme against pure dephasing errors is introduced, which allows for the implementation of error correction and of a universal set of quantum gates without error propagation. As a result, the QEC advantage increases almost exponentially with the qudit size (as in figure 7(d)), even during the implementation of stabilizers for error-correction and of a universal set of logical gates.
A more demanding task which still requires work on the theoretical side is the design of a fully quantum QEC code, able to correct a wide class of errors on the qudit and not only a specific one. Often, proposals of fully quantum codes [255] are more general and mathematically elegant, but less targeted to the investigated physical system. Hence, they could fail in providing an effective protection in case a single source of noise dominates. The challenge in this direction is to design a code which is both able to correct a generic error but also tailored to the typical noise occurring on a molecular hardware.
6. Molecular nanomagnets as quantum simulators
The implementation of a quantum simulator (QS) could be one the first targets for QIP [4], especially for a hardware based on molecular spins. Indeed, a couple of points could make this objective appealing and within reach of state-of-the-art technology: (i) a few dozens of error-mitigated qubits would suffice to outperform any classical device in simulating quantum systems, without necessarily requiring QEC. (ii) The output of the simulation of many problems of practical interest could be extracted from expectation values computed on ensemble variables, without needing single-molecule addressing and readout.
A quantum simulator (QS) is a quantum hardware whose dynamics can be controlled to mimic the evolution of a target system under investigation. This would enable the solution of many important problems in Physics and Chemistry which are nowadays intractable, due to the exponential growth of the Hilbert space with the size of the problem. In particular, molecular spins have been proposed as digital QSs, i.e. programmable quantum devices which can solve a wide variety of target models by encoding the target system into qubits and then decomposing the target evolution into a sequence of available gates.
The first proposal for a molecular QS was put forward in 2011 [15]. The elementary unit is the one shown in figure 3(b), where the distinguishability of AB/BA switch units allows one to turn on the interaction either between AB or between BA pairs along the chain. This setup enables the efficient simulation of one-dimensional translationally-invariant problems which can be easily mapped into the hardware. An interesting example is a spin 1/2 chain described by the Hamiltonian 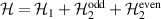 , containing local one (
, containing local one (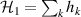 ) and two-body (
) and two-body (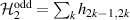 ,
, 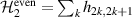 ) terms, including all the couplings between odd (
) terms, including all the couplings between odd (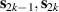 ) or even (
) or even (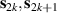 ) spin pairs, respectively. Odd (even) numbered spins can be mapped onto A (B) qubits. Then, Suzuki–Trotter decomposition (see appendix
) spin pairs, respectively. Odd (even) numbered spins can be mapped onto A (B) qubits. Then, Suzuki–Trotter decomposition (see appendix
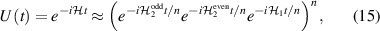
where n is the number of Trotter steps, setting the decomposition on time slices 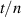 . Each of these three terms is finally decomposed into one- and two-qubit time-evolution operators on independent spin (pairs). These are recast in terms of single-qubit rotations and two-qubit
. Each of these three terms is finally decomposed into one- and two-qubit time-evolution operators on independent spin (pairs). These are recast in terms of single-qubit rotations and two-qubit 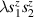 terms as outlined in appendix
terms as outlined in appendix 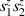 can be directly implemented by two simultaneous excitations/de-excitations of the switch, conditioned by two states of the qubit pair,
can be directly implemented by two simultaneous excitations/de-excitations of the switch, conditioned by two states of the qubit pair, 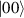 and
and 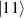 (analogously to the cϕ gates described in section 4.3). Using this approach, the value of
(analogously to the cϕ gates described in section 4.3). Using this approach, the value of 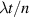 in the target evolution is controlled either by the phase difference between the exciting and de-exciting pulses or by the resonance detuning if one uses semi-resonant pulses (as detailed in appendix
in the target evolution is controlled either by the phase difference between the exciting and de-exciting pulses or by the resonance detuning if one uses semi-resonant pulses (as detailed in appendix
Other target Hamiltonians can be simulated by identifying a suitable mapping onto a qubit chain. For instance, the simulation of s = 1 models can be obtained by first encoding each spin 1 into a pair of qubits, and then restricting the dynamics to the triplet subspace. The most straightforward way to achieve this is by initializing the system in one of the triplet states and then simulate the evolution due to the target Hamiltonian  , which does not include the singlet at all, as proposed for instance in [132]. Although simple and rather inexpensive in terms of number of additional gates, this approach requires all the manipulations on the two qubits to be perfectly symmetric. Slight imperfections in the implemented unitary operators could bring the system outside from the triplet subspace, thus inducing leakage. To make the simulation more robust against this kind of errors, one could include in the target Hamiltonian a strong ferromagnetic coupling between the two qubits encoding the same spin 1 [15], which has the effect to clearly split the singlet states from the triplets of interest. In both cases, one than needs to re-write s = 1 operators into
, which does not include the singlet at all, as proposed for instance in [132]. Although simple and rather inexpensive in terms of number of additional gates, this approach requires all the manipulations on the two qubits to be perfectly symmetric. Slight imperfections in the implemented unitary operators could bring the system outside from the triplet subspace, thus inducing leakage. To make the simulation more robust against this kind of errors, one could include in the target Hamiltonian a strong ferromagnetic coupling between the two qubits encoding the same spin 1 [15], which has the effect to clearly split the singlet states from the triplets of interest. In both cases, one than needs to re-write s = 1 operators into 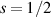 ones acting on dimers. For instance, the simulation of a zero field splitting Hamiltonian on a single spin 1
ones acting on dimers. For instance, the simulation of a zero field splitting Hamiltonian on a single spin 1 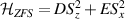 becomes (apart from a constant)
becomes (apart from a constant) 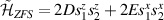 , where
, where 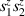 can be simulated as outlined above, while
can be simulated as outlined above, while 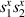 term can be obtained starting from
term can be obtained starting from  by a reference frame change, i.e. by applying
by a reference frame change, i.e. by applying  gates. The quantum simulation of this model, yielding tunneling of the magnetization for a spin 1 prepared e.g. into a
gates. The quantum simulation of this model, yielding tunneling of the magnetization for a spin 1 prepared e.g. into a 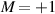 state, was proposed for the pair of nuclear qudits in the (VO)2 dimer described below. The same ideas can be extended to the simulation of generic spin
state, was proposed for the pair of nuclear qudits in the (VO)2 dimer described below. The same ideas can be extended to the simulation of generic spin  models, using 2s qubits or molecular qudits to encode each s unit.
models, using 2s qubits or molecular qudits to encode each s unit.
Finally, besides spin models, the present setup can simulate the dynamics associated with fermionic systems, such as the one-dimensional Hubbard model 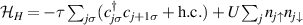 , with
, with  fermionic operators and
fermionic operators and 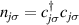 . The most common way to map fermionic into qubit operators is via the Jordan–Wigner (JW) transformation (see appendix
. The most common way to map fermionic into qubit operators is via the Jordan–Wigner (JW) transformation (see appendix 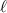 ) of spin operators [266, 267]. In practice, two qubits are required to encode each fermion. The resulting spin Hamiltonian includes
) of spin operators [266, 267]. In practice, two qubits are required to encode each fermion. The resulting spin Hamiltonian includes 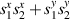 two-body terms among s or
two-body terms among s or 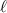 spins (originating from the hopping term in
spins (originating from the hopping term in 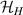 ), as well as
), as well as 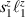 terms arising from the coupling term in
terms arising from the coupling term in 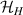 . Odd and even sites on the hardware qubit chain could be used to encode s and
. Odd and even sites on the hardware qubit chain could be used to encode s and 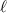 spins, but also more clever mappings can be found, as shown in [15]. Note that for the here-examined one-dimensional problem, all σz
operators in the JW mapping (equation (F1c
)) cancel and only two-body terms remain, thus greatly simplifying the problem compared to the multi-band or to the multi-dimensional Hubbard model.
spins, but also more clever mappings can be found, as shown in [15]. Note that for the here-examined one-dimensional problem, all σz
operators in the JW mapping (equation (F1c
)) cancel and only two-body terms remain, thus greatly simplifying the problem compared to the multi-band or to the multi-dimensional Hubbard model.
We conclude this subsection by noting that, being based on a potentially large array of molecules whose geometry reflects that of the target system, only controlled by global fields, this platform shares some features typical of analog QSs, which could significantly ease its practical implementation. Remarkably, also the final output of a simulation can be extracted from expectation values of observables on the whole ensemble, such as the total magnetization. Although not as universal as a fully digital QS, the proposed architecture allows one to simulate many interesting physical models and could be extended also multi-dimensional problems either by considering a spin array with the same dimension or by resorting to a more complex and less parallel implementation, without changing the hardware topology neither requiring local control.
6.1. Suitable compounds for proof-of-principle implementations
As already mentioned in section 4.3, simplified versions of the architecture described above were proposed in the following years. In particular, two families of Cr7Ni dimers with an interposed spin 1/2 switch (see figure 3(c)), and Cr7Ni rings arranged in either a parallel or slightly tilted configuration, were investigated in [211]. The former restricts the classes of target Hamiltonians which can be simulated to those invariant by permutation of the two-qubits, while the latter (see figure 9(a)) would allow one to distinguish them and hence would perfectly fit the AB scheme described above. Both systems were used to numerically simulate the transverse field Ising model [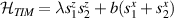 ] with 10 Trotter steps, corresponding to the subsequent implementation of 10 two-qubit and 20 single-qubit operators. This example constitutes a feasible proof-of-principle experiment, where the final output could be obtained by measuring the magnetization of the molecular crystal after the pulse sequence implementing the simulation. This lasts about 350 ns, a time which is ~ one order of magnitude shorter than typical coherence times of deuterated Cr7Ni rings [118]. This makes decoherence practically ineffective on the simulated magnetization, which reproduces very well the expected behavior, as shown in figure 9(b).
] with 10 Trotter steps, corresponding to the subsequent implementation of 10 two-qubit and 20 single-qubit operators. This example constitutes a feasible proof-of-principle experiment, where the final output could be obtained by measuring the magnetization of the molecular crystal after the pulse sequence implementing the simulation. This lasts about 350 ns, a time which is ~ one order of magnitude shorter than typical coherence times of deuterated Cr7Ni rings [118]. This makes decoherence practically ineffective on the simulated magnetization, which reproduces very well the expected behavior, as shown in figure 9(b).
Figure 9. (a) Simplified elementary unit of the QS platform proposed in [15], consisting of a pair of Cr7Ni qubits linked via a single ion. Different arrangements of the two rings (here orthogonal) can be obtained [211]. (b) Quantum simulation of the magnetization 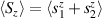 in the transverse field Ising model [
in the transverse field Ising model [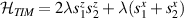 ], including the full sequence of pulses (blue circles) and the effect of decoherence with
], including the full sequence of pulses (blue circles) and the effect of decoherence with  s (red), compared with the expected evolution after Suzuki–Trotter (ST) decomposition using n = 10 (continuous black line, in good agreement with the exact evolution induced by
s (red), compared with the expected evolution after Suzuki–Trotter (ST) decomposition using n = 10 (continuous black line, in good agreement with the exact evolution induced by  , dashed line). (c) Elementary two-qubit unit of an alternative architecture, with a redox-active Ru2Co triangle acting as switch of the effective XY interaction between two Cr7Ni qubits. (d) Quantum simulation of the magnetization in the Heisenberg model in a magnetic field [
, dashed line). (c) Elementary two-qubit unit of an alternative architecture, with a redox-active Ru2Co triangle acting as switch of the effective XY interaction between two Cr7Ni qubits. (d) Quantum simulation of the magnetization in the Heisenberg model in a magnetic field [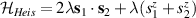 ], including also the measured values of T2 (red circles). Here no Suzuki–Trotter decomposition is needed. (e) (VO)2 dimer used as an electron-mediated nuclear spin quantum simulator, where the electronic spin dimer is used to switch on and off two-qubit gates between the nuclear spin qubits. (f) Quantum simulation of the tunneling of the magnetization in a spin 1 system, target Hamiltonian
], including also the measured values of T2 (red circles). Here no Suzuki–Trotter decomposition is needed. (e) (VO)2 dimer used as an electron-mediated nuclear spin quantum simulator, where the electronic spin dimer is used to switch on and off two-qubit gates between the nuclear spin qubits. (f) Quantum simulation of the tunneling of the magnetization in a spin 1 system, target Hamiltonian 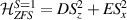 . Numerical simulations in panels (b), (d), (f) were obtained using system parameters of complexes (a), (c), (e), respectively, and initializing the system in state
. Numerical simulations in panels (b), (d), (f) were obtained using system parameters of complexes (a), (c), (e), respectively, and initializing the system in state 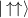 . (e), (f) Reproduced with permission from [132]. CC BY-NC 3.0.
. (e), (f) Reproduced with permission from [132]. CC BY-NC 3.0.
Download figure:
Standard image High-resolution imageAn alternative two-qubit elementary unit of a molecular quantum simulator is shown in figure 9(c). As in the scheme of figure 3(d), the switch between a pair of Cr7Ni rings is here provided by a redox active unit (a Ru2Co triangle) which in the oxidized state is diamagnetic and can be reversibly reduced into an effective  [212]. As illustrated in section 4.2, this scheme allows one to implement an iSWAP
[212]. As illustrated in section 4.2, this scheme allows one to implement an iSWAP gate, corresponding to the time evolution induced by an interaction term
gate, corresponding to the time evolution induced by an interaction term  between the two qubits. This interaction can be easily transformed into analogous
between the two qubits. This interaction can be easily transformed into analogous 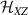 or
or 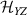 by combining the time evolution
by combining the time evolution 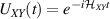 with suitable
with suitable  gates on both qubits. In particular, one can easily show that
gates on both qubits. In particular, one can easily show that 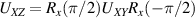 and
and 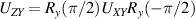 . Then, since
. Then, since ![$[\mathcal{H}_{XZ},\mathcal{H}_{XY}] = [\mathcal{H}_{XZ},\mathcal{H}_{YZ}] = [\mathcal{H}_{YZ},\mathcal{H}_{XY}] = 0$](https://content.cld.iop.org/journals/0034-4885/87/3/034501/revision1/ropad1f81ieqn298.gif) , the simulation of the Heisenberg coupling can be obtained by the product
, the simulation of the Heisenberg coupling can be obtained by the product 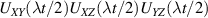 . Numerical simulations reported in figure 9(e) with real system parameters (including also the measured values of T2) show a very good agreement with the exact time evolution, thus making also the system of figure 9(d) promising for proof-of-principle experiments on a molecular crystal.
. Numerical simulations reported in figure 9(e) with real system parameters (including also the measured values of T2) show a very good agreement with the exact time evolution, thus making also the system of figure 9(d) promising for proof-of-principle experiments on a molecular crystal.
Nuclear spin-based quantum simulators can also be envisaged, where hyperfine-coupled electronic spins mediate the effective interaction between a pair of nuclear spins. To this end, a promising compound was synthesized [132], consisting of a symmetric VO dimer where the two electronic spins are coupled by a dipole-dipole interaction (see figure 9(e)). Qubits are encoded into the lowest energy states ( ) of the two
) of the two  nuclei. Along the same lines of the scheme described in figure 3(c), here the switch of the interaction between the nuclei is provided by the electronic spin dimer. Indeed, the effective qubit–qubit coupling can be turned on by a fast 2π microwave pulse dependent on the state of the two nuclear spins via the hyperfine interaction, resonant with the electronic spin transition
nuclei. Along the same lines of the scheme described in figure 3(c), here the switch of the interaction between the nuclei is provided by the electronic spin dimer. Indeed, the effective qubit–qubit coupling can be turned on by a fast 2π microwave pulse dependent on the state of the two nuclear spins via the hyperfine interaction, resonant with the electronic spin transition 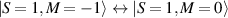 . The use of nuclear instead of electronic spins for the encoding protects information from decoherence. In parallel, two-qubit gates are implemented much faster than in standard NMR quantum computing approaches, because the effective coupling is mediated by electronic spin excitations. The VO dimer [132] was proposed as a quantum simulator of the tunneling of the magnetization in a spin 1 system, induced in an axial spin Hamiltonian by a rhombic term
. The use of nuclear instead of electronic spins for the encoding protects information from decoherence. In parallel, two-qubit gates are implemented much faster than in standard NMR quantum computing approaches, because the effective coupling is mediated by electronic spin excitations. The VO dimer [132] was proposed as a quantum simulator of the tunneling of the magnetization in a spin 1 system, induced in an axial spin Hamiltonian by a rhombic term 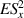 . Results are reported in figure 9(e), in very good agreement with the exact behavior (continuous line), with the inclusion of the measured
. Results are reported in figure 9(e), in very good agreement with the exact behavior (continuous line), with the inclusion of the measured 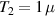 s.
s.
Another interesting application connected with quantum simulations is the adiabatic quantum algorithm proposed in [268]. The scheme was applied to a phthalocyanine molecule containing three electron spins on NO radicals and to a trans-glutaconic acid radical molecule [269] embedding one electron spin bus qubit and two nuclear client qubits [201]. The algorithm solves the factorization problem using fewer qubits compared to Shor's and is based on defining an adiabatic path from an initial hardware Hamiltonian to a target one whose ground state encodes the solution of the optimization problem [268]. The unitary evolution bringing the system to such a ground state is obtained in [269] by a Suzuki–Trotter decomposition of the target Hamiltonian evolution into a sequence of required microwave/radiofrequency pulses.
6.2. Hardware-efficient encodings based on molecular spin qudits
The larger Hilbert space of qudits can provide additional resources for quantum simulations, enabling to address problems involving quantum objects with many degrees of freedom, like nuclear or bosonic Hamiltonians [230, 231]. Indeed, despite its utmost importance for applications ranging from solid-state to high-energy Physics, the quantum simulation of models including fermionic or bosonic fields is usually inefficient on a qubit register. Indeed, on the one hand JW mapping leads in general to non-local many-body interactions in the resulting spin Hamiltonian. On the other hand, standard techniques to encode a bosonic mode into qubits either employ an exponentially large Hilbert space [270] (with a number of qubits equal to the number of boson states) or require non-local interactions between distant qubits in the array [271, 272].
Recently, a working proof-of-concept quantum simulator, based on an ensemble of nuclear 173Yb(trensal) qudits manipulated with multi-frequency radiofrequency pulses, has been realized [17]. The operativity of the simulator is demonstrated by implementing the quantum simulation of two representative problems, reproducing the correct physical behavior in both cases: an integer spin S subject to quantum tunneling of the magnetization and the transverse-field Ising model.
In general, molecular spin qudits can be used to greatly simplify the QS of multi-level problems. For instance, their multi-level structure can encode a boson mode, with the qudit levels representing the number of boson states (truncated to the number of qudit levels), as done in [231]. This scheme greatly reduces both the complexity of operations and the number of physical computational units, compared to the aforementioned qubit implementations. In particular, the Authors considered the so-called Rabi model, describing the atom-photon interaction via the Hamiltonian 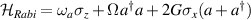 , with
, with 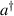 (a) bosonic creation (annihilation) operators, satisfying
(a) bosonic creation (annihilation) operators, satisfying ![$[a,a^\dagger] = 1$](https://content.cld.iop.org/journals/0034-4885/87/3/034501/revision1/ropad1f81ieqn307.gif) . It was shown how to simulate
. It was shown how to simulate  , even in the ultra-strong coupling regime (
, even in the ultra-strong coupling regime (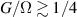 ), by employing a spin S qudit modeling the photon, coupled to a spin 1/2, describing the two-level atom.
), by employing a spin S qudit modeling the photon, coupled to a spin 1/2, describing the two-level atom.
An example assuming a simple spin 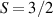 qudit is reported in figure 10. Green (black) arrows indicate transitions (induced by suitable microwave pulses) between qubit (qudit) states. The coupling between the two spins makes the excitation of each of the two units dependent on the state of the other, thus enabling full control of the system. This was exploited to compute first the ground state energy (by the variational quantum eigensolver algorithm [273], as shown in figures 10(b) and (c)) and then the time evolution of observables on the target system such as average photon number or atom excitation in a wide range of
qudit is reported in figure 10. Green (black) arrows indicate transitions (induced by suitable microwave pulses) between qubit (qudit) states. The coupling between the two spins makes the excitation of each of the two units dependent on the state of the other, thus enabling full control of the system. This was exploited to compute first the ground state energy (by the variational quantum eigensolver algorithm [273], as shown in figures 10(b) and (c)) and then the time evolution of observables on the target system such as average photon number or atom excitation in a wide range of 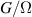 . Simulation of the hardware dynamics under the sequence of microwave pulses implementing the proposed procedures and using parameters of existing molecular systems (also including decoherence) demonstrate the effectiveness of the proposed approach. It is worth noting that this qudit-based approach could be exploited to simulate a wide range of models, including gauge fields, spin-phonon couplings and fermionic systems.
. Simulation of the hardware dynamics under the sequence of microwave pulses implementing the proposed procedures and using parameters of existing molecular systems (also including decoherence) demonstrate the effectiveness of the proposed approach. It is worth noting that this qudit-based approach could be exploited to simulate a wide range of models, including gauge fields, spin-phonon couplings and fermionic systems.
Figure 10. (a) Sequence of pulses used to fully control the coupled qudit–qubit system. In the level diagram, the energy levels of the qudit in an axial spin Hamiltonian are indicated (labeled by 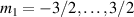 ), with different colors corresponding to different states (
), with different colors corresponding to different states (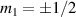 ) of the qubit and the corresponding mapping to the photon number reported on the right. Allowed transitions between qubit/qudit states are represented by arrows. (b) Variational-quantum eigensolver algorithm used to minimize the expectation value of the target Hamiltonian
) of the qubit and the corresponding mapping to the photon number reported on the right. Allowed transitions between qubit/qudit states are represented by arrows. (b) Variational-quantum eigensolver algorithm used to minimize the expectation value of the target Hamiltonian  , for
, for 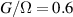 and
and 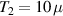 s. Red dashed line is the exact result, very close to the value obtained in the noisy simulations (blue dashed line), using the sequence of gates reported in the circuit in the inset. (c) Ground state energy E0 as a function of
s. Red dashed line is the exact result, very close to the value obtained in the noisy simulations (blue dashed line), using the sequence of gates reported in the circuit in the inset. (c) Ground state energy E0 as a function of 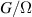 . Inset: average atom excitations/number of photons. Dashed lines: expected exact results; continuous lines: after truncation of the maximum photon number to 4 (i.e. the number of qudit levels); dots: noiseless variational quantum eigensolver results; diamonds: simulations performed on the hardware, with parameters reported in [231]. Reproduced from [231]. CC BY 3.0.
. Inset: average atom excitations/number of photons. Dashed lines: expected exact results; continuous lines: after truncation of the maximum photon number to 4 (i.e. the number of qudit levels); dots: noiseless variational quantum eigensolver results; diamonds: simulations performed on the hardware, with parameters reported in [231]. Reproduced from [231]. CC BY 3.0.
Download figure:
Standard image High-resolution image6.3. Quantum simulation of open systems
Although already envisioned by Lloyd [274], the quantum simulation of open systems has so far been much less explored. Nevertheless, it represents a very important objective. Indeed, it would allow one to understand complex behaviors related to relaxation or decoherence, which are at the basis of fundamental phenomena such as photosynthetic processes or transport and which must be necessarily kept under control in the design of novel quantum technologies. Unfortunately, these incoherent processes arise from the interaction of a relatively small subset of system qubits ( ) with a very large number of environment (
) with a very large number of environment ( ) degrees of freedom. Although the overall
) degrees of freedom. Although the overall 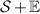 dynamics is still governed by a Schrödinger equation and hence could in principle be simulated as described in the previous section, the need to include a huge collection of qubits to model the bath makes this approach unfeasible.
dynamics is still governed by a Schrödinger equation and hence could in principle be simulated as described in the previous section, the need to include a huge collection of qubits to model the bath makes this approach unfeasible.
Therefore, one needs to focus on the dissipative dynamics of the reduced system density matrix, described by a completely-positive trace-preserving map 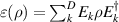 with suitable Kraus operators Ek
, and develop proper techniques to simulate it on a quantum hardware. A common approach [275] is based on implementing a unitary dynamics on an extended register (including system qubits and log2
D additional environment ones) which generates
with suitable Kraus operators Ek
, and develop proper techniques to simulate it on a quantum hardware. A common approach [275] is based on implementing a unitary dynamics on an extended register (including system qubits and log2
D additional environment ones) which generates  -
- entanglement, and then re-initializing
entanglement, and then re-initializing  qubits through local measurements [276, 277]. This last irreversible step makes the resulting dynamics on
qubits through local measurements [276, 277]. This last irreversible step makes the resulting dynamics on  non-unitary. This general approach allows one to perform a quantum simulation of both coherent and incoherent dynamics by implementing a series of dynamical maps [278] or (equivalently) by performing a digital Suzuki–Trotter decomposition of the Liouvillian operator [277]. However, due to the need to reset a subset of qubits during the simulation of each incoherent step (usually done via projective measurements), it would require to address individual-molecules (see section 8), at difference from the proposals discussed above, which could instead also be implemented on molecular crystals. A possibility in this direction is offered by a novel three-qubit supra-molecule [279], where a Cr7Ni is interposed between a Cu2+ porphyrin and a nitroxide. In this case, the very different relaxation times T1 between the constituents molecular spins (24 µs for Cr7Ni, tens to a hundred ms for the external spins) enabled to propose the system as a simulator of the incoherent dynamics of the two external qubits, with the central Cr7Ni mimicking the environment (
non-unitary. This general approach allows one to perform a quantum simulation of both coherent and incoherent dynamics by implementing a series of dynamical maps [278] or (equivalently) by performing a digital Suzuki–Trotter decomposition of the Liouvillian operator [277]. However, due to the need to reset a subset of qubits during the simulation of each incoherent step (usually done via projective measurements), it would require to address individual-molecules (see section 8), at difference from the proposals discussed above, which could instead also be implemented on molecular crystals. A possibility in this direction is offered by a novel three-qubit supra-molecule [279], where a Cr7Ni is interposed between a Cu2+ porphyrin and a nitroxide. In this case, the very different relaxation times T1 between the constituents molecular spins (24 µs for Cr7Ni, tens to a hundred ms for the external spins) enabled to propose the system as a simulator of the incoherent dynamics of the two external qubits, with the central Cr7Ni mimicking the environment ( ). After generating an entangled
). After generating an entangled  -
- state by selective resonant pulses, the
state by selective resonant pulses, the  qubit is re-initialized by waiting for its relatively fast relaxation, thus obtaining the reduced incoherent dynamics of
qubit is re-initialized by waiting for its relatively fast relaxation, thus obtaining the reduced incoherent dynamics of  . To be more specific, relaxation of the
. To be more specific, relaxation of the  qubit must be faster then the
qubit must be faster then the  qubits coherence but slower than
qubits coherence but slower than  -
- manipulations.
manipulations.
Alternatively, one can extract the final reduced  density matrix after simulation of the incoherent dynamics by full state tomography of only
density matrix after simulation of the incoherent dynamics by full state tomography of only  qubits, thus in fact summing over all possible
qubits, thus in fact summing over all possible  states, as proposed in the context of NMR quantum computing [275]. This latter method can be implemented on an ensemble of molecules and hence it is well suited to the molecular crystals described above, without requiring single-molecule addressing. A scheme for the quantum simulation of decoherence following this line was conceived, based on the five-qubit supra-molecule synthesized in [155] and shown in figure 11(a). The molecule consists of a chain of alternating Cu2+ and Cr7Ni qubits with tailored weak and strong interactions. In particular, the larger coupling identifies a core of two
states, as proposed in the context of NMR quantum computing [275]. This latter method can be implemented on an ensemble of molecules and hence it is well suited to the molecular crystals described above, without requiring single-molecule addressing. A scheme for the quantum simulation of decoherence following this line was conceived, based on the five-qubit supra-molecule synthesized in [155] and shown in figure 11(a). The molecule consists of a chain of alternating Cu2+ and Cr7Ni qubits with tailored weak and strong interactions. In particular, the larger coupling identifies a core of two 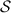 (Cr7Ni) qubits (S1 and S2 in figure 11(a)), with a switchable interaction provided by the central Cu2+ (M). The smaller one is exploited to simulate the weak coupling of the system with the environment, represented by the two external Cu2+ (E1, E2). As a prototypical test case, the Authors considered the simulation of decoherence acting on an entangled Bell pair, a typical resource for quantum teleportation experiments. Preparation of the Bell pair is achieved by combining a two-qubit controlled-Z gate (achieved by an excitation of the central M switch dependent on the state of both S1 and S2) with symmetric rotations of S1 and S2. Then, pure dephasing is simulated by implementing an evolution of E
(Cr7Ni) qubits (S1 and S2 in figure 11(a)), with a switchable interaction provided by the central Cu2+ (M). The smaller one is exploited to simulate the weak coupling of the system with the environment, represented by the two external Cu2+ (E1, E2). As a prototypical test case, the Authors considered the simulation of decoherence acting on an entangled Bell pair, a typical resource for quantum teleportation experiments. Preparation of the Bell pair is achieved by combining a two-qubit controlled-Z gate (achieved by an excitation of the central M switch dependent on the state of both S1 and S2) with symmetric rotations of S1 and S2. Then, pure dephasing is simulated by implementing an evolution of E depending on the state of S
depending on the state of S , consisting of a rotation of the environment qubits followed by a cNOT gate between each Si
-Ei
pair. The simulation time (or the
, consisting of a rotation of the environment qubits followed by a cNOT gate between each Si
-Ei
pair. The simulation time (or the 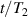 ratio) is controlled by the rotation angle. Results of the simulated error (arising from breaking entanglement via decoherence) in a quantum teleportation experiment, along with the sequence of required pulses, are reported in figures 11(b) and (c), showing a very good agreement with the expected behavior, even with the inclusion of experimentally measured coherence times of the individual sub-units.
ratio) is controlled by the rotation angle. Results of the simulated error (arising from breaking entanglement via decoherence) in a quantum teleportation experiment, along with the sequence of required pulses, are reported in figures 11(b) and (c), showing a very good agreement with the expected behavior, even with the inclusion of experimentally measured coherence times of the individual sub-units.
Figure 11. (a) Structure of the 5-spin quantum simulator with the Cr7Ni rings providing the system qubits S1 and S2, effectively interacting via a central Cu switch (M). Weakly coupled external Cu ions (E1, E2) are used to encode the environment. (b) Simulated time evolution (colored symbols) of the error in a quantum teleportation experiment for S1-S2 prepared in 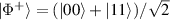 or
or 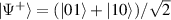 , including the measured values of T2 on Cr7Ni and Cu sub-units and compared with the ideal trend (lines). (c) Sequence of pulses for simulation of each point, effectively entangling
, including the measured values of T2 on Cr7Ni and Cu sub-units and compared with the ideal trend (lines). (c) Sequence of pulses for simulation of each point, effectively entangling  and
and  . Reproduced from [155]. CC BY 4.0.
. Reproduced from [155]. CC BY 4.0.
Download figure:
Standard image High-resolution image7. The scale-up challenge: exploiting superconducting resonators
The Hilbert space offered by properly designed magnetic molecules provides a rich playground for proof-of-concept implementations of small scale algorithms and for testing the advantages brought about by encoding information in multidimensional qudits. In parallel, the methods outlined in section 4.3 to effectively switch on and off the mutual qubit–qubit interactions at the intra-molecular level are not sufficient to build a truly scalable architecture. Yet, in order to reach a level of complexity comparable to that achieved by other platforms and, even more, to exploit the integration potential offered by the molecular approach, one needs to work with individual molecules and wire up many of them coherently.
To this aim, the most promising route is to couple individual molecular spins to superconducting lines and resonators, taking advantages from the large developments of this architecture for the control of superconducting qubits [3]. Indeed, such a solid-state platform based on circuit quantum electrodynamics (cQED) offers the possibility to selectively address and coherently communicate many molecular spin qubits in a robust and reproducible device.
7.1. Coupling molecular spins to superconducting circuits
This technology takes the classic light–matter interaction problem to a chip, in which artificial 'atoms', typically solid state qubits, interact with radiation modes of superconducting resonant circuits [3, 280, 281]. The underlying Physics can be described with the Jaynes–Cummings Hamiltonian
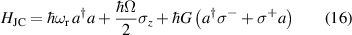
that includes a term for the isolated resonator, with  and a bosonic creation and annihilation operators and
and a bosonic creation and annihilation operators and  the frequency of the mode, a second one describing the isolated the qubit, where Ω is the transition frequency, plus a mutual interaction term. Here, G is the single qubit to single photon coupling strength. This scheme allows achieving coupling regimes that are beyond those attainable with 'real' atoms in three dimensional cavities. When G exceeds the decoherence rates of the qubit γ and of the superconducting cavity κ and the two subsystems are tuned to each other (
the frequency of the mode, a second one describing the isolated the qubit, where Ω is the transition frequency, plus a mutual interaction term. Here, G is the single qubit to single photon coupling strength. This scheme allows achieving coupling regimes that are beyond those attainable with 'real' atoms in three dimensional cavities. When G exceeds the decoherence rates of the qubit γ and of the superconducting cavity κ and the two subsystems are tuned to each other ( ), excitations over the ground state become hybridized light-matter bonding and antibonding states, whose energies differ by 2G. Besides, this strong coupling provides a tool to interface with the qubits. In particular, when the qubit and the resonator are detuned, i.e.
), excitations over the ground state become hybridized light-matter bonding and antibonding states, whose energies differ by 2G. Besides, this strong coupling provides a tool to interface with the qubits. In particular, when the qubit and the resonator are detuned, i.e.  , the resonance frequency depends on the state of the qubit, which allows performing quantum non-demolition measurements of the latter. In the same dispersive regime, the coupling of two qubits to the same cavity mode introduces an effective interaction between them, which can be exploited to generate two qubit gates.
, the resonance frequency depends on the state of the qubit, which allows performing quantum non-demolition measurements of the latter. In the same dispersive regime, the coupling of two qubits to the same cavity mode introduces an effective interaction between them, which can be exploited to generate two qubit gates.
The ability to dispersively read out and coherently communicate qubits by means of such a circuit QED scheme was first shown by experiments performed on superconducting qubits [282–284]. More recently, it has also been implemented successfully with semiconducting quantum dots [285, 286]. In both cases, the qubit-photon coupling is driven by the photon electric field, either directly as in the case of superconducting charge qubits or mediated via an effective spin-orbit interaction in the case of spin qubits in semiconductors. This interaction affords reaching strong coupling to individual qubits.
The situation is far more challenging in the case of 'real' spins, such as those present in magnetic molecules, which interact with the cavity magnetic field. The generalization of Jaynes–Cumming model (16) to this situation gives [287, 288]
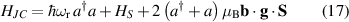
where the second term is the Hamiltonian of the spin qudit, the third accounts for its interaction via the spectroscopic tensor g with the resonator and b is the root mean squared (rms) value of the magnetic field generated by one of its photon modes. The latter depends on the rms value of the superconducting current in the resonator, which equals 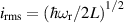 , where L is the effective resonator inductance. The role of G is now played by the transition matrix element [287]
, where L is the effective resonator inductance. The role of G is now played by the transition matrix element [287]
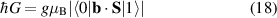
where  and
and 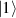 are the two logical qubit states (or the two lowest energy states of a qudit). Typical values of G for standard coplanar resonators are of the order of a few Hz, thus much smaller than the decoherence rates of molecular spin qubits
are the two logical qubit states (or the two lowest energy states of a qudit). Typical values of G for standard coplanar resonators are of the order of a few Hz, thus much smaller than the decoherence rates of molecular spin qubits  kHz and even smaller than the photon loss rate
kHz and even smaller than the photon loss rate  . The latter can reach values as low as 5–10 kHz for
. The latter can reach values as low as 5–10 kHz for 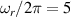 –10 GHz and resonator quality factors of 106, achievable with state-of-the-art technology.
–10 GHz and resonator quality factors of 106, achievable with state-of-the-art technology.
A way to reach stronger couplings is to work with macroscopic ensembles of N identical spins. Their collective coupling to each photon is then enhanced with respect to that of a single spin 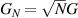 [289]. This trick has allowed observing strong coupling to diverse electronic spin systems, both inorganic [290–294] and molecular [18, 295, 296]. Also, high cooperativity coupling (
[289]. This trick has allowed observing strong coupling to diverse electronic spin systems, both inorganic [290–294] and molecular [18, 295, 296]. Also, high cooperativity coupling (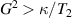 ) to the
) to the 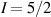 nuclear spins of 173Yb-trensal molecules has been achieved (figure 12) [19]. These results lay the basis for reading out the states in crystals of molecular spins. Combined with proper methods to coherently control them, e.g. by combining resonators with broad band transmission lines, and with suitable method to refocus the spin wave function, in order to compensate for the effect of the inhomogeneous broadening, they could afford proof-of-concept implementations of quantum simulations or even of quantum computing algorithms in these molecules. Yet, these are limited to the Hilbert space of one of them (the large number in the crystal would here serve only to amplifying the readout signal). Scaling up beyond this requires coherently coupling photons to individual molecular spins.
nuclear spins of 173Yb-trensal molecules has been achieved (figure 12) [19]. These results lay the basis for reading out the states in crystals of molecular spins. Combined with proper methods to coherently control them, e.g. by combining resonators with broad band transmission lines, and with suitable method to refocus the spin wave function, in order to compensate for the effect of the inhomogeneous broadening, they could afford proof-of-concept implementations of quantum simulations or even of quantum computing algorithms in these molecules. Yet, these are limited to the Hilbert space of one of them (the large number in the crystal would here serve only to amplifying the readout signal). Scaling up beyond this requires coherently coupling photons to individual molecular spins.
Figure 12. Circuit QED with molecular spin qudits. Top: illustrative image of a crystal of Yb-trensal molecules coupled to a lumped element superconducting resonator (left) and scheme of the electronuclear spin levels in the 173Yb-trensal isotopical derivative of this molecule (right), which encodes a d = 12 qudit. Bottom: color plots of the microwave transmission through a line coupled to a 2.93 GHz resonator (left) and to a 414 MHz (right) LC resonator. The results show transmission changes associated with a high cooperativity coupling of the resonator photon modes with the 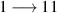 electronic spin transition and the
electronic spin transition and the 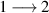 nuclear spin transition, respectively. Adapted with permission from [19].
nuclear spin transition, respectively. Adapted with permission from [19].
Download figure:
Standard image High-resolution imageEquation (18) provides a hint for the design of strategies to approach this goal, either by acting on the circuit, which determines the amplitude of b, or on the spin states. The very small coupling between spins and photons reflects the large mismatch that exists between the dimensions of the molecules and that of the resonant circuits. This suggests looking for methods which fully exploit the nanoscopic dimension of molecules by confining the magnetic component of the photon modes in mode volumes closer to the molecular size, thus contributing to locally enhance b. A direct 'brute force' approach, illustrated by figure 13, is to locally reduce the width w of the resonator transmission line [287, 297]. Near such a constriction, b scales as 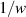 . Experiments performed on model free-radical spins deposited onto coplanar resonators [228] confirm that it is possible to reach G values close to 1 kHz for relatively modest photon frequencies (and energies)
. Experiments performed on model free-radical spins deposited onto coplanar resonators [228] confirm that it is possible to reach G values close to 1 kHz for relatively modest photon frequencies (and energies) 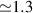 GHz. They also point to the crucial role that the molecule-circuit interface plays [179], as it limits how close individual molecules can be from the superconducting currents that generate b. Coplanar resonators impose stringent limitations on the design of the resonator geometry, which determines the effective mode volume of the resonator. A promising alternative is to use lumped- element LC resonators [19, 298–300] coupled to a readout transmission line. Since, near resonance, the magnetic energy stored in these circuits is equally shared between electric and magnetic components, working with low inductance resonators, e.g. with L made of a single micro-wire, leads to an enhancement of the current generated by each photon, thus also of G [301]. This approach, combined with state-of-the-art parametric amplifiers for the readout of the transmitted signal, has led to the implementation of magnetic resonance at the level of a few tens of spins [298–300]. Needless to say, the two methods can eventually be combined, which should allow taking G close to 100 kHz for
GHz. They also point to the crucial role that the molecule-circuit interface plays [179], as it limits how close individual molecules can be from the superconducting currents that generate b. Coplanar resonators impose stringent limitations on the design of the resonator geometry, which determines the effective mode volume of the resonator. A promising alternative is to use lumped- element LC resonators [19, 298–300] coupled to a readout transmission line. Since, near resonance, the magnetic energy stored in these circuits is equally shared between electric and magnetic components, working with low inductance resonators, e.g. with L made of a single micro-wire, leads to an enhancement of the current generated by each photon, thus also of G [301]. This approach, combined with state-of-the-art parametric amplifiers for the readout of the transmitted signal, has led to the implementation of magnetic resonance at the level of a few tens of spins [298–300]. Needless to say, the two methods can eventually be combined, which should allow taking G close to 100 kHz for 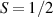 spins located on 20 nm constrictions fabricated in minimum inductance 5 GHz resonators [21].
spins located on 20 nm constrictions fabricated in minimum inductance 5 GHz resonators [21].
Figure 13. Left: image of a coplanar superconducting resonator (top) and zoom of the central transmission line (middle), in which a nanoconstriction has been fabricated by focused ion beam nanolithography. The nanobridge confines the supercurrents that generate the microwave photon field and locally enhances it (simulation at the bottom). Right: coupling energy G of single spins to photons modes of 5 GHz superconducting resonator as a function of the inductor line width w obtained with equation (18). For  spins, G is enhanced in the case of low inductance (L = 19 pH) LC lumped element resonators as compared to that achievable with coplanar resonators, showing the ability to maximize the coupling by circuit design. G also depends on the molecular spin S and on the sign of the magnetic anisotropy, showing the ability to tune the coupling by the molecular design of the spin states. Reprinted (adapted) with permission from [228]. Copyright (2020) American Chemical Society. Further permission related to the material excerpted should be directed to the ACS.
spins, G is enhanced in the case of low inductance (L = 19 pH) LC lumped element resonators as compared to that achievable with coplanar resonators, showing the ability to maximize the coupling by circuit design. G also depends on the molecular spin S and on the sign of the magnetic anisotropy, showing the ability to tune the coupling by the molecular design of the spin states. Reprinted (adapted) with permission from [228]. Copyright (2020) American Chemical Society. Further permission related to the material excerpted should be directed to the ACS.
Download figure:
Standard image High-resolution imageOne of the trademarks of the molecular approach is the ability to tune the spin properties via a careful choice of the molecular composition and structure. Therefore, besides enhancing G by designing the circuit properties, one can also attempt to improve it by molecular design of adequate spin states. From equation (18), it follows that the spin-photon matrix element can be enhanced in molecules having a spin 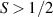 . In these systems, the level structure and the wavefunctions are determined, to a large extent, by the magnetic anisotropy. For simplicity, we consider a uniaxial spin system defined by a spin Hamiltonian
. In these systems, the level structure and the wavefunctions are determined, to a large extent, by the magnetic anisotropy. For simplicity, we consider a uniaxial spin system defined by a spin Hamiltonian 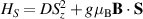 . The microwave photon field then couples states with spin projections m and
. The microwave photon field then couples states with spin projections m and 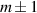 along the anisotropy axis z. Interestingly, the coupling strength between the lowest energy states depends on the sign of D [287]. For systems with easy axis anisotropy (D < 0, ground states
along the anisotropy axis z. Interestingly, the coupling strength between the lowest energy states depends on the sign of D [287]. For systems with easy axis anisotropy (D < 0, ground states 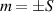 )
) 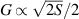 . An even larger enhancement is expected for systems with easy- plane anisotropy (D > 0), for which
. An even larger enhancement is expected for systems with easy- plane anisotropy (D > 0), for which 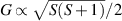 in the case of integer S (ground state m = 0) and
in the case of integer S (ground state m = 0) and 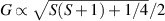 in the case of half-integer S (ground state
in the case of half-integer S (ground state 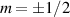 ).
).
Increasing S should not lead to a stronger decoherence, especially if we work on single molecules (where inhomogeneous broadening is not an issue) and we focus on transitions between 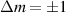 states. To further limit decoherence, one could encode the qudit in clock transition states arising at level anticrossings [168], see section 4.1. The spin-photon coupling is then dominated by the matrix element of Sz
between states
states. To further limit decoherence, one could encode the qudit in clock transition states arising at level anticrossings [168], see section 4.1. The spin-photon coupling is then dominated by the matrix element of Sz
between states 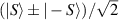 [227, 287], which leads to
[227, 287], which leads to 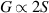 , with a further gain of a factor of two compared to an easy-plane molecular spin S. Being already protected from magnetic noise, such spin clock transitions simultaneously optimize spin coherence and the coupling to circuits [302], the two parameters that determine the strong coupling condition.
, with a further gain of a factor of two compared to an easy-plane molecular spin S. Being already protected from magnetic noise, such spin clock transitions simultaneously optimize spin coherence and the coupling to circuits [302], the two parameters that determine the strong coupling condition.
7.2. Building a scalable device
Once a strong spin-photon coupling is reached, the basic idea to scale-up a hybrid quantum processor with molecular spins integrated in a solid state device (see also [8, 21, 227]) is illustrated in figure 14. It consists of a superconducting circuit hosting multiple magnetic molecules [21]. The nodes of the quantum processor are defined by nanoscopic constrictions fabricated in the inductor line of a lumped element resonator. Spins located at these nanobridges are coherently controlled by suitably shaped local microwave pulses generated by open transmission lines. Their coupling to the resonator allows for the dispersive or resonant read out of the final states (see next section). Moreover, the resonator frequency is tuned by changing the magnetic flux through a (series of) SQUID connected in series with the inductor line, which is exploited for resonant two-qudit gates (see below) and also to better address the multiple transitions that characterize the qudits.
Figure 14. Schematic view of a hybrid quantum processor based on molecular spin qudits coupled to a superconducting circuit. Qudit states are coherently controlled by microwave pulses generated by open transmission lines. A tuneable LC resonator, whose resonance frequency can be modified by varying the magnetic flux through a SQUID connected in series with the inductor, dispersively reads out the spin states. The coupling to the resonator also generates effective couplings between quasi degenerate transitions in different qudits, thus introducing the ability of implementing conditional two-qudit gates.
Download figure:
Standard image High-resolution imageBut, more importantly for scaling up, the circuit can help to 'wire up' two of these basic units. The coupling of each spin to the resonator introduces an effective interaction between the two qudits, which depends on the relative tuning between their respective frequencies and that of the resonator. This dependence allows switching on and off this coupling, thus creating a sort of 'artificial molecular dimer' in a circuit. In the following, we examine two scenarios for such interaction, which correspond to the dispersive and resonant interaction regimes. They lead to distinct operation modes. While the former has been successfully applied to superconducting qubits, the latter might be more suitable to cope with the weaker coupling expected for molecular spins.
7.2.1. Photon mediated spin–spin interactions in the dispersive regime.
The coupling of multiple spins to a single resonator mode can be treated by an extension of equation (17) [288]. For illustrative purposes, we consider here the case of two spins S with uniaxial anisotropy and a geometry in which the external magnetic field points along the molecular axes z, while the cavity field is perpendicular to it. The Hamiltonian of the hybrid system is then

where 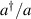 are bosonic creation/annihilation operators,
are bosonic creation/annihilation operators, 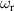 is the frequency of the resonator mode, Dj
are the ZFS parameters describing the uniaxial anisotropy of the two spins Sj
and
is the frequency of the resonator mode, Dj
are the ZFS parameters describing the uniaxial anisotropy of the two spins Sj
and 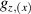 are the z(x) components of their spectroscopic splitting tensor. When
are the z(x) components of their spectroscopic splitting tensor. When 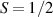 , the situation is analogous to that met with other qubits. If both spins are detuned from the resonator, i.e. the dispersive regime defined above applies to both, it is possible to derive from equation (19) a Hamiltonian for the two 'undressed' spins
, the situation is analogous to that met with other qubits. If both spins are detuned from the resonator, i.e. the dispersive regime defined above applies to both, it is possible to derive from equation (19) a Hamiltonian for the two 'undressed' spins
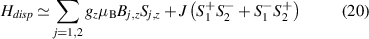
that includes an effective spin–spin interaction term with a constant
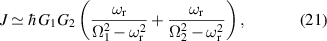
where  are the qubit-photon coupling strengths and
are the qubit-photon coupling strengths and 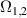 are the spin transition frequencies. This effective coupling connects transitions in the two spins (e.g.
are the spin transition frequencies. This effective coupling connects transitions in the two spins (e.g. 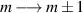 in spin 1 with
in spin 1 with  in spin 2). It induces a net evolution between these states provided that their frequencies are degenerate, i.e. when
in spin 2). It induces a net evolution between these states provided that their frequencies are degenerate, i.e. when 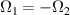 . This process takes place therefore at constant energy and involves no excitation or de-excitation of photon modes in the resonator. Energy conservation provides a way to switch on and off the interaction and, in arrays of N > 2 qubits, to select which two are on 'speaking terms', e.g. by tuning and de-tuning the frequencies at different sites via local magnetic fields. While the interaction is 'on', state
. This process takes place therefore at constant energy and involves no excitation or de-excitation of photon modes in the resonator. Energy conservation provides a way to switch on and off the interaction and, in arrays of N > 2 qubits, to select which two are on 'speaking terms', e.g. by tuning and de-tuning the frequencies at different sites via local magnetic fields. While the interaction is 'on', state  evolves into
evolves into 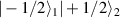 . Therefore, it allows for implementing a generalized iSWAP or
. Therefore, it allows for implementing a generalized iSWAP or  gate between the two qubits at a rate determined by
gate between the two qubits at a rate determined by 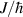 .
.
This result can be generalized to the case of  spin qudits, provided that the dispersive condition applies to all their transition frequencies [288]. The effective spin Hamiltonian (20) becomes then more complex and includes a state dependent coupling tensor. Different transitions
spin qudits, provided that the dispersive condition applies to all their transition frequencies [288]. The effective spin Hamiltonian (20) becomes then more complex and includes a state dependent coupling tensor. Different transitions 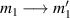 and
and 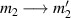 of the two qudits can be connected by adequately tuning their respective frequencies, thus giving rise to a variety of conditional gates between them. The gate operation rate scales
of the two qudits can be connected by adequately tuning their respective frequencies, thus giving rise to a variety of conditional gates between them. The gate operation rate scales 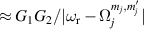 , with
, with 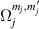 the
the 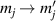 energy gap of spin j.
energy gap of spin j.
For both the qubit and qudit cases, it follows that making two-qudit operations faster than decoherence is more challenging, by the factor 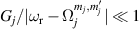 , than reaching strong coupling for each spin. This calls for exploring operation protocols beyond the dispersive limit.
, than reaching strong coupling for each spin. This calls for exploring operation protocols beyond the dispersive limit.
7.2.2. Photon mediated spin–spin interactions in the resonant regime.
An alternative proposal has been recently put forward [21] to speedup photon-mediated two-qudit gates, thus overcoming the aforementioned weakness. In [21], photons are actually exchanged by bringing the field in resonance with specific spin transitions, as outlined in figure 3(f). The only manipulation tool here is represented by the tunability of the resonator frequency, obtained via SQUID elements coupled to the circuit [303, 304]. The scheme assumes to have two distinguishable spins in a magnetic field, with at least one additional auxiliary level (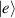 in figure 3(f)) besides those used for encoding the states of the two qudits. The effect of photon loss, more important than in the dispersive regime, is strongly limited by setting
in figure 3(f)) besides those used for encoding the states of the two qudits. The effect of photon loss, more important than in the dispersive regime, is strongly limited by setting 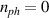 in the idle configuration. A two-qubit (qudit) cϕ gate is then implemented by (i) bringing the cavity into resonance with the first qubit energy gap. If the qubit is in the excited state
in the idle configuration. A two-qubit (qudit) cϕ gate is then implemented by (i) bringing the cavity into resonance with the first qubit energy gap. If the qubit is in the excited state 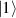 , a photon is resonantly emitted. Then (ii), the photon frequency is moved close to the
, a photon is resonantly emitted. Then (ii), the photon frequency is moved close to the 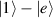 gap of the second qubit (detuned by an amount δ), yielding a (semi-)resonant Rabi oscillation between the two states. The photon is finally re-emitted and (iii) re-absorbed by the first qubit, once its frequency has been properly tuned to match its
gap of the second qubit (detuned by an amount δ), yielding a (semi-)resonant Rabi oscillation between the two states. The photon is finally re-emitted and (iii) re-absorbed by the first qubit, once its frequency has been properly tuned to match its 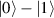 gap. At the end of the sequence, a phase ϕ (set by δ) is added to
gap. At the end of the sequence, a phase ϕ (set by δ) is added to 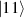 while all other two-qubit states are left unaffected, thus implementing a cϕ gate. A comparative plot of the performance of the resonant and dispersive schemes is shown in figure 15 for the quantum simulation of the Heisenberg Hamiltonian on a pair of qubits. This is a particularly good benchmark, since the simulation can be decomposed using an equal number of iSWAP
while all other two-qubit states are left unaffected, thus implementing a cϕ gate. A comparative plot of the performance of the resonant and dispersive schemes is shown in figure 15 for the quantum simulation of the Heisenberg Hamiltonian on a pair of qubits. This is a particularly good benchmark, since the simulation can be decomposed using an equal number of iSWAP or cϕ gates, as described in section 6. In this way, we focus on the capability of the two approaches, rather than on the specific algorithm decomposition. Simulations are performed by taking the best values for the spin-photon coupling reported in figure 13 and considering a SMM with S = 10 ground multiplet and easy-plane axial anisotropy, which provides a further enhancement of a factor ≈ 10 compared to a spin 1/2. In the upper panels the resulting local magnetization on the two spins is plotted, while in the lower ones the fidelity. Results obtained with the resonant approach are remarkably good, even with not too large
or cϕ gates, as described in section 6. In this way, we focus on the capability of the two approaches, rather than on the specific algorithm decomposition. Simulations are performed by taking the best values for the spin-photon coupling reported in figure 13 and considering a SMM with S = 10 ground multiplet and easy-plane axial anisotropy, which provides a further enhancement of a factor ≈ 10 compared to a spin 1/2. In the upper panels the resulting local magnetization on the two spins is plotted, while in the lower ones the fidelity. Results obtained with the resonant approach are remarkably good, even with not too large 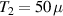 s. Then, although for short simulation angles
s. Then, although for short simulation angles 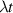 the fidelity of the two methods is similar, for larger
the fidelity of the two methods is similar, for larger  the resonant approach perform remarkably better. This is due to the practically constant gating times which are obtained by working in resonance (in the order of 3 µs), in contrast to their ~ linear increase up to
the resonant approach perform remarkably better. This is due to the practically constant gating times which are obtained by working in resonance (in the order of 3 µs), in contrast to their ~ linear increase up to 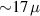 s when
s when  , as used here. All in all, large but reachable values of T2 enable the implementation of an accurate simulation of the model in the resonant regime.
, as used here. All in all, large but reachable values of T2 enable the implementation of an accurate simulation of the model in the resonant regime.
Figure 15. Quantum simulation of the Heisenberg model 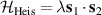 exploiting the resonant (a) or dispersive (b) approach, using a decomposition into either cϕ or iSWAP
exploiting the resonant (a) or dispersive (b) approach, using a decomposition into either cϕ or iSWAP gates. We report the local magnetization of the two spins
gates. We report the local magnetization of the two spins 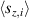 as a function of the simulation angle
as a function of the simulation angle  . Lower panels: associated fidelity. Different values of T2 are employed in the simulations, while for the resonator κ = 7.5 kHz,
. Lower panels: associated fidelity. Different values of T2 are employed in the simulations, while for the resonator κ = 7.5 kHz, 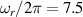 GHz and
GHz and 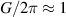 MHz. Reprinted (figure) with permission from [21], Copyright (2023) by the American Physical Society.
MHz. Reprinted (figure) with permission from [21], Copyright (2023) by the American Physical Society.
Download figure:
Standard image High-resolution imageJust as with the dispersive coupling, the resonant scheme can be extended to an arbitrary number of qudit levels and to couple molecules placed into different resonators (by enabling photon hopping between them [303]) in a completely scalable setup. Indeed, we could consider an array of resonators each hosting one or a few molecules, and characterized by a difference in their bare frequencies significantly larger than their mutual interaction. In that configuration, photon hopping is suppressed and molecules placed in different resonators can be independently addressed. In order to implement a conditional dynamics between distant molecules, one can tune the resonator frequencies to bring them into mutual resonance, thus enabling resonant photon exchange.
To conclude this section, it is worth noting that the proposed architectures based on coupling MNMs to superconducting chips fully exploit the best features of both molecular spins (namely their long coherence, chemical tunability and multi-level structure) and photons (i.e. their high mobility). Such a mobility would enable, for instance, implementation of entangling gates between distant molecules, without needing very demanding SWAP gates.
8. Single-molecule read-out
Controlling and reading out the spins of single molecules in a robust and reproducible manner is certainly challenging. In recent years, several experimental methods have been developed and tested, some with quite remarkable success. A rather direct approach, reminiscent of the spin to charge conversion methods developed for reading out spins in semiconductors [38, 39], is based on applying concepts and tools from molecular electronics to relate changes in electrical conductance with the different molecular spin states [40]. For this, molecules can be either anchored to a conducting channel, e.g. a carbon nanotube [41], which indirectly feels changes in the molecular magnetic moment, or, as it is schematically shown in figure 16, directly form a bridge between source and drain metallic nanoelectrodes opened by electromigration [40, 43, 44]. Although most molecules are insulating, some ligands can show a net conductivity when subject to adequate gate voltages. A remarkable example is provided by TbPc2 [181], shown in figure 16(a). The Tb3+ ion has a very well isolated electronic ground state defined by the maximum projections 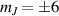 of its total angular momentum J = 6 and a nuclear spin
of its total angular momentum J = 6 and a nuclear spin 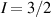 . Besides, the phthalocyanine (Pc) ligands have aromatic rings that provide conducting channels. These properties are preserved in isolated molecules, e.g. when they are evaporated onto a solid substrate [305]. The magnetic moment of the Tb3+ ion is exchange coupled to the electrons in the ligand. Then, the differential conductance through the latter shows jumps whenever the former reverses, by quantum tunneling. These tunneling events take place at avoided crossings between the different angular momentum projections, which occur at distinct magnetic fields for each nuclear spin state, thus providing a method to read out the latter [306], as sketched in figure 16(a). Besides, measuring the differential conductance allows reading out mJ
[164]. Hence, this setup allows for reading out both the molecular electronic and nuclear spin state (by measuring either the conductance or the magnetic fields at which the conductance shows jumps), finding in both cases very high readout fidelities, above 99 %.
. Besides, the phthalocyanine (Pc) ligands have aromatic rings that provide conducting channels. These properties are preserved in isolated molecules, e.g. when they are evaporated onto a solid substrate [305]. The magnetic moment of the Tb3+ ion is exchange coupled to the electrons in the ligand. Then, the differential conductance through the latter shows jumps whenever the former reverses, by quantum tunneling. These tunneling events take place at avoided crossings between the different angular momentum projections, which occur at distinct magnetic fields for each nuclear spin state, thus providing a method to read out the latter [306], as sketched in figure 16(a). Besides, measuring the differential conductance allows reading out mJ
[164]. Hence, this setup allows for reading out both the molecular electronic and nuclear spin state (by measuring either the conductance or the magnetic fields at which the conductance shows jumps), finding in both cases very high readout fidelities, above 99 %.
Figure 16. (a) Single-molecule transistor setup used to readout the state of a single TbPc2 molecule. The molecule bridges a nanoscopic gap between source and drain gold electrodes opened by electromigration. Electronic transport takes place mainly via the ligand molecules, whose charge state is controlled via a third gate terminal, bound to the central Tb3+ ion. (b) Cr4+ molecular color center, initialized and readout by laser pumping. (c) Dispersive readout of a molecular qubit exploiting a superconducting resonator. Transmission measurement in the dispersive regime allows for quantum non-demolition measurement of the state of the qubit, by inducing a shift of the bare resonator peak (dashed line), dependent on the qubit state (solid colored lines). (d) Corresponding resonant approach: by tuning the resonator frequency into resonance with the spin gap (top panels) a photon is emitted if the qubit was in 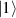 (left bottom panel) and it is not if the qubit was in
(left bottom panel) and it is not if the qubit was in 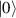 (right bottom panel), thus enabling qubit readout by single-photon detection. (e) CISS-enabled initialization (dark gray shaded area) and readout (light gray) of a molecular spin qubit, coupled to the acceptor in a donor-acceptor radical pair linked through a chiral bridge, as proposed in [20]. Photo-excitation of the donor into a singlet excited state yields spin-selective charge separation, where the transferred electron is polarized. Then, microwave pulses can be used to swap polarization from the acceptor to the qubit. In the readout stage, after possible qubit manipulations, the qubit state is swapped back to the acceptor and then only one of the two components recombines, thus in fact transforming the spin into a charge information, which can be detected by an electrometer such as a single-electron transistor. (a) Reprinted (figure) with permission from [44], Copyright (2017) by the American Physical Society. (b) Reproduced from [307]. CC BY 4.0.
(right bottom panel), thus enabling qubit readout by single-photon detection. (e) CISS-enabled initialization (dark gray shaded area) and readout (light gray) of a molecular spin qubit, coupled to the acceptor in a donor-acceptor radical pair linked through a chiral bridge, as proposed in [20]. Photo-excitation of the donor into a singlet excited state yields spin-selective charge separation, where the transferred electron is polarized. Then, microwave pulses can be used to swap polarization from the acceptor to the qubit. In the readout stage, after possible qubit manipulations, the qubit state is swapped back to the acceptor and then only one of the two components recombines, thus in fact transforming the spin into a charge information, which can be detected by an electrometer such as a single-electron transistor. (a) Reprinted (figure) with permission from [44], Copyright (2017) by the American Physical Society. (b) Reproduced from [307]. CC BY 4.0.
Download figure:
Standard image High-resolution imageThis experimental system can be combined with an excitation coil to control the states of the d = 4 qudit defined by the nuclear spin projections, whose energies are unequally spaced because of the nuclear quadrupolar interaction. Remarkably, the nuclear spin can also be coherently controlled via electric field pulses, thanks to the ability of the latter to modulate the hyperfine coupling with the Tb3+ electronic spin, which generates an effective microwave magnetic field [43]. This allowed the implementation of (sequences of) quantum operations [165] and paved the way for the first realization of a quantum algorithm, Grover's search algorithm, in a single molecular nanomagnet [44], as described in section 4.4. The same scheme has also been extended to explore the states of Tb2Pc3 molecules, hosting two mutually coupled magnetic centers [239].
In recent years, other interesting experimental methods have been explored, which have the potential to detect single molecular spins. A remarkable achievement is the realization of an optical interface with molecular spin qubits based on single Cr4+ ions [130, 307, 308]. Such 'molecular color centers' have a S = 1 spin that, combined with an easy plane magnetic anisotropy, gives rise to an m = 0 ground state singlet and a tunnel split 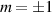 excited doublet, i.e. the same spin level scheme that characterizes NV− centers in diamond [45, 309]. The optical response is also analogous. Optical selection rules for excitation to and de-excitation from an excited S = 0 electronic state lead to a continuous pumping of the
excited doublet, i.e. the same spin level scheme that characterizes NV− centers in diamond [45, 309]. The optical response is also analogous. Optical selection rules for excitation to and de-excitation from an excited S = 0 electronic state lead to a continuous pumping of the 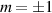 states by irradiating with a laser resonant with the transition to the S = 0 state (figure 16(c)). In addition, the photoluminiscence intensities observed after the laser excitation from the m = 0 and
states by irradiating with a laser resonant with the transition to the S = 0 state (figure 16(c)). In addition, the photoluminiscence intensities observed after the laser excitation from the m = 0 and 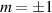 states are different. The first effect allows for the initialization of the spin state by light, whereas the second one affords reading out the spin state. A similar experiment was also recently reported on a mononuclear Eu3+ complex which thanks to very narrow optical lines allowed for optical spin initialization with 95% fidelity [308]. Even though the experiments reported to date have been performed on molecular crystals, i.e. on large spin ensembles, it seems feasible to approach the single spin detection level by improving the radiation lifetimes, e.g. via the coupling to optical cavities, or by chemically engineering narrower electronic states.
states are different. The first effect allows for the initialization of the spin state by light, whereas the second one affords reading out the spin state. A similar experiment was also recently reported on a mononuclear Eu3+ complex which thanks to very narrow optical lines allowed for optical spin initialization with 95% fidelity [308]. Even though the experiments reported to date have been performed on molecular crystals, i.e. on large spin ensembles, it seems feasible to approach the single spin detection level by improving the radiation lifetimes, e.g. via the coupling to optical cavities, or by chemically engineering narrower electronic states.
Although very appealing, these methods still lack the scalability of the circuit QED approach discussed in the previous section. In that scenario, techniques to read-out the state of individual molecules can also be devised. Similarly to photon-mediated two-qudit gates, also read-out can be operated either in the dispersive or in the resonant regime. The dispersive approach translates to molecular qudits the standard method employed to readout the state of superconducting qubits [280]. The idea is to exploit a shift of the resonator frequency induced by its dispersive coupling to a molecular spin qudit. Such a shift depends on the state of the qudit and hence can be exploited to assess the qudit state through transmission measurements on the resonator [310]. This can be understood by considering a molecular spin qubit coupled to a superconducting resonator, with the detuning 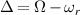 between the resonator frequency and the electronic spin gap significantly larger than G (but still
between the resonator frequency and the electronic spin gap significantly larger than G (but still 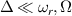 ). In this limit, one can derive [310] the effective Hamiltonian:
). In this limit, one can derive [310] the effective Hamiltonian:
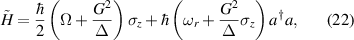
where the first term is the Stark/Lamb renormalization of the qubit gap, while the second shows the qudit-state dependent shift  of the bare resonator frequency ωr
. The latter can be detected by measuring the transmission of the resonator, as sketched in figure 16(c). The peak corresponding to the empty resonator (dashed lines) is moved either to the left or to the right (continuous lines), depending on the qubit state. The situation is easily generalized to a multi-level qudit with well distinguished gaps, in which case a peak is expected to appear at a different frequency for each qudit state [310]. Moreover, different qudits coupled to the same resonator can be selectively readout by tuning their transition frequency via local fields, thus moving them one at a time close to the resonator frequency. This, in turn, will also suppress the simultaneous two-qudit dispersive evolution.
of the bare resonator frequency ωr
. The latter can be detected by measuring the transmission of the resonator, as sketched in figure 16(c). The peak corresponding to the empty resonator (dashed lines) is moved either to the left or to the right (continuous lines), depending on the qubit state. The situation is easily generalized to a multi-level qudit with well distinguished gaps, in which case a peak is expected to appear at a different frequency for each qudit state [310]. Moreover, different qudits coupled to the same resonator can be selectively readout by tuning their transition frequency via local fields, thus moving them one at a time close to the resonator frequency. This, in turn, will also suppress the simultaneous two-qudit dispersive evolution.
The dispersive approach allows for a quantum non-demolition measurement of the state of a molecular spin qudit. Its limitation comes from the broadening of the resonance peaks (induced mainly by spin dephasing rates  ), which must be kept significantly smaller than the dispersive shift χ in order to achieve a high-fidelity readout. Moreover, the time needed for readout
), which must be kept significantly smaller than the dispersive shift χ in order to achieve a high-fidelity readout. Moreover, the time needed for readout 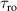 scales as
scales as 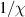 . With the best estimates for
. With the best estimates for 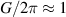 MHz from the previous section, this would lead to
MHz from the previous section, this would lead to 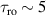 –
– s using high sensitivity detection stages, involving parametric amplification as done for superconducting circuits [311]. These values of
s using high sensitivity detection stages, involving parametric amplification as done for superconducting circuits [311]. These values of 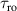 are still shorter than T1 and hence would in principle enable readout at the end of an algorithm. However, a small
are still shorter than T1 and hence would in principle enable readout at the end of an algorithm. However, a small 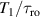 ratio limits the readout fidelity [39] and represents an important drawback for algorithms in which operations are conditioned by measurements outcomes, such as QEC.
ratio limits the readout fidelity [39] and represents an important drawback for algorithms in which operations are conditioned by measurements outcomes, such as QEC.
A more promising option comes again by operating in the resonant regime and exploiting the faster time-scale involved in resonant photon emission [21]. The scheme is outlined in figure 16(d). The frequency of the resonator embedding the molecular qudit is varied and brought into resonance with a specific qudit gap, e.g. the 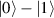 transition for a two-level qubit. Then, a photon is emitted (bright panel) and can be detected (and annihilated) by a single-photon counter only if the qubit was in the excited state
transition for a two-level qubit. Then, a photon is emitted (bright panel) and can be detected (and annihilated) by a single-photon counter only if the qubit was in the excited state 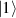 , ending up with the qubit in
, ending up with the qubit in 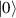 and no photons in the resonator. To restore the correct (projected) state of the qubit, one finally needs to apply a π pulse resonant with the qubit gap to bring back the qubit to the original
and no photons in the resonator. To restore the correct (projected) state of the qubit, one finally needs to apply a π pulse resonant with the qubit gap to bring back the qubit to the original  state. As a result, one gets a projective readout of the qubit. Since both photon detection and classical driving pulses can be rather fast [312],
state. As a result, one gets a projective readout of the qubit. Since both photon detection and classical driving pulses can be rather fast [312], 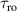 is here only limited by the time for resonant photon emission, i.e.
is here only limited by the time for resonant photon emission, i.e. 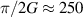 ns with
ns with 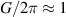 MHz. The scheme can be extended to any pair of qudit levels connected by a spin dipole matrix element. In the resonant regime, the effect of photon loss is expected to increase compared to the dispersive method, but the significant speedup strongly reduces its impact.
MHz. The scheme can be extended to any pair of qudit levels connected by a spin dipole matrix element. In the resonant regime, the effect of photon loss is expected to increase compared to the dispersive method, but the significant speedup strongly reduces its impact.
An alternative scheme to achieve single-molecule addressability and readout has been recently envisaged, based on exploiting the still little explored CISS effect [20]. The phenomenon shows an electron transmission through a chiral molecule depending on the projection of its spin along the chiral axis [313, 314]. It has been recently observed in isolated molecules in solution [315] and it is particularly evident at high (close to room) temperature [316–319]. This allows one to envision a molecular setup [20, 320] in which an electron donor and an electron acceptor are linked via a chiral bridge, as outlined in figure 16(e). An additional spin qubit can be linked to the acceptor. Within this platform, a novel spin-to-charge conversion method has been proposed, exploiting the dependence of the electron displacement on its spin projection. Such a conversion mechanism is not based on the small Zeeman splitting and hence operates also at much higher temperature compared to analogous approaches used to initialize and readout semiconductor qubits [39].
In particular, photo-excitation of the system can be used to achieve spin-selective charge separation (dark-gray shaded area in figure 16(e)), thus generating a radical pair with a well defined local spin polarization. The spin state of the acceptor can be swapped back and forth to the qubit by resonant microwave pulses (inset box in figure 16(e)), thus providing a way to initialize it even at room temperature, where the efficiency of the CISS effect in filtering the transferred electron spin is expected to be optimal [316–319].
To readout the qubit spin (light-gray shaded area in figure 16(e)), one can (i) swap the state of the qubit onto that of the acceptor and then (ii) induce spin-selective charge recombination by an external tool, such as an electric field or a laser pulse [20]. The final charge state of the donor therefore depends on the former spin of the qubit and can be readout by a sensitive electrometer, such as a readout quantum dot. Although based on an effect which is still not completely understood, this perspective approach would enable the readout of a single electronic spin at significantly higher temperatures, compared e.g. to [164, 306] or to the cQED approach [21].
9. Discussion and perspectives
A key characteristic of molecular magnetism is the strong and fruitful synergy between groups of physicists and chemists, who synthesized magnetic molecules targeted to fulfill the challenging requirements of quantum applications. Based on the achievements and open challenges discussed in the previous sections, we can now summarize what are the crucial advantages of the molecular approach and what are the steps that are still missing to realize a molecular spin quantum processor.
Compared to other players in the field, which have already reached a higher degree of maturity (in terms, for instance, of the number of qubits and gates which can be controlled), molecular spin systems display some distinctive and potentially disruptive features. Foremost, they are extremely tunable at the synthetic stage, enabling the realization of complex molecular and supramolecular structures where individual qudits are linked preserving their individual properties and coherence. This is particularly relevant for quantum simulation algorithms, most of which can be implemented even on molecular ensembles, without needing local addressability. With the perspective of building a general-purpose QC exploiting individual MNMs, each molecule can provide multiple accessible and engineerable low-energy states with potentially low decoherence. Moving from a qubit-based to a qudit-based logics helps in significantly simplifying certain quantum algorithms. Perhaps more importantly, this inherent redundancy also allows embedding quantum-error correction within each elementary unit of the quantum processor, a single molecule [8]. This latter feature could be the key to actually simplify the practical implementation of QEC, which represents a mandatory achievement to realize a general purpose QC. The multiple electronic states can also be exploited as resources for the implementation of certain operations. For instance, optical transitions that are present in some properly designed molecular systems provide means for the initialization and readout of spin states by laser pulses [130].
Decoherence represents a major challenge for the development of quantum technologies based on molecular spins. In an ensemble setup, it is dominated by reversible dephasing due to the slight inhomogeneity of the MNMs. Spin-echo techniques can remove this effect, which anyway will be absent in a single-molecule register setup. On the other hand, intrinsic coherence times of MNMs usually reflect proton spin fluctuations, and can be controlled and extended by proper chemical engineering of the ligand environment. Although in general the coherence times should still be improved, in some cases they have already overcome the threshold of 104 times the duration of elementary operations, another stepping stone for the physical implementation of a QC [22]. However, this has been achieved only on selected mononuclear compounds [121, 159], in which the ligand cage of the magnetic ion was chemically engineered to suppress decoherence (mainly by removing surrounding nuclear spins). Generalizing this approach to spins larger than 1/2 and to multi-spin systems still represents a chemical challenge. Nevertheless, theoretical models suggest that coherence can even be enhanced by properly choosing the hierarchy of spin–spin interactions in polymetallic clusters [156] and should be comparable to the case of a spin doublet for specific transitions in giant-spin molecules. This is especially true at the single molecule level, where broadening induced by distributions in the orientation of the anisotropy axes occurring in an ensemble does not matter. In addition, further improvements on coherence times are expected if individual molecules are deposited on surfaces, a much less noisy environment than a bulk crystal or a metal surface. Yet, a quantitative assessment of the impact of decoherence in the envisaged setup will require further targeted studies. Anyway, as with any platform, decoherence will ultimately limit the quantum volume attainable without error correction. The advantage of MNMs with respect to other platforms is that, on the one hand, decoherence is dominated by a single and relatively simple mechanism. On the other hand, the proposed QEC algorithms promise to tame it [120, 156, 170], even in a fault-tolerant way in perspective [265]. We stress that achieving fault-tolerant quantum computation represents the final goal for any platform, while all other error-mitigation strategies are only an intermediate step in this direction. The high level of control on the spin Hamiltonian granted by MNMs could make such a goal much closer.
Concerning actual implementations, it must be recognized that since the first proposals to use MNMs in quantum information [9], more than 20 years ago, experimental achievements have been lagging behind theoretical ones. Still, many significant experimental advances have been made in the past few years. These include the characterization and optimization of individual molecular units [13, 118, 121, 152, 158, 159, 168, 172], the realization of molecular and supramolecular structures hosting multiple and addressable spin qubits [16, 133, 135, 154, 155, 167, 208–210, 213, 220, 321], the coherent manipulation of spin dynamics via em pulses (e.g. Rabi oscillations) [125, 126, 196, 203, 322], elucidating the nature of decoherence sources and testing strategies to tame them [129, 152, 168, 180, 323], and demonstrating spin control and readout capabilities at the level of individual molecules by exploiting molecular electronics tools [43, 44, 49, 164, 165, 306]. Very recently, by using NMR techniques the first proof-of-principle quantum simulation on individual MNM qudits, via an ensemble quantum-computation paradigm has been demonstrated [17].
Yet, fewer experimental achievements have been obtained on the full readout and coherent control of multiple molecular units. The implementation of conditional gates in a register of qubits/qudits encoded in MNMs, which is a must for scaling up this technology, requires the capability to switch on at will a (weak) interaction between the two units involved. The integration of individual molecules into solid-state devices that exploit spin-to-charge conversion to extract the spin state from electron transport measurements [306] allowed the realization of an important milestone, represented by the manipulation and readout of an individual nuclear spin qudit within a single-molecule transistor [43, 44]. However, the difficulty to reproduce the experimental conditions and to address more than a single molecule makes the scalability of this architecture very challenging. At present, the most promising architecture to realize a scalable molecular spin quantum processor is based on an array of superconducting resonators, each hosting one or a few molecular spins potentially embedding QEC [21, 227]. This platform combines the requirements of scalability, individual molecule addressability and readout, and the possibility to implement two-qudit conditional gates in a completely switchable manner. Photons can be exploited not only to couple molecules in the same resonator, but also to easily entangle qudits far apart in the register, thanks to their mobility. Mediating two-qudit gates by means of circuit QED techniques presents clear advantages in the long term compared to the chemical route of synthesizing chains of weakly coupled molecular qubits. In the latter case mutual qubit–qubit couplings are hard to be completely switched off, making scalability challenging. The chemical approach can still be exploited to mediate interactions between a few qudits placed within the same resonator.
Even though some encouraging progress has been achieved by experiments on molecular spin ensembles coupled to superconducting resonators [18, 19, 178, 295, 296], the main limitation for exploiting circuit-QED techniques in this context is currently represented by reaching a strong-enough interaction between single spins and photons. The spin-photon coupling must be significantly larger than decoherence rates in order to faithfully implement both photon-mediated gates and qudit readout. This regime has not been fully achieved, but a clear route in this direction has been traced and has already yielded a gain of several orders of magnitudes in a few years [228]. Important steps forward are expected in the near future, by combining suitable chemical methods for the optimal integration of magnetic molecules onto superconducting surfaces and circuits [37, 179, 324, 325] with novel resonator designs [21, 301].
It is finally worth mentioning that the slowness of resonator-based qudit readout could be overcome by exploiting the novel CISS effect to achieve spin-to-charge conversion, as envisioned in [20]. Such a CISS-enabled readout block could be integrated into the molecular spin quantum processor, where superconducting resonators are still to be used for single-qudit manipulations and photon-mediated two-qudit gates.
All in all, although several milestones still need to be accomplished, a clear road-map for the next years can be traced. The basis for this road-map could be the blueprint for the molecular spin quantum processor presented in [21] and discussed above, with molecular spins integrated into a solid-state platform based on superconducting resonators.
Acknowledgments
We warmly thank many colleagues in the field of molecular magnetism for the fruitful collaborations and stimulating discussions, and among them in particular Roberta Sessoli for also helping us to improve the paper.
This work has received funding from the European Union Horizon 2020 research and innovation programme (FET-OPEN project FATMOLS) under Grant Agreement No. 862893, and from Fondazione Cariparma.
It was also funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.3—Call for tender No. 341 of 15/03/2022 of Italian Ministry of University and Research funded by the European Union—NextGenerationEU, award number PE0000023, Concession Decree No. 1564 of 11/10/2022 adopted by the Italian Ministry of University and Research, CUP D93C22000940001, Project title 'National Quantum Science and Technology Institute' (NQSTI).
FL acknowledges support from grant TED2021-131447B-C21 and from "Plan Complementario en Comunicación Cuántica", funded by MCIN/AEI/10.13039/501100011033, the European Union NextGenerationEU/PRTR and the CSIC Quantum Technology Platform PT-001.
We also acknowledge the European Research Council-Synergy project CASTLE (Project No. 101071533) funded by the Horizon Europe Programme.
Data availability statement
No new data were created or analysed in this study.
Appendix A: Gates from exchange interaction
A common situation in spin systems is to have pairs of spins interacting with a two-body Hamiltonian of the form 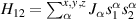 . The corresponding unitary evolution can be exploited to implement two-qubit gates. It is therefore useful to report its explicit form:
. The corresponding unitary evolution can be exploited to implement two-qubit gates. It is therefore useful to report its explicit form:
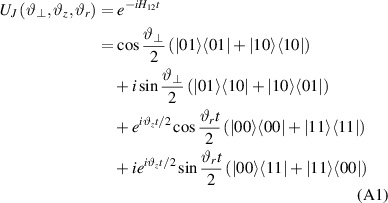
where we have introduced 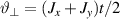 ,
, 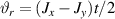 and
and 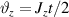 . In the case of a XY qubit–qubit coupling (
. In the case of a XY qubit–qubit coupling ( ,
, 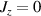 ), we obtain the so-called iSWAP
), we obtain the so-called iSWAP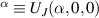 gate, which choosing
gate, which choosing 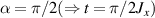 , reduces to the maximally entangling
, reduces to the maximally entangling 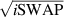 gate:
gate:
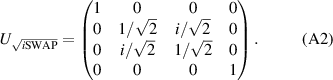
Appendix B: Universal set for qudits
Similarly to the case of qubits, a universal set of single-qudit gates can be easily identified by considering continuous rotations of arbitrary angles between pairs of states of the qudit. In particular, given a d dimensional qudit, we define planar rotations (PRs)  as
as
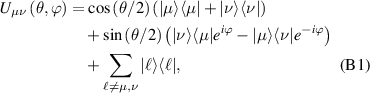
i.e. unitary transformations which only couple states 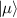 and
and 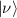 . One can show that the capability of implementing
. One can show that the capability of implementing 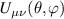 between pairs of consecutive levels is sufficient to achieve single-qudit universality [157, 238, 326]. In the case of a single spin S qudit, for instance,
between pairs of consecutive levels is sufficient to achieve single-qudit universality [157, 238, 326]. In the case of a single spin S qudit, for instance, 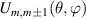 can be easily implemented by an electro-magnetic pulse resonant with
can be easily implemented by an electro-magnetic pulse resonant with 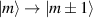 transition, characterized by the proper duration and phase, to set θ and ϕ, respectively. With more complex molecular qudits, where also transition between non-consecutive levels are allowed, more efficient decompositions of a general SU(d) rotation can be implemented, see section 4.4.
transition, characterized by the proper duration and phase, to set θ and ϕ, respectively. With more complex molecular qudits, where also transition between non-consecutive levels are allowed, more efficient decompositions of a general SU(d) rotation can be implemented, see section 4.4.
To complete the universal set, one needs to introduce also two-qudit operations. A particularly useful one is the qudit controlled-phase gate
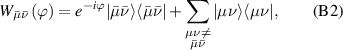
which adds the desired phase ϕ only to the 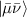 component of the two-qudit wave-function. In general, any controlled two-qudit rotation, combined with the capability of implementing an arbitrary single-qudit operation, form a universal set [232].
component of the two-qudit wave-function. In general, any controlled two-qudit rotation, combined with the capability of implementing an arbitrary single-qudit operation, form a universal set [232].
Another two-qudit gate (useful in the context of quantum simulation) is the qudit SWAP gate
gate
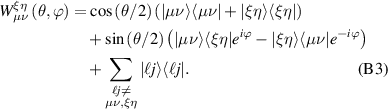
Appendix C: (Semi-)resonant driven dynamics of a spin system
The fundamental tool to process quantum information in molecular spin systems is represented by driving microwave (mw) or radio-frequency (rf) pulses inducing transitions between specific pairs of system eigenstates. The effect of these driving fields on the spin dynamics can be understood by starting from a driven two-level system and deriving analytical expressions for the time evolution of the probability amplitudes.
In particular, let us consider the system initialized in 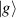 , and described by the static Hamiltonian
, and described by the static Hamiltonian 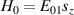 and subject to an oscillating pulse of the form
and subject to an oscillating pulse of the form 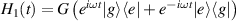 . The state at time t,
. The state at time t, 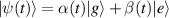 , can be analytically computed, e.g. by moving to a frame rotating at angular frequency ω, where the Hamiltonian
, can be analytically computed, e.g. by moving to a frame rotating at angular frequency ω, where the Hamiltonian 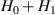 becomes time-independent, i.e.
becomes time-independent, i.e.  , with
, with 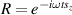 . The resulting probability amplitudes are given by
. The resulting probability amplitudes are given by
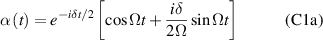
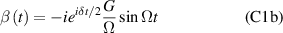
where 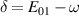 and
and 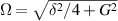 . In resonance, δ = 0,
. In resonance, δ = 0, 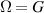 and the illustrated pulse implements an
and the illustrated pulse implements an 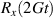 single-qubit gate.
single-qubit gate.
Off resonance, we only get a partial population transfer from 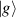 to
to 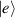 . This has an important application to implement a cϕ gate, where
. This has an important application to implement a cϕ gate, where 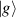 is one of the computational two-qubit states (typically
is one of the computational two-qubit states (typically 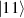 ) and
) and 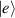 is an auxiliary level outside from the computational subspace [267], which is initially not populated and only exploited during the cϕ. In that case, a semi-resonant full-Rabi oscillation (lasting
is an auxiliary level outside from the computational subspace [267], which is initially not populated and only exploited during the cϕ. In that case, a semi-resonant full-Rabi oscillation (lasting 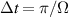 ) transfers population from
) transfers population from 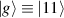 to
to 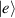 and back, adding a phase factor
and back, adding a phase factor 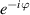 to
to 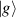 , with
, with 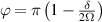 . A pulse implementing this transformation on
. A pulse implementing this transformation on 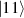 while leaving all other two-qubit states unaffected actually realizes a cϕ gate. This reduces to a cZ (i.e.
while leaving all other two-qubit states unaffected actually realizes a cϕ gate. This reduces to a cZ (i.e.  ) for δ = 0.
) for δ = 0.
Alternatively, the angle ϕ of the cϕ can be controlled by the phase difference between two resonant pulses used for excitation and de-excitation to the auxiliary state [211].
Appendix D: Incoherent dynamics
We here overview how to model the effect of noise, possibly corrupting the logical state of the register.
A widely-used and convenient way to describe the non-unitary evolution of an open quantum system is given by the operator-sum representation [1]:

with Ek
operators satisfying 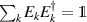 . This approach maps the initial state of the physical system, expressed by the density matrix ρ0, into the final state ρ. Alternatively, one can write a differential equation for the evolution of ρ in terms of some system operator which couple to the environment degrees of freedom. For instance, within the Born–Markov and secular approximations, the time evolution of ρ can be described by the Lindblad equation
. This approach maps the initial state of the physical system, expressed by the density matrix ρ0, into the final state ρ. Alternatively, one can write a differential equation for the evolution of ρ in terms of some system operator which couple to the environment degrees of freedom. For instance, within the Born–Markov and secular approximations, the time evolution of ρ can be described by the Lindblad equation
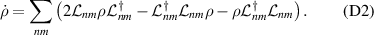
Although equation (D2) is usually deduced mathematically to guarantee complete positivity of ρ [327], the operators  can also be obtained from a microscopic modeling of the interaction between system and bath. They describe 'jumps' between eigenstates
can also be obtained from a microscopic modeling of the interaction between system and bath. They describe 'jumps' between eigenstates 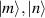 of the system Hamiltonian [328] induced by the coupling with the environment. For instance, in the case of relaxation without pure dephasing,
of the system Hamiltonian [328] induced by the coupling with the environment. For instance, in the case of relaxation without pure dephasing,  , with γnm
the transition probability between states
, with γnm
the transition probability between states 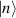 and
and 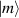 .
.
In the case of pure dephasing (the leading error for MNMs) 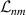 are diagonal operators, which do not alter the populations
are diagonal operators, which do not alter the populations 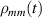 but only coherences of
but only coherences of 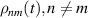 . In particular, for a set of weakly interacting spin 1/2 qubits
. In particular, for a set of weakly interacting spin 1/2 qubits 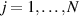 ,
, 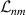 are practically equivalent to
are practically equivalent to 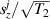 , while for a spin S ion subject to an axial Hamiltonian they correspond to
, while for a spin S ion subject to an axial Hamiltonian they correspond to 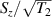 (see equation (10)). Note that an equivalent discrete description of pure dephasing on a spin 1/2 (the so-called phase-flip error in QEC) is obtained using Kraus operators
(see equation (10)). Note that an equivalent discrete description of pure dephasing on a spin 1/2 (the so-called phase-flip error in QEC) is obtained using Kraus operators 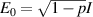 and
and 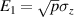 , with
, with 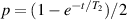 .
.
Appendix E: Metrics
In order to quantify the performance of a given quantum processor, it is useful to introduce the fidelity as a figure of merit of how close are two quantum states. We define the fidelity as [1]:
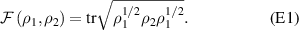
Typically, we will deal with situations in which 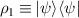 is a known pure reference state, while
is a known pure reference state, while 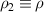 is the actual system state after experimental implementation or numerical simulation of a certain pulse sequence. In that case the fidelity can be simplified as
is the actual system state after experimental implementation or numerical simulation of a certain pulse sequence. In that case the fidelity can be simplified as
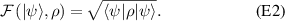
We will also consider the corresponding error probability (infidelity) 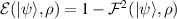 [250].
[250].
In practice, it could be difficult to compute the fidelity for a sufficiently large set of pure inputs and then to take the worst-case. As a much easier to manage alternative, one could choose a state which is known to be particularly error-prone or consider the entanglement fidelity. This corresponds to the fidelity of preserving a Bell state on the examined qubit and a perfect reference one [250]. Given the input states 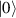 ,
, 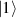 ,
, 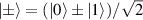 ,
,  , the entanglement fidelity becomes
, the entanglement fidelity becomes
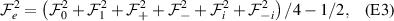
with  the fidelity on the input
the fidelity on the input  .
.
Appendix F: Digital quantum simulation
The implementation of a QS requires (i) to identify a proper mapping between target system and quantum hardware; (ii) to decompose the time evolution induced by the target Hamiltonian into a sequence of elementary steps controlled by the experimenter, i.e. one- and two-qubit gates. The mapping of  models onto an array of qubits is in general straightforward. Given their importance to describe most models of interests in Physics and Chemistry, we also recall the JW transformation [329] commonly employed to express (spinless) fermionic operators in terms of Pauli matrices:
models onto an array of qubits is in general straightforward. Given their importance to describe most models of interests in Physics and Chemistry, we also recall the JW transformation [329] commonly employed to express (spinless) fermionic operators in terms of Pauli matrices:

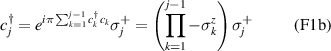

In general, for multi-dimensional problems this mapping yields non-local many-body interactions in the resulting spin Hamiltonian, with a number of spin terms which depends on the dimension of the lattice. This makes the actual simulation of such a model very demanding. Concerning point (ii), one usually exploits ideas first put forward by Lloyd in his seminal work [274]. If the target Hamiltonian  can be written as the sum of L
local terms (as in the vast majority of target problems), the simulation can be performed efficiently on the QS [4, 274]. In particular, let us consider
can be written as the sum of L
local terms (as in the vast majority of target problems), the simulation can be performed efficiently on the QS [4, 274]. In particular, let us consider  . Then, if
. Then, if 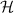 is time-independent, the corresponding time evolution is given by
is time-independent, the corresponding time evolution is given by 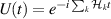 . This is still a very complex operator acting on the full register, which cannot be directly implemented. To achieve this, we exploit the Suzuki–Trotter decomposition:
. This is still a very complex operator acting on the full register, which cannot be directly implemented. To achieve this, we exploit the Suzuki–Trotter decomposition:
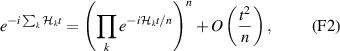
which allows us to approximate arbitrarily well the desired unitary evolution by repeating n times the gates corresponding to the product of local operators for time slices  . The digital error associated to such an approximation can be made in principle arbitrarily small by increasing n. This, however, usually also implies an increase in the number of gates and hence of the associated physical errors. Hence, in the current NISQ era, a trade-off between digital errors and other sources of noise must be found.
. The digital error associated to such an approximation can be made in principle arbitrarily small by increasing n. This, however, usually also implies an increase in the number of gates and hence of the associated physical errors. Hence, in the current NISQ era, a trade-off between digital errors and other sources of noise must be found.
After a suitable mapping, the target Hamiltonian is re-written in terms of spin 1/2 operators (acting on the qubit-based hardware). Therefore, it is useful to derive the decomposition of some common target time evolution operators into elementary gates. We focus, in particular, on the simulation of one- and two-spin terms h1 and h12 on a couple of spins. The evolution induced by  for a time t can be straightforwardly implemented by a single-qubit rotation
for a time t can be straightforwardly implemented by a single-qubit rotation 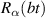 , defined in equation (2). Conversely, for two-body terms describing a generic spin–spin interaction of the form
, defined in equation (2). Conversely, for two-body terms describing a generic spin–spin interaction of the form  (
(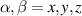 ) one can exploit the decomposition
) one can exploit the decomposition
with  ,
,  ,
, 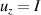 . The Ising-like evolution operator
. The Ising-like evolution operator 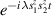 can often be directly implemented or it can be decomposed into a controlled-phase gate with
can often be directly implemented or it can be decomposed into a controlled-phase gate with 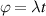 and two
and two 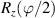 rotations of the two qubits.
rotations of the two qubits.
Footnotes
- 6
The Ni2+ ion of molecule A must be linked to two Cr3+ ions of molecule B with a precise ratio between the couplings, a requirement difficult to be met in practice.
- 7













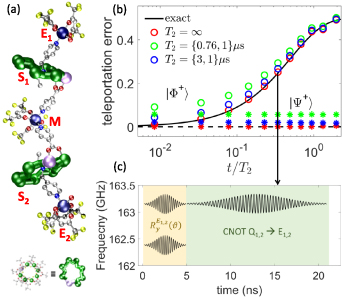

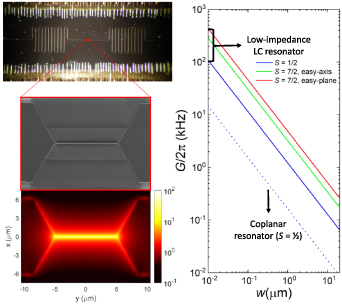
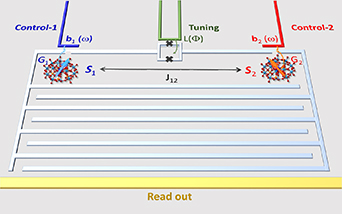


![$\epsilon = \left(\frac{t}{n}\right)^2\left[\mathcal{H}^{\mathrm{even}}_2,\mathcal{H}^{\mathrm{odd}}_2\right]/2$](https://content.cld.iop.org/journals/0034-4885/87/3/034501/revision1/ropad1f81ieqn255.gif)