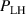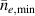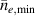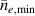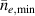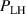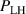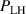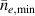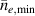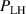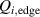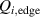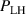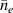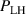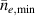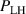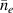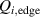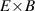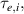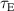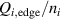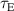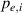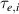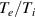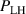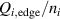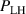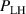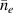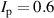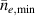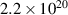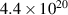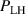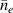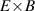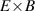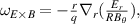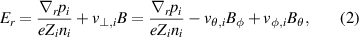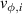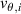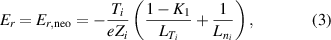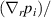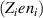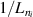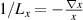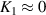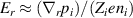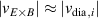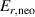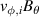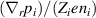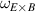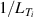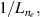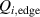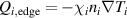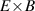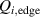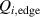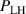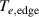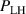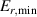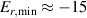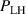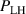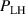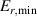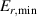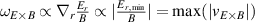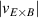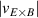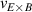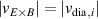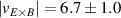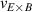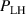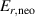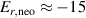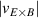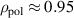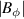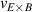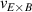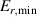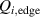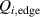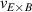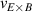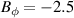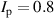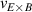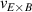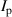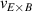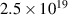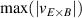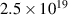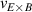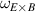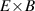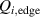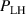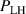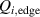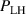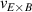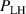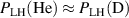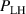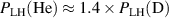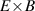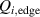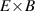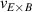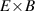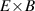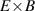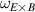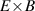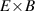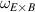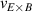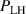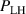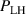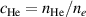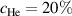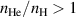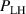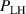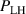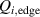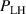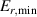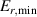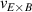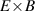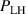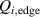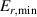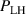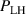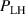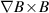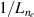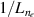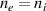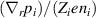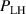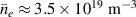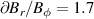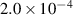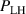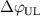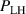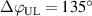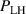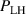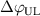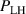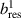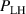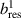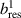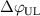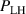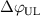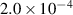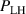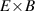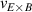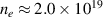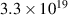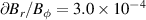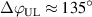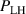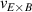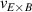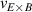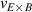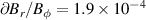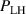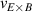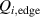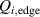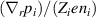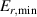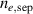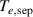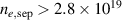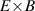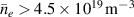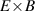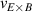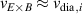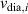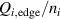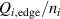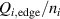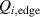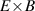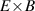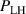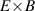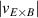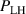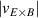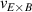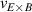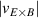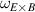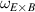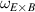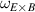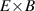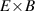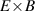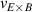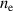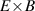Abstract
This paper presents an overview of results from L–H transition experiments that were performed at ASDEX Upgrade (AUG) with the aim of identifying the underlying mechanisms leading to H-mode confinement. With a broad variety of experiments and new diagnostic techniques, as well as modeling efforts, AUG has contributed substantially to improving our understanding of the L–H transition over the past years. In this review, the important roles of the ion heat channel and the edge radial electric field (Er) in the L–H transition physics are brought into context with known dependencies of the H-mode power threshold (), such as the impact of wall material, magnetic perturbations, and the magnetic configuration. Furthermore, experimental and theoretical results obtained at AUG on the L-mode edge turbulence are connected to the mean-field Er and its related shear flow. This led to a deeper understanding of the I-phase plasma regime, has resolved the so-called isotope effect of , and led to the development of a semi-analytical model that can describe AUG's experimental observations of the L–H transition together with the L- and H-mode density limits.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The discovery of the high confinement mode, or H-mode, and its associated improved particle and energy confinement provided a viable path to building energy-producing tokamak reactors. Since then, most reactor designs assume H-mode level plasma confinement [1–3]. Access to H-mode has, empirically, been observed above a certain applied power level, known as the H-mode power threshold (). has been found to depend on several local and global plasma parameters, such as the plasma density, the magnetic field strength, the main ion species, the wall and divertor condition and magnetic configuration [4, 5], amongst others.
A wide variety of theories and empirical scalings have been developed (see [4, 6] and references therein), but a conclusive understanding of the fundamental physics mechanisms behind the transition from L-mode into H-mode (L–H transition) has not been obtained. This makes extrapolations of the H-mode onset to future machines challenging, because these will operate in parameter spaces very different from those in present day devices. Therefore, a more robust physics-based understanding of the L–H transition is crucial to predict the H-mode access and performance of future fusion reactors correctly.
ASDEX Upgrade (AUG) has contributed greatly to our understanding of the L–H transition through a combination of experimental and theoretical works. From these contributions a clearer picture of the conditions under which the L–H transition occurs has emerged and some dependencies of could be explained. In this paper, we present an overview of L–H transition studies at AUG. In particular the importance of the edge ion heat flux for the L–H transition and its connection to the edge radial electric field (Er ) is presented in section 2. In section 3 H-mode access in different main ion composition plasmas is discussed, while in section 4 the impact of magnetic perturbations (MPs), magnetic configuration, and wall material on and Er is investigated. In section 5 we look at the I-phase and the L-mode edge turbulence and its interaction with shear flows in the context of AUG experiments. In section 6 the results from AUG L–H transition studies are summarized and conclusions are drawn.
2. Connection between the H-mode power threshold, the edge ion heat flux and the edge radial electric field
One universal feature of is its non-monotonic dependence on the line-averaged density , (see figure 1(a)), which has been observed on many tokamaks [4, 7–12]. The H-mode power threshold exhibits a minimum at a certain plasma density, named . For densities both above and below the power threshold increases. The parameter space below is known as the low density branch, while plasmas with densities above are said to be in the high density branch of the curve.
Figure 1. (a) Parabolic density dependence of the H-mode power threshold () in low-torque plasmas of pure H (blue squares), D (black circles) and He (red diamonds) at AUG with full tungsten wall. The arrow indicates the density for which is lowest (). The dashed lines show the H-mode power threshold predicted by the multi-machine scaling (see equation (1)) for pure D and H plasmas, respectively, which is valid for densities higher than (high density branch). Reproduced courtesy of IAEA. Figure from [12]. Copyright (2013) IAEA. (b) (black) and the edge ion heat flux at the L–H transition, , (red) in the low density branch, demonstrating the linear dependence of with density and the plasma current dependence of . Reproduced courtesy of IAEA. Figure from [15]. © 2014 EURATOM.
Download figure:
Standard image High-resolution imageFor the high density branch, multi-machine scalings exist [4, 5], which show an almost linear dependence on , the toroidal magnetic field Bφ and the plasma surface S. It should be noted that these scalings were obtained from experiments in which parameters like the plasma shape, the strike point positions, and the drift configuration were set such that is minimal. This was done to avoid the introduction of other dependencies, that are known to influence , into the scalings. Furthermore, these scalings are only correct, if the radiated power is small. As has been recently shown at AUG, in heavily seeded discharges the total radiated power up to the separatrix must be taken into account in order to reproduce from these scalings correctly [13]. The most commonly used scaling reads as [4]
While the increase of with density and plasma size is easily understood, the magnetic field dependence is less obvious. However, this too can be understood in connection with the paradigm of edge turbulence suppression via shear flows, which is described in more detail in sections 2.2 and 2.3. The multi-machine scaling, however, does not describe the behavior seen in the low density branch. A first explanation for the increase in below , which also depends on the applied type of auxiliary heating, was extracted from experiments at AUG [14, 15] and is connected to the critical role of the edge ion heat flux (). This is discussed in detail in section 2.1.
2.1. Connection between the edge ion heat flux and the low density branch
The first indication that the ion heat flux plays an important role for the L–H transition came from a set of low density AUG experiments heated with electron wave heating (ECRH) only, which enabled a decoupling of the electron and ion heat channels [14]. In these plasmas was measured as a function of in the low density branch. The work showed that the edge ion pressure and its gradient are important quantities at the L–H transition (see section 2.2). These observations motivated a more detailed study of the role of the ion heat channel for the L–H transition [15].
In the work of Ryter et al it was found that increases linearly with the plasma density across both the low- and high density branches and does not exhibit a minimum behavior, see e.g. figure 1(b), whereas the edge electron heat flux () displays a non-monotonic dependence on , similar to . This result was also reproduced at Alcator C-Mod where, together with the AUG data, additionally a positive Bφ dependence of at the L–H transition could be extracted (see equations (3) and (4) in [16]).
In the AUG data, the linear dependence of on was shown to be identical for plasmas with 0.6 and 1 MA plasma currents, despite there being almost a factor of two difference in between these data-sets at low density [12] (see also figure 1(b)). Note that in the high density branch, where the electron to ion heat exchange () is much stronger, no scaling of the power threshold with plasma current () is observed [12]. This is consistent with the lack of an dependence in the multi-machine scaling for the high density branch of (see equation (1)). The physics behind the dependence observed in the low density branch is explored further by Bilato et al [17]. In this work, inspired by the experimental results, Bilato et al developed a heuristic model for the H-mode power threshold based on the paradigm of edge turbulence suppression by shear flows [18] (see also section 2.2). An important quantity in this model is the ratio of the energy equi-partition time between electrons and ions, and the energy confinement time, in L-mode [17], where the latter exhibits an almost linear dependence on [19]. The model by Bilato et al reveals that depends on as soon as is comparable to .
The work of Ryter et al demonstrated that at a given density there is a threshold in that has to be reached to trigger the L–H transition. This means a critical value of the edge ion heat flux per particle () is needed to access H-mode. The threshold value can be achieved by improving the plasma confinement, i.e. increasing , or by increasing the electron to ion heat exchange , i.e. decreasing . Since , the electron-ion coupling can be influenced by changing the temperature ratio, e.g. with the heating method. In ECRH heated plasmas in the low density branch the power threshold is high, because a relatively large is required to couple enough power into the ion channel to reach the critical needed for the L–H transition. If dominant ion heating, e.g. neutral beam injection (NBI), is used, Ti and its connected heat flux (Qi ) can be increased more easily. Thus, less heating power is needed to reach the critical and is reduced, as shown in [15]. This holds, however, only for low torque plasmas. If the plasma torque is not negligible, it can be seen that both the critical needed to enter H-mode and increase with increasing toroidal edge rotation [15, 20]. The authors of these publications speculate that this behavior can be explained by the impact of the edge rotation on the edge radial electric field. This will be discussed further in section 2.2.
Another way to improve the electron-ion coupling in the low density branch is simply to increase the plasma density. As density is increased, less applied power is required to achieve the same critical at the L–H transition. Above the density minimum, in the high density branch, the increases in the efficiency of the electron-ion coupling with increasing plasma density is small compared to the increase in the number of particles, resulting in the linear increase of with density. This is the reason for the minimum observed in the H-mode power threshold as a function of plasma density.
Noting that the minimum in as a function of is due to the collisional coupling between ions and electrons, Ryter et al examined the ratio of for several AUG discharges and found that the power threshold exhibits a local minimum when this quantity is approximately equal to 9. This result held for both the and 1 MA data-sets. Based on these observations it is possible to develop a scaling for , which reproduces experimental results from multiple tokamaks devices very well and provides a prediction for in ITER deuterium operation with low torque input (see equation (3) in [15]). The density minimum in ITER is predicted to be m−3 for the half magnetic field and plasma current configuration and m−3 at full magnetic field and plasma current. This yields power thresholds of 16 and 41 MW for the half and full magnetic field and plasma current configurations, respectively, which should be feasible with the auxiliary heating systems planned for ITER [2].
The framework of a critical edge ion heat flux explains the minimum of the curve as a function of as well as the increase in the power threshold below this value. It can also unify observations made in plasmas with different heating systems, as well as with different plasma currents. However, the ion heat flux is likely not responsible for directly triggering the L–H transition. Rather, local edge quantities that are connected to , such as the radial electric field (Er ) and the ion pressure gradient, are more physics-based candidates. The relationship between the surface integrated edge ion heat flux and Er , which is a local quantity, is explored in the next section.
2.2. Connection between the edge ion heat flux and the radial electric field
One of the most commonly invoked hypotheses to explain the L–H transition is connected to the suppression of radial turbulent transport at the plasma edge by poloidally directed shear flows [18]. In this framework, the condition for the H-mode access is that the flow shearing rate () is large enough to stabilize the characteristic L-mode turbulence at the plasma edge. The shearing rate is given by with q being the safety factor, r and R the minor and major radii, respectively, and Bθ the poloidal magnetic field component [21]. Since is directly proportional to the gradient of Er , it is expected that Er and its formation in L-mode are of high importance for the L–H transition.
The background radial electric field can be determined via the radial force balance
where p, n, and v represent the pressure, density, and flow velocity of any plasma species and eZ its charge. B is the total magnetic field and Bθ and Bφ its poloidal and toroidal components, respectively. The flow perpendicular to the magnetic field, , can also be decomposed in its toroidal and poloidal components and . Although the formula holds for all plasma species (Er must be the same for all plasma species), the behavior of the main ion species, denoted with i here, is of particular interest for the formation of Er .
Assuming that the poloidal main ion rotation is determined by neoclassical theory and that the toroidal main ion rotation is small, the radial electric field can be expressed in the following form [22, 23]
where the diamagnetic pressure gradient term was re-written in terms of the logarithmic radial gradients of main ion temperature and density , with . K1 is the neoclassical flow coefficient, which depends on collisionality [23–25].
At typical AUG edge parameters the ion collisionality is in the plateau-regime [26–28] and . Thus, or , which is called the neoclassical approximation in the following. It has been found in AUG H-modes that Er can be indeed approximated in this form [29], but in L-modes it is also often observed that Er deviates from as well as that the toroidal rotation is not small and, thus, is a non-negligible contribution to Er (see sections 2.3 and 4.3).
One possible interpretation within the paradigm of turbulence suppression by background shear flows is that externally controllable quantities like density and heating power lead to a steepening of the background edge gradients in L-mode, which impact the Er gradients and their related shear flows mainly via . At the plasma edge Er typically develops a well-like structure with two gradients of opposite sign. However, it is unclear if the negative (inner) or the positive (outer) gradient is of more importance for the transition into H-mode. Therefore, in this article it is not separated between the two gradients and their connected shear layers, as either of them could be important for the H-mode access, although experiments at AUG indicate that the edge turbulence suppression starts at the location of the inner shear layer [30]. In this framework, H-mode is then achieved as soon as a 'threshold' value in is reached, i.e. one that is large enough to suppress the turbulent transport in the edge. At AUG it has been found that, when moving from L-mode towards the L–H transition it is mainly which changes, while the density gradient contribution, approximated by stays fairly constant [31, 32]. However, if by any means, e.g. wall condition, the latter is changed, then this also has an impact on the required power needed to enter H-mode, as will be shown in section 4.1.
These observations on local parameters at the plasma edge are in line with the findings of the critical role of at the L–H transition, discussed earlier in section 2.1. Although within the paradigm of turbulence suppression by shear flows, it is not itself that is expected to be important, but rather and , these quantities are all related to the main ion temperature gradient: Er via equation (2) and the edge ion heat flux via , with χi being the ion heat diffusivity. Within this picture, the increase in and the required to initiate an L–H transition observed in higher rotation plasmas can also be explained. If the increased rotation reduces the local shear, a higher applied heating power (and ) would be required to further increase the edge ion temperature gradient, compensating for the impact of the rotation, to obtain the same edge Er .
The interconnections between and Er , as they relate to , were already pointed out in [14], where detailed analysis of the edge kinetic profiles demonstrated that the edge electron temperature increases linearly with applied ECRH power at constant plasma density, whereas remains fairly constant. The same observations were also made in H plasmas in [33]. As a result, the ion pressure at the plasma edge () was observed to increase linearly with increasing plasma density at the L–H transition, as did , whereas behaves more like and at the L–H transition.
In the work of Sauter et al it was also found that the minimum of the Er well, is constant at the L–H transition ( kV m−1) for plasmas with a constant magnetic field of −2.5 T, but different densities (covering the low and high density branch of ). In that work the edge radial electric field was to a large extent not directly measured, but deduced from edge temperature and density measurements together with neoclassical theory using equation (3). Assuming now additionally that the width of the Er well is constant, as was found experimentally in H-modes at AUG [34], then the value of the Er minimum can be used as a proxy for its gradients. In conclusion, the work of Sauter et al shows experimentally, that for a wide range of plasma densities the Er gradients are constant at the L–H transition. Similar assumptions on the edge Er in L-mode plasmas were made by Maggi et al on JET data [35]. In this work the same conclusions for JET L–H transitions were drawn as previously for AUG, where they showed that an apparent threshold in the minimum value of Er is required to enter H-mode.
It should be noted that all the experiments described so far were carried out for a fixed magnetic field value and in a single magnetic field configuration, namely lower single null, favorable drift. The impact of changes in these two parameters are described in the following section and in section 4.3, respectively.
2.3. Magnetic field dependence of the H-mode power threshold
Building on the L–H transition results described in the previous sections, the relationship between the actual measured edge Er and was investigated further by Cavedon et al [36] by exploring the magnetic field dependence of (see equation (1)) in deuterium (D) and a small subset of hydrogen (H) discharges. In this work the L-mode edge Er prior to the L–H transition was measured with 1–2 ms time resolution using a fast charge exchange recombination spectroscopy (CXRS) technique [37]. Due to the limited radial resolution of this method, it was not possible to extract meaningful Er gradients from the experimental data directly. Therefore, again was used as a proxy for the Er gradients (see also section 2.2). It was observed that at the L–H transition deepens linearly with increasing magnetic field. This results in an almost constant velocity shear at the L–H transition, since . This observation is an important result to distinguish experimentally as a more fundamental quantity for the L–H transition than Er .
The work by Cavedon et al also showed that the maximum in at the L–H transition remains constant as a function of electron density for the different magnetic fields explored and that this value is consistent with earlier data-sets [14, 26]. This is shown in figure 2(b). Here, the maximum of the measured is shown for the entire data-set from the work by Cavedon et al (circles and squares) and is compared to the results from the previous works (diamonds and triangles), neither of which directly measure Er (or ), but used the neoclassical approximation . Combining all the data-sets, a threshold value of km s−1 was found at the L–H transition. Since in these data-sets varied by a factor of about three, this result provides a clear, concise explanation for the observed dependence of on Bφ (see equation (1)). A critical threshold in needed to enter H-mode automatically incorporates the observed magnetic field dependence, as has also been shown with fluid codes modelling the L–H transition (see [38] and references therein). Increasing the magnetic field reduces such that steeper Er gradients are required and, hence, a higher edge ion pressure gradient, edge ion heat flux, and , in order to obtain the same critical shear at the L–H transition. It is important to note that the same value for the critical was found in both H and D plasmas. This has important ramifications for interpretation of differences seen in between different hydrogen isotopes and will be discussed further in section 3.
Figure 2. (a) Neoclassical approximation () and Doppler reflectometry (DR) measurements (purple) of the minimum of the radial electric field well at the plasma edge in a range of plasma confinement states. At the L–H transition (black circles) a value of kV m−1 is found at AUG for a wide range of edge densities in favorable drift plasmas with T. Reproduced courtesy of IAEA. Figure from [14]. Copyright (2012) IAEA. (b) Maximum of at the L–H transition plotted against plasma edge density () for a range of favorable drift plasma discharges in which also was varied from 1.7 to 3.0 T. The figure includes the points at the L–H transition from (a) (diamonds) as well as actual measurements of the minimum by CXRS (circles) and DR (squares). Red points are measurements acquired in hydrogen and blue points are from deuterium plasmas. Reproduced courtesy of IAEA. Figure from [36]. © EURATOM 2020.
Download figure:
Standard image High-resolution imageIt is worth mentioning that the work by Cavedon et al examined the scaling of with magnetic field in the high density branch only. However, together with the previously reported results on the critical role of Er and in the low density branch [14, 15], it is likely that the magnetic field scaling of seen by Cavedon et al would also be recovered in the low density branch. As such, seems to be a more fundamental quantity for the L–H transition than Er itself, and this observation is consistent with the magnetic field scaling of at the L–H transition found in Alcator C-Mod [16], which is valid for all plasma densities.
At AUG the experimental investigations into the role of the radial electric field and its associated quantities in the L–H transition has continued with ever improving diagnostic capabilities and expanding the explored parameter space. Recent experiments pushed to even lower densities [27, 32]. It is interesting to compare the minimum of from these new measurements with the previous data-sets presented in [36]. This comparison is shown in figure 3.
Figure 3. Minimum of the experimentally determined edge at the L–H transition plotted against the plasma edge density. The measurements were made with He II spectroscopy (HES) [32] and Doppler reflectometry (DR) in D (blue circles) and H (red squares) plasmas of favorable drift configuration with T and or 1.2 MA. The data of figure 2 are also plotted in this figure for comparison. Here, the experimental data acquired with CXRS [36] are shown as grey symbols, while the data of [14, 26], using the neoclassical approximation , are shown as black symbols.
Download figure:
Standard image High-resolution imageThe new measurements of at the L–H transition, determined with He II spectroscopy (HES) [32] and Doppler reflectometry (DR), are shown as blue circles for D and red squares for H plasmas in figure 3. As shown in [32], the two Er measurement techniques exhibit excellent agreement in L-mode plasmas. This new data-set contains data from plasmas heated with ECRH only, with a constant magnetic field of −2.5 T at the geometric axis, and a plasma current of either 0.8 or 1.2 MA. For the entire covered density range, no difference in the minimum of is found between H and D plasmas, which is consistent with former observations at AUG [36], and between the low and high plasma current discharges. The latter is consistent with the findings by Ryter et al that at the L–H transition does not show any dependence on (see also section 2.1).
For comparison of the new data with the old data-sets, the data points from Cavedon et al, measured with CXRS, are shown in figure 3 as grey points, while the data points from [14, 26], for which the neoclassical approximation was applied to determine Er , are plotted in black. Above an edge density of m−3 a direct comparison between the different measurement techniques is possible. There is good agreement between the results within error bars, although the new measurements give a systematically lower than the old ones. Below an edge density of m−3, which corresponds to a plasma located in the low density branch of , a clearly lower critical is measured than is expected from the approximation . This deviation indicates not necessarily that the poloidal rotation is non-neoclassical, but that under these plasma conditions, i.e. at low density, the toroidal main ion flow is not negligible and has to be taken into account in the determination of Er , as also shown in [27].
The variation in the measured at the L–H transition does also not necessarily imply that the shear of is not constant at the L–H transition. As it is regularly observed in ECRH heated plasmas, in which the toroidal main ion flow is purely intrinsic, the latter just leads to a shift of the entire edge profile, leaving its gradients nearly unchanged, but reduces [27, 39]. This implies that the same criterion for turbulence suppression by a critical can still hold, as discussed later in section 4.2, but the assumption that the minimum of Er is a proxy for its gradients is not valid under these conditions. A quantitative assessment of the Er gradients and their related shearing rates is foreseen for this new data-set, which will require a systematic and careful study of the radial uncertainties of the measured Er profiles. It should also be noted that recent work by Silva et al [40] shows Er measurements at the L–H transition in the JET tokamak and reports on very similar observations as presented here for AUG.
In summary, the framework of a critical is able to explain the experimental observations in the low density branch of the curve and the density minimum. It is also able to unify experimental observations of in this parameter regime for plasmas with different combinations of ion and electron heating, making a more physical macroscopic quantity for understanding L–H transitions than . However, alone is not able to explain all of the experimental observations, for example, the dependence on the magnetic field is only explained by connecting to and its shear. In addition, does not provide a direct explanation for the dependence of on the main ion species or on the magnetic configuration. Instead, to understand these phenomena, local edge quantities, like Er , have to be investigated and linked to the characteristics of the edge turbulence.
3. Impact of main ion species composition on the L–H transition
A dependence of on the main ion plasma species was found already in early isotope experiments [41, 42]. For hydrogenic species scales with the inverse of the main ion mass Thus, in hydrogen (H) plasmas is about two times larger than in deuterium (D) plasmas [42]. The H-mode power threshold for pure helium (He) plasmas varies for different machines between 1 and [20, 41]. In the past years, more experimental and theoretical investigations have been performed at AUG to elucidate the reasons for the dependence of on the main ion species. The most important results of these investigations in pure D, H and He plasmas and in mixed H–He and H–D plasmas are presented in the following.
3.1. Pure H, D and He plasmas
Figure 1(a) shows the parabolic dependence of the H-mode power threshold on electron density as measured in AUG pure H, D and He plasmas. The corresponding experiments were all performed after the switch from a carbon to a tungsten wall [12] and the identification of the power threshold at low density was made possible by the extension of the ECRH systems on AUG [43]. The data show that in a metal-wall AUG [44]. Recent measurements in He plasmas at AUG could confirm this result [32], which is different from observations in carbon wall machines, where it is found that in He is higher than in D by about 40% [10, 44, 45]. The latter is also the current assumption for ITER He operation, namely that [2]. However, recent experiments at JET have also found comparable power thresholds between helium and deuterium with the ITER-like wall when considering the high density branch [46]. On the other hand, the density minimum is shifted towards higher values for He in JET, implying that at the respective density minimum, which is not observed at AUG. At AUG the density minimum and at the density minimum are the same in He as in D plasmas [12].
As can be seen in figure 1(a), also in the all metal-wall AUG is twice as high in pure H compared to pure D plasmas. Therefore, the role of the edge ion heat flux at the L–H transition was investigated also in pure H plasmas [33] and it was found that is as well twice as large in H as it is in D, but again it increases linearly with the plasma density. Although this means that there is not one critical value of at the L–H transition, which unifies observations in deuterium and hydrogen plasmas, it is also known that the turbulent transport is increased in H compared to D plasmas (see [47] and references therein). In the framework of a critical shear needed to trigger the L–H transition, this would imply that, due to the increased turbulent transport, more heating power is needed in H plasmas to establish the same critical edge gradients required at the L–H transition. This, in turn, results in a higher and a higher for H plasmas. On the other hand, one might also expect that the higher turbulent transport level in H would require a higher velocity shear at the L–H transition to be able to suppress the characteristic edge turbulence.
In several comparative experiments, the edge Er or its minimum were measured at the L–H transition in both D and H plasmas at AUG. As can already be seen from figures 2(b) and 3, the minimum of at the L–H transition is the same in D and H for a given plasma density (see section 2.3 for a description of the different data-sets). More recent Er measurements with improved diagnostic capabilities (HES and DR) [32] show that not only the minimum of Er is the same for D and H plasmas at the L–H transition, but also the width of the Er well is of comparable size. This is shown in figure 4 and justifies that in these conditions, i.e. the high density branch, can be used as a proxy for its gradients. It is also observed that for same plasma conditions, i.e. same plasma density and same heating method, the strength of both the inner and the outer Er gradient are the same between D and H, despite a factor of 2–3 difference in the amount of applied heating power (see also figure 4). Further analysis of the edge profiles has revealed that also the edge ion pressure gradient is comparable in D and H plasmas at the L–H transition [33, 48]. These experimental results confirm the hypothesis that in hydrogen plasmas a higher applied power (and edge ion heat flux) is required to obtain the same critical edge gradients at the L–H transition as seen in deuterium, on account of the higher ion heat transport. Hence, the same conditions as observed in D plasmas seem to hold quite robustly also in H, when the differences in the turbulent heat transport as a function of ion mass are taken into account. It should be noted that similar observations have also been made by Birkenmeier et al in recent isotope L–H transition experiments at JET [49, 50].
Figure 4. Experimental measurements, acquired with He II spectroscopy (HES) and Doppler reflectometry (DR), of Er profiles at the L–H transition in pure deuterium plasmas (left) and pure hydrogen plasmas (right). They reveal that the edge Er , including its gradients, is very similar for the two ion species at the respective confinement transition.
Download figure:
Standard image High-resolution imageSeveral recent theoretical works studying the turbulence in the L-mode edge have identified collisional drift-wave turbulence as the dominating transport mechanism [51–53], due to the increased collisionality in that region. This is in contrast to the ion-temperature-gradient/trapped-electron-mode instabilities typically present in the plasma core. The presence of drift-waves makes the parallel electron dynamics in the gyro-kinetic equation important for simulating the transport and the ion mass dependence enters via the electron to ion mass ratio important for the electron dynamics. As can be seen in figure 9 of [51], at high collisionality the turbulence growth-rates are expected to be a factor of two larger in H compared to D.
Within the framework of turbulence suppression by the background shear as the mechanism initiating the L–H transition, one would expect that a corresponding increase in would be required in hydrogen to enter H-mode, in seeming contradiction with the experimental data. In the work of Cavedon et al [36], as well as the newest results presented here (see figures 3 and 4), no difference in (or Er ) at the L–H transition are observed between hydrogen and deuterium. The lack of difference is potentially explained within the simulations, at least in part, by the highly non-linear response of the plasma turbulence to the shear as well as the inter-dependencies with other plasma parameters [31, 54]. Bonanomi et al showed that at low plasma β the inclusion of the shear in the simulations has only a small impact on the turbulence, while at higher β the effect is non-linear, with small increases in resulting in strong turbulence suppression [31, 54]. This effect is tied to the type and scale of the turbulent structures, with larger scale (low ky ) instabilities being found when increasing the edge plasma β. The simulations highlight the differences expected in the turbulence properties between hydrogen and deuterium plasmas, but also as a function of plasma β. In both deuterium and hydrogen plasmas β changes in response to multiple design parameters including magnetic field, plasma current, electron density and applied heating power. As such, all of these changes are expected to also impact the turbulence properties at the edge, making the constant value found over a wide range of parameters in deuterium just as unexpected as finding the same value present in both H and D plasmas.
The AUG results, in combination with the new simulations, suggest the following qualitative picture: In a given L-mode plasma, the application of external heating increases the power in the ion channel and, thus, the edge ion heat flux, the edge ion temperature gradient and the gradients in the radial electric field as well as the shear. At the same time, the increase in applied power increases the plasma pressure, altering the turbulence structures at the edge towards larger scale instabilities that are strongly, and non-linearly susceptible to shear stabilization. The strongly non-linear turbulence suppression as a function of increasing is qualitatively and to some extent quantitatively consistent with the experimental data [31, 54]. From a purely experimental perspective the data demonstrate a clear threshold for the L–H transition, which applies equally well to both D and H plasmas. The observed increase in in H compared to D directly follows from this result, when combined with the well understood changes in the edge turbulent transport.
3.2. Mixed H–D and H–He plasmas
It is also of interest to examine how changes when transitioning from one main working gas to another and in plasmas with mixed main ion species. The latter is particularly relevant for reactors that will operate with 50–50 D–T mixtures, while the former is of interest for the start-up phase of ITER operation [2]. The power threshold in D–T plasmas has recently been investigated in JET [49, 55], while experiments at AUG have focused on the behavior of in hydrogen–deuterium mixes as well as hydrogen plasmas seeded with controlled amounts of He [56]. The latter experiments were motivated by observations at JET that showed a strong reduction of in NBI heated H plasmas with modest levels of He seeding (He concentration up to 10%) [57]. As discussed in the previous section, in AUG the power threshold in H is twice as large as in D, while in He it is similar to the deuterium threshold. Hence, during the transition from a hydrogen-dominated plasma to a He plasma, it is reasonable to expect a decrease in from the H to the He level.
This transition was explored in AUG experiments in which H plasmas were seeded with controlled amounts of He up to a He concentration of 20% [56]. The obtained values, also normalized by the multi-machine scaling of D plasmas (see equation (1)) to account for the slight density increase with increasing amount of He seeding, are shown in figures 5(a) and (b), respectively. No change in the threshold is observed, inconsistent with the JET observations [57], but consistent with previous AUG results, where a reduction in when moving from H to He was only obtained at values of about 30% [44]. Note that at , with the typically low-Z impurity levels at AUG, the H concentration is still more than 50% of the electron density. However, at 30% He concentration , making it effectively a He plasma with hydrogen seeding.
Figure 5. (a) H-mode power threshold in NBI (red) and ECRH (blue) heated mixed hydrogen–helium plasmas plotted against the He concentration (in % of the electron density). The high in H plasmas does not decrease significantly with admixture of up to 20% of He, even if the density increase due to the additional He injection is taken into account, by normalizing to the multi-machine scaling [4] (b). The edge ion heat flux at the L–H transition (c) is also found to be the same independent of the He concentration and external heating source. Reproduced courtesy of IAEA. Figure from [56]. © EURATOM 2020.
Download figure:
Standard image High-resolution imageThe AUG results were all obtained in plasmas close to the density minimum. Thus, they are consistent with recent DIII-D results [58], which also show no change in the high of hydrogen at low He seeding levels () for plasmas located in the high density branch. The very strong reduction of the hydrogen power threshold by about 25% for less than 10% He seeding as observed at JET is, therefore, not reproduced by either the AUG or the DIII-D experiments.
In contrast to JET, most of the plasmas in the AUG experiments were heated with ECRH (blue circles in figure 5), also NBI heating was used for a small subset of discharges (red squares). As can be seen in figure 5, in the NBI heated plasmas is by about 20% higher than in the ECRH cases. As discussed previously in section 2, at several tokamaks such a difference in between NBI and ECRH heated plasmas is observed, which is related to the differences in torque input and toroidal edge rotation and its effect on Er . For the here presented H plasmas with He seeding the change in edge rotation alone was, however, not big enough to explain the differences in [56]. Another effect was at play, which was resolved via power balance calculations. They show that at the L–H transition is the same within the uncertainties for both the ECRH and the NBI heated plasmas and that this value remains constant over the entire range of explored He seeding levels, see figure 5(c). The differences observed in with heating method are related to the higher impact of the heat exchange term () on in H plasmas compared to D plasmas (inverse mass dependence, see section 2.1) and the dependence of on the temperature ratio , which is actively influenced by the heating method. While in ECRH heated plasmas is larger, increasing and, thus, in L-mode plasmas at the density minimum, in NBI plasmas this ratio is smaller, requiring more heating power to reach the critical needed to enter H-mode [56].
The results from these L–H experiments in mixed H–He plasmas conducted at AUG also show that in plasmas in which the heat exchange term is the dominant contribution to , the H-mode access is determined by the transport properties of the plasma core. This will also be the case in ITER PFPO-1 in which only ECRH is available [2].
At AUG the behavior of across the transition from deuterium to hydrogen dominated plasmas has also been investigated and results from the initial experiments were presented in [56]. Since then, the investigations have been expanded to cover the complete transition from hydrogen to deuterium, see figure 6, which combines the originally published data-set with the new results. and exhibit a very similar dependence on the relative hydrogen content (), with both remaining at the deuterium level until the plasma is about 50% H, as reported in [56]. Between and 1 both quantities start to increase, which is shown in figure 6(a) for and in figure 6(b) for . This results in a non-linear increase of and with , as indicated by the respective fit functions in the figure (black solid lines).
Figure 6. (a) Net input power at the L–H transition (colored symbols) and the H–L back transition (white symbols) plotted against the relative hydrogen content. Both and increase non-linearly with increasing hydrogen content, which is also indicated by the black line, a fit to the experimental data. (b) The edge ion heat flux at the L–H transition exhibits a similar increase with relative hydrogen content as . (c) The minimum of Er , which can be used as a proxy for its gradients at these plasma densities, is constant at about −11 kV m−1, independent of the hydrogen content and for both the L–H and the H–L back transition.
Download figure:
Standard image High-resolution imageBesides the L–H transition, also the H–L back transition was investigated in these mixed H–D plasmas. While colored symbols correspond to the L–H transition in figure 6, the H–L back transition is depicted with the white symbols. aligns very well with , but the lack of hysteresis, which is usually observed [12], can be ascribed to the fact that the density dependence is not captured in figure 6(a). Due to the design of the discharges, the L–H transitions occur systematically at lower plasma densities than the respective H–L back transitions. If the density increase were taken into account, a hysteresis between and would be visible.
Figure 6(c) shows the minimum of the radial electric field measured at these various transitions. Consistent with previous data-sets in pure D and H plasmas (see section 3.1), is found to remain constant at about −11 kV m−1 regardless of the main ion species mix. As can be used as a proxy for its gradients in these plasma conditions (see sections 2.3 and 3.1), this observation implies that the shear must be constant, independent of the main ion species composition. The constant shear together with the non-linear increase of and with increasing indicates, according to previous argumentation (see section 3.1), that also the L-mode edge turbulent transport increases non-linearly with increasing hydrogen content. It is foreseen to reproduce this observed dependence of the L–H transition on the effective main ion mass in gyrokinetic simulations and a semi-analytical model developed for the L–H transition at AUG (see section 5.1).
Also does not show any hysteresis and has the same value of about −11 kV m−1 at the L–H as well as at the H–L back transition. This is consistent with previous measurements of the electron pressure gradient at the L–H and H–L back transition. For medium plasma densities, where electrons and ions are coupled, it was found that the H–L back-transition occurs at the same electron pressure gradients as the L–H transition [59]. The experimentally observed lack of hysteresis in local edge quantities compared to macroscopic quantities, like the power threshold, is quite interesting, as it suggests that, despite different edge transport properties in H- and L-mode, at the L–H transition the same criterion must hold which leads to the confinement transition. This reinforces the need for self-consistent simulations of edge turbulence-flow interaction in order to reproduce an entire L–H–L cycle correctly.
4. Impact of magnetic configuration and wall condition on the H-mode power threshold
In section 2 a relatively simple explanation for the Bφ dependence of was presented. However, not only the magnetic field strength, but also the magnetic field geometry can influence . A very well known example of this is the observation that is different by roughly a factor of two depending on the direction of the ion drift relative to the active X-point of single-null magnetic configurations. When the ion drift points towards the active X-point is lower than when the ion drift points away from the active X-point. Hence, it is the practice to refer to the former configuration as 'favorable' and to the latter as 'unfavorable'. This observed difference in with drift configuration, despite being well known for many years, does not have a robust explanation. Recent AUG experiments, aimed at illuminating this dependence of [27], are presented in section 4.3.
In addition to the X-point configuration, perturbations to the magnetic field, such as those imposed for suppression of edge localized modes (ELMs), have also been observed to impact the H-mode power threshold [10, 60–66]. ITER plans to use MP coils to achieve the desired ELM suppression and ideally to apply them before the L–H transition, such that even the first ELM can be avoided. As such, any changes to the power threshold in the presence of MPs is very relevant for ITER operation. For this reason experiments to explore this issue were performed at AUG [39]. The results of these experiments are summarized in section 4.2.
These examples demonstrate that changes in the plasma edge and the scrape-off layer (SOL), either due to drifts, details of the magnetic geometry, or SOL transport can influence the confined region and . Another example of this is the influence of the wall material on the H-mode power threshold. While not intuitive, the impact of wall material on , specifically the reduction seen in metal-walled devices compared to carbon-walled machines, is a robust observation, first seen at AUG [12], and discussed in detail in section 4.1.
4.1. Wall material
AUG's gradual transition from a carbon (C) wall to a pure tungsten (W) wall provided an unprecedented opportunity to study the impact of wall material on tokamak operation, including plasma confinement, density and impurity control, pedestal transport, and the L–H transition. The wall material transition took place gradually between 2003 and 2007 [67], at which time also a cleaning of the machine was performed to remove the residual carbon from the tungsten surfaces. In 2007 and 2008 two full AUG operational campaigns were dedicated to exploring tokamak operation in the absence of low-Z wall materials. Therefore, no boronizations or other low-Z wall coating methods were employed during this time. A robust observation from these campaigns, and all subsequent campaigns in AUG with W wall, is a reduction of the H-mode power threshold by 25% compared to the C wall [12]. A similar 30% reduction of was then also observed at JET after the transition to the ITER-like wall [35].
The similarity of observations between the two machines provides additional confirmation of the ubiquity of this result, which has important ramifications for ITER. Due to its metal wall, the H-mode power threshold in ITER in D is expected to be lower than predicted by the multi-machine scaling [4]. In addition, the power threshold in hydrogen plasmas was also explored, and a similar reduction of the power threshold between the C and W wall was observed [12, 56]. As such, this effect is expected to also apply to the early non-nuclear phases of ITER operation.
The reduction of with a metal wall is not due to increased and unaccounted for radiation by the introduction of a high-Z material. This was explicitly checked in [26]. While early speculation considered plasma dilution by the increased C concentration as a potential candidate to explain the higher in the C-walled AUG [12], the work by Shao et al identified changes in the edge density profiles as a key element for the different [26]. In this work it was shown that with the W wall the L-mode electron edge density is higher at the pedestal top location and exhibits a steeper edge gradient compared to the ne profile in the C-walled AUG. This leads to an intrinsically larger logarithmic edge density gradient in a W compared to a C wall machine. The reasons for the changes in the edge density profiles arise from different divertor detachment conditions combined with a higher recycling coefficient for W, since a larger number of energetic particles is reflected from the metal wall [68].
Furthermore, in the work by Shao et al it was also found that in both W and C wall AUG the same minimum value of Er is obtained at the L–H transition and that this value is very similar to those deduced by Sauter et al [14] and later by Cavedon et al [36]. With similar assumptions as made in [14], these observations indicate that the same critical Er gradients have to be established at the L–H transition in both C- and W-walled machines. Combining this result with the observed larger logarithmic edge density gradient in the W compared to the C wall, recalling that if is assumed enters Er via (see equation (2)), gives an explanation for the reduced in a W-walled machine. With an intrinsically higher density gradient less heating power is needed to establish the same Ti and, thus, Er gradients needed for the H-mode access. This result demonstrates that Er and its related local quantities are fundamentally connected to the L–H transition physics and can unify observations made on a macroscopic scale.
4.2. Magnetic perturbations
To avoid already the first ELM, it might be necessary to apply MPs already prior to and during the L–H transition. For this reason it is important to understand how the MPs influence and act on the edge quantities important for the L–H transition. In experiments on different tokamaks [10, 60–66] it has been found that increases with increasing amplitude of the applied MPs, where also a threshold behavior is observed, and that can be increased by a factor of two compared to the value without MPs.
AUG is equipped with two rows of MP coils, which can produce perturbations with a toroidal mode number n up to 4 [69]. Therefore, also at AUG extensive L–H transition studies with MPs have been conducted in the past years. For the L–H transition experiments at AUG resonant and non-resonant n = 2 perturbations have been applied, since n = 2 perturbations are effective for ELM suppression in H-mode [70]. Initial experiments at AUG showed that the effect of by MPs depends on the density [12, 71]. In the low density branch, up to the density minimum, was not affected by the MPs. With increasing density, however, increased by up to 20% with the application of MPs. For these experiments a relative perturbation strength of – at the q = 5 magnetic surface was used.
More recent experiments [39] employed MPs with larger relative perturbation amplitudes by lowering the toroidal magnetic field strength and increasing the current in the MP coils. These experiments show that also increases at low density (), if a critical value of about – is exceeded. This result is in line with observations of other tokamaks [10, 61, 63–65]. Furthermore, it is found that the increase in depends on the alignment of the MP field, set by the differential phase angle between the MP field from the upper coil set and the lower coil set. Figure 7 shows that can increase up to 80% for –180∘. This alignment of the MPs at highest differs from the equilibrium field alignment. The same alignment is required to suppress ELMs in H-mode, but the relative radial magnetic field perturbation required to sustain ELM suppression at AUG is below the critical value for the increase of . These might be promising results for ITER, as in AUG ELM suppression can be sustained without a simultaneous increase of the H-mode power threshold.
Figure 7. versus the MP field alignment . is highest when the radial field perturbation maximizes. Reproduced from [39]. CC BY 4.0.
Download figure:
Standard image High-resolution imageLinear resistive single fluid magneto-hydrodynamic (MHD) calculations using MARS-F [72] were performed to interpret these experimental results. They show a correlation of with the resonant component of the radial field perturbation, represented by the normalized quantity [73] and calculated at the rational surface (m is the poloidal mode number). This correlation is depicted in figure 7 and it shows that including the plasma response (solid blue line) is required to predict the needed to increase . Calculations using only the vacuum field (dashed blue line) are not able to predict the dependence on correctly. Furthermore, the inclusion of a critical magnetic field perturbation strength of – in the linear MHD calculations improves significantly the reproduction of the behavior of with the radial field perturbation (solid red line) [39].
As discussed before (see section 2.2), one explanation for the L–H transition is that the velocity shear suppresses turbulent transport in the plasma edge. Previous studies at several tokamaks [61–63, 74, 75] suggested that the application of externally applied MPs induces ergodization of the magnetic field at the plasma edge in L-mode, which leads to a reversal and flattening of the Er gradients. Hence, within this picture, MPs impede access to H-mode via their impact on the edge radial electric field profile. Another possible explanation is that turbulent transport increases in the presence of MPs, which leads to a flattening of the edge kinetic profiles, which then reduces the shear in [71]. Both effects could also play together, as experimental observations and simulations on MAST indicate [75–78].
The first L–H transition studies with MPs at AUG showed that the application of MPs leads to a flattening of the edge pressure gradient profile, mainly due to a flattened temperature profile [71]. Consequently, more heating power is needed to achieve the same gradients in edge pressure profiles and, thus, the same flow shearing rate at the L–H transition. Direct Er measurements were not available for this data-set, thus, the Er gradient was approximated by the minimum of the ion or electron pressure gradient, which exhibited values between −7 and −12 kV m−1 at the L–H transition both with and without MPs, for different plasma densities and toroidal magnetic field strengths. These values are in good agreement with the observed constant minimum in in other L–H transition experiments at AUG [36].
The first comparisons of Er behavior in AUG between plasmas with and without MPs were performed in low density L-mode plasmas ( m−3) using DR measurements [79]. In this work by Conway et al a reversal of the negative Er well in the confined region to positive values, i.e. changes from the electron diamagnetic to the ion diamagnetic (IDD) drift direction, was observed, consistent with observations in other tokamaks [61–63, 75, 76]. This reversal depends both on the strength of the applied MPs and their resonances with the edge rational surfaces. Furthermore, a dependency of the Er profile on the absolute MP field orientation was found, which was different in the edge region compared to the SOL. The authors suggested that this could be related to the production of an ergodic layer in the edge region, whereas the SOL remains laminar [79].
A possible correlation of the Er reversal with the increase of was not investigated in these original experiments, but it has been revisited recently in [39]. In the work by Willensdorfer et al the edge Er and profiles were measured with DR, CXRS and HES in L-modes with and without n = 2 MPs. These experiments were performed at slightly higher densities of about m−3, with the maximum perturbation amplitude and the MP configuration such that is highest, i.e. (see also figure 7). Although the toroidal phase angle was varied, the profiles did not exhibit a toroidal asymmetry. However, in all cases in which the MPs led to an increase of the edge profiles were elevated at the L–H transition with respect to the reference L-modes without MPs, i.e. the profiles were shifted towards the IDD direction. The shear in , however, was found to be comparable to the one measured at the L–H transition without MPs. These measurements show that the minimum of (Er ) is not always a valid proxy for its shear (gradient), but they are consistent with the idea of a critical value of the shear (the Er gradient) required at the L–H transition.
In L-modes the edge profile is flatter in plasmas with MPs than in those without. As a result, more heating power is necessary in L-modes with MPs to get a steepening of the shear via to values comparable to the ones in L-modes without MPs. Moreover, the additional heating power increases Te , which reduces the plasma resistivity and, thus, the possible penetration of the MPs. In an L-mode experiment where the field perturbation was slowly ramped up, it was observed that reverses at a perturbation of about . Since this perturbation amplitude is about the same as that needed to see an increase in , these two phenomena appear to be connected. Furthermore, it was observed that the reversal occurs on a faster timescale (within 70 ms) than the ramp-up of the MP perturbation. These observations were tested against several models, which are able to predict a reversal of the profile in the presence of MPs. It was found that neoclassical toroidal viscosity cannot explain the flow reversal into the IDD drift direction, because it predicts an additional flow into the electron diamagnetic drift direction. Ergodization as well as resonant electromagnetic torque may partly explain the observations, but more sophisticated modeling including non-linear two-fluid MHD effects together with a more realistic magnetic geometry would be needed for a quantitative comparison.
Finally, MPs have also been observed to change the power threshold for I-mode access [80]. The I-mode is typically observed in unfavorable drift configuration and represents a transitional regime between L-mode and H-mode [81, 82]. It features H-mode-like energy confinement with an edge temperature pedestal, coupled with L-mode-like particle transport and L-mode-like edge density profiles. The I-mode regime itself has also been studied extensively at AUG in the past years, the interested reader is referred to [82–85], but here and in the following only observations prior to and the conditions at the transition from L- into I-mode (L–I transition) and from I- to H-mode (I–H transition) are presented. There are indications that also at the L–I transition the ion channel plays a more important role than the electron channel [80], similar to the observations made in favorable drift configuration plasmas at the L–H transition (see section 2). Experiments using n = 2 MPs demonstrate an increase in the L–I power threshold related to the flattening of the edge pressure gradient [80]. With MPs more heating power is required to re-establish the same edge pressure gradient, as found at the L–I transition without MPs. These results are reminiscent of the observations made in favorable drift plasmas demonstrating the important role of for the L–H transition (see section 2) and suggest that at least to some extent similar physics mechanisms are at play in the development of an improved confinement in general, independent of the exact magnetic configuration.
4.3. Magnetic configuration
In this section we present findings from AUG regarding H-mode access in different magnetic configurations, concentrating on the favorable and unfavorable drift configurations. At AUG it has been observed that both the power threshold to enter I-mode from L-mode () as well as the one to enter H-mode from the I-mode () are larger than [80]. Similar to a parabolic dependence on plasma density is found for , whereas does not exhibit a clear minimum at AUG [27, 80] and other machines [86]. On the other hand, only exhibits a very weak dependence on Bφ , whereas increases almost linearly with Bφ , similar to . This has been seen most clearly at Alcator C-Mod [86], but is also consistent with the AUG results for a much more limited range of magnetic field strengths [80, 82].
In the work of Ryter et al power balance analysis showed that the edge ion heat flux at the L–I transition increases linearly with plasma density. This indicates that the ion channel is also important for the I-mode access, similar as for the L–H transition in favorable drift configuration [80]. However, a quantitative comparison shows that at the L–I transition is higher than at the L–H transition, indicating that the condition to enter I-mode, and also H-mode, in unfavorable drift configuration is different to the condition to enter H-mode in favorable drift configuration. In the framework of edge turbulence suppression by shear flows (see section 2), this observation could indicate a change in the edge turbulence level or the strength of the stabilizing shear flow.
In a recent work at AUG, measurements of edge kinetic profiles and Er were compared in favorable and unfavorable drift configuration L-modes, for same heating powers and matched plasma densities [27]. It was found that the Er well at the very edge of the confined plasma is less pronounced in unfavorable drift configuration compared to favorable drift configuration, although the edge main ion pressure gradient is the same. These features can be seen in figure 8. This shallower Er well in unfavorable compared to favorable drift configuration has been observed before at AUG [87, 88] and other machines [89, 90], but could now be confirmed with new and improved Er measurement techniques [27].
Figure 8. (a) Measured edge radial electric field profiles (stars) in L-modes at matched plasma parameters of favorable (blue) and unfavorable (red) drift configuration. Although (dashed lines) is the same for both drift configurations, the Er well is shallower in unfavorable compared to favorable drift configuration. Taking into account the main ion flows, inferred from local neoclassical theory, into the predictions of Er (solid lines) can also not reproduce the differences observed in the measured Er profiles. (b) Er profiles measured with HES (circles) and DR (squares) at the L–H (violet), L–I (orange) and I–H (dark red) transition exhibit different values and different Er gradients at the respective confinement transition.
Download figure:
Standard image High-resolution imageNo significant changes in the upstream SOL-Er were found between the two drift configurations, which indicates that the altered H-mode power threshold is not directly connected to changes of SOL quantities with the drift direction. This is also confirmed by indirect measurements of the parallel SOL flows, which are considered to set a boundary condition for the intrinsic toroidal edge rotation [91]. At AUG the intrinsic toroidal edge rotation is of the same size and in the same direction for both drift configurations. Therefore, the explanation for the increased H-mode power threshold in unfavorable drift configuration given in [91] cannot explain the AUG data.
While the positive Er gradient across the separatrix is of comparable size between the two drift configurations, the shallower Er well inside the separatrix leads to a weaker (negative) Er gradient in the confined plasma and, thus, to a weaker . This is also shown in figure 8(a). Er profiles were also calculated using the radial force balance equation (see equation (2)) with neoclassical estimates of the main ion flows. This procedure utilizes the measurement of the impurity toroidal rotation to obtain the one of the main ions. The Er profiles estimated by this procedure (solid lines in the figure) cannot reproduce the differences observed in Er (symbols) between favorable and unfavorable configuration plasmas. This indicates that non-neoclassical effects are at play, which change the equilibrium Er profile and its related shear in L-mode and could, thereby, alter the condition for the H-mode onset.
In addition to measurements in L-modes at matched conditions, the radial electric field just prior to changes in confinement regime were also studied in [27]. Er profiles measured about 20 ms before the I-mode or H-mode onset show that the Er gradients can be quite different at the respective confinement transitions. The steepest Er gradients are found at the I–H transition, since the Er gradients steepen during I-mode as the ion temperature pedestal evolves. The shear levels observed at the I–H transition can be even larger than those at the L–H transition observed in favorable configurations.
For the L- to I-mode transition no clear criterion in the edge radial electric field or its shear is found. Measurements of the Er gradients at the L–I transition can be weaker, steeper, or of the same size as observed at the L–H transition in favorable configuration. In contrast, as discussed in section 2.3, the shear is observed to be quite constant at the L–H transition in favorable configuration over a wide range of plasma parameters. The measurements of Er at the L–I and I–H confinement transitions in unfavorable drift clearly demonstrate that it is not a simple single-value threshold in , which is required for the access to an improved confinement, but rather indicates that with the drift configuration also other parameters important for the L–H transition must change, such as the characteristics of the edge turbulence.
It should be noted that these observations do not exclude that close to the L–H transition also additional fluctuating shear flows, like zonal flows (ZFs) [92, 93], could become important and even trigger the transition into H-mode. A characterization of such a turbulence-flow interaction close to the L–H transition at AUG has been reported and is also introduced in section 5.2. However, the high reproducibility of the L–H transition also indicates that the gradients of the background profiles, like the main ion pressure and the equilibrium Er , must be already close to a critical threshold value, in order to establish that the transition into the improved confinement regime occurs always at the same input power for plasma discharges of identical plasma configuration.
5. L-mode turbulence properties and interaction with shear flows close to the L–H transition
In addition to investigating the nature of the stabilizing shear flow, also the L-mode edge turbulence has to be characterised to fully understand the process leading to the L–H transition. In the past years, several advances in theoretical work have been achieved on this topic by the AUG team, where it was found that the modeling capabilities of gyro-kinetic codes have to be extended close to or across the separatrix in order to capture the phenomena of the L–H transition correctly [94–96]. Experimental work closely linked to theoretical considerations that focused on the characterization and determination of edge turbulence close to and at the L–H transition was also performed.
5.1. L–H–L separation through the separatrix operational space
In a recent study by Eich and Manz the conditions for the L–H transition as well as for the density limits have been related to separatrix conditions and the characteristic edge turbulence in AUG [97]. In this experimental framework, which has also been discussed e.g. by LaBombard et al for Alcator C-Mod data [91], the boundaries for tokamak operation are determined by properties of interchange-drift-Alfvén turbulence at the separatrix. In this way the L–H transition condition as well as the density limits can be written as a combination of several dimensionless separatrix parameters and occur as boundaries in the operational space of the AUG tokamak. In practice, this translates to an existence diagram in terms of separatrix electron density, , and temperature, , as shown in figure 9.
Figure 9. The separatrix operational space of ASDEX Upgrade in terms of separatrix electron density and temperature. The blue line depicts the condition for the L–H (H–L back) transition. Reproduced from [97]. EURATOM 2021. CC BY 3.0.
Download figure:
Standard image High-resolution imageAccording to this model the L-mode edge turbulence close to the density limit ( m−3), i.e. also close to the H–L back transition, is expected to be in the regime of resistive ballooning mode turbulence, with high electron turbulent transport levels and a flattened pressure gradient. On the other hand, typical low density L–H transition experiments in AUG are expected to occur in the regime of drift-wave-dominated turbulence, where the electron turbulent transport level is rather moderate in the preceding L-mode. In the context of this model the transition into H-mode is observed when the energy transfer from the turbulence to the mean flow, via Reynolds stress, exceeds the energy input to the turbulence, which is given through the measured gradients in the edge kinetic profiles. Thus, the criterion for the L–H transition is also given by turbulence suppression through stabilizing shear flows (see also equation (8) in [97]). The picture is similar to the model developed by Kim and Diamond for the ZF generation by turbulence [98]. In the model developed by Eich and Manz the interaction between turbulence and shear flow is treated in a similar way to that of the ZF physics, although the equilibrium shear flow is assumed to be dominant [97].
A database consisting of 123 AUG discharges containing 1884 time windows with L- and H-modes of different densities and heating powers shows that the L-mode and H-mode experimental points are well separated by the proposed condition for the L–H transition of the Eich and Manz model (see figure 9). The L–H separation line in the (, ) space (blue line) corresponds to a specific combination of and Bφ , which were kept constant at 0.8 MA and 2.5 T, respectively, within the data-set displayed. Nevertheless, the condition holds more generally also for other combinations in the full experimental data-set.
Within this framework, also the crucial role of the ion heat channel in the L–H transition, which was previously found experimentally at AUG (see section 2.1) can be understood, as the contribution of the ion channel to the entire edge turbulence is the most relevant one at low densities. It is mainly this contribution to the edge turbulence which has to be suppressed by the shear flow in order to enter H-mode at low densities. Interestingly, for the H–L back transition, for which the same condition holds, it is found that also the electron channel needs to be taken into account in the turbulence generation. As a result, consistency of this model with experimental observations at AUG is found in the sense that at the L–H transition the electron heat flux exhibits a non-monotonic density dependence, as does , whereas the ion heat flux shows a linear dependence on the (separatrix) density (see also figure 5 in [97]).
5.2. Characterization of the I-phase
The I-phase is an intermediate confinement regime that occurs between the L-mode and the fully developed H-mode. The I-phase has been observed in several tokamaks in the past decades including AUG [99, 100], DIII-D [101], COMPASS [102] and EAST [103], see also references in the recent review [93]. Compared to L-mode, the I-phase already exhibits improved particle and energy confinement, although not as high as in type-I ELMy H-modes. The I-phase appears as a sequence of limit-cycle oscillations (LCOs) [99], where edge temperature and density profiles are flattened in periodic bursts or pulses [104], as a consequence of repetitive changes in edge turbulence and transport. As the I-phase forms a link between the L- and fully established H-modes, the understanding of transport changes in this regime is crucial for a full physical picture of the entire L–H–L transition cycle.
During fast L–H and H–L transitions the I-phase can be rather short, showing only a few bursts or pulsations. However, in the right parameter range, the I-phase can be held stable for several seconds, easily exceeding many energy confinement times [105, 106]. Such scenarios provide an excellent opportunity to study turbulence-flow interactions over an extended time period.
Several studies suggest that the I-phase oscillations are produced by a predator-prey-like flow-turbulence interaction [100, 101, 107–110], while other studies find them to be more ELM-like edge oscillations [104, 106, 111–113]. A combination of these two behaviors has also been described in the literature [106, 111, 114] where it was observed that the regular LCO pulsations can evolve into intermittent bursts, characterized as type-III ELMs [115]. Work at AUG has provided experimental evidence that supports both of these interpretations.
In low density I-phases, DR measurements showed the following sequence of events within one LCO period [100, 116]: the turbulence level increases until, at a certain critical threshold, a geodesic acoustic mode (GAM) oscillation is triggered together with a turbulence-driven mean flow, which adds to the equilibrium flow. The shear of this (combined) flow increases until it is large enough to reduce the turbulence level to a point where the GAM is damped, and a new cycle starts. This leads to the typical predator-prey-like behavior, with an additional threshold for the GAM oscillation. The work by Conway et al [100] also provides an existence criterion for this oscillation cycle: The averaged shearing rate of the GAM oscillations has to be comparable or larger than the turbulence de-correlation rate, and also larger than the background flow shearing rate. If the turbulence de-correlation rate is larger than the GAM flow oscillation, the plasma is in L-mode. If the flow shearing rate exceeds the turbulence de-correlation, the plasma enters H-mode [100]. The cycle described above is predominantly observed at low densities. With increasing density the GAMs are reduced by collisional damping [93]. Experimentally, the duty cycle of the LCO is also reduced, making the pulses appear more irregular and burst-like. With increasing heating power the transition from L- to I-phase appears as abrupt confinement change, followed by a more gradual evolution into a fully developed H-mode [100].
This evolution of the I-phase bursts with density and heating power is consistent with the picture of the I-phase presented by Birkenmeier et al [106] and other works [112, 114, 116] at AUG, where the I-phase oscillations were identified as type-III ELMs. In the investigated plasmas GAMs were not observed. Due to the utilization of NBI power ramps in these studies, only higher plasma densities could be achieved, which leads to a more effective collisional damping of the GAMs [93]. However, as in [100], it was observed that the I-phase develops with increasing heating power from a state with regular LCOs to a state with intermittent bursts. This evolution of the I-phase is seen both at the L–H transition and, in reversed order, at the H–L back transition. In the work by Birkenmeier et al also the magnetic signatures of the I-phase were studied, which showed an up-down asymmetry. A similar structure of the I-phase bursts on the magnetic data was observed in the M-mode at JET [104]. These oscillations could be related to up-down asymmetric parallel flow and current perturbations, as studied experimentally and theoretically in [117]. Also LCO models which additionally take into account MHD effects can reproduce a transition into an intermittent state [118], whereas models based solely on turbulence-flow interaction, like the one in [98], lead to regular LCOs only. However, all these models have in common that the underlying process leading to these LCOs is that these edge instabilities are driven by strong gradients in the edge profiles and they are stabilized by strong shear flows.
High radial and temporal resolution measurements of turbulence, mean and ZFs performed in NBI heated, high density AUG plasmas () close to the L–H or H–L back transition [112, 114] allowed two different plasma phases to be investigated in detail. The first is a transient phase, characterized by L–I–L dithers, which are the back-and forth transition from L-mode into I-phase and vice versa. These L–I–L dithers can be seen on several signals including magnetic measurements and the edge density and temperature and they occur on a time scale of a few ms. The second investigated phase was a stable I-phase with regular LCOs in the kHz (sub-ms) range. Simultaneous measurements of the edge temperature and density gradients, as well as of the flow shear (approximated by the minimum of ) showed that all quantities develop on the same time scale (time resolution of 250 µs) [112].
Measurements with a time resolution of 100 µs [112] and 1 µs [114] found that during the LCOs the turbulence level and the mean flow shear are in phase, meaning that the turbulence level is highest when the shear is lowest. Furthermore, the analysis of the LCOs in the high density I-phase revealed that at all times , where is the diamagnetic velocity of the main ions [112]. This equality implies that in these experiments the total flow shear was dominated by the edge main ion gradients and that the ZF amplitude was small compared to neoclassical flows, in agreement with observations at JFT-2M [119] and NSTX [120].
Although the physical picture forming the periodicity of the I-phase is not yet fully resolved and different theories of the details of the transport dynamics exist, it appears that the same quantities and mechanisms leading to the L–H transitions are also of major importance for the I-phase. Common to most explanations of the I-phase, and supported by the turbulence measurements, is the interaction between turbulence-driven transport and the stabilizing effect of the flow shear. It is a critical interplay between the Er gradients driving the flow and destabilizing effects like strong edge pressure gradients as the source of mode activity, leading to periodic LCOs. If turbulence dominates, the plasma is in L-mode, whereas the periodicity of the LCOs is broken towards the fully established H-mode, with a strong transport barrier allowing for steep edge gradients. The detailed measurements of turbulence properties and flow shears in such experiments is crucial to improve our understanding of the L–H and the H–L back transition.
6. Conclusions and summary
The ability to access stable, high-confinement operational regimes is key to the success of magnetic confinement fusion reactors. As such, both the experimental and theoretical fusion communities have dedicated considerable time and resources to understanding confinement transitions. These efforts have greatly improved our understanding of the conditions under which such transitions, particularly the L–H transition, occur and have enabled us to extrapolate our knowledge to future machines. However, a fundamental physics-based understanding is still lacking. The AUG team has contributed strongly to the L–H transition research and this paper has attempted to summarize these contributions, putting them into context with respect to one another, but also in comparison to results achieved at other machines.
A very well known feature of the L–H power threshold is that it is non-monotonic as a function of electron density. Experiments at AUG focusing on the low density branch examined the role of the edge ion heat flux and were able to provide a robust explanation for the non-monotonic behavior, unifying both the low- and high density branches, the plasma current scaling observed in the low density branch, and the differences in observed as a function of the heating method used. These experiments showed that a critical value of the edge ion heat flux per particle () is needed to enter H-mode, see section 2. At low density, on account of the weaker electron-ion collisional coupling, significantly higher heating power is required when pure electron heating is applied to achieve the required needed to enter H-mode, which results in the observed increase in the power threshold at low density. Within the framework of a critical threshold in to initiate the L–H transition it is possible to predict the density for which the power threshold is expected to be minimum in future machines as well as the expected power threshold. When applied to ITER, this scaling produces favorable results, yielding power thresholds that should be attainable for the auxiliary heating systems planned for ITER.
While the observed threshold in provides a compelling unification of the low- and high density branches of the L–H power threshold, it is unlikely to be directly responsible for the L–H transition. Rather, local edge quantities, such as the gradients of the radial electric field (Er ) and their connected shear flow, are the candidates to be responsible for the transition into H-mode, as they can interact with the edge turbulence. Detailed studies of these edge parameters give insight into how confinement transitions take place and provide key data for validation of theoretical models. The edge ion heat flux is, however, linked to Er via the ion temperature gradient. Experiments at AUG showed that the minimum of the Er well, which is a proxy for the much more difficult to measure shear flow, is constant at the L–H transition for a given magnetic configuration, see section 2.2. These works connected the observation of an ion heat flux threshold to a local edge parameter, and directly support the paradigm of turbulence suppression by shear flow as the mechanisms initiating the confinement transition.
The connection between the H-mode power threshold () and Er was extended to the velocity shear (), see section 2.3. Here, it was shown that the maximum of is constant at the L–H transition over a wide range of electron densities and magnetic field values, explaining the magnetic field dependence of and identifying as a more fundamental parameter for the L–H transition than Er . New results presented in the current publication extend those experiments deeper into the low density branch and show a decrease in the measured maximal values at the L–H transition, whereas the diamagnetic velocity stays relatively constant. This deviation between diamagnetic and velocity demonstrates that at low density the contributions of the main ion flows become important and the minimum of can not be used as a proxy for its shear anymore. Whether the shear itself stays constant could not be addressed in a quantitative manner due to limited radial resolution of the Er measurements. However, the results obtained comparing confinement transitions in favorable and unfavorable magnetic drift configurations show a larger variation of and its related shear at the L–H transition, see section 4.3. This observation does not confirm the idea that one single critical value of is required to enter H-mode, but rather that has to be set into relation with the edge turbulence properties. The experimental observations on at the L–H transition are also supported by recent theoretical work done at AUG showing that the impact of on the L-mode edge turbulence is strongly non-linear and depends on the background plasma parameters as well as the local turbulence characteristics.
The L–H transition and related plasma quantities have also been explored in plasmas with different main ion compositions, see section 3. In AUG, the power threshold in pure He is similar to the one of pure D plasmas, whereas the threshold in H plasmas is twice as large. Also at the L–H transition is increased by a factor of two in H compared to D plasmas, whereas the minimum of the Er well and its gradients were found to show the same values. Within a simple picture on turbulence-flow interaction one might expect that the shear required to suppress the characteristic edge turbulence is proportional to its amplitude. Hence, in H one would expect to see a higher at the transition compared to D. However, this is not what is seen in the experiments and it is also not expected from gyrokinetic simulations. Rather, the experiments show a constant at the L–H transition, independent of the main ion species composition and the simulations show strongly non-linear behavior with complex interplay between the background plasma parameters, the turbulence properties and the shear level required to impact the turbulence. Since the experimental data show a clear and consistent behavior of at the L–H transition which applies equally to D and to H plasmas, the observed increase in in H compared to D follows directly from this result: the higher level of turbulence transport in H means more input power is required to reach the critical threshold in .
The L–H power threshold is of high interest for future fusion reactors, not just for reactor operation in D–T, but also for initial commissioning phases, during which they will operate using either hydrogen or helium as the working gas to avoid neutron activation of the machine. Hence the power threshold dependence on the main ion species mix will impact multiple phases of reactor operation. The high power threshold observed in H plasmas is a particular concern for future machines, which have limited amounts of auxiliary heating power capabilities. As such, any methods of reducing the power threshold that can be identified in present experiments are of high interest. Thus, the AUG and JET results demonstrating a 25% reduction in when transitioning from a C-walled to a W-walled device, see section 4.1, are very beneficial for reactor operation. Similarly, the reduction in observed at JET when seeding low levels of He (about 10%) into H plasmas heated with NBI would indicate a promising option for the reactor commissioning phase. However, at AUG similar experiments conducted in both NBI and ECRH heated plasmas did not show any reduction of with a He concentration of up to 20%, see section 3, which indicates that in ITER a reduction of the high H-mode power threshold in H plasmas by He seeding cannot be achieved in the PFPO-1 phase, where only ECRH heating is available. The results from AUG are consistent with recent DIII-D findings, which also show no change in with up to 20% He seeding. Also, in a series of new experiments presented here, the power threshold was explored across the transition from H to D. Similar to the H to He results, no change in the power threshold is observed when seeding H into D plasmas until a 50/50 mix is achieved. Above 50% the power threshold increases smoothly until the twice as high H-mode power threshold of pure H plasmas is reached.
Another concern for future machines is that the use of MPs to suppress ELMs may result in an unforeseen increase in . Early results from AUG showed that at low density no increase in the power threshold was observed with MPs, but at higher densities an increase of up to 20% was observed. Recent AUG experiments, conducted at the density minimum of , demonstrated that an increase in the power threshold is observed if the MP amplitude is above a critical value. At AUG, the field amplitude needed to suppress ELMs is below that which results in an increase in . This is a potentially very promising result for ITER, as at AUG ELM suppression can be maintained without a simultaneous increase in the H-mode power threshold. Modeling of these experiments shows that the increase in is strongest when the MP is oriented such to maximize the plasma response. The increase in is thought to be due to the changes in the edge velocity shear, which is reduced in the presence of MPs. Therefore, with MPs more heating power is required to increase the edge gradients and increase the shear to initiate the L–H transition. Another important observation from these experiments is that the minimum of the velocity profile is higher with MPs than without. Therefore, also under these conditions, the minimum of is not a good representation for its shear.
At AUG the L–H transition has also been investigated recently by connecting the separatrix conditions of and to the edge interchange-drift-Alfvén turbulence properties. The result of this semi-analytical model approach is an existence, or operational space diagram for a large database of AUG L-mode and H-modes. Between the two well separated regimes is an identifiable boundary which can be parameterized in terms of standard plasma parameters. The underlying context of the model is still the suppression of turbulence through equilibrium shear flows. Here the role of ZFs is assumed to be sub-dominant.
The I-phase is an intermediate regime, which occurs at the transition from L-mode to H-mode and at the H–L back transition. However, the I-phase is not a transitory regime, because it can be sustained indefinitely under appropriate conditions. The study of the I-phase and its related plasma edge oscillations, so called LCOs, gives insight into the critical interplay between the stabilizing effects of shear flows and destabilizing effects, like strong edge pressure gradients, on the edge turbulence. In low collisionality plasmas at AUG the LCOs are associated with turbulence-driven GAMs. With increasing density the regular LCOs evolve to a more sporadic, bursty nature with the same magnetic signatures as type-III ELMs. At AUG the characteristics of the I-phase have been well studied experimentally and also modeled heuristically. However, fully consistent theoretical models over the full I-phase existence parameter space remain outstanding. The reproduction of the I-phase with its characteristic edge oscillations is an important aspect for models seeking to reproduce the L–H transition.
Predicting the L–H transition is a critical issue for the operational success of future magnetic confinement fusion reactors which will operate in improved confinement regimes. Therefore, present-day fusion research devices aim to improve the predictability of the H-mode power threshold under reactor conditions. The AUG team has contributed with experimental and modeling efforts to improve our understanding of the underlying physics mechanisms leading to the L–H transition. Different key parameters have been identified and the critical role of and its related shear have been shown to be important for the H-mode access. On the other hand it is also found that the investigation and characterization of the shear flow alone is not sufficient to describe all phenomena related to and observed at the L–H transition. The background shear flow has to be brought into a broader context and set in relation with the characteristic edge turbulence, which requires often another level of sophistication. First attempts to address the shear flow-turbulence interaction leading to the L–H transition have been made experimentally and theoretically at AUG, but more comparisons and detailed analysis are foreseen in the near future. This is possible as both the modeling and measurement capabilities are rapidly improving and they are evermore able to capture the different aspects of the L–H transition and the entire concept of shear flow-turbulence interaction correctly.
Acknowledgments
The authors would like to thank C Angioni, T Pütterich, F Ryter and E Wolfrum for fruitful discussions and valuable input. This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.