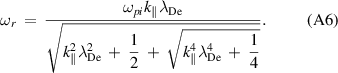Abstract
The dissipation of ion-acoustic surface waves in a fully ionized and semi-bounded plasma is investigated by solving the dispersion integral formulated by employing the specular reflection boundary condition. Non-zero ion temperature and ion-ion collisions are considered in the dielectric permittivity. The calculated damping rate is composed of the collisionless Landau damping and the collisional dissipation. The distinctions between them are addressed here. It is found that the collisionless damping is significant in the region where the wavelength is larger than the electron Debye length. The collisional dynamics, however, as well as the ion temperature, dominates the wave damping when the wavelength is smaller than the electron Debye length.
Export citation and abstract BibTeX RIS
1. Introduction
This paper discusses the effects of collision and temperature on the damping of surface ion-acoustic waves that propagate in a semi-bounded plasma. Research on the propagation and stability of surface waves in various types of plasma such as semi-bounded, slabs and columns has a long history [1–4]. After the pioneering work of Trivelpiece and Gould [1], a lot of information on the properties and propagation characteristics of surface waves has been accumulated [5]. The effects of finite temperature, density inhomogeneity [2], collisions between particles [6], dusty media with the presence of nonspherical grains [7], quantum plasma [8], etc, on the propagation of surface waves are a few examples and they still attract great interest since all plasmas are in some fashion bounded. The stability problem in a variety of confined configurations has also been extensively investigated [9].
We are motivated to conduct an analysis on the collisional damping of surface ion-acoustic waves that propagate in a fully ionized plasma. For low-frequency ion-acoustic waves, the ion collisions may provide a significant role in the damping of the waves if the ion mean free path is much smaller than the wavelength. Electron collisions may only be important for high-frequency electron plasma waves [10]. For weakly ionized plasma, the collision between ions and neutral particles is the most important component of wave dissipation [11, 12]. For completely ionized plasma, we consider the collisions between ions only because the Coulomb force between the charged particles falls very slowly with distance, the collisions with large impact parameters would play a major role in the collisional processes. Thus, the effect of collisions between ions and electrons on the ion-acoustic wave is neglected here. A large body of literature on surface waves has stimulated research activities on plasmas containing noble electrons and ions, so there is not enough information on the effect of collisional damping on the propagation and stability of surface waves. In addition, the influence of the ion-ion collision on the surface mode of ion-acoustic waves including Landau damping has not been investigated yet. Therefore, this work is motivated to present a general description of ion-acoustic waves propagating at the boundary surface of a plasma including the ion-ion collision, which seems to affect the dispersive property. Hence, the physical characteristics of electrostatic ion-acoustic surface waves are investigated to determine the wave frequency and the corresponding Landau damping rate including the ion collisional effect by using the transverse truncation method. Moreover, it is expected that the functional perturbation method with the transverse truncation approximation used in this work can provide insightful view points on the stable and unstable modes of surface plasma waves and also be useful to studies of the propagation of surface waves in the presence of the complex collective behaviors. The influence of compressible density of plasma species is not considered in this work since the ion collision effect on the propagation of the surface ion-acoustic wave including Landau damping based on the specular reflection condition is the main purpose of the current work. This situation occurs in nano-devices where the plasma is separated from the wall and spatially confined by the external field. As in the case of volume ion-acoustic wave in unbound plasma, surface ion-acoustic waves exist even if the ion thermal motion is completely ignored. Then, it is expected that the Landau dissipation on the wave would prevail. In this work, we take account of the ion temperature, although it is much less than the electron temperature. Thus, the effect of ion temperature as well as the effect of collision on the wave dissipation will be discussed. In order to obtain the analytic form for the damping rate as much as possible, we resort to the specular reflection boundary condition and the transverse truncation method which will be explained in the next section. We show that the total damping rate is the addition of a collisional damping rate arising from the ion thermal motion to a collisionless Landau damping rate arising from the wave-particle interaction.
2. Derivation of the damping rate
We consider the case of longitudinal waves, in particular the low-frequency ion-acoustic mode existing in isotropic plasma with  where
where 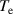 and
and 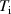 are the temperature of electrons and ions, respectively. In such a case (
are the temperature of electrons and ions, respectively. In such a case (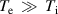 ) with wave frequencies in the range
) with wave frequencies in the range 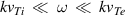 , the collisional modification of the low-frequency ion-acoustic oscillations can be made on the longitudinal dielectric permittivity. Here,
, the collisional modification of the low-frequency ion-acoustic oscillations can be made on the longitudinal dielectric permittivity. Here,  and
and 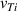 are the thermal speed of electrons (e) and ions (i), respectively, defined by
are the thermal speed of electrons (e) and ions (i), respectively, defined by  (j = e, i). To calculate the damping rate of the surface ion-acoustic mode which is caused by collisions between the charged particles, the effective collision frequency
(j = e, i). To calculate the damping rate of the surface ion-acoustic mode which is caused by collisions between the charged particles, the effective collision frequency  is considered in the longitudinal dielectric permittivity. When the particle collision is not too frequent, under the condition
is considered in the longitudinal dielectric permittivity. When the particle collision is not too frequent, under the condition 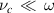 and
and 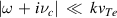 , the longitudinal dielectric permittivity can be written as [13]
, the longitudinal dielectric permittivity can be written as [13]
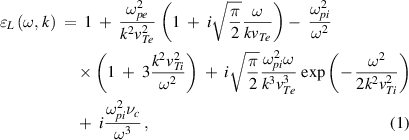
where  is the plasma frequency of the particle species j (= e, i). In the frequency range of the ion-acoustic wave, equation (1) can be reduced to [9]
is the plasma frequency of the particle species j (= e, i). In the frequency range of the ion-acoustic wave, equation (1) can be reduced to [9]
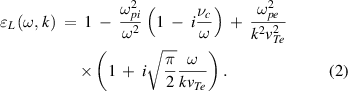
Note that in the low-frequency range the electron collisions do not contribute to the dissipation of longitudinal oscillations. For a fully ionized plasma, the collisions between charged particles prevail. Under the condition 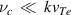 , the collisional effect due to electrons may be neglected since the wavelength is much smaller than the electron mean free path. Then, the dissipative collisional process is insignificant. However, under the condition,
, the collisional effect due to electrons may be neglected since the wavelength is much smaller than the electron mean free path. Then, the dissipative collisional process is insignificant. However, under the condition, 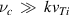 , ion collisions must be accounted for in the dissipative part of the dielectric permittivity. The collisional correction in the case of fully ionized plasmas is given by
, ion collisions must be accounted for in the dissipative part of the dielectric permittivity. The collisional correction in the case of fully ionized plasmas is given by  where
where  is the ion-ion collision frequency [9].
is the ion-ion collision frequency [9].
We consider an isotropic plasma occupying the half-space defined by the region 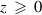 and bounded by a vacuum half-space (
and bounded by a vacuum half-space (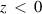 ). This semi-bounded plasma is uniform and unmagnetized. We assume that the curl of electric field vanishes, so the analysis is limited to electrostatic. The perturbation about the equilibrium state is weak. If the characteristic length of the plasma is much greater than the scale length of the inhomogeneity, we can set the specular reflection boundary condition for the perturbed plasma distribution function
). This semi-bounded plasma is uniform and unmagnetized. We assume that the curl of electric field vanishes, so the analysis is limited to electrostatic. The perturbation about the equilibrium state is weak. If the characteristic length of the plasma is much greater than the scale length of the inhomogeneity, we can set the specular reflection boundary condition for the perturbed plasma distribution function  at
at  . This condition must contain all the information on the interaction of plasma particles at the surface satisfying the condition [14]
. This condition must contain all the information on the interaction of plasma particles at the surface satisfying the condition [14]

It is well established that the dispersion equation for surface waves can be derived by applying the general electrodynamic boundary conditions and by equating the surface impedance of the semi-bounded plasma and that of the vacuum half-space. In [13], the surface impedance of the semi-bounded isotropic plasmas is calculated as
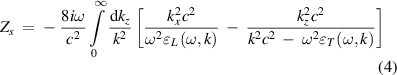
and the surface impedance of the vacuum half-space is given by
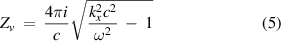
where 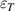 is the transverse dielectric permittivity. Now we apply the boundary condition, i.e. the continuity of the tangential components of the electromagnetic fields for
is the transverse dielectric permittivity. Now we apply the boundary condition, i.e. the continuity of the tangential components of the electromagnetic fields for 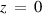 and equate
and equate 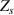 and
and 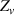 to yield the dispersion equation for surface waves such as
to yield the dispersion equation for surface waves such as
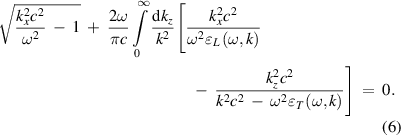
In the limit of electrostatic perturbation  , the dispersion equation for longitudinal surface waves in semi-bounded plasma can be obtained as
, the dispersion equation for longitudinal surface waves in semi-bounded plasma can be obtained as
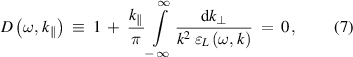
where  and
and  are the parallel and the perpendicular components of the wave vector
are the parallel and the perpendicular components of the wave vector  and
and 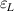 is given by equation (2) for the ion-acoustic wave in the fully ionized plasma. The component
is given by equation (2) for the ion-acoustic wave in the fully ionized plasma. The component 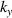 is set to zero since the y-coordinate has a translational invariance for the plasma bounded by the plane
is set to zero since the y-coordinate has a translational invariance for the plasma bounded by the plane  and thus can be ignored in our geometry. The finiteness of the fields would yield the continuity of the tangential components of the electric fields at
and thus can be ignored in our geometry. The finiteness of the fields would yield the continuity of the tangential components of the electric fields at 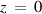 . This condition can be applied to yield equation (7) by equating the surface impedance of the semi-bounded isotropic plasma and the surface impedance of the vacuum half-space. Here, equation (7) can be used for our model in which the existence of a sufficiently sharp plasma surfaces is presumed. Hence, all plasma quantities with the dimension of physical length such as the Debye length usually exceed the size of the density variation near the interface. We are dealing with a linearized theory in which the perturbation is small. Then, the expansion of
. This condition can be applied to yield equation (7) by equating the surface impedance of the semi-bounded isotropic plasma and the surface impedance of the vacuum half-space. Here, equation (7) can be used for our model in which the existence of a sufficiently sharp plasma surfaces is presumed. Hence, all plasma quantities with the dimension of physical length such as the Debye length usually exceed the size of the density variation near the interface. We are dealing with a linearized theory in which the perturbation is small. Then, the expansion of 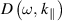 is a useful technique to find the damping rate for the surface waves. Let
is a useful technique to find the damping rate for the surface waves. Let 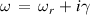 where
where 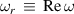 and
and  . We also let
. We also let 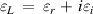 where
where 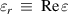 and
and 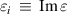 . If
. If  and
and 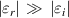 , the expansion of
, the expansion of 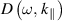 about
about  gives
gives  . The dielectric permittivity
. The dielectric permittivity  in equation (7) allows us to write
in equation (7) allows us to write 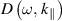 in the form
in the form
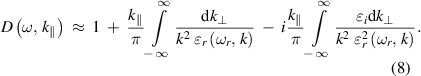
Therefore, the damping rate of the wave can be formulated succinctly as
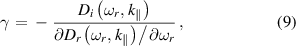
where 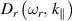 and
and 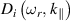 are the real and the imaginary part of the dispersion integral given by, respectively,
are the real and the imaginary part of the dispersion integral given by, respectively,
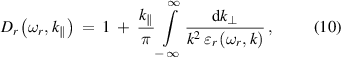
and
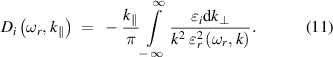
The dispersion relation of the surface ion-acoustic wave is obtained by evaluating 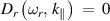 , i.e.
, i.e.
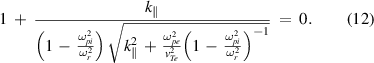
Therefore, the wave frequency is found as
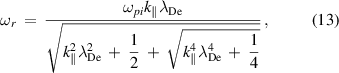
where  is the electron Debye length. Surface ion-acoustic waves are possible only in the frequency range where
is the electron Debye length. Surface ion-acoustic waves are possible only in the frequency range where 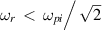 [14], and the above result satisfies this condition for the whole spectrum. In the region where
[14], and the above result satisfies this condition for the whole spectrum. In the region where  is small, we can see immediately that the frequency increases in proportion to
is small, we can see immediately that the frequency increases in proportion to 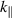 and converges to
and converges to  as
as 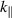 increases.
increases.
We now proceed to the analysis of damping rate for the ion-acoustic surface waves in a semi-bounded plasma. We are interested in the case where analytical solutions can be possible. Unlike 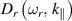 , it is very difficult to calculate
, it is very difficult to calculate 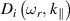 by directly performing the integration. Therefore, we use an approximate approach named the transverse truncation method to execute the integral in the imaginary part
by directly performing the integration. Therefore, we use an approximate approach named the transverse truncation method to execute the integral in the imaginary part  . According to the condition of
. According to the condition of 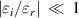 and weak contribution of the perpendicular component
and weak contribution of the perpendicular component  of the wave vector to the function
of the wave vector to the function  near the interface, the transverse truncation analysis, i.e.
near the interface, the transverse truncation analysis, i.e. ![${\left[ {{\varepsilon _i}\left( {{\omega _r},\,k} \right)/{\varepsilon _r}\left( {{\omega _r},\,k} \right)} \right]_{{k_ \bot }\, = \,0}}$](https://content.cld.iop.org/journals/0741-3335/63/11/115011/revision2/ppcfac1f6aieqn62.gif) can be applied to extract the physical information on the imaginary part
can be applied to extract the physical information on the imaginary part  . Hence, the constraint of the smallness of
. Hence, the constraint of the smallness of  provides a very novel method and is useful for surface wave calculations, especially for surface waves propagating in semi-bounded plasmas. Near the sharp interface, the imaginary part
provides a very novel method and is useful for surface wave calculations, especially for surface waves propagating in semi-bounded plasmas. Near the sharp interface, the imaginary part 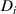 is then approximated as follows,
is then approximated as follows,
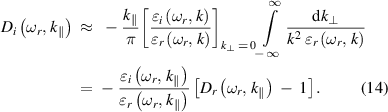
After substituting the expressions for  ,
, 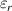 and
and  into equation (14), we obtain
into equation (14), we obtain  in the form,
in the form,
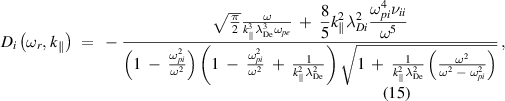
where 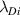 is the ion Debye length. Finally, the damping rate for the surface wave in the completely ionized plasma is calculated as
is the ion Debye length. Finally, the damping rate for the surface wave in the completely ionized plasma is calculated as
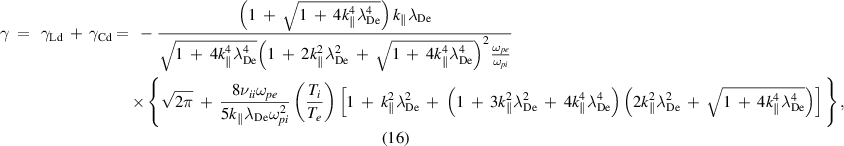
where 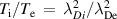 . Here,
. Here,  represents the collisionless Landau damping:
represents the collisionless Landau damping:
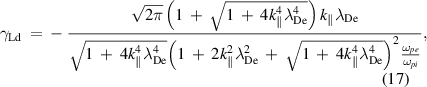
and 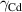 stands for the collisional dissipation:
stands for the collisional dissipation:
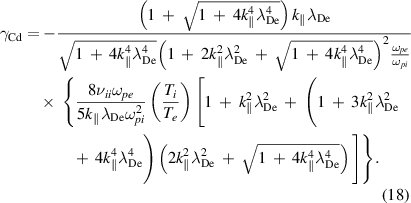
3. Discussions and results
The magnitude of damping rate for the surface ion-acoustic mode given by equation (16) is plotted in figures 1 and 2 for different values of collision frequency and ion temperature. In these figures, the damping rate, the wave number, the collision frequency and the electron plasma frequency are scaled to the dimensionless physical quantities  ,
, 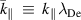 ,
, 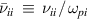 and
and  (=40 is assumed for numerical results), respectively. In figure 1, the collisional damping is compared to the collisionless damping. As
(=40 is assumed for numerical results), respectively. In figure 1, the collisional damping is compared to the collisionless damping. As 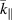 increases, the collisionless Landau damping rate
increases, the collisionless Landau damping rate  increases initially and then decreases to zero after reaching the maximum value (solid line). It can be seen that the damping rate increases as the collision increases: the dashed line for
increases initially and then decreases to zero after reaching the maximum value (solid line). It can be seen that the damping rate increases as the collision increases: the dashed line for  and the dotted line for
and the dotted line for  . Therefore, it can be said that the damping rate is enhanced by the collision. However, we see from figure 1 that the collisional damping is significant for
. Therefore, it can be said that the damping rate is enhanced by the collision. However, we see from figure 1 that the collisional damping is significant for  , i.e. ion-ion collision is important when the wavelength is much smaller than the electron Debye length. This feature becomes more evident by taking the limits for the damping rate. For
, i.e. ion-ion collision is important when the wavelength is much smaller than the electron Debye length. This feature becomes more evident by taking the limits for the damping rate. For  , i.e. in the short wavelength limit, the damping rate becomes
, i.e. in the short wavelength limit, the damping rate becomes
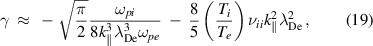
Figure 1. Damping rate for the surface ion-acoustic wave in the fully ionized plasma as a function of  for
for 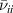 = 0 (solid line), 0.01 (dashed line) and 0.02 (dotted line) when
= 0 (solid line), 0.01 (dashed line) and 0.02 (dotted line) when 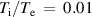 .
.
Download figure:
Standard image High-resolution imageFigure 2. Damping rate for the surface ion-acoustic wave in the fully ionized plasma as a function of 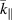 for
for 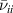 = 0 (solid line), 0.01 (dashed line) and 0.02 (dotted line) when
= 0 (solid line), 0.01 (dashed line) and 0.02 (dotted line) when 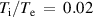 .
.
Download figure:
Standard image High-resolution imagewhich can be further reduced to  . Therefore, for a large wave number, the collisionless Landau damping is ignorable, and the collision term is dominant.
. Therefore, for a large wave number, the collisionless Landau damping is ignorable, and the collision term is dominant.
As well as the dynamic role of collisions on the dissipation of surface ion-acoustic waves, the ion temperature is also important in the fully ionized plasma. If the ions are cold, i.e. 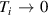 , then the dissipation becomes purely collisionless Landau damping. In fact, the effect of ion-ion collision on the damping is important only for
, then the dissipation becomes purely collisionless Landau damping. In fact, the effect of ion-ion collision on the damping is important only for 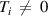 , regardless of the range of
, regardless of the range of  . Figure 2 is provided to compare with figure 1 to see the effect of ion temperature. Figures 1 and 2 are drawn for
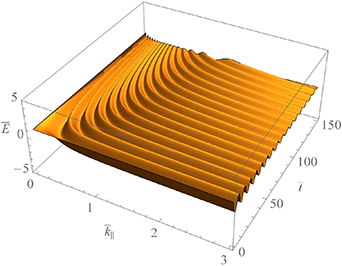
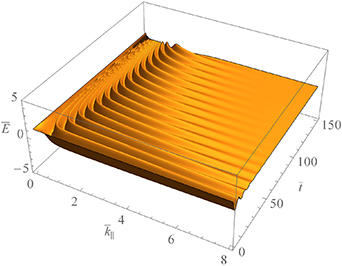
. Figure 2 is provided to compare with figure 1 to see the effect of ion temperature. Figures 1 and 2 are drawn for  and 0.02, respectively, with the same variation of collision rate. We easily observe that the ion temperature enhances the collisional damping rate as indicated in equation (19). Finally, the variation of the wave amplitude is drawn in figures 3–5 to show visually how the perturbed surface ion-acoustic wave would dissipate over time at an arbitrary point on the boundary. The normalized form of the perturbed wave can be written as
and 0.02, respectively, with the same variation of collision rate. We easily observe that the ion temperature enhances the collisional damping rate as indicated in equation (19). Finally, the variation of the wave amplitude is drawn in figures 3–5 to show visually how the perturbed surface ion-acoustic wave would dissipate over time at an arbitrary point on the boundary. The normalized form of the perturbed wave can be written as ![$\bar E\,\, = \,\,{e^{\bar \gamma \bar t}}\,\operatorname{Re} \left[ {{e^{i\left( {{{\bar k}_\parallel }\bar x\, - \,{{\bar \omega }_r}\bar t} \right)}}} \right]$](https://content.cld.iop.org/journals/0741-3335/63/11/115011/revision2/ppcfac1f6aieqn95.gif) where
where  is the scaled time and
is the scaled time and 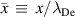 is the scaled position of the wave. Figure 3 shows the change of
is the scaled position of the wave. Figure 3 shows the change of  in time for
in time for 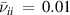 and
and  . It can be seen that the perturbation of the wave rapidly decreases around
. It can be seen that the perturbation of the wave rapidly decreases around 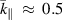 at which the damping rate peaks. If the collision rate and the ion temperature increase, the attenuation of the perturbation will be noticeable as
at which the damping rate peaks. If the collision rate and the ion temperature increase, the attenuation of the perturbation will be noticeable as  increases past the peak. This property is seen in the large
increases past the peak. This property is seen in the large 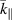 area in figure 4 where
area in figure 4 where 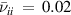 and
and  are used. As equation (19) implies, the strong dissipation can be seen more clearly in figure 5 where the range of
are used. As equation (19) implies, the strong dissipation can be seen more clearly in figure 5 where the range of 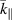 is further expanded. In weakly ionized plasmas, it is shown that the collisional moment [15] should include both Coulomb and change-exchange scattering. Hence, the investigation of the dissipation of ion-acoustic surface waves in a weakly ionized and semi-bounded plasma will also be treated elsewhere since the fractional force in weakly coupled plasmas can also be caused by the charge-exchange with neutral species. For surface wave experiments, the radially resolved probe measurements of the electron energy distribution have been obtained in an argon discharge [16] and the stationary microwave discharge in helium gas was investigated by applying field radial decay measurements with optical spectroscopy methods [17]. The excitation of a surface plasma wave was investigated by a relativistic electron beam over a plasma cylinder [18]. In addition, the experiment for the excitation of surface plasma waves was carried out by using an intense short laser pulse [19]. However, the experimental investigations on the dissipation of ion-acoustic surface waves has not been carried out in a fully ionized and semi-bounded plasma. So, in the future, we may observe and resolve the decay of ion-acoustic surface waves in a semi-bounded plasma including the influence of ion collisions.
is further expanded. In weakly ionized plasmas, it is shown that the collisional moment [15] should include both Coulomb and change-exchange scattering. Hence, the investigation of the dissipation of ion-acoustic surface waves in a weakly ionized and semi-bounded plasma will also be treated elsewhere since the fractional force in weakly coupled plasmas can also be caused by the charge-exchange with neutral species. For surface wave experiments, the radially resolved probe measurements of the electron energy distribution have been obtained in an argon discharge [16] and the stationary microwave discharge in helium gas was investigated by applying field radial decay measurements with optical spectroscopy methods [17]. The excitation of a surface plasma wave was investigated by a relativistic electron beam over a plasma cylinder [18]. In addition, the experiment for the excitation of surface plasma waves was carried out by using an intense short laser pulse [19]. However, the experimental investigations on the dissipation of ion-acoustic surface waves has not been carried out in a fully ionized and semi-bounded plasma. So, in the future, we may observe and resolve the decay of ion-acoustic surface waves in a semi-bounded plasma including the influence of ion collisions.
Figure 3. Variation of the perturbed surface ion-acoustic wave as a function of 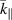 and
and  at an arbitrary point on the plasma-vacuum boundary when
at an arbitrary point on the plasma-vacuum boundary when 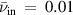 and
and 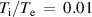 .
.
Download figure:
Standard image High-resolution imageFigure 4. Variation of the perturbed surface ion-acoustic wave as a function of 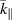 and
and  at an arbitrary point on the plasma-vacuum boundary when
at an arbitrary point on the plasma-vacuum boundary when  and
and 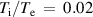 .
.
Download figure:
Standard image High-resolution imageFigure 5. Variation of the perturbed surface ion-acoustic wave as a function of  and
and  at an arbitrary point on the plasma-vacuum boundary when
at an arbitrary point on the plasma-vacuum boundary when 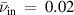 and
and 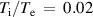 (with extended
(with extended  range).
range).
Download figure:
Standard image High-resolution image4. Summary
The effect of collisional damping of the surface ion-acoustic wave is investigated for a fully ionized plasma separated sharply by a vacuum. Hence, the physical properties of an ion-acoustic surface wave are investigated to determine the wave frequency and the Landau damping rate including the influence of the ion collisional effect. It has been shown that the ion temperature, as well as the ion-ion collision rate, can play an important role in the dissipation of the surface ion-acoustic wave. It has been found that the collisionless Landau damping is significant for a wavelength larger than the electron Debye length, but the collision rate and the ion temperature dominate over the Landau damping in the range where the wavelength is smaller than the electron Debye length. Surface waves possess a lot of advantages over bulk waves since they can produce plasmas with more spatially uniform density profiles, resulting in a wide range of applications such as gas discharge for surface treatment of solids, laser physics, gas detoxification, medical industry, etc. Since the collisional frequency is not often small under experimental conditions for plasma wave research, one should take into account the collision frequency for the dielectric permittivity of the plasma if the deviation of the experimental results from the theoretical dispersion diagram is evident. The mirror reflection model employed in this work would be especially useful to describe the confinement of plasma particles in metals and semiconductor plasmas. Moreover, the specular reflection condition and the transverse truncation method will be quite useful for the analysis of plasma confined within a finite layer such as a thin slab in a variety of applicational devices. It is shown that the functional perturbation method with the transverse truncation method used in this work provide insightful view points on the stable and unstable modes of surface waves and would also be useful to explore the propagation mode of surface waves in the presence of complex collective behaviors which provide complex character of the plasma susceptibility. In this work, it is shown that the collisionless damping is significant in the region where the wavelength is larger than the electron Debye length. In addition, it is shown that the collision dynamics dominates the wave damping when the wavelength is smaller than the electron Debye length. In this case, the relation between the thickness of the layer and the wavelength of the wave is expected to be an important factor for the propagation and damping of the wave. It should be pointed out that the methods used here would be helpful to understand the physics of ion-acoustic surface waves propagating in various geometric shapes.
Acknowledgments
The work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (NRF-2019R1A2C1003363).
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
: Appendix
Appendix. Derivation of the wave frequency
The frequency of ion-acoustic wave can be derived from 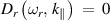 where
where 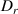 is defined by equation (10) as
is defined by equation (10) as
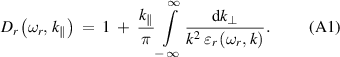
The real part of the permittivity in equation (A1),  , can be found as
, can be found as
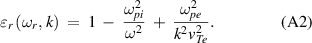
If we insert equation (A2) into equation (A1), we get
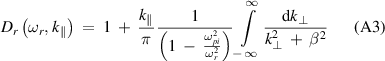
where

The integral in equation (A3) can be evaluated in the complex  -plane. Picking up the residue at the pole
-plane. Picking up the residue at the pole  , we obtain the following result:
, we obtain the following result:
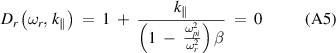
which is equivalent to equation (12). If we solve equation (A5) for 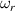 with the condition
with the condition 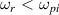 , one finally obtains the wave frequency in the form:
, one finally obtains the wave frequency in the form: