Abstract
A theoretical analysis is presented for the stimulated Raman scattering (SRS) driven by multiple beams with certain frequency differences or bandwidths. The concomitant electrostatic modes are excited by the scattering lights when the pump beams share a common electron plasma wave to drive SRS. This coupling can be suppressed when the frequency difference of the two beams is three times larger than the SRS growth rate of a single beam, where the beams develop their scattering lights independently. To mitigate SRS further under the multibeam irradiation, polychromatic pumps are introduced to reduce the SRS saturation level, where the weakly coupled common modes are heavily damped in hot plasmas. The sidescattering driven by polychromatic light in inhomogeneous plasmas is significantly reduced due to the wavevector mismatch of daughter waves. Particle-in-cell simulations confirm our theoretical analysis and demonstrate that the strength of multibeam SRS and the hot electron production in inhomogeneous plasmas can be controlled at a low level by polychromatic light with a few percentage bandwidth ( ), even in the non-linear regime.
), even in the non-linear regime.
Export citation and abstract BibTeX RIS
1. Introduction
Stimulated Raman scattering (SRS) [1–3], the decay of a pump laser into a scattered light and an electron plasma wave, is one of the major obstacles to inertial confinement fusion (ICF) [4–7]. In ICF experiments, many laser beams are applied in order to compress and heat the fusion targets uniformly and sufficiently, either in the direct-drive or the indirect-drive scheme [6, 8–10]. In these cases, the SRS excitation from neighboring laser beams may be coupled by a common daughter wave [11–14]. Comparing with a single beam, multibeam SRS is described at least in two dimensional geometry [10, 15]. Different from crossed beam energy transfer [16–20] and polarization control [21, 22] via ion acoustic waves, multibeam SRS is a kind of absolute instability in inhomogeneous plasmas under a certain particular configuration. This instability can lead to significant loss of pump energies and generation of hot electrons [23]. Therefore, the mitigation of multibeam SRS is important for ICF research. A few ideas have been proposed to control laser plasma instabilities, such as the proven laser smoothing techniques [24, 25], temporal profile shaping pulse composed of a spike train of uneven duration and delay (STUD) [26], external DC magnetic fields [27], etc.
Parametric instabilities driven by incoherent pumps are attracting increasing interest. Thomson et al proposed that the parametric instabilities can be reduced by the broadband when the bandwidth is much larger than the linear growth rate [28, 29]. Kruer et al investigated the non-linear evolution of instabilities driven by broadband pumps via simulations [30–32]. Later work showed a good agreement between simulations and theoretical models [33, 34]. Pesme et al reviewed the early studies of parametric instabilities driven by an incoherent pump, and established the validity regions for the statistical description [35]. Santos et al proposed the general dispersion relation of the broadband radiation based upon a generalized Wigner-Moyal statistical theory [36]. Some early experiments were performed to observe the bandwidth effects [37, 38]. SRS driven by a single polychromatic light, which is composed of many beamlets with different frequency, has been studied in homogeneous and inhomogeneous plasmas [39, 40]. Such light is found potentially to be effective for the suppression of parametric instabilities in ICF [41]. Low-coherence high-power laser drivers have achieved a series of developments [42]. Polychromatic light under ICF conditions can be generated, for example, by the modulation of high power intense laser in tenuous plasmas [43, 44]. Multiple beams with different central frequencies can out-way the difficulty in producing bandwidth on one beam. Mitigation of cross beam energy transfer using wavelength detuning has been observed in experiments [45, 46]. However, the collective SRS excited by multiple polychromatic beams still needs to be explored. In the following, we propose a theoretical model of multibeam SRS coupling by a common electron plasma wave in homogeneous plasmas. Based upon this model, we discuss the mitigation of SRS by polychromatic lights according to the multibeam dispersion relation. Then, the multibeam SRS developed by polychromatic light in inhomogeneous plasmas is discussed according to the wavevector matching condition and saturation coefficient. Finally, the theoretical predictions are validated by particle-in-cell (PIC) simulations.
2. Theoretical analysis of SRS driven by multiple polychromatic lights
2.1. SRS driven by multibeam in homogeneous plasmas
Without loss of generality, we firstly consider that two beams drive SRS sharing the same Langmuir wave in a homogeneous plasma. When the laser bandwidth Δω0 is much smaller than the growth rate Γ [39], the coupling equations for plasma density perturbation 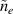 and scattering lights are:
and scattering lights are:
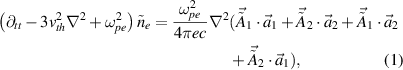
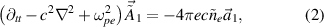
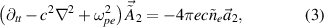
where  and
and 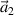 are the amplitude of beam 1 and beam 2, respectively, vth
is the electron thermal velocity, and ωpe
is the frequency of electron plasma wave.
are the amplitude of beam 1 and beam 2, respectively, vth
is the electron thermal velocity, and ωpe
is the frequency of electron plasma wave. 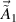 and
and  are the scattering perturbations developed by beam 1 and beam 2, respectively. The relation between laser intensity Ii
and ai
is given by
are the scattering perturbations developed by beam 1 and beam 2, respectively. The relation between laser intensity Ii
and ai
is given by ![$I_{i}(\mathrm{W}\,\mathrm{cm}^{-2}) = 1.37\times 10^{18}a_{i}^2/[\lambda(\mu \mathrm{m})]^2$](https://content.cld.iop.org/journals/0741-3335/63/5/055006/revision3/ppcfabe75aieqn7.gif) , where i denotes the ith beam.
, where i denotes the ith beam.
The coupling terms  and
and 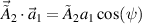 indicate that one of the pump beams is coupled by the scattering light developed by the other laser to excite the Langmuir wave, where ψ is the angle between the polarizations of the two beams. Therefore, two Langmuir waves
indicate that one of the pump beams is coupled by the scattering light developed by the other laser to excite the Langmuir wave, where ψ is the angle between the polarizations of the two beams. Therefore, two Langmuir waves 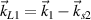 and
and  are developed from the partially shared scattering lights. One notes that equations (1)–(3) can be reduced to the single laser case under
are developed from the partially shared scattering lights. One notes that equations (1)–(3) can be reduced to the single laser case under  . The interaction of two pump beams can be projected into the plane of their wavevectors, where we always have cos(ψ) = 1 for s-polarized (electric field of light is perpendicular to the plane) lasers. However, one has cos(ψ) ≤ 1 for p-polarized (electric field of light is parallel to the plane) lasers, where the equality only exists for the special case that
. The interaction of two pump beams can be projected into the plane of their wavevectors, where we always have cos(ψ) = 1 for s-polarized (electric field of light is perpendicular to the plane) lasers. However, one has cos(ψ) ≤ 1 for p-polarized (electric field of light is parallel to the plane) lasers, where the equality only exists for the special case that 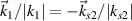 . In the following discussions, two pump lasers both with s-polarization are considered due to the relatively larger growth rate.
. In the following discussions, two pump lasers both with s-polarization are considered due to the relatively larger growth rate.
Multibeam SRS developed by pump beams with a same frequency have been discussed in the previews works [11, 47]. Two resonant modes 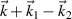 and
and  can be found from the Fourier analysis of the coupling terms
can be found from the Fourier analysis of the coupling terms 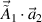 and
and 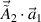 . Here we consider that the two beams are along the same propagation direction
. Here we consider that the two beams are along the same propagation direction 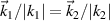 and with different frequencies
and with different frequencies 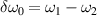 . By doing the Fourier analysis of equations (1)–(3) in the plane of
. By doing the Fourier analysis of equations (1)–(3) in the plane of  and
and  , one obtains the dispersion relation:
, one obtains the dispersion relation:
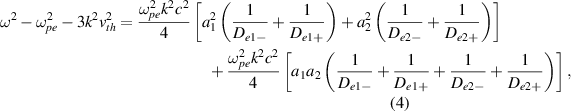
where 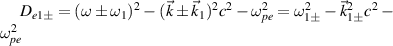 ,
, 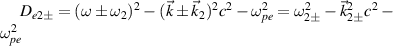 , ωi
and
, ωi
and  are the frequency and wavevector of ith beam, respectively. We have
are the frequency and wavevector of ith beam, respectively. We have 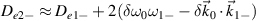 with
with 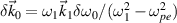 . The modulus of
. The modulus of 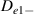 is in the order of
is in the order of  , and
, and 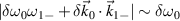 , where Γ is the imaginary part of ω. When
, where Γ is the imaginary part of ω. When 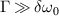 , the backscattering mode
, the backscattering mode 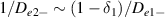 with
with 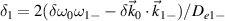 . Therefore, the two beams are strongly coupled under a small bandwidth
. Therefore, the two beams are strongly coupled under a small bandwidth 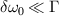 . On the contrary,
. On the contrary, 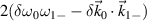 is the dominant term of
is the dominant term of 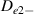 under a broad bandwidth
under a broad bandwidth 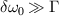 , and correspondingly the two beams are decoupled [29, 35].
, and correspondingly the two beams are decoupled [29, 35].
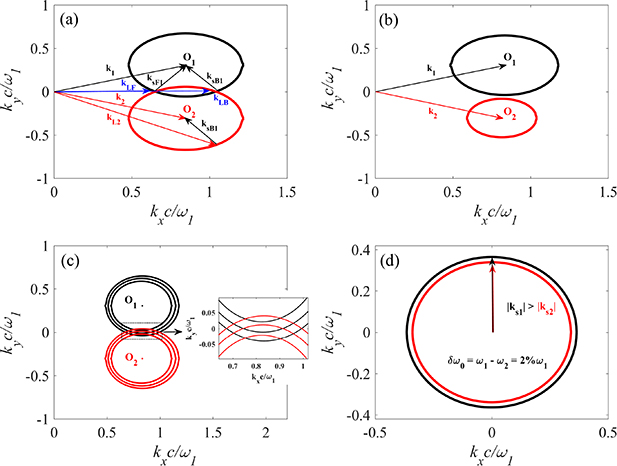
Figure 1(a) shows the wavenumber distribution of the SRS growth rate in the rectangular coordinates by solving equation (4). The plasma density is 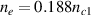 , and electron temperature is Te
= 2keV, where nc1 is the critical density for beam 1. The incident angles of the two beams in plasma are equal
, and electron temperature is Te
= 2keV, where nc1 is the critical density for beam 1. The incident angles of the two beams in plasma are equal 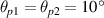 , and with the same amplitude
, and with the same amplitude 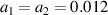 and different frequencies
and different frequencies 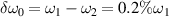 . The two scattering lights have a small frequency difference equal to 0.2%ω1, and both of them are shared by the pumps. One finds that the instability regions of the two beams are overlapped under this condition. Therefore, the instability region width Δk is the major factor for the coupling of different instability modes.
. The two scattering lights have a small frequency difference equal to 0.2%ω1, and both of them are shared by the pumps. One finds that the instability regions of the two beams are overlapped under this condition. Therefore, the instability region width Δk is the major factor for the coupling of different instability modes.
Figure 1. Distributions of the SRS growth rate Γ driven by two beams in the wavenumber space and the θ-δω0 plane. The plasma density is 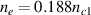 , and the electron temperature is Te
= 2keV. (a) The two pump beams are in the same direction
, and the electron temperature is Te
= 2keV. (a) The two pump beams are in the same direction 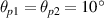 with the frequency difference
with the frequency difference 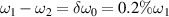 , and the amplitudes of the two beams are
, and the amplitudes of the two beams are 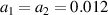 . (b) The frequency difference is
. (b) The frequency difference is 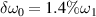 , and the incident angles are
, and the incident angles are  and
and 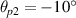 . The other parameters are the same with (a). (c) The growth rate as a function of angle between the vectors of the two pumps for different δω0. The other parameters are same to (b). (d) The beam 2 is a polychromatic light composed by two decoupled beamlets. The beamlet frequencies are
. The other parameters are the same with (a). (c) The growth rate as a function of angle between the vectors of the two pumps for different δω0. The other parameters are same to (b). (d) The beam 2 is a polychromatic light composed by two decoupled beamlets. The beamlet frequencies are 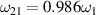 and
and 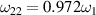 with amplitude
with amplitude 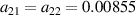 , which has energy equal to beam 1.
, which has energy equal to beam 1.
Download figure:
Standard image High-resolution imageThe instability regions of the scattering lights are decoupled 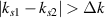 , when the frequency difference satisfies
, when the frequency difference satisfies 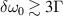 [39]. Under this condition, the pump lasers will develop their respective scattering lights independently, and equations (1)–(3) are reduced to:
[39]. Under this condition, the pump lasers will develop their respective scattering lights independently, and equations (1)–(3) are reduced to:



By doing the Fourier analysis of equations (5)–(7) in the plane of 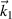 and
and 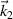 , one obtains the dispersion relation:
, one obtains the dispersion relation:
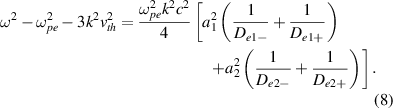
Figure 1(b) shows the phase space of two beams with different incident angles  ,
, 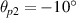 and the frequency difference
and the frequency difference  . The wavenumber difference of scattering lights
. The wavenumber difference of scattering lights 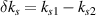 is larger than the instability region width Δki
of ith beam. Therefore, their scattering lights are no longer shared by each other. Two common Langmuir waves can be found in figure 1(b), where the backscattered common wave
is larger than the instability region width Δki
of ith beam. Therefore, their scattering lights are no longer shared by each other. Two common Langmuir waves can be found in figure 1(b), where the backscattered common wave 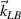 with the largest growth rate is the major instability mode when the scattering lights are decoupled. Figure 1(c) presents the growth rate as a function of angle between the vectors of the two pumps for different δω0. One finds that the growth rate of the collective SRS slightly decreases with the enhancement of δω0, when the scattering lights have been decoupled. However, the growth rate Γ can be significantly reduced by the incident angle, and therefore the frequency difference can separate the two instability regions at a certain large θ.
with the largest growth rate is the major instability mode when the scattering lights are decoupled. Figure 1(c) presents the growth rate as a function of angle between the vectors of the two pumps for different δω0. One finds that the growth rate of the collective SRS slightly decreases with the enhancement of δω0, when the scattering lights have been decoupled. However, the growth rate Γ can be significantly reduced by the incident angle, and therefore the frequency difference can separate the two instability regions at a certain large θ.
Here we introduce the polychromatic light, which is composed of many beamlets with different frequencies  [39, 40], where ai
is the normalized amplitude of ith beamlet with a carrier frequency ωi
and a random phase φi
, and N is the beamlets number. The bandwidth of the polychromatic light is
[39, 40], where ai
is the normalized amplitude of ith beamlet with a carrier frequency ωi
and a random phase φi
, and N is the beamlets number. The bandwidth of the polychromatic light is  . The beamlets of polychromatic light can propagate in different directions, such as the case with N = 2 shown in figure 1(b). And also, they can propagate in the same direction, as the example with N = 2 shown in figure 1(a). To keep the pump energy conserved between normal laser beam a0 and polychromatic light a, the beamlet amplitude is
. The beamlets of polychromatic light can propagate in different directions, such as the case with N = 2 shown in figure 1(b). And also, they can propagate in the same direction, as the example with N = 2 shown in figure 1(a). To keep the pump energy conserved between normal laser beam a0 and polychromatic light a, the beamlet amplitude is 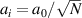 .
.
In analogy to the above two-beam analysis, the dispersion relation is easily extended to N beams case which can describe the collective SRS driven by polychromatic light
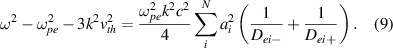
Equation (9) also can be obtained from the generalized Wigner–Moyal statistical theory with the photon distribution function 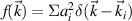 , where δ function has been used here [36]. An example is displayed in figure 1(d), where the polychromatic beam 2 is composed of two beamlets with different frequencies, and the beam 1 is a normal laser with uniform amplitude a1 = 0.012. The beamlet amplitude of the polychromatic light is a2i
≈ 0.00855, which has an equal energy to beam 1. There are four common electrostatic modes can be found in figure 1(d), and the highest growth rate is reduced with comparing to figure 1(b). One also finds that the mitigation effects on multibeam SRS are different from the single beam model. The instability regions can be completely separated by the decoupled beamlets in the same propagation direction. However, they may still have intersections in the multibeam configurations with different incident angles. One notes that the wavenumber difference δkL
of backward SRS is larger than that of forward SRS, as shown in figure 1(d). This is mainly because the frequency difference not only reduces the radius of the wavenumber circle
, where δ function has been used here [36]. An example is displayed in figure 1(d), where the polychromatic beam 2 is composed of two beamlets with different frequencies, and the beam 1 is a normal laser with uniform amplitude a1 = 0.012. The beamlet amplitude of the polychromatic light is a2i
≈ 0.00855, which has an equal energy to beam 1. There are four common electrostatic modes can be found in figure 1(d), and the highest growth rate is reduced with comparing to figure 1(b). One also finds that the mitigation effects on multibeam SRS are different from the single beam model. The instability regions can be completely separated by the decoupled beamlets in the same propagation direction. However, they may still have intersections in the multibeam configurations with different incident angles. One notes that the wavenumber difference δkL
of backward SRS is larger than that of forward SRS, as shown in figure 1(d). This is mainly because the frequency difference not only reduces the radius of the wavenumber circle 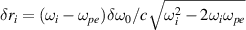 , but also shifts the center to the left
, but also shifts the center to the left 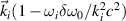 . The frequency difference for the mitigation of forward SRS is
. The frequency difference for the mitigation of forward SRS is  which is larger than the threshold for backward SRS [36]. Therefore, forward SRS and modulation instability are less sensitive to the small bandwidth. Generally, backward SRS dominates in the kinetic regime
which is larger than the threshold for backward SRS [36]. Therefore, forward SRS and modulation instability are less sensitive to the small bandwidth. Generally, backward SRS dominates in the kinetic regime  due to the high growth rate, where λD
is the Debye length. Forward SRS is insufficient to heat a large number of electrons independently, and the control of backward SRS is important for the suppression of hot electrons in the convective regime. Note that forward SRS may be excited by the beat of beamlets when the bandwidth is larger than the frequency of the plasma wave [48]. In this work, we mainly consider the bandwidth effect around
due to the high growth rate, where λD
is the Debye length. Forward SRS is insufficient to heat a large number of electrons independently, and the control of backward SRS is important for the suppression of hot electrons in the convective regime. Note that forward SRS may be excited by the beat of beamlets when the bandwidth is larger than the frequency of the plasma wave [48]. In this work, we mainly consider the bandwidth effect around  , where the corresponding plasma density for the beat wave excitation is
, where the corresponding plasma density for the beat wave excitation is 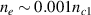 . Note that this density is much smaller than the usually concerned plasma density in ICF.
. Note that this density is much smaller than the usually concerned plasma density in ICF.
In a brief summary, the scattering lights are decoupled from each other when the frequency difference of pump beams satisfies  , and therefore the linear growth rate is reduced. For further mitigation, polychromatic light can be used as the pump beams, which can significantly mitigate the multibeam SRS by dividing the common mode to multiple decoupled common modes, and the weak modes are heavily damping in hot plasmas.
, and therefore the linear growth rate is reduced. For further mitigation, polychromatic light can be used as the pump beams, which can significantly mitigate the multibeam SRS by dividing the common mode to multiple decoupled common modes, and the weak modes are heavily damping in hot plasmas.
2.2. SRS driven by multibeam in inhomogeneous plasmas
According to the above analysis about multibeam SRS in homogeneous plasmas, the wavevector matching condition 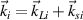 and frequency matching condition
and frequency matching condition  of ith beam are the necessary conditions for the excitation of collective SRS, where
of ith beam are the necessary conditions for the excitation of collective SRS, where 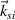 and ωsi
are the wavevector and frequency of the scattering light, respectively. In inhomogeneous plasmas, multibeam SRS is developed in the resonant region where the matching conditions are satisfied, and then convective amplified in the propagation. For the multibeam SRS with a common electron plasma wave, the frequency matching condition
and ωsi
are the wavevector and frequency of the scattering light, respectively. In inhomogeneous plasmas, multibeam SRS is developed in the resonant region where the matching conditions are satisfied, and then convective amplified in the propagation. For the multibeam SRS with a common electron plasma wave, the frequency matching condition 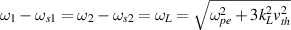 will be satisfied when the wavevector matching condition
will be satisfied when the wavevector matching condition 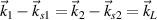 is satisfied at plasma density ne
. Therefore, we study the multibeam parametric instability in inhomogeneous plasmas based on the wavevector matching condition in the rectangular coordinates
is satisfied at plasma density ne
. Therefore, we study the multibeam parametric instability in inhomogeneous plasmas based on the wavevector matching condition in the rectangular coordinates  and
and 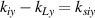 . According to the dispersion relation of scattering light
. According to the dispersion relation of scattering light 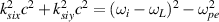 , one obtains the relation for (
, one obtains the relation for ( ) as follows:
) as follows:
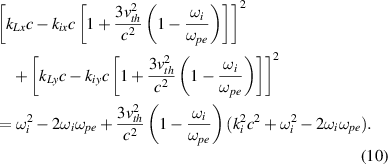
Equation (10) indicates that the wavenumber distribution of kL
is a circle with its center ![$O_i(k_{ix}[1+3v_{th}^2/c^2(1-\omega_i/\omega_{pe})],k_{iy}[1+3v_{th}^2/c^2(1-\omega_i/\omega_{pe})])$](https://content.cld.iop.org/journals/0741-3335/63/5/055006/revision3/ppcfabe75aieqn87.gif) . One notes that the center Oi
is the wavevector of incident light
. One notes that the center Oi
is the wavevector of incident light 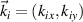 , and the radius is
, and the radius is  for cold plasma vth
= 0. The thermal modification for both Oi
and ri
are in the order of
for cold plasma vth
= 0. The thermal modification for both Oi
and ri
are in the order of 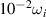 . Considering a small change of the plasma density δne
, the change of wavevector radius is
. Considering a small change of the plasma density δne
, the change of wavevector radius is
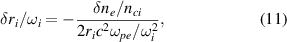
where nci is the critical density for ith beam. Based on equation (11), we know that the radius ri decreases with the plasma density ne .
The above discussion is valid for both homogeneous and inhomogeneous plasmas. Considering for a plasma with inhomogeneous density in the longitudinal direction  , one has a relation for the incident angle in vacuum θv
and the angle of the pump beam in plasma
, one has a relation for the incident angle in vacuum θv
and the angle of the pump beam in plasma 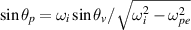 . As an example, we firstly consider two pump beams with the same frequency
. As an example, we firstly consider two pump beams with the same frequency  , and the incident angles
, and the incident angles 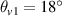 and
and 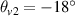 , respectively. The wavevector distribution of multibeam SRS at
, respectively. The wavevector distribution of multibeam SRS at 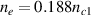 and Te
= 0 is presented in figure 2(a). Two intersections
and Te
= 0 is presented in figure 2(a). Two intersections 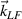 and
and 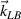 can be found, which are similar to figure 1(b). The longitudinal projection of the wavevector
can be found, which are similar to figure 1(b). The longitudinal projection of the wavevector 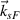 is in the forward direction, and the longitudinal projection of the wavevector
is in the forward direction, and the longitudinal projection of the wavevector 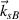 is in the backward direction. Note that the scattering light of beam 1
is in the backward direction. Note that the scattering light of beam 1 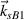 is a seed mode for beam 2 to drive a concomitant electrostatic mode
is a seed mode for beam 2 to drive a concomitant electrostatic mode 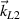 . Therefore, parts of the scattering lights are shared in the process of multibeam SRS coupling by a common electron plasma wave. One obtains
. Therefore, parts of the scattering lights are shared in the process of multibeam SRS coupling by a common electron plasma wave. One obtains 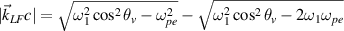 and
and 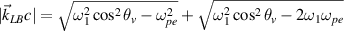 from equation (10) at kLy
= 0 and vth
= 0. A critical point is found at
from equation (10) at kLy
= 0 and vth
= 0. A critical point is found at  , i.e.
, i.e. 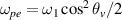 , where the propagation of the scattering light is perpendicular to the density gradient, and therefore the SRS instability is absolute [23]. The multibeam SRS sharing a common Langmuir wave will be developed only when
, where the propagation of the scattering light is perpendicular to the density gradient, and therefore the SRS instability is absolute [23]. The multibeam SRS sharing a common Langmuir wave will be developed only when  is satisfied.
is satisfied.
Figure 2. Wavevector matching conditions for multibeam SRS in the rectangular coordinates. (a)–(c) The incident angles of beam 1 and beam 2 in vacuum are 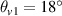 and
and 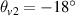 , respectively. Plasma density is
, respectively. Plasma density is 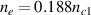 . (a) The frequencies of the two beams are equal, and electron temperature is Te
= 0. (b) The frequency difference of the two beams is
. (a) The frequencies of the two beams are equal, and electron temperature is Te
= 0. (b) The frequency difference of the two beams is 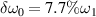 , and the electron temperature is Te
= 2 keV. (c) The bandwidth of the polychromatic light is
, and the electron temperature is Te
= 2 keV. (c) The bandwidth of the polychromatic light is  , and electron temperature is Te
= 2 keV. (d) Wavenumber distributions of the scattering lights driven by two-color pump beams with frequency difference
, and electron temperature is Te
= 2 keV. (d) Wavenumber distributions of the scattering lights driven by two-color pump beams with frequency difference  . The plasma density is
. The plasma density is 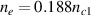 .
.
Download figure:
Standard image High-resolution imageNow we consider the case when there is a frequency difference between the two beams. A similar example to the above case with  and Te
= 2 keV is displayed in figure 2(b). The plasma density ne
is
and Te
= 2 keV is displayed in figure 2(b). The plasma density ne
is 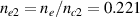 for beam 2, which is larger than
for beam 2, which is larger than 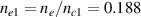 due to
due to 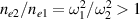 . As discussed above, the radius ri
decreases with the increasing of plasma density. One finds a smaller circle O2 as compared to O1 in figure 2(b), and the two circles no longer intersect. Therefore, the frequency difference of pump beams can change the position of absolute SRS region where
. As discussed above, the radius ri
decreases with the increasing of plasma density. One finds a smaller circle O2 as compared to O1 in figure 2(b), and the two circles no longer intersect. Therefore, the frequency difference of pump beams can change the position of absolute SRS region where 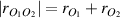 , i.e.
, i.e.
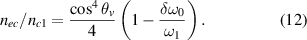
Equation (12) shows that the density for the multibeam absolute SRS is slightly reduced by the frequency difference. As an example, the density for absolute SRS is  for beams with δω0 = 0,
for beams with δω0 = 0, 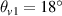 and
and 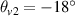 . When the frequency difference is increased to
. When the frequency difference is increased to 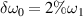 , the absolute SRS region is changed to
, the absolute SRS region is changed to 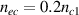 . Considering the absolute SRS developed by N beams, the absolute SRS regions are different for every two beams, when different frequency differences are introduced to the multibeam. The instability is mitigated due to the intense one common electrostatic field is divided to multiple submodes. Moreover, the frequency difference can also suppress the concomitant electrostatic modes as
. Considering the absolute SRS developed by N beams, the absolute SRS regions are different for every two beams, when different frequency differences are introduced to the multibeam. The instability is mitigated due to the intense one common electrostatic field is divided to multiple submodes. Moreover, the frequency difference can also suppress the concomitant electrostatic modes as  .
.
The wavenumber distribution of SRS driven by two polychromatic lights with bandwidth 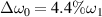 and beamlets number N = 2 is shown in figure 2(c). The plasma density is
and beamlets number N = 2 is shown in figure 2(c). The plasma density is  and the incident angles are
and the incident angles are 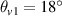 and
and 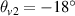 . One finds that the common mode is divided to multiple submodes with different frequency
. One finds that the common mode is divided to multiple submodes with different frequency  . When
. When 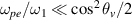 , we have:
, we have:
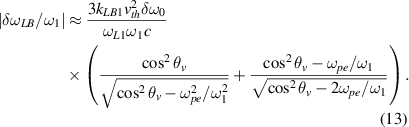
Based upon our previous work [40], the coupling of Langmuir waves will be reduced if there is a frequency difference between the pump beams, which leads to the reduction of Rosenbluth gain saturation coefficient [49, 50]. Considering a linear density profile in the longitudinal direction 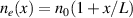 , where L is the density scale length. The saturation coefficient of the common mode kLB
driven by two normal lasers
, where L is the density scale length. The saturation coefficient of the common mode kLB
driven by two normal lasers 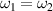 with an equal amplitude
with an equal amplitude  is
is 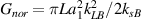 [23]. The saturation coefficient is reduced by the frequency difference between different common modes
[23]. The saturation coefficient is reduced by the frequency difference between different common modes ![$G_{brb} = G_{nor}[1+\cos(\delta\omega_{LB}\beta)]$](https://content.cld.iop.org/journals/0741-3335/63/5/055006/revision3/ppcfabe75aieqn129.gif) , where
, where  for low density plasmas, and νp
is the damping rate of plasma wave [40]. Considering polychromatic pumps with N beamlets, Langmuir waves are weakly coupled due to their frequency shifts equation (13), and multibeam SRS is heavily damped if
for low density plasmas, and νp
is the damping rate of plasma wave [40]. Considering polychromatic pumps with N beamlets, Langmuir waves are weakly coupled due to their frequency shifts equation (13), and multibeam SRS is heavily damped if 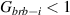 for every two common modes. Here we consider that Gbrb − i
= 1, and every beamlet shares different common modes with all the other beamlets, i.e. there are N2 common Langmuir waves. Note that the parity of N has little effect on the final result under
for every two common modes. Here we consider that Gbrb − i
= 1, and every beamlet shares different common modes with all the other beamlets, i.e. there are N2 common Langmuir waves. Note that the parity of N has little effect on the final result under 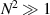 . The amplification coefficient for polychromatic light can be estimated as
. The amplification coefficient for polychromatic light can be estimated as 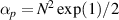 , and the amplification coefficient for normal lasers with the same energy is αn
= exp(N/2) based upon
, and the amplification coefficient for normal lasers with the same energy is αn
= exp(N/2) based upon  . The ratio
. The ratio 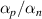 is found to be less than one
is found to be less than one 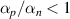 for
for 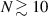 . Generally, the amplification coefficients of polychromatic light αp
is a function of Nm
, and the amplification coefficients of normal lasers is
. Generally, the amplification coefficients of polychromatic light αp
is a function of Nm
, and the amplification coefficients of normal lasers is 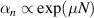 , where m is a finite exponent, and
, where m is a finite exponent, and 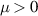 is a constant. The relation
is a constant. The relation 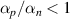 always can be satisfied for a large enough N. Therefore, the saturation level of Langmuir waves can be reduced by broadband light with large numbers of beamlets.
always can be satisfied for a large enough N. Therefore, the saturation level of Langmuir waves can be reduced by broadband light with large numbers of beamlets.
The wavenumber distribution of the scattering light driven by ith beam is 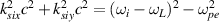 , which can be reduced to
, which can be reduced to  for cold plasma. Different from the Langmuir wave, the circle center of the scattering light wavemumber is the origin of the coordinates (0, 0), and the radius is
for cold plasma. Different from the Langmuir wave, the circle center of the scattering light wavemumber is the origin of the coordinates (0, 0), and the radius is 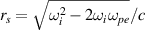 . The phase space of scattering lights can be separated when the two beams have a frequency difference
. The phase space of scattering lights can be separated when the two beams have a frequency difference 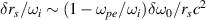 . An example is shown in figure 2(d), where the scattering lights are driven by two-color pumps with frequency difference
. An example is shown in figure 2(d), where the scattering lights are driven by two-color pumps with frequency difference 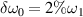 . Therefore, polychromatic light can detune the scattered seed lights in the development of concomitant electrostatic field.
. Therefore, polychromatic light can detune the scattered seed lights in the development of concomitant electrostatic field.
When the incident angles are large enough  , multibeam SRS will no longer share with the same Langmuir wave. Sidescattering in the perpendicular direction of the density gradient is an absolute instability in inhomogeneous plasmas [51]. According to equation (1), most of the scattering lights are detuned from the polychromatic pump beam. The scattering light
, multibeam SRS will no longer share with the same Langmuir wave. Sidescattering in the perpendicular direction of the density gradient is an absolute instability in inhomogeneous plasmas [51]. According to equation (1), most of the scattering lights are detuned from the polychromatic pump beam. The scattering light 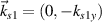 cannot be shared by beam 2 if
cannot be shared by beam 2 if 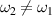 , as shown in figure 2(d). Therefore, SRS sidescattering can be mitigated by the polychromatic light when the intense sidescattering wave is broken up into many weak beamlets. In one-dimensional geometry, there exists a secondary amplification of the scattering lights with different frequency in inhomogeneous plasmas. For an example, the scattering light
, as shown in figure 2(d). Therefore, SRS sidescattering can be mitigated by the polychromatic light when the intense sidescattering wave is broken up into many weak beamlets. In one-dimensional geometry, there exists a secondary amplification of the scattering lights with different frequency in inhomogeneous plasmas. For an example, the scattering light  developed by beam 1 ω1 at
developed by beam 1 ω1 at 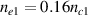 will be amplified again by beam 2
will be amplified again by beam 2  at
at 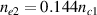 where the frequencies of the scattering lights are equal
where the frequencies of the scattering lights are equal 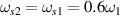 . However, the 90∘ sidescattering light
. However, the 90∘ sidescattering light 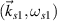 developed at
developed at  is no longer perpendicular to the density gradient at
is no longer perpendicular to the density gradient at 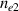 . The angle between the two scattering lights is
. The angle between the two scattering lights is
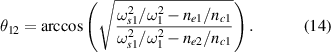
The wavevector mismatch 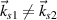 mitigates the secondary amplification even though their frequencies are equal
mitigates the secondary amplification even though their frequencies are equal  .
.
Multibeam can be coupled by a same scattering light under ksy
= 0 in inhomogeneous plasmas. A particular region is the density around 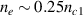 , where the wavevector of SRS scattering light is
, where the wavevector of SRS scattering light is 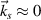 , and SRS is an absolute instability due to the group velocity of the scattering light is
, and SRS is an absolute instability due to the group velocity of the scattering light is 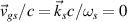 . Considering an example that the plasma density is
. Considering an example that the plasma density is 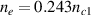 and electron temperature is Te
= 3 keV. The incident angles of the two normal lasers are
and electron temperature is Te
= 3 keV. The incident angles of the two normal lasers are 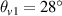 and
and 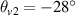 , respectively. The wavevector of the scattering light is
, respectively. The wavevector of the scattering light is 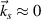 , and
, and 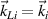 is satisfied for the wavevector matching condition. Therefore, both beam 1 and beam 2 can share with the same scattering light
is satisfied for the wavevector matching condition. Therefore, both beam 1 and beam 2 can share with the same scattering light 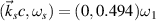 . One notes that the frequency of the scattering light satisfies
. One notes that the frequency of the scattering light satisfies  . The absolute instability region
. The absolute instability region ![$[\omega_1/2-a_1|k_1|c/4,\omega_1/2+a_1|k_1|c/4]$](https://content.cld.iop.org/journals/0741-3335/63/5/055006/revision3/ppcfabe75aieqn171.gif) for beam 1 can be obtained from equation (8) under vth
= 0, a2 = 0 and
for beam 1 can be obtained from equation (8) under vth
= 0, a2 = 0 and 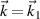 [52]. The pump beams will no longer share with a common scattering light when
[52]. The pump beams will no longer share with a common scattering light when 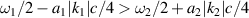 , i.e.
, i.e.
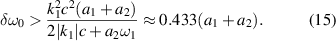
The above threshold indicates that multiple pump beams will be decoupled by the frequency difference in the sharing with a common scattering light. For example, comparing to the normal lasers with intensity  , absolute multibeam SRS with a common scattering light will be mitigated by the polychromatic lights with N = 20 and bandwidth
, absolute multibeam SRS with a common scattering light will be mitigated by the polychromatic lights with N = 20 and bandwidth  . According to the threshold for developing absolute SRS in inhomogeneous plasmas, one knows that absolute SRS can be considerably suppressed when the decoupled beamlets satisfy
. According to the threshold for developing absolute SRS in inhomogeneous plasmas, one knows that absolute SRS can be considerably suppressed when the decoupled beamlets satisfy 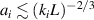 [50]. Note that two-plasmon decay instability also can be effectively mitigated when equation (15) is satisfied [40, 53].
[50]. Note that two-plasmon decay instability also can be effectively mitigated when equation (15) is satisfied [40, 53].
3. Simulations for the mitigation of multibeam SRS in inhomogeneous plasmas with polychromatic light
3.1. Coupling of two beams via a common electrostatic wave
To validate the mitigation of multibeam SRS by polychromatic light, we have performed several two-dimensional (2D) simulations mainly for direct drive by using the OSIRIS code [54, 55]. The space and time given in the following are normalized by the laser wavelength in vacuum λ and the laser period τ. The plasma occupies a region from x = 5λ to x = 115λ with the density profile ![$n_e(x) = 0.18\exp[(x-5)/1000]n_{c1}$](https://content.cld.iop.org/journals/0741-3335/63/5/055006/revision3/ppcfabe75aieqn177.gif) . The mass of the ion is
. The mass of the ion is 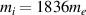 with a charge Z = 1. The initial electron and ion temperatures are Te
= 2 keV and Ti
= 700 eV, respectively. Two s-polarized semi-infinite pump lasers with a uniform amplitude are incident from the left boundary of the simulation box.
with a charge Z = 1. The initial electron and ion temperatures are Te
= 2 keV and Ti
= 700 eV, respectively. Two s-polarized semi-infinite pump lasers with a uniform amplitude are incident from the left boundary of the simulation box.
Firstly, we consider the case of two normal beams with an equal amplitude 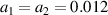 , and different frequencies
, and different frequencies 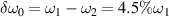 . The incident angles are
. The incident angles are 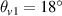 and
and  . The spatial distribution of the pump beams at t = 1200τ is displayed in figure 3(a). One finds that an intense electrostatic field has been excited in the crossed region of the two beams based on figure 3(b). According to equation (10), the beams are still coupled by the common Langmuir wave under
. The spatial distribution of the pump beams at t = 1200τ is displayed in figure 3(a). One finds that an intense electrostatic field has been excited in the crossed region of the two beams based on figure 3(b). According to equation (10), the beams are still coupled by the common Langmuir wave under 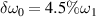 . Therefore, an intense Langmuir wave is developed around
. Therefore, an intense Langmuir wave is developed around  as shown in figure 3(c). Note that the wavenumber circle of beam 1 is larger than that of beam 2 as discussed above. The pump beams no longer share with the common Langmuir wave when the frequency difference is increased to
as shown in figure 3(c). Note that the wavenumber circle of beam 1 is larger than that of beam 2 as discussed above. The pump beams no longer share with the common Langmuir wave when the frequency difference is increased to  , as exhibited in figure 3(d). The larger growth rate of beam 2 leads to the more intense electrostatic field around
, as exhibited in figure 3(d). The larger growth rate of beam 2 leads to the more intense electrostatic field around 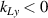 by comparing to beam 1. The simulation results presented in figures 3(c) and (d) validate that the common electrostatic modes are different for every two beams, when different frequency differences are introduced to the pump beams. Based upon figure 3(e) we know that the growth of electrostatic energy excited by normal lasers is reduced by the frequency difference
by comparing to beam 1. The simulation results presented in figures 3(c) and (d) validate that the common electrostatic modes are different for every two beams, when different frequency differences are introduced to the pump beams. Based upon figure 3(e) we know that the growth of electrostatic energy excited by normal lasers is reduced by the frequency difference 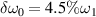 , due to the mitigation of the concomitant electrostatic fields. When the two instability regions are totally separated at
, due to the mitigation of the concomitant electrostatic fields. When the two instability regions are totally separated at 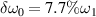 , the growth rate is further reduced.
, the growth rate is further reduced.
Figure 3. Spatial distributions of (a) electromagnetic field and (b) electrostatic field at t = 1200τ. (c) Fourier spectrum of Langmuir wave at t = 1200τ. (a)–(c) The frequency difference between the two beams is 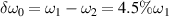 . (d) Fourier spectrum of Langmuir wave at t = 1200τ under
. (d) Fourier spectrum of Langmuir wave at t = 1200τ under 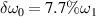 . The electron temperature is Te
= 2 keV. (e) Temporal growth of electrostatic energies developed by two beams with different frequency differences.
. The electron temperature is Te
= 2 keV. (e) Temporal growth of electrostatic energies developed by two beams with different frequency differences.
Download figure:
Standard image High-resolution imageNext, we study the mitigation of SRS with polychromatic light. As an comparison, we have performed a simulation for two normal lasers 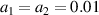 with an equal frequency
with an equal frequency 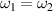 . The incident angles are
. The incident angles are 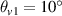 and
and 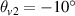 . The plasma parameters are the same to the above simulation example. According to equations (8) and (10), we know that the wavevector of beam 1 is
. The plasma parameters are the same to the above simulation example. According to equations (8) and (10), we know that the wavevector of beam 1 is 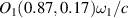 , and the backscattering common mode is the major instability mode with wavenumber
, and the backscattering common mode is the major instability mode with wavenumber 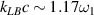 at plasma density
at plasma density  , which are very close to the simulation results presented in figure 4(a), where
, which are very close to the simulation results presented in figure 4(a), where  and
and 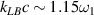 . The wavevector of the scattering light developed by beam 1 is
. The wavevector of the scattering light developed by beam 1 is 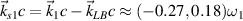 , and the wavevector of the other scattering light is
, and the wavevector of the other scattering light is 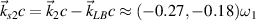 as shown in figure 4(b). One notes that two concomitant electrostatic modes
as shown in figure 4(b). One notes that two concomitant electrostatic modes 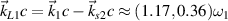 and
and 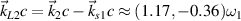 are induced by the scattering light from the other beam.
are induced by the scattering light from the other beam.
Figure 4. Wavenumber distributions of (a) Langmuir wave and (b) scattering light at t = 1500τ. The pump beams are normal lasers without bandwidth. Wavenumber distributions of Langmuir wave driven by polychromatic light with different bandwidth (c)  at t = 1500τ, (d)
at t = 1500τ, (d)  at t = 3000τ, and (e)
at t = 3000τ, and (e) 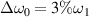 at t = 3000τ. (f) Temporal growth of electrostatic energies developed by pump beams with different bandwidth. Electron energy distribution under different bandwidth at (g) t = 3000τ and (h) t = 6000τ. Ne
is the electron number. The incident angles of beam 1 and beam 2 in vacuum are
at t = 3000τ. (f) Temporal growth of electrostatic energies developed by pump beams with different bandwidth. Electron energy distribution under different bandwidth at (g) t = 3000τ and (h) t = 6000τ. Ne
is the electron number. The incident angles of beam 1 and beam 2 in vacuum are 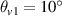 and
and 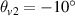 , respectively. Plasma density of the beam overlapping region is
, respectively. Plasma density of the beam overlapping region is 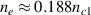 . The initial electron temperature is Te
= 2 keV.
. The initial electron temperature is Te
= 2 keV.
Download figure:
Standard image High-resolution imageTo keep the energy conservation of normal laser a1 and polychromatic light, the amplitude of each beamlet is 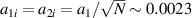 under N = 19. We find that the intensities of the common Langmuir wave and the concomitant electrostatic field are significantly reduced by the polychromatic lights with bandwidth
under N = 19. We find that the intensities of the common Langmuir wave and the concomitant electrostatic field are significantly reduced by the polychromatic lights with bandwidth 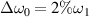 at t = 1500τ, with comparing figure 4(c) to figure 4(a). As discussed above, the different submodes are weakly coupled, and therefore the whole instability saturation level is reduced by the polychromatic lights. However, the multibeam SRS has not been totally suppressed, due to the weak coupling of the beamlets under a relatively small bandwidth
at t = 1500τ, with comparing figure 4(c) to figure 4(a). As discussed above, the different submodes are weakly coupled, and therefore the whole instability saturation level is reduced by the polychromatic lights. However, the multibeam SRS has not been totally suppressed, due to the weak coupling of the beamlets under a relatively small bandwidth 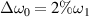 . Therefore, one finds multiple electrostatic submodes around
. Therefore, one finds multiple electrostatic submodes around  at t = 3000τ as shown in figure 4(d). When the bandwidth is increased into
at t = 3000τ as shown in figure 4(d). When the bandwidth is increased into 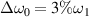 , only a much weak common Langmuir wave is developed at t = 3000τ, known from figure 4(e). The temporal growth of the electrostatic energies developed by pump beams with different bandwidth are shown in figure 4(f). One finds that the growth rate in the linear regime
, only a much weak common Langmuir wave is developed at t = 3000τ, known from figure 4(e). The temporal growth of the electrostatic energies developed by pump beams with different bandwidth are shown in figure 4(f). One finds that the growth rate in the linear regime 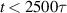 and the saturation level at t = 3000τ are reduced by the bandwidth, which are consistent with our theoretical conclusions. When the interactions evolve into the non-linear regime for Δω0 = 0 and
and the saturation level at t = 3000τ are reduced by the bandwidth, which are consistent with our theoretical conclusions. When the interactions evolve into the non-linear regime for Δω0 = 0 and 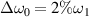 , the electrostatic energies slowly grow with time. Note that the linear growth of the electrostatic energies of Δω0 = 0 is larger than that of
, the electrostatic energies slowly grow with time. Note that the linear growth of the electrostatic energies of Δω0 = 0 is larger than that of 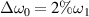 , i.e.
, i.e.  . Therefore, the mitigation of multibeam SRS by polychromatic light can also be found in the non-linear regime. When the bandwidth is enhanced to
. Therefore, the mitigation of multibeam SRS by polychromatic light can also be found in the non-linear regime. When the bandwidth is enhanced to 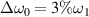 , the collective SRS is found to be still in the linear regime at t = 6000τ. The intensity of Langmuir waves directly leads to the strength of hot electrons. The single common electrostatic field is divided to many weak modes with different wavevectors, and the hot electron productions are mitigated when the weak coupling modes are heavily damped. The electron energy distribution at the end of linear regime t = 3000τ and the fully non-linear regime t = 6000τ are presented in figures 4(g) and (h). For normal laser beams, the common electron plasma wave heats a large number of electrons together with the two concomitant electrostatic modes. Polychromatic lights with bandwidth
, the collective SRS is found to be still in the linear regime at t = 6000τ. The intensity of Langmuir waves directly leads to the strength of hot electrons. The single common electrostatic field is divided to many weak modes with different wavevectors, and the hot electron productions are mitigated when the weak coupling modes are heavily damped. The electron energy distribution at the end of linear regime t = 3000τ and the fully non-linear regime t = 6000τ are presented in figures 4(g) and (h). For normal laser beams, the common electron plasma wave heats a large number of electrons together with the two concomitant electrostatic modes. Polychromatic lights with bandwidth  can effectively reduce the electron hot tail even in the fully non-linear regime. The electron hot tail is sufficiently suppressed by polychromatic lights with bandwidth
can effectively reduce the electron hot tail even in the fully non-linear regime. The electron hot tail is sufficiently suppressed by polychromatic lights with bandwidth 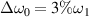 . Different from homogeneous plasmas, the simulation results conform that an effective mitigation can be found at a relatively small bandwidth
. Different from homogeneous plasmas, the simulation results conform that an effective mitigation can be found at a relatively small bandwidth 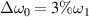 in inhomogeneous plasmas in both linear and non-linear regimes, because the electrostatic strength is reduced by the wavenumber detuning outside the resonant region [40, 48, 56].
in inhomogeneous plasmas in both linear and non-linear regimes, because the electrostatic strength is reduced by the wavenumber detuning outside the resonant region [40, 48, 56].
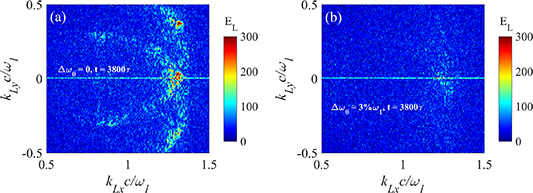
To validate the mitigation effects in a relatively broad plasma density range, we have performed the simulations for the beam overlapping region [0.14, 0.19]nc1
, with L = 900λ. The mass of the ion is  with an effective charge Z = 1, and the other parameters are the same to the above simulations. The wavenumber distributions of Langmuir wave at the same time for different bandwidth have been displayed in figure 5. One still finds a well mitigation of multibeam SRS by polychromatic light with bandwidth
with an effective charge Z = 1, and the other parameters are the same to the above simulations. The wavenumber distributions of Langmuir wave at the same time for different bandwidth have been displayed in figure 5. One still finds a well mitigation of multibeam SRS by polychromatic light with bandwidth 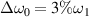 . Generally, the whole level of SRS can be controlled if the intensities of Langmuir wave and scattering light are mitigated in the high density region where the growth rate and saturation level are relatively higher.
. Generally, the whole level of SRS can be controlled if the intensities of Langmuir wave and scattering light are mitigated in the high density region where the growth rate and saturation level are relatively higher.
Figure 5. Wavenumber distributions of Langmuir wave at t = 3800τ for different bandwidth (a) Δω0 = 0 and (b)  . Plasma density range of the beam overlapping region is [0.14, 0.19]nc1
.
. Plasma density range of the beam overlapping region is [0.14, 0.19]nc1
.
Download figure:
Standard image High-resolution image3.2. Coupling of two beams via a common scattering light
The above simulations indicate that polychromatic lights with bandwidth 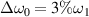 can effectively mitigate the intensity of multibeam SRS coupling by a common Langmuir wave. Here we study the excitation of multibeam SRS sharing with the same scattering light near 0.25nc1
. The plasma occupies a region from x = 5λ to x = 75λ with the density profile
can effectively mitigate the intensity of multibeam SRS coupling by a common Langmuir wave. Here we study the excitation of multibeam SRS sharing with the same scattering light near 0.25nc1
. The plasma occupies a region from x = 5λ to x = 75λ with the density profile ![$n_e(x) = 0.236\exp[(x-5)/1000]n_{c1}$](https://content.cld.iop.org/journals/0741-3335/63/5/055006/revision3/ppcfabe75aieqn230.gif) . The electron and ion temperatures are Te
= 3 keV and Ti
= 1 keV, respectively.
. The electron and ion temperatures are Te
= 3 keV and Ti
= 1 keV, respectively.
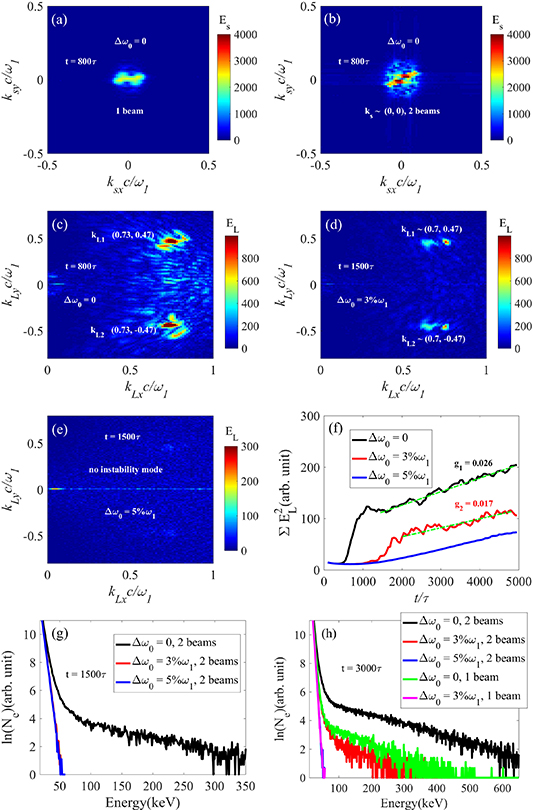
We consider first that SRS excited by normal laser beams. Figure 6(a) shows the wavenumber distribution of scattering light developed by a single normal laser with a uniform amplitude a1 = 0.01 and incident angles 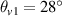 . One finds that the wavevector of the scattering lights is around
. One finds that the wavevector of the scattering lights is around 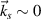 . Next, we perform the simulation with two normal laser beams
. Next, we perform the simulation with two normal laser beams 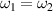 , their uniform amplitudes are equal
, their uniform amplitudes are equal 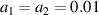 , with the incident angles
, with the incident angles  and
and  . The wavevectors of the scattering lights driven by two normal lasers are also around
. The wavevectors of the scattering lights driven by two normal lasers are also around 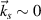 , and the collective instability has been fully developed at t = 800τ as presented in figure 6(b). The intensity of the scattering lights for two normal beams is higher than that of single beam, known from the comparison between figures 6(a) and (b). Therefore, the two beams share with the same scattering light in the development of SRS. Figure 6(c) shows that the two beams develop their respective Langmuir waves independently, where
, and the collective instability has been fully developed at t = 800τ as presented in figure 6(b). The intensity of the scattering lights for two normal beams is higher than that of single beam, known from the comparison between figures 6(a) and (b). Therefore, the two beams share with the same scattering light in the development of SRS. Figure 6(c) shows that the two beams develop their respective Langmuir waves independently, where  and
and  .
.
Figure 6. (a) Wavenumber distribution of scattering light driven by single one laser without bandwidth at t = 800τ. Wavenumber distributions of (b) scattering light and (c) Langmuir wave driven by two normal lasers without bandwidth at t = 800τ. Wavenumber distributions of Langmuir wave driven by polychromatic light with different bandwidth (d) 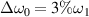 at t = 1500τ, and (e)
at t = 1500τ, and (e)  at t = 1500τ. (f) Temporal growth of electrostatic energies developed by pump beams with different bandwidth. Electron energy distributions under different bandwidth or beam number at (g) t = 1500τ and (h) t = 3000τ. The incident angles of beam 1 and beam 2 in vacuum are
at t = 1500τ. (f) Temporal growth of electrostatic energies developed by pump beams with different bandwidth. Electron energy distributions under different bandwidth or beam number at (g) t = 1500τ and (h) t = 3000τ. The incident angles of beam 1 and beam 2 in vacuum are 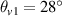 and
and 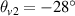 , respectively. Plasma density of the beam overlapping region is
, respectively. Plasma density of the beam overlapping region is 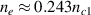 . The initial electron temperature is Te
= 3 keV.
. The initial electron temperature is Te
= 3 keV.
Download figure:
Standard image High-resolution imageFinally, we validate the mitigation effect of polychromatic light. To keep the energy conservation between normal laser a1 and polychromatic light, the amplitude of each beamlet is 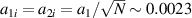 for N = 19. According to figure 6(d), we know that the intensity of Langmuir waves has been reduced by the polychromatic lights with bandwidth
for N = 19. According to figure 6(d), we know that the intensity of Langmuir waves has been reduced by the polychromatic lights with bandwidth 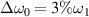 . The wavevector projection kLx
has a broad range, due to the coupling of beamlets with different frequencies. When the bandwidth is increased to
. The wavevector projection kLx
has a broad range, due to the coupling of beamlets with different frequencies. When the bandwidth is increased to  , no instability can be found at t = 1500τ in figure 6(e). Therefore, weak coupling modes are developed under
, no instability can be found at t = 1500τ in figure 6(e). Therefore, weak coupling modes are developed under 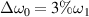 , where the bandwidth is smaller than the threshold equation (15)
, where the bandwidth is smaller than the threshold equation (15) 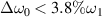 . However, no obvious instability mode can be found when the threshold is satisfied
. However, no obvious instability mode can be found when the threshold is satisfied 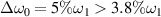 , where the submodes are much weak and heavily damped by the high electron temperature. The temporal growth of the electrostatic energies shown in figure 4(f) further validates that the bandwidth can reduce the growth rate and the saturation level of multibeam SRS with sharing a common scattering light. Polychromatic light can effectively mitigate the collective SRS in both linear and non-linear regimes. The electron energies are diagnosed at the end of linear regime t = 1500τ and the fully non-linear regime t = 3000τ, and the distributions are shown in figures 6(g) and (h). The electron energy distribution of
, where the submodes are much weak and heavily damped by the high electron temperature. The temporal growth of the electrostatic energies shown in figure 4(f) further validates that the bandwidth can reduce the growth rate and the saturation level of multibeam SRS with sharing a common scattering light. Polychromatic light can effectively mitigate the collective SRS in both linear and non-linear regimes. The electron energies are diagnosed at the end of linear regime t = 1500τ and the fully non-linear regime t = 3000τ, and the distributions are shown in figures 6(g) and (h). The electron energy distribution of 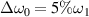 is almost overlapped by that of
is almost overlapped by that of 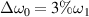 at t = 1500τ, when their electrostatic energies have little difference. A comparison has been made for the mitigation effects of single beam and two beams at t = 3000τ. Generally, the bandwidth threshold for mitigation of multibeam SRS is larger than that of one-beam case, due to the relatively higher growth rate of the former. The intensity of SRS driven by two polychromatic beams with bandwidth
at t = 1500τ, when their electrostatic energies have little difference. A comparison has been made for the mitigation effects of single beam and two beams at t = 3000τ. Generally, the bandwidth threshold for mitigation of multibeam SRS is larger than that of one-beam case, due to the relatively higher growth rate of the former. The intensity of SRS driven by two polychromatic beams with bandwidth 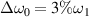 is comparable to that of one normal laser. Note that SRS is considerably suppressed by one beam with
is comparable to that of one normal laser. Note that SRS is considerably suppressed by one beam with 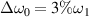 , and the same mitigation effect is found at a larger bandwidth
, and the same mitigation effect is found at a larger bandwidth  for two beams, where their distributions are almost overlapped and no hot electrons can be found at this time. Therefore, polychromatic light with bandwidth
for two beams, where their distributions are almost overlapped and no hot electrons can be found at this time. Therefore, polychromatic light with bandwidth 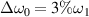 is enough to reduce the hot electron production even in the non-linear regime.
is enough to reduce the hot electron production even in the non-linear regime.
4. Summary
We have theoretically and numerically studied the development and mitigation of SRS excited by multiple intersecting beams. One of the pump beams is coupled by the scattering light developed by another beam to excite the Langmuir wave. The excitation of the concomitant modes can be suppressed when the frequency difference  . Common Langmuir waves are detuned from each other, when different frequency differences are introduced between two beams. For further mitigation, polychromatic light is introduced, which is composed of many beamlets with different frequencies. Based upon the inhomogeneous plasma model, the saturation level of multibeam SRS is reduced by the polychromatic light, since the weakly coupled common modes are heavily damped in hot plasmas. Moreover, broad bandwidth can mitigate the absolute SRS sidescattering in inhomogeneous plasmas by detuning the wavevectors of the daughter waves. PIC simulations mainly for direct drive validate the theoretical analysis, and show that the frequency difference between two beams can decouple the daughter waves in the collective SRS. The strength of multibeam SRS and the hot electron production in inhomogeneous plasmas can be controlled at a low level by use of polychromatic light with a few percentage bandwidth (
. Common Langmuir waves are detuned from each other, when different frequency differences are introduced between two beams. For further mitigation, polychromatic light is introduced, which is composed of many beamlets with different frequencies. Based upon the inhomogeneous plasma model, the saturation level of multibeam SRS is reduced by the polychromatic light, since the weakly coupled common modes are heavily damped in hot plasmas. Moreover, broad bandwidth can mitigate the absolute SRS sidescattering in inhomogeneous plasmas by detuning the wavevectors of the daughter waves. PIC simulations mainly for direct drive validate the theoretical analysis, and show that the frequency difference between two beams can decouple the daughter waves in the collective SRS. The strength of multibeam SRS and the hot electron production in inhomogeneous plasmas can be controlled at a low level by use of polychromatic light with a few percentage bandwidth ( ), even in the non-linear regime.
), even in the non-linear regime.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos. 12005287, 11775144 and 1172109), the Natural Science Foundation of Shanghai (No. 19YF1453200), and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant Nos. XDA25050800 and XDA25050100). The authors would like to acknowledge the OSIRIS Consortium, consisting of UCLA and IST (Lisbon, Portugal) for providing access to the OSIRIS 4.0 framework.