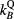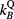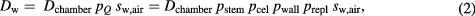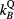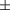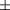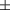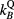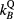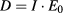Radiation dosimetry in magnetic fields with Farmer-type ionization chambers: determination of magnetic field correction factors for different magnetic field strengths and field orientations

For the study, six Farmer-type chambers, including the PTW 30013 (radius 3 mm) and five custom-built ionization chambers with the same design, but varying inner radii from 1 mm to 6 mm, were used (see figure 1(d)). The behavior of these chambers has been described previously by Legrand et al (2012a, 2012b). The cavity length of all chambers is 23 mm. The wall consists of a 0.335 mm thick PMMA layer which is coated with graphite of 0.09 mm thickness. The central electrode has a diameter of 1.15 mm and a length of 21.2 mm and is made of aluminum. The chamber stem is built of layers of various materials, including PMMA, graphite and aluminum, among others. In the following, the chambers are referred to as R_i (where i  =  (1, 6), corresponds to their inner radius).

Zoom In Zoom Out Reset image size

The charge reading per monitor unit (MU) of the six Farmer-type chambers was measured in magnetic fields. Therefore, the chambers were positioned in a self-designed and 3D-printed water tank (material: VeroClear RDG810, density: 1.18–1.19 g cm⁻³, size ca. 3.5  ×  12  ×  15 cm³, see figures 1(a) and (b)) with their reference point at 10 cm water equivalent depth in accordance with the TRS-398 dosimetry protocol (Andreo et al 2006). Thus, a layer of 5 cm water was used for backscatter material. The bias voltage of the chambers was set to 400 V. The thickness of the water tank was limited to 3.5 cm, such as to fit between the pole shoes of the electromagnet (Schwarzbeck AGEM 5520, Germany). The maximally achievable magnetic field strength was 1.1 T. A description of the magnet can be found in Stefanowicz et al (2013). A water circulating system was integrated into the water tank to limit the increase of the water temperature due to heating of the magnet to less than 0.2 °C per measurement series.

The chambers were positioned with 3D-printed holders that fixed the chamber stem at the top of the water tank. Care was taken to ensure that there were no air bubbles near the sensitive volume of the chambers.

All irradiations were performed with 100 MU using a horizontal beam of the 6 MV linear accelerator (linac, Artíste, Siemens Medical Solutions Inc., PA, USA). A maximum field strength of below 1 mT was measured at the linac head. Thus, no influence of the magnetic field on the beam generation was assumed. The source to surface distance (SSD) was set to 100 cm. To avoid significant back scatter from the pole shoes of the electromagnet, a radiation field of 3  ×  10 cm² was used.

The magnetic field was oriented perpendicular to the beam as well as to the chamber axis. The magnetic field strength ranged between 0.0 T and 1.1 T, corresponding to electric currents from 0.0 A to 14.11 A, respectively. Each set of measurements of different field strength was repeated three times with a randomized order of magnetic field strength to avoid systematic effects from magnetic hysteresis.

2.3.1. Simulation geometry.

The Farmer-type chambers were modeled using the C++ class library egspp of the Monte Carlo code EGSnrc (Kawrakow 2000, Kawrakow et al 2009). The materials and dimensions of the chambers were obtained from data sheets provided by PTW (details see section 2.1) and µCT images (Inveon^®, Siemens, Germany). The stems of the chambers were modeled in detail according to the µCT scans (see figure 1(e)). In particular, care was taken to ensure that any air gaps in the chamber stem were modeled correctly. The ionization chamber models were placed in a 50  ×  50  ×  50 cm³ water phantom. The reference points of the chambers were positioned at reference depth, i.e. at 10 cm water-equivalent depth, in accordance with the TRS-398 protocol (Andreo et al 2006). As beam source, a 6 MV photon spectrum collimated to a field size of 3  ×  10 cm² was used (Mohan et al 1985). According to the experimental set-up, an SSD of 100 cm was used. A schematic drawing of the simulation set-up is displayed in figure 2.

Zoom In Zoom Out Reset image size

The calculation of the dose to the sensitive chamber volume was performed using the egs_chamber user code (Wulff et al 2008b). To reduce calculation time, variance reduction techniques such as local photon cross-section enhancement and range-based Russian Roulette were employed.

Homogeneous magnetic field strengths ranging from 0.0 T to 3.0 T were used in the simulations, employing a customized magnetic field macro (provided by Dr Kawrakow, see appendix for Fano cavity test results with this magnetic field macro). To assure correct simulation of the electrons in the magnetic field, a maximum step length of 0.025 times the gyration radius of the electron was used.

Moreover, a maximum global energy loss in an electron step of ESTEPE  =  0.1 and a maximum first elastic scattering moment per step of XIMAX  =  0.1 were used. Spin-off effects were turned off. The default transport cut-off energies were used (ECUT  =  0.521 MeV, PCUT  =  0.01 MeV).

2.3.2. Definition of dead volumes.

2.3.3. Magnetic field orientation.

2.3.4. Calculation of ${\rm k_{B}^{{\rm Q}}}$ and perturbation factors.

To correct for the altered chamber response in magnetic fields, $k_{B}^{{\rm Q}}$ as well as perturbation factors were calculated. The correction factor $k_{B}^{{\rm Q}}$ for the beam quality Q obtained for the reference field can be calculated as the ratio of dose to water D_w and measured signal M with and without magnetic field B (O'Brien et al 2016). Assuming that the mean energy deposited in air per Coulomb charge does not change with magnetic field strength, $k_{B}^{{\rm Q}}$ factors can be calculated with Monte Carlo simulations by

$$\begin{align} \displaystyle k_{B}^{{\rm Q}}=~\frac{\left( {{D}_{{\rm w}}}/M \right)_{{\rm Q}}^{B}}{{{({{D}_{{\rm w}}}/M)}_{{\rm Q}}}}=~\frac{\left( {{D}_{{\rm w}}}/{{D}_{{\rm chamber}}} \right)_{{\rm Q}}^{B}}{{{({{D}_{{\rm w}}}/~{{D}_{{\rm chamber}}})}_{{\rm Q}}}},\nonumber \end{align} \tag{ 1 }$$

where D_chamber denotes the dose to the air volume of the chamber.

Moreover, the dose to water D_w can also be expressed as

$$\begin{align} \displaystyle {{D}_{{\rm w}}}=~{{D}_{{\rm chamber}}}~{{p}_{Q~}}{{s}_{{\rm w,air}}}={{D}_{{\rm chamber}}}~{{p}_{{\rm stem}}}~{{p}_{{\rm cel }~ }}{{p}_{{\rm wall }~ }}{{p}_{{\rm repl }~ }}{{s}_{{\rm w,air}}},\nonumber \end{align} \tag{ 2 }$$

where p_Q denotes the overall perturbation factor, s_w,air the averaged stopping power ratio of water and air and p_stem, p_cel, p_wall, and p_repl represent the perturbation factors due to the stem, central electrode, wall and replacement, respectively. The perturbation factors were calculated as described by Wulff et al (2008a). The approach is illustrated in figure 3.

Zoom In Zoom Out Reset image size

To calculate the correction factor $k_{B}^{{\rm Q}}$ and perturbation factors under reference conditions, the 10 cm  ×  10 cm IAEA phase space of a 6 MV Siemens Primus linac (Pena et al 2007) was used as beam source. The remaining simulation geometry and parameters were set as described in section 2.3.1.

The dose to water D_w at the point of measurement was calculated in a water-filled cylindrical volume of 1 cm radius and 0.025 cm height.

The averaged stopping-power ratios between water and air were determined with the help of the user code SPRRZnrc (Rogers et al 2013) in a water phantom at the depth of measurement. An electron cut-off energy of 10 keV was used (Wulff et al 2008a).

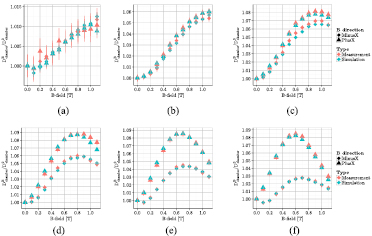
The measured relative signal of the charge reading per MU in the presence of the magnetic field to the response without magnetic field is depicted in figure 4 for all six chambers and both magnetic field orientations perpendicular to beam and chamber axis. The chamber response shows a complex dependence on magnetic field strength, chamber radius and magnetic field orientation. For the chambers R₃ to R₆, the response increases up to a certain magnetic field strength and decreases beyond. The maximum increase in  +X-direction was observed for chamber R₄ at 0.9 T (8.8%), while in the ‒X-direction the maximum increase was obtained for chamber R₃ at 1.0 T (7.0%). Moreover, switching the magnetic field orientation has only a minor influence on the response of the small chambers (R₁–R₃, around 1%), whereas the impact increases for chambers with larger radii (up to 6% for the R₆ chamber). The magnetic field strength at which the maximum response occurs decreases for increasing chamber radii.

Zoom In Zoom Out Reset image size

Figure 5 shows the results of the simulations for chambers R₃ and R₆, when the sensitive volume is considered to consist of the whole air volume below the guard electrode in the chamber. The measured response is shown for comparison. In contrast to the measurement, the increase in chamber response is slightly larger in the ‒X-direction than in the  +X-direction. Moreover, the difference in response between both magnetic field orientations is smaller in the simulations. Particularly for the R₆ chamber, a large disagreement between measurement and simulation can be observed.

Zoom In Zoom Out Reset image size

In order to investigate the influence of dead volumes, the spatial dose distributions in the air volume of the chambers were analyzed. The results for chamber R₃ are presented in figure 6.

Zoom In Zoom Out Reset image size

The statistical uncertainty (standard deviation) of all scoring regions is below 0.4%, with a mean uncertainty of 0.2%. Figures 6(a)–(c) show the resulting dose maps integrated over the azimuthal sections for 0.0 T, −1.0 T and  +1.0 T in X-direction, respectively. If no magnetic field is applied, the dose distribution inside the air volume is rather homogenous (figure 6(a)). In contrast, when a magnetic field of 1.0 T is applied in the ‒X-direction, dose hot spots of up to  +35% and cold spots of  −20% relative to the mean chamber dose without magnetic field are found at the guard electrode and at the chamber tip, respectively. This effect is simply due to deflection of the electrons towards the chamber stem by the Lorentz force. The opposite effect occurs for a 1.0 T magnetic field in the  +X direction. Here, low dose regions are formed at the chamber stem, while high dose regions are found at the chamber tip.

Figures 6(d)–(f) display the dose distribution for 0.0 T, −1.0 T and  +1.0 T in the transversal plane at the reference point for discretized azimuthal segments. The beam is directed from bottom to top of the figures. The statistical uncertainty of all scoring regions is below 0.7%, with a mean uncertainty below 0.4%. Without magnetic field, the dose distribution is again rather homogeneous, showing only a small dose decrease at the beam exit behind the central electrode. In the presence of a magnetic field, the dose is concentrated at the beam entrance side with dose hot spots of about  +35%, while dose cold spots of  −26% are observed at the beam exit side originating from the lateral deflection of secondary electrons.

Thus, the assumption of a cylindrical dead volume at the guard electrode can lead to a significant change in the simulated chamber response.

Figure 7 displays the simulation results of the response for the R₃ chamber with cylindrical dead volumes of different thicknesses adjacent to the guard electrode. The larger the dead volume, the larger is the difference in response between the  +X and –X magnetic field orientation: The response for the  +X-direction increases with an increase in thickness of the dead volume, since the low dose region (see figure 6(c)) is excluded, while the effect is opposite for the ‒X-direction due to the exclusion of the high dose region close to the chamber stem (see figure 6(b)). Therefore, it was possible to adapt the simulation results to the measurements by adjusting the thickness of the dead volume. Figure 8 shows the best fit of the thickness of the dead volumes for all six chambers. The thickness of the dead volumes for the R₁, R₂, R₃, R₄, R₅ and R₆ are 0.08 cm, 0.09 cm, 0.11 cm, 0.19 cm, 0.22 cm and 0.26 cm, respectively. A very good agreement between measurement and simulation was obtained with a root-mean squared deviation of 0.2% and a maximum deviation of 0.9% for the R₄ chamber at 1.1 T in  +X-direction.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

With the simulation models adapted to the measurement, the response was investigated also with respect to the magnetic field orientations that could not be realized by means of our experimental set-up. Figures 9 and 10 display the dose distribution inside the air cavity of the chamber R₃ for a 1.0 T magnetic field in $\pm$Y (parallel to the chamber axis) and $\pm$Z direction (parallel to the beam). Only minor changes relative to the dose distribution without magnetic field can be observed along the chamber axis. The doses increase slightly in vicinity of the central electrode and towards the guard electrode. In the transversal plane, the dose distribution is disturbed according to the Lorentz force: For a magnetic field in $\pm$Y-direction and electrons traveling in beam direction, the Lorentz force points on average in $\pm$X-direction, thus hot (up to  +34%) and cold spots (down to  −39%) arise at the $\pm$X sides of the chamber (see figures 9(d)–(f)). For a magnetic field in $\pm$Z-direction, one can observe a dose increase at the beam entrance side of the chamber (see figures 10(e) and (f)) (up to  +9%).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The corresponding responses for the magnetic field in $\pm$Y- and $\pm$Z-direction are shown in figure 11.

Zoom In Zoom Out Reset image size

For a magnetic field in $\pm$Y-direction, the chamber response again describes a complex dependence on magnetic field strength, chamber radius and field orientation. The dependence on the field orientation, however, is much smaller than for the case where the chamber axis is perpendicular to the beam and the magnetic field. The response of the small chambers R₁ and R₂ increases by  +1.3% for 3.0 T. For the larger chambers, a maximum response evolves, whose magnitude and position depend on the chamber radius. The larger the chamber radius, the smaller is the perturbation of the chamber response. It can be noted that for an increasing chamber radius, the magnetic field strength at which the maximum perturbation occurs decreases. The largest chamber, R₆, exhibits a maximum increase of the response of  +0.3% at 0.7 T. Since the ionization chamber models are rotationally symmetric and the electron energy fluence points mostly in beam direction, no significant dependence on the magnetic field orientation in Y-direction is found.

For a magnetic field in $\pm$Z-direction, the response increases monotonically with an increasing magnetic field. The chamber response changes only slightly, around  +1.0% for 1.0 T. Except for chamber R₁, no significant dependence on the chamber radius and the magnetic field orientation can be observed for this geometry.

The magnetic field correction factors $k_{B}^{{\rm Q}}$ calculated for a 10  ×  10 cm² reference field for all three magnetic field directions using equation (1) are shown in figure 12. Numerical values of the commercial R₃ chamber (PTW 30013) are given in table A1 (supplementary material (stacks.iop.org/PMB/62/6708/mmedia)). Since the dose to water changes only slightly with increasing magnetic field strength (around  −0.3% for a 1.0 T field in X-direction/−0.2% for 1.0 T in Y-direction/+0.1% for 1.0 T in Z-direction), the $k_{B}^{{\rm Q}}$ graphs reveal approximately the inverse shape of the response curves. For a magnetic field perpendicular to beam and chamber axis ($\pm$X-direction), $k_{B}^{{\rm Q}}$ decreases towards a minimum, depending on the chamber radius (maximum change of  −7.6% for the R₄ chamber at 0.8 T), and rises again for higher magnetic field strengths.

Zoom In Zoom Out Reset image size

With a magnetic field parallel to the chamber axis ($\pm$Y-direction), $k_{B}^{{\rm Q}}$ also first decreases towards a minimum with increasing magnetic field strength. In this case, smaller chamber radii exhibit a larger decrease (maximum decrease  −2.5% for the smallest R₁ chamber at 3.0 T). The correction factor of the largest chamber R₆ reduces only by about  −0.5% at 0.7 T, before rising again towards unity. For a magnetic field parallel to the beam ($\pm$Z-direction), $k_{B}^{{\rm Q}}$ decreases monotonically with increasing field strength, presenting a decrease of about  −0.8% at 1.0 T. Only minor influence of the chamber radius can be observed for this configuration.

The perturbation factors associated with the chamber stem, central electrode, wall and replacement of the water by air are shown in figure 13 for all six chambers and for a magnetic field in $\pm$X-, $\pm$Y- and $\pm$Z-direction, respectively. All perturbation factors show a clear dependence on the chamber radius, magnetic field strength and orientation. However, only for a magnetic field oriented along the X-direction an influence of the magnetic field orientation on the perturbation factors was found.

Zoom In Zoom Out Reset image size

The magnetic field in  +X-direction causes a steeper increase in the stem perturbation factor p_stem than a field in ‒X-direction, since in this case, the electrons in the water region replacing the chamber stem are deflected towards the cavity where they deposit additional dose. The stems of the R₁ and R₂ chambers were built slightly differently from the other chamber stems, which may be the reason for the small shift in their p_stem perturbation factors compared with the other ones. For a magnetic field in $\pm$Y-direction, p_stem decreases monotonically for the R₁ and R₂ chambers (maximally by  −0.7% at 3.0 T for the R₂ chamber), while it monotonically increases for the chambers R₄–R₆ (maximally by  +0.9% at 3.0 T for the R₆ chamber). A magnetic field in $\pm$Z-direction causes p_stem to approach towards unity for all chambers at a high magnetic field strength.

The central electrode perturbation factor p_cel presents again a maximum depending on the chamber radius for a magnetic field in $\pm$X-direction. The field orientation has only a minor impact on p_cel, however. The highest variation in p_cel due to the field direction is observed for the R₁ chamber with  +3.6% at 1.5 T. For the case of the magnetic field in the Y-direction, a minimum perturbation factor is observed for the large chambers. In contrast, for a magnetic field in $\pm$Z-direction, p_cel decreases monotonically for higher field strengths. For both cases of the field in Y- and Z-direction, however, the smaller the chamber radius, the higher is the deviation from unity of p_cel. The largest decrease can be found for the R₁ chamber with  −1.5% at 3.0 T for a magnetic field in $\pm$Y-direction.

The wall perturbation factor p_wall increases for all magnetic field directions with increasing field strength by about 1–2% at 3.0 T, except for the  +X-direction. For this direction, p_wall first decreases slightly by about  −0.2% to 0.7–0.8 T for the R₃–R₆ chamber, before increasing again for higher field strengths. The increase in p_wall is shallower for the  +X-direction, when the electrons enter the cavity from the chamber stem side, compared to the  −X-direction, as there is no wall in this region and thus less perturbation. The p_wall value is smaller for smaller chamber radii.

The replacement perturbation factor p_repl shows a minimum, depending on the chamber radius, for a magnetic field in $\pm$X-direction, before it increases again at higher field strengths. The maximum decrease can be observed for the R₅ chamber with  −8.0% at 0.6 T. This perturbation factor is the main contributing factor to the $k_{B}^{{\rm Q}}$ correction factor showing a very similar shape to $k_{B}^{{\rm Q}}$. For a magnetic field in $\pm$Y- and $\pm$Z-direction p_repl, changes only slightly, decreasing monotonically with increasing field strength.

A complex behavior of the chamber response curves was found in measurements and simulations depending on the chamber radius and the magnetic field strengths as well as on the field direction. As described by Meijsing et al, this behavior can be explained by the number of electrons, their track length and their energy dependent stopping power inside the chamber air cavity (Meijsing et al 2009). The average number of electrons entering the chamber cavity depends on the magnetic field direction, since more electrons can reach the sensitive volume via the stem and the dead air volume than via the chamber tip. The larger the chamber radius, the larger is the difference in the number of electrons entering the cavity for the two magnetic field directions. In general, the average number of electrons reaching the sensitive volume decreases with the magnetic field in  −X-direction and exhibits a maximum for magnetic fields in  +X-direction, as can be seen in figure 14(a).

Zoom In Zoom Out Reset image size

The average electron track length within the cavity rises with increasing magnetic field strength up to a certain field strength, before decreasing again for higher magnetic field strengths (see figure 14(b)). The larger the chamber, the smaller is the maximum increase in track length relative to that at 0 T. A possible explanation may be the decreasing surface to volume ratio with increasing radius. As expected, no significant influence of the magnetic field direction on the mean track length was observed.

The size of the sensitive volume has an important impact on the response curve of Farmer-type chambers in magnetic fields, especially when the average direction of the Lorentz force is along the chamber axis. As the electric field inside the chamber air cavity may be disturbed, especially close to the guard electrode, dead volumes can occur, reducing the size of the sensitive volume. A reduction of the electric field near the chamber stem and thus the existence of dead volumes was also observed by Butler et al (2015). They studied dose maps of several chambers, including a PTW 30013 Farmer chamber that corresponds to the R₃ chamber used in the present study, and found that there is a signal reduction near the chamber stem, which can be explained by a decreased electric field. The charge created in these dead volumes is then not collected by the central electrode, but e.g. by the guard electrode. Therefore, these volumes have to be excluded from the sensitive chamber volume in the simulations. In our simulations, the dead volumes were approximated as cylindrical volumes. Realistic dead volumes, however, might be more toroidal-shaped due to the electric field distribution at the guard electrode.

The adjusted dead volume has to be considered as an effective dead volume and its determination is also affected by inherent limitations of efficient Monte Carlo particle transport, i.e. the cut-off energies.

In principle, the adjustment of the dead volume in the Monte Carlo simulation could also be affected by the orientation between the magnetic field and the ionization chamber, as the simulation does not consider trajectories of electrons with energies below 10 keV. In a measurement, however, different magnetic field orientations may change the angular distribution of these low-energy electrons and thus the measured charge.

If the average direction of the Lorentz force lies in the plane perpendicular to the chamber axis, however, the residual range of low-energy electrons is expected to be of minor importance as in this case, the electrons are not deflected towards or away from the guard electrode and therefore the dose distribution is more homogeneous in the cavity including the dead volume near the guard electrode.

In contrast, if the Lorentz force is on average directed along the chamber axis, hot or cold dose spots arise within the dead air volume. Therefore, excluding the air volume near the guard electrode from the sensitive volume in the simulation changes the chamber response curve significantly. In this work, the thickness of the simulated dead volume was adjusted until measured and simulated chamber response curves agreed. Experimentally, the dead volume can in principle be determined by scanning the chamber across a small slit beam or with a step-like dose profile and measuring the signal (Butler et al 2015, Ketelhut and Kapsch 2015). With this method, dosimetric response maps can be determined. However, the measurement has to be very precise to be able to detect dead volume below 1 mm in height for the R₁ chamber. Moreover, to investigate the effect of the magnetic field, a set-up of this experiment in a magnetic field would be desired. Therefore, the scope of this work was to develop virtual chamber models that reproduce the response measurements rather than the exact measurement of the sensitive volumes of the chambers. These models were further-on used to study other orientations of chamber, beam and magnetic fields.

The response curve for a magnetic field parallel to the chamber axis or parallel to the beam revealed smaller changes compared with the case of a magnetic field perpendicular to beam and chamber axis. Again, the changes in response can be explained by the average track length and the number of electrons inside the sensitive volume: For a magnetic field in $\pm$Y-direction, the average electron path length inside the cavity increases slightly with increasing field strength, whereas the amount of electrons decreases for higher field strengths. Both values increase continuously for a magnetic field in $\pm$Z-direction. Moreover, no dependence on the field orientation could be observed for a field in $\pm$Y- or $\pm$Z-direction. A magnetic field in $\pm$Y-direction causes a Lorentz force on average in $\pm$X-direction, thus along the rotationally-symmetric direction of the chamber. Therefore, no change in response can be observed when reversing the orientation of the field in the simulation. In reality, the chambers might be not perfectly rotationally-symmetric, which might have an influence on the response when reversing the magnetic field in $\pm$Y-direction. A magnetic field in $\pm$Z-direction leads to a focusing of electrons along the  +Z-direction for both orientations and thus to no changes in response for both Z-directions.

Therefore, a set-up with a magnetic field parallel to the chamber axis or, if possible, parallel to the beam would be better suited for reference dosimetry in magnetic fields since smaller correction factors would be needed and simulations would be less error-prone when potential dead volumes are not simulated correctly. This agrees with the findings of O'Brien et al, stating that the correction factors are minimized, when the chamber is aligned parallel to the magnetic field (O'Brien et al 2016).

However, when recommending a set-up for reference dosimetry, the influence of a misalignment of the chamber needs to be considered. Smit et al performed measurements with a Farmer ionization chamber in a magnetic field rotating from a parallel alignment of chamber and magnetic field towards a perpendicular alignment: They showed that for a chamber set-up parallel to the magnetic field a misalignment of 10 degrees changes the response by less than 0.6%, whereas such a misalignment causes a change in response of only 0.4% for a chamber set-up perpendicular to the field (Smit et al 2013). This suggests a similar impact of set-up uncertainties for both alignments, but a detailed analysis of the influence of realistic set-up uncertainties on dose measurements in magnetic fields still needs to be performed.

Magnetic field correction and perturbation factors can be calculated with the help of Monte Carlo simulations. It was found that the $k_{B}^{{\rm Q}}$ correction factors can be minimized by selecting the magnetic field in $\pm$Y- or $\pm$Z-direction, i.e. oriented along the chamber axis or along the beam direction. As elaborated upon already in sections 4.1 and 4.3, this effect can be explained by the number and the path length of the electrons entering the cavity.

For the same reason, the changes of the perturbation factors are largest for magnetic fields in $\pm$X-direction. For this direction, p_stem and p_wall vary around 1%, p_cel around 4%. The largest influence factor on the overall perturbation factor and thus on the magnetic field correction factor $k_{B}^{{\rm Q}}$, is p_repl, with changes of up to  −8.0%. For a magnetic field in $\pm$Y-direction, p_stem changes by about 1%, and p_cel, p_wall and p_repl by about 2%. The smallest changes in perturbation factors can be found for a magnetic field in $\pm$Z-direction with variation in p_stem of around 0.2%, and of around 1% in p_cel, p_wall and p_repl.

In general, for most of the investigated directions the absolute values of the chamber stem, central electrode and chamber wall perturbation factors deviate the most from unity for smaller chamber radii. The chamber wall as well as the central electrode are largest relative to the chamber radius for the small chamber R₁, thus they have the biggest influence for this chamber.

In the current IAEA protocol, the stem perturbation factor is ignored in the k_Q calculation (Andreo et al 2006). This is acceptable without a magnetic field since the p_stem value differs only by below 0.4% from unity. However, applying a magnetic field of 1.5 T in  +X- or of 3.0 T in $\pm$Y-direction can change this factor to values that differ by around 1% from unity depending on the magnetic field direction and the chamber radius. Thus, for these field orientations, the p_stem factor should be included in the $k_{B}^{{\rm Q}}$ calculation. For a magnetic field in $\pm$Z-direction, the p_stem factor is close to unity, thus in this case the stem perturbation factor may still be ignored.

The central electrode perturbation factor changes with magnetic field strength and decreases with field strength for a magnetic field in Y- and Z-direction, since here, more electrons can reach the electrode and thus more perturbation occurs at higher field strengths. In contrast, the p_wall perturbation factor increases at higher magnetic field strengths. Again, more perturbation occurs, since more electrons reach the cavity, when no wall is present. The p_wall factors for the R₁ and R₂ chamber are below unity without magnetic field, because parts of their walls were slightly modified by the vendor to fit the chamber stem that was adapted from the R₃ chamber.

Our experimental set-up deviates in some points from the recommended set-up for reference dosimetry. The radiation field size was limited to a 3  ×  10 cm² compared to the reference 10  ×  10 cm² field size. To estimate the effect of the different field sizes, a simulation with both field sizes was performed. The calculated magnetic field correction factors for a 3  ×  10 cm² and a 10  ×  10 cm² field differed maximum by only 0.4% for all investigated magnetic field strengths.

For the calculation of the magnetic field correction and perturbation factors, given in the results, the 10  ×  10 cm² reference field was used.

The experimental electromagnet itself had an influence on the measurement due to scattering. With the magnet (without magnetic field) around the phantom, +1.1% more signal was recorded than without the magnet (Bakenecker 2014). However, since relative measurements have been performed, this should have no significant effect on the measured values.

Hackett et al and Agnew et al described that small air gaps have a large effect on measurements with ionization chambers (Hackett et al 2016, Agnew et al 2017). In addition to the visual check for air bubbles, the response of the R₃ chamber was measured three times within a time period of several months. A very good reproducibility of the response measurements with a maximum deviation of 0.3% ensured that no accidentally trapped air perturbed the measurement.

The PTW 30013 chamber (R₃) was also used by Agnew et al for measurements in magnetic fields irradiated with a ⁶⁰Co source (Agnew et al 2017). For comparison of our simulation chamber model, the response measurement was simulated using a 10  ×  10 cm² field produced with a ⁶⁰Co spectrum (Rogers et al 1988). Although the simulation was performed in water instead of the experimental Perspex phantom and a different SSD was used, a good agreement with a mean squared difference of 0.4% was obtained (maximum difference 0.7%), confirming our chamber model.

In the chamber response simulation described in section 2.3.1, a 6 MV spectrum was used as beam source. To estimate the influence of small differences in the spectrum, $k_{B}^{{\rm Q}}$ correction factor calculations were performed for the R₃ chamber with different 6 MV spectra from the literature (spectrum of an Elekta SL25 (Sheikh-Bagheri and Rogers 2002) as well as spectra produced from the IAEA phase space files of Siemens Primus (Pena et al 2007), Varian Clinac 600C (Brualla et al 2009), Varian Clinac iX linacs): The $k_{B}^{{\rm Q}}$ factor calculated for 10  ×  10 cm² field sizes generated with the different spectra differed on average by 0.1% (maximum difference 0.5%). Thus, small changes in the beam spectrum have only a small influence on the $k_{B}^{{\rm Q}}$ factors.