Abstract
'That it is possible to find the form of the Lorentz transformations without requiring the speed of light to be the same in every inertial system is rediscovered about every thirty years and, rightly, forgotten.' This proposition alongside the doctoral dissertation of Hendrik Smid in 1986 provides food for thought: Is the light postulate of special relativity, which gives the speed of light  in vacuum its status of maximum and unchanging speed, indeed not necessary? What kind of physical world are you then left with? What could be the value of discussing this in class? In this paper we show how the Lorentz transformation, which describes the relationship between two coordinate systems moving relative to each other at a constant speed, can indeed be derived by replacing the light postulate by another assumption, namely the requirement of closure under composition of transformations that relate inertial frames of reference (i.e. two successive coordinate transformations of certain type can be written as one transformation of the same type). Although well known in specialised literature of physics research, the remarkable insight that
in vacuum its status of maximum and unchanging speed, indeed not necessary? What kind of physical world are you then left with? What could be the value of discussing this in class? In this paper we show how the Lorentz transformation, which describes the relationship between two coordinate systems moving relative to each other at a constant speed, can indeed be derived by replacing the light postulate by another assumption, namely the requirement of closure under composition of transformations that relate inertial frames of reference (i.e. two successive coordinate transformations of certain type can be written as one transformation of the same type). Although well known in specialised literature of physics research, the remarkable insight that  is somehow buried in nature is hardly mentioned in pre-university and bachelor's physics courses and textbooks. Yet, the presented comprehensible approach may support the understanding and plausibility of the abstract subject of special relativity. Mathematics may go too far for an average pre-university student, but this subject would certainly not be out of place in an undergraduate physics course or a physics teacher course. Although many teachers do not know that the light postulate of special relativity can be replaced by another assumption or may not appreciate such replacement as part of their teaching of the topic, it offers in our opinion an opportunity to inform students that a critical look at postulates and an investigation of alternatives is an essential part of the nature of science.
is somehow buried in nature is hardly mentioned in pre-university and bachelor's physics courses and textbooks. Yet, the presented comprehensible approach may support the understanding and plausibility of the abstract subject of special relativity. Mathematics may go too far for an average pre-university student, but this subject would certainly not be out of place in an undergraduate physics course or a physics teacher course. Although many teachers do not know that the light postulate of special relativity can be replaced by another assumption or may not appreciate such replacement as part of their teaching of the topic, it offers in our opinion an opportunity to inform students that a critical look at postulates and an investigation of alternatives is an essential part of the nature of science.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Many countries have recently introduced special relativity in secondary school physics in order to expose students to modern physics [1] and several teaching and learning sequences have been developed [2–7]. The postulates of special relativity and the Lorentz transformation, which describes the relationship between two coordinate systems moving relative to each other at a constant speed, play a role in almost all of them. The quotation of Smid [8] in the abstract suggests that the Lorentz transformations may equally be derived without using the light postulate. More accurately stated, one can replace the light postulate in the set of physical arguments used for the standard derivation of the Lorentz transformation (e.g. [9]) by the requirement that the coordinate transformations are closed under composition (i.e. two successive coordinate transformations of certain type can be written as one transformation of the same type). This remarkable result pointing towards the existence of a universal constant is well known in specialised literature of physics research [10–15]. The required mathematics knowledge and skills may go too far for an average pre-university student. But the topic would certainly not be out of place in a physics (teacher) course at undergraduate level, when students may be expected to have the mathematical competencies needed. We will show that a minimum of calculus, algebra and matrix algebra is sufficient to understand our teacher/student-friendly derivation. Apart from this, it is still worth conveying the fascinating result to younger students in a qualitative way so that they learn that having a critical look at foundational assumptions in theory formation and searching for alternatives are activities that scientists actually do in research practice.
When the special theory of relativity was introduced after many years of experimentation into the current upper secondary physics pre-university curriculum in the Netherlands and when it became one of four optional subdomains of which two have to be selected for the school examination of physics 4 , school physics teachers were not too worried. In contrast with the compulsory subdomain Quantum World of the country-wide examination [16], the explanation in the lecture halls of concepts such as inertial frames of reference, the Michelson–Morley experiment, and the premise that the speed of light in vacuum is the same in every inertial frame of reference were still fresh in many teachers' minds. Nor were the mathematical derivations and algebraic manipulation too great an obstacle for the teachers.
The derivation of the formula for time dilation is an example of mathematical simplicity, which allows its discussion with upper secondary physics students. Imagine a thought experiment in which an observer in a frame of reference at rest measures that it takes a proper time interval  for a pulse of light to move vertically from the origin of the frame of reference to the ceiling. The height of the ceiling is then equal to
for a pulse of light to move vertically from the origin of the frame of reference to the ceiling. The height of the ceiling is then equal to  . From the viewpoint of an observer with an inertial frame of reference moving parallel to the ceiling at velocity
. From the viewpoint of an observer with an inertial frame of reference moving parallel to the ceiling at velocity  to the right and passing by with coinciding origin in his/her frame of reference and the rest fame at the moment when the pulse of light is emitted, the light takes an oblique path; s/he measures a larger time interval
to the right and passing by with coinciding origin in his/her frame of reference and the rest fame at the moment when the pulse of light is emitted, the light takes an oblique path; s/he measures a larger time interval  for the light signal to reach the ceiling and a longer path length of
for the light signal to reach the ceiling and a longer path length of  that the pulse of light needs to reach the ceiling. In this time interval, the moving frame of reference is shifted
that the pulse of light needs to reach the ceiling. In this time interval, the moving frame of reference is shifted  to the right; see figure 1. The ratio of
to the right; see figure 1. The ratio of  and
and  can be determined by the Pythagorean theorem and basic algebraic manipulation leads to the well-known time dilation formula
can be determined by the Pythagorean theorem and basic algebraic manipulation leads to the well-known time dilation formula  , where
, where  is the so-called Lorentz factor.
is the so-called Lorentz factor.
Figure 1. Rectangular triangle used for the derivation of the time dilation formula via the Pythagorean theorem.
Download figure:
Standard image High-resolution imageAt first sight, there seems nothing wrong with the above derivation of the formula for time dilation and many students will be completely satisfied with it. Yet intuition causes some friction here: a critical student might note that the difference between  and
and  arises from the fact that for the vertical side of the triangle and for the hypotenuse both the velocity of light has been used (and not, for instance,
arises from the fact that for the vertical side of the triangle and for the hypotenuse both the velocity of light has been used (and not, for instance,  ). The light postulate of special relativity, which states that the speed of light in vacuum is the same for observers moving at constant speed relative to each other, is hidden in it. Telling that this status of
). The light postulate of special relativity, which states that the speed of light in vacuum is the same for observers moving at constant speed relative to each other, is hidden in it. Telling that this status of  as maximum and unchanging speed of light is just the inevitable consequence of experimental results found by Michelson and Morley does not usually win the critical student over. It may help if the teacher notes that our intuition is simply formed in a world in which it seems as if the speed of light is infinite and that we therefore cannot escape from judging the results of the denial thereof, i.e. theory of relativity, as illogical and counterintuitive. If the speed of light, for example, were as small as the speed of a spacecraft, everyone would notice that time depends on the speed of the observer with the time measurement device and thus perceive time as unreliable. This is why we have chosen Einstein's expression 'time is suspect!' [17, p 48] as the title of this paper.
as maximum and unchanging speed of light is just the inevitable consequence of experimental results found by Michelson and Morley does not usually win the critical student over. It may help if the teacher notes that our intuition is simply formed in a world in which it seems as if the speed of light is infinite and that we therefore cannot escape from judging the results of the denial thereof, i.e. theory of relativity, as illogical and counterintuitive. If the speed of light, for example, were as small as the speed of a spacecraft, everyone would notice that time depends on the speed of the observer with the time measurement device and thus perceive time as unreliable. This is why we have chosen Einstein's expression 'time is suspect!' [17, p 48] as the title of this paper.
The suspect would even be greater when a teacher discusses with students the case that in the frame at rest as well as in the moving frame at the moment that the origins of their frames of reference coincide a pulse of light is going vertically from the origin to ceiling of the same height: each observer now thinks that the pulse of light emitted in the frame of reference of the other observer takes longer time to reach the ceiling than in his/her own frame of reference.
Yet it would be nice to add that the light postulate does not appear out of the blue, but is embedded in the mathematical relationship between a frame of reference at rest and a moving inertial frame of reference. Three necessary and understandable conditions for the yet-to-be-determined coordinate transformation between two inertial frames of reference turn out to lead, even without the light postulate, to the Lorentz transformation containing a constant velocity  that, incidentally, can still be finite or infinite, or equal to the speed of light
that, incidentally, can still be finite or infinite, or equal to the speed of light  .
.
But before we go into this derivation of the Lorentz transformation we first address a possible student's question: 'Why do we talk about the Lorentz transformation and not about the Einstein transformation?' The obvious, but incorrect answer is: 'Lorentz was the first person who wrote about it.' This would give the false image that theory formation in science is generally the result of work of a single person. It is true that Hendrik Lorentz did pioneering work in the context of electromagnetism: he came up with a transformation that made the electric and magnetic fields independent of the possible speed of an observer. He also formulated the notion of length contraction as explanation of the null result of the Michelson–Morley experiment. But other scientists contributed in the same period to the theory formation. Henri Poincaré was one of them and he introduced the name Lorentz transformation [18–21], probably in recognition of the leading role that Lorentz played. However, Lorentz did not believe in the physical reality of  : for him it only served as the auxiliary variable 'local' time. It was Einstein in 1905 who explained the fundamental physical value of the transformation, generalised it to uncharged particles, and derived the transformation from his relativity postulate and light postulate. By the way, the title of Einstein's work [22] refers indirectly to the work of Lorentz.
: for him it only served as the auxiliary variable 'local' time. It was Einstein in 1905 who explained the fundamental physical value of the transformation, generalised it to uncharged particles, and derived the transformation from his relativity postulate and light postulate. By the way, the title of Einstein's work [22] refers indirectly to the work of Lorentz.
2. Derivation of the Lorentz transformation
We consider two inertial frames of reference  and
and  with position-time coordinates
with position-time coordinates  and
and  , respectively. The frame of reference
, respectively. The frame of reference  moves relative to
moves relative to  with constant velocity
with constant velocity  along the
along the  axis. One may think of a frame of reference
axis. One may think of a frame of reference  at rest and a moving frame of reference
at rest and a moving frame of reference  (see figure 2).
(see figure 2).
Figure 2. Two inertial frames moving with respect to each other along the  -axis with constant velocity
-axis with constant velocity  and the general transformation between the frames of reference.
and the general transformation between the frames of reference.
Download figure:
Standard image High-resolution imageWe derive in this section the coordinate transformation from the frame of reference  at rest to the moving frame of reference
at rest to the moving frame of reference  on the basis of the following three assumptions:
on the basis of the following three assumptions:
- (i)Exchangeability of frames of reference: frame
 moves relative to
moves relative to  with velocity
with velocity  along the
along the  axis.
axis. - (ii)Space-time is homogeneous (i.e. the origin of the frames of reference can be located anywhere) and space is isotropic (i.e. it does not matter which direction is called positive).
- (iii)The composition of two coordinate transformations is again a coordinate transformation of the same kind.
These three assumptions turn out to be sufficient for the derivation of the Lorentz transformation without using the light postulate of a maximum speed of light in vacuum.
In the derivation we do not scale time to the dimension of length for three reasons: (i) in this way we get the form of the Lorentz transformation commonly found in physics textbooks; (ii) scaling is a technique that does not get much attention in education and therefore may be more confusing; and (iii) the argumentation and algebra are similar for the derivation with and without time scaling. However, one could argue that it is from physical point of view more elegant to work in the coordinate transformation with scaled time coordinates  and
and  that have, just like the spatial coordinates
that have, just like the spatial coordinates  and
and  the dimension of length. Here,
the dimension of length. Here,  and
and  are yet unknown scale factors with the dimension of velocity. By the way, teaching and learning sequences in special relativity at secondary school level that use spacetime Minkowski diagrams show that teachers expect that students can in fact deal with scaling (in this case with the speed of light
are yet unknown scale factors with the dimension of velocity. By the way, teaching and learning sequences in special relativity at secondary school level that use spacetime Minkowski diagrams show that teachers expect that students can in fact deal with scaling (in this case with the speed of light
 ). In a supplementary document the authors present the derivation of the Lorentz transformation with time scaling included.
). In a supplementary document the authors present the derivation of the Lorentz transformation with time scaling included.
2.1. Derivation without time scaling
From the homogeneity of space-time follows that coordinate transformations between the frames of reference are linear mappings that depend continuously on the velocity  (cf [11, 13, 23]). The coordinates
(cf [11, 13, 23]). The coordinates  of the frame of reference
of the frame of reference  at rest can be converted into the coordinates
at rest can be converted into the coordinates  of the moving frame of reference
of the moving frame of reference  via a velocity-dependent linear mapping, which we denote by the matrix
via a velocity-dependent linear mapping, which we denote by the matrix  . So:
. So:
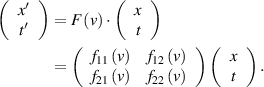
The reverse transformation is also possible; the only thing that changes is the direction of the velocity
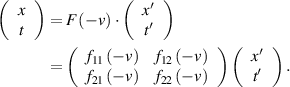
The exchangeability of the frames of reference implies that  and
and  are each other's inverse; in matrix form this can be written as:
are each other's inverse; in matrix form this can be written as:
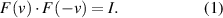
Assuming that space is isotropic so that it does not matter which direction we call positive, reverting the direction means that the frame of reference  moves with velocity
moves with velocity  in the opposite direction with respect to the frame of reference
in the opposite direction with respect to the frame of reference  and that we get:
and that we get:
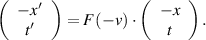
In matrix form we can write this as the following equation:
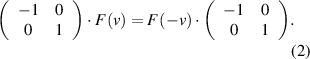
The third assumption about the coordinate transformation can be mathematically expressed as:
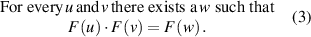
The matrix assumptions (1)–(3) for the coordinate transformation  determine its mathematical formula:
determine its mathematical formula:
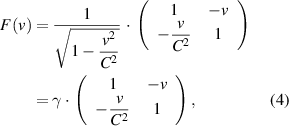
where  is a constant and
is a constant and  . We will prove this below.
. We will prove this below.
From equations (1) and (2), and from multiplication properties of the determinant of a matrix follows that
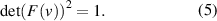
So  . Because
. Because  and the coordinate transformation
and the coordinate transformation  depends continuously on velocity
depends continuously on velocity  , it must be true that
, it must be true that
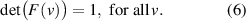
This formula simplifies the computation of the formula of the inverse matrix of  , which according to the matrix condition (1) equals
, which according to the matrix condition (1) equals  . Elementary linear algebra leads to:
. Elementary linear algebra leads to:
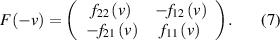
We can rewrite the matrix equation (2) as
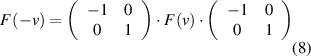
and obtain from this
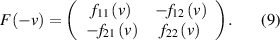
Formulas (8) and (9) imply that  and that we can write
and that we can write
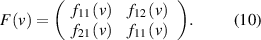
Now, let  coincide with the origin of the moving frame of reference
coincide with the origin of the moving frame of reference  . Then
. Then  and thus
and thus  , which can be rewritten as
, which can be rewritten as
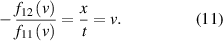
This means that we can rewrite formula (10) of  as
as
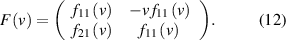
We introduce in the crucial matrix element  a new, in principle velocity-dependent quantity,
a new, in principle velocity-dependent quantity,  defined as
defined as
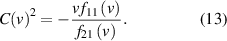
The coordinate transformation  can now be written as
can now be written as
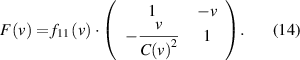
Because  for all v (formula (6)) it follows from expression (14) for
for all v (formula (6)) it follows from expression (14) for  that
that
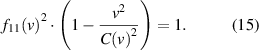
So we can rewrite the coordinate transformation  as
as
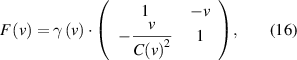
where  .
.
Let us now compute the composition of two coordinate transformation with velocities u and v, respectively. Matrix multiplication gives:
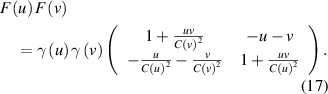
Assumption (iii) states that the composition must be a coordinate transformation of the same kind and in particular the diagonal elements must be equal to each other. This implies in formula (17) that in fact  for all velocities
for all velocities
 and
and
 . In other words,
. In other words,  is independent of velocity
is independent of velocity
 and thus equal to some constant
and thus equal to some constant  .
.
Without experimental data we do not know whether this constant
 is a finite number or infinity. Taking the limit for
is a finite number or infinity. Taking the limit for  yields the Galilean transformation:
yields the Galilean transformation:
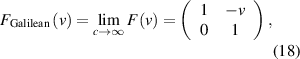
that is,  and
and  , and the classical mechanics addition formula of velocities can be applied. However, when C is finite, time is transformed and therefore dependent on the relative velocity v of the inertial frames: 'time is suspect!' The addition formula is now more complicated and follows from rewriting formula (17) as
, and the classical mechanics addition formula of velocities can be applied. However, when C is finite, time is transformed and therefore dependent on the relative velocity v of the inertial frames: 'time is suspect!' The addition formula is now more complicated and follows from rewriting formula (17) as

Thus velocities  and
and  add up to a velocity
add up to a velocity  given by
given by
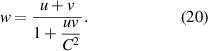
In conclusion, we have found the Lorentz transformation  without reference to the light postulate of a maximum speed of light, constant for all inertial frames of reference. Only some constant
without reference to the light postulate of a maximum speed of light, constant for all inertial frames of reference. Only some constant  with the dimension of velocity pops up in the derivation. There is at this stage yet no reason to identify this constant
with the dimension of velocity pops up in the derivation. There is at this stage yet no reason to identify this constant  with the light of speed -
with the light of speed - . What we know about
. What we know about  is that if an object moves in one inertial frame of reference with velocity
is that if an object moves in one inertial frame of reference with velocity  , then it moves in any other inertial frame of reference with the same velocity. Applying the linear mapping defined in formula (4) to the case of
, then it moves in any other inertial frame of reference with the same velocity. Applying the linear mapping defined in formula (4) to the case of  leads to
leads to  . We will come back to this in the final example of section 3. In other words,
. We will come back to this in the final example of section 3. In other words,  is an invariant speed, i.e. it is the same in all inertial frames of reference. Moreover,
is an invariant speed, i.e. it is the same in all inertial frames of reference. Moreover,  is a maximum as any existing larger velocity would violate causality. Maxwell's theory of electromagnetism stipulates that the speed at which electromagnetic waves travel in vacuum is constant in any inertial frame of reference and light is an electromagnetic wave. No experiments have contradicted this. As a result, we can identify
is a maximum as any existing larger velocity would violate causality. Maxwell's theory of electromagnetism stipulates that the speed at which electromagnetic waves travel in vacuum is constant in any inertial frame of reference and light is an electromagnetic wave. No experiments have contradicted this. As a result, we can identify
 with the speed of light
with the speed of light
 . Alternatively, application of the relativity postulate to Maxwell's equations yields the Lorentz transformation with the identification
. Alternatively, application of the relativity postulate to Maxwell's equations yields the Lorentz transformation with the identification 
3. Discussion
In the previous section we have shown that knowledge and skills in elementary calculus and linear algebra are sufficient to derive the Lorentz transformation without the light postulate of special relativity. But physics theory cannot do without experimental validation: one cannot escape from experimental determination of the speed of light. This is probably why the proposition alongside the doctoral dissertation of Smid [8], quoted in the abstract, contains the word 'rightly'. Yet, our approach shows how fundamental the Lorentz transformation actually is! An elegant aspect of the primarily mathematical approach is that one can find on the basis of rather simple principles about space and time transformations, depending on the choice of an unknown speed  , either classical or relativistic transformations. Maybe Einstein already realised in 1916 that the Lorentz transformation could be derived without the light postulate: his derivation and sigh 'Das hätte ich einfacher sagen können' (I could have said that more simply) [24] do point at this.
, either classical or relativistic transformations. Maybe Einstein already realised in 1916 that the Lorentz transformation could be derived without the light postulate: his derivation and sigh 'Das hätte ich einfacher sagen können' (I could have said that more simply) [24] do point at this.
The simplicity and the ease of acceptance of the assumption that a composition of transformations of certain type is again a transformation of the same kind does not automatically mean that it replaces the light postulate in education. Actually this is not what we advocate: certainly at secondary school level, the derivation of the light postulate from the new assumption is, as we wrote upfront, probably too difficult for the students. We are just of opinion that inclusion of the discussion of postulates and alternatives adds to the scientific literacy of students, as described by Hodson [25, 26]. They learn more about the way scientists work, not in solitude but within in a research community, and gain a better understanding of the history and philosophy of science. Improving students' scientific literacy, presenting concepts of modern physics in authentic contexts, and increasing their motivation and engagement with modern physics were in many countries also driving forces in the curriculum reforms in the last two decades [e.g. 27–29].
Change of an underpinning assumption in the special relativity theory also does not provide an easy solution for many of the students' difficulties that are reported in the research literature. This is clear when one reads about student's alternative conceptions in the review and analysis of the body of research on special relativity theory education at secondary and undergraduate level by Alstein et al [1] and references herein. But one must keep in mind that this review study is restricted to articles that address conceptual understanding of special relativity and Galilean relativity 'without presupposing an understanding of the formalism of Lorentz transformation or spacetime geometry.' [p 2] So, these authors take the stand that at secondary and lower undergraduate level a conceptual approach to special relativity theory, in which abstract concepts are expressed through the use of thought experiments [2], rather than mathematical of geometrical formalism, which can be derived as a complement afterwards. They developed a teaching and learning approach in which the light postulate, which is notoriously difficult for students to grasp [3, 30, 31], is chosen as a central concept and in which students perform relativistic thought experiments using event diagrams as reasoning tool, try different interpretations of the light postulate, and experience how the new concepts meet the requirements for a good theory [2]. This interesting instructional sequence was developed as part of a design research-based doctoral study [32], but as the authors [2, p 96] admit: 'the current version of our design cannot be directly implemented in the classroom as it relies heavily on a teacher working closely with students individually to guide their reasoning.' Yet such detailed studies have great value in exploring challenges and opportunities with regard to teaching special relativity at secondary and lower undergraduate level.
Inspired by the analysis of college physics textbooks by Dimitiadi and Halkia [3], Alstein et al [1] organised their overview of learning difficulties of secondary and lower undergraduate students into three main categories: (i) frames of reference; (ii) postulates of special relativity theory; and (iii) relativistic effects such as relativity of simultaneity, time dilation and length contraction. Any description of relative motion is inextricably linked to the concept of frames of reference, in which observers perform measurements to determine spatial and temporal coordinates of events by means of measuring rods and synchronised clocks, and to an operational definition of the time of a distant event. Understanding of the transformation of measurement outcomes found in several frames of reference is therefore of key importance in any approach to the special relativity theory. Actually similar difficulties exist in Galilean relativity education. Below we describe research findings about students' alternative of frames of reference.
Many students consider a frame of reference as local instead of infinite: it never extends beyond the object where the observer is [33, 34] and an observer can only know what happens at his/her location [35]. Many students link every observer or object to a private frame of reference; so they think that there can be no more than one observer in a frame of reference. In other words, many students fail to consider a frame of reference as a system of observers that determines the same position and time for any event, and they interpret statements of the frame-dependence of the time of an event to mean that signals are received from events at different times by observers at different locations [35]. Conversely, Scherr et al [36] showed that students tend to treat observers at the same position as being in the same frame of reference, regardless of their relative motion. Many students (initially) see motion and velocity as an intrinsic property of a moving object and find it therefore difficult to refer to velocities and trajectories with respect to a frame of [37, 38]. Some students think that events may be simultaneous for one observer and not simultaneous for another person, even when both observers are located in the same frame of reference, and many students cannot give an answer only depending on the location of the observer when his or her velocity is mentioned as if the movement contaminated the event [39]. Many students consider length as a property of an object that cannot change and therefore they look at length contraction as an optical illusion and they think that, when several observers do not get the same measurements of length, some of them must have made a mistake [3]. Students frequently do not spontaneously or consciously consider alternative frames of reference besides the default frame of reference, which is generally the earth. Many of them tend to believe that in special relativity theory there is a 'privileged observer' position and that time dilation and length contraction happen only for the moving observer [30]. Scherr et al [36] pointed out that many of the student difficulties may arise from too vague and/or unclear definitions of basic concepts such as frame of reference, event, observer, 'intelligent observer' (taking signal travel time into account), simultaneity, and spacetime leading to the construction of a conceptual framework in which the ideas of absolute and relative simultaneity harmoniously coexist (see also [40]). Entire conferences [41] have been devoted to students difficulties with frames of reference and ways to overcome obstacles. Much attention has gone and still goes into development of ICT-based learning activities that enrich students' experiences, allow them to engage with more abstract and sometimes counterintuitive physics concepts through simulations, and help them deepen their understanding of modern physics. In conclusion, Scherr et al [42] concluded that many students who study special relativity at the undergraduate to graduate levels fail to develop a functional understanding, partly because of a lack of understanding of more basic, underlying concepts. These authors found [p 1247] that 'after standard instruction many students lack operational definitions for fundamental ideas such as time of an event, simultaneity, and reference frame—concepts that should be familiar to them from Galilean relativity.'
Recently, Hughes and Kersting [43] pointed out how the language of special relativity can mislead and confuse students, or even worse is a likely source of misconceptions. In particular, the words 'observer' and 'observation' may blur the distinction between seeing and measuring. For example, the formula for length contraction does not describe what one sees, but what one measures. What is measured corresponds to a specific measuring procedure in which simultaneously separate coordinates on a moving object are located. In contrast, what is seen depends on the differing time light takes to reach the eyes of the observer for different parts of a moving object. Similar confusion happens with time dilation. Research in quantum physics education also suggests that secondary school students tend to conceptualise 'observation' as seeing rather than measuring.
In light of the above discussion of student difficulties linked to frames of reference, we believe that students may only better understand that formulas in special relativity mainly deal with measurement when they are at early stages of education already deeply exposed to frames of reference and apply them in many exercises in classical mechanics, Galilean relativity, and finally in special relativity. Then students may learn to understand how measurement is inextricably linked to a choice of a frame of reference. Scaling of an axis is actually nothing else than choosing another unit of the quantity linked to that axis. Students better learn at an early stage how coordinate transformations link differing frames of reference: rotation changes the orientation, and translation allows for a differing choice of the origin. After such a learning path full of discussion of frames of reference and coordinate transformations, students can understand that the Lorentz transformation is just another transformation of a two-dimensional space, only a little bit more complicated than they have seen before. They may better understand the Lorentz transformation and not believe anymore that the transformation of time constitutes a correction for signal travel time, a misconception reported by Scherr et al [36].
Use of the Lorentz transformation does not necessarily mean that the student performs calculations. Use can also be in the form of qualitative algebraic reasoning. In this way, for example the loss of simultaneity among equivalent observers and other relativistic effects such as time dilation and length contraction can be analysed by students. As concrete example we discuss the spacecraft question designed by Scherr et al [36]. It involved two volcanoes. Mt. Rainier and Mt. Hood, that erupt simultaneously in the frame of reference  of an observer at rest on the ground, midway between the volcanoes. A spacecraft moving at a given constant relativistic velocity
of an observer at rest on the ground, midway between the volcanoes. A spacecraft moving at a given constant relativistic velocity  from Mt. Rainier to Mt. Hood is directly over Mt. Rainier when it erupts. Event 1 and Event 2 are defined to be 'Mt. Rainier erupts' and 'Mt. Hood erupts,' respectively. The question is what the order of eruptions is in the moving frame of reference
from Mt. Rainier to Mt. Hood is directly over Mt. Rainier when it erupts. Event 1 and Event 2 are defined to be 'Mt. Rainier erupts' and 'Mt. Hood erupts,' respectively. The question is what the order of eruptions is in the moving frame of reference  of the spacecraft, i.e. does event 1 occur before, after, or at the same time as event 2 in the frame of reference of the spacecraft observer. A correct answer can be obtained by qualitative reasoning, by use of spacetime diagrams, and by application of the Lorentz transformation. We discuss the latter approach. The spatial separation between the two events in the frame of reference
of the spacecraft, i.e. does event 1 occur before, after, or at the same time as event 2 in the frame of reference of the spacecraft observer. A correct answer can be obtained by qualitative reasoning, by use of spacetime diagrams, and by application of the Lorentz transformation. We discuss the latter approach. The spatial separation between the two events in the frame of reference  is defined as
is defined as  , where
, where  and
and  are the locations of event 1 and event 2, respectively. Taking the positive direction to be directed from Mt. Rainier to Mt. Hood we have
are the locations of event 1 and event 2, respectively. Taking the positive direction to be directed from Mt. Rainier to Mt. Hood we have  and
and  . Similarly the temporal separation between the two events is defined as
. Similarly the temporal separation between the two events is defined as  , where
, where  and
and  are the times at which event 1 and event 2 occur, respectively. In this question
are the times at which event 1 and event 2 occur, respectively. In this question  because the volcanoes erupt simultaneously. The Lorentz transformation relates measurements in the ground frame
because the volcanoes erupt simultaneously. The Lorentz transformation relates measurements in the ground frame  and the spacecraft frame
and the spacecraft frame  . The general Lorentz transformation of time is
. The general Lorentz transformation of time is  and specialises in this case to
and specialises in this case to  because
because  ,
,  and
and  . A negative value of
. A negative value of  means that in the spacecraft reference frame Mt. Hood erupts before Mt. Rainier. We believe that the above reasoning is less error-prone than many other approaches. The final result is of course still counterintuitive.
means that in the spacecraft reference frame Mt. Hood erupts before Mt. Rainier. We believe that the above reasoning is less error-prone than many other approaches. The final result is of course still counterintuitive.
We end this paper with the following thought experiment that shows how the Lorentz transformation can be used to illustrate the light postulate. The mathematics does not go beyond upper secondary level. Consider an observer in the origin of a three-dimensional frame of reference  at rest. When s/he creates a flash of light at time
at rest. When s/he creates a flash of light at time  , then the light will be after time
, then the light will be after time  on a sphere with radius
on a sphere with radius  , where c is the speed of light in vacuum. A second observer in a spacecraft with constant velocity passes at time
, where c is the speed of light in vacuum. A second observer in a spacecraft with constant velocity passes at time  the origin of S, thus exactly at the time of emission of the flash of light. What shape has the light in his/her moving frame of reference
the origin of S, thus exactly at the time of emission of the flash of light. What shape has the light in his/her moving frame of reference  . To simplify the algebra, we rewrite the Lorentz transformation and its inverse in the following more symmetric format:
. To simplify the algebra, we rewrite the Lorentz transformation and its inverse in the following more symmetric format:
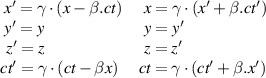
where
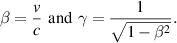
These transformations can be used to explain that the second observer also concludes that the light will be after some time on a sphere in his reference frame. First, square the equation  and rewrite it as
and rewrite it as  . Substitute the inverse Lorentz transformation:
. Substitute the inverse Lorentz transformation:
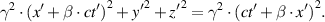
Expand the brackets in the previous equation and use the relation  to rewrite it as
to rewrite it as  . Thus, in the frame of reference of the second observer, the light will be after time
. Thus, in the frame of reference of the second observer, the light will be after time  on a sphere with radius
on a sphere with radius  . This mathematical approach, well within reach of upper secondary students, does not obscure physical aspects and does not hinder the process of acquiring physical intuition of special relativity. On the contrary, it shows that the constancy of the speed of light in vacuum in any frame of reference does not come out of the blue.
. This mathematical approach, well within reach of upper secondary students, does not obscure physical aspects and does not hinder the process of acquiring physical intuition of special relativity. On the contrary, it shows that the constancy of the speed of light in vacuum in any frame of reference does not come out of the blue.
Data availability statement
No new data were created or analysed in this study.
Footnotes
- 4
Besides special theory of relativity, the three other optional subdomains in the school examination program are biophysics, geophysics and elementary particle physics. Two of these four subdomains must be elected for school assessment.
Biographies

André Heck earned MSc degrees in mathematics and chemistry, and a doctoral degree in mathematics and science education. He is senior lecturer at the Faculty of Science of the University of Amsterdam. His research area is the application of ICT in mathematics and science education.

Hans Jordens earned a doctoral degree in theoretical physics, and in physics and mathematics education. He worked ten years as teacher at a secondary school and thirty years as lecturer at the University of Groningen, Netherlands. During 35 years he was involved in many physics and science competitions for secondary education amongst which the International Physics Olympiad, of which he was president for 10 years.

Peter Uylings graduated in physics and mathematics, and he obtained his PhD in theoretical physics. He worked part-time as teacher at a secondary school and as physics teacher educator. After retirement he went back to his first love in physics research and restarted work in the field of atomic physics.
Supplementary data (<0.1 MB DOCX)






