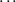Abstract
The paper Pendulum: the partial and global approach combines a historic introduction to the theoretical treatment of pendulum motion with presentation of data from measurements on a single pendulum. This comment focuses on the presentation and analysis of experimental data, and how the use of dimensionless variables in graphs would make use of the mathematical properties, placing the single measurement in a more general context, including mass-independence and the isochronism (for small angles). The concept of 'effective weight' used by Coelho is then discussed in relation to inertial forces and the principle of equivalence between inertial and gravitational mass.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In a recent paper, Coelho [1] claims to take a global perspective on pendulum motion. After the introductory discussion about a historical approach to the derivation of the equation of motion follows a presentation of the results of a single experiment. The author then proceeds to deriving a well-known relation for the tension in a string during pendulum motion, and the abstract suggests that the paper 'provides a mathematical insight into the phenomenon suitable for the high school student'. This comment focuses on the presentation and analysis of experimental data, and how the use of dimensionless variables in graphs would make use of the mathematical properties, and place the results of the single experiment in a more general context.
Coelho [1] states that 'Research in physics education has ... shown dynamically relevant aspects of pendulum motion'. This is, of course, not true. The dynamical aspects of pendulum motion were clear long before Physics Education (PER) was established as a research field. What is shown by PER is that students and sometimes even teachers tend to forget about the centripetal acceleration when asked about the acceleration in a pendulum (e.g. [2, 3]). It is very likely that the same students, if asked to calculate the forces in the lowest point, would be able to do so. When students in a focus group were asked what would happen if there were a force equilibrium in the lowest point, they quickly realized what they had missed [4].
2. Data collection, presentation and interpretation
The first figure in [1] shows results, expressed in Newton, for a single pendulum with given mass and three different starting angles. The data were collected in one particular location, with a specified value of the local acceleration of gravity, g (not 'local gravitational constant'). These can hardly be considered global results! The well-known relations, also derived in [1], show that the maximum values for the tension 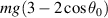 , deviate from mg twice as much as the minimum value
, deviate from mg twice as much as the minimum value 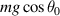 (which is omitted from their tables). This relation hold also for very large angles, as seen e.g. in [5], and is compatible with the graph in the first figure in [1].
(which is omitted from their tables). This relation hold also for very large angles, as seen e.g. in [5], and is compatible with the graph in the first figure in [1].
Their data collection used the force sensor in a PASCO Smart Cart. The cart, which has a mass of 0.245 kg according to specifications [6], was fitted with two lead sheets to prevent it from spinning. No information is given about the dimensions of the sheets, only that the total mass was 3.0042 kg. The author fails to discuss if the resulting bob is well represented by a point particle or if there is a need to take the moment of inertia into account. The Smart Cart also includes accelerometer and rotation sensors, which would enable additional validation of the measured data, as done e.g. by Monteiro and coworkers using a smartphone to study the motion of a physical pendulum for large angles [7].
2.1. Dimensionless variables
For a more global approach, the data can be presented in terms of the tension in the string divided by mg. The data can also be expressed in terms of a vector 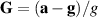 , often referred to as a 'G-force' and expressed in units of g. This vector is independent of the mass of the pendulum bob, and is also what would be measured by an accelerometer sensor, whether the built-in sensor of a Smart Cart or a smartphone. A graph of dimensionless data with
, often referred to as a 'G-force' and expressed in units of g. This vector is independent of the mass of the pendulum bob, and is also what would be measured by an accelerometer sensor, whether the built-in sensor of a Smart Cart or a smartphone. A graph of dimensionless data with 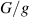 on the vertical axis and
on the vertical axis and 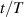 on the horizontal axis can represent the motion of a pendulum independent of mass, length and acceleration of gravity, as long as the approximation of a point-like bob on a massless string is valid. An example is shown in figure 1.
on the horizontal axis can represent the motion of a pendulum independent of mass, length and acceleration of gravity, as long as the approximation of a point-like bob on a massless string is valid. An example is shown in figure 1.
Figure 1. Dimensionless graph of forces in the motion of a mathematical pendulum, for the starting angles 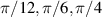 and
and 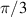 . The graphs were constructed as
. The graphs were constructed as 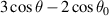 for
for 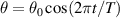 , thus neglecting deviations from the small-angle approximation
, thus neglecting deviations from the small-angle approximation 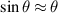 in the equation of motion for the pendulum. The vertical green lines mark times during the first half period where the tension in the string has the size mg. The vertical red lines mark the deviation from mg for the maximum and minimum values of the tension.
in the equation of motion for the pendulum. The vertical green lines mark times during the first half period where the tension in the string has the size mg. The vertical red lines mark the deviation from mg for the maximum and minimum values of the tension.
Download figure:
Standard image High-resolution imageIn the Conclusion section of [1], Coelho states, without motivation, that the curves cross for different starting angles when the tension in the string has the value mg. He also claims that the figure 'clearly shows us that the thread supports more than the weight of the body in the laboratory for about a quarter of the period', which, however, is clearly inconsistent with the graphs in their first figure. The value is closer to 60%, as discussed below.
2.2. When does the tension in the string equal mg?
The period T of a pendulum is found to be essentially independent of the amplitude, as noticed already by Galileo. This 'isochronism' holds only for small angles, where 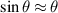 and the period for pendulum of length L is given by
and the period for pendulum of length L is given by 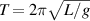 . The time dependence of the pendulum angle can then be written as
. The time dependence of the pendulum angle can then be written as 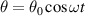 , where
, where 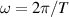 .
.
The part of the period where the tension in the string has the value mg can be obtained by setting 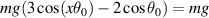 , or:
, or:

The small angle expansion for the cosine function gives
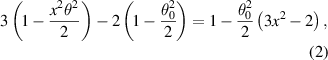
which equals 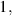 independent of θ0, if
independent of θ0, if 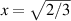 . Using the relation
. Using the relation 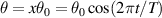 we find that the value of tension in the force should equal mg for a time:
we find that the value of tension in the force should equal mg for a time:
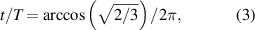
after the pendulum is at the maximum angle. This gives 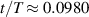 , as marked in figure 1. The tension in the force thus reaches mg after about 10% of the period (or 20% of a half period) which is compatible with the data shown in the first figure in [1]. The same value, mg, for the tension of the string is obtained after 40%, 60% and 90% of the period.
, as marked in figure 1. The tension in the force thus reaches mg after about 10% of the period (or 20% of a half period) which is compatible with the data shown in the first figure in [1]. The same value, mg, for the tension of the string is obtained after 40%, 60% and 90% of the period.
3. Action, reaction, interaction
Most physics educators would probably be unhappy with the free-body diagram suggested in the second figure of [1].
Coelho [1] claims that 'The effective weight of the body and the tension of the thread form an action-reaction pair'. However, this differs from the usual physics education context where action-reaction pairs are the related Newton's third law and involve an interaction. The forces in an action-reaction pair are both of the same type and act on different bodies. The reaction force to the force from the string on the bob is, instead, the force from be bob on the string, which should not be drawn in the same free-body diagram as the forces acting on the bob!
The text claims that 'The centripetal force and the radial component of the weight are balanced by the tension of the thread' (The author probably meant 'centrifugal—centre-fleeing. Students often confuse the terms). After an extended exposure to statics, students may be tempted to include the inertial 'centrifugal force' to obtain a force balance. However, forces in accelerated motion are not balanced. Real forces—unlike inertial forces ('pseudoforces')—are the result of interactions and are independent of the reference system chosen to describe the motion. There is no such thing as 'centrifugal' or 'centripetal' interactions!
Users of inertial forces may invoke the d'Alembert principle from 1743, which can be seen as rewriting Newton's second law as 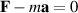 . It is rarely used or even mentioned in modern physics textbooks. This principle:
. It is rarely used or even mentioned in modern physics textbooks. This principle:
'
evolved when understanding and experience with dynamics were extremely limited and was a means of explaining dynamics in terms of the principles of statics, which were more fully understood. This excuse for using an artificial situation to describe the real one is no longer justified, as today a wealth of knowledge and experience with dynamics strongly supports the direct approach of thinking in terms of dynamics rather than statics.' [8] (p 249)
Coelho defines an 'effective weight', R, as what is measured by the force sensor. Other authors (e.g. [9, 10]) talk about an 'operational weight'. Mathematically, this operational weight can be defined by the expression, 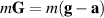 and builds on the equivalence between inertial and gravitational mass, which makes an acceleration feel exactly like a gravitational field in the opposite direction. The 'Equality of Inertial and Gravitational Mass' was discussed in chapter XX of Einstein's book 'Relativity: The Special and General Theory' [11], but the equivalence applies also in Newtonian mechanics!
and builds on the equivalence between inertial and gravitational mass, which makes an acceleration feel exactly like a gravitational field in the opposite direction. The 'Equality of Inertial and Gravitational Mass' was discussed in chapter XX of Einstein's book 'Relativity: The Special and General Theory' [11], but the equivalence applies also in Newtonian mechanics!
4. Conclusion
The pendulum involves many different areas of mechanics, although 'Usually all that is covered is the period of the pendulum for small angles and how it depends on the length of the string and not on the mass of the bob' [3]. (Exceptions include [12].) Pendulum motion is a good example for introducing dimensional analysis and dimensionless quantities. As discussed e.g. by Richards [13], the use of dimensionless quantities to present results leads to more globally applicable relations.
The article by Coelho [1] gives an interesting background to Newton's laws and ways of deriving the equations of motion. However, the treatment of data lacks attention to detail and the presentation of free-body diagrams with its only implicit use of inertial forces can easily lead to increased confusion about topics known to cause difficulties for many students.
Data availability statement
No new data were created or analysed in this study.
Biographies

Ann-Marie Pendrill, Prof. Em. has a research background in computational atomic physics at University of Gothenburg. She was the director of the Swedish National Resource Centre for Physics Education at Lund University 2009–2019. She enjoys using playground swings for physics teaching.