Abstract
When thinking about Olympic winter sports and watching events on television, people mostly focus on events where the chances of success are high for fellow-countrymen. For example, in the Netherlands speed skating is considered the main winter sports event. But with Kimberley Bos there is now also a Dutch medal candidate for the Winter Olympics 2022 in the skeleton discipline. Where speed skaters prepare in summer for the winter season with roller skates, Bos trains on an athletics track with a self-built board on wheels as a replacement for the skeleton. British athletes on the other hand can choose the bobsleigh and skeleton push-start track at the University of Bath for their summer preparation. We prepare for the upcoming Winter Olympics 2022 by taking a physics view on advanced sleighing. We show how school physics helps understanding the motion of athletes in bobsleigh and skeleton and increases respect for the athletes' performance.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
There are three types of winter sleighing sports: bobsleigh, luge, and skeleton. The main goal in these disciplines is to descend a winding track through an ice channel with a sleigh as quickly as possible. In bobsleigh, a team of two or four athletes descends in a steerable sleigh in which the athletes sit behind a cowling; solo bobsleigh takes place in Beijing only in the women's monobob event. In luge, the athlete lays alone or with a partner on the back, feet forward. In skeleton, the athlete lays prone on the sleigh, head forward, as discussed in section 3. Besides the number of athletes (one, two or four) and the posture on the sleigh, there are also major differences in starting technique (run-up/push-off), number of runners (skates) per sleigh (two or four), weight of athletes plus sleigh, dimensions of the sleigh, steering and braking technique, start and finish location on the race track, and the number of runs (two or four) in a competition. In competitions, a fast start is essential for a good run time and during the run the sleigh must be controlled in such way that is safe, but at the same time shortest and fastest route is followed. We apply classical mechanics taught at secondary school to model the start and the entire run in a bobsleigh and skeleton event on a race track. We use computer models to supplement the experiments and questions for students normally found in physics textbooks about the movement of an object on an inclined plane. With these models, we explore which factors influence the run time most, how a push-start track can be best designed, what the ideal route is in a circular bend, and how wide a bend must be in order that  -forces are not too large.
-forces are not too large.
2. A model of downhill sleighing
Simple models already help to come to grips with the most important factors that influence the run time with a bobsleigh or skeleton. Figure 1 shows the force diagram for a two-man bobsleigh with total mass 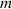 sliding down on an inclined plane with inclination angle
sliding down on an inclined plane with inclination angle  , subject only to gravity force
, subject only to gravity force  (with acceleration of gravity
(with acceleration of gravity  ), the normal force
), the normal force 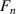 , and the frictional force
, and the frictional force  . The frictional force is the sum of the sliding friction force
. The frictional force is the sum of the sliding friction force  (with the coefficient of friction
(with the coefficient of friction  ) and the drag force
) and the drag force  , with air density
, with air density  , frontal area of the bobsleigh
, frontal area of the bobsleigh  , aerodynamic drag coefficient
, aerodynamic drag coefficient  , and speed
, and speed  ). The normal force is not computed by the usual formula,
). The normal force is not computed by the usual formula, 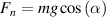 , but via the average vertical acceleration
, but via the average vertical acceleration  on the race track with the many bends. As suggested in figure 1, this give a larger value of
on the race track with the many bends. As suggested in figure 1, this give a larger value of  The value of
The value of  is actually greater than
is actually greater than  for race tracks because of the strong centripetal force acting on the bobsleigh in bends of the track. The equation of motion is:
for race tracks because of the strong centripetal force acting on the bobsleigh in bends of the track. The equation of motion is:
Figure 1. Approximation of a complete run of a race track by sleighing straight downhill. The force diagram involves an average normal force that is, due to the bends in the track, a function of gravitational and centripetal forces.
Download figure:
Standard image High-resolution image

where  and
and  is the weight of the bobsleigh plus the two athletes and optionally extra weight to reach the maximum allowed weight of 390 kg.
is the weight of the bobsleigh plus the two athletes and optionally extra weight to reach the maximum allowed weight of 390 kg.
The maximum speed, which is the terminal speed  for a long inclined plane, can be calculated by setting the total acceleration equal to zero and solving it for
for a long inclined plane, can be calculated by setting the total acceleration equal to zero and solving it for  . Contrary to what many students think, this terminal speed does not depend on the starting speed
. Contrary to what many students think, this terminal speed does not depend on the starting speed  . The formula is:
. The formula is:

It is beyond the secondary school curriculum, but the equation of motion can actually be solved exactly (the above differential equation for velocity  is separable and the resulting integral can be evaluated; the answer can be found in [1]) and there exist explicit formulas for the distance travelled at a certain time, for the speed at a certain distance travelled, and for the run time for a given track length.
is separable and the resulting integral can be evaluated; the answer can be found in [1]) and there exist explicit formulas for the distance travelled at a certain time, for the speed at a certain distance travelled, and for the run time for a given track length.
What is within reach of students is a computer model to simulate the descent of the sleigh with the athletes. This allows exploration of the effect of a change of a parameter value to the run time. Figure 2 shows a screenshot of a Coach 7 model with a simulation of a 4-man bob run on the Whistler Sliding Centre track in Canada, which has a length of 1450.4 m and an average slope of 9%. These track details can be found on the website of the International Bobsleigh and Skeleton Federation (IBSF) [2]. For realistic parametric values, we use data from experimental studies [3]: 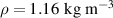 ,
,  ,
,  (2-man bob) and
(2-man bob) and  (4-man bob),
(4-man bob),  ,
,  ,
,  (2-man bob),
(2-man bob),  (4-man bob),
(4-man bob),  (2-woman bob),
(2-woman bob),  (2-man bob),
(2-man bob),  (4-man bob) and
(4-man bob) and  (2-woman bob). The simulation stops as soon as the length of the track is reached and the run time is read out. The run time for the 4-man bob on Whistler's track in the simulation is 51.149 s.
(2-woman bob). The simulation stops as soon as the length of the track is reached and the run time is read out. The run time for the 4-man bob on Whistler's track in the simulation is 51.149 s.
Figure 2. Graphical computer model in Coach of a run with a 4-man bob on the Whistler Sliding Centre track.
Download figure:
Standard image High-resolution imageTo comprehend figure 2 it is useful to know that the modelling tool of Coach [4] is a graphical system dynamics based modelling environment which involves quantities commonly called levels that change in time by inflows and outflows. In our modelling activity we have position and velocity as level variables and acceleration as inflow. Physical flow and information flow determine the system's behaviour over time. Information flow is best understood as an indication of dependencies between variables. These variables can be levels, flows, parameters, and auxiliary variables. These relations are made explicit graphically and very specific via mathematical formulas. The graphical model actually represents a computer model, which provides in many cases an iterative numerical solution of a system of differential equations, e.g. via a Runge–Kutta algorithm.
Computer simulations with systematically changed parameter values reveal the influence of various factors on the run time. Table 1 shows the results when we change one parameter value by 10%. It shows that the starting speed and the coefficient of friction influence the run time most. By using a computer model in this way, students hopefully see the power of modelling: models not only describe the given situation, but also enable predictions and improvements. In this particular case, students can see that modelling suggests that for achieving best results one focuses on reducing the friction of the runners with the ice as much as possible, on training methods that lead to a higher initial velocity, or on selecting athletes that can deliver more power to get the sleigh in motion.
Table 1. Effects of parameter changes on run time (reference value is 51.149 s) for a simulated 4-man bobsleigh race on the Whistler Sliding Centre track.
| Parameter | Reference value | New value | New run time (s) | Difference in time (s, and in %) |
|---|---|---|---|---|

| 0.3 | 0.33 (+10%) | 51.315 | 0.166 (0.32%) |

| 0.4 m2 | 0.44 (+10%) | 51.315 | 0.166 (0.32%) |

| 0.008 | 0.0088 (+10%) | 51.461 | 0.312 (0.61%) |

| 630 kg | 567 kg (−10%) | 51.333 | 0.185 (0.36%) |

| 9 m/s | 8.1 m s−1 (−10%) | 52.050 | 0.901 (1.76%) |
3. Modelling the push-start of bobsleigh and skeleton
Figure 3, taken from Roberts' doctoral thesis [5], shows the four phases of the start in skeleton and the profile of the beginning of the bobsleigh track. The athlete drives off the fixed starting block with maximum force and sprints about 15 m over a slope with a declination of 2%. During this acceleration phase one runner of the sleigh glides through a deep groove in the ice track. After 15 meters, the first time measurement takes place. After this, the athlete loads onto the sleigh with a dive and settles into the race position while the IBSF rules prescribe a gradient of 12% for the next 50 m of the track. At the end of this phase another time measurement takes place. The starting time is defined as the time difference between these two measurements. So the first 15 m of the push start is not part of the run time: time measurement starts only after 15 m and the athlete decides how long to run and when to load onto the sleigh. The same applies to the bobsleigh start except that it involves in most events several athletes, who at some point load into the cockpit of the bobsleigh (see www.youtube.com/watch?v=SFAgC6lHaog).
Figure 3. The vertical profile of a push-start track, showing the four phases of a skeleton start. Reproduced with permission from [5].
Download figure:
Standard image High-resolution imageIn this section we want to model the push-start of bobsleigh and skeleton. To this end we extend a model of sprinting for track and field events. Heck and Ellermeijer [6] have investigated several models for such sprinting events. The simplest model for the start of a sprint, the so-called Keller model, can be adapted for the first 15 m of a skeleton start or bobsleigh start. The Keller model for the start of a sprint on an athletics track lead to the following equation of motion:

with starting speed  , a maximum propulsion force
, a maximum propulsion force  per kg body weight, and a resistance term
per kg body weight, and a resistance term  for certain constant
for certain constant  . For Usain Bolt, the following parameter values can be used
. For Usain Bolt, the following parameter values can be used  and
and  [6]. The only necessary adjustments to the Keller model for the first 15 m of the skeleton or bobsleigh start are the introduction of the inclined plane, the sliding of the sleigh with only sliding friction due to the low speed, and the number of athletes involved in the start (one, two or four), delivering the propulsion force. As an example, we look at the start of a 2-man bobsleigh with two equally heavy athletes. The equation of motion now becomes
[6]. The only necessary adjustments to the Keller model for the first 15 m of the skeleton or bobsleigh start are the introduction of the inclined plane, the sliding of the sleigh with only sliding friction due to the low speed, and the number of athletes involved in the start (one, two or four), delivering the propulsion force. As an example, we look at the start of a 2-man bobsleigh with two equally heavy athletes. The equation of motion now becomes

with total mass 
 , acceleration of gravity
, acceleration of gravity  , inclination angle
, inclination angle  , and coefficient of friction
, and coefficient of friction  .
.
Figure 4 shows a graphical Coach model of this motion equation and a simulation of the bobsleigh start performed by two Usain Bolt-like bobsledders, i.e.  . For the other parameters, the following values have been chosen:
. For the other parameters, the following values have been chosen:  ,
,  , and
, and  . For comparison, the graph windows also show the magenta coloured background graphs of the distance travelled and speed of Usain Bolt's sprint start on an athletics track according to Keller's model with the same parameter choices. Of course, the heavy bobsleigh increases the time needed to sprint 15 m and the speed at that point of the track is less than in sprinting without a sleigh, but the results are still impressive.
. For comparison, the graph windows also show the magenta coloured background graphs of the distance travelled and speed of Usain Bolt's sprint start on an athletics track according to Keller's model with the same parameter choices. Of course, the heavy bobsleigh increases the time needed to sprint 15 m and the speed at that point of the track is less than in sprinting without a sleigh, but the results are still impressive.
Figure 4. Graphical Coach model of the equation of motion for the start of a 2-man bob and a simulation of a start performed by two Usain Bolt-like athletes.
Download figure:
Standard image High-resolution imageThis model of the push-start can of course be supplemented with the previously discussed model for gliding on an inclined plane with a prescribed inclination angle of 6.85°. In a simulation, the speed after 60 m, i.e. the starting speed of the run, can be determined. This starting speed is a good indication of a fast run time in bobsleighing; this is less true for skeleton, which indicates that an error during the run is less easy to correct than in bobsleighing and quickly leads to a slower run time. The steering of the skeleton, especially in bends, is subtle and done by body posture adjustments. For example, if the athlete pushes the skeleton with the left shoulder down, possibly applying less pressure to the sleigh with the right knee, then the left runner will have more friction than the right glider and the skeleton will turn to the left due to the torque of forces on the sleigh.
4. How to design a push-start track?
In the abstract we already mentioned that British athletes can practise their start at the bobsleigh and skeleton push-start track of the University of Bath. Also in the Netherlands there was such a facility in Harderwijk from 2005 until 2018. Figure 5, taken from [7], shows a technical diagram of this push-start track: the upper part is designed according to the IBSF track regulations [8]; the lower part shows an uphill ramp to decelerate the wheeled sleigh and athlete(s) with a slope of 28.7%, which is connected to the downhill ramp via a circular piece of the track.
Figure 5. Technical diagram showing the design of the former Dutch push-start track in Harderwijk. Reproduced with permission from [7].
Download figure:
Standard image High-resolution imageNeglecting friction and knowing the maximum speed  and the height
and the height  when the athlete loads onto the sleigh, we can apply the law of conservation of energy to compute the extra height
when the athlete loads onto the sleigh, we can apply the law of conservation of energy to compute the extra height  reached on the uphill ramp compared to the initial height
reached on the uphill ramp compared to the initial height  . We get the relation
. We get the relation  . Using the following parameter values for the push-start track
. Using the following parameter values for the push-start track

we compute  . The total height reached on the uphill ramp is therefore 10.07 m. With a slope of 28.7%, this means a scaffolding over a distance of 35.1 m. These numbers are also written on the technical diagram (taken from [7]). Actually, a smaller distance suffices when one takes friction forces into account. But for this result one must rely on computer modelling again.
. The total height reached on the uphill ramp is therefore 10.07 m. With a slope of 28.7%, this means a scaffolding over a distance of 35.1 m. These numbers are also written on the technical diagram (taken from [7]). Actually, a smaller distance suffices when one takes friction forces into account. But for this result one must rely on computer modelling again.
The motion from the moment of loading onto/in to the wheeled sleigh until the moment that the sleigh reaches the highest position on the uphill extension ramp (with velocity equal to zero) can be simulated with a computer model that takes into account rolling friction in a rolling motion without slipping and aerodynamic friction. On the straight ramps of the push-start track, the model is more or less the same as in figure 2, but now we can use the usual formula for the normal formal force  (see also [9]). Only in the circular part of the track that connects the two straight ramps we must take the centripetal acceleration into account when determining the normal force acting on the sleigh with the athlete(s) and use instead the formula
(see also [9]). Only in the circular part of the track that connects the two straight ramps we must take the centripetal acceleration into account when determining the normal force acting on the sleigh with the athlete(s) and use instead the formula
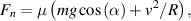
where  is the radius of the circular part of the track with arc length approximately equal to
is the radius of the circular part of the track with arc length approximately equal to  . Figure 6 shows the simulation of the displayed graphical model for parameter values
. Figure 6 shows the simulation of the displayed graphical model for parameter values  ,
,  ,
,  . The simulation stops automatically when the velocity gets close to zero. The graphs beneath the graphical model are the distance-time graph (left) and the velocity-time graph (right).
. The simulation stops automatically when the velocity gets close to zero. The graphs beneath the graphical model are the distance-time graph (left) and the velocity-time graph (right).
Figure 6. Graphical Coach model of the motion of a wheeled sleigh with the athlete on the push-start track from loading the sleigh until reaching the highest position on the uphill extension ramp.
Download figure:
Standard image High-resolution image5. What does physics say about bends?
When a sleigh from a straight part of the ice channel enters a circular bend in the track, it will go up along the side of the ice channel. After all, inertia predicts that, without additional forces, the sleigh will continue to go straight. In order to make the transitions from the straight to the bend and vice versa from the bend to straight less abrupt and to prevent capsizing of the bobsleigh, the entrance and exit of a bend are designed with transition curves. This ensures that the transition to the part in the bend where the ice channel resembles a curved halfpipe (half a cylinder) can go smoothly if no steering errors are made. Figure 7 shows schematically what the force scheme is on the bobsleigh with crew that has speed  on a circular bend with radius
on a circular bend with radius 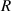 , assuming that there is no downhill slope during the bend. We denote the weight of the bobsleigh with crew as
, assuming that there is no downhill slope during the bend. We denote the weight of the bobsleigh with crew as  and the angle of tilting of the bobsleigh as
and the angle of tilting of the bobsleigh as  .
.
Figure 7. Force diagram for a model of a bobsleigh in a bend and viewed from the front, assuming that there is no downhill slope during the bend.
Download figure:
Standard image High-resolution imageThe sleigh follows an ideal course in the ice channel in a bend when the sum of the gravity force and the normal force is equal to the centripetal force acting on the bobsleigh. Then there is no lateral motion of the sleigh. In mathematical terms, there are two conditions:  and
and  . It follows that
. It follows that  . The normal force
. The normal force  can also be computed with Pythagoras Theorem as
can also be computed with Pythagoras Theorem as
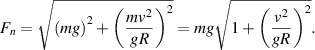
With this formula we can not only compute the ideal course of the bobsleigh with crew in a circular bend, but also determine how wide a circular bend in the race track must be to match the IBSF track rules [9]. The same formula, with tension instead of normal force, is also found with the conical pendulum. One of the track rules is that  -force (i.e. the force experienced by the athletes divided by
-force (i.e. the force experienced by the athletes divided by  ) may not exceed the value 5 and thus
) may not exceed the value 5 and thus  must be true, that is
must be true, that is  . When
. When  , this means that
, this means that  . When the radius of a circular bend is equal to 28 m, then the tilting angle (
. When the radius of a circular bend is equal to 28 m, then the tilting angle ( ) is equal to 78.5°. Capsizing of the bobsleigh is already lurking: a small steering error and fun may be over. According to the IBSF track rules, the maximum permitted
) is equal to 78.5°. Capsizing of the bobsleigh is already lurking: a small steering error and fun may be over. According to the IBSF track rules, the maximum permitted  -force may only last 2 s. A simple calculation leads to the conclusion that for the given speed and radius the bend you can only stay safe in a bend of
-force may only last 2 s. A simple calculation leads to the conclusion that for the given speed and radius the bend you can only stay safe in a bend of  . For a bend of
. For a bend of  passed at a speed of
passed at a speed of  or more the radius of the bend must be greater than 28 m. This is a fine example of how physics helps in designing the bobsleigh track and preventing fatal accidents, as unfortunately happened on the Whistler Sliding Centre track at the 2010 Winter Olympics.
or more the radius of the bend must be greater than 28 m. This is a fine example of how physics helps in designing the bobsleigh track and preventing fatal accidents, as unfortunately happened on the Whistler Sliding Centre track at the 2010 Winter Olympics.
6. Conclusion
To conclude on a positive note: if you have become interested in applications of physics in winter sports, we recommend the readable book of Mark Denny [1]. It also goes into the physics of other winter sports like speed skating, figure skating, ice hockey, curling, skiing, ski jumping and snowboard. We share his reaction, when we watch winter sports events, to wonder about the physics involved. Modelling and in particular computer modelling allow us to come to grips with some of our questions raised. We hope and expect that students can be motivated in this way to learn and appreciate the kind of physics that underlies (winter) sports and to become familiar with the methods applied in biomechanics. Anyway, we believe that it will increase their scientific literacy
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Biographies

André Heck earned MSc degrees in mathematics and chemistry, and a doctoral degree in mathematics and science education. He is senior lecturer at the Faculty of Science of the University of Amsterdam. His research area is the application of ICT in mathematics and science education.

Peter Uylings graduated in physics and mathematics, and he obtained his PhD in theoretical physics. He worked part-time as teacher at a secondary school and as physics teacher educator. After retirement he went back to his first love in physics research and restarted work in the field of atomic physics.







