Abstract
Fermat's principle states that a light ray refracted across different media will traverse the fastest path as the physics for Snell's law. A geometric proof of Fermat's principle will be demonstrated as an intuitive approach to learn high school geometry and physical optics. It will be proved explicitly by showing that all alternative paths need more traversal time to complete their journey.
Export citation and abstract BibTeX RIS
1. Introduction
Refraction describes the bending of the light path as the light passes across the boundary separating two media with different indexes of refraction. Note that the index of refraction of a medium, n ≡ c/v, is defined as the speed of light in vacuum c divided by the speed of light v in the medium.
There are several different approaches to show that light will be refracted according to Snell's law when it passes across the boundary separated by n1-medium and n2-medium [1–9]. Note that we have used the notation ni
-medium to represent medium with refraction index ni
for i
 1, 2. One of the ingenious way to explain the physics of Snell's law is the Fermat's principle. The principle states that light will traverse the fastest path [1]. This principle also has to do with the development of the well-known variational principle. Since then, there has been curios about how light ray 'knows' which path is the least traversal time path. According to Feynman's path integral, each different path has its own probability. The fastest path is nothing but the most probable path with maximum probability and hence served as the physical path. Feynman and Fermat do not, however, explain why this is happening. Hence the underlying physics of Snell's law is not only interesting but also educational for high school students.
1, 2. One of the ingenious way to explain the physics of Snell's law is the Fermat's principle. The principle states that light will traverse the fastest path [1]. This principle also has to do with the development of the well-known variational principle. Since then, there has been curios about how light ray 'knows' which path is the least traversal time path. According to Feynman's path integral, each different path has its own probability. The fastest path is nothing but the most probable path with maximum probability and hence served as the physical path. Feynman and Fermat do not, however, explain why this is happening. Hence the underlying physics of Snell's law is not only interesting but also educational for high school students.
The conventional proof requires, however, the knowledge of differentiation that is not known to most high school students. It is therefore difficult for most high school students to appreciate the underlying nature of the variational principle and how nature works in a simple and elegant manner. Therefore, a more intuitive picture of Fermat's principle should be helpful and heuristic for high school students. Hence we will try to provide a simple geometric proof for this purpose. In particular, we will show that the geometric proof is quite intuitive once appropriate auxiliary constructs such as auxiliary (helping) lines and helping circles are present.
2. Ratio of light speed in a helping triangle ΔAOF
We will start by proving a simple lemma that will be helpful in the geometric proof the Fermat's principle. The straight line L passing through point O in figure 1 represents the interface (boundary) of two different media with refraction indices n1 and n2. Here n1-medium is on the left hand side and n2-medium is on the right hand side of the line L, respectively.
Figure 1. Ratio of light speed is given by  .
.
Download figure:
Standard image High-resolution imageNote that a line segment between points A and O is written as 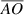 . The length of the line segment
. The length of the line segment  is the distance between points A an O. For simplicity, we will follow the convention that
is the distance between points A an O. For simplicity, we will follow the convention that 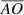 is also used to represent the length of the line segment
is also used to represent the length of the line segment  . Line passing through two different points E, O will be denoted as line
. Line passing through two different points E, O will be denoted as line 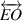 in this paper. In addition, we will also define path S as the line path starting from point A to point O and ending at point B that obeys the Snell's law
in this paper. In addition, we will also define path S as the line path starting from point A to point O and ending at point B that obeys the Snell's law  . Here the angle of incidence
. Here the angle of incidence  and angle of refraction
and angle of refraction 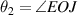 with respect to the normal of the interface L are also shown in figure 1.
with respect to the normal of the interface L are also shown in figure 1.
Note that  according to the definition of index of refraction n = c/v. Here vi
denotes the speed of light in ni
-medium. The vectors
according to the definition of index of refraction n = c/v. Here vi
denotes the speed of light in ni
-medium. The vectors  and
and  denotes the incident light and refracted light, respectively, that obeys the Snell's law. Besides, the auxiliary dotted line
denotes the incident light and refracted light, respectively, that obeys the Snell's law. Besides, the auxiliary dotted line  is the extension of the line
is the extension of the line 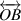 with the property that the length of the line segments are equal:
with the property that the length of the line segments are equal: 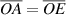 . The auxiliary lines
. The auxiliary lines  and
and  are both perpendicular to the horizontal axis with points F and J both on the horizontal axis. Moreover, the auxiliary line
are both perpendicular to the horizontal axis with points F and J both on the horizontal axis. Moreover, the auxiliary line 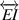 is parallel to horizontal axis and intersects with line
is parallel to horizontal axis and intersects with line  at the point K. As a result, the length of the line segments are also equal:
at the point K. As a result, the length of the line segments are also equal:  .
.
Now we are ready to prove lemma 1 with the help of line segments 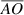 and
and 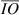 shown in figure 1.
Lemma 1.
shown in figure 1.
Lemma 1.
lemma Ratio of light speed  equals the ratio
equals the ratio  .
.
The proof of lemma 1 goes as follows. As shown in the figure, the length 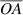 equals the length of the line segment
equals the length of the line segment 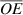 , i.e.
, i.e.  . Hence
. Hence
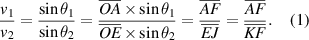
This follows from the facts that 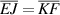 shown above.
shown above.
It can also be shown that:

from the symmetry between the similar triangles ΔFAO and ΔKAI. As a result, we prove the lemma that  .
.
Fermat's principle states that 'the path taken by a ray between two given points is the path that can be traversed in the least time.' It is also known as the principle of least time. The key to a geometric proof is the physical picture described by lemma 1. Indeed, the physical picture of lemma 1 can be stated as: the traversal time for light in n1-medium to propagate the distance 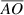 is the same as the traversal time for the light in n2-medium to propagate the distance
is the same as the traversal time for the light in n2-medium to propagate the distance  .
.
3. Fermat principle and path S
Fermat's principle predicts that light ray takes the fastest path when it crosses the interface from n1-medium into n2-medium. And the resulting path obeys Snell's law. Conventional proof of Fermat's principle requires differentiation to derive the fastest path as an extremum of the traversal time required among all different paths. We will present a geometric proof in this section without the help of calculus. First of all, we will try to prove that: traversal time of path S will not be enough for all other paths to propagate from point A in n1-medium to the same endpoint B in n2-medium.
For convenience, we will define path II (A → C → B) as an alternative path following the vectors  and
and  in figure 2. Hence we need to prove that traversal time for path S (A → O → B) will only be enough for path II (A → C → B) to reach the point with a distance
in figure 2. Hence we need to prove that traversal time for path S (A → O → B) will only be enough for path II (A → C → B) to reach the point with a distance  away from its destiny point B.
away from its destiny point B.
Figure 2. Fermat principle for path II and path Snell.
Download figure:
Standard image High-resolution imageAs shown in figure 2, the proof will become more transparent if a helping circle A centered at point A with radius 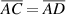 is drawn as an auxiliary construct. Note that only part of the arc is shown for all circles drawn in figure 2. In addition, we can also draw helping circle B centered at point B with radius
is drawn as an auxiliary construct. Note that only part of the arc is shown for all circles drawn in figure 2. In addition, we can also draw helping circle B centered at point B with radius 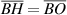 and helping circle
and helping circle  with radius
with radius 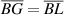 , respectively. Another helping circle O centered at point O with radius
, respectively. Another helping circle O centered at point O with radius  is also drawn in figure 2. Finally, we will draw a helping circle
is also drawn in figure 2. Finally, we will draw a helping circle 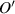 centered at point O with radius
centered at point O with radius  . Note that point L is the point of intersection of the helping circle
. Note that point L is the point of intersection of the helping circle  and the helping line
and the helping line 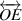 .
.
With the help of helping circle A and helping circle B, it is apparent that (1) path S (A → O → B) propagates an additional distance 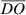 in n1-medium as compared to the path II (A → C → B), and (2) path II (A → C → B) propagates an additional distance
in n1-medium as compared to the path II (A → C → B), and (2) path II (A → C → B) propagates an additional distance  in n2-medium as compared to the path S (A → O → B).
in n2-medium as compared to the path S (A → O → B).
The proof of the principle is then to prove that the traversal time for a light ray to propagate through the distance  in n1-medium is smaller than the traversal time for the light ray to propagate through the distance
in n1-medium is smaller than the traversal time for the light ray to propagate through the distance 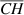 in n2-medium. Another observation is that with the help of lemma 1, it can be shown that: the traversal time Δt for light to propagate from D → O in n1-medium equals the traversal time for the light ray to propagate from G → H in n2-medium.
in n2-medium. Another observation is that with the help of lemma 1, it can be shown that: the traversal time Δt for light to propagate from D → O in n1-medium equals the traversal time for the light ray to propagate from G → H in n2-medium.
This is proved by an observation that, according to lemma 1, when light ray reaches point O from point D in n1-medium, the light ray in n2-medium can only propagate the distance 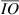 . It is clearly shown in figure 2 that
. It is clearly shown in figure 2 that 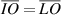 because points I and L are both on the helping circle O. In addition, it is also apparent that
because points I and L are both on the helping circle O. In addition, it is also apparent that  because
because 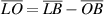 ,
,  . Hence the identity follows from the fact that
. Hence the identity follows from the fact that  and
and 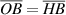 as shown above.
as shown above.
Hence we can make the conclusion that the traversal time Δt for light to propagate from point D to point O in n1-medium is only enough for the light ray to propagate from point G to point H in n2-medium. Consequently, light rays propagate through path II requires more time to go through the distance  as compared to path S.
as compared to path S.
Note that the length of 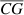 will decrease as point C, the entering point of an alternative path into n2-medium, approaches point O, the prescribed entering point chosen by path S. Similarly, the length of
will decrease as point C, the entering point of an alternative path into n2-medium, approaches point O, the prescribed entering point chosen by path S. Similarly, the length of  will keep increasing after point C crosses the point O. As a result, we proved the Fermat principle that path S is indeed the least-time refracted path from point A in n1-medium to point B in n2-medium.
will keep increasing after point C crosses the point O. As a result, we proved the Fermat principle that path S is indeed the least-time refracted path from point A in n1-medium to point B in n2-medium.
4. Conclusion
There are a number of different approaches to show that light will be refracted according to Snell's law when it passes across the boundary separated by n1-medium and n2-medium. One of the ingenious way to understand the physics of Snell's law is the Fermat's principle. The principle states that light will traverse the fastest path. A simple geometric proof without the help of calculus should be helpful and heuristically for most high school students. Therefore we have successfully provided a more intuitive and geometric picture of Fermat's principle.
Acknowledgments
This paper is supported in part by the Ministry of Science and Technology (MOST) of Taiwan under Contract No. MOST 109-2112-M-009-001.
Data availability statement
No new data were created or analyzed in this study.
Biographies

W F Kao is a theoretical physicist, a professor in the Institute of Physics, National Yang Ming Chiao Tung University. He has a PhD in physics. He enjoys teaching, works on the physics of the early Universe.



