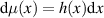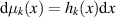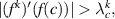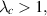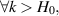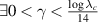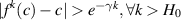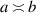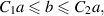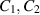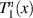Topological synchronisation or a simple attractor?

It is worth noticing that in the next section we will compute the D_q spectrum in a few cases by using the characterization (8) and not the definition (7) in terms of the correlation integral.

We point out, however, that it is in general not enough to have a weak convergence of the measures to ensure the convergence of the D_q spectrum. Suppose for instance that the master system has an absolutely continuous invariant measure $\textrm d\mu(x) = h(x) \textrm dx$ and that, for k close enough to 1, so does the measure of the slave system $\textrm d\mu_k(x) = h_k(x) \textrm dx$. If $h(x)\sim_{x_0} \text{const} |x-x_0|^{\alpha},$ with $-1\lt\alpha\lt0$ as, for instance, it is the case for some quadratic map along the orbit of the critical point, then the local dimension of µ at x₀ is $\alpha +1\lt1$ and it is easily seen (see the detailed computations in the proof of Proposition 5.1) that the D_q spectrum is not constant. Moreover, if we further assume that, for all k < 1, h_k is a piecewise constant function converging in L¹ to h, it is easy to see that the D_q spectrum for µ_k is constant equal to 1 for all k < 1, so that there is no convergence to the spectrum of the master map.

The map f is of class C⁴ and it must be:

• a Collet-Eckmann S-unimodal map verifying $|(f^{\,k})^{^{\prime}}(f(c))|>\lambda_c^k,$ with $\lambda_c>1,$ $\forall k>H_0,$ where H₀ is a constant larger than 1.
• a Benedicks-Carleson map: $\exists 0 \lt \gamma \lt \frac{\log \lambda_c}{14}$ such that $|{\,{f}}^{\,{k}}(c)-c|>e^{-\gamma k}, \forall k>H_0$.

With the symbol $a\asymp b$ we mean that a is bounded from below and above as $C_1a\leqslant b\leqslant C_2a,$ with $C_1, C_2$ two positive constants.

The continuity of T₁ and of T₂ and therefore of ψ is sufficient.

In other words we are supposing that the $\{\omega _{n}\}_{n\geqslant 1}$ are mutually independent. This is of course not true when ω_n is distributed as $T_{1}^{n}(x)$, with x chosen Leb-a.e. but it becomes asymptotically true since T mixes exponentially fast with respect to µ.