Abstract
We generalize leading-order asymptotics of a form of the heat content of a submanifold (van den Berg & Gilkey 2015) to the setting of time-dependent diffusion processes in the limit of vanishing diffusivity. Such diffusion processes arise naturally when advection–diffusion processes are viewed in Lagrangian coordinates. We prove that as diffusivity ɛ goes to zero, the diffusive transport out of a material set S under the time-dependent, mass-preserving advection–diffusion equation with initial condition given by the characteristic function  , is
, is  . The surface measure
. The surface measure 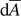 is that of the so-called geometry of mixing, as introduced in (Karrasch & Keller 2020). We apply our result to the characterisation of coherent structures in time-dependent dynamical systems.
is that of the so-called geometry of mixing, as introduced in (Karrasch & Keller 2020). We apply our result to the characterisation of coherent structures in time-dependent dynamical systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr Hinke M Osinga
Footnotes
- 1
- 2
To see this, we first observe that the Markov property of SDEs [1, theorem 9.2.3] yields a time-1 transition function pɛ satisfying
![${p}_{\varepsilon }(x,A)={E}_{x,0}[{\mathbb{1}}_{A}({X}_{1}^{\varepsilon })]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) for
for  and measurable
and measurable  . The definition of the inner product
. The definition of the inner product  yields
yields
- 3
Observe that t ↦ ψ(t, ɛ) is monotone (and hence measurable) and finite (cf [8, chapter 5, corollary 1.2]). By the monotone convergence theorem, if tn → t from below, then ψ(tn , ɛ) → ψ(t, ɛ). In particular, the almost-everywhere (in t) bound from the integral form of Grönwall's lemma (see [6, appendix B.2]) holds everywhere.




![${p}_{\varepsilon }(x,A)={E}_{x,0}[{\mathbb{1}}_{A}({X}_{1}^{\varepsilon })]$](https://content.cld.iop.org/journals/0951-7715/34/10/7303/revision2/nonac18b1ieqn68.gif)