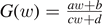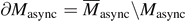Abstract
We establish the existence of chimera states, simultaneously supporting synchronous and asynchronous dynamics, in a network of two symmetrically linked star subnetworks of identical oscillators with shear and Kuramoto–Sakaguchi coupling. We show that the chimera states may be metastable or asymptotically stable. If the intra-star coupling strength is of order ɛ, the chimera states persist on time scales at least of order 1/ɛ in general, and on time-scales at least of order 1/ɛ2 if the intra-star coupling is of Kuramoto–Sakaguchi type. If the intra-star coupling configuration is sparse, the chimeras are asymptotically stable. The analysis relies on a combination of dimensional reduction using a Möbius symmetry group and techniques from averaging theory and normal hyperbolicity.
Export citation and abstract BibTeX RIS
Recommended by Dr Lev Tsimring
Footnotes
- 3
Here
 stands for Landau's symbols for order functions. So,
stands for Landau's symbols for order functions. So,  is: there exists ɛ0 ⩾ 0 and K ⩾ 0 such that 0 ⩽ t ⩽ K|δ(ɛ)| for 0 ⩽ ɛ ⩽ ɛ0.
is: there exists ɛ0 ⩾ 0 and K ⩾ 0 such that 0 ⩽ t ⩽ K|δ(ɛ)| for 0 ⩽ ɛ ⩽ ɛ0. - 4
We select initial conditions satisfying the restrictions for system be in M and we add a small random uniform vector with each coordinate drawn from the interval (0, 0.01).
- 5
For all simulations involving the BA networks, we integrate the equations using an explicit Runge–Kutta method of order four.
- 6
The complete Möbius group consists of all fractional linear transformations
 of the complex plane such that ad − bc ≠ 0 but we only consider the subgroup that preserves the unit circle. As in related literature we refer to this subgroup as the Möbius group.
of the complex plane such that ad − bc ≠ 0 but we only consider the subgroup that preserves the unit circle. As in related literature we refer to this subgroup as the Möbius group. - 7
Here we mean the topological boundary, that is,
 .
.