Normalized solutions for fractional nonlinear scalar field equations via Lagrangian formulation

We study existence of solutions for the fractional problem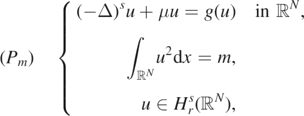$({P}_{m})\quad \left\{\begin{aligned}{(-{\Delta})}^{s}u+\mu u=g(u)& \quad \text{in}\enspace {\mathbb{R}}^{N},\\ {\int }_{{\mathbb{R}}^{N}}{u}^{2}\mathrm{d}x=m,\\ u\in {H}_{r}^{s}({\mathbb{R}}^{N}),\end{aligned}\right.$

where N ⩾ 2, s ∈ (0, 1), m > 0, μ is an unknown Lagrange multiplier and 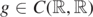$g\in C(\mathbb{R},\mathbb{R})$ satisfies Berestycki–Lions type conditions. Using a Lagrangian formulation of the problem (P_m), we prove the existence of a weak solution with prescribed mass when g has L² subcritical growth. The approach relies on the construction of a minimax structure, by means of a Pohozaev's mountain in a product space and some deformation arguments under a new version of the Palais–Smale condition introduced in Hirata and Tanaka (2019 Adv. Nonlinear Stud.19 263–90); Ikoma and Tanaka (2019 Adv. Differ. Equ.24 609–46). A multiplicity result of infinitely many normalized solutions is also obtained if g is odd.