Method of nose stretching in Newton's problem of minimal resistance

We consider the problem 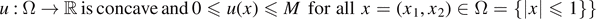$\mathrm{inf}\left\{\int {\int }_{{\Omega}}{\left(1+\vert \nabla u\left({x}_{1},{x}_{2}\right){\vert }^{2}\right)}^{-1}\mathrm{d}{x}_{1}\enspace \mathrm{d}{x}_{2}:\;\text{the}\;\text{function}\right.$ $\left.u:{\Omega}\to \mathbb{R}\;\text{is}\;\text{concave}\;\text{and}\;0{\leqslant}u\left(x\right){\leqslant}M\text{for}\enspace \text{all}\enspace x=\left({x}_{1},{x}_{2}\right)\in {\Omega}=\left\{\vert x\vert {\leqslant}1\right\}\right\}$ (Newton's problem) and its generalizations. In the paper by Brock, Ferone, and Kawohl (1996) it is proved that if a solution u is C² in an open set 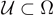$\mathcal{U}\subset {\Omega}$ then  det  D²u = 0 in $\mathcal{U}$. It follows that graph ${\left.\left(u\right)\rfloor \right.}_{\mathcal{U}}$ does not contain extreme points of the subgraph of u. In this paper we prove a somewhat stronger result. Namely, there exists a solution u possessing the following property. 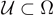If u is C¹ in an open set $\mathcal{U}\subset {\Omega}$ then graph 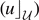$\left({\left.u\rfloor \right.}_{\mathcal{U}}\right)$ does not contain extreme points of the convex body C_u = {(x, z): x ∈ Ω, 0 ⩽ z ⩽ u(x)}. As a consequence, we have 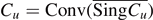${C}_{u}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\left(\bar{\text{Sing}{C}_{u}}\right)$, where SingC_u denotes the set of singular points of ∂C_u. We prove a similar result for a generalization of Newton's problem.