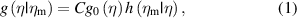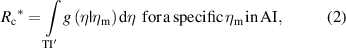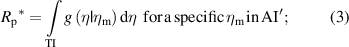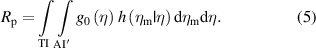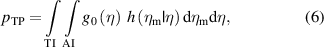Abstract
Probability of conforming items of a finite sample of items is evaluated when conformity assessment (CA) of each item is based on comparison of measured item property values with their acceptance and/or tolerance limits. Two models of probabilities of false decisions on conformity of the whole sample are developed. The first model considers a specific sample of items that already underwent a CA process. A Poisson binomial distribution is applied to calculate the number of the sample items having good (conforming) true property values. The second model, applying a multinomial distribution, treats a generic sample of items potentially drawn from a common population. This model allows evaluating probabilities of false decisions on conformity of the sample items (false positives and negatives), as well as probabilities of correct decisions (true positives and negatives). Applicability of both the models is demonstrated using data of simulated and experimental case studies. These methods extend the existing framework for evaluation of probabilities of true and false decisions in the CA of individual items to the whole sample. The proposed approach provides quality indexes for such a sample, that can be applied in quality inspection and CA of products and objects in industry and trade, environmental monitoring, and other fields. In particular, this approach may be helpful for solving the inspection problem of a production lot, when the minimal number of non-conforming items in a sample for rejecting the whole lot is to be determined.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Indications on how to assess the conformance of a quantitative scalar property of a single item (a product, material, object, etc.) to certain requirements are provided in JCGM 106 [1], based on a Bayesian approach. The conformity assessment (CA) of an item consists in verifying whether a certain property of the item, the measurand [2], lies within a specification/tolerance interval (TI) prescribed in a standard or another documented information source based on a scientific study. The TI limits are considered as limits of true property values. Anyway, the true value of the measurand remains unknown since only an inference on it can be made based on the obtained measured value. Moreover, to know the measured value with perfect accuracy is impossible, since it always has an associated measurement uncertainty [3]. Therefore, CA decisions to accept or reject an item are made using a factory acceptance interval of permissible measured values. Such interval is usually established considering the factory experience (the dataset of previous measured values) and the measurement uncertainty. This is why to know the acceptance interval (AI) with perfect accuracy is also impossible. An AI can be set as different from the TI (larger or smaller), depending on the consumer's or the producer's interests taken into account at the factory. A direct comparison of a measured value with the specification/tolerance limits, taken as true values, is still influenced by the measurement uncertainty associated with the measured value. Thus, the uncertainty principle in CA holds that a decision on conformity or nonconformity (to accept or reject an item) cannot be certain, and risks/probabilities of false/incorrect decisions are generally different from zero [4].
Influence of measurement uncertainty on CA decisions was reported in numerous studies, e.g. [5, 6]. Cost aspects of false conformity decisions and corresponding optimization of AI were also analyzed, for example in the papers [7, 8], but they are out of the scope of the present work.
Specific and global risks of false decisions for both the consumer and the producer at CA of a single item are defined in [1]. A consumer's risk is the probability of accepting the item when it should have been rejected, since the measured value is in the AI, whereas the true value is outside the TI. A producer's risk is the probability of falsely rejecting a conformant item when the measured value is outside the AI, whereas the true value is inside the TI. There is a substantial difference between specific and global risks. When the items under CA come from a common population (e.g. from a stable production process) and are tested according to the required measurement method, the specific risks are related to one specific item whose property has already been measured. On the other hand, the global risks are related to an item that could be potentially picked from that population at random and whose property value would be measured by that measurement method. Hence, a global risk can be seen as the fraction of items that could be erroneously accepted or rejected. In this sense, it characterizes the population of items globally. Note that specific risks are related to conditional probabilities (conditional to the measured value of a specific item property), whereas global risks are based on probabilities of joint events (of the true and the measured value of the property lying within certain intervals at the same time).
The approach, developed for a quantitative scalar property of a single item [1] can be extended for solving wider CA problems. CA of multicomponent materials or objects, for example, is not reducible to a risk calculation made component-by-component, i.e. separately for each component property, such as content or concentration in that material or object. When, for an item, more than one measured property values undergo CA (e.g. in food or environmental analysis), and for each particular property the risks of false decisions are moderate, nonetheless the total risk of a false decision on the material as a whole might still be substantial. Multivariate approaches [9] and evaluation of total risks for multicomponent objects were proposed in that respect [10, 11].
There are series of standards, e.g. ISO 3951 for inspection by variables [12] and ISO 2859 for inspection by attributes [13], aimed to determine appropriate sampling plans for lot-by-lot inspection of quality characteristics. They follow a frequentist, not Bayesian approach. A Bayesian counterpart for this purpose is currently under development [14, 15]. The idea is to consider as the target variable the (true) proportion of nonconforming items in the lot or production from which a sample is taken [16]. Then, an appropriate prior probability density function (PDF) for the target variable (like the beta prior), and a suitable likelihood function for the number of items assessed as nonconforming in the lot can allow calculating specific and global risks, hence broadening the JCGM 106 scope to a lot inspection, with a focus on the proportion of nonconforming items in the lot.
The goal of the work described in the present paper is evaluation of the probabilities of true and false decisions in CA of a finite sample of N items. Such probabilities are different from those calculated separately on each sample item and provide a quality index of the whole sample. The items may be batches or lots of a material, drug, or food, produced at a factory continuously. They may be also goods, e.g. gauge blocks or jewelry. Evaluation of such probabilities is especially important for characterization of a new technological process; when a supplier of raw materials was changed; a key person from the staff and/or a part of the production equipment was replaced; etc. In other words, this is a tool useful for an intermediate analysis of the production success at its installation and any improvement, as well as for monitoring environmental changes.
2. Modeling
The proposed modeling of the probabilities characterizing conformity of a finite sample of items is based on the use of risks of false decisions in CA of each single item according to JCGM 106.
2.1. Risks of false decisions according to JCGM 106—a reminder
The property undergoing CA is the measurand Y, which is regarded as a random variable with possible values η [1]. The information on Y available ahead of the measurement is modeled by a prior PDF g0(η). The measurement process is described by a likelihood function h(ηm|η) of true value η given measured values ηm, which is the PDF of possible ηm values of the measuring system output Ym at the true value Y = η of the measurand. Then, the post-measurement state of knowledge on Y is derived as the posterior PDF g(η|ηm):
where C is a normalizing constant.
The conformance of an η value to a TI is assessed by checking whether a corresponding measured value ηm, inevitably affected by uncertainty, falls into an AI. Risks of false decisions for the consumer (c) and the producer (p) are defined on the base of equation (1) as:
- -specific risks R* (for a specific item)
- -global risks R (for an item chosen at random from the population of such items)
TI' and AI' in the equations above denote the range of true and measured values, respectively, that are complementary to the TI and the AI. Equations (2) and (3) require that the posterior PDF (1) be integrated over the relevant intervals TI' and TI, whereas equations (4) and (5) consist of the double integration of the joint PDF f(η, ηm) = g0(η) h(ηm|η) of variables Y and Ym.
There are also the probabilities p of true positive (TP) and true negative (TN) decisions, respectively:
2.2. Two approaches to model risks in CA of a finite sample of items
The acronyms 'good measured value ηm' (GMV), 'bad measured value ηm' (BMV), 'good true value η' (GTV) and 'bad true value η' (BTV) are used further to indicate occurrences of the events {ηm ∈ AI}, {ηm ∉ AI}, {η ∈ TI} and {η ∉ TI}, respectively.
2.2.1. Specific risks and probabilities of conformity decisions related to a finite sample of items.
The number of GTVs of the sample can generally differ from the number of the observed GMVs because of the measurement uncertainties. Starting from the observation of how many GMVs of the sample are obtained, it is important to make inference on the probable number of GTVs in that sample.
A discrete random variable V can be applied which counts how many items' true property values ηi, i = 1, ..., N, are GTVs, either corresponding to good measured property values GMVs or being hidden behind some BMVs. The variable V is then the sum of N independent Bernoulli random variables, each with its own success probability P(Yi ∈ TI|ηmi ). Such conditional probabilities are, respectively, 1 − Rci *, when ηmi is a GMV, and Rpi *, when ηmi is a BMV, as shown in figure 1.
Figure 1. Modeling scheme for conformity assessment of a finite sample of N items whose measured values are either GMV or BMV, corresponding to either GTV or BTV.
Download figure:
Standard image High-resolution imageThe sum of N independent Bernoulli variables, not necessarily identically distributed, is a Poisson binomial random variable by definition [17]. When all success probabilities are equal, the Poisson binomial distribution reduces to the ordinary binomial distribution.
Without losing generality, considering the K items with GMVs as the first K in the sample (as depicted in figure 1), random variable V would be distributed as V∼ Poisson binomial (1 − Rc1 *, ..., 1 − RcK *, Rp(K+1) *, ..., RpN *) and the probability that at least J true values are actually conforming in the sample would be given by P(V ⩾ J) = 1 − P(V < J). Values of J can vary between 0 and N.
Evaluation of P(V ⩾ J) allows quantifying the reliability of statements such that 'the number of sample items having a true property value within its TI, i.e. actually conforming, is at least J'. In particular, the probability P at J = K refers to the case when the number of the sample items having conforming true values is at least the same as the number of the accepted (good) measured values.
Addressing the inverse task by setting a desired value P(V ⩾ J), one can answer the question 'which is the corresponding maximum number J of the actually conforming sample items?'
2.2.2. Global risks and probabilities of conformity decisions related to a finite sample of items.
Consider a finite sample of N items drawn from a virtual infinite population. CA of the items is characterized by global risks of false decisions by equations (4) and (5) and probabilities of correct decisions by equations (6) and (7). A certain number K1 of items of the sample may have bad true property values, but show GMVs, at the same time. Such events (BTV∩GMV) are classified as false positive. Other K2 items, classified as false negative, have simultaneously good true property values, but BMVs (GTV∩BMV). The remaining are TP K3 items, having both good true and measured property values (GTV∩GMV), and TN K4 items, when both true and measured property values are bad (BTV∩BMV). Probabilities of these events are the elements of the confusion matrix in figure 2.
Figure 2. Confusion matrix of probabilities by equations (4)–(7) of the joint events relevant to true and measured values of each item property.
Download figure:
Standard image High-resolution imageNote that the probabilities in the confusion matrix satisfy the relation Rc + Rp + pTP + pTN = 1, and the four categories of the events (BTV∩GMV, GTV∩BMV, GTV∩GMV, and BTV∩BMV) are disjoint, hence K1 + K2 + K3 + K4 = N. The discrete random variable W able to model such events (at the sampling without replacement and sample size equal to N) has a multinomial probability mass function (PMF) [18], i.e. W ∼ multinomial (N; Rc, Rp, pTP, pTN). Therefore, the probability that a finite sample will consist of N items pertaining to either of the discussed categories is given by P(W= [K1, K2, K3, K4]).
It is obvious that probability P depends on the sample size N and the measurement uncertainty of the test results (that affect the value of its distributional parameters Rc, Rp, pTP, pTN). Evaluation of P may be helpful for setting thresholds for false positives and negatives, as well as for TPs and TNs, in order to satisfy requirements to the properties of a tested product or an environmental compartment, such as ambient air around of a factory/stone quarry.
3. Results and discussion
Both models are applied to the data of simulated and experimental case studies. Functions available in R packages 'PoissonBinomial' [19] and 'stats' [20] have been used for modeling PMFs and cumulative distributions functions of Poisson binomial and multinomial discrete random variables, respectively.
3.1. Examples of CA of a finite sample considering the specific risks
3.1.1. A simulated sample of ten items.
As a simulated example, a sample of N = 10 items (with arbitrary property units) was drawn from a population of the imagined items. The prior distribution g0(η) is assumed to be a standard normal distribution N(0, 1). Also for the likelihood function h(ηm|η) a normal distribution N(η, u) is chosen with measurement uncertainty u equal to 0.1, 0.5 and 1 of the standard deviation of the prior distribution. Consequently, the posterior distribution is also following a normal law with parameters provided in JCGM 106 [1, A.13 and A.14, respectively]. A CA with respect to the upper tolerance limit coinciding with the upper acceptance limit TU = AU = 1, is considered.
The N = 10 simulated measured values are reported in table 1, together with their corresponding posterior probability values P(ηi ⩽ TU|ηi m) = ∫TI g(ηi |ηmi ) dηi , calculated for the different uncertainty values. These probabilities correspond to 1 − Rci * when ηmi is in the AI (ηmi ⩽ AU), and to Rpi * for ηmi outside the AI (ηmi > AU). Only the fifth observation (1.69) is outside AI, that is, larger than AU = 1. Its producer's risk increases for increasing uncertainty, contrary to all the others values 1 − Rci *. This is a known result in the context of risks of false decisions: when the measurement uncertainty increases, also the standard deviation of the resulting posterior PDF increases, leading to a larger producer risk for any out-of-tolerance measured value, and to a larger consumer risk (hence a smaller 1 − Rci *) for any accepted measured value.
Table 1. Simulated sample of N = 10 measured values and corresponding probabilities P(ηi ⩽ TU = 1|ηmi ), rounded to two decimal digits, for increasing uncertainty values, when a standard normal prior and a normal likelihood (with standard deviation equal to measurement uncertainty) model the CA process.
| Probabilities P(ηi ⩽ TU = 1|ηmi ) | ||||
|---|---|---|---|---|
| Uncertainty values u | ||||
| i | Measured values ηmi | 0.1 | 0.5 | 1 |
| 1 | 0.733 | 1.00 | 0.87 | 0.81 |
| 2 | 0.934 | 0.94 | 0.80 | 0.77 |
| 3 | 0.557 | 1.00 | 0.92 | 0.85 |
| 4 | −0.049 | 1.00 | 0.99 | 0.93 |
| 5 | 1.685 | 0.00 | 0.39 | 0.59 |
| 6 | −0.685 | 1.00 | 1.00 | 0.97 |
| 7 | 0.198 | 1.00 | 0.97 | 0.90 |
| 8 | −0.923 | 1.00 | 1.00 | 0.98 |
| 9 | 0.376 | 1.00 | 0.95 | 0.87 |
| 10 | −0.170 | 1.00 | 0.99 | 0.94 |
Hence, nine from ten items of the sample in table 1 are conforming (considering their measured value), and one only the fifth item (i = 5) has a measured value outside the AI. For this item, the probability reported in table 1 is the specific producer's risk R5p*. For the other nine items having GMVs, the probability values in table 1 are complementary to the consumer's risk values, 1 − Rci * (i = 1, ..., 10, i ≠ 5). Both producer's and complementary to consumer's risks are the probabilities of the events when the true value is in its TI, i.e. conforming, while the measured value is outside or inside the AI, respectively. Therefore, the random variable V∼ Poisson binomial(1 − Rc1*, ..., 1 − Rc4*, Rp5*, 1 − Rc6*, ..., 1 − Rc10*) counts how many GTVs can be in such sample.
This is an important information on the quality of the sample. Despite the evidence of only one non-conforming measured value, it would be useful to know which is the probability of the actual number of GTVs in that sample: a number of GTVs smaller than that of the observed GMVs would certainly be not so unlikely. Figure 3 shows the PMF of the variable V when u = 1. Note that this plot, and following ones relevant to PMFs and corresponding cumulative distribution functions of discrete random variables, display functions taking value only at integer numbers on the abscissa. Segments between successive points are displayed just for an easier readability of the plots. The mode of the PMF in figure 3 coincides with the number (9) of GMVs, yet showing a nonnegligible probability P(V = 8) = 28 % of having eight GTVs, for example, and an even more worrying (cumulative) probability P(V < 9) = P(V ⩽ 8) = 42 % of a number of GTVs smaller than that observed in the sample of measured values. On the other side, there is a significant probability (20 %) that the sample contains all good items, i.e. that the number of GTVs is equal to 10.
Figure 3. PMF of Poisson binomial variable V for the simulated case study in table 1 at uncertainty u = 1, i.e. probability values P(V = J), for J = 0, 1, ..., 10.
Download figure:
Standard image High-resolution imageThe cumulative distribution of V can be used to answer the question 'which is the maximum number of GTVs that can be in the sample at a certain level of confidence?' Figure 4 shows probability values P(V ⩾ J) for J = 0, 1, ..., 10 at the three considered measurement uncertainty values. For u = 0.5 and at a probability of at least 95 %, for example, the number of GTVs cannot be larger than 8, since P(V ⩾ 8) = 95 %, whereas P(V ⩾ 9) = 72 %.
Figure 4. Probability values P(V ⩾ J), for J = 0, 1, ..., 10, when V is a Poisson binomial variable for the simulated case study in table 1.
Download figure:
Standard image High-resolution imageR code for the calculations made in the present section (section 3.1.1) and the main (not rounded) results are available as supplementary material to the paper.
Note that the 'dpbinom' function of the R package 'PoissonBinomial' works correctly without any limitation of the sample size. However, the machine time should be considered: a sample size of 108 items requires about 30 s calculation with a Windows 10 Pro PC with a 2.50 GHz processor and 32 GB RAM.
3.1.2. A sample of test results of total suspended particulate matter in ambient airs.
The modeling developed in section 2.2.1 is applied to data of an experimental case study of concentration of total suspended particulate matter (TSPM) in ambient air, monitored around three stone quarries in a period of three consecutive years. Experimental details are available in the report [21], the dataset is kept at Zenodo [22]. In the present work, only N = 220 test results (measured values) related to air around the first quarry were considered.
The regulations of air quality prescribe the upper specification/tolerance limit for TSPM concentration TU = 0.2 mg m−3. The relative measurement uncertainty associated with the TSPM measured values was urel = 7 %. Only seven measured values out of 220 were found to be out of specification. A lognormal prior PDF and a normal likelihood were applied to model, respectively, the distribution of the TSPM true values and the dispersion of the measured values around a true value. Based on these distributional assumptions and the regulation by which AU = TU, specific consumer's and producer's risks were already calculated in [21] for any GMVs (ηm ⩽ 0.2 mg m−3) and BMVs (ηm > 0.2 mg m−3). The detected seven BMVs and corresponding specific risks Rpi * are listed in table 2. The remaining 213 GMVs and the probabilities of GTVs equal to 1 − Rci * were calculated according to [21] and the R codes therein.
Table 2. BMVs and corresponding Rpi * values for the experimental case study of a sample of N = 220 test results (measured values of concentration of TSPM in ambient air) considered as items.
| i | BMVs | Rpi * |
|---|---|---|
| 1 | 0.204 | 0.52 |
| 2 | 0.210 | 0.37 |
| 3 | 0.210 | 0.37 |
| 4 | 0.210 | 0.37 |
| 5 | 0.223 | 0.14 |
| 6 | 0.224 | 0.12 |
| 7 | 0.231 | 0.06 |
The Poisson binomial random variable V, counting how many GTVs could be in that sample, has 220 parameter values: the 7 Rpi * values corresponding to the out-of-specification test results, and the 213 values of 1 − Rci * corresponding to the other GMVs. Figure 5 shows the PMF of V, zoomed on the interval [200, 220].
Figure 5. Zoomed PMF of Poisson binomial variable V for the case study of a sample of N = 220 items.
Download figure:
Standard image High-resolution imageIn case the national regulation required the quarry owner to have less than nine out-of-specification test results in the monitoring period of three years, the owner was fine, since it had only seven such results. However, if the true values of TSPM concentration in air were considered instead of the measured ones, the probability of not conforming items less than 9 would be P(#BTVs < 9) = P(#BTVs ⩽ 8) = P(#GTVs ⩾ 212) = P(V ⩾ 212) = 80 %. Hence, the probability of not being compliant with the regulation may be perceptible, since P(#BTVs ⩾ 9) = 1 − P(#BTVs < 9) = 20 %.
3.2. Examples of CA of a finite sample considering the global risks
3.2.1. Simulated samples of 10 and 100 items.
Global consumer's and producer's risks for the simulated example in section 3.1.1 are calculated according to JCGM 106 [1, A.15 and A.16, respectively], and the probabilities of TPs and TNs are calculated according to equations (6) and (7). Their values, rounded to two decimal digits, are shown in table 3 for the considered uncertainty values.
Table 3. Global consumer's and producer's risks and probabilities of true positives and negatives calculated for the considered uncertainty values, when a normal prior and a normal likelihood are used for modeling the CA of a simulated sample of ten items.
| Uncertainty values u | |||
|---|---|---|---|
| Risks and probabilities | 0.1 | 0.5 | 1 |
| Rc | 0.01 | 0.03 | 0.05 |
| Rp | 0.01 | 0.06 | 0.13 |
| pTP | 0.83 | 0.78 | 0.71 |
| pTN | 0.15 | 0.12 | 0.11 |
For a simulated sample of size N= 10 and another sample of size N = 100 drawn from the same population, three different requirements are set in this study for comparison purposes, from the less to the more stringent:
- (a)K1 ⩽ 10 % N and K2 ⩽ 10 % N and K3 ⩾ 80 % N;
- (b)K1 ⩽ 5 % N and K2 ⩽ 5 % N and K3 ⩾ 80 % N;
- (c)K1 ⩽ 5 % N and K2 ⩽ 5 % N and K3 ⩾ 80 % N and K4 ⩽ 15 % N.
Conditions (a) and (b) imply a small amount of the sample items being false positives and negatives and a reasonably high fraction of TPs (equal to or larger than 80 %). Condition (c) includes also a limit for the fraction of the sample items being TNs (equal to or less than 15 %).
Figures 6 and 7 show the dependence of probabilities P, for random variable W, on measurement uncertainty u, when N= 10 and 100, respectively, at the mentioned conditions (a), (b), and (c), and the distributional parameters of W reported in table 3.
Figure 6. Probabilities P of the multinomial variable W modeling the simulated case study vs. measurement uncertainty u at conditions (a), (b) and (c), when N = 10.
Download figure:
Standard image High-resolution imageFigure 7. Probabilities P of the multinomial variable W modeling the simulated case study vs. measurement uncertainty u at conditions (a), (b) and (c), when N = 100.
Download figure:
Standard image High-resolution imageA larger measurement uncertainty leads to smaller probabilities P at all the considered conditions. In other words, satisfaction of conditions (a), (b) and (c) is less easily achievable for increasing measurement uncertainty associated with the measured property values. At the same measurement uncertainty, satisfaction of more stringent conditions to CA is less probable. However, for larger sample size N the influence of conditions like (a), (b) and (c) on the probabilities P is mitigated.
R code for the calculations made in the present section (section 3.2.1) and the main (not rounded) results are also available as supplementary material to the paper.
Note that the 'rmultinom' function of the R package 'stats' proved to correctly work without any limitation of the size of the sample. The machine time for a sample size of 108 items, coupled with a number of 107 Monte Carlo randomly generated values, required only 3 s calculation on a Windows 10 Pro PC with a 2.50 GHz processor and 32 GB RAM.
3.2.2. A sample of test results of a sausage chemical composition.
The model developed in section 2.2.2 was applied to a dataset of test results of a sausage chemical composition [23]. Contents of four main components of the sausage were measured: fat, protein, moisture, and salt. The contents' specification/tolerance limits were accompanied here by a mass balance constraint: the sum of true values of the component contents was limited by 100 %. Measurement methods and uncertainties, assumptions of appropriate multivariate PDF for the prior distribution and the likelihood function, as well as corresponding total global consumers' risk value Rtotal(c) = 0.006 and corresponding producers' risk value Rtotal(p) = 0.017 related to a sausage item (batch) were reported in [23]. Those total risks were evaluated for CA of chemical composition of the sausage in whole, as a multicomponent product.
Therefore, the following PMF parameters of the multinomial variable W were considered in this example: Rc = 0.006, Rp = 0.017, pTP = 0.970, pTN = 0.007, where pTP and pTN values were hypothesized for illustration purposes, such that Rc + Rp + pTP + pTN = 1. Probabilities P of the variable W for N = 100 batches of sausages of the same kind were evaluated at the following conditions:
- (a)P(K1 ⩽ 5 % N, K2 ⩽ 5 % N, K3 ⩾ 80 % N) = 99.2 %
- (b)P(K1 ⩽ 1 % N, K2 ⩽ 1 % N, K3 ⩾ 90 % N) = 43.0 %
- (c)P(K1 ⩽ 1 % N, K2 ⩽ 1 % N, K3 ⩾ 99 % N, K4 ⩽ 1 % N) = 19.5 %.
The P values above mean that more than 99 % of the produced batches may encompass at maximum five false positives and false negatives, and at least 80 TPs. Again, the percentage of batches with desirable characteristics decreases dramatically for more stringent requirements: less than 20 % of the batches may encompass at maximum 1 false positive, 1 false negative and 1 TN, and at least 99 TPs.
4. Conclusions
Two models for evaluation of probabilities of true and false decisions in CA of a finite sample of items are developed using discrete PMFs. Four categories of the events for each item of the sample are considered: (1) bad true and good measured property values, (2) good true and bad measured values, (3) good true and good measured values, and (4) bad true and bad measured values.
The first model is related to the concept of specific risks of false decisions in CA of an item by JCGM 106. Starting from the number of items of the sample with bad and good measured property values and the values of corresponding specific risks of false decisions, the model estimates the number of the sample items with GTVs.
The second model is related to the concept of global risks in CA of an item by JCGM 106, assigning probabilities of false and true positives and negatives of the sample items.
Both proposed models, therefore, depend on the accuracy in the evaluation of specific and global risks for each item: inaccuracy in those values affects also the results provided by the models. For example, when the hypotheses made for the prior modeling of a production process (prior PDF) and/or those for the measurement/test process (likelihood function) need to be changed or updated, corresponding changes influence also probabilities of true conforming items in any sample drawn from that population.
Evaluation of probabilities of true and false decisions in CA of a finite sample of items extends the framework of the JCGM 106 related to an individual item at a time. The models and their numerical implementations, demonstrated with applications to the simulated and experimental examples, are conceptually and practically easy. They are applicable in industry and trade, as in environmental monitoring and other fields.
Acknowledgments
The authors are grateful to Rainer Göb and Steffen Uhlig for their useful feedback on a preliminary elaboration of the proposed modeling, and to Walter Bich for his valuable viewpoint on a draft version of this manuscript.
The authors wish also to thank two anonymous referees for their precious feedback on the first version of the paper.
Data availability statement
The data that support the findings of this study are openly available. Data, codes and results relevant to section 3.1.1 and 3.2.1 are available as supplementary material to the present publication. Data relevant to section 3.1.2 are openly available at [22], whereas data relevant to section 3.2.2 are enclosed into the supplement data of [23] and are available upon request from the authors.