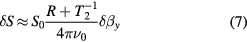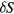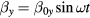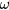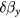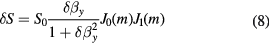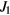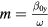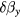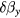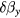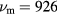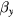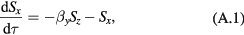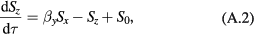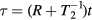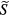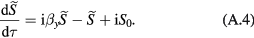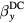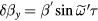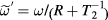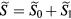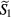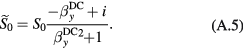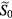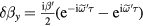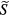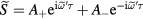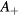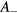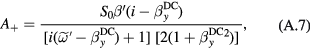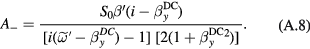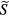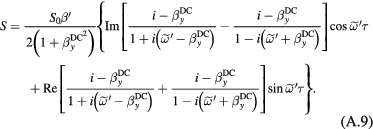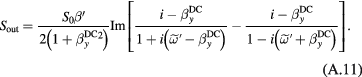Abstract
Optically pumped magnetometers (OPM) can be used in various applications, from magnetoencephalography to magnetic resonance imaging and nuclear quadrupole resonance (NQR). OPMs provide high sensitivity and have the significant advantage of non-cryogenic operation. To date, many magnetometers have been demonstrated with sensitivity close to 1 fT, but most devices are not commercialized. Most recently, QuSpin developed a model of OPM that is low cost, high sensitivity, and convenient for users, which operates in a single-beam configuration. Here we developed a theory of single-beam (or parallel two-beam) magnetometers and showed that it is possible to achieve good sensitivity beyond their usual frequency range by tuning the magnetic field. Experimentally we have tested and optimized a QuSpin OPM for operation in the frequency range from DC to 1.7 kHz, and found that the performance was only slightly inferior despite the expected decrease due to deviation from the spin-exchange relaxation-free regime.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
Optically pumped atomic magnetometers (OPMs) [1, 2] are the most sensitive cryogen-free magnetic-field sensors, which contain a vapor of alkali-metal atoms as the source of optically polarized electron spins by a pump laser beam and measure a weak external magnetic field by detecting the Faraday rotation of linearly polarized light or the absorption of a circularly polarized light with a probe laser beam. The leading high sensitivity magnetic-field sensors had been for a long time superconducting quantum interference device (SQUID) magnetometers; however, recently OPMs have been demonstrated that outperform SQUIDs [2], with the advantage of non-cryogenic operation. OPMs can have potential applications ranging from fundamental science [3, 4] to industry. Recently a commercial 15 fT/Hz1/2 QuSpin prototype OPM was released, which is compact, low cost, and simple to operate. It was targeted for magneto- encephalography (MEG) and magneto-cardiography (MCG) applications, so it was designed to operate in a limited frequency range, below 200 Hz. It has a single-beam configuration, and such a configuration is not optimal for high frequency operation. However, many applications, such as nuclear magnetic resonance (NMR) [5, 6], magnetic resonance imaging (MRI) [7, 8], detection of radio-frequency (RF) signals in general, and even MEG and MCG in some cases, need a much broader frequency range. An example of an MEG application that requires a kHz range is the detection of magnetic field of a single neuron or a small group of neurons. Other examples where the 0–200 Hz range is insufficient are the Earth Field NMR detection at 2 kHz frequency and MagViz NMR applications that need frequency on the order of 1 kHz to extract signals from aluminum cans without raising much ambient noise [9, 10]. In case of MagViz, multiple low-cost reliable sensors such as those produced by QuSpin or by others based on a single-beam design would be of great advantage. Finally, underground or underwater radio-communication also can greatly benefit from expanding the frequency range: while lower frequencies are desirable for larger penetration depth, higher frequencies increase the communication speed.
In this paper, we theoretically studied a single-beam (parallel beam) configuration and found that even though it is not optimal for high-frequency operation, the frequency operation range can be still expanded from a typical 200 Hz of spin-exchange relaxation-free (SERF) magnetometers to much higher frequencies. This theory is validated experimentally using a single-beam QuSpin OPM [11]. By introducing modifications to its initial operation mode and bypassing a built-in low-pass filter we investigate the QuSpin OPM sensitivity in the range of 0–1.7 kHz. The upper bound of the range is chosen by considering the sensitivity of other simpler, already commercially available sensors, such as a search-coil magnetometer [12].
Analysis of the response of the single-beam OPM in a broad frequency range
In an OPM with the single-beam configuration, a single circularly polarized laser beam serves to both pump and probe the electron spins inside the OPM vapor cell. The laser beam passing through the cell is sent to a photodetector with a transimpedance amplifier to retrieve the magnetic signals. Unlike the two-beam configuration, where pump and probe beams are individually adjusted for the best pumping and probing efficiency, there are several compromises: the pump and probe beam intensities, polarizations, and wavelengths in general should be different, while in the single-beam configurations they are the same. The noise from the pump beam is minimized in the two-beam configuration. Further simplification in some implementations (QuSpin OPM in particular) is that no polarizing beam splitter is used to reduce intensity fluctuation noise, but instead a modulating field is applied to suppress the effects of the laser noise. Two cases need to be distinguished when operating an OPM with the single-beam configuration: when the modulation field is applied [13] or when DC offset fields are applied to tilt the spins from the probe-pump direction to enable linear sensitivity to small fields [14]. Note that the OPM signal is proportional to the spin projection along the beam direction whether one circularly polarized laser beam is used to probe and pump the spins (QuSpin implementation),an elliptically polarized single beam [13], or two parallel beams [14] one circularly polarized to pump spins and the other linearly polarized to probe them.
When a magnetic field changes very slowly, the steady-state solution of the Bloch equation, which describes the response of a SERF OPM in the single-beam or parallel beam configuration to the magnetic field, can be used [14], which gives the OPM signal S
where is the equilibrium spin polarization, is the optical pumping rate, is the longitudinal relaxation time, is the normalized magnetic field components, is the gyromagnetic factor relating Larmor frequency to the magnetic field, and is the transverse relaxation time approximately equal to in the SERF regime. We defined the z-axis as the laser beam direction; x- and y-axes are orthogonal to the beam and can be chosen arbitrary owing to the axial symmetry of the problem. When x and z components of the field are zeroed, equation (1) can be simplified:
For two field components applied in the y direction, one large (DC offset field) and one small , which is measured field, the change in the OPM signal due to the small field will be:
This equation can be used to determine the optimal offset field, [14], giving
In case of applying the modulation field at low frequency , , (thus the quasi-static approximation (equation (2)) is still valid) and detection of the first harmonic, the result is quite similar: the optimal value of is approximately 0.71 and
In the dynamic regime for a rapidly varying magnetic field where the quasi-static approximation is not applicable (x and z components of the field are still zeroed for simplicity), the solution of the Bloch equation for a small field should be used, equation (A.9) in the appendix. The response (sensitivity) is maximized near the resonance, which leads to the following simplified equation:
where is a non-small DC offset field and we neglected small terms near resonance: the in-phase counter-rotating term (the second term in equation (A.10)), the total out- of-phase term (equation (A.11)), and unity in the denominator of the factor in front of Re in equation (A.10) (for specific experiments in the following sections this approximation applies at frequencies >200 Hz). Equation (6) can be also rewritten in terms of resonance frequency for the given offset field to show that the OPM response decreases inversely with the resonance frequency:
This behavior differs from that of the steady-state solution, where the OPM signal had some optimal independent of frequency. Also at high enough frequency, the OPM bandwidth implicitly included in the definition of and cancels, so the spin-exchange broadening will not directly affect the signal . In this case, the sensitivity can be increased by increasing the optical depth, to which the OPM signal is proportional in addition to . The optical depth, in turn, is the product of density and path length, so either or both can be used to improve OPM sensitivity.
When the modulation field is applied in the dynamic regime where the is not small, the solution of Bloch equation to a small field gives at the modulation frequency [13]
where and are Bessel functions of the first kind and is the modulation index. The product of the Bessel functions has a maximum of 0.34 at m = 1.08, so for small slow varying fields
This solution assumes slow-varying , which is the case below 200 Hz in SERF OPMs. For fast varying by solving the Bloch equation we find that the OPM signal decreases inversely with the frequency of after it exceeds the OPM 1/T2, similarly to the case with the DC offset field considered earlier here (equations (6) and (7)). Thus for the detection of magnetic signal at high frequency, the modulation method does not improve OPM sensitivity.
Experimental setup
The sensitivity study of a QuSpin OPM (SERF vector type) at high frequency was conducted with the experimental setup shown in figure 1. It consists of a cylindrical ferrite magnetic shield (18 cm diameter and 38 cm height) inserted into a three-layer open mu-metal co-axial cylindrical shield (23 cm inner diameter, 29 cm outer diameter, and 69 cm height), a system of coils inside the ferrite shield to generate fields and gradients, the QuSpin OPM positioned in the center of the coil system, and a computer interface based on National Instrument hardware and LabView software. The coil system serves to fine-tune magnetic fields and gradients to maximize the OPM sensitivity. In addition, a square Helmholtz coil with 2.5 cm side length was mounted near the OPM vapor cell to provide an oscillating calibration field, which frequency can be scanned. The residual noise of the ferrite shield and the coil system is about a few fT in the frequency range we study here, much lower than the intrinsic noise of the OPM.
Figure 1. Experimental setup to investigate the sensitivity of the QuSpin OPM at high frequency range (not scaled).
Download figure:
Standard image High-resolution imageThe OPM sensor head shown in figure 2 is a compact, self-contained unit with all the necessary optical components, including a semiconductor laser for optical pumping, optics for laser beam conditioning, a 3 × 3 × 3 mm 87Rb vapor cell containing about 1 amagat of buffer gases, and silicon photodiodes. The outside dimensions of the head are L 8 cm × W 1.4 cm × H 2.1 cm. The cell was electrically heated to a temperature of 160° C to achieve the optimal Rb vapor density. The sensor head is connected with a 5 m cable to a small electronics controller, which is placed outside the mu-metal shield to minimize any possible magnetic interference. The output from the electronics controller is an analogue voltage proportional to magnetic field of interest. The electronics controller connects to a PC via a USB connector and sensor operation is controlled by a LabView software. The operation of the OPM is fully-automated with a single mouse click.
Figure 2. Schematic showing the basic operation of the QuSpin OPM. (1) 795 nm laser. (2) Collimating lens. (3) Linear polarizer. (4) Circular polarizer. (5) Light beam. (6) Reflecting prisms. (7) Vapor cell. (8) Photodiode. (Coils not shown). The amplitude of the two components of the magnetic field that are perpendicular to the beam can be simultaneously measured via assessment of changes in the light intensity at the photodiode.
Download figure:
Standard image High-resolution imageA 795 nm laser (figure 2) tuned to the D1 transition of 87Rb is used to spin-polarize the rubidium atoms, and the intensity of laser light transmitted through the cell is detected using a photodiode (thus the OPM output is a voltage signal and it can be converted to a magnetic field signal with the known calibration field). The sensor includes three electromagnetic coils which can be used to null any static field components in the cell; subsequent field changes (due to external field) can then be detected via the change in transmitted light intensity which they produce. The transmitted intensity manifests a zero-field resonance, which is a Lorentzian function of the magnetic field components transverse to the laser beam, with a full width half maximum of 30 nT.
Because the spins are initially aligned along the laser beam direction resulting in quadratic response to the applied field (see discussion below), in the conventional QuSpin operation regime a modulation field is applied to increase the magnetometer response to small low-frequency fields. The modulation amplitude and frequency Hz are optimized for the best OPM sensitivity at low frequency. In the presence of the measured magnetic field of some frequency , two sidebands are formed and , and after demodulation and filtering, the signal with the initial frequency of the measured magnetic field is restored. This is done with a QuSpin built-in lock-in amplifier and a low-pass filter. In addition, the unprocessed signal from the photodiode is also available, which is not demodulated or filtered and contains hence two sidebands in the presence of modulation. This signal is not suppressed when the measured field frequency is increased beyond 200 Hz. In the experiment we used this raw signal to maximize the response of the OPM at different frequencies and measured the OPM sensitivity.
Experimental measurements
The theoretical analysis indicates that at low frequency the modulation method is beneficial, especially because it reduces laser technical noise by shifting the measured signal to high frequency, and at high frequency, modulation does not give any benefit and leads to some additional complexities of signal processing. Thus we experimentally investigated the QuSpin OPM sensitivity using the modulation method below 400 Hz and the DC offset field method in the range of 600–1700 Hz. The calibration coil shown in figure 1 generated oscillating magnetic fields with a constant amplitude of 40 pTrms at different frequencies with intervals of 200 Hz, using a function generator. The measurements of the OPM voltage signal were done with a spectrum analyzer and the recorded voltage noise spectra were converted to the OPM field noise using the known calibration field. Within each interval the OPM bias fields were optimized, which was done by optimization of each field component and five first-order gradients in sequence (the coil system shown in figure 1), and iterating the procedure several times to achieve convergence.
The measured response of the OPM (i.e. the measured OPM signal amplitude) to the calibration field at different frequencies is shown in figure 3. The first three data were measured with the modulation field applied, while the rest of the data with the optimized DC offset field applied. It can be seen that at low frequency with the modulation method (equation (9)) the OPM signals are about two times smaller than that when the optimized DC offset field is applied (equation (4)) in quasi-static approximation, in qualitative agreement with the theoretical analysis in the above. Also, the OPM signal when the optimal offset field is applied for the specific frequency decreases as the function of frequency as predicted by equation (7). When the amplitude of the calibration field was increased and decreased by 10 times, the observed OPM signal also 10 times increased and decreased. We confirmed that the results were reproducible.
Figure 3. OPM response to the oscillating calibration field at different frequencies. The three leftmost points are obtained when the modulation field was applied (the normal QuSpin OPM operation) and the rest are obtained when the optimized DC offset field was applied, different for each frequency.
Download figure:
Standard image High-resolution imageFigure 4 indicates the result of the OPM signal trend with frequency and also of the OPM projected sensitivity, which is a combination of all field noise spectra at different frequencies that are converted from all the measured voltage spectra by the constant amplitude of the calibration field, 37.5 pTrms/Hz1/2 at the setting of the spectrum analyzer where the voltage spectra were recorded. We found that the OPM sensitivity (solid red curve) decreases gradually with the frequency. In the range below 1400 Hz, the sensitivity is almost invariant on the order of 20 fT/Hz1/2. From 1400 to 1800 Hz it changes from 20 to 100 fT/Hz1/2. From our theoretical analysis we also expect that the OPM will continue this trend, since the voltage noise is roughly the same at high frequency but the response of the OPM decreases inversely with frequency (see equation (7)). This specific behavior is due to the single-beam (parallel beam) configuration. In other RF OPMs, the sensitivity is expected to be constants in a wide range of frequencies [17].
Figure 4. Field noise measurements of the OPM at different frequencies and projected sensitivity (solid red curve).
Download figure:
Standard image High-resolution imageConclusions and discussions
In summary, we have showed theoretically that the frequency operation range of a single-beam or parallel beam OPM can be expanded well beyond its traditional frequency range. Experimentally, we demonstrated the satisfactory operation of a small-cell commercial QuSpin OPM outside its conventional range of frequency <200 Hz, without applying a modulation field. We found that a comparable sensitivity of 20 fT/Hz1/2 can be reached in a much wider range <1.6 kHz. The OPM sensitivity is limited by the low power of the used laser that was mounted inside the OPM head. Better sensitivity is expected if the OPM is further developed to address some limitations of the current design. Applications in NMR, MRI, nuclear quadrupole resonance (NQR), underground communications, MEG, and MCG can be readily developed.
While OPMs in general can have very high sensitivity in a wide range of frequencies, the specific QuSpin OPM due to its design constrains actually loses sensitivity at frequencies above 1.8 kHz, and becomes less competitive than search coils [12], except for applications in which measurements are performed at small distances, for example, in the detection of NMR signals or neuronal activities. The small size can improve the sensitivity of NMR detection directly in micro-fluidic remote NMR detection mode [15] and in flux transformer-based anatomic MRI detection [8, 16]. From the point of view of minimal detection quantity, the reduction in distance from say 20 mm (a typical stand-off from a SQUID sensor) to 5 mm (current QuSpin stand-off) would increase the signal 64 times! Many other applications would benefit from the simplicity of OPM operation and its small footprint.
With regard to high frequency OPMs, in general, they have already demonstrated impressive sensitivity [17, 18], but they are not commercially available and are not as simple to operate as the QuSpin OPM. The first demonstration of high-sensitivity performance (2 fT/Hz1/2) with the analysis of fundamental noise was done in [17] and subsequent experiments with RF OPMs established the new sensitivity record for atomic magnetometers (0.25 fT/Hz1/2) [18]. In parallel, various novel applications of RF OPMs in NMR [6], MRI [8], and NQR [18] detection were introduced. Some research has been devoted to improving and simplification of the design. For example, it was shown that fT sensitivity can be achieved with a room-temperature paraffin-coated cell, at low temperature of operation and reduced power requirements for lasers [19, 20]. However, the bandwidth was very small, of Hz level, while applications such as MRI or radio communication require much wider bandwidth. Overall, currently there are no commercially available high-sensitive high-frequency OPMs. Because QuSpin has already optimized design and made OPMs commercially available, we anticipate that by extending the operating range of the QuSpin OPM, many applications can be immediately enabled.
Acknowledgments
This work was supported by the US DOE through the LANL/LDRD program.
Appendix.: Analytical solution of the Bloch equation in the dynamic regime
The OPM operating in the SERF regime can be described by the Bloch equation [14].When the z-axis is oriented along the pump-probe beam direction and x and z components of a magnetic field are zerod in terms of the dimensionless field introduced in the text, the Bloch equation can be rewriten as:
where is the dimensionless time. To solve this system of two first order differential equations, the transverse components of the spin can be written in the complex form:
which gives a first order differential equation,
We consider two fields applied in the y direction, one non-small DC offset field and one small rapidly oscillating field at the dimesionless frequency . The two spin componets can be decomposed as , where the first term is given by the zero-order steady-state solution, when is set to zero:
By substituting into equation (A.4), we get
Since the oscillating field can be decomposed into two counter-rotating fields, , the can be expressed as . To determine and , we substitute these equations into equation (A.6), which gives
The OPM signal is proportional to aligned along the probe beam direction, hence the imaginary part of (see equation (A.3)) is the OPM signal :
Thus, the in-phase and out-of-phase components, and , of the OPM signal are given by
When the offset field is tuned to operate OPM at resonance (i.e. ), the change in the OPM signal due to the small oscillating field can be simplified as
Here we neglected the counter-rotating term because of the condition (or ) in the dynamic regime and the out-of-phase component since its contribution at the resonance frequency vanishes. We also neglected unity in the denominator in front of Re.



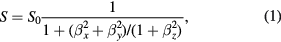




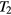
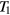

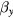
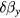
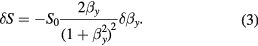
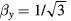



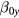

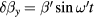

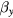

![${{B}_{y}}\left[{{\beta}_{y}}=\frac{\gamma {{B}_{y}}}{\left(R+T_{2}^{-1}\right)}\right]$](https://content.cld.iop.org/journals/0957-0233/28/3/035104/revision2/mstaa58b4ieqn018.gif)