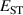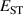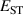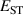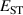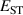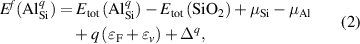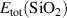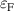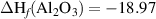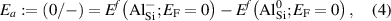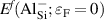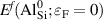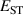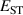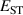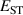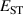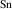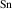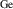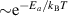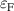Abstract
A major shortcoming of ultrawide-bandgap (UWBG) semiconductors is unipolar doping, in which either n-type or p-type conductivity is typically possible, but not both within the same material. For UWBG oxides, the issue is usually the p-type conductivity, which is inhibited by a strong tendency to form self-trapped holes (small polarons) in the material. Recently, rutile germanium oxide (r-GeO2), with a band gap near 4.7 eV, was identified as a material that might break this paradigm. However, the predicted acceptor ionization energies are still relatively high (∼0.4 eV), limiting p-type conductivity. To assess whether r-GeO2 is an outlier due to its crystal structure, the properties of a set of rutile oxides are calculated and compared. Hybrid density functional calculations indicate that rutile TiO2 and SnO2 strongly trap holes at acceptor impurities, consistent with previous work. Self-trapped holes are found to be unstable in r-SiO2, a metastable polymorph that has a band gap near 8.5 eV. Group-III acceptor ionization energies are also found to be lowest among the rutile oxides and approach those of GaN. Acceptor impurities have sufficiently low formation energies to not be compensated by donors such as oxygen vacancies, at least under O-rich limit conditions. Based on the results, it appears that r-SiO2 has the potential to exhibit the most efficient p-type conductivity when compared to other UWBG oxides.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Ultrawide-bandgap (UWBG) oxide semiconductors are of great interest to power electronics [1]. Among these materials, monoclinic gallium oxide (β-Ga2O3), with a band gap of 4.8 eV, has thus far proven to be the most promising [2]. However, the lack of p-type conductivity in Ga2O3 restricts device designs [3] and impedes its use in optoelectronic applications where both electron and hole conductivity are necessary (for instance, both electron and hole conductivity are necessary for fabricating bipolar junction transistors, high efficiency LEDs and laser diodes [1]). Holes have a tendency for self-trapping and are strongly bound to acceptor impurities [4, 5], making them ineffective dopants. The tendency to form self-trapped holes in Ga2O3 also makes it difficult to use polarization doping approaches that have proven successful in wide bandgap nitrides [6, 7], since any field-ionized holes would subsequently form small hole polarons that are practically immobile at room temperature. In general, strong hole trapping has been predicted in a wide range of UWBG oxides [8, 9], casting doubt on whether any member of this materials class could be made p-type conductive.
Recently, there has been a prediction that rutile germanium oxide (r-GeO2) may exhibit both n-type and p-type conductivity [10]. Unlike other UWBG semiconductors, in which self-trapped holes (STHs) are rather stable [8, 9], STHs in r-GeO2 were predicted to be nearly isoenergetic with free holes. However, the predicted acceptor impurity ionization energies of 0.4 eV in r-GeO2 [9, 10] are higher than in gallium nitride [11], implying reduced doping efficiencies by significantly limiting the concentration of free holes at typically required device operating temperatures.
The results of [10] raise the question of whether r-GeO2 is an outlier or whether there are other UWBG materials in which p-type conductivity could be achieved; or if this feature is related to the rutile crystal structure. We note that STHs were found to be stable in r-TiO2 [8], and other studies have found that hole trapping affects acceptor impurities as well [12–14]. In SnO2, hole localization at acceptor impurities leads to acceptor ionization ranging from 0.6 to 1 eV [15, 16]. However, these trends have not been examined against changing the metal cation in the rutile crystal structure (i.e. from Sn to Ti, Ge and Si).
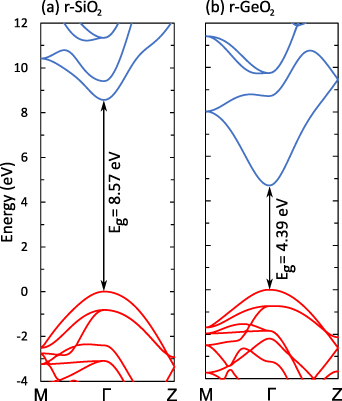
Here the properties of acceptor dopants in the four rutile oxides TiO2, SnO2, GeO2, and SiO2 are calculated and compared using hybrid density functional theory (DFT). In agreement with previous results, high ionization energies are found for acceptors in r-SnO2, though those in r-TiO2 are only ∼0.5 eV, i.e. similar to r-GeO2. Rutile SiO2, also known as stishovite, is identified as an outlier. r-SiO2 has a very similar electronic structure to r-GeO2 (see figure 1), though with a much larger band gap of 8.5 eV. Despite this very large bandgap, our calculations indicate that acceptor ionization energies are rather small in this material. Furthermore, donor defects and impurities have relatively high formation energies, suggesting that hole compensation can be mitigated, enabling efficient p-type conductivity.
Figure 1. Calculated band structures of (a) SiO2 and (b) GeO2 in the rutile crystal structure. The valence-band maximum (VBM) is set to 0 eV, valence bands are in red, and conduction bands are in blue.
Download figure:
Standard image High-resolution image2. Methods
To calculate the properties of acceptors in the rutile oxides we perform hybrid DFT calculations with the projector-augmented wave method [17] as implemented in the VASP code [18]. The HSE hybrid functional [19] with 32% mixing and a 0.2 Å−1 screening parameter are employed for all oxides, as in previous work [9]. This provides an excellent description of the band gaps, in good agreement with experimental data, except in the case of TiO2 where a 25% mixing is required to give a band gap close to the experimental value. Note that adjusting the Hartree–Fock mixing parameter slightly changes the equilibrium lattice parameters of the material, yet the hole-trapping behavior remains unaffected. The structure and electronic properties of SiO2, GeO2, SnO2, and TiO2 in the rutile crystal structure, calculated with HSE, are listed in table 1.
Table 1. Structure and electronic properties of the rutile SiO2, GeO2, SnO2, and TiO2, compared with the experimental data [24, 25]. Band gaps (in eV), average bond lengths (b, in Å), hole effective masses (), hole self-trapping energies (, in eV).
| Bandgap (eV) | a (Å) | c (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Material | calc. | exp. | calc. | exp. | calc. | exp. | b (Å) | (eV) | ||
| SiO2 | 8.57 | 8.74 [20] | 4.16 | 4.18 | 2.66 | 2.67 | 1.77 | 1.084 | 1.589 | — |
| GeO2 | 4.69 | 4.68 [21] | 4.40 | 4.41 | 2.87 | 2.86 | 1.88 | 1.104 | 1.587 | 0.01 |
| TiO2 | 3.14 | 3.03 [22] | 4.60 | 4.59 | 2.95 | 2.96 | 1.96 | 4.982 | 4.317 | 0.19 |
| SnO2 | 3.54 | 3.60 [23] | 4.73 | 4.74 | 3.18 | 3.19 | 2.05 | 1.305 | 1.579 | 0.21 |
The hole self-trapping energy () represents the stability of the localized hole accompanied by a local lattice distortion, and it is defined as:
where is the total energy of a supercell representing the perfect bulk crystal, is the total energy of a supercell with a self-trapped hole, with the hole localized on one oxygen atom,  v is the energy of the valence-band maximum (VBM), and is the q-dependent correction due to the finite size of the supercell [26]. As defined, a positive from equation (1) indicates that the STH is stable relative to a free hole, delocalized and occupying the VBM single-particle state, while a negative indicates that the delocalized hole will be energetically favored.
v is the energy of the valence-band maximum (VBM), and is the q-dependent correction due to the finite size of the supercell [26]. As defined, a positive from equation (1) indicates that the STH is stable relative to a free hole, delocalized and occupying the VBM single-particle state, while a negative indicates that the delocalized hole will be energetically favored.
The calculated for each oxide is also listed in table 1. For rutile TiO2 and SnO2, STHs are energetically stable with near 0.2 eV, in agreement with prior studies [8]. For GeO2, is slightly positive as in previous work [9, 10], indicating that the STH is barely more stable than the delocalized free hole. In contrast, the STH could not be stabilized in r-SiO2 (hence no value is listed for its table 1). We note that the magnitude of energies are inversely proportional to the bond length of the rutile oxide, suggesting that a more compact lattice destabilizes STHs.
Calculations of dopants and defects in this work use 72-atom rutile supercells, and follow the established formalism [27]. Using the aluminum acceptor impurity substituting on the silicon site (Al) in SiO2 as an example, the formation energy of Al in charge state q is given by:
where is the total energy of a supercell containing the Al impurity in charge state q, and is the total energy of perfect SiO bulk using the same supercell. Any electrons added to or removed from the supercell are exchanged with the electron reservoir in the semiconductor host, i.e., the Fermi level (), which is referenced to the VBM (εv ) of SiO . The final term in equation (2), , is the charge-state dependent correction due to the finite size of the supercell [26, 28].
The removed Si atom is placed in a reservoir of energy µSi, referenced to the energy per atom of the Si crystal, and its range is limited by the enthalpy of formation of SiO2 [ eV], so it can take values between 0 eV (the Si-rich limit) and −11.50 eV (the O-rich limit). Analogous considerations apply to µO, which is referenced to the energy per atom of the spin-polarized O2 molecule.
The chemical potential for the impurity is limited by the formation of secondary phases; in the case of Al, µAl is limited by the formation of Al2O3 through the relation:
where ΔHf (Al2O3) is the formation enthalpy of Al2O3 [ eV].
With the formation energy of different charge states for an impurity at a particular site, the thermodynamic transition levels can be determined. In the case of an acceptor such as Al in SiO2, the () level corresponds to the acceptor ionization energy (Ea ) and is given as:
where and represent the formation energies of the − and 0 charge states of Si when the Fermi level is at 0 eV (i.e., at the VBM). Note that these transition levels have no dependence on the atomic chemical potentials.
Band alignments are determined using surface-slab calculations. This approach aligns the VBM with respect to the averaged electrostatic potential within each oxide to the vacuum level, giving a common reference and avoiding lattice mismatch and strain effects [29]. Nonpolar (110) surfaces are used for these calculations, with 16 bilayers of oxide (at least 20 Å of material) together with 25 Å of vacuum. Atoms within 5 Å of the surfaces were permitted to relax, while the interior atoms remained fixed to mimic the bulk material.
3. Results and discussion
3.1. Bulk properties
The calculated electronic and structural properties of the bulk rutile oxides in table 1 show that all band gaps are in good agreement with experimental values and with prior hybrid functional calculations [8, 10]. The hole self-trapping energies in table 1 show that in both r-SnO2 and r-TiO2, STHs are energetically favored, which is consistent with prior calculations [8]. In contrast, E for r-GeO2 is near 0 eV (meaning that the STH is basically isoenergetic with the free hole [9, 10]), while for r-SiO2 the STH cannot be stabilized. The trends in among the rutile oxides cannot fully be explained by comparing their hole effective masses (mh ), which reflect the flatness of the valence band near the VBM. These are also listed in table 1 for various directions. SnO2 and TiO2 have the largest mh , and also the most stable STHs (however, while mh is largest in TiO2, is larger for SnO2). In contrast, mh are smallest for GeO2 and SiO2, in which the STH is least stable.
Another correlation is found between the stability of the STH and the average bond length (b) in the oxide. In figure S1, for each material is plotted as a function of b, illustrating this trend. SnO2, with the largest bond lengths, has the most stable STHs. In contrast, the smallest bond lengths occur in r-SiO2, for which STHs are unstable. This is rationalized by noting that a substantial local lattice distortion, typically an increase of a few percent in the bond lengths, is required to form the STH [8]; in the more compact oxides, such distortions incur larger strain energy penalties, destabilizing the STH.
Despite very different band gaps, r-GeO2 and r-SiO2 exhibit similar electronic properties. In addition to having similar effective masses and STHs being barely stable in the former and unstable in the latter, their bulk band structures are quite similar, as shown in figure 1. Like r-GeO2, r-SiO2 has a dispersive valence and conduction band [10], which distinguishes them from other UWBG oxides [9]. Other than the 4 eV band gap difference, r-SiO2 also features a much smaller distance between the first and second conduction bands compared to r-GeO2.
3.2. Acceptor ionization energies
The focus of this work is on group-III substitutional acceptors, as these provide the lowest ionization energies in r-GeO2 [10]. Note that acceptors substituting on the O site, such as N, are deep in r-SiO2 as they are in r-GeO2 [10]. For N, the states in the gap are derived from the impurity orbitals, and not related to STHs which come from O-related orbitals. Although molybdenum has recently been suggested [30] as a potential p-type dopant, in our calculations we find that Mo acts as a deep donor in GeO2 (see figure S2 in the supplementary material). This behavior is consistent with the predicted deep-donor behavior of Mo in Ga2O3 [31].
It has previously been established that acceptor ionization energies for polaronic acceptors correlate with [9], i.e. in materials for which STHs are stable, acceptor impurities tend to give deep levels in the gap. Polaronic acceptors here refer to those dopants whose deep acceptor behavior is driven by trapped hole polarons [32]. For example, in Ga2O3, with a calculated of 0.53 eV, acceptor ionization energies are in excess of 1 eV [5]. In contrast, for r-GeO2 is near 0 eV, and acceptor ionization energies are near 0.5 eV [10]. Thus, the magnitude can be seen as a proxy for p-type dopability. Following this rationale, TiO2 and SnO2 should have acceptor ionization energies larger than GeO2, while those of SiO2 should be smaller.
The acceptor ionization energies listed in table 2 show that this correlation mostly holds for the rutile oxides. Acceptor ionization energies are largest in SnO2, which is consistent with that oxide having the largest and the longest bond lengths. Acceptor ionization energies are smallest for r-SiO2, which has the smallest and the shortest bond lengths.
Table 2. Calculated acceptor ionization energies (in eV) for group-III impurities substituting on the metal sites in the rutile oxides.
| Material | B | Al | Ga | In |
|---|---|---|---|---|
| SiO2 | 1.01 | 0.22 | 0.24 | 0.33 |
| GeO2 | 1.17 | 0.57 | 0.47 | 0.61 |
| TiO2 | 0.57 | 0.53 | 0.51 | 0.62 |
| SnO2 | 1.67 | 1.06 | 0.91 | 0.87 |
For SnO2, B has the largest ionization energy at 1.67 eV, which we attribute to a large size mismatch between the B and Sn cations. The small size of B impurity allows it to displace into a planar configuration, bonding to three oxygen atoms, allowing a hole to localize on a fourth oxygen neighbor representing a B⋯O broken bond. Similar behavior has been observed for B impurities in AlN [33]. The ionization energies of Al (1.06 eV), Ga (0.91 eV), and In (0.87 eV) in SnO2 are smaller, and are consistent with prior calculations [15, 16].
The results for r-TiO2, which are also consistent with previous calculations [12, 13], show smaller ionization energies, near 0.5 eV. These ionization energies are close to those reported for r-GeO2, despite the STH being more stable in r-TiO2. Note that the differences in ionization energies between acceptors in r-TiO2 and in r-GeO2 are surprisingly small (except for B), considering the large differences in the hole effective masses in the two materials.
For r-GeO2, the ionization energies for group-III acceptors fall within 0.4–0.6 eV (except for B, again due to offsite displacements caused by a large size mismatch). These ionization energies are the lowest among the oxides here, except for r-SiO2 (as will be discussed below), aligning with previous studies [9, 10]. Although these ionization energies are considerably lower than those of other UWBGO and of Ga2O3 in particular, they are likely not low enough to lead to effective p-type conductivity. Only a very small fraction of the impurities will be ionized at room temperature, due to the exponential dependence on the ionization energies, i.e. .
As for the other rutile oxides, B has the highest ionization energy in r-SiO2 (1.01 eV). This is again due to substantial offsite displacements of B from the Si lattice site, due to its small ionic radius. However, the acceptor ionization energies of In, Ga, and Al fall within 0.22–0.33 eV. These acceptor levels are lower than in r-GeO2 by at least 0.2 eV in each case. In fact, these energies are similar to Mg acceptors in gallium nitride [11], which exhibits sufficient p-type conductivity to enable light-emitting solid-state devices.
When holes are trapped at acceptors in r-SiO2, the nearby configuration is quite similar to r-GeO2. Figure 2 shows the isosurfaces of the hole single-particle state associated with the neutral charge state of the aluminum acceptor in GeO2 and SiO2, along with bond lengths near the impurity. Hole localization is limited by the small Si–O bond lengths of this material. This is illustrated by a comparison between the bond lengths around the Al substitutional acceptor in its neutral charge state, shown in figure 2. For r-GeO2, localization of the hole at an oxygen adjacent to Al causes the bond lengths around that oxygen to increase by an average of about 5% of the bulk r-GeO2 bond length. Bond lengths around the oxygen adjacent to Al at which the hole is localized in r-SiO2 increase by a similar amount (an average of 4%). Note that in Mg-doped GaN, the wavefunction of the hole is also quite localized at a nearest-neighbor N atom, yet the ionization energy derived from total energies is relatively small [32].
Figure 2. Isosurfaces of the wavefunction squared of the hole trapped adjacent to (a) Al in r-GeO2 and (b) Al in r-SiO2, along with bond lengths (black, in Å). All isosurfaces are set to 5% of the maximum. Note that for clarity, only one plane of the oxide (perpendicular to the octahedral axis) is shown (plotted using VESTA [34]).
Download figure:
Standard image High-resolution imageFrom these results, we conclude that the distinguishing feature in r-SiO2 is that it destabilizes trapped holes due its compact structure. With the smallest bond length among rutile oxides, hole trapping in r-SiO2 incurs the largest energetic penalty, raising the relative energy of the neutral charge state, with its local lattice distortion, and decreasing the acceptor ionization energy. This behavior can be highlighted by examining quartz SiO2, which has a much less compact crystal structure and in which holes are well known to be self-trapped or trapped at acceptor impurities [35]. Using the same hybrid functional calculations as for r-SiO2, we find that hole localization is far more prevalent in quartz SiO2. For instance, Al in quartz has an ionization energy of 1.33 eV (over 1 eV larger than in r-SiO2).
3.3. Hole compensation in r-SiO2
While group-III acceptors appear to be promising p-type dopants, their potential efficacy could be limited by compensating donor defects. This compensation might come from either native donor defects (such as silicon interstitials or oxygen vacancies) or from group-III interstitial donors (i.e. self compensation). To assess this possibility, the formation energies of these donors have been calculated and compared with the acceptor dopants under different chemical potential conditions.
Plotted in figure 3 are the formation energies of different dopants and defects in r-SiO2 as a function of the Fermi level, for both O-rich (figure 3(a)) and Si-rich (figure 3(b)) conditions. Sii and Ali are found to be highly charged donors; similar behavior was found in [10]. is a deep donor in r-SiO2, and is stable in the 2+ charge state when the Fermi level is near the VBM. When the Fermi level approaches the CBM, becomes negatively charged. Similar behavior has been reported for in other UWBG oxides such as Al2O3 [36].
Figure 3. Formation energies versus Fermi level for acceptor impurities and compensating defects under (a) O-rich and (b) Si-rich conditions for r-SiO2.
Download figure:
Standard image High-resolution imageSi-rich conditions are less conducive to p-type doping: and Sii have far lower formation energies than the group-III acceptor dopants when is within 2 eV of the VBM. Thus, these donor defects are expected to incorporate and strongly compensate holes in any p-type doping attempt with Al or Ga, at least under equilibrium.
In contrast, the O-rich condition shown in figure 3(a) is far more promising for achieving p-type conductivity. Here, Al has a lower formation energy than both and Sii over the entire band gap; Ga is only less stable than when is 0.1 eV from the VBM. Furthermore, although Al can incorporate as an interstitial donor (Al), this species is much higher in energy than the Al acceptor under O-rich conditions. These results indicate that doping r-SiO2 with Al (or Ga) should lead to p-type conductivity, at least under O-rich conditions.
3.4. Limitations of r-SiO2
Although r-SiO2 shows characteristics of a p-type-dopable UWBG oxide, it does exhibit a few major limitations. As mentioned earlier, it is a metastable phase, and α-quartz is lower in energy by 0.24 eV/formula unit. This will likely make material growth difficult. While r-SiO2 has been observed in nature, it is only stable at very high pressures, and no commercializable synthesis is known [37].
Furthermore, like r-GeO2, [21, 38] its minimum-gap transition (VBM–CBM) is calculated here to be dipole-forbidden. Though the transition between the next-lowest CBM and the VBM is bright, this would hamper the potential development of r-SiO2 for light-emitting applications, at least those based on band-to-band transitions.
A final drawback of r-SiO2 is that donor dopants are deep, due to the high-lying position of its CBM. The transition levels of donors in r-SiO2 are compared to those in r-GeO2 in figure 4, plotted together with the band offsets between the two materials. Note that these offsets differ substantially from a prior study [39] which used the mBJ functional that severely underestimates UWBG oxide band gaps. GeO2 does feature shallow donor dopants (such as F and Sb) [10]. In contrast, despite r-SiO2 exhibiting acceptors with low ionization energies, the donor impurities exhibit deep levels, limiting n-type conductivity. This is attributed to the high-lying position of the CBM, which is nearly 4 eV higher on an absolute scale than r-GeO2, as shown in figure 4. In fact, all three donor dopants examined here are negative-U centers [40] and exhibit a deep () level well below the CBM. This behavior, which would make these donors ineffective n-type dopants, arises from the s states of the donor impurities existing well below the high-lying CBM of r-SiO2.
Figure 4. Dopant transition levels in r-SiO2 (left) and r-GeO2 (right). Donor levels (representing the () transition level) are shown in red, while acceptor ionization energies (representing the () transition level) are shown in blue. The dotted line for the Sb, P, and F donors in GeO2 represents an effective-mass-like state (i.e. shallow donors).
Download figure:
Standard image High-resolution imageDespite the shortcomings of r-SiO2, the results here clearly indicate that p-type doping of this UWBG semiconductor might be possible. Wide bandgaps and oxygen-derived valence bands typically result in polaronic acceptor behavior and a lack of p-type doping. Yet, our calculations indicate that a highly compact structure, with short metal-oxygen bond legths, prevents this from occurring in rutile silicon dioxide. This suggests that other highly compact oxides where strain energies prevent STH formation may be a fruitful area of research for finding other p-type possible UWBG materials.
4. Summary and conclusions
Rutile SiO2 is identified here as a p-type dopable UWBG oxide by means of hybrid functional calculations. The rutile oxides SnO2 and TiO2 are susceptible to strong hole localization, but self-trapped holes in r-SiO2 are unstable due to its short Si–O bond lengths. Although holes do localize at acceptor impurities such as aluminum, the resulting ionization energies are much smaller than in the other rutile oxides and are comparable to those in gallium nitride. Moreover, group-III acceptor impurities are predicted to be impervious to compensation by native donor defects or by interstitial donors in O-rich conditions. Despite its promise for p-type conductivity, donor impurities are found to be deep centers, and the minimum-gap transition is optically dark. Nevertheless, these results identify a few important characteristics for the host oxide semiconductor to exhibit p-type conductivity upon doping. These include having short metal-bond lengths and strain energies high enough to destabilize self-trapped holes, in addition to growing or processing the material under appropriate conditions to avoid hole compensation by native defects or impurities.
Acknowledgments
We thank Emmanouil Kioupakis and Sieun Chae for fruitful discussions. This work was supported by the Office of Naval Research through the Naval Research Laboratory's Base Research Program. Computations were performed at the DoD Major Shared Resource Centers at AFRL and the Army ERDC. A J was supported by the ONR Summer Faculty Research Program under grant to ProSource 360 Consulting Services (Grant Number. N000141812728) and managed at NSWC Carderock by the Office of Technology and Innovation.
Data availability statement
The data cannot be made publicly available upon publication due to legal restrictions preventing unrestricted public distribution. The data that support the findings of this study are available upon reasonable request from the authors.

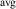
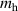
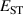
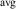

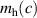
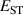
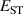
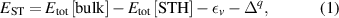
![$E_\textrm{tot}[\textrm{bulk}]$](https://content.cld.iop.org/journals/0953-8984/36/8/085501/revision2/cmad0a11ieqn10.gif)
![$E_\textrm{tot}[\textrm{STH}]$](https://content.cld.iop.org/journals/0953-8984/36/8/085501/revision2/cmad0a11ieqn11.gif)