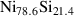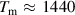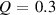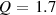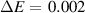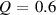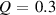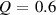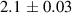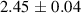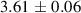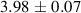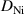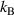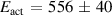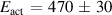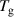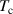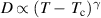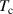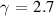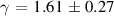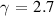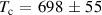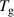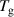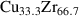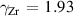Abstract
Nickel self-diffusion was measured for a Ni77Si23 alloy in the liquid state over a temperature range of about 400 K through quasielastic neutron scattering. At the two lowest temperature points the derived diffusion coefficients deviate from a high-temperature Arrhenius-type behaviour and indicate a change in dynamics above the liquidus temperature. A fit with a power-law temperature dependence as predicted by the mode coupling theory for the liquid to glass transition can describe the diffusion coefficients quite well over the whole measured temperature range. The obtained results agree with predictions from a classical molecular dynamics (MD)-simulation, which evidenced an increasing glass forming ability with increasing silicon content. A crossover to a super-Arrhenius behaviour was reported for metallic glass formers above the liquidus temperature and the here investigated NiSi alloy demonstrates the same signature.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
During processing a lot of metallic materials undergo a step in the liquid phase. The particle dynamics of liquid metals and alloys plays a crucial role in technological important processes like solidification and welding [1]. For example, diffusion coefficients are important transport parameters influencing the solidification process at the liquid–solid interface and hence the formation of different phases. From the application point of view NiSi compounds might have potential as high temperature and oxidation resistant alloys. However, if crystallization can be avoided during the freezing process the liquid can be undercooled and the material can be transformed into a glass [2, 3].
The binary solid NiSi compound has a rich phase diagram [4]. Which of the solid phases is chosen upon cooling is influenced by the composition and by process parameters like cooling rate and melt undercooling [5, 6]. MD-simulations showed that the molar volume of a NiSi melt decreases at first with rising Si concentration hinting to strong interactions between the particles [7]. A consequence of this mixing effect might be the tendency for an increased glass forming ability with increasing Si content [7]. For example, the eutectic composition can be undercooled several hundreds K [8]. A neutron diffraction experiment on silicon-rich compositions revealed an influence on the atomic structure due to the ability of silicon to form covalent bonding in the melt [9].
The changes in structure with Si-content will consequently influence the dynamics as well. A powerful experimental method to measure self-diffusion coefficients is quasielastic neutron scattering (QENS) to fill the gap in available experimental diffusion coefficients. In a QENS study on the Ni self-diffusion of silicon-rich compounds a factor 5 faster Ni diffusion was demonstrated in comparison to pure liquid nickel [10, 11]. On the nickel-rich side of the phase diagram surface tension measurements have been performed for a Ni–5 wt% Si alloy over a wide temperature range. The derived viscosity and diffusion coefficients were described by an Arrhenius law across the whole temperature range [12]. Classical MD-simulations have been performed on Ni-rich compositions to elucidate the dynamics of these compounds over a wide temperature range from the hot liquid to the supercooled state [7, 13]. With increasing Si-content up to 25 at% Si the glass forming ability increased. The simulated self-diffusion showed with increasing Si concentration a deviation from the high-temperature Arrhenius-type behaviour for the diffusion coefficients [7]. This deviation in dynamics occurred above the melting point. Similar transitions in the diffusion coefficients above the liquidus temperature from a high-temperature Arrhenius-type behaviour have been reported for known metallic glass formers [14]. However, for monatomic liquid and undercooled Ni an Arrhenius-type behaviour for the diffusion coefficients was reported [11], in agreement with the temperature dependence of the derived D-values for the Ni-rich Ni–5 wt% Si alloy [12]. Yet, the collective dynamics of monatomic liquid metals demonstrates a dynamical crossover within the equilibrium liquid state, suggesting that the correlated particle movements experience a distinct change above the melting point [15–20].
To unveil the changes of the Ni self-diffusion coefficient in a Ni75Si25 composition in the liquid and undercooled state a QENS experiment using a levitation technique was performed [21]. Within four temperature points no evidence for a transition to a non-Arrhenius behaviour could be deduced. Therefore a more detailed study was in order to be performed with a sample covering a much larger beam cross section compared to the levitation experiment to increase the statistics. As a consequence more temperature points can be measured to increase the accuracy for a detection of deviations from an Arrhenius behaviour. Here we present the temperature dependence of the self-diffusion coefficients of Ni77Si23 over a 400 K wide temperature range to elucidate the supposed changes in self-dynamics of Ni above the melting point.
2. Experimental details
Weighted Ni and Si powder of high purity was filled into an annular alumina can to obtain the Ni77Si23 composition. The melting temperature of this alloy is K, deduced from the phase diagram [8]. This value was then later confirmed during the QENS experiment. Reducing the temperature by 20 K below the lowest measured temperature (T = 1453 K) resulted in a spectrum evidencing solid-like features and confirmed the value derived from the phase diagram. The outer diameter of the can is 18 mm and the gap size is 1 mm. The wall thickness is 1.5 mm. The sample was installed into a vacuum high-temperature furnace, which has a temperature limit of 1873 K. The powder sample was heated up to 1773 K for several hours to melt the powder components into an alloy. Measurements were performed with the OSIRIS spectrometer of the ISIS Facility, UK [22, 23]. This indirect time-of-flight spectrometer was operated in the PG002 setting of the analyser bench, which provides an energy resolution of (full width at half maximum (FWHM)) eV. A dynamic range of −0.7 –1.5 meV was covered in a 25 Hz setting with a momentum range from Å−1 to Å−1.
The incoherent neutron cross section of Ni is 5.2b and the coherent one is 13.3b, whereas the incoherent cross section of Si is practically zero and the coherent one is 2.163b [24]. Due to the smallness of the structure factor at small Q-vectors the QENS measurement will be mainly sensitive to the self-dynamics of nickel through the incoherent cross section. Towards larger Q-vectors more and more coherent contributions will add to the signal. The first peak of the total structure factor of liquid Ni is at Å−1 [25, 26] and liquid NiSi shows the first peak at Å−1 [9, 27] for a wide range of compositions. Hence the experiment was covering wave vectors about half of the size where the structure factor maximum lies. Nine temperatures between 1453 K and 1843 K were measured [28]. For each temperature several runs were performed with a total measurement time of between 8 and 12 h per temperature. An empty can measurement was performed at 1673 K in addition.
After conversion from time of flight into energy transfer, a detector efficiency correction and a constant energy binning ( meV) was applied. Then the empty can was subtracted with appropriately calculated absorption factors according to the method of Paalman and Pings [29]. The data reduction and analysis steps were undertaken within the Mantid framework [30]. Finally a multiple scattering correction was performed. To this end the twice scattered neutrons were calculated with a Monte Carlo method [31, 32]. As an appropriate input signal the incoherent Lovesey model [33] was used with parameters resembling liquid Ni. Figure 1 shows a spectrum at Å−1 measured at T = 1535 K. Included is the empty can measurement for the same wave vector and a measurement with a vanadium standard, representing the energy resolution. The vanadium measurement has been peak normalized. Clearly visible is the quasielastic broadening of the line due to the Ni diffusion and also the non-negligible amount of the empty can and furnace contribution which needs to be subtracted properly. The calculated signal from twice scattered neutrons is also depicted. It is only a small contribution of the total signal which is subtracted and will not influence the overall results very much. A small multiple scattering contribution is expected because the incoherent scattering power of the sample is less than 10% and the coherent scattering contribution to multiple scattering is largely reduced due to the smallness of wave vectors covered in the spectrometer setup, which excludes the main structure factor ( Å−1) of the liquid completely.
Figure 1. A spectrum at Å−1 is displayed for a temperature of T = 1535 K. The empty can measurement is included as well as a run with a vanadium standard. The calculated twice scattered neutron signal (triangles) is also included.
Download figure:
Standard image High-resolution imageSelf-diffusion on long time and length scales can be described with the diffusion equation for the density correlation function of a tagged particle. The spatial and time Fourier transformed solution of the diffusion equation is a single Lorentzian with a Q-dependent half width at half maximum [34]:
At small Q vectors, in the hydrodynamic limit (Q → 0), a Lorentzian is the exact lineshape for the diffusion behaviour and . The proportionality constant D is the self-diffusion coefficient for translational diffusion on long distances. To extract the line width a fit with a single Lorentzian function convoluted with the resolution function was applied. Included into the fit was a linear sloping background and an elastic contribution to take care of possible remains of the empty cell subtraction.
3. Results and discussion
Figure 2(a) shows spectra from three temperatures for a Q-vector of Å−1 to demonstrate the increased broadening of the quasielastic line with increasing temperature. The line depicts the quasielastic contribution of the fit with a Lorentzian convoluted with the resolution of the spectrometer. In figure 2(b) three spectra at wave vectors Å−1, Å−1 and Å−1 are shown for T = 1673 K on a logarithmic scale. For visibility purposes the energy binning has been increased in the figure. The wave vector dependent increase in linewidth is a signature for translational diffusion. Included are the total fits as full lines and the quasielastic contribution from the diffusing Ni atoms as dashed lines. The overall good fit and the statistics of the data do not recommend the use of a more sophisticated model.
Figure 2. Plot (a) displays three spectra at T = 1453 K, T = 1583 K and T = 1843 K for Å−1. Plot (b) shows three spectra at three Q-vectors for a temperature of T = 1673 K on a logarithmic scale. The dashed lines depict fits with a Lorentzian curve of the quasielastic contribution convoluted with the resolution function and the full lines are the total fit to the spectra.
Download figure:
Standard image High-resolution imageFrom the Lorentzian fits we obtain the wave vector dependent FWHM which are presented in figure 3 for three temperatures. The expected Q2 behaviour at small Q for translational diffusion is evident, which then seems to change to a saturation value at larger Q-vectors. This could be caused by a change of the self-diffusion process and/or the increasing influence of the coherent scattering. For the determination of diffusion coefficients we restrict the data analysis to Q-vectors smaller than Å−1. In this Q-range we fitted the diffusion law: . In figure 4 the line widths for four temperature are plotted against Q2. The slope of the linear fit represents the diffusion coefficient. The fit results are included as lines.
Figure 3. The deduced FWHM from the Lorentzian fits are plotted for three temperatures over the whole explored wave vector range.
Download figure:
Standard image High-resolution imageFigure 4. The deduced FWHM from the Lorentzian fits are plotted against Q2. The lines depict fits with .
Download figure:
Standard image High-resolution imageThe derived diffusion coefficients from the fits are presented in figure 5 on a logarithmic scale against the inverse temperature. Resulting diffusion coefficients are depicted from fits of the multiple scattering corrected data (stars) and from an analysis of the data without multiple scattering correction (triangle down). The error bars are smaller than the symbol size. In table 1 the diffusion coefficients are listed. Only at the lowest temperatures, when the line width is smallest, the multiple scattering correction imposes a modest change to smaller values. For an Arrhenius-type activated diffusion process a linear dependence would be expected in this representation. The two lowest temperature data points appear to deviate from a linear dependence independent of the analysis method.
Figure 5. Diffusion coefficients from Ni77Si23 with (stars) and without (triangle down) multiple scattering correction are plotted. Included are the previous data from Ni75Si25 [21], for liquid Ni [11] and the values for [10].
Download figure:
Standard image High-resolution imageTable 1. Ni diffusion coefficients.
| Temperature (K) | D (10−5 (cm2 s−1)) |
|---|---|
| 1453 | |
| 1483 | |
| 1533 | |
| 1583 | |
| 1623 | |
| 1673 | |
| 1723 | |
| 1773 | |
| 1843 |
Included are from the previously measured Ni75Si25 alloy (rings) [21]. These values are distinctly smaller with a similar slope in this representation. This difference in diffusion coefficients might be related to the composition change or a systematic error in the temperature calibration of the previous measurement cannot be excluded. Diffusion coefficients for liquid and undercooled pure nickel (full circles) [11] are very similar to the ones in Ni77Si23, except towards the highest temperatures. However, the diffusion coefficients for the silicon rich compound Ni20Si80 (triangle up) on the opposite side of the phase diagram are much larger. Here the Ni atoms can move through the open silicon structure much faster.
The temperature dependence of a diffusion process in a liquid can be described by an Arrhenius law: with the Boltzmann constant, T the temperature and the activation energy for the diffusion process. Experimental diffusion coefficients of many liquid metals and alloys seem to follow an Arrhenius-type equation over a certain temperature range [35, 36]. Different temperature dependence have also been proposed for liquid metals, for example T2 [37]. On a logarithmic scale the Arrhenius behaviour results in a linear dependence and the slope represents the activation energy.
From a fit with an exponential process for temperatures between 1533 K and 1773 K we obtain an activation energy of meV (see figure 6). Note the highest temperature diffusion coefficient seems to deviate to larger values than expected from the Arrhenius-behaviour, an observation already made in the previous study [21]. Whether this deviation is significant and indicates a change in the hot-liquid dynamics needs further investigations, even though this temperature range presents an experimental challenge. For the Ni75Si25 alloy a similar activation energy of meV [21] has been obtained and for liquid and undercooled Ni a meV has been reported [11]. The nickel rich systems show similar diffusion coefficients and activation energies. In contrast, the silicon-rich NiSi melts demonstrate a smaller activation energy of meV [10] and the lower activation energy has been related to the factor 5 faster Ni self-diffusion in these compounds. Moving within the phase diagram the activation energy and also the diffusion coefficients are changing according to the local environment the nickel atoms experience.
Figure 6. The diffusion coefficients are plotted against the inverse temperature on a logarithmic scale. The line depicts a fit with an Arrhenius-type behaviour and the dashed line for a power-law behaviour. Included as a dotted line is also the power-law fit with the parameters from the MD simulation [13].
Download figure:
Standard image High-resolution imageHowever, for the two lowest temperatures the fit with an Arrhenius-type activation process deviates from the measured diffusion coefficients (see figure 6). Below 1533 K the mobility of the Nickel atoms slows down more than expected from the high temperature Arrhenius-type process. Beyond an Arrhenius-type behaviour theoretical models exist for the temperature dependence of the diffusion coefficient, in particular when the supercooled state is approached. Mode coupling theory (MCT) of the liquid to glass transition predicts a slowing down of dynamics on a quantitative basis in a temperature range above the glass transition temperature [38]. Within this theory a critical temperature is central for the dynamics, where structural relaxation becomes frozen. One prediction of the theory is that towards self-diffusion is described by a power-law behaviour in contrast to an Arrhenius-law [39]: . The power-law has been found correct in the vicinity of in metallic glass formers, for example, for the Ni self-diffusion in a four-component metallic glass [40]. For a hard sphere system a was predicted by theory [41]. An exponent has been reported for the Ni-diffusion in a four component metallic glass former [40]. However, for the monatomic liquid Ni an Arrhenius-type behaviour was concluded [11]. In the 5% silicon concentration of the simulated NiSi alloy no departure of an Arrhenius-law was observed in the MD-simulation [7]. For a Ni 5 wt% Si compound derived viscosity diffusion data were presented which were described by an Arrhenius-type behaviour [12]. The monatomic liquid Ni and the high Ni concentration alloys do not indicate a non-Arrhenius behaviour for the diffusion coefficients above the melting point.
However, with increasing Si concentration the dynamics changes. MD-simulations of the Ni75Si25 composition showed that the diffusion coefficients and viscosity can be described by a power-law behaviour up to about twice the glass temperature , far above the melting temperature [13]. For this composition an exponent for the power-law for the Ni self-diffusion coefficient of and a K was reported. A fit with a power-law was applied over the whole temperature range, which is included as a dashed line in figure 6. We obtain K and from the fit. This exponent is in very good agreement with the result from the MD-simulation, however there is a difference in . Both fit parameters are strongly correlated and a fit with a fixed , assuming a similar dynamics as in the glass forming Ni compound [40, 42], would deliver a K and hence in perfect agreement with the MD simulation. There might also be a temperature offset in the simulated alloys, because the simulated melting temperatures for the low Si-content simulated alloys appear to be lower than the values expected from the phase diagram. To demonstrate the difference to the power-law fit with the parameters from the MD-simulation a fit with the respective parameters was added in figure 6 as a dotted line. It indicates that the deviation towards a non-Arrhenius behaviour will occur at lower temperature as expected from a 300 K lower . Besides this difference we emphasize the existence of a departure from an Arrhenius-type behaviour around 100 K above the melting point in this alloy.
MCT is quite successful to describe the dynamics of glass formers in a particular range of temperatures above the glass transition temperature. Within MCT the driving force for the slowing down of dynamics is the particle density and a critical slowing down of the relaxation dynamics occurs for hard sphere systems, independent of the interaction potential [38]. Yet other theoretical frameworks exist to describe the phenomena occurring from a liquid to the glass. A different approach relates the changes within the glass transition to the multidimensional potential energy landscape [3]. The super-Arrhenius increase of viscosity for a fragile glass former can be understood as an increasing activation energy towards the glass transition, which is related to more cooperative particle rearrangements needed with lower temperature [3]. The picture of cooperatively rearranging regions has been invoked to describe the processes towards the glass transition. The mean inherent potential energy of a particle decreases with temperature and hence a larger energy is needed to sample the potential energy landscape with a consequent slowing down of the dynamics. At the same time the number of accessible configurations is reduced and concomitant the configurational entropy, which is related to the number of minima in the potential energy landscape, is reduced. An investigation of the enthalpy–entropy relationship revealed that the onset of non-Arrhenius behaviour of the diffusion coefficient might be related to the sensing of the roughness of the energy landscape of a particle and hence the changes in the configurational entropy plays an important role [43]. A different viewpoint towards the fragility of metallic glass formers relates the repulsive ion–ion interaction with fragility [44]. Here the interaction potential and hence the underlying potential energy landscape is directly connected to the temperature dependence of the viscosity. This model was further on applied to non-metallic fragile liquids [45].
The glass transition temperature is often found to be about 20%–30% lower than [39], therefore we could estimate to find at about 800 K in our composition. With this estimate the observed deviation from the high-temperature Arrhenius-behaviour around 1543 K sets in around at twice . This observation agrees with the changes in the diffusion coefficients reported in the MD-simulation study for the Ni diffusion in Ni75Si25 [13]. A MD-simulation study for the glass forming binary melt demonstrated that both self-diffusion coefficients follow a power-law behaviour with an exponent of and [46], similar to the value obtained here for Ni. In this compound a deviation from the high temperature Arrhenius-type behaviour was also observed about few hundred degrees above the liquidus temperature [47], which points to a more widespread behaviour in alloys susceptible to glass formation. Indeed, further support for a change in dynamics above the melting point was reported in a MD-simulation on the alloy [48]. A transition in transport parameters from Arrhenius to super-Arrhenius behaviour was found at about twice the glass transition temperature. In a QENS and MD-simulation study on a four-component metallic glass former a deviation in the diffusion coefficient from the high-temperature Arrhenius behaviour was observed [49]. It was argued that the onset of correlated dynamics below a crossover temperature at about is responsible for a change in dynamics. It has been reported that 11 metallic glass formers show an Arrhenius crossover at about from a high-temperature Arrhenius behaviour in the diffusion coefficients to a low temperature super-Arrhenius behaviour [14]. This crossover was related to an increased cooperative motion in the liquid below this crossover temperature range. More and more collective particle motions are involved in the single particle mobility towards lower temperature and this interplay between single particle diffusion and collective particle rearrangements emphasize the importance of collective dynamics for the tagged particle dynamics with decreasing temperature. The here investigated Ni77Si23 alloy demonstrates a similar behaviour as the cited metallic glass formers and we argue that the deviation from the Arrhenius behaviour above the melting point is caused by the influence from collective particle dynamics. For metallic glasses the importance of collective atomic motions of string-like entities has been stressed as the fundamental process for diffusion around the glass transition temperature [50].
Consequently the collective dynamics in this NiSi alloy needs to be investigated experimentally to reveal the interrelation of single and collective particle dynamics within the solidification process. In the MD-simulation the viscosity shows a transition to a power-law behaviour at a similar temperature range [13] and an experimental confirmation of this behaviour would be interesting to observe. Furthermore, the dynamics with increasing Si content across the phase diagram should be investigated. At the end point of the phase diagram, pure Si, MD-simulations exhibit a non-Arrhenius behaviour of the diffusion coefficient with a critical temperature from a power-law fit of about 700 K below the melting temperature [51]. Therefore, the evidence for non-Arrhenius behaviour might be not obviously recognizable above the melting point in pure Si. However, with a small concentration of Ni within the silicon environment a separation in dynamics might occur. The measurements of the Ni diffusion coefficient Ni20Si80 show a separation in dynamics between the Ni and Si atoms. However, the does not exhibit a deviation from an Arrhenius-type behaviour in the investigated temperature range [10]. Therefore the non-Arrhenius behaviour above the liquidus temperature might be restricted to the part of the phase diagram around the eutectic composition.
4. Conclusions
A QENS experiment on Ni77Si23 was performed with the aim to reveal the Ni self-diffusion coefficient over a wide range of temperatures. Nine temperatures were measured in a temperature range of about 400 K above the melting point. The experiment sensed the single particle dynamics of Ni and modelling with Fick's diffusion law in the low Q-range revealed the diffusion coefficients. The diffusion coefficients evidence a deviation from a high-temperature Arrhenius-type behaviour about 100 K above the melting point. A power-law dependence, originated from a theory for the liquid to glass transition, is able to describe the diffusion coefficients over the whole temperature range. This result agrees with predictions from a MD-simulation for a Ni75Si25 alloy, even though there is a difference between the derived critical temperatures. An estimate for the glass transition temperature puts the deviation from the Arrhenius behaviour at about . This estimated temperature agrees well with a crossover temperature for a departure to a super-Arrhenius behaviour for the diffusion coefficients seen in bulk metallic glass formers. To support the evidence for non-Arrhenius behaviour above the liquidus temperature in Ni77Si23 measurements of the macroscopic shear viscosity could be performed. This result puts the Ni77Si23 alloy into the same class of materials with bulk metallic glass formers and separates this alloy from the behaviour of monatomic metals. That temperature range indicates a crossover of the alloy melt to a state with reduced mobility with an increased influence of cooperative particle movements. The change in diffusion dynamics can be understood as a signature for the beginning solidification process above the melting point. Further experimental studies to reveal the collective particle dynamics would be desirable to elucidate the interplay of single and collective particle dynamics towards solidification.
Acknowledgments
I am grateful to the superb support of the ISIS furnace group. This work was supported by the Science and Technology Facilities Council, STFC.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.