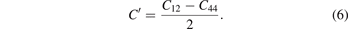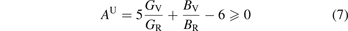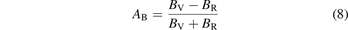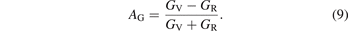Abstract
First-principles calculations are used to study the structure, magnetism and mechanical anisotropy properties of M6C (M = Fe, Mo) carbides. The stability of alloy carbide M6C can be improved when Mo atoms occupy the 48f Wyckoff position. Fe3Mo3C with Mo atoms occupying 48f position and Fe atoms occupying 16d and 32e positions has the best structural stability. The magnetic moment is triggered when the Fe content is approximately 0.5, suggesting that there exists a critical value between the paramagnetic nature and ferromagnetism. Carbides with Fe content above 0.5 have stronger magnetism. Higher Fe content corresponds to the stronger chemical bonding of carbides, resulting in improved elastic properties when Mo atoms are held in 48f position. The special carbides Fe4Mo2C and Fe3Mo3C (Fe at 48f site, Mo at 16d and 32e sites) correspond to the excellent mechanical properties. These results are helpful in providing a theoretical foundation of the possible direction for the advances of the excellent physical properties in Mo-containing steel.
1. Introduction
Alloy carbides have an important effect on the properties of structural steels, such as in the strengthening and ductiling of microalloyed steels [1–3]. Molybdenum carbides can be used to enhance the resistance to static fracture of components steel, for example springs, bolts and power plant structural parts [4–6]. The carbides are mainly composed of M6C, M3C, M23C6 and M7C3 (M = Fe, W or Mo) [7–10]. M6C is an interstitial carbide with a complex densely arranged structure and mainly composed of Fe, Mo and C to form a complex ternary alloy carbide [11]. M6C has a significant impact on the hardness, toughness and elastic anisotropy of steel materials, especially the elastic properties [12–14]. Therefore, it is necessary to find a new carbide with excellent mechanical properties.
M6C can be synthesized by means of experiments [7, 15, 16]. Suchida et al [15] synthesized ternary carbide Fe3M3C (M = Mo, W) from a mixed powder of Fe/M/C = 1:1:1 with the aid of mechanical activation or mechanical synthesis. Hou et al [16] found that the strong magnetic field could promote the precipitation of M6C and further studied the precipitation mechanism of M6C carbides in Fe–C–Mo alloys by using strong magnetic fields. Only Fe3Mo3C and Fe4Mo2C carbides were observed in the precipitated phase of M6C [7]. However, the relationship between the content of Fe and Mo and the magnetic free energy of Fex Mo6−x C (x = 2, 3, 4) carbides is investigated, ignoring the study of the magnetism of all M6C carbides [17]. Oh et al [18] found that M6C carbides provide vacant sites which coalesce along the fracture zone during the creep rupture test, but the relationship between the crystal structure of these carbides and the corresponding mechanical property has not been further analyzed. Hence, it is necessary to predict the stability, magnetic properties and mechanical properties of all types of M6C from theoretical calculations and to seek the relationship between the structure, magnetism and mechanical properties.
In this work, the reaction energy, magnetic moment and elastic constant of all (Fe, Mo)6C carbides are implemented by first-principles calculations. Here, the stability of M6C carbides is explained on the basis of the reaction energy. The calculation of the magnetic moment is used to research the relationship between magnetism and Fe content. The elastic constants are calculated to investigate the brittleness and toughness behaviour of carbides at the atomic level. Based on the relation between the elastic constants, the deformation behaviour of carbides towards different directions can be correspondingly analysed.
2. Calculation methods
A first-principles density functional theory calculation program based on the basis group of pseudopotential plane waves is used for calculation [19, 20]. For exchange-related functions, because the Fe atom contains exist four unpaired electrons in the 3d orbital, the generalized gradient approximation (GGA) is chosen in this work. The GGA based on the Perdew–Burke–Ernzerhof functional is better than the local density approximation at reflecting spin polarization [21–23]. In the calculation of structural optimization and mechanical performance, the k-point grid settings in the Brillouin zone are 4 × 4 × 4 and 3 × 3 × 3, respectively. The cut-off energy of the plane wave base group is 500 eV, and the energy convergence accuracy is 10−5 eV atom−1. In the process of optimizing the crystal structure, the crystal structure is fully relaxed until the stress applied to all atoms is less than 0.02 eV Å−1. In this process, both the unit cell parameters and the atomic positions are optimized. Due to the addition of Fe atoms, the magnetic properties will affect the properties of the carbides, so spin polarization is considered in all calculations. All calculations were performed using the spin polarization method (spin = 2 in the INCAR file). Moreover, the strong magnetism of Fe and the anti-parallel local magnetic moment of Mo provided a basis for setting the initial value of the magnetic moment in the INCAR file (2 and 0 μB for Fe and Mo atoms, respectively). After obtaining a stable unit cell structure, the elastic constants are calculated according to the stress–strain method [24].
3. Results and discussion
3.1. Structure and stability of all kinds of M6C (M = Fe, Mo)
The crystal structure of M6C (M = Fe, Mo) is a face-centered cubic (space group Fd m) structure [25]. Figure 1(a) shows a schematic diagram of the M6C crystal structure. There are 112 atoms in the unit cell, including four nonequivalent sites: (1) 16d (yellow ball, the position occupied by metal atoms), the symmetry is m; (2) 32e (blue ball, the position occupied by metal atoms), the symmetry is 3 m; (3) 48f (red ball, the position occupied by metal atoms), the symmetry is 2 mm; (4) 16c (black ball, position occupied by carbon atoms), the symmetry is m. The structure in figure 1(a) can be split into the two structures in figures 1(b) and 1(c). The structure of figure 1(b) is composed of 16d and 32e metal atoms. Figure 1(b) is mainly composed of eight equivalent clusters (figure 1(d)). The cluster is composed of five tetrahedrons. Metal atoms with 48f site and carbon atoms form the framework of figure 1(c). The structure of figure 1(c) is mainly composed of six equivalent structures (figure 1(e)), one of which is made of six metal atoms and one carbon atom. The carbon atom is in the centre of an octahedron structured by six metal atoms.
Figure 1. (a) Schematic diagram of M6C structure. Yellow (16d), blue (32e), and red (48f) balls represent metal atoms, while black (16c) balls represent carbon atoms. (b) The framework composed of black and blue atoms. (c) Structure consisted by red and carbon atoms. (d) The cluster consists of two types of tetrahedra, one of which consists of one black atom and three blue atoms, and the other of which consists of four blue atoms. (e) The octahedron is made up of six atoms of red sites. The carbon atom inserts inside.
Download figure:
Standard image High-resolution imageTable 1 shows the relationship between the lattice parameters and Fe content after the structure is optimized. The optimized lattice parameters are in good agreement with the previous experimental and theoretical results [11, 26]. With increasing Fe content, the carbide lattice parameters decrease. This is actually because the radius of Mo atoms is larger than that of Fe atoms [27].
Table 1. The lattice parameters, formation and reaction energies of carbide with Fe occupying different Wyckoff positions during the substitution of Mo atoms by Fe. Fe3Mo3C has two different crystal structures. Here, Fe3Mo3C-I represents Fe at 48f site, Fe3Mo3C-II represents Mo at 48f site.
| Phase | Fe occupied sites | a, b, c (Å) | ΔH (eV atom−1) | ΔEr (eV atom−1) |
|---|---|---|---|---|
| Mo6C | — | 11.73 | 0.09 | 0 |
| FeMo5C | 16d | 11.49 | 0.05 | −0.30 |
| Fe2Mo4C | 32e | 11.27 | −0.03 | −0.87 |
| 11.26 [26] | −0.055 [27] | |||
| Fe3Mo3C-I | 48f | 11.27 | 0.46 | 2.56 |
| Fe3Mo3C-II | 16d, 32e | 11.03 | −0.06 | −1.09 |
| 11.077 [11] | −0.093 [27] | |||
| Fe4Mo2C | 16d, 48f | 11.00 | 0.35 | 1.77 |
| Fe5MoC | 32e, 48f | 10.77 | 0.19 | 0.70 |
| Fe6C | 16d, 32e, 48f | 10.48 | 0.15 | 0.37 |
Formation energy is the energy absorbed or released by different kinds of atoms from their elemental state into a compound [28]. It can be defined as E(AB) − E(A) − E(B), where E(A) and E(B) are the energies of the A and B atoms in its elemental state, respectively. E(AB) is the energy of the compound AB. The precipitation of compounds is closely related to the formation energy [27]. The formation enthalpy (ΔH) of each atom in (Fe, Mo)6C is shown in equation (1):
Without considering the zero-point vibration energy, the formation energy (ΔE) is equal to the formation enthalpy (ΔH) at T = 0 K and P = 0 Pa [27]. By analysing the calculated results, it is possible to determine which kind of carbides tend to precipitate [29, 30].
Some researchers [31–33] pointed out that it is inadequate to predict the stability of a compound by forming energy. In this work, the formation energy is calculated for comparison with previous research [21], ensuring the accuracy of our energy calculation. Recently, the reaction energy (ΔEr) was used to predict the stability of a compound [34]. The ΔEr is described in equation (2):
The process of Fe replacing Mo atoms can be understood by the following formula: xFe + Mo6C = Fex Mo6−x C + xMo. The negative reaction energy indicates that the energy of products is lower than the energy of reactants in equation (2). This shows that this substitution is feasible and that the product can exist stably. In contrast, a positive reaction energy indicates that the reaction cannot proceed, and the compound will not exist. It can be seen from table 1 that only FeMo5C, Fe2Mo4C and Fe3Mo3C-II have negative ΔEr, and the reaction energies are −0.299 eV atom−1, −0.871 eV atom−1 and −1.088 eV atom−1, respectively. The reaction energies of these three carbides FeMo5C, Fe2Mo4C and Fe3Mo3C-II are less than 0, and Fe3Mo3C-II has the lowest reaction energy. This result indicates that in M6C, the stability sequence is Fe3Mo3C-II > Fe2Mo4C > FeMo5C and the Fe3Mo3C-II carbide has the best stability.
Moreover, Fe atoms tend to occupy the Wyckoff positions of 16d and 32e (table 1). Due to the substitution of Fe atoms, the structure of the product changed after substitution, which affected the change in the magnetic properties [25]. In the following section, the magnetic evolution with different Fe or Mo atoms is investigated by first-principles calculations.
3.2. Magnetic evolution with the Fe/Mo atom
Figure 3 shows the relationship between the volume evolution of M6C, the magnetic moment and the concentration of Fe atoms. The black fitting dotted line represents the change in the volume (V) with the content of Fe atoms (xFe), and the result of fitting equation is shown in equation (3):
According to the black fitting curve, the volume of the carbide gradually decreases with increasing Fe content. The blue fitting dashed line represents the relationship between the magnetic moment (M) of carbides and the content of Fe atoms, and the result of fitting equation is described in equation (4):
From these two fitting curves, the magnetic moment of the carbides increases with increasing Fe atom content, and the structure of the carbides also changes with increasing Fe atom content. The magnetism of carbide is closely related to structure [17]. Based on figure 1(d), the further research of magnetism and structure is carried out between the 16d and 32e Wyckoff positions. In M6C, there are four carbides with Fe occupying the 32e Wyckoff position: Fe2Mo4C, Fe3Mo3C-II, Fe5MoC and Fe6C. From figure 3, it can be seen that the magnetic moment for Fe2Mo4C and Fe3Mo3C-II are almost 0. The relationship between magnetic moments and bond lengths of Fe5MoC and Fe6C is further studied. The magnetic moments of Fe (32e) of Fe5MoC and Fe6C are 1.45 μB and 2.14 μB, and the bond lengths between 16d and 32e are 2.3639 and 2.2727 , respectively. Consequently, this is consistent with the conclusion that the longer bond length corresponds to smaller magnetic moment [35]. The Wyckoff sites or Fe content may affect the magnetic properties of carbides.
Firstly, the influence of the 48f Wyckoff site or Fe content on the magnetic properties of alloy carbides has been systematically studied. New carbides are formed after Fe gradually replaces Mo, and the magnetic properties will correspondingly change. The calculation results show that Mo6C is nonmagnetic, which is consistent with the results in reference [36]. Fe6C has the strongest magnetic properties. As shown in figure 3 (blue symbols), the concentration of Fe atoms (xFe) below 0.5, the magnetic moment of the carbide is almost 0. It means that xFe has hardly effect on the magnetic moment of the carbide. The magnetic moment of carbides gradually rises when xFe is above 0.5. In other words, the iron content of 0.5 triggers the magnetic transition which indicates that there exists a critical value between the paramagnetic nature and ferromagnetism.
For the explanation of magnetic origin, Fe2Mo4C (concentration of Fe atoms xFe < 0.5), Fe3Mo3C-I (xFe = 0.5), Fe3Mo3C-II (xFe = 0.5) and Fe4Mo2C (xFe > 0.5) four carbides are selected to research physical mechanism about the magnetism near the critical value 0.5. The state densities of these four carbides are shown in the figure 2. It can be seen from the observation figure 2(a) that the density of states of Fe and Mo atoms is mainly contributed by the d orbital, and the density of states of Fe, Mo and C atoms is symmetric up and down, resulting in the alloy carbide Fe2Mo4C (xFe < 0.5) with non-magnetic. Figures 2(a) and (c) that the total state densities of Fe2Mo4C (xFe < 0.5) and Fe3Mo3C-II (xFe = 0.5) are relatively symmetric, which is consistent with the result that the total magnetic moment is close to 0. It can be seen from figures 2(b) and (d) that the total state densities of Fe3Mo3C-I (xFe = 0.5) and Fe4Mo2C (xFe > 0.5) are not symmetrical up and down, indicating that these two carbides are magnetic.
Figure 2. The explanation of the origin of the magnetism according to the partial and total density of states: Fe2Mo4C (xFe < 0.5), Fe3Mo3C-I (xFe = 0.5), Fe3Mo3C-II (xFe = 0.5) and Fe4Mo2C (xFe > 0.5).
Download figure:
Standard image High-resolution imageBesides the above discussion of the symmetry on the magnetism, the co-contribution of the atoms (Fe, Mo and C) has been investigated in the following parts. Firstly the focus was put on the Fe atom. From figure 2(b), the spin-up state density of the d orbital of Fe (48f) atom is significantly higher than that of the spin-down state density for Fe3Mo3C-I (xFe = 0.5). This provides the Fe atom a large positive magnetic moment. By observing the density of states in the d orbital of Fe (48f) atom, it can be found that the density of states of the spin-up in the −4–0 eV energy range is significantly different from that in the spin-down. Therefore, the magnetism of Fe atom is mainly contributed by the energy range of −4–0 eV, and the magnetism of Fe3Mo3C-I (xFe = 0.5) is mainly contributed by the d orbital of Fe atom.
Except for the main influence of the Fe atom, the other atoms (Mo and C) has been discussed as well. In the energy range of −8–4 eV, the spin-up state density of the d orbital of Mo (16d) and Mo (32e) atoms is lower than that of the spin-down state density. The magnetic moment direction of Mo atom is negative. Moreover, the s orbital of C atom is mainly distributed in the −12 to −8 eV region, and the total state density presents asymmetric property. The spin polarization of C atom is mainly due to its s orbital contribution.
Furthermore, the critical content essentially corresponds to the crystal structure when Fe atoms lies at 48f Wyckoff position. It is worthy to point out that the preference of Fe atoms at 48f Wyckoff position has the stronger magnetism than that of Fe atoms at 16d and 32e sites. It coincides with the results that the site preference of the atom significantly influences the magnetism evolution [37, 38].
Moreover, in order to illuminate the relationship between Wyckoff site (or Fe content) and the magnetism, the influence of the nearest neighbor (NN) bond lengths of magnetic carbides on the magnetism has been investigated. It is noted that magnetic carbide refers to the carbide with Mo at 48f position. From figure 3, the NN bond lengths of magnetic carbides are given in table 2, the NN Fe–C bond length slowly decreases with the increasing of Fe content. The shorter Fe–C bond length corresponds to a stronger magnetism, the phenomenon occurs in the special Fe content when xFe > 0.5. This result agrees with the relationship between magnetism and bond length [35]. In essence, the special Fe content represents the different site preference. Therefore, the site preference of the atom plays an important role in the magnetic property of carbide.
Figure 3. Effect of Fe content on the magnetic moment and cell volume of carbide. The calculated magnetic moment (left longitudinal coordinates, blue color) was obtained by means of first-principles calculations, and the volume (V) dependence on the concentration of Fe atoms (xFe) is shown in the right ordinate (black colour). Noting that the triangle represented the references [11, 26] for the various tendencies of V with xFe.
Download figure:
Standard image High-resolution imageTable 2. The NN Fe–C bond length and magnetic moment in magnetic carbides.
| Carbides | NN Fe–C bond length (Å) | Magnetic moment (μB) |
|---|---|---|
| Fe3Mo3C-I | 2.0816 | 4.8945 |
| Fe4Mo2C | 2.0451 | 5.5205 |
| Fe5MoC | 2.0063 | 8.0944 |
| Fe6C | 1.9832 | 11.8803 |
Actually, the site preference determines not only the magnetism but the other properties, such as the electron structure [39], the stability [40], anisotropic elastic moduli, intrinsic hardness and tensile property [3, 34, 41]. In the section 3.3, the anisotropic and mechanical properties has been summarized for understanding the dependence of the anisotropic and mechanical properties on the site preference.
3.3. Mechanical properties
3.3.1. Characteristics for different kinds of moduli in M6C carbides
The elastic constant (Cij ) is an important parameter of crystalline materials [30]. Many mechanical properties are related to elastic constants, such as bulk modulus (B), shear modulus (G), Young's modulus (E), B/G ratio and Poisson's ratio (σ). For the cubic crystal structure, only these three elastic constants (C11, C12, and C44) need to be calculated [42]. Under the conditions of 0 K and 0 Pa, the calculation results of elastic constants of alloy carbide M6C are shown in table 3. The elastic constants of a cubic crystal structure need to meet the Born–Huang's criteria of mechanical stability in equation (5) [42]:
Table 3. Calculation of the elastic constant (GPa) and melting point of (Fe, Mo)6C.
| Phase | C11 | C12 | C44 | C11 − C12 | C11 + 2C12 | Melting point (K) |
| Mo6C | 420.444 | 195.675 | 95.172 | 224.769 | 811.794 | 3037.824 |
| 401.5 [27] | 173.8 [27] | 92.5 [27] | ||||
| FeMo5C | 431.300 | 210.490 | 88.954 | 220.81 | 852.28 | 3101.983 |
| 411.3 [27] | 194.6 [27] | 92.2 [27] | ||||
| Fe2Mo4C | 459.743 | 203.964 | 118.864 | 255.779 | 867.671 | 3270.081 |
| 438.6 [27] | 189.3 [27] | 126.2 [27] | ||||
| Fe3Mo3C-I | 213.412 | 152.543 | 55.459 | 60.869 | 518.498 | 1814.265 |
| 239.2 [27] | 183.4 [27] | 61.9 [27] | ||||
| Fe3Mo3C-II | 478.923 | 202.330 | 141.596 | 276.593 | 883.583 | 3383.435 |
| 478.2 [27] | 177.8 [27] | 130.2 [27] | ||||
| Fe4Mo2C | 243.089 | 182.447 | 35.681 | 60.642 | 607.983 | 1989.656 |
| 317.8 [27] | 239.5 [27] | 8.9 [27] | ||||
| Fe5MoC | 159.412 | 18.975 | 69.654 | 140.437 | 197.362 | 1495.125 |
| Fe6C | 286.895 | 115.629 | 80.941 | 171.266 | 518.153 | 2248.549 |
| 304.7 [27] | 126.1 [27] | 86.8 [27] |
From table 3, the elastic constants of all (Fe, Mo)6C satisfy the above criteria of mechanical stability (equation (5)), indicating that they are all mechanically stable. Moreover, it can be found that the value of C11 is larger than that of C12 and C44 in all (Fe, Mo)6C, which indicates that these carbides are the most difficult to compress along the x-axis. The calculation results are relatively consistent with the results of the literature [27], indicating that the elastic parameter settings and results are reliable in this work.
Voigt–Reuss–Hill theory [43–46] is used to calculate the bulk modulus (B) and shear modulus (G) of the M6C carbides. The bulk modulus is estimated as , and the shear modulus is estimated as G = (Gv + GR)/2, where Gv = (C11 − C12 + 3C44)/5 and . Then, Young's modulus (E) and Poisson's ratio (σ) can be calculated from the bulk modulus and shear modulus, where E = 9BG/(3B + G) and σ = (3B − 2G)/2(3B + G) [47]. In addition to above related moduli and Poisson's ratio, the Cauchy pressure (C') also can be used to describe the mechanical properties of materials [48], which can be expressed as equation (6) [49]:
Firstly, the bulk modulus can reflect the strength of the material [50]. In figure 4, comparing C11 and bulk modulus, it can be found that the bulk modulus has a similar growth trend as C11. This is because C11 corresponds to bulk modulus to some extent. The order of bulk modulus is Fe3Mo3C-II > Fe2Mo4C > FeMo5C > Mo6C > Fe4Mo2C > Fe3Mo3C-I > Fe6C > Fe5MoC. Among them, the Fe3Mo3C-II alloy carbide has the largest bulk modulus, which is as high as 294.53 GPa, indicating that the Fe3Mo3C-II is the most difficult to compress under external force. On the contrary, the Fe5MoC is most easily compressed under the action of an external force. Secondly, the shear modulus can represent an ability to resist shear strain [3]. The shear modulus ranges from 33.43–140.27 GPa. Fe3Mo3C-II alloy carbide has the strongest resistance to shear strain, while Fe4Mo2C has the smallest shear modulus (table 4). Meanwhile, Young's modulus represents the stiffness of the material, the larger Young's modulus corresponds the stronger the stiffness [48, 50]. From table 4, the Young's modulus of Fe3Mo3C-II is the largest with 363.15 GPa, indicating that Fe3Mo3C-II has the strongest stiffness. Whereas Fe4Mo2C corresponds the smallest Young's modulus (95.06 Gpa), implying that the excellent ductility for Fe4Mo2C. Interestingly, the carbides of Mo atoms at 48f site (Mo6C, FeMo5C, Fe2Mo4C, Fe3Mo3C-II) have larger bulk modulus, shear modulus and Young's modulus than other carbides. In order to further enlighten the interaction among elastic properties and 48f site, the melting points has been calculated.
Figure 4. The change in the M6C modulus with Fe content. The orange shadow indicates that with increasing Fe content, both the modulus and C11 of M6C show a rising trend. The blue shadow suggests that the modulus and C11 did not increase with increasing Fe content. Note that the red inverted triangle is considered as the reference [27] for the shear modulus.
Download figure:
Standard image High-resolution imageTable 4. Calculated elastic modulus, including bulk modulus (B), shear modulus (G), Young's modulus (E), B/G, Poisson's ratio (σ) and Cauchy pressure (C') of (Fe, Mo)6C.
| Phase | B (GPa) | Gv (GPa) | GR (GPa) | G (GPa) | B/G | E (GPa) | σ | C' (GPa) |
|---|---|---|---|---|---|---|---|---|
| Mo6C | 270.60 | 102.06 | 101.38 | 101.72 | 2.66 | 271.18 | 0.33 | 50.25 |
| FeMo5C | 284.09 | 97.53 | 96.45 | 96.99 | 2.93 | 261.25 | 0.35 | 60.77 |
| Fe2Mo4C | 289.22 | 122.47 | 122.32 | 122.40 | 2.36 | 321.79 | 0.31 | 42.55 |
| Fe3Mo3C-I | 172.83 | 45.45 | 41.73 | 43.59 | 3.96 | 120.63 | 0.38 | 48.54 |
| Fe3Mo3C-II | 294.53 | 140.28 | 140.26 | 140.27 | 2.10 | 363.15 | 0.29 | 30.37 |
| Fe4Mo2C | 202.66 | 33.54 | 33.32 | 33.43 | 6.06 | 95.06 | 0.42 | 73.38 |
| Fe5MoC | 65.79 | 69.88 | 69.88 | 69.88 | 0.94 | 154.82 | 0.11 | -25.34 |
| Fe6C | 172.72 | 82.82 | 82.75 | 82.79 | 2.09 | 214.14 | 0.29 | 17.34 |
The melting point of carbides with cubic structure can be predicted as [51], the calculated results are listed in table 3. The melting points of Mo6C, FeMo5C, Fe2Mo4C and Fe3Mo3C-II are relatively higher compared to other carbides, meaning that they have stronger chemical bonding. It agrees with the argument that the higher melting point corresponds to the stronger chemical bonding [52]. The carbides that Mo atoms at 48f site have relatively higher chemical bonding than carbides of Fe atoms at 48f site. Hence, Mo atoms at 48f site has a predominant contribution for the elastic properties of carbides.
According to the above discussion, Fe3Mo3C-II express the outstanding performance no matter what kinds of elastic parameters including bulk modulus, shear modulus and Young's modulus. This provides a good theoretical basis for Fe3Mo3C-II to improve the strength and stiffness of materials in the future applications.
3.3.2. Toughness and brittleness prediction from the extension for different kinds of moduli in M6C carbides
According to Pugh's theoretical research [53], the toughness and brittleness of the material have a great relationship with the rate of B/G, Poisson's ratio and Cauchy pressure (C'). The critical value of B/G is 1.75 [54]. If the value of B/G is above 1.75, the carbide exhibits relatively good ductility. In contrast, this material has better brittleness. According to table 4, only the B/G value of Fe5MoC is below 1.75, whereas the B/G values of other carbides are larger than 1.75. Fe5MoC carbide has the worst ductility. Among them, the B/G value of Fe4Mo2C is the largest, indicating that Fe4Mo2C has the best ductility.
Poisson's ratio is usually used to analyze the toughness and brittleness of materials [30]. Poisson's ratio uses 1/3 as the threshold cut-off value. If Poisson's ratio is greater than 1/3, then the material exhibits plasticity [55]. Table 4 shows that the Poisson's ratio of Fe5MoC is lowest, only 0.11. The Poisson's ratio value of the Fe4Mo2C carbide is the largest, reaching 0.42, implying Fe4Mo2C has the best ductility in M6C. It can be found that the change trend of Poisson's ratio and the change trend of the B/G value are consistent.
The Cauchy pressure (C') can be used to describe the bonding properties between atoms [48]. When the Cauchy pressure is positive, metal bonds are dominant in the structure cell and the material exhibits ductility [56, 57]. And the value of the Cauchy pressure is positively correlated with the ductility of the material. From table 4, only the Cauchy pressure of Fe5MoC is less than 0. In (Fe, Mo)6C carbides, the Cauchy pressure value of Fe5MoC is the smallest, indicating that its ductility is the worst. The Cauchy pressure value of the Fe4Mo2C carbide is the largest, as high as 73.38 GPa, indicating that Fe4Mo2C has the best ductility.
Based on the above calculated results (table 4), the toughness and brittleness of (Fe, Mo)6C are analyzed from three aspects: B/G ratio, Poisson's ratio and Cauchy pressure. The analysis results consistently show that Fe5MoC has the worst ductility among M6C, indicating that it is more brittle than the other carbides. Fe4Mo2C has the largest values of B/G (6.06), Poisson's ratio (0.42) and Cauchy pressure (73.38 Gpa) which demonstrates the special carbide has the property of relatively better strength and toughness. Therefore, it is reasonable to predict that Fe4Mo2C has the potential as an alternative material to improve the wear resistance of materials.
3.3.3. The prediction of deformation according to the anisotropic investigation
The study of the elastic anisotropy of materials is of great significance to the improvement of their properties. The cracks generated in the material are closely related to its elastic anisotropy. There are many ways to characterize the elastic anisotropy of materials [58]. The most common method is to evaluate the elastic anisotropy through the universal anisotropic index (AU) and anisotropic index ratio (AB and AG). The corresponding empirical is as equations (7)–(9) [59, 60]:
In the equations, BV, BR, GV and GR are the modulus values calculated by the Voigt [45] and Reuss [43] methods. AB and AG characterize the anisotropy of the bulk modulus and shear modulus of the carbide, respectively. However, AU represents the characterization of the elastic anisotropy of the carbide. When the values of AU, AB and AG of carbide are all 0, it indicates isotropy. Otherwise, it is anisotropic. Carbides with the larger AU, AB and AG correspond to stronger mechanical anisotropy. It can be seen from table 5 that only the AG value of Fe5MoC is zero, meaning that the shear modulus of Fe5MoC is isotropic, and the shear modulus of other carbides is anisotropic. It is obvious that the AB values of all carbides are 0, because the same bulk modulus is obtained by both the Voigt and Reuss methods. Except Fe5MoC, the order of anisotropic strength of other alloy carbides is Fe3Mo3C-I > FeMo5C > Mo6C > Fe4Mo2C > Fe2Mo4C > Fe6C > Fe3Mo3C-II. The AU value of Fe3Mo3C-I is the largest, indicating that the carbide has the strongest elastic anisotropy.
Table 5. Calculated values for the universal anisotropic index (AU) and anisotropic index ratio (AB and AG) of (Fe, Mo)6C.
| (Fe, Mo)6C | AU | AB | AG |
|---|---|---|---|
| Mo6C | 0.034 | 0 | 0.0033 |
| FeMo5C | 0.056 | 0 | 0.0056 |
| Fe2Mo4C | 0.006 | 0 | 0.0006 |
| Fe3Mo3C-I | 0.446 | 0 | 0.0427 |
| Fe3Mo3C-II | 0.001 | 0 | 0.0001 |
| Fe4Mo2C | 0.033 | 0 | 0.0033 |
| Fe5MoC | 0 | 0 | 0 |
| Fe6C | 0.004 | 0 | 0.0004 |
In fact, the simplest and most intuitive method is to characterize the elastic anisotropy of the compound by drawing a three-dimensional graph. M6C belongs to the cubic crystal system. Therefore, the spherical coordinate diagram of each direction of Young's modulus of the cubic structure is drawn by the following empirical equations (10) and (11) [61]:
In the equations, Sij is the flexibility coefficient representing elasticity, which can be obtained by Cij conversion. n1, n2, and n3 are cosines representing different directions. Figures 5(a)–(h) and 6(a)–(c) show the three-dimensional view of the Young's modulus of M6C and the projection of M6C on the three planes (100), (010) and (001), respectively.
Figure 5. The surface constructions of Young's modulus (Fe, Mo)6C carbides for (a) Mo6C, (b) FeMo5C, (c) Fe2Mo4C, (d) Fe3Mo3C-I, (e) Fe3Mo3C-II, (f) Fe4Mo2C, (g) Fe5MoC, (h) Fe6C.
Download figure:
Standard image High-resolution imageFigure 6. The projection of Young's modulus of (Fe, Mo)6C on (a) (100), (b) (010) and (c) (001) crystal plane, respectively.
Download figure:
Standard image High-resolution imageThe anisotropic strength of the carbide can be understood in different orientations according to the surface constructions of Young's modulus in figures 4 and 5. The surface constructions of the carbides (Mo6C (a), FeMo5C (b), Fe3Mo3C-I (d), Fe4Mo2C (f)) deviates from the ideal sphere. The phenomenon suggests that those carbides have a larger anisotropy in figure 4. It is worthy to point out that the surface constructions of Fe3Mo3C-I (figure 5(d)) deviates most from the ideal sphere, implying it has the strongest anisotropy. The three-dimensional surface constructions of Fe2Mo4C (c), Fe3Mo3C-II (e), Fe5MoC (g) and Fe6C (h) in figure 5 are nearly spherical, it can be inferred that these carbides have weak anisotropy. The results of three-dimensional anisotropy diagram of Young's modulus are basically consistent with the calculated anisotropy factor. It shows that the calculated elastic anisotropy results are reliable.
According to the projection of the Young's modulus on the three planes (100), (010) and (001), more details of the anisotropy of the Young's modulus of M6C can be found. The projection graphics represent the strength of Young's modulus along different directions on one plane. From figures 6(a)–(c), it is evident that the projection of Young's modulus of these carbides possess the same contour profile on the three planes (100), (010) and (001). In order to further explain the anisotropy characteristics of the contour profile, figure 6(a) was selected as an example. It is interested that the larger C44 (table 3) corresponds to the bigger projection ring (figure 6(a)), because Young's modulus is mainly resulted from C44. Fe3Mo3C-II has the largest elliptic ring, implying that it has the strongest stiffness. The projection of Fe3Mo3C-I deviates the most from the ideal circle indicating its significant anisotropic property. The crystal orientation of the largest Young's modulus can be confirmed from the plane projection. It can be found that the maximum and minimum Young's modulus of Fe3Mo3C-I are along the [111] direction and the [100] direction, respectively. This means that the [111] direction is harder to deform than [100] direction. This provides theoretical guidance for the directional research in experiments and is of great significance to the design of new structural steels.
4. Conclusions
The structural, magnetic and mechanical anisotropic properties of alloy carbide M6C (M = Fe, Mo) are researched by first-principles calculations. The key conclusions are as follows:
- (a)Mo atoms tend to occupy 48f Wyckoff position, whereas Fe atoms prefer to occupy 16d and 32e Wyckoff positions. The Fe3Mo3C-II (Mo at 48f site, Fe at 16d and 32e sites) has the best stability.
- (b)(Fe, Mo)6C are nonmagnetic at the concentration of Fe atoms (xFe) below 0.5. When xFe is higher than 0.5, the magnetic moment of (Fe, Mo)6C rises with increasing of Fe content. The preference of Fe atoms at 48f Wyckoff position has the stronger magnetism than that of Fe atoms at 16d and 32e sites.
- (c)Higher Fe content corresponds to the stronger chemical bonding of carbides, resulting in improved elastic properties when Mo atoms are held in 48f position.
- (d)Fe4Mo2C has the best ductility, and Fe3Mo3C-I has the strongest Young's modulus anisotropy. This is of guiding significance for the directional design of new material properties.
Acknowledgments
This work was financially supported by the National Natural Science Foundation of China (Grant Nos. 12174296 and U1532268), The Key Research and Development Program of Hubei Province (Grant No. 2021BAA057), Excellent Young and Middle-aged Science and Technology Innovation Team in Colleges and Universities of Hubei Province (Grant No. T201903) and 111 projects. The work was carried out at the National Supercomputer Centre in Tianjin, and the calculations were performed on TianHe-1(A).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).



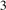


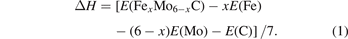
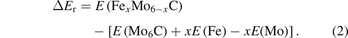
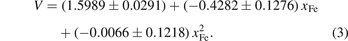
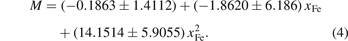



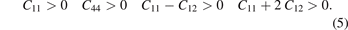

![${G}_{\mathrm{R}}=5\left[\left({C}_{11}-{C}_{12}\right){C}_{44}\right]/[4{C}_{11}+3\left({C}_{11}-{C}_{12}\right)]$](https://content.cld.iop.org/journals/0953-8984/34/28/285703/revision2/cmac68bdieqn7.gif)