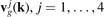Abstract
We study the evolution of initial temperature profiles in a two-dimensional isolated harmonic graphene lattice. Two heat transfer problems are solved analytically and numerically. In the first problem, the evolution of a spatially sinusoidal initial temperature profile is considered. This profile is usually generated in real experiments based on the transient thermal grating technique. It is shown that at short times the amplitude of the profile decreases by an order magnitude and then it performs small decaying oscillations. A closed-form solution, describing the decay of the amplitude at short times is derived. It shows that due to symmetry of the lattice, the anisotropy of the ballistic heat transfer is negligible at short times, while at large times it is significant. In the second problem, a uniform spatial distribution of the initial temperature in a circle is specified. The profile is the simplest model of graphene heating by an ultrashort localized laser pulse. The corresponding solution has the symmetry of the lattice and many local maxima. Additionally, we show that each atom has two distinct temperatures corresponding to motions in zigzag and armchair directions. Presented results may serve for proper statement and interpretation of laboratory experiments and molecular dynamics simulations of unsteady heat transfer in graphene.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Description of heat transfer in low-dimensional systems at micro- and nanoscale is one of the topical problems for modern mechanics and physics of solids. Unique mechanical, thermal, and other properties of 2D materials are discussed e.g. in the review [1]. In such materials, significant deviations from conventional macroscopic heat transfer laws are observed. In particular, recent experimental and theoretical works show that the Fourier law, assuming linear dependence of the heat flux on the temperature gradient, is usually violated in low dimensions (see e.g. [2]). Development of alternative heat transfer models is then required.
In the literature, the majority of real experiments on heat transfer are carried out in the so-called nonequilibrium steady state [3–6], notably a stationary heat transfer between two thermal reservoirs having different constant temperatures is considered. It is shown that the effective thermal conductivity, defined as the ratio of the heat flux and the temperature gradient, significantly depends on the system size (distance between the reservoirs). Therefore, conductivity cannot be regarded as a material constant. The nonequilibrium steady-state formulation is widely used in analytical [7] and numerical [8] studies on heat transfer. Dependence of the effective thermal conductivity on system size allows distinguishing ballistic, diffusive, and anomalous heat transfer regimes. Moreover, it allows determining some characteristics on the fundamental solution of unsteady problems (see e.g. paper [9]). However, the information provided by the nonequilibrium steady-state experiments and simulations is insufficient for a complete description of unsteady heat transfer. Therefore, in the present paper, we consider the unsteady formulation of the problem. More specifically, we consider evolution of initial temperature profiles in the isolated lattice.
Significant progress in the analytical description of unsteady ballistic heat transfer has been achieved in the harmonic approximation [10–19]. In particular, an equation describing unsteady ballistic heat transfer in the Hooke's crystal 4 was derived in papers [12, 13]. Generalization of results [12] for the case of one- and two-dimensional scalar lattices with arbitrary harmonic interactions was carried out in paper [14]. The influence of interactions with non-nearest neighbors on heat transfer in harmonic one-dimensional chains was studied in paper [15]. Unsteady heat transfer problems with heat supply were solved e.g. for the damped one-dimensional chain [16], two-dimensional scalar square lattice [17], and scalar graphene lattice [18]. A theory describing unsteady heat transport in polyatomic lattices has been formulated in paper [19]. In the present work, we employ this theory for analytical description of heat transport in harmonic graphene lattice.
Heat transport in graphene is studied in many theoretical and experimental works (see e.g. review [20] and references therein). Mostly, the steady-state formulation described above is considered. Papers on the unsteady heat transfer in graphene are scarce and mostly based on numerical simulations. For example, propagation of a planar thermal wave in graphene was investigated using molecular dynamics in paper [21]. In paper [22], one-dimensional problem of thermal contact between hot and cold half-spaces was simulated using molecular dynamics and Boltzmann transport equation. Several analytical solutions of ballistic heat transport problems were obtained in paper [19] using a simple model with pair interactions between particles. This model is irrelevant for simulation of the in-plane heat transfer in graphene. Therefore we consider a graphene model with more realistic multi-body interactions.
In the present paper, we investigate peculiarities of unsteady ballistic heat transfer in the harmonic graphene lattice performing in-plane oscillations. We present analytical and numerical solutions of two heat transfer problems. In the first problem, the initial temperature profile is sinusoidal. This profile is chosen because in real experiments it can be generated via the transient thermal grating technique [23, 24]. We show analytically that in this problem the anisotropy of heat transfer can be neglected at short times, while at large times it is significant. In the second problem, a uniform spatial distribution of the initial temperature is specified in a circle. We show that the solution of this problem has symmetry of the lattice and many local maxima. Additionally, the presence of two distinct kinetic temperatures, corresponding to two spatial directions, is demonstrated.
2. Nomenclature
Here and below matrices are denoted by bold italic symbols, while invariant vectors, e.g. position vector, are denoted by bold symbols. The following notation is used:
- a is an equilibrium interatomic distance;
- ak , k = 1, ..., 6, are vectors connecting atoms from a unit cell with the nearest neighbors;
- A(t) is an amplitude of the sinusoidal temperature profile;
- bj , j = 1, 2 are primitive vectors of the lattice;
-
 are vectors of the reciprocal basis;
are vectors of the reciprocal basis; - i, j are unit vectors of the Cartesian system;
- k is the wave vector;
- M is the mass of a carbon atom;
-
ωj
(k),
 , are jth branch of dispersion relation and corresponding group velocity;
, are jth branch of dispersion relation and corresponding group velocity; - rn,m is the position vector of the unit cell {n, m};
- T(rn,m , t) is kinetic temperature of the unit cell {n, m}, proportional to mathematical expectation of its kinetic energy;
- T (rn,m , t) is 4 × 4 temperature matrix of the unit cell {n, m};
- T0(r) is an initial temperature field;
- TF, TS are 'fast' and 'slow' components of the temperature field, describing changes in temperature due to equalization of kinetic and potential energies and due to heat transfer respectively;
-
 are x, y components of vectors of displacements Un,m
, Vn,m
for atoms from the unit cell {n, m}.
are x, y components of vectors of displacements Un,m
, Vn,m
for atoms from the unit cell {n, m}.
3. Statement of the problem
In this section, we present equations describing in-plane motions of an isolated harmonic graphene lattice and initial conditions, corresponding to a given initial temperature profile. For simplicity, the out-of-plane vibrations are ignored. This simplification is justified by the fact that in harmonic approximation in-plane and out-of-plane vibrations of a stretched graphene are formally decoupled. However the question on the accuracy of this approximation for realistic values of bending stiffness and pretension of graphene requires additional investigation. We refer to paper [19] for analysis of ballistic heat transfer by out-of-plane vibrations. Also, we consider the perfect lattice, although it was shown that defects and chemical functionalization significantly change graphene's properties [25, 26].
3.1. Lattice geometry
Graphene has a regular honeycomb lattice with a unit cell containing two carbon atoms (see figures 1(a) and (b)). Each atom has two independent translational degrees of freedom; as a result, the unit cell has four degrees of freedom. Unit cells are numbered by pairs of indices {n, m}. Position vectors of unit cells {n, m} and {s, p} are related as 5

Here primitive vectors of the lattice, b1, b2, are represented in Cartesian basis i, j as
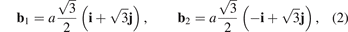
where a is an equilibrium bond length in graphene; in figure 1(b) vector i is horizontal and vector j is vertical.
Figure 1. Graphene lattice (a) and corresponding unit cell (b). Carbon atoms are located in the nodes of the lattice. Reproduced with permission from [27]. [Copyright © 2019 The Royal Society. All rights reserved].
Download figure:
Standard image High-resolution imageVectors a1, ..., a6 connect two atoms of the unit cell with their nearest neighbors (figure 1(b)). The vectors are introduced such that a4 = −a1, a5 = −a2, a6 = −a3.
3.2. Equations of motion and initial conditions
We consider the equations of motion for two atoms from the unit cell with indices {n, m}. Each atom has two degrees of freedom. Displacements of atoms from the unit cell {n, m} are denoted as 2D vectors Un,m
, Vn,m
. Following [27], we use the harmonic approximation for the potential energy of the lattice. Each atom is connected with three nearest neighbors by linear springs (bonds) with stiffness c. Additionally, the nearest bonds between particles are connected by angular springs with stiffness g. Equations of motion for this system were obtained using the Euler–Lagrange formalism in paper [27]. For the sake of completeness, we derive these equations in the appendix

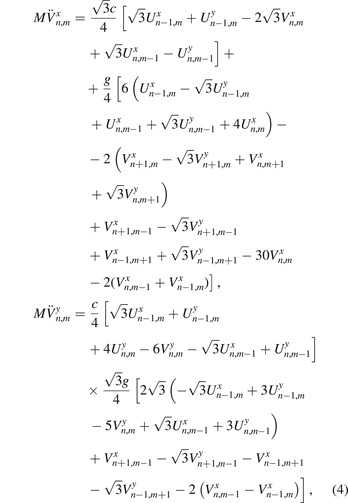
where M is the mass of the carbon atom; c, g are stiffnesses of linear and angular springs respectively. In further calculations, we use the following values of parameters for graphene:
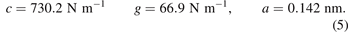
In paper [28] it is shown that the given values of stiffnesses yield correct in-plane elastic moduli of graphene.
We consider random initial conditions corresponding to a given initial kinetic temperature profile T0(rn,m ) (see definition (10)):
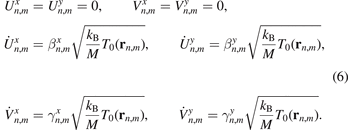
where kB is the Boltzmann constant. It is assumed that the function T0 is defined for all points of the graphene plane and slowly changes at distances of order of the interatomic distance. In (6), parameters 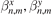 and
and 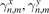 are uncorrelated random values with zero mathematical expectation and unit variance, i.e.
are uncorrelated random values with zero mathematical expectation and unit variance, i.e.
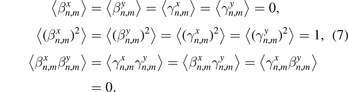
Here and below 〈‥〉 stands for the mathematical expectation. We note that the initial conditions (6) are such that mathematical expectations of kinetic energies (and temperatures (9)), corresponding to four degrees of freedom of the unit cell are equal.
3.3. Kinetic temperatures
To define thermodynamic properties of the system, we consider an infinite number of realizations with random initial conditions (6). Initially, kinetic temperatures corresponding to four degrees of freedom of the unit cell are equal. Further it is shown that during ballistic heat transfer these temperatures are generally different. Therefore we introduce the temperate matrix [19], T , such that
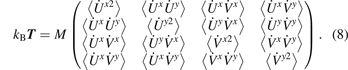
In this subsection, arguments rn,m , t of temperatures as well as indices n, m of velocities are omitted for brevity.
The diagonal elements of the temperature matrix define the kinetic temperatures, corresponding to four degrees of freedom of the unit cell:
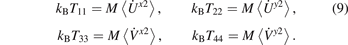
We also introduce the conventional (average) kinetic temperature as

Under initial conditions (6), all temperatures are equal at t = 0, i.e. Tii = T = T0.
The main goals of the present paper are to investigate evolution of the temperature field in the harmonic graphene lattice and to show that during ballistic heat transport the temperatures Tii are different.
4. Analytical solution for an arbitrary initial temperature profile
In this section, we present an analytical solution of the heat transfer problem with arbitrary initial temperature profile T0 in graphene.
4.1. Dispersion relation
Ballistic heat transfer is carried out by elastic waves traveling in the lattice. Therefore description of the heat transfer requires knowledge of the dispersion relation for the lattice and corresponding group velocities (see e.g. papers [10–12, 14, 19]). To obtain the dispersion relation we seek the solution of equations of motion (3) and (4) in the form of plane waves
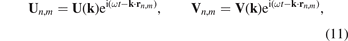
where i2 = −1; U(k), V(k) are the amplitudes of the waves; ω is a frequency; rn,m
stands for position vector of the unit cell; k is a wave vector represented in a reciprocal basis 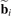 such that
such that 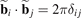 :
:

Here and below k1, k2 ∈ [0; 1] are dimensionless components of the wave vector. Taking formulae (12) into account, we substitute (11) into (3) and (4). The substitution leads to a homogeneous system of four linear equations with respect to components of the amplitudes. The system has nontrivial solutions only if its determinant is equal to zero. This condition yields quartic equation with respect to ω2. Solving the equation numerically, we obtain the dispersion surfaces ωj (k1, k2), j = 1, 2, 3, 4. Plots of the surfaces are presented in paper [27].
Given known the dispersion relation, the group velocities 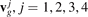 are calculated as
are calculated as

Further, the frequencies ωj
and group velocities 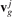 are employed for description of the heat transfer.
are employed for description of the heat transfer.
4.2. General solution
Analytical description of the ballistic heat transfer, presented e.g. in paper [19], is based on the assumption that the initial temperature field T0 slowly changes in space on the distances of order of the interatomic distance. Using this assumption the following formulae, describing evolution of the temperature field, are derived:

where k1, k2 are defined by formula (12). Detailed derivation of formula (14) is given in paper [19].
In formula (14), the first term, TF, describes high-frequency oscillations of the temperature caused by local transition to thermal equilibrium at short times. This process in the graphene lattice is considered in detail in paper [27]. In particular, it is shown that TF practically vanishes at times of order of ten periods of atomic vibrations. Here we focus on behavior of the second term, TS, describing slow changes in the temperature profile due to ballistic heat transport. Characteristic time scale of the heat transfer is much larger than the time scale of the transition to thermal equilibrium (see section 6.1 for details). Therefore in further analysis TF is neglected.
In the following section, formula (14) is employed for description of evolution of sinusoidal and circular initial temperature profiles.
5. Simulation setup
In all further numerical simulations, a square graphene sheet under periodic boundary conditions is considered. Numerical integration of equations of motion (3), (4) with initial conditions (6) is carried out using symplectic leap-frog integrator with empirically chosen time-step of 1.76 × 10−3
τ*, where  . Calculations are performed using the in-house C++ code combined with compute united device architecture to increase the performance [34]. For each realization, random velocities of atoms (6) with normal distribution are set using the cuRAND library [35]. Then forces acting on atoms are calculated using the right part of equations (3) and (4). At every time step, all forces acting on a single atom from the neighbor atoms are computed by a single graphic processor unit (GPU) thread. If the number of atoms exceeds the number of threads then each thread consequently computes the forces acting on several atoms. Then, the threads integrate the equations of motion to obtain the velocities and displacements of the atoms. At reference steps, kinetic energies of the atoms, corresponding to motion in x and y directions, are saved. To compute the kinetic temperatures, the kinetic energies for each atom are then averaged over realizations (see formula (9)).
. Calculations are performed using the in-house C++ code combined with compute united device architecture to increase the performance [34]. For each realization, random velocities of atoms (6) with normal distribution are set using the cuRAND library [35]. Then forces acting on atoms are calculated using the right part of equations (3) and (4). At every time step, all forces acting on a single atom from the neighbor atoms are computed by a single graphic processor unit (GPU) thread. If the number of atoms exceeds the number of threads then each thread consequently computes the forces acting on several atoms. Then, the threads integrate the equations of motion to obtain the velocities and displacements of the atoms. At reference steps, kinetic energies of the atoms, corresponding to motion in x and y directions, are saved. To compute the kinetic temperatures, the kinetic energies for each atom are then averaged over realizations (see formula (9)).
6. Sinusoidal initial temperature profile
In this section, we investigate anisotropy of ballistic heat transport in graphene by solving two problems with spatially sinusoidal initial temperature profiles in zigzag and armchair directions. This particular profile is chosen for two reasons. Firstly, the profile can be realized in experiments by two crossed laser pulses (see references on transient thermal grating for more details [23, 24]). Secondly, since the temperature varies only in one spatial direction then the heat transfer problem is quasi one-dimensional and it requires much less computational resources than truly two-dimensional problems (e.g. the one considered in section 7).
6.1. Analytical solution in the integral form
We consider sinusoidal initial temperature profile in the direction given by unit vector e (e.g. for zigzag e = i, while for armchair e = j):
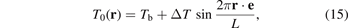
where Tb, ΔT are constants such that Tb > ΔT; L is the wavelength of sine. In this case, the general solution (14) is simplified. Additionally, we obtain an approximate solution in the closed form.
Substituting formula (15) into (14) after some transformations yields

Formula (16) shows that the temperature profile remains sinusoidal at any moment in time. Therefore instead of calculating the entire temperature field, we only compute amplitude, A, of the sine defined as

Substitution of (16) into (17) yields
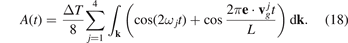
According to formula (16), TF and TS have different time scales, proportional to 1/ω* and L/c* respectively, where 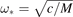 , c* = ω*
a. The first time scale is determined by frequencies of vibrations of individual atoms. The second time scale is determined by a time required for a sound wave to pass distance L. The ratio of these time scales, L/a, is usually a large parameter. Therefore the time scales are well separated. In further calculations, we focus on behavior of sine at large times of order of L/c*. Neglecting the first term in brackets in formula (18), we obtain
, c* = ω*
a. The first time scale is determined by frequencies of vibrations of individual atoms. The second time scale is determined by a time required for a sound wave to pass distance L. The ratio of these time scales, L/a, is usually a large parameter. Therefore the time scales are well separated. In further calculations, we focus on behavior of sine at large times of order of L/c*. Neglecting the first term in brackets in formula (18), we obtain
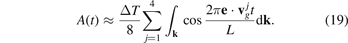
Formula (18) shows that time evolution of amplitude A depends on direction, e, of the initial thermal perturbation. Therefore, in general, the ballistic heat transport in graphene is anisotropic, although graphene's in-plane elastic properties are isotropic for small strains [36]. The accuracy of formula (19) is examined below.
6.2. Closed-form solution at short times
How strong is the anisotropy of ballistic heat transfer in graphene? To address this question, we derive an approximate expression for A(t) at short times.
Consider behavior of A(t) at 1/ω* ≪ t ≪ L/c*. Series expansion of the cosine in (19) then yields
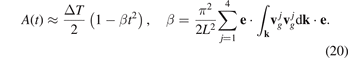
It is seen that the dependence of A on the direction e is determined by the second rank tensors 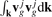 . Since the graphene lattice has the third order symmetry then all these tensors are spherical and then
. Since the graphene lattice has the third order symmetry then all these tensors are spherical and then

Numerical evaluation of the integrals in (21) yields

where c* = ω*
a, and  .
.
The complete solution (19) and approximate short-time solution (20) are shown in figure 2. It is seen that at times t ∼ L/c* sinusoidal profiles in zigzag (e = i) and armchair (e = j) directions decay almost identically, as predicted by formula (20).
Figure 2. Decay of amplitude of the sinusoidal temperature profiles in zigzag (solid red line) and armchair (dashed blue line) directions, calculated by formula (19). Approximate solution (20) is shown by dotted green line.
Download figure:
Standard image High-resolution imageThus for t < L/c* the decay of amplitude, A, of the sinusoidal temperature profile is described by the parabola (20). For symmetry reasons, the coefficient of the parabola is independent on the direction, e, of the initial temperature perturbation. Therefore at short times the anisotropy of heat transfer is negligible. The behavior of the amplitude at larger times is considered below.
6.3. Numerical simulations
In this subsection, we compare analytical predictions with results of numerical solution of equations of motion (3) and (4) with initial conditions (6).
Sinusoidal temperature profiles in zigzag (x = r ⋅ i) and armchair (y = r ⋅ j) directions are considered, i.e.

Analytical solutions of heat transfer problems with initial condition (23) are given by formula (16) with e = i and e = j. Since the profile remains sinusoidal then we only compute its amplitude A. Analytical expression for A is given by (19). Integral in this formula is evaluated numerically. The first term in this integral, describing high frequency oscillations of temperature, is neglected.
When solving the equations of motion (3) and (4) numerically, we obtain the temperature field T(r, t) and calculate the amplitude, A, as
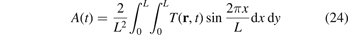
for the temperature profile in zigzag (x) direction (for the armchair direction the formula is similar). Note that in contrast to (17), formula (24) involves additional averaging in y direction. The averaging is added to reduce the influence of randomness of the initial conditions. The temperature field in formula (24) is calculated by averaging kinetic energies of particles with respect to large number 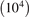 of realizations. In simulations ΔT/Tb = 0.9901, L = 182a. We note that since the lattice is harmonic then neither absolute values of ΔT, Tb nor their ratio influence the results shown below.
of realizations. In simulations ΔT/Tb = 0.9901, L = 182a. We note that since the lattice is harmonic then neither absolute values of ΔT, Tb nor their ratio influence the results shown below.
Comparison of predictions of formula (19) with results of numerical solution of equations of motion are shown in figure 3. It is seen that analytical and numerical results are in a good quantitative agreement. Figure 3 demonstrates several specific features of ballistic heat transport in graphene. Firstly, the curves corresponding to zigzag and armchair directions practically coincide for t < L/c*. Therefore at short times the heat transfer is nearly isotropic, as predicted by formula (20). For t ≫ L/c*, the anisotropy is significant. The anisotropy is caused by the fact that propagation of short waves in graphene is directional dependent. Secondly, the decay of amplitude at large times is non-monotonic. This is due to ballistic (wave) nature of heat transfer. Thirdly, in both directions the amplitude decays inversely proportional to time (see the subplot in figure 3), while in systems with the Fourier heat transport the decay is exponential.
Figure 3. Decay of amplitude of the sinusoidal temperature profiles, A/ΔT, for zigzag (circles, solid red line) and armchair (triangles, dashed blue line) directions. Analytical solution (19) (solid and dashed lines) and results of numerical solution of equations of motion (triangles and circles) are shown.
Download figure:
Standard image High-resolution imageNote that, strictly speaking, the rate of decay of the amplitude should be estimated using asymptotic methods, e.g. the stationary phase method [29]. However, in two dimensions application of this method is not straightforward and requires a separate study, which is beyond the scope of the present paper. Therefore in this paper, we limit our-self to less rigorous numerical arguments. The inset plot in figure 3 shows the oscillations of the function Ac* t/(ΔTL) over the time scale corresponding to the main plot. The amplitude of these oscillations neither decrease nor increase in time. We have checked numerically that similar behavior is also observed at large times (at least up to c* t/L = 150). Therefore we conclude that the amplitude decays approximately as 1/t in the most interesting time interval in which the changes in temperature are most noticable.
7. Circular initial temperature profile
In this section, we consider time evolution of a circular initial temperature profile:

where R is the radius of the circle with non-zero initial temperature. In further calculations R = 7.04 a ≈ 10 Å.
The main goal is to show that during the heat transfer kinetic temperatures T11 and T22, corresponding to two spatial directions, are different. Additionally, we show how the kinetic energies, obtained in numerical simulations and averaged over realizations, converge to prediction of the analytical solution (14).
7.1. Comparison with the analytical solution
In this subsection, we compare results of numerical solution of equations of motion with the analytical solution (14).
In numerical simulations, we consider two square samples of length L = 182a and L = 1818a. We compute the temperature profiles in these samples at t = 15.91τ* and t = 176.8τ* respectively. These moments in time are chosen such that the temperature front reaches the boundary of the corresponding sample.
To construct the analytical solution, we substitute the initial temperature distribution (25) into the general solution (14). Integral in this formula is evaluated numerically. Temperature profiles at t = 15.91τ* and t = 176.8τ* calculated using formula (14) are shown in figure 4.
Figure 4. Temperature profiles T/T1 in graphene at t = 15.91τ* (a) and (c) and at t = 176.8τ* (b) and (d) in samples with circular distribution of initial temperature (25). Isometric (a) and (b) and top (c) and (d) views are shown.
Download figure:
Standard image High-resolution imageTo compare analytical solution (14) with numerical simulation results, we consider convergence of the temperature field with respect to number of realizations. In each realization, kinetic energies of all atoms are calculated. To compute the temperature field, the kinetic energies are averaged over 10, 102, 104 and 105 realizations (see figure 5). Figure 5 shows that the temperature field converges with increasing number of realizations. The convergence is practically achieved for 104 realizations.
Figure 5. Temperature profile T/T1 in graphene at t = 15.91τ* in samples with circular distribution of initial temperature (25). Results of molecular dynamics simulations averaged over 1 (a), 102 (b), 104 (c), and 105 (d) realizations are shown.
Download figure:
Standard image High-resolution imageWe also check that numerical results converge to the analytical solution (14). For this purpose we plot the distribution of temperature T(x, 0) along the x axis (see figure 6) at t = 15.91τ* and at t = 176.8τ*. In this calculation, atoms that are at a distance less than or equal to 0.5a from the x axis are taken into account. If two atoms belong to the same unit cell then the average of their temperatures is plotted. To compute the temperatures, kinetic energies of the atoms are averaged over 105 realizations for a small sample and over 104 realizations for a large one. Figure 6 shows that the analytical solution (14) describes results of numerical simulations with acceptable accuracy.
Figure 6. Distribution of kinetic temperature along the x axis (T|y=0/T1) at t = 15.91τ* (a) and at t = 176.8τ* (b) in samples with circular distribution of initial temperature (25). Analytical solution (16) (solid black line) and results of numerical simulations (dashed red line) are shown.
Download figure:
Standard image High-resolution image7.2. Peculiarities of the solution
In this subsection, we discuss several peculiarities of the solution, shown in figures 5 and 6.
To start, we consider similar problem in a material with the Fourier heat transfer. In this case, the temperature profile has Gaussian-like shape, i.e. it has one local maximum at the center and it monotonically decrease with increasing distance from the center. In other words, the hottest point is always at the center of the sample.
In the case of ballistic heat transfer, the shape of the temperature field is qualitatively different. Firstly, the temperature profile has well-defined circular front, moving with the maximum group velocity. Secondly, in addition to the local maximum at the center, there are multiple local maxima, moving with different speeds. Thirdly, the position of the global maximum of the temperature changes in time, i.e. the hottest point is not always at the center. For example, at t = 15.91τ* the hottest point is at the center, while at t = 176.8τ* there are six identical hottest points located at distance about 600a from the center (see figures 5 and 6). At larger times, the hottest points move along the main lattice directions and form a regular hexagon.
To explain these peculiarities, we analyze the analytical solution (14). The solution may be interpreted in terms of the kinetic theory of heat transfer 6 . In the kinetic theory, the temperature is carried out by quasi-particles moving with group velocities. These quasi-particles are sometimes erroneously associated with phonons. We believe that they should be associated with the wave-packets (see discussion in paper [37]). Then the kinetic temperature at some point is proportional to density of quasi-particles at this point. Formula (14) shows that there are four types of quasi-particles, corresponding to four branches of the dispersion relation. Initially, the quasi-particles are uniformly distributed in a circle. Since the quasi-particles move freely then their motion is completely determined by the distribution of group velocities.
We compute the distribution of group velocities as follows. We calculate absolute values of the group velocities  at vertices of the square mesh
at vertices of the square mesh  ,
, 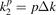 , s, p = 0, ..., Nk
− 1, where Δk = 1/Nk
. The values of group velocities form four arrays of length
, s, p = 0, ..., Nk
− 1, where Δk = 1/Nk
. The values of group velocities form four arrays of length 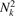 . These arrays are sorted in ascending order and maximum group velocities
. These arrays are sorted in ascending order and maximum group velocities 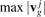 are calculated. Each interval from 0 to
are calculated. Each interval from 0 to 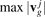 is divided into equal segments of length Δv. Number of array elements in all these intervals is calculated. Then the distribution function is calculated as
is divided into equal segments of length Δv. Number of array elements in all these intervals is calculated. Then the distribution function is calculated as
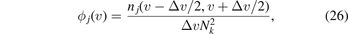
where nj (v − Δv/2, v + Δv/2) is a number of elements from array j in the interval from v − Δv/2 to v + Δv/2. Function ϕj (v) shows the relative number of quasi-particles with velocities close to v. Further we assume that each quasi-particle carries the same amount of thermal energy [37] (see formula (14)).
The functions (26) are shown in figure 7. It can be noted that the maximum group velocities  are equal to 0.583c*, 0.795c*, 0.535c*, and 0.277c* respectively. It is seen that the distributions are non-uniform. In particular, three out of four distributions have multiple sharp local maxima. The most pronounced maxima are at points 0.068c*, 0.277c*, 0.424c*, 0.517c*, 0.525c*, 0.795c*. Since the temperature is proportional to the density of quasi-particles then the presence of local maxima on distributions causes the maxima of the temperature field shown in figures 4–6. In particular, the highest maxima in figure 6(b) (at x/a ∼ 580 and x/a ∼ 620) are formed by the quasi-particles moving with velocities close to 0.517c* and 0.525c*. Since the difference between the velocities is small then these maxima merge at short times and form a single maxima at x/a ∼ 50 (see figure 6(a)).
are equal to 0.583c*, 0.795c*, 0.535c*, and 0.277c* respectively. It is seen that the distributions are non-uniform. In particular, three out of four distributions have multiple sharp local maxima. The most pronounced maxima are at points 0.068c*, 0.277c*, 0.424c*, 0.517c*, 0.525c*, 0.795c*. Since the temperature is proportional to the density of quasi-particles then the presence of local maxima on distributions causes the maxima of the temperature field shown in figures 4–6. In particular, the highest maxima in figure 6(b) (at x/a ∼ 580 and x/a ∼ 620) are formed by the quasi-particles moving with velocities close to 0.517c* and 0.525c*. Since the difference between the velocities is small then these maxima merge at short times and form a single maxima at x/a ∼ 50 (see figure 6(a)).
Figure 7. The distribution functions ϕj (v) show the relative number of quasi-particles with velocities close to v. Functions ϕ1 (red solid), ϕ2 (black dashed), ϕ3 (blue dotted), ϕ4 (magenta dot dashed) correspond to four branches of the dispersion relation.
Download figure:
Standard image High-resolution imageThus interpretation of the analytical solution (14) in terms of the kinetic theory yields simple explanation of the presence of multiple local maxima of the temperature field (hot points) shown in figures 4–6. The hot points are formed by the quasi-particles moving at speeds corresponding to maxima of the distribution function ϕj , defined by formula (26).
7.3. Two distinct kinetic temperatures
The theory suggests that in heat conducting harmonic crystals the kinetic temperatures, corresponding to different degrees of freedom of the unit cell, are generally different (see paper [19] for discussion). In particular, in papers [19, 38] this phenomenon have been observed in the harmonic one-dimensional chain with alternating masses. In this subsection, we show that this phenomenon is also present in the graphene lattice.
The presence of several distinct temperatures is demonstrated by numerical solution of the problem with circular initial temperature profile (25). Simulation results show that during heat transfer each atom has two distinct temperatures, corresponding to motions in zigzag (x) and armchair (y) directions even though initially these temperatures are equal. For each unit cell, the temperatures (9) satisfy the relations (except for a small number of cells, where all four temperatures are equal):

To demonstrate this phenomenon, we plot temperatures (9) of individual atoms at t = 15.91τ*, obtained in computer simulation (see figures 8(a) and (b)). Figure 8(a) shows temperatures T11/T1 and T33/T1 corresponding to motion along the x axis, while figure 8(b) shows temperatures T22/T1 and T44/T1 corresponding to motion along the y axis. It is seen that kinetic energies of thermal motion (and corresponding kinetic temperatures) are significantly different.
Figure 8. Temperatures corresponding to motion of atoms along x axis (T11 ≈ T33, left) and y axis (T22 ≈ T44, right) at t = 15.91τ*. The temperatures are normalized by the initial temperature T1. Simulations result are averaged over 105 realizations. Initial temperature distribution is given by (25).
Download figure:
Standard image High-resolution image8. Conclusions
We have presented analytical and numerical solutions of two heat transfer problems. The solutions revealed several peculiarities of purely ballistic heat transfer in the graphene lattice.
In the first problem, sinusoidal initial temperature profile in different spatial directions was considered. It was shown that amplitude of the temperature profile decays by an order of magnitude at short times (t < L/c*). At this time scale, the anisotropy of heat transfer is negligible. Decay of the amplitude is independent on the direction in which the initial temperature profile is specified. For all directions, it is described by simple approximate formula (20). At larger times (t ≫ L/c*), the amplitude performs small oscillates, decaying inversely proportional to time. The oscillations are directional dependent and therefore the effect of anisotropy is significant. The anisotropy should be taken into account when performing real experiments with quasi-ballistic regime of heat transfer (e.g. at low temperatures).
Similar phenomenon (isotropy at short times and anisotropy ant large times) was observed in a different graphene model in paper [19]. However in [19], no theoretical explanation of this phenomenon have been given. We have shown that the isotropy at short times is caused by the third order symmetry of the lattice.
In the second problem, constant initial temperature in a circle was specified. The solution of this problem demonstrates several peculiar features. The temperature profile has a front moving with the maximum group velocity and multiple local maxima. The global maxima (the hottest point) is located at the center of the specimen at short times only. At large times, the temperature has six identical global maxima moving along symmetry axes of the lattice. Additionally, the temperature field has multiple local maxima. These peculiarities were explained using interpretation of the results in terms of the kinetic theory and analysis of distribution of group velocities.
It was also shown that during the heat transfer each atom has two distinct temperatures, corresponding to motions in zigzag and armchair directions. The presence of several temperatures in the ballistic regime was predicted by the theory developed in paper [19]. The theory suggests that in general, the number of temperatures is equal to the number of degrees of freedom for the unit cell (four in the case of graphene). Our calculations show that in graphene only two out of four temperatures are different.
Presented results were obtained using the harmonic graphene model with purely ballistic regime of heat transfer. In real graphene, anharmonic effects are always present. However, in papers [30–33] it was shown that at small spatial and short time scales the behavior of weakly anharmonic crystals is described by harmonic models with acceptable accuracy. Therefore we believe that similar phenomena will be observed in anharmonic graphene models and real experiments.
Acknowledgments
The authors are deeply grateful to AM Krivtsov and SN Gavrilov for useful and stimulating discussions. Comments of the anonymous reviewers are highly appreciated. Work of VA Kuzkin and AY Panchenko was supported by the Russian Science Foundation (Grant No. 21-71-10129).
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Appendix A.: Equations of motion for the harmonic graphene lattice
In this appendix, we derive equations of motions (3)and (4) for two atoms in a unit cell. It is assumed that atoms are connected with the nearest neighbors by linear spring with stiffness c. Additionally, the neighboring bonds are connected by angular springs with stiffness g. The resulting equations of motion can be represented in the form

where 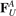 ,
, 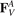 are forces caused by linear springs, while
are forces caused by linear springs, while 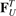 ,
, 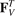 are forces caused by angular springs;
are forces caused by angular springs;  stands for the second derivative with respect to time. Forces caused by the linear springs are given by
stands for the second derivative with respect to time. Forces caused by the linear springs are given by
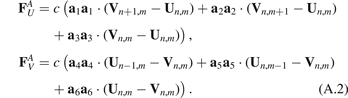
Here c is an axial stiffness, a4 = −a1, a5 = −a2, a6 = −a3.
The angular part of interaction corresponds to the change of the angle between the interatomic bonds. As long as any angle can be described with positions of three atoms this type of interatomic potential can be referred to as triple interaction. According to the figure A.1(a) atoms in the unit cell take part in 14 triple interactions.
Figure A.1. Angles numbering in honeycomb lattice (a), reproduced with permission from [27]. [Copyright © 2019 The Royal Society. All rights reserved]. Angle between two carbon bonds (b).
Download figure:
Standard image High-resolution imageConsider forces caused by one angular spring (see figure A.1(b)). The potential energy of this spring is

Here Θ = Θ(r0, r1, r2) is a function of position vectors of the atoms. For small Θ − Θ0 formula (A.3) can be approximated by
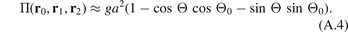
Hence, angular interaction is an example of the triple interaction, meaning it is determined by the positions of three neighboring atoms. We introduce new variables η and ζ such that

Then specific forces acting to the atoms can be found using the following expressions:

Here the first index is a number of atom on which the force is acting, while the second and the third indices are numbers of the neighboring atoms involved in the interaction. Note that the forces satisfy the relation Fijk = Fikj .
To calculate the derivatives of cos Θ in (A.6), we represent it as

and use the well-known relation
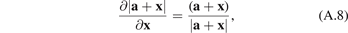
where a is some vector constant and x is a vector variable. Then
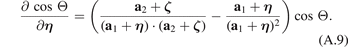
Similarly, for sin Θ we obtain

Relations for the 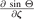 and
and 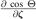 can be found in a similar way.
can be found in a similar way.
Given known the forces Fj caused by individual angular springs, the total forces are calculated as

Here the indices j, k show the angles to be taken into account to calculate the corresponding force using (A.6) (see figure A.1).
Substitution of formulae (A.2) and (A.11) into (A.1) yields equations of motion in the vector form. Projections of these equations onto x and y axes yield formulae (3) and (4).
Footnotes
- 4
One-dimensional harmonic chain consisting of identical particles interacting with the nearest neighbors via identical springs.
- 5
Here and below position vector of the unit cell is defined as the vector connecting the origin with center of mass of the cell in the undeformed state.
- 6