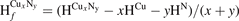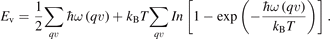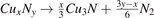Predicted stable high-pressure phases of copper-nitrogen compounds

To investigate the stabilities of various Cu_x N_y structures, the formation enthalpies of them (per atom) were calculated as ${\mathrm{H}}_{f}^{\mathrm{C}{\mathrm{u}}_{x}{\mathrm{N}}_{y}}=({\mathrm{H}}^{\mathrm{C}{\mathrm{u}}_{x}{\mathrm{N}}_{\mathrm{y}}}-x{\mathrm{H}}^{\mathrm{C}\mathrm{u}}-y{\mathrm{H}}^{\mathrm{N}})/(x+y)$, where ${\mathrm{H}}^{\mathrm{C}{\mathrm{u}}_{x}{\mathrm{N}}_{y}}$, H^Cu and H^N are enthalpies of Cu_x N_y (per f.u.), Cu (per atom) and N (per atom) reference systems at corresponding pressure. Based on calculated enthalpies, the convex hull diagrams for Cu–N compounds were plotted in figures 1(a)–(e). Any structure whose formation enthalpy lies on the convex hull (solid lines) could be considered stable and synthesizable.

Zoom In Zoom Out Reset image size

As shown in figure 1, four kinds of Cu–N compounds can be deemed stable at high-pressures. They are Pnnm-CuN₂, I-CuN₃, II-CuN₃ and P2₁/m-CuN₅. Among them, the P2₁/m-CuN₅ was previously proposed to be metastable at ambient condition [35]. While the other three are all newly discovered stable Cu–N structures. The crystal structures (supercell models) of them are presented in figures 1(g)–(j). The schematic of the pressure-composition phase diagram for the Cu–N compounds at 0 K are also shown in figure 1(f), with the pressure regions where these four predicted Cu_x N_y structures are stable marked by different colors. Pnnm-CuN₂ is thermodynamically stable within the pressure range between 20 to 150 GPa. For CuN₃ compounds, two kinds of structures, I-CuN₃ and II-CuN₃, are stable in the pressure range from 48–150 GPa. The phase transition between these two phases occurs at ∼84 GPa, as shown in figure 2(b). We also found that the P2₁/m-CuN₅, which was previously reported to be metastable at ambient condition, is stable between 45–75 GPa. But it should be acknowledged that this pressure-composition phase diagram for Cu–N compounds is based on static DFT calculations at temperature of 0 K. The finite temperature effects will be discussed in the following.

Zoom In Zoom Out Reset image size

As mentioned above, the P6₃/mmc-CuN₂ is not the most favorable CuN₂ structure (0 K DFT result) within the pressure range studied, as shown in figure 1. But in experiment [32], P6₃/mmc-CuN₂ has been synthesized at the pressure of 52 GPa and temperature above 1500 K. To understand this discrepancy, we further calculated the phonon spectra and then the lattice vibrational energies at 1500 K. As shown in figure 2(a), the enthalpy of newly discovered Pnnm-CuN₂ was set to 0, which acts as the reference enthalpy. The relative enthalpies of P6₃/mmc-CuN₂ are presented. Black, red and blue solid lines represent relative enthalpies based on calculated total-energy (T = 0 K), total-energy plus zero-point energy (ZPE) correction and plus vibrational energies (TS term with T = 1500 K), respectively. ZPE correction does not change the relative enthalpy of P6₃/mmc-CuN₂ much. But the finite temperature effects at 1500 K shift the relative enthalpy curve downwards by 20–35 meV atom⁻¹, making the P6₃/mmc-CuN₂ phase thermodynamically more stable than Pnnm-CuN₂ at pressure lower than 60 GPa. This result rationalizes the experimentally observed P6₃/mmc-CuN₂ structure and provides useful guidance for future experimental exploration of Pnnm-CuN₂ phase.

For the phase transition between I-CuN₃ and II-CuN₃, the ZPE correction and finite temperature effects were also studied and then shown in figure 2(b). Both ZPE and vibrational energy corrections increase the phase transition pressure between I-CuN₃ and II-CuN₃. The vibrational energy (E_v) introduced by the phonon of lattice at finite temperature is expressed as

$$\begin{equation*}{E}_{\text{v}}=\frac{1}{2}\sum\limits _{qv}\;\hslash \omega \left(qv\right)+{k}_{\text{B}}T\sum\limits _{qv}\;In\left[1-\mathrm{exp}\left(-\frac{\hslash \omega \left(qv\right)}{{k}_{\text{B}}T}\right)\right].\end{equation*}$$

According to the formula of the added free energy of phonon, both the ZPE (T = 0) and the vibrational energy (T > 0) of lattice are positively correlated with the averaged vibrational frequency integrated in the whole q-space and all branches of phonon. By the careful examination of the two CuN₃ structures, we found that an adding of nitrogen–nitrogen bond is associated with the structural transformation from I-CuN₃ to II-CuN₃. In a unit cell, I-CuN₃ has five nitrogen–nitrogen bonds while II-CuN₃ contains six, both of which correspond to the high frequency peaks of optical modes in the density states of phonon, as shown in supplementary figure S1. Although I-CuN₃ has a double bond (N=N, bond length of 1.19 Å) with the highest frequency of 53 THz, the added N–N bond in II-CuN₃ helps a larger averaged frequency than that of I-CuN₃. Thus, the ZPE and vibrational energy at finite temperature in II-CuN₃ are larger than those in I- CuN_3, and additional pressure is needed to overcome these energy differences between the two phases. The phase transition from I-CuN₃ to II-CuN₃ occurs at ∼84 GPa. Notably, this structural transformation is associated with the increasing the N–N bond and the appearance of metal-metal bond. In I-CuN₃, metal ions are effectively separated by nitrogen ions with the edge-shared polyhedrons to avoid the formation of Cu–Cu bond. However, strong compression weakens the Cu–N bonds and strengthens the N–N and Cu–Cu bonds for II-CuN₃, which is consistent with the claim in a previous review that the pressure will favor the formation of homonuclear bonds instead of heteronuclear bonds [44]. The calculated phonon dispersions of these four Cu–N compounds under different pressures are shown in figure S2. There are no imaginary phonon frequencies in the whole Brillouin zone, indicating the dynamic stabilities of them.

Figure 1 gives the atomic structures of the above four Cu–N compounds (supercell models). For CuN₂, both of newly discovered Pnnm-CuN₂ in figure 1(g) and previously synthesized P6₃/mmc-CuN₂ [32] contain the octahedrally coordinated Cu atoms. Each Cu atom is bonded to six N atoms. N atoms exist in the form of N₂ dimer. The N–N distance of N₂ dimer is 1.22 Å in Pnnm-CuN₂ and 1.2 Å in P6₃/mmc-CuN₂, being typical N=N bond. With the increase of nitrogen content, the N₂ dimer in the CuN₂ transform to a two-dimensional (2D) nitrogen sheet in I-CuN₃/II-CuN₃ and then to the cyclo-N₅ ⁻ ring in P2₁/m-CuN₅. For P2₁/m-CuN₅ and II-CuN₃, the distances between N atoms in the cyclo-N₅ ⁻ ring and N sheet are about 1.3 Å and 1.28 Å, which lies between the N–N single bond (1.45 Å) and N=N double bond lengths (1.25 Å) [26, 45]. The distances between nitrogen atoms in I-CuN₃ are 1.19 Å, 1.26 Å and 1.29 Å, and there is an N=N (1.19 Å). Indeed, the criterion depending on bond length to decide N–N or N=N bond is just only an empirical method, though this method has been adopted by many previous works [1, 6, 23, 26]. The bond strength is strongly related to the phonon vibration frequency. Experiments take Raman or infrared spectroscopy to determine single and double bonds. In theoretical calculation, it is reasonable to use phonon vibration frequency to judge single or double bonds. We illustrated the phonon density of states for these four high pressure phases at the same pressure of 55 GPa in figure S3. There are two distinct high frequency peaks with frequencies of about 48 (Pnnm-CuN₂) and 50 THz (I-CuN₃), which obviously correspond to two double bonds in the two structures. If we treat the N–N bonds of cyclo-N₅ ring in P2₁/m-CuN₅ as single bonds with the maximal frequency of 40 THz, and those peaks between the two frequencies may be considered as the mixed bond of N=N and N–N. The bond lengths of N–N are labeled at supplementary figure S4. The crystallographic parameters and unit-cell structures of these Cu_x N_y compounds are also provided in supplementary table S1 and figure S4.

The electronic band structures of these four Cu–N compounds at different pressures are presented in figure 3. The Pnnm-CuN₂, I-CuN₃ and II-CuN₃ are metals at pressure of 55, 70 and 150 GPa, respectively. The P2₁/m-CuN₅ at 55 GPa is a semiconductor with an indirect band gap energy of 0.073 eV, based on PBE functional calculation. Hybrid HSE06 functional calculation leads to a much larger band-gap value (1.28 eV), but with similar dispersion of energy bands. The band-gap energy decreases with the increased pressure, as shown in figure S5. The special local structure with the formation of the closed aromatic cyclo-N₅ ring and the ionic interaction between the cyclo-N₅ ⁻ and Cu⁺ in P2₁/m-CuN₅ are the origin of the band gap. The N–N bond lengths in P2₁/m-CuN₅ vary slightly between 1.31 and 1.34 Å, which agree very well with previously reported semiconductive aromatic cyclo-N₅ ⁻ compounds, such as CuN₅ [35], LiN₅ [46], NaN₅ [7] and MgM₁₀ [1]. We found that the appearance of P2₁/m-CuN₅ phase in 45 to 75 GPa is correlated with the formation of electronic band gap, which lowers the energy of electronic states approached to Fermi level. The increased pressure will gradually close the band gap (figure S5), and lifted the energy of electronic states, which leads to the instability of P2₁/m-CuN₅ at high pressures.

Zoom In Zoom Out Reset image size

In order to further analyze the bonding characteristics, we have performed the Bader charge and electron localization function (ELF) calculations and showed the results in figure 4. The covalent bond and lone pair can be represented by a high ELF value (≫0.5); while the ELF value ≪0.5 and close to 0.5 are often indicators of ionic bonds and metal bonds. The calculated ELF suggested the valance bonding between N atoms, the ionic bonding between N and Cu atoms and lone pairs at several N atoms. The Bader charge results also show that copper in these four structures exist as Cu⁺ ion. Our ELF and Bader charge analysis also show that the bonding in the N₅ ⁻ anion is covalent and stabilized by the electron transferred from nearby Cu atom, as show in figure S6. The formation of a large sharp peak of Cu–N antibonding approaching to Fermi level in figure S7 also suggested the ionic interaction between Cu⁺ and N₅ ⁻. The effect of pressure on charge transfer has also been investigated. As shown in figure S8, the pressure has little effect on the Bader charge results within the pressure range studied by us. The calculated COHP for these four Cu–N compounds are presented in figure S7. The integrated COHP values of Cu–N bonds and N–N bonds are −2 to −4 eV pair⁻¹ and −14 to −16 eV pair⁻¹, indicating that the N–N bonds are stronger than the Cu–N bonds, which is consistent with our ELF analysis.

Zoom In Zoom Out Reset image size

Previous experiment has provided the Rietveld refinement of synchrotron XRD pattern of P6₃/mmc-CuN₂ [32]. To provide additional information for future experiments, the simulated XRD patterns of Pnnm-CuN₂, P6₃/mmc-CuN₂, I-CuN₃, II-CuN₃ and P2₁/m-CuN₅ at corresponding pressures have been obtained with λ = 0.3344 Å which is known as the wavelength of the incident x-ray beam, in order to keep consistent with that of the XRD pattern of experimental P6₃/mmc-CuN₂ [32]. Among them, the data of Pnnm-CuN₂ and P6₃/mmc-CuN₂ are presented in figure 5, shown along with the experimental result for P6₃/mmc-CuN₂. The rest of them are plotted in figures 5(b)–(e). The Miller indices (h k l) for each XRD peaks have been marked. By comparing our simulated XRD patterns with the experimental one, the calculated XRD pattern of P6₃/mmc-CuN₂ agrees much better with the experimental obtained XRD data, supporting that the previously synthesized CuN₂ is indeed P6₃/mmc-CuN₂ phase. In addition, we hope the simulated XRD patterns of Pnnm-CuN₂, I-CuN₃, II-CuN₃ and P2₁/m-CuN₅ structures can provide insights for further experimental efforts to find them.

Zoom In Zoom Out Reset image size

The N-rich compounds were considered as promising high-energy-density materials. Especially, the cyclo-N₅ ⁻ has been extensively studied because of the high chemical energy stored in it. At last, we investigated the explosive performances of these novel stable Cu–N compounds by calculating the energy-densities of them. In the dissociation of $C{u}_{x}{N}_{y}\to \frac{x}{3}C{u}_{3}N+\frac{3y-x}{6}{N}_{2}$, the calculated energy densities for Pnnm-CuN₂, I-CuN₃, II-CuN₃ and P2₁/m-CuN₅ are 1.57, 2.39, 2.62 and 2.74 kJ g⁻¹, respectively. These values are higher than those of the two known structures, P6₃/mmc-CuN₂ (1.57 kJ g⁻¹) and Pm $\bar{3}$ m-CuN₃ (1.51 kJ g⁻¹), similar to the CO/N₂, TATB and RDX (1–3 kJ g⁻¹) [47], but lower than the TNT (4.3 kJ g⁻¹) and HMX (5.7 kJ g⁻¹) [45].