Abstract
We analyse the knotting behaviour of linear polymer melts in two types of soft-core models, namely dissipative-particle dynamics and hybrid-particle-field models, as well as their variants with slip-springs which are added to recover entangled polymer dynamics. The probability to form knots is found drastically higher in the hybrid-particle-field model compared to its parent hard-core molecular dynamics model. By comparing the knottedness in dissipative-particle dynamics and hybrid-particle-field models with and without slip-springs, we find the impact of slip-springs on the knotting properties to be negligible. As a dynamic property, we measure the characteristic time of knot formation and destruction, and find it to be (i) of the same order as single-monomer motion and (ii) independent of the chain length in all soft-core models. Knots are therefore formed and destroyed predominantly by the unphysical chain crossing. This work demonstrates that the addition of slip-springs does not alter the knotting behaviour, and it provides a general understanding of knotted structures in these two soft-core models of polymer melts.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
There has been a considerable activity in the development and use of soft-core polymer models, i.e., models where the nonbonded interactions between monomers do not approach a singularity at short intermonomer distances, but assume a finite value. The value is low enough, say of the order of 10kB T (kB being Boltzmann's constant), so that it does not even present 'practical infinity' in a simulation. Such models are engineered to reproduce static structural and thermodynamic properties of hard-core excluded-volume models as well as possible, with little attention given so far to their ability or disability to capture the propensity for polymer chains to form knots. As a consequence of the soft interactions, however, monomers can (infrequently) pass through each other, which leads to a qualitatively incorrect polymer dynamics. Polymer chains do not entangle, regardless of their length, they are not forced to reptate around each other, and each one moves like a chain in a solvent, not like a chain in a polymer melt. We have employed two different classes of such soft-core models. The first is dissipative-particle dynamics (DPD) [1], a very coarse-grained particle model with one bead representing a substantial fraction of a real polymer chain. The second is hybrid-particle-field molecular dynamics (hPF-MD) [2], whose base particle model can be of arbitrary resolution from atomistic to low-resolution coarse-grained. It treats, however, the nonbonded interactions not pairwise but mediated by a density field. This necessarily leads to them becoming effectively soft-core. Both methods are introduced in more detail below.
To re-introduce qualitatively correct polymer dynamics, we have augmented both DPD and hybrid-particle-field (hPF) by so-called slip-springs [3, 4]. These are temporary bonds between normally nonbonded beads, which migrate along polymer chains, disappear and reappear according to their own dynamics. We and others have shown that they can very effectively mimic the effects of excluded-volume interactions, chain-noncrossability and entanglements, and that they restore reptation dynamics to the soft-core models of polymer melts [5–10]. At the same time, it has been shown that the introduction of slip-springs does not alter the polymer structure. Descriptors on the monomer scale [radial distribution function (RDF)], the chain scale (radius of gyration) and bulk scale (density) are identical to within the error bars between soft-core models with and without slip-springs, for the case of polymer melts. (For polymers in solution, there is a small, predictable and well-understood contraction of the radius of gyration [11].) In contrast, there is a structural difference at the monomer scale, e.g. in the RDF, between a soft-core model and its parent hard-core model. (In the case of hPF, for example, both models are available.) Predictably, the field description allows a closer approach or even overlap of particles [12]. On larger scale structures, however, hPF and the hard-core model agree [13].
It is the purpose of the present contribution to compare our models in terms of their knot structure, which is yet another descriptor, whose scale is on the order of the chain size. In a melt of long-enough polymer chains, some will invariably contain knots [14]. The average number of knots and their topologies depend on chain length, chain stiffness [15] but also on chain-crossability, i.e. hard-core vs soft-core description [16]. In particular, it is possible that models, which produce otherwise identical polymer structures, differ in the number of knots. Similarly, there is the possibility for the models to differ in the speed of knot formation and destruction, as different mechanisms may prevail. We therefore investigate the knotting/unknotting dynamics via a correlation-function analysis.
We are in a position to compare the same polymer melts at different levels of modelling. For the hPF-series, we have the (i) parent hard-core MD model, the (ii) soft-core hPF description derived from it, and the (iii) hPF description with slip-springs added. We can therefore not only compare knotting differences between hard and soft core (i) and (ii). We can also study, whether the slip-spring emulation of entangled dynamics leads to a change of knottedness (compare (ii) and (iii)). The latter comparison can also be made for our DPD models without and with slip-springs (there is no parent hard-core model for DPD, since it is a top–down multiscale approach). We keep the analysis simple and restrict it to the simplest and most common knot topology, mathematically denoted as 31 knot, known to sailors as overhand knot [17]. This knot involves only a single polymer chain, i.e. it does not tie two chains together. We want to know the probabilities of our models to contain knots and, thus, supplement their structural characterization. We do not wish, however, to dive into a full analysis of more complicated knots. This is all the more justified, as there is little evidence for the knottedness of a polymer melt influencing its more practical properties, such as mechanical or rheological. This is probably associated with the synthetic challenge to experimentally prepare and characterize polymers with a defined knot structure.
2. Methods and model
2.1. Hybrid-particle-field molecular dynamics
The hPF-MD approach and its applications to atomistic and coarse-grained (bio)macromolecular systems have been extensively presented in previous publications [2, 12, 13, 18–25]. Here, we briefly recall the main ideas. In hPF-MD, the intramolecular interactions (bond, angle...) are the same as the standard molecular dynamics (MD) simulations, while pairwise interactions between nonbonded particles in standard MD simulations are transformed into an interaction of a particle with an external potential depending on the density field. For a system composed of two different types of particles, the potential energy in the density field is
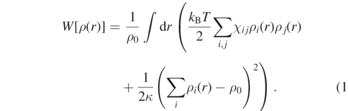
By applying the saddle point approximation, it is possible to obtain the mean-field external potential  acting on an individual particle (type i) at position r from the functional derivative of the potential energy W[ρ(r)] with respect to the local density:
acting on an individual particle (type i) at position r from the functional derivative of the potential energy W[ρ(r)] with respect to the local density:
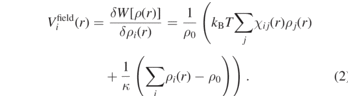
Here, the Flory–Huggins parameter χij represents the strength of the mean field interaction between particles of type i and j, ρ0 is the average number density of the system, κ is the compressibility factor for the system, and ρi and ρj are number densities of particles of type i and j in the density field at position r, respectively. The forces acting on particles are computed by interpolating the gradients of the external potential on spatial grids. More details about the implementation of density fields and its force calculations in MD simulations can be found in references [2, 22, 26]. Replacing hard-core nonbonded pair interaction by the interaction with a field on a lattice turns MD into an O(N) algorithm, but also makes the nonbonded interactions necessarily soft-core. Polymer chains are thus able to cross each other and fail to show entangled dynamics such as reptation [27]. To remedy this shortcoming, we recently employed slip-springs in hPF-MD simulations of polymer melts, which successfully restored their entangled dynamics [7].
We study a model system of polystyrene melts, which has been introduced in previous publications [12, 13, 21]. The coarse-grained force field of polystyrene melts was originally developed by Qian and co-workers [28]. In this model, two different bead types (R and S) are defined to reproduce the tacticity of the polymer chain with the bead placed at the centre of mass of the repeating unit. Coarse-grained atactic polystyrene chains are created by randomly generating the sequence of R and S beads. Specifically, by using the iterative Boltzmann inversion method [29] to retain probability distribution functions of their all-atom counterparts, coarse-grained bond interactions, namely bonds, angles and dihedral angles, are derived. The coarse-grained nonbonded interactions are computed through the density-functional field, whose update time interval is Δtfield = 1 hPF-MD time step. In this density-functional field, the grid spacing is chosen as 0.55 nm, comparable to the average bond length between connected coarse-grained beads. The latter is l ≈ 0.52 nm for both standard MD and hPF simulations. The Flory–Huggins parameter χ is 0 for a homogeneous polymer melt. To probe the effect of different incompressibility conditions, two incompressibility parameters κ = 0.1 and 0.05 mol × kJ−1 are employed. Their influence on the monomer diameter is derived from the potential of mean force (PMF) between monomers. Specifically, the PMF is computed by Boltzmann inversion of the intermolecular RDF, and the monomer diameter is identified as the length where it equals 0. This definition can be applied in the same way to both MD with pairwise interactions and to hPF. The resulting monomer diameters for MD and the two hPF models with κ = 0.05 and κ = 0.1 are 1.01 nm, 1.24 nm, and 1.27 nm, respectively. All details of the simulated systems such as the number of chains, chain length, box sizes and the total number of slip-springs in hPF simulations (if present at all) are listed in table 1.
Table 1. Simulation details of MD simulations with regular hard-core pairwise interactions, hPF simulations without slip-springs and with slip-springs (SSPF). N, M, l and NSS are the number of monomers per chain, the number of chains in the system, the length of the cubic simulation box and the total number of slip-springs in SSPF simulations, respectively.
| System code | N | M | l (nm) | NSS |
|---|---|---|---|---|
| MD-100 | 100 | 300 | 17.48 | |
| MD-200 | 200 | 150 | 17.48 | |
| MD-400 | 400 | 75 | 17.48 | |
| MD-600 | 600 | 50 | 17.48 | |
| MD-750 | 750 | 40 | 17.48 | |
| hPF-100 | 100 | 300 | 17.48 | |
| hPF-200 | 200 | 150 | 17.48 | |
| hPF-400 | 400 | 75 | 17.48 | |
| hPF-600 | 600 | 50 | 17.48 | |
| hPF-750 | 750 | 40 | 17.48 | |
| hPF-1000 | 1000 | 30 | 17.48 | |
| SSPF-100 | 100 | 300 | 17.48 | 86 |
| SSPF-200 | 200 | 150 | 17.48 | 161 |
| SSPF-400 | 400 | 75 | 17.48 | 199 |
| SSPF-600 | 600 | 50 | 17.48 | 211 |
| SSPF-750 | 750 | 40 | 17.48 | 216 |
All simulations are performed using GPU-accelerated large-scale molecular simulation toolkit (GALAMOST [26]) package with our version of the slip-spring model. The initial configurations are obtained from the reference MD simulations after their density is converged at a temperature of T = 500 K. The equilibration of the hPF systems is achieved by utilizing the fast equilibration procedure reported previously [12]. Specifically, we perform a pure hPF simulation to pre-equilibrate the system up to 4 × 108 steps, with the grid spacing slowly decreasing from lgrid ≈ 1 nm to lgrid ≈ 0.55 nm. The mean squared internal distance is tracked throughout the equilibration step to ensure a complete equilibration [30]. Data are then collected from production simulations continued from these equilibrated systems with lgrid ≈ 0.55 nm. Both hPF simulations with and without slip-springs are run in an NVT ensemble using a Langevin thermostat with a frictional coefficient of 226 g × mol−1 × ps−1.
Slip-springs are modelled by employing a soft Lennard-Jones potential with its parameters mapped to the corresponding hard-core MD systems. The slip-spring bond length follows a Gaussian distribution, whose mean value is close to half of the tube diameter of polystyrene melts  [31]. It should be noted here that the slip-spring bond length in hPF models is longer than that employed in DPD models compared to the respective bead sizes. Slip-spring motion is governed by a Monte Carlo (MC) algorithm. In our example CG-PS systems, the MC motion of slip-springs is activated every ΔtMC = 100 hPF time steps (3 ps). This is close to the relaxation time of a single monomer, which we estimated as the transition time of the monomer's mean squared displacement g1(t) from ballistic (g1(t) ∼ t2) to Rouse motion (g1(t) ∼ t0.5). The mobility of slip-springs is controlled by a hopping frequency vhop, which is a control parameter determined by matching corresponding experimental or MD simulation data. In the present model, comparison with MD diffusion coefficients yielded vhop = 1.25 × 10−4 ps−1. We note that this implementation of a hopping-frequency-controlled migration is slightly different from our original slip-spring model [5, 6], where MC blocks have a fixed amount of time steps. Nonetheless, both methods successfully restore entanglement dynamics. If a slip-spring reaches a chain end, it attempts a relocation move. Slip-springs are only allowed to relocate from one chain end to another: in a relocation attempt, a new slip-spring is created by connecting a randomly chosen chain end to any other bead within a distance closer than 0.95 × dT ≈ 7.125 nm. A Metropolis MC trial between the initial and the new slip-spring position determines whether the relocation is successful; the 'loosing' slip-spring is discarded. More details about the implementation of slip-springs in the coarse-grained polystyrene (CG-PS) model can be found in reference [25].
[31]. It should be noted here that the slip-spring bond length in hPF models is longer than that employed in DPD models compared to the respective bead sizes. Slip-spring motion is governed by a Monte Carlo (MC) algorithm. In our example CG-PS systems, the MC motion of slip-springs is activated every ΔtMC = 100 hPF time steps (3 ps). This is close to the relaxation time of a single monomer, which we estimated as the transition time of the monomer's mean squared displacement g1(t) from ballistic (g1(t) ∼ t2) to Rouse motion (g1(t) ∼ t0.5). The mobility of slip-springs is controlled by a hopping frequency vhop, which is a control parameter determined by matching corresponding experimental or MD simulation data. In the present model, comparison with MD diffusion coefficients yielded vhop = 1.25 × 10−4 ps−1. We note that this implementation of a hopping-frequency-controlled migration is slightly different from our original slip-spring model [5, 6], where MC blocks have a fixed amount of time steps. Nonetheless, both methods successfully restore entanglement dynamics. If a slip-spring reaches a chain end, it attempts a relocation move. Slip-springs are only allowed to relocate from one chain end to another: in a relocation attempt, a new slip-spring is created by connecting a randomly chosen chain end to any other bead within a distance closer than 0.95 × dT ≈ 7.125 nm. A Metropolis MC trial between the initial and the new slip-spring position determines whether the relocation is successful; the 'loosing' slip-spring is discarded. More details about the implementation of slip-springs in the coarse-grained polystyrene (CG-PS) model can be found in reference [25].
2.2. Dissipative-particle dynamics
DPD [1, 32, 33] is a mesoscopic simulation method that describes particle interactions in terms of purely pairwise conservative, dissipative, and random contributions. The coarse-grained, soft-core conservative force allows for large integration steps at low computational costs, which makes DPD a popular technique for simulations of soft matter [34]. The coupled dissipative and random forces account for the system's friction and act as a thermostat. Here, we follow the methodology of Groot and Warren [1], where the conservative force between two beads i and j is linear and defined by a cutoff radius rc and a repulsion parameter aij (equation (3)).
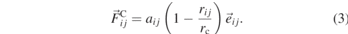
Polymer chains are modelled using a standard bead-spring model, where DPD beads are connected by a weak Hookean spring in addition to their nonbonded interactions. As a computationally inexpensive answer to the physical shortcomings of soft-core conservative interactions, slip-springs have been employed in DPD simulations of polymer melts [5, 6, 8] and solutions [35, 36] by different groups. In this study, we follow the work of Langeloth et al [5]: initially, a fixed number of slip-springs is distributed between pairs of nonbonded beads, following a similar distance criterion as in the slip-spring hPF model. During the simulation, slip-springs are allowed to migrate along the chains governed by a Metropolis MC criterion. If slip-springs reach the end of a chain, a relocation move to a different, randomly chosen chain end is attempted as described in the previous subsection. Slip-springs are frozen after a number of MC migration attempts and act as fixed bonds in the next set of DPD steps. By performing alternating blocks of MC and DPD steps, entanglement dynamics such as reptation and constraint release are restored. For further details, we refer to the initial work in reference [5].
In addition to unrestricted melts, we present simulations of systems confined by an array of nanotubes (figure 1). Nanotubes are modelled by a purely repulsive potential and placed on a hexagonal grid in the xy-plane. They are infinite in z-direction. The nanotubes are positioned in the centre and on the corners of the simulation box, so that one periodic image contains two tubes. They interact with DPD beads via the conservative potential: in a modified version of equation (3), aij
and rij
are replaced by the nanotubes' repulsion parameter aNT,i
and the distance between a bead and their 'surface' rNT,i
. A nanotube's surface is defined by its radius RNT, which is also used to evaluate its effective excluded volume  , where lz
is the box size in z-direction. The nanotubes' repulsion parameter aNT,i
is chosen to be twice as repulsive as the regular aij
. Notably, interactions between beads and nanotubes are still soft-core, which theoretically allows beads to penetrate the tubes. In this case, rNT,i
becomes formally negative. However, we have not observed polymers crossing into the nanotubes, so the repulsion appears to be large enough to keep them out.
, where lz
is the box size in z-direction. The nanotubes' repulsion parameter aNT,i
is chosen to be twice as repulsive as the regular aij
. Notably, interactions between beads and nanotubes are still soft-core, which theoretically allows beads to penetrate the tubes. In this case, rNT,i
becomes formally negative. However, we have not observed polymers crossing into the nanotubes, so the repulsion appears to be large enough to keep them out.
Figure 1. Simulation box of a polymer melt confined by an array of nanotubes. Nanotubes are placed on a hexagonal grid on the xy-plane and are infinite in z-direction. They are modelled by a purely repulsive potential which acts as a barrier of particles at a distance RNT from the nanotube centre (see text). The hexagonal symmetry relates the box dimensions lx
, ly
and the nanotubes' radii and distances RNT, dNT as  and dNT = ly
− 2RNT.
and dNT = ly
− 2RNT.
Download figure:
Standard image High-resolution imageDPD simulation results are presented in reduced units: time, distance, mass, and energy are given in units of tDPD, rc, mDPD, and kB
T, respectively. If need be, our simulations can be mapped onto a polystyrene model [36]. All DPD parameters are taken from reference [1] for a density of  . The repulsion parameters for bead-bead and bead-nanotube interactions are
. The repulsion parameters for bead-bead and bead-nanotube interactions are  and
and  . Bonds and slip-springs have a force constant of
. Bonds and slip-springs have a force constant of  . The integration step is Δt = 0.06 tDPD. The monomer radius is 1 rc by definition, and an average bond length of l ≈ 1.21 rc emerges from the sum of bonded and nonbonded interactions.
. The integration step is Δt = 0.06 tDPD. The monomer radius is 1 rc by definition, and an average bond length of l ≈ 1.21 rc emerges from the sum of bonded and nonbonded interactions.
Our simulations feature chains of length N = 25, 50, 75, 100, and 150. For the unconfined melts, 1668, 834, 556, 417, and 278 of these chains are simulated in a cubic  box, respectively. Chains under confinement are investigated for different nanotube surface-to-surface distances dNT. On a hexagonal grid, only two of the parameters dNT, RNT, lx
, and ly
can be chosen independently. Here, we fix the nanotube radius at RNT = 10 rc and the x-dimension as lx
= 38, 42, 48 and 56 rc with lx
> ly
. Consequently,
box, respectively. Chains under confinement are investigated for different nanotube surface-to-surface distances dNT. On a hexagonal grid, only two of the parameters dNT, RNT, lx
, and ly
can be chosen independently. Here, we fix the nanotube radius at RNT = 10 rc and the x-dimension as lx
= 38, 42, 48 and 56 rc with lx
> ly
. Consequently,  and dNT = ly
− 2RNT = 1.9, 4.2, 7.7, 12.3 are determined. The z-length is lz
= 21 rc for all systems. To match a density of
and dNT = ly
− 2RNT = 1.9, 4.2, 7.7, 12.3 are determined. The z-length is lz
= 21 rc for all systems. To match a density of  in the accessible volume Vbox − 2VNT, the total number of beads in the dNT = 1.9, 4.2, 7.7 and 12.3 systems is set to 12 900, 25 000, 45 000, and 74 500, respectively. Exceptions are the
in the accessible volume Vbox − 2VNT, the total number of beads in the dNT = 1.9, 4.2, 7.7 and 12.3 systems is set to 12 900, 25 000, 45 000, and 74 500, respectively. Exceptions are the ![$\left({d}_{\text{NT}}=4.2,N=\left[75,150\right]\right)$](https://content.cld.iop.org/journals/0953-8984/33/24/244001/revision5/cmabef25ieqn12.gif) and
and ![$\left({d}_{\text{NT}}=12.3,N=\left[75,150\right]\right)$](https://content.cld.iop.org/journals/0953-8984/33/24/244001/revision5/cmabef25ieqn13.gif) systems where the total number of beads is 24 900 and 74 550, respectively, to allow an integer number of chains. Simulations are performed with and without slip-springs for every setup. If present, the number of slip-springs is always 10% of the total number of beads. Details of the slip-spring method can be found in reference [5]. Here, we use the same block sequence lengths of 500 DPD steps and 500 MC migration attempts, a pattern chosen to match the spatial correlation of slip-springs in both blocks [5]. The unconfined melts are equilibrated for 5 × 105 (N = [25, 50, 75]) and 1.5 × 106 (N = [100, 150]) time steps, which is longer than any chains' longest relaxation time. Production runs are performed for 3 × 106 time steps. All confined melts are equilibrated for 106 (N = [25, 50, 75]) and 2 × 106 (N = 100, 150) time steps, while data is extracted from 106 (N = [25, 50, 75]) and 5 × 106 (N = [100, 150]) time steps of production. If not denoted otherwise, errors are the standard deviation of the mean of all chains.
systems where the total number of beads is 24 900 and 74 550, respectively, to allow an integer number of chains. Simulations are performed with and without slip-springs for every setup. If present, the number of slip-springs is always 10% of the total number of beads. Details of the slip-spring method can be found in reference [5]. Here, we use the same block sequence lengths of 500 DPD steps and 500 MC migration attempts, a pattern chosen to match the spatial correlation of slip-springs in both blocks [5]. The unconfined melts are equilibrated for 5 × 105 (N = [25, 50, 75]) and 1.5 × 106 (N = [100, 150]) time steps, which is longer than any chains' longest relaxation time. Production runs are performed for 3 × 106 time steps. All confined melts are equilibrated for 106 (N = [25, 50, 75]) and 2 × 106 (N = 100, 150) time steps, while data is extracted from 106 (N = [25, 50, 75]) and 5 × 106 (N = [100, 150]) time steps of production. If not denoted otherwise, errors are the standard deviation of the mean of all chains.
2.3. Knot analysis
In order to describe a knot in a chain mathematically, the chain is required to be closed. The Alexander polynomials [37] are then used as topological invariants to characterize the knots. In this work, we utilize the Kymoknot software [38] (version 1.0), which enables us to analyse knots in open and closed polymers. For the closure of open chains, the minimally-interfering closure scheme [38, 39] is applied. Within this closure scheme, two distinct ways of connecting the chain ends are compared—they are either connected by direct bridging, or via the closest points of the convex hull of the chain portion. The end-to-end distance of the chain is thus compared with the sum over the distances between the chain ends and their closest points on the convex hull. If the former is smaller, simple bridging is applied, otherwise the chain is closed via the convex hull. This closure scheme has shown to be robust and computationally efficient and leads to the least amount of additional entanglements [39].
The smallest region of the chain that has the same topology as the entire chain after closure is considered as the knotted region. Various search schemes can be used for determining knots in a polymer chain which may return different knotted regions [38]. We use a bottom-up approach, which starts from very short, unknotted portions of the chain. These portions are gradually increased until the physical knot of the chain portion equals the knotting type of the whole chain. The remainder of the chain is unknotted. The knot size is then defined as the number of beads within the knotted region.
The kinetics of the constant transition between the knotted and the unknotted state can be analysed as well. For a single chain i, we introduce a state function hi (t), which equals 1 if chain i contains at least one knot and is 0 otherwise. We then define a correlation function C(t) for the knotting dynamics using this state function:
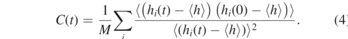
Here, we average over all M chains in the system. The relaxation time of a knot τK is obtained as the integral of the correlation function C(t)
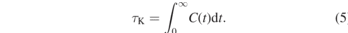
3. Results
3.1. Comparison between hard-core molecular dynamics and soft-core hybrid-particle-field simulations
In this section, we discuss the differences in the knotting behaviour of our hard-core standard MD model and the soft-core hPF model derived from it. In the hPF model, the softness of nonbonded interactions can be controlled by tuning the compressibility parameter κ. Specifically, a smaller value of κ gives a less compressible system, in which less particle overlapping occurs. The chain dimensions of all polystyrene models are shown in figure 2. Among these models, the chain structures are found to be consistent, indicating that the soft-core and hard-core natures do not necessarily alter polymer structural properties on the chain scale. Both the ensemble-averaged squared end-to-end distance  and radius of gyration
and radius of gyration  show the expected linear scaling with the number of monomer N (dashed lines in figure 2) [40]. It should be noted that the compressibility parameter κ must have an impact on the structural behaviour of polymer chains; here, the structural deviation for the employed range of κ is within 3%.
show the expected linear scaling with the number of monomer N (dashed lines in figure 2) [40]. It should be noted that the compressibility parameter κ must have an impact on the structural behaviour of polymer chains; here, the structural deviation for the employed range of κ is within 3%.
Figure 2. Mean squared end-to-end distance  (upper set of symbols) and radius of gyration
(upper set of symbols) and radius of gyration  (lower set of symbols) of polystyrene melts derived from MD and hPF simulations employing different compressibility parameters κ. The lines indicate a linear scaling with the number of monomers N.
(lower set of symbols) of polystyrene melts derived from MD and hPF simulations employing different compressibility parameters κ. The lines indicate a linear scaling with the number of monomers N.
Download figure:
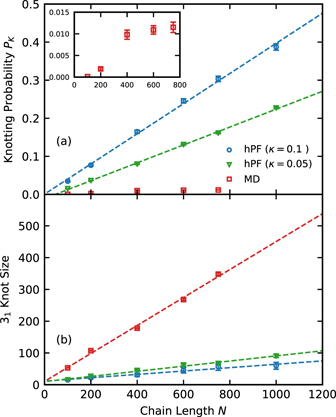
Standard image High-resolution imageNext, we examine the knotting probability and knot size in both soft-core and hard-core models using the knotting analysis presented in subsection 2.3. As shown in figure 3(a), the knotting probability PK of hPF models is profoundly higher than the MD models over the whole range from N = 100 to N = 750 monomers. Moreover, the knotting probability PK of hPF models continuously increases with the polymer chain length N. A linear fit yields slopes of k ≈ 3.9 × 10−4 and k ≈ 2.3 × 10−4 for the hPF models with κ = 0.1 and κ = 0.05, respectively. This indicates that the knotting probability in hPF models with κ = 0.1 is almost 50% higher than that with κ = 0.05. It is noted that the linearity of the knotting probability with the chain lengths in hard-core MD simulations is not as evidently seen as that in the soft-core models. This probably comes from the rather small low statistical value of PK in MD simulations. Nevertheless, the knotting probability in hard-core MD models is sufficiently low in comparison to the soft-core models, implying that the degree of overlapping plays an important role. We further investigate the knot size where we focus on the dominating simple trefoil (31) knot. As illustrated in figure 3(b), the average size detected in the MD model is significantly larger than that in hPF models. Linear fits reveal that approximately 44% of all monomers of any chain are involved in one trefoil 31 knot in the MD model. In contrast, only ∼5% and ∼8% of the monomers per chain form a 31 knot in the hPF models with κ = 0.1 and κ = 0.05, respectively. With the similar characteristic ratio of the polystyrene melt in hPF and MD models, the overestimated knotting probability and underestimated knot size are expected to be intimately related to the soft-core interactions, implying that the overlapping of particles facilitates the localization and occurrence of the formation of a trefoil 31 knot. Recently, Meyer et al [16] studied the knotting properties of generic polymer models with various characteristic ratios using MD simulations and compared their results with the random walk (RW) polymer model. The RW model is found to overestimate the knotting probability and underestimate the knot size in comparison with the simulation model with hard-core repulsive interactions, consistent with our observations in hPF and MD models.
Figure 3. Knotting in polystyrene chains derived from hPF and MD simulations. (a) Shows the probability PK to find at least one knot in a chain of length N. hPF simulations are performed with different compressibility parameters κ. Dashed lines are linear fits with slopes of 3.9 × 10−4 and 2.3 × 10−4 for κ = 0.1 and 0.05, respectively. The inset shows a close-up of the MD results. The average size of a 31 trefoil knot in numbers of monomers is shown in (b) as a function of the chain length N. Dashed lines are linear fits with slopes of 0.05, 0.08 and 0.44 for hPF simulations with κ = 0.1 and 0.05 and MD chains, respectively.
Download figure:
Standard image High-resolution image3.2. Comparison between soft-core models with and without slip-springs
In this section, we study the influence of slip-springs, which are initially designed to mimic the chain entanglements for dynamical properties, on the knotting behaviour of soft-core hPF and DPD models. The typical reptation behaviour of polymer melts was recovered by the introduction of slip-springs to these soft-core models in prior studies [5, 7]. The effect of slip-springs on the conformational properties of polymer chains (e.g. the radius of gyration) in the melt state was found to be negligible. How slip-springs, as artificial ad hoc interactions, affect the self-entanglements (knottedness) of polymer chains is still unknown.
3.2.1. Hybrid-particle-field simulations
We analyse the knotting behaviour in terms of the probability PK to carry at least one knot in hPF models of polystyrene melts with and without slip-springs at various chain lengths. As displayed in figure 4(a), PK of the hPF chains with slip-springs is in good agreement with that without slip-springs at all investigated chain lengths. Figure 4(b) shows the average trefoil 31 knot size for chain lengths between N = 100 and 750 in hPF models with and without slip-springs. Consistent with previous observations for hPF, we find the 31 knot size in hPF simulations with slip-springs to increases with increasing chain length. No significant difference is observed between systems with and without slip-springs. Both of these analyses suggest that slip-springs indeed have a negligible effects on the self-entanglements (knottedness) of polymer chains in hPF simulations within the tested parameter space.
Figure 4. Probability PK for a chain to carry at least one knot (a) and the average size of a 31 trefoil knot in numbers of monomers (b) as a function of the chain length N. Systems are hPF simulations with κ = 0.1, with and without slip-springs.
Download figure:
Standard image High-resolution image3.2.2. Dissipative-particle dynamics simulations of polymer melts
DPD simulations of polymer melts with and without slip-springs are investigated for their probability PK to carry at least one knot per chain, as well as the size of the simple 31 trefoil knot. The results are shown as a function of the number of beads N in figures 5(a) and (b), respectively. They are comparable with those of the hPF model in terms of slip-springs, which show no significant impact on the knotting probability or the knot size. The knotting probability as well as the average knot size of the 31 trefoil knots both increase roughly linearly with the chain length.
Figure 5. Probability PK for a chain to carry at least one knot (a) and the average size of a 31 trefoil knot in numbers of beads (b) as a function of chain length N. Systems are DPD simulations with and without slip-springs. Error bars are within the symbol size.
Download figure:
Standard image High-resolution image3.2.3. Dissipative-particle dynamics simulations of confined polymer melts
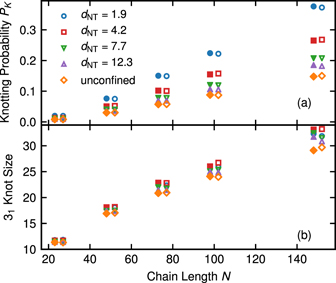
We finally study the knottedness of DPD chains confined by a regular array of nanotubes for different distances dNT between two nanotubes and thus different degrees of confinement. Generally, confinement increases the polymer's compactness. An example plot of the squared radius of gyration  as a function of the chain length N is given as figure A1 in the supplementary information (https://stacks.iop.org/JPCM/33/244001/mmedia) for the strongest confinement (dNT = 1.9) and the unconfined systems.
as a function of the chain length N is given as figure A1 in the supplementary information (https://stacks.iop.org/JPCM/33/244001/mmedia) for the strongest confinement (dNT = 1.9) and the unconfined systems.  shrinks by roughly 35–40% for dNT = 1.9, however, the scaling of
shrinks by roughly 35–40% for dNT = 1.9, however, the scaling of  with N − 1 is barely affected. Further findings concerning the static and dynamic polymer properties will be reported elsewhere. The probability PK of chains of length N to carry at least one knot is given in figure 6(a). Consistent with the observations made for unconfined melts, simulations with and without slip-springs are barely distinguishable. As the distance between the nanotubes dNT decreases, the confined chains assume more compact structures, which is associated with a higher knottedness. For a chain length of N = 150, PK is 18% in the pure melt, while it increases to 39% for a strongly confined system with a nanotube distance of dNT = 1.9. For short chains (N ⩽ 50), the radius of gyration is of similar size as the range of the interstice region between three nanotubes. We do, however, still observe a distinct effect: for N = 25, we see an increase in PK from 0.8% (unconfined) to 2.0% (dNT = 1.9), which is comparable to the increase detected for longer chains. We briefly study the knottedness of a chain as a function of its confinement: a plot of the knotting probability PK against the squared radius of gyration
with N − 1 is barely affected. Further findings concerning the static and dynamic polymer properties will be reported elsewhere. The probability PK of chains of length N to carry at least one knot is given in figure 6(a). Consistent with the observations made for unconfined melts, simulations with and without slip-springs are barely distinguishable. As the distance between the nanotubes dNT decreases, the confined chains assume more compact structures, which is associated with a higher knottedness. For a chain length of N = 150, PK is 18% in the pure melt, while it increases to 39% for a strongly confined system with a nanotube distance of dNT = 1.9. For short chains (N ⩽ 50), the radius of gyration is of similar size as the range of the interstice region between three nanotubes. We do, however, still observe a distinct effect: for N = 25, we see an increase in PK from 0.8% (unconfined) to 2.0% (dNT = 1.9), which is comparable to the increase detected for longer chains. We briefly study the knottedness of a chain as a function of its confinement: a plot of the knotting probability PK against the squared radius of gyration  for various chain lengths and degrees of confinement can be found in figure A2 (supplementary information). For a fixed confinement, PK and
for various chain lengths and degrees of confinement can be found in figure A2 (supplementary information). For a fixed confinement, PK and  show the expected linear relation, as they are both linked by the chain length (
show the expected linear relation, as they are both linked by the chain length ( ). For a fixed chain length N, on the other hand, the knotting probability increases with decreasing
). For a fixed chain length N, on the other hand, the knotting probability increases with decreasing  . However, we did not find a trivial relation between them, e.g. by a power law. This is likely due to the alignment of chains parallel to the nanotubes, and the therefore anisotropic nature of the confinement.
. However, we did not find a trivial relation between them, e.g. by a power law. This is likely due to the alignment of chains parallel to the nanotubes, and the therefore anisotropic nature of the confinement.
Figure 6. Probability PK for a chain to carry at least one knot (a) and the average size of a 31 trefoil knot in numbers of beads (b) as a function of chain length N. Systems are DPD simulations with (full symbols) and without slip-springs (empty symbols). The melt is confined by a regular, hexagonal array of nanotubes with different inter-tube distances dNT. For clarity, the symbols carry an offset of −2 (slip-springs), +2 (no slip-springs). Error bars are within the symbol size.
Download figure:
Standard image High-resolution imageThe average 31 knot size for all systems containing nanotubes (figure 6(b)) reveals a rather weak confinement effect. The influence of slip-springs is negligible, and the slight deviations for longer chains (N ⩾ 100) are likely of statistical nature. Interestingly, the decreasing nanotube distance appears to lead to an increase in the knot size, where a maximum is reached for dNT = 4.4. By analysing the spatial components of the radius of gyration, we find that chains are elongated parallel to the nanotubes. Therefore, generally, chains tend to form larger knots when brought into confinement. However, the size of the interstice region between three nanotubes decreases with decreasing nanotube distance. The size of the radius of gyration of longer chains (N ⩾ 50) thus competes with the diameter of this interstice region, especially for short nanotube surface-to-surface distances. In the case of dNT = 1.9, a larger fraction of chains are spread over multiple interstitial regions. In this case, knots might be formed in parts of the chain that are confined within the interstitial region, leading to smaller knot sizes.
3.3. Comparison with different models
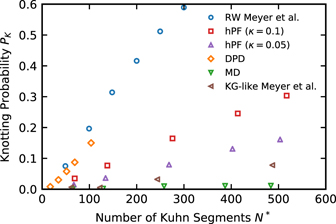
We lastly compare the observed knottedness of our DPD and hPF chains with results reported for different limiting models. We focus on the knotting probabilities of systems without slip-springs. As discussed above, the same observations apply for the slip-spring systems. Recently, Meyer et al [16] investigated the knotting probabilities in self-avoiding model polymer chains with an adjustable bending potential and compared them to those of a RW. We follow their approach to compare the knotting probability of our models on the chains' Kuhn scale: by utilizing the ratio N⋆ = N/C∞, we normalize both the DPD and hPF chain lengths N to the number of Kuhn segments per chain. Here, C∞ is the characteristic ratio and derived from the bond length l between two beads as  . The results are shown in figure 7 along with the data reported in reference [16] for their fully flexible chain and the RW. The fully flexible chain consists of purely repulsive Lennard-Jones beads and a harmonic bond known to reproduce the same chain structures as finitely extensible (FENE) bonds. This, along with a reported characteristic ratio of C∞ = 2.1, makes it very similar to the standard Kremer–Grest (KG) model (C∞,KG = 1.7) [41, 42]. We thus refer to it as a KG-like chain. Coarse-grained MD chains, hPF chains with κ = 0.1 and 0.05, and DPD chains have characteristic ratios of C∞ = 1.55, C∞ = 1.49, C∞ = 1.45 and C∞ = 1.45, respectively, which were derived from their bond lengths of 0.52 nm (hPF) and 1.21 rc (DPD). We find the knotting probability of our hard-core MD simulations to be in the range of, but lower than, that of KG-like chains. The difference probably arises from the different number densities of these two models, as higher densities in polymer systems are known to favour higher knotting probabilities [16]. However, a comparison of both models' number densities is not straightforward and depends on the spatial quantity utilized for mapping. The knotting probability increases for the κ = 0.05 and κ = 0.1 hPF models and the DPD model, respectively, with those of the DPD chain being somewhat lower than for the RW. We note that the Kuhn-scale-reduced DPD model should be taken with a grain of salt, as the mapping of DPD chains usually happens on even coarser scales; however, it serves well for the comparison between models. The PK of the less compressible hPF model (κ = 0.05) lies between those of the more flexible hPF (κ = 0.1) and DPD chains and the hard-core MD model. These results are generally consistent with the findings of Meyer et al: comparing their fully-flexible KG-like chain and the RW, they identify the knotting behaviour to be closely connected to the models' bond–bond correlation functions: since the formation of a knot requires a negative correlation on the respective length scale, the bond–bond correlations as well as their fluctuations determine at which scale and how likely knots are formed [16]. For hard-core models, knots are thus rather rare. In the soft-core limit, RWs allow many and strongly localized knots. Meyer et al conclude that 'real' polymer chain melts, such as the KG-like chain, are rather poorly described by RWs on a local scale [16]. It becomes apparent from figure 7 that soft-core models, especially our DPD system, are much closer to the RW on all scales. Consequently, their knotting probability is much closer to a RW than to a KG-like chain. However, weak local repulsion still exists, and the full knotting probability of the RW is not yet reached. The deviations from a local random-walk behaviour become stronger with increasing excluded-volume effects when going from DPD to the κ = 0.1 and κ = 0.05 hPF models and the hard-core MD model, which all have bending potentials. This causes a decrease of the knotting probability. We note that, if need be, the local structure of hard-core MD or KG-like chains can at least in parts be restored to the hPF models by tuning the compressibility parameter κ.
. The results are shown in figure 7 along with the data reported in reference [16] for their fully flexible chain and the RW. The fully flexible chain consists of purely repulsive Lennard-Jones beads and a harmonic bond known to reproduce the same chain structures as finitely extensible (FENE) bonds. This, along with a reported characteristic ratio of C∞ = 2.1, makes it very similar to the standard Kremer–Grest (KG) model (C∞,KG = 1.7) [41, 42]. We thus refer to it as a KG-like chain. Coarse-grained MD chains, hPF chains with κ = 0.1 and 0.05, and DPD chains have characteristic ratios of C∞ = 1.55, C∞ = 1.49, C∞ = 1.45 and C∞ = 1.45, respectively, which were derived from their bond lengths of 0.52 nm (hPF) and 1.21 rc (DPD). We find the knotting probability of our hard-core MD simulations to be in the range of, but lower than, that of KG-like chains. The difference probably arises from the different number densities of these two models, as higher densities in polymer systems are known to favour higher knotting probabilities [16]. However, a comparison of both models' number densities is not straightforward and depends on the spatial quantity utilized for mapping. The knotting probability increases for the κ = 0.05 and κ = 0.1 hPF models and the DPD model, respectively, with those of the DPD chain being somewhat lower than for the RW. We note that the Kuhn-scale-reduced DPD model should be taken with a grain of salt, as the mapping of DPD chains usually happens on even coarser scales; however, it serves well for the comparison between models. The PK of the less compressible hPF model (κ = 0.05) lies between those of the more flexible hPF (κ = 0.1) and DPD chains and the hard-core MD model. These results are generally consistent with the findings of Meyer et al: comparing their fully-flexible KG-like chain and the RW, they identify the knotting behaviour to be closely connected to the models' bond–bond correlation functions: since the formation of a knot requires a negative correlation on the respective length scale, the bond–bond correlations as well as their fluctuations determine at which scale and how likely knots are formed [16]. For hard-core models, knots are thus rather rare. In the soft-core limit, RWs allow many and strongly localized knots. Meyer et al conclude that 'real' polymer chain melts, such as the KG-like chain, are rather poorly described by RWs on a local scale [16]. It becomes apparent from figure 7 that soft-core models, especially our DPD system, are much closer to the RW on all scales. Consequently, their knotting probability is much closer to a RW than to a KG-like chain. However, weak local repulsion still exists, and the full knotting probability of the RW is not yet reached. The deviations from a local random-walk behaviour become stronger with increasing excluded-volume effects when going from DPD to the κ = 0.1 and κ = 0.05 hPF models and the hard-core MD model, which all have bending potentials. This causes a decrease of the knotting probability. We note that, if need be, the local structure of hard-core MD or KG-like chains can at least in parts be restored to the hPF models by tuning the compressibility parameter κ.
Figure 7. Comparison of the knotting probability PK as a function of the number of Kuhn segments N⋆ = N/C∞ for different models. The characteristic ratio C∞ is 1.55, 1.49, 1.45 and 1.45 for MD, (hPF, κ = 0.1 and 0.05), and DPD simulations, respectively. Probabilities for the fully flexible KG-like model and the RW are taken from reference [16].
Download figure:
Standard image High-resolution image3.4. Dynamics of knot formation and destruction
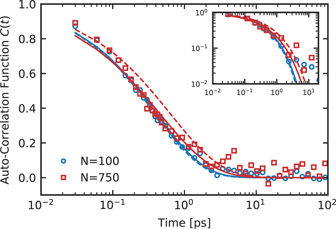
In addition to the static properties related to knotting, we investigate the dynamics of the knotted-to-unknotted transition in the hPF model. Figure 8 displays the autocorrelation function (ACF) of this transition in hPF simulations of polystyrene melts without (a) and with slip-springs (b). In both models, the ACFs exhibit no chain-length dependence. Moreover, we find that the ACFs decay to zero in about ∼10 ps. In order to quantitatively characterize the relaxation time of knot formation dynamics, we fit the ACF by a stretched exponential function
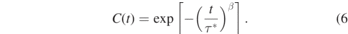
One example is shown in figure 9 for hPF simulations (κ = 0.1) of N = 100 and N = 750 with (solid lines) and without slip-springs (dashed lines). The relaxation time τknot is then calculated as

where Γ represents the complete gamma function. The calculated relaxation times are summarized in table 2. The relaxation time τknot evidently does not depend on the chain length. The knot relaxation happens on a time scale comparable to the time which a monomer needs to diffuse its own diameter. The same results are observed for our DPD models (not shown). Indeed, these results of fast knotting dynamics are not surprising. In the soft-core hPF model, the nonbonded interactions are so soft that the bonds can cross each other. As illustrated in the inset of figure 8(b), the knotted-to-unknotted transition can easily take place at the monomer length and time scale. This transition is essentially insensitive to the chain length and effectively dictated by the monomer relaxation time. A similarly fast relaxation of knotted structures in soft-core models has qualitatively been observed by Meyer et al, who also reported a change in knotting probabilities on drastically shorter time scales than the structural chain relaxation. Moreover, slip-springs in our systems are expected to alter the polymer dynamics only above the entanglement length (Ne) and time (τe) scales. This is consistent with the observation in table 2 that the knot formation dynamic is genuinely unaffected by the addition of slip-springs.
Figure 8. Autocorrelation function of the knotted-to-unknotted interconversion C(t) in hPF simulations without (a) and with slip-springs (b) with a compressibility parameter of κ = 0.1 as a function of chain length N. The inset in (b) is a cartoon of the transition between knotted (i) and unknotted (ii) state via bond-crossing on the scale of single beads.
Download figure:
Standard image High-resolution imageFigure 9. Stretched exponential fits to the knot formation ACFs of hPF simulations (κ = 0.1) with (solid lines) and without (dashed lines) slip-springs for polystyrene chains composed of 100 monomers (blue) and 750 monomers (red). The inset shows the same data in a double-logarithmic presentation.
Download figure:
Standard image High-resolution imageTable 2. Relaxation times of knot formation of hPF simulations (κ = 0.1) with and without slip-springs of polystyrene melts at chain length N ranging from 100 monomers to 750 monomers.
| τknot(ps)/N | 100 | 200 | 400 | 600 | 750 |
|---|---|---|---|---|---|
| hPF | 0.52 | 0.70 | 0.36 | 0.55 | 1.19 |
| hPF + slip-springs | 0.55 | 0.62 | 0.89 | 0.89 | 0.70 |
4. Conclusion
For linear polymer chains in the melt, we have investigated the probability to form knots, the number of monomers involved in an average trefoil knot, as well as the dynamics of knot formation and destruction. The focus was on two series of soft-core polymer models, which we have developed and used in recent years. Firstly, there is the hPF model. For this model, we tested both the standard variant [2] and a variant with slip-springs for better reproduction of entangled dynamics [7]. The interesting aspect of the hPF series of models is that there is also a reference model from which they were derived. This is a veteran hard-core coarse-grained MD model of polystyrene [28]. Secondly, there are two DPD models, one without, the other with slip-springs [5]. No parent hard-core model is available here. We are, thus, able to not only characterize our models for their knotting behaviour, but also to compare, on the one hand, hard-core and soft-core models and, on the other hand, the effect of slip-springs on the knotting properties. It is obvious that the introduction of soft-core nonbonded repulsions leads to a massive increase in the probability for a chain to be knotted, cf e.g. figure 3(a). Throughout all polymer lengths, the increase is more than one order of magnitude (the precise ratio is hard to calculate, because of the very small number of knots of the hard-core model and the resulting noisy statistics). Within the knotting map of polymer models of different hardness or softness, our hard-core CG-PS is in the same class as the KG model as one of the standard hard-core polymer models (figure 7). However, the soft-core DPD model, but also the hPF models, are much closer to the knotting pattern of the random walk, which is the ultimate soft-core model. The knottedness of the hPF model can be tuned, within limits, by manipulating its compressibility, which is linked to the softness of the nonbonded repulsion. The knot size, i.e. the number of monomers participating in a knot, is about 5 times larger for the hard-core models. It should be stressed that, in all other structural aspects, hard-core and soft-core models are identical, with the foreseeable and well-understood exception of the pair-correlation function at short distances [2].
The introduction of slip-springs to a soft-core model (hPF or DPD) influences dramatically the polymer dynamics: it restores successfully the proper reptation motion to the soft-core models [5–7]. However, slip-springs have next to no effect on the knotting probability (figures 4(a) and 5)(a), including for melts under heavy confinement (figure 6(a)). Soft-core models with slip-springs may lead to a marginally smaller knot size than the same models without slip-springs (figures 4(b), 5(b) and 6(b)). It is not clear, however, if this deviation is statistically significant, and it is only found for the longest chains studied.
The investigation of the dynamics of reversible knot formation and destruction sheds some light on the knot formation mechanism in soft-core models. It turns out that all knotting and unknotting happens on the time-scale of single-monomer mobility. In other words, soft-core polymers do not form knots by running one chain end through an existing loop, but by monomers or short chain-segments exchanging positions. This mechanism is not altered by the introduction of slip-springs, as slip-springs enforce a long-time entangled-like dynamics on the polymer chains without actually preventing chains from crossing one another. Therefore, they have no effect on the short-time motion of monomers. The question as to whether the reason for our hard-core model to have much fewer knots than either soft-core model is thermodynamic (hard-core and soft-core models do have different Hamiltonians) or kinetic (hard-core models are forced to physically tie the knot, rather than taking the short-cut of chain-crossing) cannot be answered in this contribution. The hard-core model has too few knotting and unknotting events to calculate a reliable relaxation time for the process.
Note added in the revised manuscript
After the initial submission of this article, a study of knots in soft-core polymer models was published by Zhang et al [43]. Their findings further confirm the importance of local chain properties on their knotting probability, and are generally in line with ours.
Acknowledgments
Fruitful discussions with Peter Virnau are gratefully acknowledged. This work has been funded by the Collaborative Research Centre Transregio 146 'Multiscale Simulation Methods for Soft Matter', project A8, of the Deutsche Forschungsgemeinschaft.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.