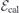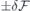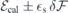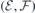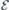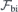Abstract
Point defects in solids are promising single-photon sources with application in quantum sensing, computing and communication. Herein, we describe a theoretical framework for studying electric field effects on defect-related electronic transitions, based on density functional theory calculations with periodic boundary conditions. Sawtooth-shaped electric fields are applied perpendicular to the surface of a two-dimensional defective slab, with induced charge singularities being placed in the vacuum layer. The silicon vacancy (VSi) in 4H-SiC is employed as a benchmark system, having three zero-phonon lines in the near-infrared (V1, V1' and V2) and exhibiting Stark tunability via fabrication of Schottky barrier or p-i-n diodes. In agreement with experimental observations, we find an approximately linear field response for the zero-phonon transitions of VSi involving the decay from the first excited state (named V1 and V2). However, the magnitude of the Stark shifts are overestimated by nearly a factor of 10 when comparing to experimental findings. We discuss several theoretical and experimental aspects which could affect the agreement.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Point defects in semiconductors are rapidly becoming contenders for a host of quantum applications, with properties such as spin manipulation and single-photon emission at room temperature, enabling technologies that range from quantum sensing and information processing to quantum cryptography and communication. Hitherto, the nitrogen-vacancy (NV) center in diamond has been at the forefront, enabling high-sensitivity magnetometers with nanoscale resolution [1], and exhibiting both coherent spin manipulation at room temperature [2] and entanglement between two NV center spins [3]. However, as far as device processing and fabrication is concerned, diamond technology lacks maturity, the fraction of the total NV emission channeled into the zero-phonon line (ZPL) is low (at about 4%) [4], and coupling NV centers to waveguides to enhance emission intensities was shown to have a detrimental effect on spin and emission stability [5, 6].
Over recent years, silicon carbide (and the 4H polytype in particular) has emerged as a competitive alternative to diamond, offering a more mature fabrication technology and greater ease of combining defect centers with various devices [7]. Several candidate defects exist, with the silicon vacancy (VSi), the silicon-carbon divacancy (VSi
VC), the nitrogen-vacancy center (NC
VSi) and the carbon-antisite vacancy pair (CSi
VC) all being room-temperature single-photon sources and exhibiting millisecond spin coherence times under cryogenic conditions [8–13]. However, only one charge state of each defect center exhibits the required properties, with the others remaining dark and without the option of optically controlling and reading out the spin state. For the case of the Si vacancy, the bright charge state is the negative one (represented as  ).
).
Charge-state control over qubit contender defects in 4H-SiC was first demonstrated for VSi and VSi VC by employing dual excitation [14], but the optical approach lacks the option of selective and controlled toggling between specific defect charge states. Recently, electrical charge-state control over VSi and VSi VC was optically detected by monitoring the photoluminescence (PL) emission intensity from defects situated within 4H-SiC membranes in the vicinity of electrodes [15] or in the intrinsic region of 4H-SiC p-i-n diodes [16, 17], and embedded within the depletion region of Ni/4H-SiC Schottky barrier diodes (SBDs) [18]. The electrical approach is particularly interesting as it enables control over not only the intensity, but also the energy, of single-photon emission from qubit defects via the Stark effect [19]. This has been demonstrated for defects such as NV in diamond [20, 21], and also VSi [18, 22] and VSi VC [15, 17, 23] in 4H-SiC.
Importantly, emission from solid-state systems is highly susceptible to local fluctuations related, for instance, to strain and electromagnetic fields. Thus, local inhomogeneities surrounding a defect center will diminish the uniformity of photon energies originating from that specific emitter. Emission tuning, for example via the Stark effect, therefore presents a means towards obtaining high-fidelity and identical photons from solid-state light sources, enabling integration with present and future quantum technologies and facilitating operation of relevant defects as electric field sensors. Moreover, the nature of the Stark shift may help to elucidate defect-related properties such as the local environment, the defect symmetry and the degeneracy of its electronic states. With that in mind, we report on a theoretical method for studying Stark shifts of transitions between electronic states of defects in semiconductors. We will use the negatively charged Si vacancy in 4H-SiC as a model system, and compare the results with observations reported in the literature.
A Si vacancy can inhabit two distinct lattice locations in 4H-SiC, namely the hexagonal (h) and pseudo-cubic (k) sites. These sites have C3v
point group symmetry and essentially differ on the relative positions of their second neighbors and farther atoms. In the ground state, both the 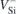 (h) and
(h) and  (k) defects have spin 3/2 and adopt a
(k) defects have spin 3/2 and adopt a 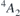 spin-quartet state [24]. To simplify our analysis, we will disregard any fine structure of the many-body states due to spin–orbit and zero-field effects. Within a one-electron picture, the ground state corresponds to a
spin-quartet state [24]. To simplify our analysis, we will disregard any fine structure of the many-body states due to spin–orbit and zero-field effects. Within a one-electron picture, the ground state corresponds to a  configuration as shown on the left-hand side of figure 1(a), with the corresponding one-electron states being depicted in figure 1(b). Besides the singlet and doublet states in the gap, the four carbon radicals of VSi (represented as gray spheres) give rise to a fourth one-electron state which is resonant with the valence band, and is labeled a1,R. This state does not participate in the optical activity of the center.
configuration as shown on the left-hand side of figure 1(a), with the corresponding one-electron states being depicted in figure 1(b). Besides the singlet and doublet states in the gap, the four carbon radicals of VSi (represented as gray spheres) give rise to a fourth one-electron state which is resonant with the valence band, and is labeled a1,R. This state does not participate in the optical activity of the center.
Figure 1. (a) Schematics of the one-electron configurations involved in the luminescent transitions from exited states,  and 4
E, into the 4A2 ground state. Arrows (pointing upwards and downwards) and circles correspond to electrons (with spin-up and spin-down) and holes bound to
and 4
E, into the 4A2 ground state. Arrows (pointing upwards and downwards) and circles correspond to electrons (with spin-up and spin-down) and holes bound to  . The symmetry character of the one-electron states is also indicated. Hatched areas represent crystalline states limited by the valence band top (Ev) and conduction band bottom (Ec). (b) Isosurfaces of the a1 and e states in the gap for ψ = ±0.03 at k = Γ. Si and C atoms are represented as white and gray spheres, respectively. The location of the missing Si atom is indicated as a black dot. (c) Configuration coordinate diagram representing two possible luminescent transitions from the
. The symmetry character of the one-electron states is also indicated. Hatched areas represent crystalline states limited by the valence band top (Ev) and conduction band bottom (Ec). (b) Isosurfaces of the a1 and e states in the gap for ψ = ±0.03 at k = Γ. Si and C atoms are represented as white and gray spheres, respectively. The location of the missing Si atom is indicated as a black dot. (c) Configuration coordinate diagram representing two possible luminescent transitions from the  excited state into 4A2 ground state. The system either combines a radiative decay (with energy Erad) with a non-radiative relaxation step (releasing a Franck–Condon energy EFC), for instance via multi-phonon emission, or it undergoes a zero-phonon transition maximizing the energy of the emitted photon (EZPL).
excited state into 4A2 ground state. The system either combines a radiative decay (with energy Erad) with a non-radiative relaxation step (releasing a Franck–Condon energy EFC), for instance via multi-phonon emission, or it undergoes a zero-phonon transition maximizing the energy of the emitted photon (EZPL).
Download figure:
Standard image High-resolution imageThree different zero phonon lines (ZPLs) are attributed to 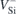 in 4H-SiC. They are labeled V1 and V1', arising from the decay of two different but close-lying excited states of the same defect center, and V2. V1/V1' and V2 have been assigned to the h and k configurations of VSi, respectively [25]. The corresponding ZPL energies fall in the near-infrared range (860–916 nm), and are thus better suited for integration with fiber optical communication than, e.g., the NV center in diamond which emits in the red. All three lines have been interpreted as arising from spin-down channel radiative transitions involving two close-lying excited states, namely
in 4H-SiC. They are labeled V1 and V1', arising from the decay of two different but close-lying excited states of the same defect center, and V2. V1/V1' and V2 have been assigned to the h and k configurations of VSi, respectively [25]. The corresponding ZPL energies fall in the near-infrared range (860–916 nm), and are thus better suited for integration with fiber optical communication than, e.g., the NV center in diamond which emits in the red. All three lines have been interpreted as arising from spin-down channel radiative transitions involving two close-lying excited states, namely 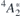 and 4
E. Their corresponding one-electron configurations are depicted in figure 1(a). While
and 4
E. Their corresponding one-electron configurations are depicted in figure 1(a). While 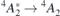 transitions, which involve
transitions, which involve  and
and  , give rise to the V1 (EZPL = 1.438 eV) and V2 (EZPL = 1.352 eV) ZPLs, respectively,
, give rise to the V1 (EZPL = 1.438 eV) and V2 (EZPL = 1.352 eV) ZPLs, respectively,  in
in  leads to the V1' emission line (EZPL = 1.443 eV) [26]. It is expected that analogously to
leads to the V1' emission line (EZPL = 1.443 eV) [26]. It is expected that analogously to  (h),
(h),  (k) should produce a V2' counterpart. So far, and despite many attempts, such a signal has escaped detection.
(k) should produce a V2' counterpart. So far, and despite many attempts, such a signal has escaped detection.
In figure 1 we suggest that the excited states of 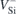 possess a pseudo-acceptor character. Accordingly, they consist of an electron strongly bound to
possess a pseudo-acceptor character. Accordingly, they consist of an electron strongly bound to 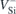 (red colored downward arrows) whose negative charge secures a weakly bound hole (red circles). This picture, where the
(red colored downward arrows) whose negative charge secures a weakly bound hole (red circles). This picture, where the 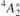 state is effectively a double negatively charged vacancy (
state is effectively a double negatively charged vacancy ( ) perturbed by a diffuse hole, is coherent with the fact that the V1 and V2 ZPL energies are very close to the calculated energy difference between the first and second acceptor levels of VSi in 4H-SiC, E(=/−) − E(−/0) = 1.4 eV [18, 27] (the small discrepancy being accounted for by a meV-range hole binding energy).
) perturbed by a diffuse hole, is coherent with the fact that the V1 and V2 ZPL energies are very close to the calculated energy difference between the first and second acceptor levels of VSi in 4H-SiC, E(=/−) − E(−/0) = 1.4 eV [18, 27] (the small discrepancy being accounted for by a meV-range hole binding energy).
In reference [18], a pronounced quadratic Stark shift was shown for the V1' ZPL upon application of a bias to SBD devices along the hexagonal crystallographic axis (0001). Similar behavior was subsequently reported in reference [22], but now adding the effect of the electric field applied along the crystallographic basal direction as well. Here, the observation of a two-fold splitting of the V1' line nicely accounted for the double degeneracy of the 4 E excited state. A Stark shift was also reported for the V1 ZPL [22]. In this case, approximately linear and quadratic shifts were observed when the field was along the main axis and parallel to the basal plane, respectively.
Despite several reports on the calculation of Stark shifts using first principles methods (see for instance reference [28] on C–O and C–N bonds in small molecules and references [29, 30] about hexagonal boron nitride), this effect has not been addressed for the case of defects in solids. In principle, the combination of reasonable accuracy with the ability to account for the electronic structure of thousands of atoms makes the Kohn–Sham formalism to density functional theory (DFT) the method of choice for such a calculation. However, a major difficulty arises upon the incorporation of a macroscopic field into the Hamiltonian, which desirably should be constructed from first-principles, and mostly uses three-dimensional periodic boundary conditions. Additionally, since we may be dealing with defects with open-shell or metallic-like states, we cannot employ the Berry-phase theory of polarization [31]. While a possible approach involves the incorporation of a sawtooth-shape potential across the periodic cell [32], in the case of a solid, numerical instabilities hamper the calculations due to the superposition of strongly varying potential 'teeth' with the atomic potentials. Note that according to the Poisson equation, this method effectively translates into placing two parallel sheets of high charge density with opposite sign within the supercell. Of course, the above is not an issue for the calculation of molecules within open boundary conditions [28], not even for defects in surfaces and 2D-materials calculated in 3D-supercells [29, 33], where the potential 'teeth' can be placed within vacuum regions.
Herein, we propose that Stark shifts of defect states in bulk semiconductors can still be evaluated using 3D periodic boundary conditions. To that end, we use periodic slabs separated by thick vacuum layers wherein we place the field 'teeth' (section 2). Semi-local and hybrid DFT calculations are employed to investigate the effect of macroscopic fields on the ground and excited states of 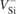 (h) and
(h) and  (k). We describe a calibration step that should be performed for the case of non-centrosymmetric materials (like 4H-SiC), where a polarization is induced by the asymmetric slab surfaces (section 3). The field dependence of the
(k). We describe a calibration step that should be performed for the case of non-centrosymmetric materials (like 4H-SiC), where a polarization is induced by the asymmetric slab surfaces (section 3). The field dependence of the  zero-phonon transition energies is obtained within the delta-self consistent field approach (Δ-SCF), and the results are compared to experimental data (section 4). Finally, we draw several remarks and conclusions in section 5.
zero-phonon transition energies is obtained within the delta-self consistent field approach (Δ-SCF), and the results are compared to experimental data (section 4). Finally, we draw several remarks and conclusions in section 5.
2. Methodology
The calculations reported below employ the Kohn–Sham density functional method as implemented in the Quantum ESPRESSO software [34, 35]. Importantly, this particular code allows for simultaneously (i) constraining the occupation of the one-electron states (needed for studying ground and excited states of  ), (ii) the use of supercells with arbitrary shape (hexagonal for the case of 4H-SiC), (iii) applying an external periodic electric field, (iv) solving the Kohn–Sham problem self-consistently (subject to the external field and occupancy constraints), (v) the use of charged supercells, and finally (vi) calculating the forces on atoms, relaxing the atomistic structure and finding the total energy. Most results reported below employ the semi-local functional of Perdew, Burke and Ernzerhof (PBE) [36] for describing the many-body electronic interactions. A limited number of calculations were carried out using a non-local hybrid functional as proposed by Song, Yamashita and Hirao [37], and in this case they are flagged with the 'Gau-PBE' label. Unfortunately, due to the complexity of the calculations, numerical instabilities frustrated any attempt to obtain self-consistent hybrid-DFT energies for the excited states when subject to electric fields. Hence, calculated transition dipole and polarizability values were found within the PBE level.
), (ii) the use of supercells with arbitrary shape (hexagonal for the case of 4H-SiC), (iii) applying an external periodic electric field, (iv) solving the Kohn–Sham problem self-consistently (subject to the external field and occupancy constraints), (v) the use of charged supercells, and finally (vi) calculating the forces on atoms, relaxing the atomistic structure and finding the total energy. Most results reported below employ the semi-local functional of Perdew, Burke and Ernzerhof (PBE) [36] for describing the many-body electronic interactions. A limited number of calculations were carried out using a non-local hybrid functional as proposed by Song, Yamashita and Hirao [37], and in this case they are flagged with the 'Gau-PBE' label. Unfortunately, due to the complexity of the calculations, numerical instabilities frustrated any attempt to obtain self-consistent hybrid-DFT energies for the excited states when subject to electric fields. Hence, calculated transition dipole and polarizability values were found within the PBE level.
The effect of core electrons was accounted for by using norm-conserving pseudopotentials [38, 39], whereas the valence was described by a plane-wave basis. Accordingly, energy cut-offs of  eV and
eV and  were found sufficient to provide convergence with respect to the quality of the Kohn–Sham wave functions and potential/density fields, respectively. An external electric field with magnitude
were found sufficient to provide convergence with respect to the quality of the Kohn–Sham wave functions and potential/density fields, respectively. An external electric field with magnitude 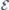 was applied by adding a sawtooth term to the local potential along the z-coordinate (parallel to the c-axis of 4H-SiC). The slope of the sawtooth potential was
was applied by adding a sawtooth term to the local potential along the z-coordinate (parallel to the c-axis of 4H-SiC). The slope of the sawtooth potential was  across the whole cell, except within a short 0.1 Å interval where it ramped-up to comply with the periodic boundary conditions. In order to avoid the superposition of artificial charge density singularities (induced by the potential 'teeth') with the SiC electronic states, we employ vacuum-separated 4H-SiC periodic slabs with Si and C surface atoms saturated by hydrogen. The potential 'teeth' were therefore placed inside the vacuum region.
across the whole cell, except within a short 0.1 Å interval where it ramped-up to comply with the periodic boundary conditions. In order to avoid the superposition of artificial charge density singularities (induced by the potential 'teeth') with the SiC electronic states, we employ vacuum-separated 4H-SiC periodic slabs with Si and C surface atoms saturated by hydrogen. The potential 'teeth' were therefore placed inside the vacuum region.
Figure 2(a) shows a side view of a hydrogen-terminated slab used in this study with a hexagonal (h) lattice plane at its center. The figure also shows a VSi(h) defect as indicated by a black dot. An analogous slab with a pseudo-cubic middle layer was employed to study VSi(k). The limits of the whole supercell are indicated by the box, which in the case of a pristine slab encloses a total of 300 atoms, including 25 hydrogen atoms on each face. The primitive lattice vectors of bulk 4H-SiC (a1 = a2 and a3) and positive direction of the applied electric field are also shown. The lateral size of the supercell was 5a1 = 15.356 Å, whereas the axial length was 2a3 = 20.103 Å. The vacuum width was about 1/3 of the total length of the supercell. For sampling the Brillouin zone, we used a 2 × 2 × 1 mesh of k-points for all PBE-level calculations, while Γ-sampling was used for the hybrid Gau-PBE calculations.
Figure 2. (a) Side view of a hydrogen-terminated h-plane centered 4H-SiC slab used in this study with a VSi(h) defect located in the middle (black dot). The limits of the supercell are indicated by the box. Primitive lattice vectors (a1 and a3), crystallographic directions and positive direction of the applied electric field (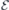 ) are also shown. Silicon, carbon and hydrogen atoms are represented as white, gray and black spheres, respectively. (b) Analysis of the electrostatic potential across a pristine slab for zero electric field (left) and when the applied field is
) are also shown. Silicon, carbon and hydrogen atoms are represented as white, gray and black spheres, respectively. (b) Analysis of the electrostatic potential across a pristine slab for zero electric field (left) and when the applied field is 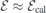 (right, see text). The data presented includes the xy-averaged electrostatic potential energy (ϕxy
), the rolling-averaged potential (ϕRA) and the macroscopic potential in the slab (ϕm
) as found from a linear fit to the ϕRA data near the center of the slab. (c) Calculated local field in the middle of h- and k-centered pristine slabs against the applied electric field,
(right, see text). The data presented includes the xy-averaged electrostatic potential energy (ϕxy
), the rolling-averaged potential (ϕRA) and the macroscopic potential in the slab (ϕm
) as found from a linear fit to the ϕRA data near the center of the slab. (c) Calculated local field in the middle of h- and k-centered pristine slabs against the applied electric field,  . Best linear fits to the data are also shown (see equation (2)).
. Best linear fits to the data are also shown (see equation (2)).
Download figure:
Standard image High-resolution imageThe coordinates of the hydrogen atoms saturating the surfaces were optimized in a first step (keeping all SiC atoms locked to their crystalline coordinates). This avoided the appearance of any spurious gap states due to residual strain in the Si–H and C–H bonds. During all subsequent atomic relaxations, the Si–H and C–H surface pairs were kept frozen and only inner layer atoms were allowed to move. Further constraints included the charge state (negative), the one-electron occupancy (for excited states) and the presence of the external field. Tolerances for the largest force during ionic relaxations and for the self-consistent total energy were 0.01 eV Å−1 and 1 μeV, respectively. Finally, we computed the ZPL energy, EZPL, according to the delta-self consistent field (Δ-SCF) method [40–42]. As depicted in figure 1(c), EZPL is found from the energy difference between the minimum energy configurations of excited and ground states under the effect of an external field. This approach naturally accounts for any Frank–Condon relaxation contribution, EFC, to the ZPL energies.
3. Electric field calibration
The effect of the polarization induced by the asymmetric slab surfaces can be seen on the left-hand-side graph of figure 2(b), where we plot the xy-averaged electrostatic potential, ϕxy
(z), across a pristine slab (red line) and its rolling average, ϕRA(z), obtained within a window of width a3 = 10.05 Å. The presence of an induced dipole is demonstrated by a non-vanishing slope of ϕRA within the slab under zero-field conditions ( ). Here, any defect introduced into the slab will be subject to a local macroscopic field
). Here, any defect introduced into the slab will be subject to a local macroscopic field
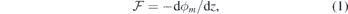
where ϕm is the macroscopic electrostatic potential across the slab. In the present context, the expression macroscopic refers to a space-averaged quantity that is free of atomic-scale variations. We found ϕm from a linear fit to ϕRA in the central region of the slab (straight black line in figure 2(b)).
To first order (linear media), a change in an externally applied electric field ( ) induces a proportional variation in the local field within the slab (
) induces a proportional variation in the local field within the slab (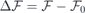 ),
),
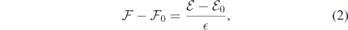
where 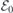 and
and 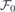 are arbitrary and
are arbitrary and  is the effective slab screening constant. For the sake of convenience we rewrite the above as
is the effective slab screening constant. For the sake of convenience we rewrite the above as
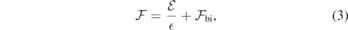
where we set  and
and 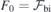 , the latter representing the built-in field induced across the slab mentioned above. Both
, the latter representing the built-in field induced across the slab mentioned above. Both  and
and  can be found by linear fitting of equation (3) to a set of
can be found by linear fitting of equation (3) to a set of 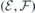 data points from defect-free slab calculations. Importantly, we can calibrate the applied field, that is, we can find the field
data points from defect-free slab calculations. Importantly, we can calibrate the applied field, that is, we can find the field  which neutralizes the built-in field, as well as its effect on defects introduced in the slab. The result of this condition is shown on the right-hand-side plot in figure 2(b). Of course, calibration of
which neutralizes the built-in field, as well as its effect on defects introduced in the slab. The result of this condition is shown on the right-hand-side plot in figure 2(b). Of course, calibration of  is only necessary when the slab surfaces induce an internal field (e.g., slabs made of non-centrosymmetric materials). Although not unique, the procedure can be summarized by the following steps:
is only necessary when the slab surfaces induce an internal field (e.g., slabs made of non-centrosymmetric materials). Although not unique, the procedure can be summarized by the following steps:
- (a)From a zero-field calculation (using a pristine slab), estimate the spurious built-in field as
 ;
; - (b)Find an estimate for
 as
as  , where
, where  s is the static dielectric constant of the material. For SiC we employ
s is the static dielectric constant of the material. For SiC we employ  s = 10;
s = 10; - (c)Chose a local field range
 and corresponding applied field range
and corresponding applied field range  (see below for further details);
(see below for further details); - (d)Calculate from first-principles a set of
 data points within the selected
data points within the selected  -field range;
-field range; - (e)
After obtaining the values of  and
and  (for h- and k-centered slabs), we are ready to introduce a silicon vacancy into the slab and probe its response to an arbitrary field
(for h- and k-centered slabs), we are ready to introduce a silicon vacancy into the slab and probe its response to an arbitrary field  . For that, we set the applied field to
. For that, we set the applied field to 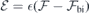 and monitor the Stark shift using a second-order expansion in the local field,
and monitor the Stark shift using a second-order expansion in the local field,
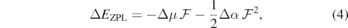
where Δμ and Δα are the respective changes in dipole moment and polarizability between the excited and ground states [43]. Although in general the dipole moment and polarizability of a defect state are, respectively, vectorial and second-rank tensorial quantities, equation (4) is reduced to a scalar form, reflecting the fact that we will analyze the Stark shifts for fields along the c-axis of the crystal.
Figure 2(c) shows the best linear fits to the calculated  data points obtained for h-centered and k-centered pristine slabs. The built-in fields in the slabs, as found from the fittings to equation (3), are
data points obtained for h-centered and k-centered pristine slabs. The built-in fields in the slabs, as found from the fittings to equation (3), are 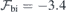 MV m−1 and −2.6 MV m−1 (horizontal dashed lines), while the slab dielectric constants are
MV m−1 and −2.6 MV m−1 (horizontal dashed lines), while the slab dielectric constants are  = 10.1 and 11.4 for the h- and k-centered slabs, respectively. The calculated values of
= 10.1 and 11.4 for the h- and k-centered slabs, respectively. The calculated values of  are rather close to the measured static dielectric component parallel to the c-axis for bulk 4H-SiC (
are rather close to the measured static dielectric component parallel to the c-axis for bulk 4H-SiC ( || = 10.03 [44]). We emphasize that the geometry of the inner layers of the slabs were fully relaxed for each value of
|| = 10.03 [44]). We emphasize that the geometry of the inner layers of the slabs were fully relaxed for each value of  . This implies that the screening response accounts for both electronic polarization (ion-clamped conditions) as well as for ionic polarization effects.
. This implies that the screening response accounts for both electronic polarization (ion-clamped conditions) as well as for ionic polarization effects.
The bare field that has to be imposed in order to offset the local field to zero is  MV m−1 and 29.6 MV m−1 for h- and k-slabs, respectively (vertical dashed lines in figure 2(c)). Hence, if we consider probing VSi defects with fields
MV m−1 and 29.6 MV m−1 for h- and k-slabs, respectively (vertical dashed lines in figure 2(c)). Hence, if we consider probing VSi defects with fields  , the applied field
, the applied field  will be in the range
will be in the range  .
.
Before moving on to the results section, we leave a few remarks regarding accuracy issues. According to experiments [18, 22], local fields of up to about  MV m−1 lead to Stark shifts of the V1 and V1' lines in the meV range. These correspond to changes in the electric dipole and polarizability on the order of Δμ ∼ 1 D and Δα ∼ 103 Å3. From the point of view of conducting the calculations, the convergence tolerance of the total energy should be tight enough as to provide us with a sub-0.1 meV numerical error in energy differences. Among the most important issues to take care of, we single out (i) keeping the Si–H and C–H units frozen during all calculations and (ii) when finding the ground state of a defect under a particular field, one should start the self-consistent calculation with the solution found from a previous calculation, ideally from one with a close electric field.
MV m−1 lead to Stark shifts of the V1 and V1' lines in the meV range. These correspond to changes in the electric dipole and polarizability on the order of Δμ ∼ 1 D and Δα ∼ 103 Å3. From the point of view of conducting the calculations, the convergence tolerance of the total energy should be tight enough as to provide us with a sub-0.1 meV numerical error in energy differences. Among the most important issues to take care of, we single out (i) keeping the Si–H and C–H units frozen during all calculations and (ii) when finding the ground state of a defect under a particular field, one should start the self-consistent calculation with the solution found from a previous calculation, ideally from one with a close electric field.
Another important issue is to make sure that electrons do not leak out from nor get poured into defect states upon the application of the field (ex. into surface states or into excited states). This can be inspected by closely monitoring the population of the band structure, to ensure that the 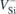 defect state ordering envisaged in figure 1(a) is maintained throughout the calculations.
defect state ordering envisaged in figure 1(a) is maintained throughout the calculations.
Due to electronic confinement along the direction perpendicular to the slab surfaces, the calculated band-gap (within PBE) is Eg = 2.6 eV. This is considerably larger than the gap width of bulk 4H-SiC (Eg = 2.0 eV using the same theory level), but closer to the experimental figure (3.2 eV). This artificial, albeit convenient, effect is expected to reduce the overestimated and detrimental resonances between gap states and crystalline states that typically affect local and semi-local calculations.
Single determinant calculations of EZPL values usually yield absolute accuracies of around ∼0.1 eV [45]. This figure is at least two orders of magnitude larger than the largest Stark shifts observed for V1/V1' and V2 lines [18, 22]. However, we are actually interested in the shift ΔEZPL, whose calculation involves the energy difference between two systems which differ only by a slight perturbation of the electron density, due to a small change in the electric field magnitude. As for other differential quantities, such as vibrational mode frequencies with typical error bars of a few tens of cm−1, the geometries and electronic structure of the differentiating states remain very similar and the results benefit from cancellation of systematic errors (e.g., due to finite size effects or basis incompleteness).
Finally, the nearly linear behavior of 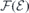 in figure 2(c) and the screening response of the slabs to external fields (showing values of
in figure 2(c) and the screening response of the slabs to external fields (showing values of  close to the experimental figure) give us confidence in the method.
close to the experimental figure) give us confidence in the method.
4. Results and discussion
We now report on the application of the above methodology for the case of VSi in 4H-SiC. After calibration of the field, we calculated the change in the zero-phonon transition energies with the local field amplitude. The one-electron occupancy was kept fixed to enforce the electronic configurations of the S = 3/2 states of 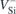 (see figure 1(a)). The optical transitions referred to as V1/V1' and V2/V2', respectively attributed to
(see figure 1(a)). The optical transitions referred to as V1/V1' and V2/V2', respectively attributed to  (h) and
(h) and 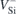 (k), are spin-conserving and involve changes in the occupancy of the minority-spin channel. Although V2' has not been detected experimentally, possibly due to a lifetime- or dynamical-related broadening effect or overlap with the phonon-side bands of V1 and V2, we still consider it in our analysis for the sake of completeness.
(k), are spin-conserving and involve changes in the occupancy of the minority-spin channel. Although V2' has not been detected experimentally, possibly due to a lifetime- or dynamical-related broadening effect or overlap with the phonon-side bands of V1 and V2, we still consider it in our analysis for the sake of completeness.
V1 and V2 arise from  transitions, whereas V1' and V2' involve
transitions, whereas V1' and V2' involve  transitions. The ground state organizes as
transitions. The ground state organizes as ![${}^{4}A_{2}\equiv {\Gamma }_{\mathrm{v}}\left({\uparrow}{\downarrow}\right)+\left[{a}_{1}\left({\uparrow}\right)+e\left(x\enspace {\uparrow},y\enspace {\uparrow}\right)\right]$](https://content.cld.iop.org/journals/0953-8984/33/7/075502/revision3/cmabc804ieqn71.gif) , while first and second excited states are
, while first and second excited states are ![${}^{4}A_{2}^{{\ast}}\equiv {\Gamma }_{\mathrm{v}}\left({\uparrow} {\circ}\right)+\left[{a}_{1}\left({\uparrow}{\downarrow}\right)+e\left(x\enspace {\uparrow},y\enspace {\uparrow}\right)\right]$](https://content.cld.iop.org/journals/0953-8984/33/7/075502/revision3/cmabc804ieqn72.gif) and 4
E ≡ Γv(↑ ◦) + [a1(↑) + e(x ↑↓, y ↑)], respectively [46]. In this notation, localized states in the forbidden gap are enclosed within square brackets, upward and downward arrows stand for occupied spin-up and spin-down states, respectively, while the small circle refers to the lack of an electron which has been promoted to a higher-lying state. Doublet states are resolved into x and y components. The label Γv identifies a state that results from mixing between valence band states with a resonating a1,R
state of the defect (see figure 1(a)). In the excited state configurations, Γv holds a diffuse hole overlapping the vacancy. In practice, Γv is taken as the highest occupied valence band state of the pristine slab, i.e., just below a1 in the energy scale. Notably, the V1' and V2' luminescent transitions involve a degenerate and open-shell initial (excited) state. In this case, a Jahn–Teller distortion is expected to take place. To account for that, we allowed the structures to relax without symmetry constraints. The distortion is not affected by the electric field—the latter is invariant with respect to all operations of the C3v
point group of the VSi defect. Further details of this problem have been addressed elsewhere [26] and fall outside the scope of the present work.
and 4
E ≡ Γv(↑ ◦) + [a1(↑) + e(x ↑↓, y ↑)], respectively [46]. In this notation, localized states in the forbidden gap are enclosed within square brackets, upward and downward arrows stand for occupied spin-up and spin-down states, respectively, while the small circle refers to the lack of an electron which has been promoted to a higher-lying state. Doublet states are resolved into x and y components. The label Γv identifies a state that results from mixing between valence band states with a resonating a1,R
state of the defect (see figure 1(a)). In the excited state configurations, Γv holds a diffuse hole overlapping the vacancy. In practice, Γv is taken as the highest occupied valence band state of the pristine slab, i.e., just below a1 in the energy scale. Notably, the V1' and V2' luminescent transitions involve a degenerate and open-shell initial (excited) state. In this case, a Jahn–Teller distortion is expected to take place. To account for that, we allowed the structures to relax without symmetry constraints. The distortion is not affected by the electric field—the latter is invariant with respect to all operations of the C3v
point group of the VSi defect. Further details of this problem have been addressed elsewhere [26] and fall outside the scope of the present work.
Table 1 reports the calculated ZPL energies for the 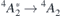 and
and  transitions of
transitions of  (h) and
(h) and  (k) in the slabs. The calculations reported in table 1 were all carried out with
(k) in the slabs. The calculations reported in table 1 were all carried out with  , i.e., the field in the vacuum layer was
, i.e., the field in the vacuum layer was  . Quantities outside parentheses were obtained according to the Δ-SCF method using fully relaxed structures. On the other hand, results within parentheses were found from the energy difference of two spin-down Kohn–Sham eigenvalues of the
. Quantities outside parentheses were obtained according to the Δ-SCF method using fully relaxed structures. On the other hand, results within parentheses were found from the energy difference of two spin-down Kohn–Sham eigenvalues of the  ground state, which involve the electron exchange during the transition. Unfortunately, self-consistency of the Kohn–Sham problem proved exceedingly difficult to achieve for excited state calculations. While this was still possible for the lower energy
ground state, which involve the electron exchange during the transition. Unfortunately, self-consistency of the Kohn–Sham problem proved exceedingly difficult to achieve for excited state calculations. While this was still possible for the lower energy  transitions,
transitions,  transition energies could not be obtained, except when using the Kohn–Sham energies from
transition energies could not be obtained, except when using the Kohn–Sham energies from 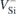 ground states alone (quantities enclosed in parentheses in table 1). Within the latter approach, we found a ∼50 meV monoclinic splitting of the two degenerate
ground states alone (quantities enclosed in parentheses in table 1). Within the latter approach, we found a ∼50 meV monoclinic splitting of the two degenerate  transitions due to Jahn–Teller unfolding of the e-states. Table 1 reports only the lower transition energy counterpart.
transitions due to Jahn–Teller unfolding of the e-states. Table 1 reports only the lower transition energy counterpart.
Table 1. Calculated (Calc.) excited-to-ground state transition energies EZPL for the 4
 4
A2 and 4
E → 4
A2 transitions of
4
A2 and 4
E → 4
A2 transitions of 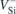 (h) and
(h) and 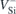 (k). Quantities outside parentheses were obtained from the total energies of fully relaxed defects in the ground and excited states of
(k). Quantities outside parentheses were obtained from the total energies of fully relaxed defects in the ground and excited states of  . The ZPL energies within parentheses were found from energy differences between the unoccupied and occupied Kohn–Sham eigenvalues within the band gap of the respective ground state. Assignments of V1/V1' and V2 to the experimental data (Exp.) are also included [47]. ND stands for not detected. All values are in eV.
. The ZPL energies within parentheses were found from energy differences between the unoccupied and occupied Kohn–Sham eigenvalues within the band gap of the respective ground state. Assignments of V1/V1' and V2 to the experimental data (Exp.) are also included [47]. ND stands for not detected. All values are in eV.
| Defect | Transition | Calc. | Exp. | ZPL |
|---|---|---|---|---|
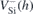
|
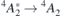
| 1.32 (1.38) | 1.438 | V1 |

| (1.44) | 1.443 | V1' | |

|

| 1.26 (1.35) | 1.352 | V2 |

| (1.39) | ND | V2' |
The experimental values from reference [47] are shown next to the calculations in table 1. In general, the calculated figures match rather well the experimental data and they differ by less than 10%. As discussed at the end of section 3, this agreement benefits from the artificial opening of the band gap due to the slab boundary conditions. Notably as well, in agreement with the experiments, all calculated ZPL energies related to VSi(h) are invariably higher than the analogous quantities for VSi(k). Hybrid-DFT calculations of the 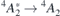 transitions using the Gau-PBE functional overestimate experimental data by about 0.2 eV. For the sake of comparison, we calculated selected ZPL transition energies using bulk orthorombic (hexagonal) supercells without vacuum comprising 96 (400) atoms. We computed VSi(h) transition energies of 1.414 eV (1.412 eV) for the
transitions using the Gau-PBE functional overestimate experimental data by about 0.2 eV. For the sake of comparison, we calculated selected ZPL transition energies using bulk orthorombic (hexagonal) supercells without vacuum comprising 96 (400) atoms. We computed VSi(h) transition energies of 1.414 eV (1.412 eV) for the 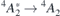 transition, and 1.428 eV for
transition, and 1.428 eV for  . Comparing with the literature, our zero-field transition energies land slightly below other computed values [25, 26], but show similar agreement (below ∼10% difference) with experiment. Indeed, the slight underestimation of experimental data found herein (see table 1) can be attributed to the use of a semi-local functional. Reference [25] reported hybrid-level values of 1.541 eV for V1 and 1.443 eV for V2, the overestimation likely arising from the use of the HSE06 functional. Reference [26] computed ZPL energies of 1.450 eV and 1.385 eV for V1 and V2, respectively, but reported higher transition energies for the second electronic
. Comparing with the literature, our zero-field transition energies land slightly below other computed values [25, 26], but show similar agreement (below ∼10% difference) with experiment. Indeed, the slight underestimation of experimental data found herein (see table 1) can be attributed to the use of a semi-local functional. Reference [25] reported hybrid-level values of 1.541 eV for V1 and 1.443 eV for V2, the overestimation likely arising from the use of the HSE06 functional. Reference [26] computed ZPL energies of 1.450 eV and 1.385 eV for V1 and V2, respectively, but reported higher transition energies for the second electronic  excitations at 1.792 eV and 1.953 eV, respectively, for V1' and V2'.
excitations at 1.792 eV and 1.953 eV, respectively, for V1' and V2'.
Regarding the Kohn–Sham based results, besides being derived from quantities with a weak physical meaning, they do not account for a small Franck–Condon relaxation energy in the excited state. This explains why they slightly overestimate their Δ-SCF counterparts. Despite the insufficiencies, they reproduce the observed V1 and V2 energy ordering and they allow us to suggest that the V2' transition energy is a few tens of meV below V1' and close to V1.
Figure 3 represents the field dependence of the 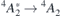 transitions of
transitions of  at h- (figure 3(a)) and k-sites (figure 3(b)) as calculated using the Δ-SCF method at PBE level. The solid lines represent the best fits of equation (4) to the first-principles data (black circles). Considering the magnitude of the fields applied, approximately linear Stark shifts were found for both VSi(h) and VSi(k). A strictly linear Stark effect is often not observed in non-centrosymmetric defects. A notable example is the NV center in diamond [20]. The weak parabolic dependence of ΔEZPL on
at h- (figure 3(a)) and k-sites (figure 3(b)) as calculated using the Δ-SCF method at PBE level. The solid lines represent the best fits of equation (4) to the first-principles data (black circles). Considering the magnitude of the fields applied, approximately linear Stark shifts were found for both VSi(h) and VSi(k). A strictly linear Stark effect is often not observed in non-centrosymmetric defects. A notable example is the NV center in diamond [20]. The weak parabolic dependence of ΔEZPL on  could be explained by field-induced couplings of defect and crystalline states [43]. From the fittings to the data we found variations of the electric dipole moment and polarizability as Δμ = 1.46 D and Δα = −640 Å3 for VSi(h), and Δμ = 3.92 D and Δα = −920 Å3 for VSi(k) (1D = 3.34 × 1030 C m and
could be explained by field-induced couplings of defect and crystalline states [43]. From the fittings to the data we found variations of the electric dipole moment and polarizability as Δμ = 1.46 D and Δα = −640 Å3 for VSi(h), and Δμ = 3.92 D and Δα = −920 Å3 for VSi(k) (1D = 3.34 × 1030 C m and 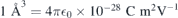 ). The relative error bars for dipole and polarizability changes are less than 1% and about 10%, respectively. We note that because of the nearly linear dependence of
). The relative error bars for dipole and polarizability changes are less than 1% and about 10%, respectively. We note that because of the nearly linear dependence of  , the offset applied to the field of
, the offset applied to the field of  MV m−1 during the calibration step (see section 3) has little impact on the results.
MV m−1 during the calibration step (see section 3) has little impact on the results.
Figure 3. Calculated Stark shift (black circles) of the 4
 4
A2 zero-phonon transition involving the decay from the first excited state into the ground state of (a) VSi(h) and (b) VSi(k). Solid lines represent the best fits of equation (4) to the data, from which the transition dipole moment and polarizability changes (Δμ and Δα, respectively) were extracted.
4
A2 zero-phonon transition involving the decay from the first excited state into the ground state of (a) VSi(h) and (b) VSi(k). Solid lines represent the best fits of equation (4) to the data, from which the transition dipole moment and polarizability changes (Δμ and Δα, respectively) were extracted.
Download figure:
Standard image High-resolution imageOur results indicate little contribution from the polarizability change to the Stark effect, instead hinting towards a dominance of the dipole moment difference between excited and ground states. While a small Δα value (which leads to an approximately linear character) has been observed for V1 with the field along the c-axis [22], the calculated value of Δμ for VSi(h) overestimates the respective measured figure for V1 by about a factor of 10.
We can only hypothesize several reasons for the above discrepancy. Firstly, it is possible that the slab employed is too thin (additional SiC layers should be included) or the vacuum width should be increased. Further, the semi-local treatment of the many-body electronic exchange correlation interactions could be insufficient to accurately describe the difference in coupling of the electric field to the  and
and  electronic configurations. Another possibility is the inherent inaccuracy of the simple single-determinant wave functions to describe excited states. These are among the issues that need to be addressed in the future in order to further investigate the applicability of the present method for the calculation of Stark shifts of electronic transitions for defects in semiconductors.
electronic configurations. Another possibility is the inherent inaccuracy of the simple single-determinant wave functions to describe excited states. These are among the issues that need to be addressed in the future in order to further investigate the applicability of the present method for the calculation of Stark shifts of electronic transitions for defects in semiconductors.
In comparison to other centers, we note that the calculated Δμ values are close to those observed for the divacancy in 4H-SiC (Δμ ≈ 2 D) [15] and to the NV center in diamond (Δμ ≈ 0.8–1.5 D) [20, 21]. Regarding the polarizability, we know that small molecules [48] and quantum dots [49] usually yield positive values for Δα. This is in line with the view that excited states are generally nodal and therefore more polarizable than ground states. However, we found Δα < 0 for the  transitions of
transitions of  in 4H-SiC. Considering the error bars of the measurements, we cannot consider a disagreement with the observations [22]. As a matter of fact, negative values for Δα are also possible for defects in semiconductors, one prominent case being NV in diamond [20].
in 4H-SiC. Considering the error bars of the measurements, we cannot consider a disagreement with the observations [22]. As a matter of fact, negative values for Δα are also possible for defects in semiconductors, one prominent case being NV in diamond [20].
Finally, we should keep in mind that the theoretical approximations and limitations discussed above are not exclusively accountable for the discrepancies between theory and measurements. Several difficulties affect the measurement of Stark shifts as well. Perhaps the most severe is the determination of the electric field that is actually acting on a specific defect. For instance, the often used Lorentz local field approximation may turn out to be inadequate, or the complexity of the sample structure combined with the scatter of the defect distribution can easily frustrate an accurate quantification of Δμ and Δα.
5. Concluding remarks
We present a first-principles methodology to calculate Stark shifts of electronic transitions of defects in semiconductors using periodic boundary conditions. The method is applied to the silicon vacancy in 4H-SiC, with the electric field response of its PL transition energies being investigated by DFT within the Δ-SCF method.
Our approach involves the use of a periodic supercell comprising a semiconductor slab adjacent to a vacuum layer. The surfaces of the slab were passivated by hydrogen termination, and an external electric field with variable amplitude was applied along the surface normal (in parallel to the (0001)- or c-axis). To this end, we added a sawtooth potential to the Hamiltonian, placing the potential 'teeth' in the vacuum region to avoid the superposition of induced charge density singularities with the electronic states of the slab.
For the case of non-centrosymmetric materials (like 4H-SiC), the presence of inequivalent surfaces on the 4H-SiC slab induce a built-in field. A calibration of the external field is carried out to neutralize the built-in field and find the zero-field condition in the slab bulk.
The calculated zero-field transition energies for VSi(h) and VSi(k) account for the experimental data (V1/V1' and V2 PL lines) within an error bar of about 0.1 eV. The energy ordering of the transitions are also in line with the measurements. Such an agreement exceeds the expectations for the present level of theory—typical semi-local approximated exchange correlation functionals underestimate excitation energies by a factor of 0.5–0.6. We suggest that the agreement artificially profits from the opening of the band gap due to electronic confinement in the slab terminated by hydrogen and vacuum.
Regarding the Stark shifts, within the range of electric fields considered ( MV m−1), we found approximately linear Stark shifts for the
MV m−1), we found approximately linear Stark shifts for the  transitions of both VSi(h) and VSi(k). These corresponded to transition dipole changes of Δμ = 1.46 D and Δμ = 3.92 D, respectively, with a numerical error bar below 1%. While an approximately linear Stark shift was observed for V1 [22], the calculated Δμ overestimates the measurement by about a factor of 10. We discuss several reasons which could affect the quality of the theory and should be addressed in the future (for instance, slab geometry and exchange–correlation description level), but also aspects that impact on the interpretation of the observations, in particular the knowledge of the magnitude and direction of the field directly affecting the defects.
transitions of both VSi(h) and VSi(k). These corresponded to transition dipole changes of Δμ = 1.46 D and Δμ = 3.92 D, respectively, with a numerical error bar below 1%. While an approximately linear Stark shift was observed for V1 [22], the calculated Δμ overestimates the measurement by about a factor of 10. We discuss several reasons which could affect the quality of the theory and should be addressed in the future (for instance, slab geometry and exchange–correlation description level), but also aspects that impact on the interpretation of the observations, in particular the knowledge of the magnitude and direction of the field directly affecting the defects.
Acknowledgments
Financial support was kindly provided by the Research Council of Norway and the University of Oslo through the Frontier research project FUNDAMeNT (No. 251131, FriPro ToppForsk-program). The Research Council of Norway is acknowledged for the support to the Norwegian Micro- and Nano-Fabrication Facility, NorFab, Project No. 245963. Some of the computations were performed on resources provided by UNINETT Sigma2 - the National Infrastructure for High Performance Computing and Data Storage in Norway. JC thanks the support of the i3N project, references UIDB/50025/2020 and UIDP/50025/2020, financed by the Fundação para a Ciência e a Tecnologia in Portugal and support by the NATO SPS programme (Project No. 985215).