Abstract
We report the single-crystal synthesis and detailed investigations of the cage-type superconductor Sc5Ru6Sn18, using powder x-ray diffraction (XRD), magnetization, specific-heat and muon-spin relaxation (µSR) measurements. Sc5Ru6Sn18 crystallizes in a tetragonal structure (space group I41/acd) with lattice parameters a = 1.387(3) nm and c = 2.641(5) nm. Both DC and AC magnetization measurements prove the type-II superconductivity in Sc5Ru6Sn18 with Tc ≈ 3.5(1) K, a lower critical field  = 157(9) Oe and an upper critical field,
= 157(9) Oe and an upper critical field, 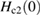 = 26(1) kOe. The zero-field electronic specific-heat data are well fitted using a single-gap BCS model, with
= 26(1) kOe. The zero-field electronic specific-heat data are well fitted using a single-gap BCS model, with 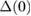 = 0.64(1) meV. The Sommerfeld constant γ varies linearly with the applied magnetic field, indicating s-wave superconductivity in Sc5Ru6Sn18. Specific-heat and transverse-field (TF) µSR measurements reveal that Sc5Ru6Sn18 is a superconductor with strong electron–phonon coupling, with TF-µSR also suggesting a single-gap s-wave character of the superconductivity. Furthermore, zero-field µSR measurements do not detect spontaneous magnetic fields below Tc, hence implying that time-reversal symmetry is preserved in Sc5Ru6Sn18.
= 0.64(1) meV. The Sommerfeld constant γ varies linearly with the applied magnetic field, indicating s-wave superconductivity in Sc5Ru6Sn18. Specific-heat and transverse-field (TF) µSR measurements reveal that Sc5Ru6Sn18 is a superconductor with strong electron–phonon coupling, with TF-µSR also suggesting a single-gap s-wave character of the superconductivity. Furthermore, zero-field µSR measurements do not detect spontaneous magnetic fields below Tc, hence implying that time-reversal symmetry is preserved in Sc5Ru6Sn18.
Export citation and abstract BibTeX RIS
1. Introduction
In 1957, Bardeen, Cooper, and Schrieffer (BCS) explained superconductivity by using the concept of Cooper pairs [1], implying electrons with equal and opposite spins and crystal momenta, which pair together. Understanding the pairing mechanism in unconventional superconductors is a challenging task. In conventional s-wave superconductors, only the gauge symmetry is broken. However, in the case of unconventional pairing, besides the global gauge symmetry (responsible for the Meissner and Josephson effects [2]) other symmetries of the Hamiltonian might be broken in the superconducting state, including spin-rotation, lattice-point and translation-group symmetries. Studying such broken symmetries in superconductors is crucial and it can be achieved by investigating the symmetry properties of the order parameter, 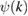 . Depending on the parity of superconducting order parameter [3], superconductors with an inversion center may be classified in either even parity spin-singlet (S = 0) or in odd parity spin-triplet pairing states (S = 1). For instance, a few compounds, such as the 4d-electron system Sr2RuO4 [4, 5] or the 5f-electron system UGe2 [6] have been reported to be spin-triplet superconductors.
. Depending on the parity of superconducting order parameter [3], superconductors with an inversion center may be classified in either even parity spin-singlet (S = 0) or in odd parity spin-triplet pairing states (S = 1). For instance, a few compounds, such as the 4d-electron system Sr2RuO4 [4, 5] or the 5f-electron system UGe2 [6] have been reported to be spin-triplet superconductors.
Besides modifying the properties of the system, broken symmetry may lead to some interesting unconventional behavior. Superconductivity itself is one of the best examples of a symmetry-breaking phenomenon. Time-reversal symmetry (TRS) breaking is another interesting example. TRS breaking is a rare phenomenon and has been observed only in a few unconventional superconductors, such as Sr2RuO4 [4], LaNiC2 [7], Re6Zr [8], Re24Ti5 [9]. TRS breaking can be probed with the help of zero-field muon spin-relaxation (ZF-µSR) technique, by detecting the occurrence of tiny spontaneous magnetic fields, below the onset of superconductivity. The presence of such spontaneous fields restricts the pairing symmetry of the superconducting states. TRS breaking is associated with a special kind of superconducting states having a degenerate representation. The two or more degenerate superconducting phases lead to a spatially inhomogeneous order parameter near the resulting domain walls; which, in turn, create spontaneous supercurrents and hence, spontaneous magnetic field in those regions [3]. TRS breaking fields may also originate from the intrinsic magnetic moments due to spin-polarization (in case of spin-triplet pairing) and the relative spin-angular momentum associated with the Cooper pairs [10]. Recently, some of the noncentrosymmetric superconductors, such as Re6Zr [8] and La7Ir3 [11], with a mixed singlet-triplet pairing, were found to exhibit TRS breaking. However, it has been established theoretically [12] and experimentally [13] that the presence of singlet-triplet mixing not necessarily implies a broken TRS.
Compounds with cage-like structures have attracted remarkable attention due to their peculiar features. There are three major classes of cage-type compounds which are being studied extensively, i.e., skutterudites (RT4X12), β-pyrochlore oxides (AOs2O6) and Ge/Si clathrates [14]. Exotic phenomena such as heavy-fermion superconductivity or exciton-mediated superconductivity were discovered in these materials. These compounds consist of 3D skeletons which surround large atomic cages, in which small atoms are situated. Because of a strong electron-phonon coupling and weak structural couplings, the small atoms can 'rattle' with large atomic excursions, ultimately leading to a rattling vibration. Such rattling of small atoms might result in interesting phenomena, such as strong-coupling superconductivity in AOs2O6 [15]. A specific case of cage-type compounds is given by R5Rh6Sn18 (R = Sc, Y, Lu). These crystallize in a tetragonal structure with space group I41/acd and Z = 8, where Z represents the number of formula units per unit cell (R occupies sites of different symmetry [16]). R5Rh6Sn18 exhibit superconductivity at 5 K (Sc), 3 K (Y) and 4 K (Lu) [17], respectively. The superconducting properties of Lu5Rh6Sn18 and Y5Rh6Sn18 compounds have been studied [2, 18]. Unconventional superconductivity has been observed in both Lu5Rh6Sn18 and Y5Rh6Sn18, where the former has an isotropic superconducting gap, while the latter shows anisotropic gap. In addition, ZF-µSR studies reveal the presence of spontaneous magnetic fields, hinting at TRS breaking. However, the superconductivity of ruthenate stannides R5Ru6Sn18 is largely unexplored. This motivated us to study the superconducting properties of Sc5Ru6Sn18 and to search for possible TRS breaking in this compound.
In this paper, we report on the superconducting properties of the cage-type superconductor Sc5Ru6Sn18 investigated via magnetization, specific-heat, and µSR measurements. The symmetry of the superconducting gap was studied using TF-µSR, whereas ZF-µSR measurements could not detect the spontaneous magnetic fields below Tc, hence indicating that the TRS is preserved in Sc5Ru6Sn18. We also report on the calculated critical current density (Jc) as obtained from the isothermal hysteresis loops in Sc5Ru6Sn18.
2. Experimental methods
Single crystals of Sc5Ru6Sn18 were grown using a Sn-flux method with Sc-powder (99.99%), Ru-powder (99.99%) and Sn-shot (99.99%) as the starting materials. The typical dimensions of the crystals used in our investigations were 2.5 × 2.8 × 2.5 mm3 as shown in the inset of figure 1. The smaller crystals were crushed into powder for x-ray diffraction (XRD) measurements (using a Bruker AXS GmbH D2 Phaser desktop x-ray diffractometer) with Cu-Kα radiation. The quality of the single crystal was verified using a 2D XRD technique with omega scan without crystal rotation. Well-defined spots on the 2D image indicated a good crystalline quality. The magnetization was measured using a superconducting quantum interference device (SQUID) magnetometer (Quantum Design) at temperatures down to 1.8 K and magnetic fields up to 20 kOe. The specific-heat measurements were performed in various magnetic fields (up to 30 kOe) in the temperature range 1.8–10 K, using the heat-capacity option of a physical property measurement system (PPMS) (Quantum Design). The temperature dependence of AC susceptibility was again studied with PPMS, using a small (5 Oe) ac-driving field with frequencies up to 10 kHz.
Figure 1. Powder XRD pattern of Sc5Ru6Sn18. All the peaks were indexed successfully to a tetragonal R5M6Sn18 (R = rare earth, M = transition metal) phase. The inset shows the single crystal used in our study. The hexagonal-shaped plane was identified with the (1 1 2) plane by means of x-ray reflection.
Download figure:
Standard image High-resolution imageThe ZF-µSR measurements were carried out at the pulsed muon beam of the RIKEN-RAL Muon Facility at ISIS (United Kingdom). In this case the sample temperature was varied from about 30 K (>Tc) down to 1.5 K (<Tc) with cooling being performed in a helium-flow type cryostat (Janis Co.). Helium exchange gas was used to achieve good temperature homogeneity. The asymmetry parameter is defined as A(t) = [F(t) − αB(t)]/[(F(t) + αB(t)], where F(t) and B(t) represent the muon events recorded in the forward and backward counters, respectively. α is a geometrical factor, which accounts for the different solid angles and efficiencies of the two detectors, as viewed from the sample position. The time dependence of A(t), also known as the µSR time spectrum, was measured. The TF-µSR measurements were carried out in the superconducting mixed state in an applied field of 300 Oe, using the general-purpose surface (GPS) muon instrument located at the πM3 beamline of the Swiss Muon Source of the Paul Scherrer Institute in Villigen, Switzerland.
3. Results and discussion
3.1. Crystal structure
Figure 1 shows the room temperature powder XRD pattern for Sc5Ru6Sn18 with the scattering angle 2θ varying between 20°–80°. All the peaks in the pattern can be well indexed using a tetragonal structure with lattice constants a = 1.387(3) nm and c = 2.641(5) nm, which give a unit cell volume = 5.080(5) 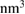 and a density ρ = 7.8(3) g cm−3 (space group I41/acd.) The obtained values are in good agreement with those previously reported on the R5M6Sn18 (R = rare earth, M = transition metal) family of compounds [19, 20].
and a density ρ = 7.8(3) g cm−3 (space group I41/acd.) The obtained values are in good agreement with those previously reported on the R5M6Sn18 (R = rare earth, M = transition metal) family of compounds [19, 20].
3.2. Magnetization
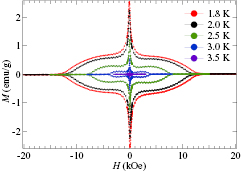
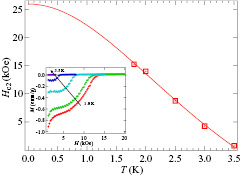
Figure 2 shows the hysteresis curves of Sc5Ru6Sn18 recorded at various temperatures below Tc, characterized by symmetric M–H loops. The M(H) curves exhibit a butterfly shape, typical of type-II superconductors. The symmetry of the hysteresis loop (or the lack of it) allows one to distinguish between pinning- and surface- (or geometrical barrier) induced hysteresis, with flux pinning known to produce symmetric hysteresis loops [21], as in our case. The lower-Hc1 and upper-Hc2 field values were determined from the magnetization data. The lower critical field, Hc1, is defined as the point where the field-dependent magnetization starts to deviates from linearity (see inset in figure 3) [22]. Since the actual magnetic field around the sample is larger than the applied magnetic field due to the demagnetizing effects by a factor of 1/(1 − N), where N is the demagnetizing factor, we have to correct the Hc1 values for such an effect [23]. We have estimated the value of N from the rectangular prism approximation which is based on the dimensions of the crystal [24] and we get N = 0.39. The main panel of figure 3 shows the temperature variation of corrected values of Hc1, which can be fitted by the relation [25]:
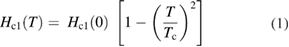
where Hc1(0) is the lower critical field at zero-temperature. The fit gives Hc1(0) = 157(9) Oe.
Figure 2. Magnetization hysteresis curves of a Sc5Ru6Sn18 crystal, recorded at different temperatures in an applied magnetic field normal to the (1 1 2) plane.
Download figure:
Standard image High-resolution imageFigure 3. Temperature dependence of Hc1 for Sc5Ru6Sn18 (squares) and fit to equation (1) (solid line). Inset: magnetization curves for Sc5Ru6Sn18 for temperatures in the 1.8–3.5 K range. Hc1 is defined as the field where M(H) curve starts to deviate from the linearity.
Download figure:
Standard image High-resolution imageThe upper critical field is defined as the point where the magnetization curve touches the zero magnetic moment line (see inset in figure 4). The main panel in figure 4 shows the temperature variation of Hc2, which can be fitted using the Ginzburg–Landau equation given by [25]:
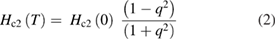
where 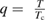 and Hc2(0) is the upper critical field at zero-temperature. The fit gives Hc2(0) = 26(1) kOe. From this, we estimate a Ginzburg–Landau coherence length,
and Hc2(0) is the upper critical field at zero-temperature. The fit gives Hc2(0) = 26(1) kOe. From this, we estimate a Ginzburg–Landau coherence length, 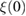 ≈ 11.26(3) nm, by using the relation [25]:
≈ 11.26(3) nm, by using the relation [25]:
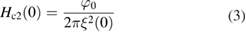
where φ0 = 2.07 × 10−15 Tm2, is the quantum of the magnetic flux. In addition, we can estimate the Ginzburg–Landau penetration depth using the relation [25]:
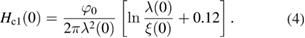
Figure 4. Temperature dependence of Hc2 for Sc5Ru6Sn18 (squares) and a fit to equation (2) (solid line). Inset: magnetization curves for Sc5Ru6Sn18 for temperatures in the 1.8–3.5 K range. Hc2 is defined as the field at which the magnetization becomes zero.
Download figure:
Standard image High-resolution imageBy using 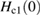 = 157(9) Oe and
= 157(9) Oe and 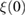 ≈ 11.26(3) nm, we obtain
≈ 11.26(3) nm, we obtain 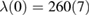 nm.
nm.
Finally, the Ginzburg–Landau parameter ( ) is obtained from the relation
) is obtained from the relation 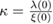 . By using the values for
. By using the values for 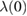 and
and 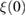 , we find κ ≈ 23(2) >
, we find κ ≈ 23(2) > 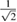 , the latter indicating that Sc5Ru6Sn18 is indeed a strong type-II superconductor. The zero-temperature thermodynamic critical field was estimated by using the relation [25],
, the latter indicating that Sc5Ru6Sn18 is indeed a strong type-II superconductor. The zero-temperature thermodynamic critical field was estimated by using the relation [25],
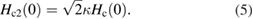
By using the values for Hc2(0) = 26(1) kOe and κ ≈ 23(2), we get 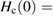 799(6) Oe.
799(6) Oe.
The field dependence of the critical current density (Jc) was derived from the width ΔM of the magnetization curve, by using the Bean model [26, 27]:
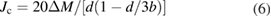
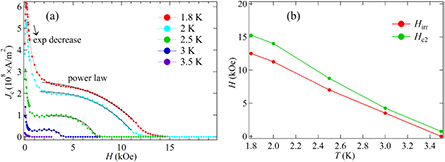
where d (mm) and b (mm) are the sample dimensions (d < b). In our case d = 1.25 mm and b = 1.40 mm. The critical current density (Jc) is expected to have a maximum at the lower critical field, whereas above this threshold it decreases rapidly with the increasing field. Figure 5(a) shows Jc as a function of the magnetic field at various temperatures. Above the threshold field, for each isothermal measurement, initially Jc shows an exponential decrease followed by a power-law variation, in good agreement with the previous reports [28, 29]. We obtain Jc(1.8 K) ~ 6(3) × 108 A m−2. The de-pairing current is given by the relation:
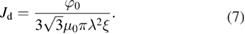
Figure 5. (a) Variation of the critical current density (Jc) with the applied magnetic field for different temperatures for a single crystal of Sc5Ru6Sn18. The critical current density shows a peak near the lower critical field (Hc1) and an ensuing exponential decrease followed by a power-law (Ha) variation versus applied field. The Jc(1.8 K) ~ 6 × 108 A m−2 is obtained at a low field of 150 Oe. (b) Phase diagram showing the variation of the irreversibility (Hirr) and upper critical (Hc2) fields for Sc5Ru6Sn18.
Download figure:
Standard image High-resolution imageBy using the previously obtained values of ξ(0) = 11.26(3) nm and λ(0) = 260(7) nm, we find Jd = 3.07(5) × 1010 A m−2. The long coherence length implies a high pinning energy and flux-lines that do not move easily [30]. The material might have a large concentration of weak pinning centers, which ultimately leads to collective pinning. In the scenario of collective pinning, the critical current density depends strongly on the magnetic field and is typically small. This behavior has been observed, e.g., in case of layered inhomogeneous superconductors [31]. The irreversibility field (Hirr), at which the magnetic hysteresis disappears, is determined by the criterion Jc = 2 × 107 A m−2 [28]. The variation of the Hirr and Hc2 with temperature is shown in figure 5(b). We note that the irreversibility field is comparable to the upper critical field (Hc2), a rather plausible result considering that the material has a low Tc and a high coherence length [30].
3.3. AC susceptibility
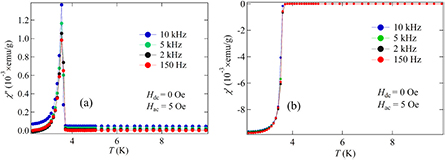
To further confirm the superconducting transition temperature we measured the ac magnetic susceptibility in the temperature range 1.8–10 K, with Hac = 5 Oe and Hdc = 0 Oe. Figure 6(a) shows the imaginary part of the ac susceptibility, while figure 6(b) shows the real part, corresponding to the out-of-phase and in-phase components, respectively (with respect to the ac field). The real part of the ac susceptibility versus temperature, represents the transition from the Meissner state (perfect shielding) to the complete penetration of the ac magnetic field inside the sample. On the other hand, the imaginary part of the ac susceptibility represents the ac losses occurring when the ac field penetrates the sample. As shown in figure 6(a), χ'' has a sharp transition near Tc = 3.6 K. The transition in χ'' is independent of the frequency of the driving ac field. The appearance of a peak in χ'' is commonly associated with the superconducting transition. When the temperature is far below the critical temperature and the magnetic field is smaller than the lower critical field Hc1, the screening current generated by the ac field is confined to regions near the sample surface. Hence, no magnetic flux enters the sample and the ac losses are minimal; consequently χ'' is almost zero. As the temperature is raised, the magnetic field starts penetrating the sample and ac losses start increasing. The maximum in χ'' occurs when the ac field fully penetrates the sample.
Figure 6. (a) Temperature dependence of the imaginary part of ac susceptibility for Hdc = 0 Oe and Hac = 5 Oe and different frequencies for Sc5Ru6Sn18. (b) Temperature dependence of the real part of ac susceptibility measured in identical conditions.
Download figure:
Standard image High-resolution image3.4. Specific heat
The specific heat in the superconducting state is one of the key parameters to reflect closely the superconducting gap and its symmetry. Therefore, we measured and analyzed in detail the zero-field specific heat of Sc5Ru6Sn18. The electronic specific heat (Ce/T) of the sample was obtained after subtracting the phonon contribution from the raw experimental data. As shown in the inset of figure 7, the normal-state specific heat was fitted using the relation C/T = γ + βT2 + δT4 for 14 K2 ⩽ T2 ⩽ 42 K2 to obtain γ = 36.93(6) mJ mol−1 K−2, β = 2.5(5) mJ mol−1 K−4 and δ = 1.2(9) mJ mol−1 K−6. The Debye temperature θD = 205(1) K was calculated using the relation:
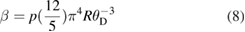
where p = 29 is the number of atoms in one formula unit and R = 8.314 J K−1 mol−1. The density of states at the Fermi level  was estimated from [32]:
was estimated from [32]:
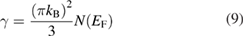
where kB is the Boltzmann constant. By using the previously obtained γ value, we obtain 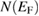 = 15.24(6) states/eV per formula unit. The strength of electron-phonon coupling can be estimated by the McMillan equation [33]:
= 15.24(6) states/eV per formula unit. The strength of electron-phonon coupling can be estimated by the McMillan equation [33]:
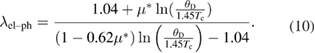
Figure 7. Temperature dependence of the zero-field electronic specific heat of Sc5Ru6Sn18. The solid line refers to a fit using a fully-gapped s-wave model. Inset: raw C/T data versus T2. The solid line shows the fit to  , which is used to calculate the phonon contribution to the specific heat.
, which is used to calculate the phonon contribution to the specific heat.
Download figure:
Standard image High-resolution imageHere  is the Coulomb repulsion parameter. By inserting the values for θD = 205(1) K and Tc = 3.5(1) K, we get
is the Coulomb repulsion parameter. By inserting the values for θD = 205(1) K and Tc = 3.5(1) K, we get 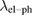 = 0.64(4), which indicates that Sc5Ru6Sn18 is a strongly coupled superconductor.
= 0.64(4), which indicates that Sc5Ru6Sn18 is a strongly coupled superconductor.
The calculated density of states N(EF) and the effective mass of quasiparticles m*, depend on the many-body electron-phonon interactions. These quantities are related to the bare band-structure of density of states Nband(EF) and 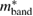 by the following relations [34]:
by the following relations [34]:
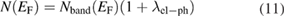
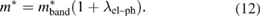
By using the values of 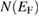 and
and 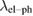 in equation (11), we get
in equation (11), we get 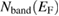 = 9.270(6) states eV−1 f.u. By using
= 9.270(6) states eV−1 f.u. By using 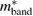 =
= 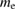 (the free electron mass), in equation (12), we obtain 1.644
(the free electron mass), in equation (12), we obtain 1.644 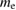 for the mass of the quasiparticles.
for the mass of the quasiparticles.
The density of states can be used to estimate the Fermi velocity, vF, which is related to 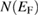 by [35],
by [35],
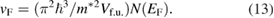
Where 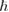 = Planck's constant/2π,
= Planck's constant/2π, 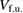 =
= 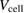 /2 is the volume per formula unit. Using the values of m*,
/2 is the volume per formula unit. Using the values of m*, 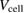 and
and 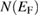 , we get
, we get 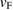 = 1.94(7) × 107 cm s−1 for Sc5Ru6Sn18. We can further estimate the mean free path
= 1.94(7) × 107 cm s−1 for Sc5Ru6Sn18. We can further estimate the mean free path 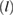 of the superconducting carriers by using the relation
of the superconducting carriers by using the relation 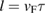 , where
, where  is the mean free scattering time, given by
is the mean free scattering time, given by 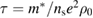 , where
, where 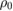 is the residual resistivity and
is the residual resistivity and 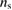 is the superconducting carrier density. The latter is given by
is the superconducting carrier density. The latter is given by 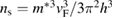 , assuming a spherical Fermi surface [35]. Using the value of
, assuming a spherical Fermi surface [35]. Using the value of 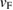 , we get
, we get 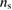 = 7.05(2) × 1026 carriers m−3. By combining these expressions we get [35],
= 7.05(2) × 1026 carriers m−3. By combining these expressions we get [35],
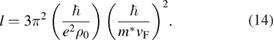
Putting 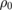 = 200 µ
= 200 µ cm (resistivity data not shown here) and the above estimated values of
cm (resistivity data not shown here) and the above estimated values of 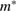 and
and 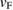 , we get l = 8.14(5) nm.
, we get l = 8.14(5) nm.
The normalized electronic specific heat Ce/γT is plotted versus the normalized temperature T/Tc as shown in figure 7. The normalized specific heat jump at Tc is 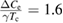 for γ = 36.93(6) mJ mol−1 K−2. Since such a value is higher than the BCS value of 1.43 (for a weakly coupled superconductor), it again indicates a strong electron-phonon coupling in Sc5Ru6Sn18.
for γ = 36.93(6) mJ mol−1 K−2. Since such a value is higher than the BCS value of 1.43 (for a weakly coupled superconductor), it again indicates a strong electron-phonon coupling in Sc5Ru6Sn18.
The temperature dependence of specific heat in the superconducting state is best modelled by an s-wave single-gap BCS expression of the normalized entropy S [34]:
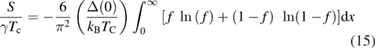
where ![$ \newcommand{\e}{{\rm e}} f\left(\xi \right)={{\left[\exp \left(\frac{E\left(\xi \right)}{{{k}_{{\rm B}}}T} \right)+1 \right]}^{-1}}$](https://content.cld.iop.org/journals/0953-8984/30/31/315803/revision2/cmaacf65ieqn050.gif) is the Fermi function,
is the Fermi function, 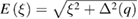 , where
, where 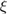 is the energy of electrons in the normal state, measured with respect to the Fermi energy,
is the energy of electrons in the normal state, measured with respect to the Fermi energy, 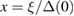 ,
, 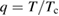 and
and ![$\Delta (q)=\Delta (0)~\tanh \left[1.82{{\left(1.018\left(\left(\frac{1}{q} \right)-1 \right) \right)}^{0.51}} \right]$](https://content.cld.iop.org/journals/0953-8984/30/31/315803/revision2/cmaacf65ieqn055.gif) is the temperature dependence of the superconducting gap. The normalized electronic specific heat is given by the expression [34]:
is the temperature dependence of the superconducting gap. The normalized electronic specific heat is given by the expression [34]:
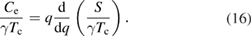
The electronic specific heat (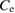 ) in the superconducting state is described by equation (16), while it is equal to
) in the superconducting state is described by equation (16), while it is equal to 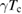 in the normal state. The specific heat data were fitted to equation (16) as shown in the figure 7. The fit gives a superconducting gap,
in the normal state. The specific heat data were fitted to equation (16) as shown in the figure 7. The fit gives a superconducting gap,  = 0.64(1) meV.
= 0.64(1) meV.
The Sommerfeld constant (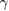 ) is calculated by fitting the
) is calculated by fitting the 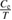 versus T data for various fields using the relation [36]:
versus T data for various fields using the relation [36]:
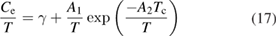
where 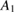 and
and 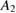 are constants.
are constants.
The single gap s-wave superconductivity in Sc5Ru6Sn18 is also confirmed by the magnetic-field dependence of the electronic specific-heat coefficient (Sommerfeld constant), γ(H). In a single-gap type-II superconductor, the Sommerfeld constant is proportional to the vortex density. When the applied magnetic field is increased, the density of vortices increases too, which, in turn, result in an increase of the quasiparticle density of states. Consequently, γ turns out to be proportional to the applied magnetic field in case of a nodeless and isotropic s-wave superconductor [34, 36, 37]. On the other hand, in case of nodes in the superconducting gap, Volovik predicted a nonlinear relation given by  [38]. The field dependence of
[38]. The field dependence of 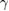 is shown in figure 8. The linear relation between
is shown in figure 8. The linear relation between 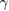 and
and 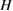 confirms the single-gap s-wave superconductivity in Sc5Ru6Sn18.
confirms the single-gap s-wave superconductivity in Sc5Ru6Sn18.
Figure 8. Sommerfeld constant γ versus normalized field 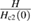 for Sc5Ru6Sn18. The solid line shows the linear relation between γ and field, which indicates the s-wave nature of superconductivity in Sc5Ru6Sn18.
for Sc5Ru6Sn18. The solid line shows the linear relation between γ and field, which indicates the s-wave nature of superconductivity in Sc5Ru6Sn18.
Download figure:
Standard image High-resolution imageThe condensation energy 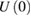 can be estimated from the relation:
can be estimated from the relation:
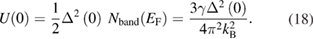
Using the previously obtained values of 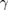 = 36.93(6) mJ mol−1 K−2 and
= 36.93(6) mJ mol−1 K−2 and 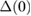 = 0.64(1) meV, we get
= 0.64(1) meV, we get  = 156.8(9) mJ mol−1.
= 156.8(9) mJ mol−1.
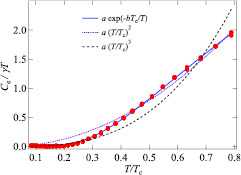
To further confirm the characteristics of the superconducting gap function, we analyzed 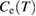 by fitting the data by means of different functional forms, i.e.,
by fitting the data by means of different functional forms, i.e., 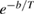 ,
,  and
and 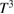 , corresponding to the expected temperature dependence of a superconducting gap which is isotropic, has line nodes or linear point nodes, respectively. As can be seen in figure 9, well below
, corresponding to the expected temperature dependence of a superconducting gap which is isotropic, has line nodes or linear point nodes, respectively. As can be seen in figure 9, well below 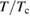 = 0.8, data are best modelled by the exponential function,
= 0.8, data are best modelled by the exponential function, 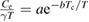 . The quadratic and cubic fits instead are rather poor. Similar exponential fits have been used to model the superconducting gap of other superconductors with comparable transition temperatures [9, 39, 40]. Thus, the above analysis confirms that Sc5Ru6Sn18 has an isotropic gap and s-wave pairing.
. The quadratic and cubic fits instead are rather poor. Similar exponential fits have been used to model the superconducting gap of other superconductors with comparable transition temperatures [9, 39, 40]. Thus, the above analysis confirms that Sc5Ru6Sn18 has an isotropic gap and s-wave pairing.
Figure 9. Temperature dependence of the zero-field electronic specific heat for Sc5Ru6Sn18 in the superconducting phase. The solid, dotted and dashed lines are fits to the data using three different models (see text for details).
Download figure:
Standard image High-resolution imageWe can estimate the London penetration depth at T = 0 K, 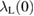 , using the relation [25]:
, using the relation [25]:
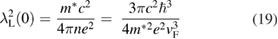
where c is the speed of light in vacuum. Putting the values of all parameters, we get 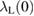 = 245(6) nm. The BCS coherence length
= 245(6) nm. The BCS coherence length  can be estimated from
can be estimated from 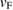 and the superconducting energy gap
and the superconducting energy gap 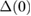 using the relation [41]:
using the relation [41]:

Putting the values of 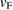 = 1.94(7) × 107 cm s−1 and
= 1.94(7) × 107 cm s−1 and 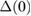 = 0.64(1) meV, we get
= 0.64(1) meV, we get 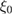 = 63.72(9) nm. We find that BCS coherence length (
= 63.72(9) nm. We find that BCS coherence length (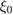 ) is much larger than the mean free path l = 8.14(5) nm,
) is much larger than the mean free path l = 8.14(5) nm,  = 0.12
= 0.12 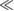 1, which indicates that the superconductivity in Sc5Ru6Sn18 is in the moderate dirty limit.
1, which indicates that the superconductivity in Sc5Ru6Sn18 is in the moderate dirty limit.
3.5. µSR
Figure 10(a) shows the TF-µSR spectra collected above (5 K) and below (1.5 K) the superconducting transition temperature, Tc. The fast decay of muon-spin polarization below Tc indicates an inhomogeneous field distribution due to the flux line lattice (FLL) in the vortex state. The time-domain spectra were fit by using the following model [9]:
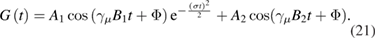
Figure 10. (a) Transverse field µSR time spectra of Sc5Ru6Sn18 measured at T = 1.5 and 5 K in a magnetic field, H = 300 Oe. The solid lines show fits to the data using equation (21). (b) Temperature dependence of the normalized muon spin-depolarization rate 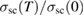 collected in an applied magnetic field, H = 300 Oe. The solid line represents a fit by an isotropic s-wave superconducting gap using equation (23).
collected in an applied magnetic field, H = 300 Oe. The solid line represents a fit by an isotropic s-wave superconducting gap using equation (23).
Download figure:
Standard image High-resolution imageHere A1 and A2 are the initial muon-spin asymmetries, whereas B1 and B2 are the local fields sensed by muons implanted in the sample and the sample holder. 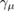 = 2π × 135.53 MHz T−1 is the muon gyromagnetic ratio, Φ is the phase factor and σ is the Gaussian relaxation rate. Since the sample holder is non-magnetic, B2 coincides with the applied magnetic field.
= 2π × 135.53 MHz T−1 is the muon gyromagnetic ratio, Φ is the phase factor and σ is the Gaussian relaxation rate. Since the sample holder is non-magnetic, B2 coincides with the applied magnetic field.
In the superconducting state, the Gaussian relaxation rate σ contains contributions from both the FLL (σsc) and the nuclear magnetic moments (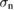 ), such that:
), such that:

By using equation (22), one can estimate the FLL-related relaxation rate 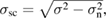 since
since 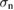 is expected to be temperature independent in the measured temperature range and is determined from the measurements made above Tc. Considering that
is expected to be temperature independent in the measured temperature range and is determined from the measurements made above Tc. Considering that 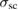 is directly related to the superfluid density, the temperature dependence of
is directly related to the superfluid density, the temperature dependence of 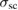 provides hints on the superconducting gap and its symmetry. Further,
provides hints on the superconducting gap and its symmetry. Further, 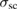 can be modeled by [42–44]:
can be modeled by [42–44]:
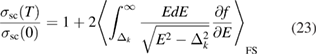
where f and E are the same as defined in equation (15). The curved brackets represent an average over the Fermi surface (FS). The superconducting gap is defined by 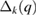 =
=  , (
, (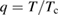 ), which contains an angular dependent part
), which contains an angular dependent part 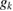 and a temperature dependent part
and a temperature dependent part 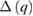 , which can be approximated as
, which can be approximated as ![$\Delta (q)=\Delta(0)~\tanh \left[1.82{{\left(1.018(\left(\frac{1}{q} \right)-1) \right)}^{0.51}} \right]$](https://content.cld.iop.org/journals/0953-8984/30/31/315803/revision2/cmaacf65ieqn102.gif) . As shown in figure 10(b), the temperature dependence of the normalized FLL-related relaxation rate
. As shown in figure 10(b), the temperature dependence of the normalized FLL-related relaxation rate 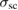 (T)/
(T)/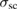 (0), can be fitted by a single-gap isotropic s-wave using equation (23) (for single gap s-wave model,
(0), can be fitted by a single-gap isotropic s-wave using equation (23) (for single gap s-wave model, 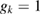 ), with
), with 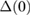 = 0.64(1) meV and
= 0.64(1) meV and 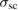 (0) = 0.178
(0) = 0.178 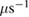 . This implies a ratio
. This implies a ratio 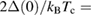 4.25(4), i.e., higher than 3.53 expected for a weakly coupled BCS superconductor. This further confirms the strong electron–phonon coupling in Sc5Ru6Sn18 and is consistent with the results obtained from specific-heat data.
4.25(4), i.e., higher than 3.53 expected for a weakly coupled BCS superconductor. This further confirms the strong electron–phonon coupling in Sc5Ru6Sn18 and is consistent with the results obtained from specific-heat data.
The effective penetration depth (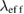 ) for small applied fields, such that
) for small applied fields, such that 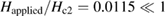 , is given by the relation [9, 45]:
, is given by the relation [9, 45]:
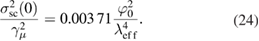
Using  (0) = 0.178
(0) = 0.178 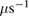 , we get
, we get 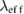 = 774 nm. The effective penetration depth
= 774 nm. The effective penetration depth 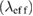 and London penetration depth
and London penetration depth 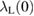 are related by
are related by 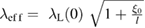 [25]. Using
[25]. Using 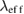 = 774 nm,
= 774 nm,  = 63.72(9) nm and l = 8.14(5) nm, we get,
= 63.72(9) nm and l = 8.14(5) nm, we get, 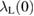 = 258(7) nm, which is comparable to the value estimated using m* and
= 258(7) nm, which is comparable to the value estimated using m* and 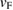 and the magnetization measurements. This confirms the validity of our fitting model.
and the magnetization measurements. This confirms the validity of our fitting model.
To probe the occurrence (or absence) of TRS breaking in Sc5Ru6Sn18, we performed ZF-µSR experiments. The availability of 100% spin-polarized muon beams, along with the large muon gyromagnetic ratio, make ZF-µSR a very useful technique to detect the spontaneous internal fields, as has been shown in previous studies of Y5Rh6Sn18 [18] and Sr2RuO4 [4]. In general, in absence of an external magnetic field, the onset of the superconducting phase does not induce any changes in the ZF-muon spin-relaxation rate. However, in the case of TRS breaking, the presence of tiny spontaneous currents leads to the associated weak magnetic fields, which are detected by ZF-µSR as an increase in the muon spin-relaxation rate. Since the expected effects are rather small, we measured carefully the muon spin-relaxation rates both above and below Tc.
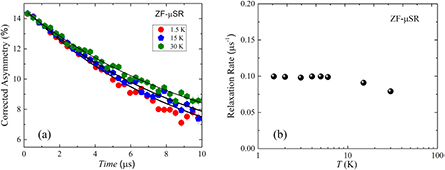
The ZF-µSR time-domain data for three representative temperatures (1.5, 15 and 30 K, i.e., below and above Tc) are shown in figure 11(a). Muons stopped in the silver sample holder give rise to a time independent background signal. Since no precession signals were observed in the entire 1.5–30 K temperature range, we rule out the possibility of significant internal fields and consequently, of any long range magnetic order in Sc5Ru6Sn18. In this scenario, the only possibility is that the muon-spin relaxation is due to the static, randomly distributed local fields, arising from the nuclear moments close to the muon-stopping site. In this case, the muon-spin depolarization can be described by the Kubo–Toyabe (KT) function:
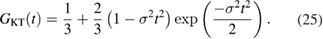
Figure 11. (a) ZF-µSR time spectra of Sc5Ru6Sn18 measured at various temperatures. The solid lines are the best-fit results by using the function A(T) = A0GKT(t) exp(−λ1t). (b) Temperature dependence of the muon-spin relaxation rate (see text for details). The temperature independent behavior below 10 K suggests the absence of spontaneous internal magnetic fields at the muon site, indicating that time reversal symmetry is unlikely to be broken in Sc5Ru6Sn18.
Download figure:
Standard image High-resolution imageAfter subtracting the background due to the silver sample holder, the ZF-µSR spectra could be analyzed by using the function:
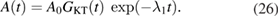
Here, A0 is the initial asymmetry at t = 0. GKT can be treated as a temperature-independent parameter (within the µSR time window [46]). λ1 is the muon-spin relaxation rate, considered to reflect the fluctuations of surrounding electronic spins lying close to the muon. Solid lines in figure 11(a) are the best-fit results by using equation (26). Figure 11(b) shows the temperature dependence of λ1, as obtained from the fits of the time spectra. Here λ1 shows a slight enhancement with decreasing temperature, starting from T > Tc. This would mean that some unpaired electronic spins still remain, thus causing the observed muon-spin depolarization behavior.
A key result of the ZF-µSR data is the almost temperature independent λ1 below ~10 K, especially when crossing Tc i.e. upon entering the superconducting phase. In conventional BCS type s-wave superconductors, no effects are expected in the ZF-µSR data in the superconducting state. On the other hand, when TRS is broken, ZF-µSR time spectra are modified due to the appearance of spontaneous magnetic fields below Tc. This is typically the case for the Cooper pairs with a p-wave symmetry, as, e.g. in Sr2RuO4 [4]. As shown in figure 11(b), since the time spectra do not show any relevant changes (within statistical errors), we must conclude that a TRS breaking is unlikely in the superconducting state of Sc5Ru6Sn18.
Note that the TRS breaking depends on the pairing symmetry of the electrons in the superconducting state. The TRS can be broken if the superconducting state has degenerate representations, as is the case of triplet superconducting states [4]. However, in the case of singlet-superconducting states, where the superconducting state has non-degenerate representations, the TRS may not be broken. While TRS breaking is possible in systems with strong spin–orbit coupling such as Y5Rh6Sn18 [18], it might still be conserved in systems with weak spin–orbit coupling, such as Sc5Ru6Sn18.
3.6. Cooper pair breaking
In case of type-II superconductors, the breaking of Cooper pairs upon applying an external magnetic field may happen via two mechanisms: orbital or Pauli paramagnetic limiting field effects [34]. In case of an orbital pair-breaking mechanism, Cooper pairs break when the field-induced kinetic energy of the pair exceeds the superconducting condensation energy. On the other hand, in case of the Pauli paramagnetic effect, it is energetically favorable for electron spins to point in the direction of the applied magnetic field, thus decoupling from their partner, which results in the splitting of the Cooper pair [34]. For a BCS superconductor the orbital limit of the upper (i.e. orbital) critical field is given by the Werthamer–Helfand–Hohenberg (WHH) expression [47, 48]:
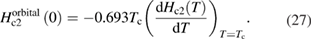
The slope 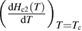 is estimated from the
is estimated from the  phase diagram (see figure 4) and is equal to 8.1(1) kOe K−1 in our case, which gives an orbital upper limiting field,
phase diagram (see figure 4) and is equal to 8.1(1) kOe K−1 in our case, which gives an orbital upper limiting field, 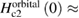 19.18 kOe. The Pauli limiting field,
19.18 kOe. The Pauli limiting field, 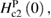 within the BCS theory is given by [49, 50]:
within the BCS theory is given by [49, 50]:

For 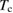 = 3.5 K,
= 3.5 K, 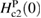 ≈ 65.1 kOe. The Maki parameter [51],
≈ 65.1 kOe. The Maki parameter [51], 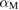 , is used to measure the relative strength of the orbital and Pauli limiting field values and is given by the expression:
, is used to measure the relative strength of the orbital and Pauli limiting field values and is given by the expression:
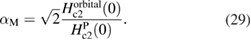
From this relation, we get 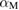 ≈ 0.29, which means that in our case,
≈ 0.29, which means that in our case,  is much larger than
is much larger than  , hence implying that the upper critical field is limited by the orbital effects and the Pauli paramagnetic effect is negligible as indicated by a small value of Maki parameter. For Sc5Ru6Sn18, the calculated
, hence implying that the upper critical field is limited by the orbital effects and the Pauli paramagnetic effect is negligible as indicated by a small value of Maki parameter. For Sc5Ru6Sn18, the calculated 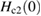 is close to the orbital limiting field and is much smaller than the Pauli limiting field.
is close to the orbital limiting field and is much smaller than the Pauli limiting field.
4. Summary
After succefully growing single crystals of Sc5Ru6Sn18, their superconducting properties were investigated by means of powder XRD, DC and AC magnetization, specific heat and µSR measurements. The powder XRD pattern was indexed as a tetragonal structure with lattice constants, a = 1.387(3) nm, c = 2.641(5) nm, which imply a density of 7.8(3) g cm−3. We find that Sc5Ru6Sn18 is a type-II superconductor with Tc ≈ 3.5(1) K, a lower critical field 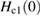 = 157(9) Oe and an upper critical field
= 157(9) Oe and an upper critical field 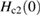 = 26(1) kOe. The zero-temperature thermodynamic critical field is estimated to be
= 26(1) kOe. The zero-temperature thermodynamic critical field is estimated to be 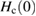 = 799(6) Oe. With a coherence length,
= 799(6) Oe. With a coherence length, 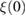 = 11.26(3) nm and a penetration depth,
= 11.26(3) nm and a penetration depth, 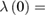 260(7) nm, Sc5Ru6Sn18 has a Ginzburg Landau parameter, κ = 23(2). The Bean model was used to calculate the critical current density, providing Jc(1.8 K) ~ 6 × 108 A m−2 at 150 Oe. The de-pairing current (Jd) is estimated to be 3.07 × 1010 A m−2.
260(7) nm, Sc5Ru6Sn18 has a Ginzburg Landau parameter, κ = 23(2). The Bean model was used to calculate the critical current density, providing Jc(1.8 K) ~ 6 × 108 A m−2 at 150 Oe. The de-pairing current (Jd) is estimated to be 3.07 × 1010 A m−2.
Our analysis of the normal-state specific heat yields a Sommerfeld coefficient, γ = 36.93(6) mJ mol−1 K−2, corresponding to a density of states at the Fermi level, N(EF) = 15.24(6) states/eV f.u. The superconducting transition is revealed by a sharp jump at Tc = 3.5(1) K, with 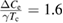 for γ = 36.93(6) mJ mol−1 K−2, which is higher than the BCS value of 1.43 for a weakly coupled superconductor, which indicates strong electron–phonon coupling in Sc5Ru6Sn18. The electronic specific heat can be fitted with a single-gap BCS model with
for γ = 36.93(6) mJ mol−1 K−2, which is higher than the BCS value of 1.43 for a weakly coupled superconductor, which indicates strong electron–phonon coupling in Sc5Ru6Sn18. The electronic specific heat can be fitted with a single-gap BCS model with 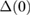 = 0.64(1) meV. The Sommerfeld constant γ exhibits a linear variation with the applied magnetic field, indicating an s-wave superconducting pairing in Sc5Ru6Sn18. TF-µSR measurements reveal that Sc5Ru6Sn18 is a strongly coupled superconductor. TF-µSR measurements also suggest an s-wave character of the superconducting gap. ZF-µSR measurements do not show the presence of spontaneous internal magnetic fields and hence, indicate a preserved TRS in Sc5Ru6Sn18. In table 1, we have summarized the experimentally estimated parameters of Sc5Ru6Sn18, along with those of Y5Rh6Sn18 [18] and Lu5Rh6Sn18 [2]. It is clear that most of the parameters of Sc5Ru6Sn18 are comparable with the corresponding parameters of Y5Rh6Sn18 and Lu5Rh6Sn18, except for
= 0.64(1) meV. The Sommerfeld constant γ exhibits a linear variation with the applied magnetic field, indicating an s-wave superconducting pairing in Sc5Ru6Sn18. TF-µSR measurements reveal that Sc5Ru6Sn18 is a strongly coupled superconductor. TF-µSR measurements also suggest an s-wave character of the superconducting gap. ZF-µSR measurements do not show the presence of spontaneous internal magnetic fields and hence, indicate a preserved TRS in Sc5Ru6Sn18. In table 1, we have summarized the experimentally estimated parameters of Sc5Ru6Sn18, along with those of Y5Rh6Sn18 [18] and Lu5Rh6Sn18 [2]. It is clear that most of the parameters of Sc5Ru6Sn18 are comparable with the corresponding parameters of Y5Rh6Sn18 and Lu5Rh6Sn18, except for 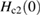 . Other compounds of the R5M6Sn18 family are currently being investigated to clarify the nature of the TRS breaking mechanism in this class of caged-type superconducting compounds.
. Other compounds of the R5M6Sn18 family are currently being investigated to clarify the nature of the TRS breaking mechanism in this class of caged-type superconducting compounds.
Table 1. Superconducting parameters of Sc5Ru6Sn18, Y5Rh6Sn18 [18] and Lu5Rh6Sn18 [2].
| Parameter | Unit | Sc5Ru6Sn18 | Y5Rh6Sn18 | Lu5Rh6Sn18 |
|---|---|---|---|---|
| Tc | K | 3.5(1) | 3 | 4(1) |
| Hc2(0) | kOe | 26(1) | 43 | 72.4 |
| γ | mJ mol−1 K−2 | 36.93(6) | 38.13(3) | 48.1(5) |
| ΔCe/γTc | 1.6 | 1.95 | 2.06 | |
| 2Δ(0)/kBTc | 4.25(4) | 4.26(4) | 4.26(4) | |
| θD | K | 205(1) | 183(2) | 157(2) |
| m* | 1.64(4) me | 1.21me | 1.32me | |
| ns | carriers m−3 | 7.05(2) × 1026 | 2.3 × 1028 | 2.6 × 1026 |
| Hc1(0) | Oe | 157(9) | ||
| Hc(0) | Oe | 799(6) | ||
| Jc(1.8 K) | A m−2 | 6(3) × 108 | ||
| Jd | A m−2 | 3.07(5) × 1010 | ||
| λ(0) | nm | 260(7) | ||
| ξ(0) | nm | 11.26(3) | ||
| κGL | 23(2) | |||
| λeff(0) | nm | 774(8) | ||
| N(EF) | states/eV f.u. | 15.24(6) | ||
| l | nm | 8.14(5) |
Acknowledgments
We acknowledge the Ministry of Science and Technology (MOST) of Taiwan, which supported the work, via the grants: MOST 104-2221-M-006-010-MY3, MOST 104-2119-M-006-017-MY3. DK would like to acknowledge MOST for the postdoctoral fellowship under project grant number MOST 105-2811-M-006-022. TS and TS acknowledge support from SNF—the Swiss National Science Foundation. Part of this work is based on experiments performed at the Swiss Muon Source µ, Paul Scherrer Institute, Villigen, Switzerland. We thank M R Lees for fruitful discussion.