Abstract
We introduce cascaded parity-time (PT)-symmetric artificial sheets (e.g. metasurfaces or frequency selective surfaces) that may exhibit multiple higher-order laser-absorber modes and bidirectional reflectionless transmission resonances within the PT-broken phase, as well as a unidirectional reflectionless transmission resonance associated with the exceptional point (EP). We derive the explicit expressions of the gain–loss parameter required for obtaining these modes and their intriguing physical properties. By exploiting the cascaded PT structures, the gain–loss threshold for the self-dual laser-absorber operation can be remarkably lowered, while the EP remains unaltered. We further study interferometric sensing based on such a multimodal laser-absorber and demonstrate that its sensitivity may be exceptionally high and proportional to the number of metasurfaces along the light propagation direction.
Export citation and abstract BibTeX RIS
1. Introduction
Parity-time (PT)-symmetry (space-time reflection symmetry) takes its roots from open quantum physics systems [1], where non-Hermitian Hamiltonians commute with parity and time reversal operators, and thus may exhibit real eigenvalues and eigenstates. This intriguing property was first discovered by Bender and Boettcher in 1998 [2], and ever since then, PT-symmetry has attracted tremendous interests due to its potential in novel applications, such as unidirectional reflectionless wave propagations [3, 4], invisibility cloaks [5, 6], negative refractions [7], loss-induced oscillators [8], and single-mode microlasers [9], to name a few. Exploration of these emerging applications lies in spectral singularities in PT-symmetric systems, such as exceptional points (EPs) and coherent perfect absorber-laser (CPAL) points. EPs are spectral degeneracies that indicate a transition of eigenvalues from real to complex-conjugate pairs, splitting the system into the exact PT-symmetric phase and the broken PT-symmetric (PT-broken) phase. In the PT-broken region, eigenvalues may diverge both to zero and infinity at CPAL points, leading to scattering anomalies, namely a device that can be switched from the lasing mode to the coherent perfect absorption (CPA) mode under different initial conditions [10–15].
EPs and CPAL points have unveiled the next-generation optical [1, 16–21], plasmonic [22] and electronic [23–30] sensors with remarkably enhanced sensitivity [31–36]. For example, sensors operating around the EPs were recently shown to possess a high sensitivity as a result of bifurcation of eigenvalues and eigenstates [22, 28, 34, 37–40]. It is worthwhile noting that the eigenvalue splitting scales with the nth root of the applied perturbation, where n is the order of the EP [41]. Very recently, 'monochromatic' sensors operating near the CPAL frequency were proposed to make interferometric sensors with ultrahigh sensitivity and low phase/flicker noises. In [10], a CPAL sensor made of a PT-symmetric pair of artificial electromagnetic sheets (e.g. active and passive metasurfaces) was studied, and limits of detection and sensitivity were derived. It was shown that the output factor in response to conductive perturbation ( ) or reactive perturbation [
) or reactive perturbation [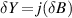 ] is given by:
] is given by: 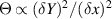 , where
, where 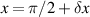 is the electrical length between the gain and loss layers at the operating angular frequency
is the electrical length between the gain and loss layers at the operating angular frequency  [10]. Intuitively, the sensitivity, defined as the slope of the output factor function, can be very large when the phase error
[10]. Intuitively, the sensitivity, defined as the slope of the output factor function, can be very large when the phase error  is infinitesimally small. The CPAL-based PT sensor was experimentally demonstrated in the electronics domain by means of the lumped elements circuits [11], where gain and loss elements were sourced from a negative-resistance converter and a shunt resistor, respectively, and a radio-frequency sensor was treated as a variable resistor or variable capacitor that changes the system's reflection or transmission responses. It was demonstrated that the CPAL-based PT sensor can outperform traditional sensors based on the Fabry–Perot interferometers in terms of sensitivity and resolvability [10, 11] under similar admittance perturbations.
is infinitesimally small. The CPAL-based PT sensor was experimentally demonstrated in the electronics domain by means of the lumped elements circuits [11], where gain and loss elements were sourced from a negative-resistance converter and a shunt resistor, respectively, and a radio-frequency sensor was treated as a variable resistor or variable capacitor that changes the system's reflection or transmission responses. It was demonstrated that the CPAL-based PT sensor can outperform traditional sensors based on the Fabry–Perot interferometers in terms of sensitivity and resolvability [10, 11] under similar admittance perturbations.
2. Results and discussion
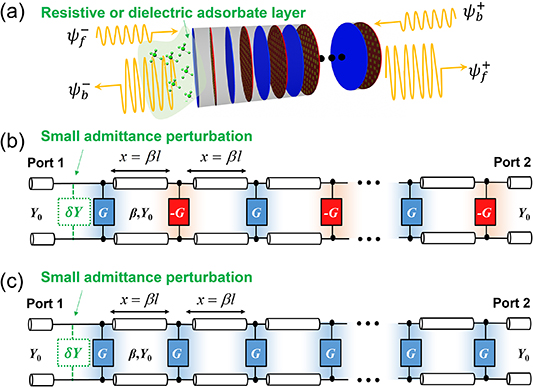
In this work, we further study the cascaded PT-symmetric metasurfaces that can have higher-order CPAL points, as illustrated in figure 1(a). Characteristics of the PT-symmetric multimodal laser-absorber can be described using the two-port transmission line network model shown in figure 1(b). Here, we consider isotropic and uniform metasurfaces with negative and positive equivalent surface conductances, 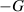 and
and  displaying a delicate balance between gain and loss, necessary for the PT symmetry condition. For the sake of simplicity, we assume that metasurfaces have purely real surface conductances and zero surface susceptances associated with reactive or stored energy. These gain and loss components are separated by a transmission line segment with characteristic admittance
displaying a delicate balance between gain and loss, necessary for the PT symmetry condition. For the sake of simplicity, we assume that metasurfaces have purely real surface conductances and zero surface susceptances associated with reactive or stored energy. These gain and loss components are separated by a transmission line segment with characteristic admittance  and an electrical distance
and an electrical distance  where
where  and
and 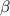 are the physical length and the phase constant of the line. This requires the physical length between two metasurfaces to be a quarter of the wavelength, which is sufficiently large for considering the metasurfaces to be isolated devices [42, 43]. Here, we define a dimensionless gain–loss parameter
are the physical length and the phase constant of the line. This requires the physical length between two metasurfaces to be a quarter of the wavelength, which is sufficiently large for considering the metasurfaces to be isolated devices [42, 43]. Here, we define a dimensionless gain–loss parameter  which is also regarded as the non-Hermiticity of the PT system. The incoming and outgoing waves from the left
which is also regarded as the non-Hermiticity of the PT system. The incoming and outgoing waves from the left  and right
and right  ports can be related by a
ports can be related by a  transfer matrix
transfer matrix  as:
as:  where the subscripts
where the subscripts  and
and 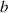 represent the forward and backward propagation flows. Since the PT-symmetric systems are reciprocal,
represent the forward and backward propagation flows. Since the PT-symmetric systems are reciprocal, 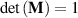 and
and 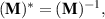 leading to
leading to 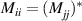 and
and  where
where  . Let us now consider PT systems comprising
. Let us now consider PT systems comprising  pairs of active and passive metasurfaces separated by an electrical length of
pairs of active and passive metasurfaces separated by an electrical length of 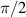 . The explicit expressions for the elements in
. The explicit expressions for the elements in 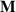 can be written as:
can be written as:
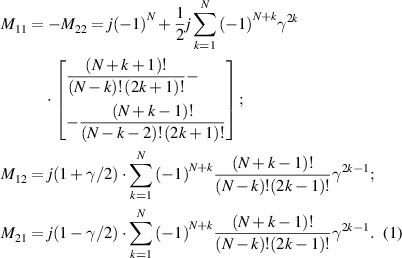
Figure 1. (a) Schematics and (b) the associated transmission line network model for the PT-symmetric electromagnetic system formed by cascaded artificial sheets with balanced gain and loss. Here, we assume that these artificial sheets are made of isotropic optical metasurfaces. In the optical region, active metasurfaces can be built using thin elements with photo-pumped gain. In the low-frequency regions, such as radio frequency (RF) and microwave frequencies, artificial sheets can be realized with active and passive metasurfaces as functional extensions of frequency selective surfaces (FSSs). The active FSS or metasurface can be built using thin metallic inclusions loaded with biased negative resistance converters.
Download figure:
Standard image High-resolution imageThe time-harmonic convention of 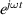 is adopted throughout this study (see supplementary material for derivation of M (available onilne at stacks.iop.org/JPD/55/085301/mmedia)). The relationship between the forward- and backward-propagating waves can be specified by a scattering matrix
is adopted throughout this study (see supplementary material for derivation of M (available onilne at stacks.iop.org/JPD/55/085301/mmedia)). The relationship between the forward- and backward-propagating waves can be specified by a scattering matrix 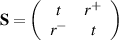 as:
as: 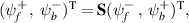 where
where  and
and  refer to transmission and reflection coefficients. The above-mentioned scattering coefficients are associated with
refer to transmission and reflection coefficients. The above-mentioned scattering coefficients are associated with  as:
as: 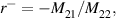
 and
and  The transition between the exact and broken PT-symmetry can be characterized by observing the evolution of scattering matrix eigenvalues,
The transition between the exact and broken PT-symmetry can be characterized by observing the evolution of scattering matrix eigenvalues,  as the gain–loss parameter
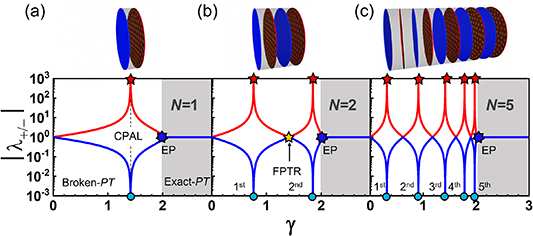
as the gain–loss parameter  is swept, as shown in figure 2(a). For the typical PT-symmetric metasurface system illustrated in the inset of figure 2(a), the eigenvalues and eigenstates coalesce into a single degenerate eigenmode at the EP (
is swept, as shown in figure 2(a). For the typical PT-symmetric metasurface system illustrated in the inset of figure 2(a), the eigenvalues and eigenstates coalesce into a single degenerate eigenmode at the EP (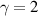 ), which divides the system into (a) the exact PT-symmetric phase where eigenvalues are nondegenerate and unimodular, and (b) the PT-symmetry-broken (or PT-broken) phase where eigenvalues are non-unimodular. In the PT-broken regime, there is a self-dual spectral singularity
), which divides the system into (a) the exact PT-symmetric phase where eigenvalues are nondegenerate and unimodular, and (b) the PT-symmetry-broken (or PT-broken) phase where eigenvalues are non-unimodular. In the PT-broken regime, there is a self-dual spectral singularity  at which eigenvalues diverge simultaneously to zero and infinity, standing respectively for the CPA and laser modes. At the CPAL point, the two modes with completely different optical properties can be switched by proper adjustment of the complex amplitude ratio between the uniform plane waves normally incident from the left and right directions. For the PT systems made of
at which eigenvalues diverge simultaneously to zero and infinity, standing respectively for the CPA and laser modes. At the CPAL point, the two modes with completely different optical properties can be switched by proper adjustment of the complex amplitude ratio between the uniform plane waves normally incident from the left and right directions. For the PT systems made of  pairs of active and passive metasurfaces, the phase transition always takes place at the EP (
pairs of active and passive metasurfaces, the phase transition always takes place at the EP ( ), resulting in the unidirectional reflectionless transmission, known also as anisotropic transmission resonance. Moreover, it is worth mentioning that there are
), resulting in the unidirectional reflectionless transmission, known also as anisotropic transmission resonance. Moreover, it is worth mentioning that there are  CPAL points and
CPAL points and 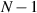 bidirectional reflectionless points (which are analogous to Fabry–Perot transmission resonance (FPTR)), whose generalized expressions can be written as:
bidirectional reflectionless points (which are analogous to Fabry–Perot transmission resonance (FPTR)), whose generalized expressions can be written as:
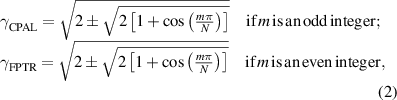
where  . Figures 2(b) and (c) show the eigenvalue evolutions for cascaded PT-symmetric metasurface systems with
. Figures 2(b) and (c) show the eigenvalue evolutions for cascaded PT-symmetric metasurface systems with  and
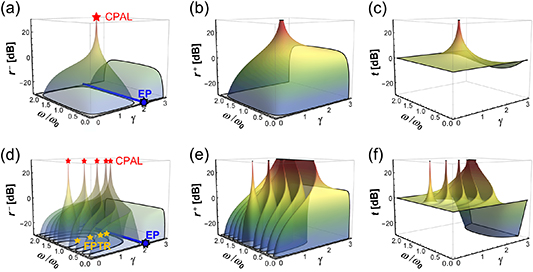
and  respectively. Figures 3(a)–(f) plot the calculated magnitudes of reflection and transmission coefficients for the PT-symmetric metasurface systems in figures 2(a) and (c), respectively. By inspecting figure 2, we find that if more than one pair of PT-symmetric metasurfaces are used (i.e. N ⩾ 2), the system can have multiple CPAL points in the PT-broken phase, so-called higher-order CPAL modes. On the other hand, despite the number of cascaded metasurfaces, there is always one EP, which gives the unidirectional reflectionless transmission (
respectively. Figures 3(a)–(f) plot the calculated magnitudes of reflection and transmission coefficients for the PT-symmetric metasurface systems in figures 2(a) and (c), respectively. By inspecting figure 2, we find that if more than one pair of PT-symmetric metasurfaces are used (i.e. N ⩾ 2), the system can have multiple CPAL points in the PT-broken phase, so-called higher-order CPAL modes. On the other hand, despite the number of cascaded metasurfaces, there is always one EP, which gives the unidirectional reflectionless transmission (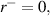
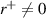 and
and  ) at
) at  as can be seen in figure 3. Importantly, the results obtained from equation (2) (figure 4(a)) show that min(
as can be seen in figure 3. Importantly, the results obtained from equation (2) (figure 4(a)) show that min( ) decreases as the number of active and passive metasurface pairs increase. Such results may be beneficial for laser and amplifier applications. In principle, when a large number of cascading metasurfaces are used, min(
) decreases as the number of active and passive metasurface pairs increase. Such results may be beneficial for laser and amplifier applications. In principle, when a large number of cascading metasurfaces are used, min( ) could be close to zero, implying that the gain–loss parameter threshold can be greatly reduced. Additionally, the upper bound on the CPAL effect is
) could be close to zero, implying that the gain–loss parameter threshold can be greatly reduced. Additionally, the upper bound on the CPAL effect is 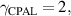 which is also the boundary between the exact PT-symmetric phase and the PT-broken phase. Also, in figure 3, we note that there exist
which is also the boundary between the exact PT-symmetric phase and the PT-broken phase. Also, in figure 3, we note that there exist 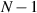 bidirectional reflectionless transmission resonances, with
bidirectional reflectionless transmission resonances, with  and
and  associated with the FPTRs. Unlike an EP, these FPTR points with symmetric scattering properties exist in the PT-broken phase and do not lead to the phase transition. In contrast, the bidirectional reflectionless transparency is obtained at the FPTR points where the sum of the reflection coefficient phases on the right and left walls (i.e. the first and last metasurfaces) and the phase change inside the structure (i.e. a round trip bounce inside the cavity) must be equal to zero or an integer multiple of
associated with the FPTRs. Unlike an EP, these FPTR points with symmetric scattering properties exist in the PT-broken phase and do not lead to the phase transition. In contrast, the bidirectional reflectionless transparency is obtained at the FPTR points where the sum of the reflection coefficient phases on the right and left walls (i.e. the first and last metasurfaces) and the phase change inside the structure (i.e. a round trip bounce inside the cavity) must be equal to zero or an integer multiple of 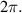 FPTR points also exist in a PT-symmetric metasurface pair with the electrical distance of its gap equal to
FPTR points also exist in a PT-symmetric metasurface pair with the electrical distance of its gap equal to 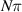 [7]. Increasing the number of cascaded active and passive metasurfaces would not only reduce the gain–loss parameter threshold for CPAL, but also reduce it for FPTR. It is interesting to note that the EP-associated unidirectional reflectionless transparency is insensitive to the electrical distance between metasurfaces and thus could be wideband but being quite sensitive to the gain–loss parameter. On the contrary, the FPTR-associated bidirectional reflectionless transparency is sensitive only to the electrical distance, instead of the gain–loss parameter. Finally, both the electrical length and the gain–loss parameter are important for the CPAL effect, as can be seen in figure 3. This may explain the high-Q nature of the CPAL modes.
[7]. Increasing the number of cascaded active and passive metasurfaces would not only reduce the gain–loss parameter threshold for CPAL, but also reduce it for FPTR. It is interesting to note that the EP-associated unidirectional reflectionless transparency is insensitive to the electrical distance between metasurfaces and thus could be wideband but being quite sensitive to the gain–loss parameter. On the contrary, the FPTR-associated bidirectional reflectionless transparency is sensitive only to the electrical distance, instead of the gain–loss parameter. Finally, both the electrical length and the gain–loss parameter are important for the CPAL effect, as can be seen in figure 3. This may explain the high-Q nature of the CPAL modes.
Figure 2. Variation of the eigenvalues of S with the gain–loss parameter 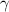 for the multimodal emitter-absorber based on the PT-symmetric system with
for the multimodal emitter-absorber based on the PT-symmetric system with  equal to (a) 1, (b) 2 and (c) 5. For all cases, an exceptional point (EP, marked by blue stars) dividing the system into exact- and broken-PT regimes is fixed at
equal to (a) 1, (b) 2 and (c) 5. For all cases, an exceptional point (EP, marked by blue stars) dividing the system into exact- and broken-PT regimes is fixed at 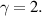 In the broken-PT regime, the eigenvalues become infinity (laser mode) and zero (CPA mode) at the CPAL points (marked by the red star and the blue circle), whose number depends on the number of gain–loss metasurface pairs. Here, the CPAL modes are labeled by 1st, 2nd, etc. Additionally, when
In the broken-PT regime, the eigenvalues become infinity (laser mode) and zero (CPA mode) at the CPAL points (marked by the red star and the blue circle), whose number depends on the number of gain–loss metasurface pairs. Here, the CPAL modes are labeled by 1st, 2nd, etc. Additionally, when  , there will exist
, there will exist 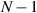 FPTRs in the broken-PT region, marked by the yellow stars.
FPTRs in the broken-PT region, marked by the yellow stars.
Download figure:
Standard image High-resolution imageFigure 3. (a)–(c) Contours of reflection coefficients (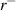 and
and 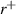 ) and transmission coefficient (t) for the PT-symmetric metasurface system as a function of the normalized angular frequency
) and transmission coefficient (t) for the PT-symmetric metasurface system as a function of the normalized angular frequency 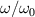 and the gain–loss parameter
and the gain–loss parameter  for the PT-symmetric bilayer metasurface in figure 2(a). Figures (d)–(f) are similar to (a)–(c), but for higher-order PT system with N = 5. Here, the CPAL points, EP, and FPTR points are labeled by the red, blue, and yellow stars, respectively.
for the PT-symmetric bilayer metasurface in figure 2(a). Figures (d)–(f) are similar to (a)–(c), but for higher-order PT system with N = 5. Here, the CPAL points, EP, and FPTR points are labeled by the red, blue, and yellow stars, respectively.
Download figure:
Standard image High-resolution imageFigure 4. (a) Evolution of 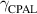 with the number of active and passive metasurface pairs. (b) Output coefficient versus the normalized angular frequency for CPA (dashed lines) and laser (solid lines) modes of the PT-symmetric metasurface systems with
with the number of active and passive metasurface pairs. (b) Output coefficient versus the normalized angular frequency for CPA (dashed lines) and laser (solid lines) modes of the PT-symmetric metasurface systems with  ; here, all the CPAL modes in (a) were calculated using equation (2).
; here, all the CPAL modes in (a) were calculated using equation (2).
Download figure:
Standard image High-resolution imageThe system's self-dual CPA-laser properties can be monitored by the output factor  defined as the ratio of the total intensity of outgoing waves to that of incoming waves:
defined as the ratio of the total intensity of outgoing waves to that of incoming waves:
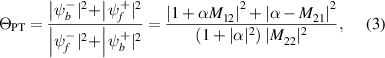
where 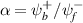 is the complex amplitude ratio of two incoming plane waves. The CPA mode is obtained by setting
is the complex amplitude ratio of two incoming plane waves. The CPA mode is obtained by setting  while the system is switched to the laser mode if
while the system is switched to the laser mode if 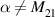 . Such a result is valid for arbitrary
. Such a result is valid for arbitrary 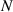 . Figure 4(b) shows the corresponding output factors for the CPAL modes highlighted in figure 4(a). Remarkably, it can be seen from figure 4(b) that the emitter-absorber property can be switched at the same frequency by properly adjusting the gain–loss parameter and the complex-amplitude ratio of input waves, following the guidelines provided in equations (1) and (2). We find that the much narrower linewidth (or larger Q-factor) can be obtained in the lower-order laser and CPA modes, as can be seen in figure 4(b).
. Figure 4(b) shows the corresponding output factors for the CPAL modes highlighted in figure 4(a). Remarkably, it can be seen from figure 4(b) that the emitter-absorber property can be switched at the same frequency by properly adjusting the gain–loss parameter and the complex-amplitude ratio of input waves, following the guidelines provided in equations (1) and (2). We find that the much narrower linewidth (or larger Q-factor) can be obtained in the lower-order laser and CPA modes, as can be seen in figure 4(b).
Next, we will discuss the sensing functions of cascaded PT metasurface systems locked at the CPAL points. When a small admittance perturbation, such as gaseous surface absorbates or micro liquids, is attached on the first metasurface, a shunt admittance  is introduced to the system, as depicted in figure 5(a). In this case, the device could be radically switched from a CPA to a laser, and vice versa [10]. Such a modal transition could result in dramatic changes in the output coefficient. In other words, the slope of
is introduced to the system, as depicted in figure 5(a). In this case, the device could be radically switched from a CPA to a laser, and vice versa [10]. Such a modal transition could result in dramatic changes in the output coefficient. In other words, the slope of 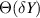 may be very steep, suggesting that a CPAL-based sensor can have an unprecedented sensitivity. Assuming that the system is initially operating at the fundamental CPA mode, the output coefficient as a function of a small conductance perturbation
may be very steep, suggesting that a CPAL-based sensor can have an unprecedented sensitivity. Assuming that the system is initially operating at the fundamental CPA mode, the output coefficient as a function of a small conductance perturbation 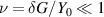 can be derived as:
can be derived as:
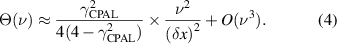
Figure 5. (a) Schematic of multimodal CPAL-based PT-symmetric metasurface sensing system and (b) its equivalent transmission line network model; here, the shunt admittance is introduced by a thin dielectric or conductive layer, which respectively correspond to surface susceptance  and surface conductance
and surface conductance 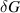 , as discussed in [10]. (c) An equivalent transmission line network of cascaded FPC metasurface structure.
, as discussed in [10]. (c) An equivalent transmission line network of cascaded FPC metasurface structure.
Download figure:
Standard image High-resolution imageEquation (4) is also applicable to a reactive perturbation  . The result in equation (4) remains applicable when
. The result in equation (4) remains applicable when  is replaced with
is replaced with 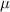 . In [10], we have experimentally demonstrated that the output coefficient of a single-mode PT-based CPAL is
. In [10], we have experimentally demonstrated that the output coefficient of a single-mode PT-based CPAL is 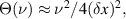 so the slope depends on an augment factor of
so the slope depends on an augment factor of  . For a system with multiple CPAL modes, the slope of
. For a system with multiple CPAL modes, the slope of 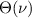 is related also to an extra augment factor,
is related also to an extra augment factor,  and it is intuitive when
and it is intuitive when  approaches its upper bound (i.e.
approaches its upper bound (i.e. 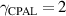 ), the slope of
), the slope of  could also become infinity. This ensures unprecedented sensitivity even when fabrication errors in stacking the metasurfaces (which increases
could also become infinity. This ensures unprecedented sensitivity even when fabrication errors in stacking the metasurfaces (which increases  ) are taken into account. In theory, an infinite slope could be obtained when
) are taken into account. In theory, an infinite slope could be obtained when  is large or when
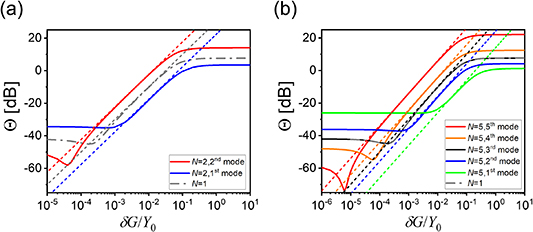
is large or when 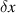 is infinitesimally small, both leading to an unprecedentedly high sensitivity. Figures 6(a) and (b) compare variations of the output coefficients with conductive perturbation for the multimodal CPAL sensors with
is infinitesimally small, both leading to an unprecedentedly high sensitivity. Figures 6(a) and (b) compare variations of the output coefficients with conductive perturbation for the multimodal CPAL sensors with  and
and  ; here, all CPAL modes are presented for making a fair comparison. It is seen from figure 6 that for certain CPAL modes, sensitivity plotted in the logarithm scale can be much greater than that of the single-mode CPAL.
; here, all CPAL modes are presented for making a fair comparison. It is seen from figure 6 that for certain CPAL modes, sensitivity plotted in the logarithm scale can be much greater than that of the single-mode CPAL.
Figure 6. Variations of the output coefficient with the conductive perturbation for the multimodal CPAL sensors in figure 5(a) with different numbers of active and passive metasurface pairs: (a) 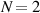 and (b)
and (b)  . The results for a single mode CPAL sensor (i.e. PT bilayer metasurfaces) are given with the dash-dots line.
. The results for a single mode CPAL sensor (i.e. PT bilayer metasurfaces) are given with the dash-dots line.
Download figure:
Standard image High-resolution imageHere, we also compare the optimum sensitivity of multimodal CPAL sensors with that of interferometric sensors made of multilayered Fabry–Perot cavity (FPC)-based CPA. A multilayered FPC-based CPA comprises passive metasurfaces with surface conductance 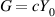 where c is a positive real number, with its equivalent transmission line network model shown in figure 5(c). Inside an FPC, the electrical length between neighboring metasurfaces
where c is a positive real number, with its equivalent transmission line network model shown in figure 5(c). Inside an FPC, the electrical length between neighboring metasurfaces  For the simplest FPC made of two passive metasurface walls, the CPA effect can be obtained when eigenvalues of the scattering matrix are 1 and 0 at the operating frequency (see figure 7(a)) and the phase offset between two incoming waves is
For the simplest FPC made of two passive metasurface walls, the CPA effect can be obtained when eigenvalues of the scattering matrix are 1 and 0 at the operating frequency (see figure 7(a)) and the phase offset between two incoming waves is 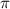 (i.e.
(i.e.  ). Figure 7(b) reports the dependencies of eigenvalues on
). Figure 7(b) reports the dependencies of eigenvalues on  at the operating frequency
at the operating frequency 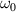 for multilayered FPC (
for multilayered FPC ( ). By applying the proper
). By applying the proper  and electrical length
and electrical length  into multilayered FPC, we could explicitly derive the transfer matrix:
into multilayered FPC, we could explicitly derive the transfer matrix:  From equation (3), we know that the CPA effect is obtained when
From equation (3), we know that the CPA effect is obtained when 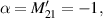 and together with the above results, one may straightforwardly understand that
and together with the above results, one may straightforwardly understand that 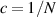 is the generalized CPA condition for FPCs. Such a result is clearly seen in figure 7(b), as c required for making a CPA decreases when N increases. After substituting
is the generalized CPA condition for FPCs. Such a result is clearly seen in figure 7(b), as c required for making a CPA decreases when N increases. After substituting  and
and  into equation (3), as well as introducing a small conductive and reactive perturbation to the first metasurface, the output coefficients of the multilayered FPC-based CPA can be approximately expressed as:
into equation (3), as well as introducing a small conductive and reactive perturbation to the first metasurface, the output coefficients of the multilayered FPC-based CPA can be approximately expressed as:
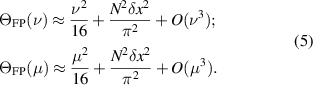
Figure 7. (a) Contours of eigenvalues as a function of angular frequency  and the dimensionless parameter
and the dimensionless parameter 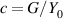 for an FPC interferometer formed by a pair of resistive metasurfaces. (b) Dependencies of eigenvalues on the normalized surface conductance c and the number of resistive metasurface pairs
for an FPC interferometer formed by a pair of resistive metasurfaces. (b) Dependencies of eigenvalues on the normalized surface conductance c and the number of resistive metasurface pairs  at the operating frequency
at the operating frequency 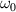 ; here, the dashed lines and solid lines represent the two eigenvalues of the system,
; here, the dashed lines and solid lines represent the two eigenvalues of the system, 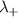 and
and  .
.
Download figure:
Standard image High-resolution imageIt is therefore evident that sensitivity related to the slope of 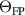 is ∼
is ∼ , independent of the number of metasurfaces. Moreover, the lowest output coefficient is
, independent of the number of metasurfaces. Moreover, the lowest output coefficient is  showing that increasing
showing that increasing 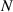 could only interfere with the detection result for small
could only interfere with the detection result for small  and
and  . Figures 8(a) and (b) compare the optimum slope of the output coefficients for the interferometric sensors made of multimodal CPAL in figure 2 (
. Figures 8(a) and (b) compare the optimum slope of the output coefficients for the interferometric sensors made of multimodal CPAL in figure 2 (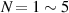 ) and its passive FPC counterparts, under similar conductive and reactive perturbations; here we assume that
) and its passive FPC counterparts, under similar conductive and reactive perturbations; here we assume that  From figure 8, it is evident that under the same amount of conductive or reactive perturbations, the CPAL sensor can outperform the traditional passive FPC sensor in terms of sensitivity, resolvability, and the limit of detection. We find that the sensitivity of multimodal FP sensors does not increase with
From figure 8, it is evident that under the same amount of conductive or reactive perturbations, the CPAL sensor can outperform the traditional passive FPC sensor in terms of sensitivity, resolvability, and the limit of detection. We find that the sensitivity of multimodal FP sensors does not increase with  . Instead, increasing
. Instead, increasing  only degrades the sensing performance and the range of detection, as can be understood from inspection of equation (5). Such an outcome is opposite to what can be observed in the multimodal CPAL sensors in figure 6. Our theoretical results demonstrate that the multimodal CPAL sensors based on suitable PT-symmetric metasurfaces could outperform conventional sensors based on the passive cavity or resonator.
only degrades the sensing performance and the range of detection, as can be understood from inspection of equation (5). Such an outcome is opposite to what can be observed in the multimodal CPAL sensors in figure 6. Our theoretical results demonstrate that the multimodal CPAL sensors based on suitable PT-symmetric metasurfaces could outperform conventional sensors based on the passive cavity or resonator.
Figure 8. Comparison of output coefficient variations between multimodal CPAL sensors (solid lines) and multimodal Fabry–Perot CPA sensors (dashed lines) of the same number of metasurfaces under (a) conductive perturbation and (b) reactive perturbation; here, only the maximum sensitivity of each type of sensor is displayed.
Download figure:
Standard image High-resolution imageFinally, we also propose feasible methods to practically implement the proposed multimodal CPAL devices in the optical region. At optical frequencies, an active metasurface with negative surface conductance can be made by lithographically patterning a thin layer of gain medium, such as an optically-pumped 2D mono- or bi-layer [15, 44–47], organic dyes [48], or some semiconductors [49]. A passive metasurface with positive surface conductance can be made of a patterned resistive film. The cascaded PT structures including the dielectric spacers can be fabricated using sequential thin-film deposition, typical in complimentary metal-oxide semiconductor processes. When the CPAL device is used for sensing, the admittance perturbation could be due to surface adhesion of gases, aqueous solutions, or aerosols. In addition, surface absorbates can also change the surface admittance of a passive/active metasurface made of monolayer or few-layer 2D materials.
3. Conclusions
In summary, we have introduced multimodal CPAL and FPTR devices based on cascaded PT-symmetric metasurfaces with scalar surface conductances. We have derived the analytical expression for the EP, as well as the CPAL points and FPTR points existing in the PT-broken phase. A multimodal CPAL can have a reduced gain–loss threshold for achieving the self-dual emitter-absorber property, since the threshold decreases as the number of active and passive metasurface pairs increases. Additionally, we have analyzed changes in output factor when responding to surface conductive or reactive perturbations. We have shown theoretically that a multimodal CPAL sensor has the ability to sense an infinitesimal change in surface properties such as the adhesion of a thin dielectric or conductive film. Further, the sensitivity of this innovative CPAL sensor is proportional to the number of metasurfaces used to build the PT system. We envision that many applications including optical switches, modulators, lasers, and interferometric sensors may benefit from the proposed multimodal PT optical devices.
Acknowledgments
PYC would like to thank the NSF ECCS-1917678 Grant for supporting this work.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflict of interest
There are no conflicts to declare.