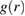Abstract
The free energy of hard-sphere systems provides a direct link between the particle-scale structure and macroscopic thermodynamic properties. Here, we employ this framework to investigate the shear-induced structure of a colloidal glass, and link it to its macroscopic mechanical and thermodynamic state. We measure the nonequilibrium free energy under shear from the free volumes of the particles, and monitor its evolution with the applied strain. Unlike crystals, for which the elastic energy increases quadratically with strain due to affine particle displacements, for glasses the free energy decreases due to non-affine displacements and dissipation, reflecting the ability of the glass to reach deeper free-energy minima. We model this decrease using the nonaffine shear modulus and a standard viscous dissipative term. Our model and measurements allow us to disentangle the complex contributions of affine and nonaffine particle displacements in the transient shear deformation of glasses.
Export citation and abstract BibTeX RIS
1. Introduction
Unlike crystals that deform reversibly under small applied strain, amorphous materials such as glasses deform irreversibly even at vanishingly small deformations. This relaxation is a generic property of glasses and central to their mechanical properties, such as elasticity, time-dependent anelasticity, and plastic flow, and its understanding remains a major challenge. This property of glasses is fundamentally connected to the lack of inversion symmetry: in most crystals, the lattice point symmetry guarantees local balance of forces by affine displacements, while in glasses, the amorphous short-range order precludes force balance by affine displacements alone, leading to additional non-affine motions to restore force balance locally under applied shear [1]. The usual description of glasses is also very different from crystals, involving a free-energy landscape picture in which the glasses seek to find ever lower free-energy minima by thermally activated hops over energy barriers. Such hops may also be shear-induced, causing accelerated aging due to the system being driven into deeper free-energy minima. These concepts have remained, however, rather abstract, because a direct connection between the shear-induced (non-affine) atomic displacements and the free energy is lacking for the simple reason that both are almost impossible to measure. Disentangling the complex contributions of affine and non-affine displacements and connecting them to the free-energy landscape of amorphous materials therefore remains a crucial challenge.
Colloidal glasses, on the other hand, do allow for a direct observation of single-particle dynamics, and consequently they have become much-studied model systems for the microscopic degrees of freedom of amorphous solids. Hard-sphere particles are known to undergo a colloidal glass transition at volume fraction  [2]; since there are no interactions between the particles other than collisions, the free energy is uniquely defined by the entropy of the particles. Theory [3–6] and recent experiments [7, 8] have shown that the particle configurations then provide a direct route to the free energy of the system that is determined by geometry only. This opens up new opportunities to elucidate, experimentally, the relation between microscopic degrees of freedom and important bulk thermodynamic quantities of deformation.
[2]; since there are no interactions between the particles other than collisions, the free energy is uniquely defined by the entropy of the particles. Theory [3–6] and recent experiments [7, 8] have shown that the particle configurations then provide a direct route to the free energy of the system that is determined by geometry only. This opens up new opportunities to elucidate, experimentally, the relation between microscopic degrees of freedom and important bulk thermodynamic quantities of deformation.
In this paper, we experimentally study the shear deformation of glasses and connect the shear-induced microscopic structure to the macroscopic free energy of deformation. The main finding is that the free energy of the glass decreases with increasing deformation, whereas that of the crystal increases. To provide a quantitative analysis we then use a recent theoretical framework that generalizes Born's stability criterion for crystals to amorphous solids. In the model, strain-induced forces that balance by symmetry in centrosymmetric crystals, require additional non-affine displacements in amorphous solids to be relaxed. The framework we develop relates affine and non-affine displacements in amorphous solids, allowing us to link them to the elastic moduli, stress and free energy of the glass. The conclusion is that the free energy decrease is due to the non-affine displacements that allow the glass to find deeper free energy minima. This leads to a simple particle-scale picture of the transient deformation that is typical to glasses: the loss of interparticle contacts in the extensional sectors of the shear plane leads to loss of connectivity between the particles entailing a proliferation of non-affine displacements that enables the flow under the applied shear.
2. Experiments
We use a colloidal glass consisting of sterically stabilized fluorescent polymethylmethacrylate (PMMA) particles with a diameter of d = 1.5 μm and a polydisperity of  , suspended in a density and refractive index-matching mixture of cycloheptyl bromide and cis-decalin. A dense glassy suspension with particle volume fraction
, suspended in a density and refractive index-matching mixture of cycloheptyl bromide and cis-decalin. A dense glassy suspension with particle volume fraction 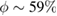 , above the colloidal glass transition
, above the colloidal glass transition  is prepared by diluting suspensions centrifuged to a sediment. At this high volume fraction, structural relaxations occur very slowly; at rest, we measure a glass relaxation time of
is prepared by diluting suspensions centrifuged to a sediment. At this high volume fraction, structural relaxations occur very slowly; at rest, we measure a glass relaxation time of  s by confocal microscopy as the time in which the particles' mean-square displacement becomes equal to their radius [9]. The suspension is loaded in a cell between two horizontal, parallel plates 65 μm apart. A piezoelectric translation stage moves the top plate, applying shear at very slow rates between
s by confocal microscopy as the time in which the particles' mean-square displacement becomes equal to their radius [9]. The suspension is loaded in a cell between two horizontal, parallel plates 65 μm apart. A piezoelectric translation stage moves the top plate, applying shear at very slow rates between 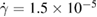 s−1 and
s−1 and  s−1, of the order of the inverse relaxation time; these shear rates are significantly smaller than in other studies on colloidal flows [10–13]. The plates are immersed in a colloidal reservoir; hence the sheared suspension can dilate under constant osmotic pressure. We image the individual particles using confocal microscopy, and determine their positions in three dimensions with an accuracy of 0.03 μm in the horizontal, and 0.05 μm in the vertical direction [9]. This way, we follow the particle-scale structure of the glass under applied shear, from the undeformed state at strain
s−1, of the order of the inverse relaxation time; these shear rates are significantly smaller than in other studies on colloidal flows [10–13]. The plates are immersed in a colloidal reservoir; hence the sheared suspension can dilate under constant osmotic pressure. We image the individual particles using confocal microscopy, and determine their positions in three dimensions with an accuracy of 0.03 μm in the horizontal, and 0.05 μm in the vertical direction [9]. This way, we follow the particle-scale structure of the glass under applied shear, from the undeformed state at strain  to
to 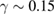 .
.
To link the structure to the thermodynamic properties of the sheared glass, we determine the free energy from the particle configurations obtained with confocal microscopy [7]. The central quantity of interest is then the free energy of deformation defined as  , i.e. the difference between the free energy
, i.e. the difference between the free energy 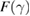 of the deformed state under a strain γ, and the free energy
of the deformed state under a strain γ, and the free energy 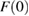 of the unstrained glass at rest [14]. This quantity encodes the local affine and nonaffine distortions of the glass structure together with irreversible rearrangements due to relaxation. To determine it, we generate a Voronoi tessellation that divides the space into distinct, non-overlapping convex polyhedra. The free volume
of the unstrained glass at rest [14]. This quantity encodes the local affine and nonaffine distortions of the glass structure together with irreversible rearrangements due to relaxation. To determine it, we generate a Voronoi tessellation that divides the space into distinct, non-overlapping convex polyhedra. The free volume 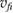 associated with a Voronoi cell i is then defined as the volume accessible to the center of mass of the particle, and is generated from the Voronoi cell by moving the faces normally inside over a distance of half the particle diameter. Note that this method is applicable to high densities [3], especially for a glassy system [7] where the particles are densely packed. The total free energy of the hard-sphere system can then be expressed directly in terms of only the free volume as
associated with a Voronoi cell i is then defined as the volume accessible to the center of mass of the particle, and is generated from the Voronoi cell by moving the faces normally inside over a distance of half the particle diameter. Note that this method is applicable to high densities [3], especially for a glassy system [7] where the particles are densely packed. The total free energy of the hard-sphere system can then be expressed directly in terms of only the free volume as 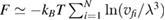 , where
, where  is the thermal wavelength [3, 7]. This allows us to track both reversible (equilibrium) [14] and irreversible (nonequilibrium) [15] contributions to the free energy of deformation.
is the thermal wavelength [3, 7]. This allows us to track both reversible (equilibrium) [14] and irreversible (nonequilibrium) [15] contributions to the free energy of deformation.
3. Results and discussion
For a uniformly sheared, purely elastic crystal, the free energy should increase quadratically with applied strain, similar to the elastic deformation of a spring. This is indeed what we find when we construct an affine shear deformation on a computer-generated hard-sphere face-centered cubic (fcc) crystal, and use our method to compute the free energy (figure 1(c), open stars and blue fitting curve). Here, the particle volume fraction  was preserved using periodic boundary conditions. The curvature of the parabola indicates the elastic modulus, which we determine to be
was preserved using periodic boundary conditions. The curvature of the parabola indicates the elastic modulus, which we determine to be  , in good agreement with
, in good agreement with 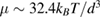 determined for
determined for 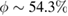 in simulations [16]. In contrast, in the experiments, when we shear a colloidal glass, we measure a surprising decrease of the free energy (figure 1(c), colored closed symbols and black down-curved fit). This monotonic decrease indicates that microscopic degrees of freedom other than affine motions dominate the deformation with increasing strain.
in simulations [16]. In contrast, in the experiments, when we shear a colloidal glass, we measure a surprising decrease of the free energy (figure 1(c), colored closed symbols and black down-curved fit). This monotonic decrease indicates that microscopic degrees of freedom other than affine motions dominate the deformation with increasing strain.
Figure 1. Changes in free energy and volume fraction upon deformation of crystals and glasses. Sketches of a sheared crystal (a) and glass (b) at strain 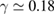 . (c) Free energy per particle as a function of strain in two types of systems: a constructed fcc cystal displaying purely affine deformation (stars and up-curved blue parabolic fit) and experimental deformation of a colloidal glass at different shear rates (filled symbols and down-curved fit according to our model). Also indicated are the predicted affine (solid and dashed red upward curves) and non-affine components (light gray shaded area), and dissipation (dark gray shaded area). The affine component is given by
. (c) Free energy per particle as a function of strain in two types of systems: a constructed fcc cystal displaying purely affine deformation (stars and up-curved blue parabolic fit) and experimental deformation of a colloidal glass at different shear rates (filled symbols and down-curved fit according to our model). Also indicated are the predicted affine (solid and dashed red upward curves) and non-affine components (light gray shaded area), and dissipation (dark gray shaded area). The affine component is given by  according to the first two terms of equation (1). Symbols indicate shear rates of
according to the first two terms of equation (1). Symbols indicate shear rates of 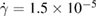 s−1 (black squares),
s−1 (black squares), 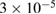 s−1 (red circles),
s−1 (red circles), 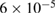 s−1 (olive triangles), 10−4 s−1 (blue triangles),
s−1 (olive triangles), 10−4 s−1 (blue triangles),  s−1 (orange diamonds). Enlarged section of the free energy data in the inset (highest shear rates only) clearly shows the initial parabolic increase of the free energy at small strain, well fitted by the affine component only. A relaxation event leads to sudden free energy drop at a strain of ∼0.05. The shear modulus corresponding to the parabolic increase is ∼
s−1 (orange diamonds). Enlarged section of the free energy data in the inset (highest shear rates only) clearly shows the initial parabolic increase of the free energy at small strain, well fitted by the affine component only. A relaxation event leads to sudden free energy drop at a strain of ∼0.05. The shear modulus corresponding to the parabolic increase is ∼ , roughly an order of magnitude smaller than shear moduli determineed by step-stress [17] or oscillatory measurements [18], possibly reflecting its frequency dependence. Reproduced from [17]. © IOP Publishing Ltd. All rights reserved. (d) Particle volume fraction change
, roughly an order of magnitude smaller than shear moduli determineed by step-stress [17] or oscillatory measurements [18], possibly reflecting its frequency dependence. Reproduced from [17]. © IOP Publishing Ltd. All rights reserved. (d) Particle volume fraction change 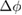 versus strain at shear rate 10−4 s−1 for the glass with initial volume fraction
versus strain at shear rate 10−4 s−1 for the glass with initial volume fraction 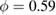 . The inset shows the predicted volume fraction change versus strain in a simple expansion for marginal solids (see text).
. The inset shows the predicted volume fraction change versus strain in a simple expansion for marginal solids (see text).
Download figure:
Standard image High-resolution imageLooking more closely, the data points suggest that the glass free energy in fact follows an upwards parabolic curvature initially (red solid curve). After this initial increase, at 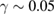 , the free energy decreases abruptly, followed by another parabolic increase (red dashed curve), followed by another abrupt decrease, etc. These sudden drops suggest occurrence of significant relaxation events after some elastic loading. Such intermittency has been observed as important hallmark in the relaxation of stressed glasses, and we see it here even in the bulk free energy. This intermittency leads to an overall decreasing trend in the free energy, signaling significant relaxation of the glass under shear.
, the free energy decreases abruptly, followed by another parabolic increase (red dashed curve), followed by another abrupt decrease, etc. These sudden drops suggest occurrence of significant relaxation events after some elastic loading. Such intermittency has been observed as important hallmark in the relaxation of stressed glasses, and we see it here even in the bulk free energy. This intermittency leads to an overall decreasing trend in the free energy, signaling significant relaxation of the glass under shear.
A possible mechanism decreasing the free energy is dilation; glasses can dilate under shear, increasing the free volume, and hence decreasing the free energy. Therefore, we monitored, by particle counting, the volume fraction change upon deformation. However, we find that the changes are small; initially, the volume fraction even increases, indicating some compaction of the material, before it saturates at a constant value in the strain window where the free energy decreases; see figure 1(d). Clearly, dilation cannot account for the decrease in free energy. The small amount of compaction observed (figure 1(d)) can result from the osmotic pressure of the colloidal reservoir that is in direct particle exchange with the sheared colloidal layer. This compaction is in contrast to what is expected for sheared marginal elastic solids. We compute the dilation and resulting volume fraction change for sheared marginal elastic solids following [19]; see appendix. The resulting strain-dependent volume fraction  decreases considerably with deformation (figure 1(d), inset) to as much as 40% in the relevant range of strain values, in stark contrast to what we observe in our experiments on colloidal glasses (figure 1(d)).
decreases considerably with deformation (figure 1(d), inset) to as much as 40% in the relevant range of strain values, in stark contrast to what we observe in our experiments on colloidal glasses (figure 1(d)).
Since dilation cannot explain the decrease in the free energy, we looked at other structural changes. We computed the pair correlation function 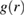 that indicates the probability of finding a particle at a distance r with respect to the ideal gas distribution. Resolving
that indicates the probability of finding a particle at a distance r with respect to the ideal gas distribution. Resolving  in the shear plane, we observe a significant distortion of the average nearest-neighbor structure under deformation, as shown in figure 2(a), where we plot the difference of
in the shear plane, we observe a significant distortion of the average nearest-neighbor structure under deformation, as shown in figure 2(a), where we plot the difference of 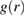 between the deformed and undeformed states. Clearly, nearest neighbour distances become extended in the dilation direction and reduced in the compression direction, as expected for the shear geometry and consistent with earlier work [11, 20, 21]. At the same time, the angle-averaged nearest neighbor distance remains essentially unchanged as shown in the appendix (figure B1), confirming the overall constant density of the glass in agreement with figure 1(d). As a result of the anisotropic distortion, particles become crowded along the compression direction, and less dense along the dilation direction, as schematically shown in figure 2(b). This is reflected in the height of
between the deformed and undeformed states. Clearly, nearest neighbour distances become extended in the dilation direction and reduced in the compression direction, as expected for the shear geometry and consistent with earlier work [11, 20, 21]. At the same time, the angle-averaged nearest neighbor distance remains essentially unchanged as shown in the appendix (figure B1), confirming the overall constant density of the glass in agreement with figure 1(d). As a result of the anisotropic distortion, particles become crowded along the compression direction, and less dense along the dilation direction, as schematically shown in figure 2(b). This is reflected in the height of  , which is a measure of the number of nearest neighbors. As shown in figure 2(c), this height decreases significantly in the dilation direction, indicating neighbor loss, while it becomes only slightly larger along the compression direction, indicating only some neighbor gain. This imbalance results from the asymmetry of the hard-core repulsion rendering further approach of nearest neighbors prohibitively difficult. As the neighbor loss is not balanced by neighbor gain, this leads to an overall loss of neighbours and to destabilization. The resulting imbalance of forces causes the particles to move non-affinely to restore the local force balance [1, 22]. Because these nonaffine displacements perform internal work against the potential of mean force (the potential-field of our 'lattice'), this process results in an overall negative contribution to the free energy [23–25]. We note that by looking in the shear plane, we have focused here on the most obvious nonaffine contributions; non-affine rearrangements may exist in other planes as well (see e.g. recent work on a sheared emulsion in [26]), but are typically less dominant, as shown by the three-dimensional nature of shear rearrangements in colloidal glasses [27].
, which is a measure of the number of nearest neighbors. As shown in figure 2(c), this height decreases significantly in the dilation direction, indicating neighbor loss, while it becomes only slightly larger along the compression direction, indicating only some neighbor gain. This imbalance results from the asymmetry of the hard-core repulsion rendering further approach of nearest neighbors prohibitively difficult. As the neighbor loss is not balanced by neighbor gain, this leads to an overall loss of neighbours and to destabilization. The resulting imbalance of forces causes the particles to move non-affinely to restore the local force balance [1, 22]. Because these nonaffine displacements perform internal work against the potential of mean force (the potential-field of our 'lattice'), this process results in an overall negative contribution to the free energy [23–25]. We note that by looking in the shear plane, we have focused here on the most obvious nonaffine contributions; non-affine rearrangements may exist in other planes as well (see e.g. recent work on a sheared emulsion in [26]), but are typically less dominant, as shown by the three-dimensional nature of shear rearrangements in colloidal glasses [27].
Figure 2. Shear-induced loss of structural connectivity. (a) Particle pair correlation function  in the shear plane. Color indicates the difference of
in the shear plane. Color indicates the difference of  of the sheared glass (
of the sheared glass ( s−1) with respect to the undeformed state. (b) Schematic of the corresponding nearest-neighbor configuration under applied shear. The number of particles moving out of the cage in the extension direction is larger than that moving in along the compression direction, leading to net loss of connectivity. (c) Measured maximum of
s−1) with respect to the undeformed state. (b) Schematic of the corresponding nearest-neighbor configuration under applied shear. The number of particles moving out of the cage in the extension direction is larger than that moving in along the compression direction, leading to net loss of connectivity. (c) Measured maximum of  in the compression (black squares) and extension (red circles) axis (plotted in logarithmic scale) as a function of strain (linear scale). The black fitting line has slope −0.9.
in the compression (black squares) and extension (red circles) axis (plotted in logarithmic scale) as a function of strain (linear scale). The black fitting line has slope −0.9.
Download figure:
Standard image High-resolution imageTo obtain a quantitative description of the free energy of deformation, we first consider the affine part, 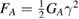 , where the shear modulus
, where the shear modulus 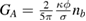 in the linear regime, according to the Born–Huang theory of lattice dynamics [28]. Here, nb is the number of nearest neighbors and κ the spring constant associated with a nearest-neighbor bond. In our hard-sphere glass, the 'bonds' between neighbors arise from the entropic attraction (akin to depletion attraction) [29] that relates the first peak of the radial distribution function
in the linear regime, according to the Born–Huang theory of lattice dynamics [28]. Here, nb is the number of nearest neighbors and κ the spring constant associated with a nearest-neighbor bond. In our hard-sphere glass, the 'bonds' between neighbors arise from the entropic attraction (akin to depletion attraction) [29] that relates the first peak of the radial distribution function 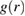 to an attractive minimum in the pair potential of mean force
to an attractive minimum in the pair potential of mean force  . This also defines the effective elastic spring constant as
. This also defines the effective elastic spring constant as ![$\kappa=[d^{2}V_{{\rm eff}}/dr^{2}]_{r=\sigma}$](https://content.cld.iop.org/journals/0022-3727/51/32/324002/revision2/daad03aieqn046.gif) between two bonded neighbors. The number of bonded neighbors is given by the integral of the first peak of
between two bonded neighbors. The number of bonded neighbors is given by the integral of the first peak of  , which yields
, which yields  for the static hard-sphere glass5. Under applied shear, this value decreases as the loss of neighbors in the dilation direction is not balanced by the particle gain in the compression direction [20, 31]. We model this loss of neighbors by assuming that the local cage dynamics is governed by the Smoluchowski equation with shear [32]. The general spherically averaged solution is
for the static hard-sphere glass5. Under applied shear, this value decreases as the loss of neighbors in the dilation direction is not balanced by the particle gain in the compression direction [20, 31]. We model this loss of neighbors by assuming that the local cage dynamics is governed by the Smoluchowski equation with shear [32]. The general spherically averaged solution is ![$ \newcommand{\e}{{\rm e}} g(r, \gamma)=\exp[-V_{{\rm eff}}/kT+h(r)\gamma]$](https://content.cld.iop.org/journals/0022-3727/51/32/324002/revision2/daad03aieqn049.gif) with
with 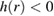 , which after integration translates to
, which after integration translates to ![$ \newcommand{\e}{{\rm e}} n_b(\gamma) = n_{b}^{0}\exp[-A\gamma]$](https://content.cld.iop.org/journals/0022-3727/51/32/324002/revision2/daad03aieqn051.gif) , corresponding to a decrease of the height
, corresponding to a decrease of the height 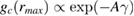 of the first peak of
of the first peak of 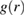 in the extension direction. This estimate is in excellent agreement with the exponential dependence shown in figure 2(c); the numerical factor A follows from a fit to the data, and we obtain A = 0.96.
in the extension direction. This estimate is in excellent agreement with the exponential dependence shown in figure 2(c); the numerical factor A follows from a fit to the data, and we obtain A = 0.96.
The reduced connectivity leads to growing non-affine contributions decreasing the shear modulus. Assuming that the rigidity of the material breaks down at the isostatic limit nb = 6 [23], the total shear modulus 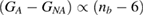 , meaning that
, meaning that 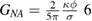 . The total reversible free energy then follows from integration:
. The total reversible free energy then follows from integration: ![$F_{el}(\gamma)= \frac{1}{5\pi}\frac{\kappa\phi}{\sigma} [n_b(\gamma)- 6]\gamma^2$](https://content.cld.iop.org/journals/0022-3727/51/32/324002/revision2/daad03aieqn059.gif) . This total elastic part of the free energy, with fitting parameters specified below, indeed fits the initial parabolic increase of the free energy as shown by the red curve in figure 1(c).
. This total elastic part of the free energy, with fitting parameters specified below, indeed fits the initial parabolic increase of the free energy as shown by the red curve in figure 1(c).
To account for the relaxation-related decrease of the free energy, we also include a term related to irreversible rearrangements. We model these irreversible changes here by a standard continuum dissipative term. In standard dissipation, the dissipated energy associated with continuously ramping the strain at strain rate  is
is 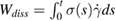 , where the stress
, where the stress  [33] with
[33] with  the (strain dependent) relaxation modulus. Using a standard viscoelastic model, the relaxation modulus has the general form
the (strain dependent) relaxation modulus. Using a standard viscoelastic model, the relaxation modulus has the general form ![$ \newcommand{\e}{{\rm e}} G(t)=G+G_{R}\exp[-t/\tau]^{\beta}$](https://content.cld.iop.org/journals/0022-3727/51/32/324002/revision2/daad03aieqn064.gif) , where
, where 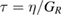 is the global relaxation time, η the viscosity [34] and
is the global relaxation time, η the viscosity [34] and  , with G0 the instantaneous (infinite-frequency) shear modulus. For the standard linear viscoelastic solid [33], one has
, with G0 the instantaneous (infinite-frequency) shear modulus. For the standard linear viscoelastic solid [33], one has  , while for many glassy materials the relaxation is stretched-exponential with
, while for many glassy materials the relaxation is stretched-exponential with 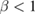 . Thus, inserting the stretched-exponential expression for
. Thus, inserting the stretched-exponential expression for 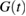 in the integral, and using
in the integral, and using  , one obtains Wdiss as a function of
, one obtains Wdiss as a function of 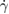 , γ and GR. Focusing on the limit of very low
, γ and GR. Focusing on the limit of very low  as in our experiment, the leading term in a Taylor expansion around
as in our experiment, the leading term in a Taylor expansion around 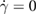 is
is 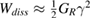 , independent of β.
, independent of β.
The total nonequilibrium free energy of deformation then is  , where F0 is the strain-independent, 'ground-state' energy of the metastable minimum (inherent structure) of the glass,
, where F0 is the strain-independent, 'ground-state' energy of the metastable minimum (inherent structure) of the glass,  , with
, with  the elastic (reversible) energy containing both affine and non-affine contributions, and
the elastic (reversible) energy containing both affine and non-affine contributions, and 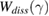 the dissipated energy due to irreversible rearrangements. Using the terms derived above, the final expression for the free energy of deformation is
the dissipated energy due to irreversible rearrangements. Using the terms derived above, the final expression for the free energy of deformation is

To test our model quantitatively, we simultaneously fit the free energy data in figure 1(c) using equation (1) (black line) and stress–strain curves of a colloidal glass measured independently with a rheometer [13]; see figure 3. Here, the stress is computed by adding the elastic and viscous contributions: 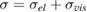 , where
, where 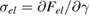 , and the standard viscous expression
, and the standard viscous expression 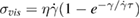 . We obtain excellent simultaneous fits up to large strains, validating our model for the nonequilibrium free energy with elastic and viscous components. The calculated number of nearest neighbors (figure 3, inset) decreases with strain, reflecting the loss of connectivity and the propagation of non-affine contributions. This decrease of nearest neighbors saturates eventually as shown in the experimental
. We obtain excellent simultaneous fits up to large strains, validating our model for the nonequilibrium free energy with elastic and viscous components. The calculated number of nearest neighbors (figure 3, inset) decreases with strain, reflecting the loss of connectivity and the propagation of non-affine contributions. This decrease of nearest neighbors saturates eventually as shown in the experimental  for strains
for strains 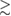 0.1; see figure 2(c).
0.1; see figure 2(c).
Figure 3. Comparison of model prediction (blue line) and experimental data (black squares) of stress σ as a function of strain γ (log–log scale). To measure the stress reliably at these small shear rates, we used smaller particles with diameter d1 = 50 nm, resulting in shear stresses larger by a factor 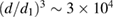 . All data were measured at the same volume fraction
. All data were measured at the same volume fraction  and similar Peclet number. The black line has slope 1 to guide the eye. Inset: theoretical prediction of the average number of nearest neighbors (log scale) as a function of strain (linear scale).
and similar Peclet number. The black line has slope 1 to guide the eye. Inset: theoretical prediction of the average number of nearest neighbors (log scale) as a function of strain (linear scale).
Download figure:
Standard image High-resolution imageIn summary, we connect the microscopic structure of sheared glasses to their nonequilibrium free energy of deformation by combining colloidal shear experiments with generalized stability theory of amorphous materials. Nonaffine contributions decrease the shear modulus and thereby the initial elastic (parabolic) rise of the free energy, while dissipation—modeled here by a standard continuum dissipative term—explains the overall decrease of the non-equilibrium free energy with strain. The applied shear thus allows the glass to explore lower free energy states by forcing structural rearrangements that would otherwise be frozen or take much longer time by thermal aging alone. The measured decrease of the free energy under deformation is indeed of the order of, albeit a bit smaller than the free energy decrease of 0.1–0.2 kBT obtained upon aging the glass for a few days. This decrease should saturate at larger strain (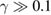 ), when the glass acquires a steady-state structure under the applied constant shear rate. Our results thus provide insight into the role of non-affine displacements and dissipation in the transient deformation of glasses [14]. While our hard-sphere colloidal glass allows direct measurement of the free energy and underlying microscopic distortions, the proposed mechanism should apply to molecular glasses as well. For those molecular glasses, the strong hard-core repulsion is replaced by a steep repulsive potential (
), when the glass acquires a steady-state structure under the applied constant shear rate. Our results thus provide insight into the role of non-affine displacements and dissipation in the transient deformation of glasses [14]. While our hard-sphere colloidal glass allows direct measurement of the free energy and underlying microscopic distortions, the proposed mechanism should apply to molecular glasses as well. For those molecular glasses, the strong hard-core repulsion is replaced by a steep repulsive potential ( r12) leading to similar shear-induced loss of connectivity and growth of non-affine dynamics.
r12) leading to similar shear-induced loss of connectivity and growth of non-affine dynamics.
Acknowledgments
This work is funded by the Netherlands Organization for Scientific Research (NWO). PS acknowledges support by a Vici fellowship from NWO. We thank D Frenkel, E Lerner, G Petekidis, and M Hoffmann for useful discussions.
Appendix A. Dilatancy of marginal solids
To estimate the dilatancy of a marginal solid, following [19], we compute the dilatant strain in a quasistatic response of an isotropic elastic solid according to

where Rp is the Reynolds coefficient. This Reynolds coefficient is defined as
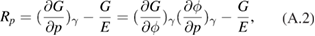
where 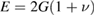 is the Young's modulus, G the shear modulus and
is the Young's modulus, G the shear modulus and  the Poisson ratio. Thus, the free energy can be expressed as
the Poisson ratio. Thus, the free energy can be expressed as

The volume fraction of the dilated system follows as
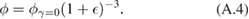
A.1. For hard-sphere crystals
The equation of state is, within the framework of cell theory [35, 36],

where  ,
,  , and
, and  is the particle volume. Thus,
is the particle volume. Thus,

Values of the shear modulus as a function of volume fraction can be obtained from [16]. 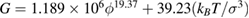 . By interpolating this data to the volume fraction of our computer generated crystal,
. By interpolating this data to the volume fraction of our computer generated crystal,  , we obtain G = 48.5
, we obtain G = 48.5  and E = 129
and E = 129  , where the hard-sphere diameter d = 1.5
, where the hard-sphere diameter d = 1.5 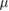 m. It then follows that the Reynolds coefficient
m. It then follows that the Reynolds coefficient
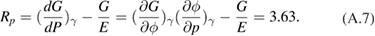
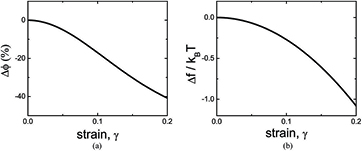
The resulting change of volume fraction with respect to this dilatancy Rp is shown in figure A1(a), and the corresponding free energy change is shown in figure A1(b).
Figure A1. Volume fraction and (a) resulting free energy change of sheared crystal (b) as a function of shear strain in the linear approximation.
Download figure:
Standard image High-resolution imageA.2. For hard-sphere glasses
The equation of state is [37]
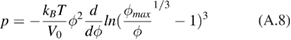

where 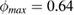 .
.
Thus, we determine that

The shear modulus as a function of volume fraction of our hard-sphere glass can be obtained from [36]. By interpolation, we determine that for our volume fraction, 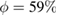 ,
, 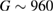
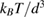 and
and 
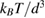 . With these values, we obtain
. With these values, we obtain 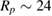 . The resulting change of volume fraction is shown in figure A2(a), and the corresponding free energy change is shown in figure A2(b).
. The resulting change of volume fraction is shown in figure A2(a), and the corresponding free energy change is shown in figure A2(b).
Figure A2. Volume fraction and (a) resulting free energy change (b) as a function of strain for a sheared glass with linear dilatancy.
Download figure:
Standard image High-resolution imageAppendix B. Experimental evidence of negligible dilatancy in the glass
In the main text, we investigate the dilatancy in the sheared glass by monitoring the volume fraction by particle counting. Here, we present an alternative way to check for dilation based on the angle-averaged pair correlation function that indicates the probability of two particles to be separated by a distance r. We estimate the dilation in the deformed state from the minimum of the mean-square difference  between the
between the  curves of the deformed and undeformed glass as a function of a linear stretching α that transforms r to
curves of the deformed and undeformed glass as a function of a linear stretching α that transforms r to  . We show
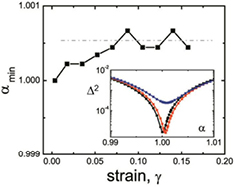
. We show 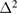 as a function of α in figure B1, inset; its minima are at
as a function of α in figure B1, inset; its minima are at  , all very close to 1, indicating neither compression nor dilation. Close evaluation of the minima
, all very close to 1, indicating neither compression nor dilation. Close evaluation of the minima  for all deformed states in the interested strain window confirms this, indicating maybe a small compression of less than one per mill in deformed states compared to the quiescent state (figure B1, main panel). Similarly to the manuscript, these closely constant values contrast with the strong dilatancy predicted by the linear theory, and indicate substantial nonlinear behavior, even at small strain.
for all deformed states in the interested strain window confirms this, indicating maybe a small compression of less than one per mill in deformed states compared to the quiescent state (figure B1, main panel). Similarly to the manuscript, these closely constant values contrast with the strong dilatancy predicted by the linear theory, and indicate substantial nonlinear behavior, even at small strain.
Figure B1. Dilation parameter  versus shear deformation determined from the minimum of the mean-square difference of
versus shear deformation determined from the minimum of the mean-square difference of 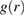 of the deformed and undeformed glass (inset). Dash-dotted line is a guide to the eye.
of the deformed and undeformed glass (inset). Dash-dotted line is a guide to the eye.
Download figure:
Standard image High-resolution imageFootnotes
- 5
Unlike in the liquid, a good part of the bonded nearest neighbors in the glass is long-lived, and contributes to the long-time elasticity of the glass [30].
- 6
This shear-induced cage breakdown may be even bigger than what we can infer here on the basis of the static
 . The static
. The static  includes also those neighbors which fluctuate very fast over long distances, and hence do not contribute to stress-transmission and elasticity. The decrease of the number of neighbors as derived from the behavior of
includes also those neighbors which fluctuate very fast over long distances, and hence do not contribute to stress-transmission and elasticity. The decrease of the number of neighbors as derived from the behavior of  is therefore probably an underestimation of the real decrease, which might be stronger if one could separate the contributions of slow (permanent) and fast (non-permanent) neighbors.
is therefore probably an underestimation of the real decrease, which might be stronger if one could separate the contributions of slow (permanent) and fast (non-permanent) neighbors.