Abstract
We introduce a specific four-particle, four degree-of-freedom model and calculate the rotation that can be achieved by purely internal torques and forces, keeping the total angular momentum zero. We argue that the model qualitatively explains much of the ability of a cat to land on its feet even though released from rest upside down.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
We are interested in the ability of a cat to always land on its feet when dropped from rest upside down. It has been well known for a long time that non-rigid bodies can perform zero angular momentum turns. Some general references are [1–3]. The problem of the falling cat has interested many investigators since the time of Maxwell. Historical references can be found in Kane [4] and in Fredrickson [5]. The purpose here is to present a model that makes a quantitative treatment of the problem accessible to undergraduates.
To study the cat we introduce a simple model which we believe catches the essentials of the kinematics of this phenomenon. This is not uncontroversial, however. There are in fact two schools of thought in the literature regarding the kinematic mechanism of the cat turn.
One is the 'legs in—legs out' sequence with a relative twist of the front and hind legs. This is the mechanism described by our model. It is also used in text book explanations (e.g. Walker [6]) and it has been studied by Kaufman [7] who, however, argues that this mechanism is not sufficient to explain the 180° turn. Other studies of this general type can be found in [8–11].
The other school claims that tilted rotating cylinders (called 'tuck and turn' by Kaufman [7]) is the main mechanism. This model seems to be the most popular nowadays and it is advocated by Kane [4], Edwards [12], Galli [13], Iwai et al [14] and Wikipedia [15]. There is a YouTube video of the motion of this model [16]. One notes that in these models the front and hind legs of the cat remain parallel (no twist).
There are many photograph sequences (e.g. in [4, 5]) and You Tube videos [17, 18] of falling cats. The most conspicuous feature of these is a considerable twist of the front relative to the hind of the cat. Their relative angle appears to approach 180° (π radians). Since this feature is not part of the tilted cylinder models it seems that the 'legs in—legs out' models can not be totally wrong.
Various authors discuss the problem in terms of advanced concepts such as gauge theories [3] or non-holonomic systems and geometric phases [19]. Others are interested in the ability of the cat to survive falls from large heights and their terminal velocity [18, 20]. Here we will focus on the 180° turn and describe it in the simplest terms possible.
We first present our model system. The extension of the legs from the horizontal axis through the centre of mass and their angles of rotation about this axis are the primary variables. The two angles are then replaced by the relative, or twist, or torsion, angle ψ and the mean, or average, or rotation, angle φ. A differential equation giving the (zero angular momentum) rotation angle as a function of the twist and leg extensions is the derived. It is shown that the system can rotate 180° by a single twist of 180°.
2. The model system
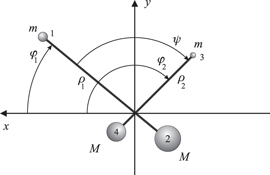
The model is a four-particle system, shown in figures 1 and 2. It consists of an axle of length L. About the end points two perpendicular rods can rotate. These have particles attached at the end points, one heavy of mass M and one light of mass m. Both rods have their centres of mass on the axle, so if the distance to m from the axle is ρ, the distance to M is μρ with μ = m/M.
Figure 1. The model system consists of two light rods with particles attached at the end points. On each rod there is one heavier particle with mass M and one lighter with mass m. The centres of mass G1 and G2 of the rods are on an axle of length L connecting them and the centre of mass G of the system is at the midpoint of this axle. The two rods can rotate about the axle. The particles are represented by spheres and those further from the viewer are shown as smaller. One rod represents the front legs of the cat, the other the hind legs.
Download figure:
Standard image High-resolution imageWe will assume that the relative angle of the two rods and the length of the rods can be changed by means of internal torques and forces, while there is no external torque acting on the system. The centres of mass of the rods will then remain on the axle. The only external forces are the weights of the particles and these can be represented by a resultant acting downwards at the common centre of mass G. In the freely falling reference frame there are no external forces acting.
We describe the system using the angles φ1 and φ2 shown in figure 2. The distances of the lighter masses to the axis through the centres of mass are denoted ρ1 and ρ2 respectively. There are thus four degrees-of-freedom and the corresponding coordinates are φ1, φ2, ρ1, ρ2.
Figure 2. The model system seen along the rotation z-axis through the centres of mass of the rods. The z-axis points into the paper. The distances from the z-axis to the heavier particles are μρ1 and μρ2 respectively. Since the centres of mass are on the z-axis μ = m/M. The cylindrical coordinates ρk, φk (k = 1, 2) are shown, as well as the relative angle ψ. The spheres representing the particles further from the viewer are shown as smaller thus indicating the third-dimension.
Download figure:
Standard image High-resolution image2.1. Model angular momentum
We now introduce cylindrical (polar) coordinates ρ, φ, and z and corresponding unit vectors 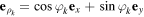 ,
, 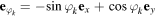 . In terms of these we have for the position vectors
. In terms of these we have for the position vectors 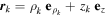 and for the velocities
and for the velocities 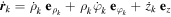 . The position vectors of the four particles of the model system, relative to the centre of mass G, are
. The position vectors of the four particles of the model system, relative to the centre of mass G, are




Here L is the distance between the centres of mass of the rods and μ = m/M ensures that the centres of mass are on the z-axis. The velocities are then




The angular momentum of the system with respect to the centre of mass has four contributions and these are
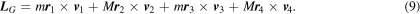
Straightforward calculation simply gives

since all other terms cancel.
2.2. Two new variables
Assume now that the there is no external torque and that angular momentum is zero initially. We then have the simple relationship

Let us define the mean angular velocity  and relative angular velocity
and relative angular velocity 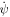 through
through
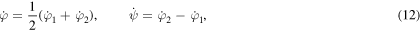
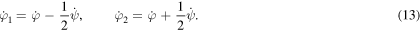
The zero angular momentum equation (11) then gives

From this equation we see that if 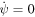 , so is
, so is 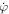 . It is also clear that if ρ1 = ρ2 then
. It is also clear that if ρ1 = ρ2 then 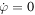 . There will thus only be a mean angular velocity if both
. There will thus only be a mean angular velocity if both  and
and 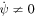 .
.
2.3. Differential equation of rotation
Equation (14) gives the mean angular velocity of our model system

We put

since only this combination of length changes will affect the mean angular velocity. This gives us the differential equation

We now wish to find functions f(t), ψ(t) that are such that after some time T, the duration of the fall, the mean angle φ has changed by π (180°),

To model the cat the functions f(t), ψ(t), and 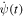 should all start and end with zero values
should all start and end with zero values
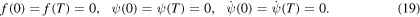
This corresponds to the cat starting and ending its fall with equally long front and hind legs, which are parallel and non-rotating. To model the cat the relative angle ψ(t) should change from zero to some maximum value and back to zero since this is the what photos and videos indicate. This means that the function 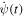 changes sign once. For the system to keep rotating in the same direction the function f(t) must therefore change sign at the same time.
changes sign once. For the system to keep rotating in the same direction the function f(t) must therefore change sign at the same time.
2.4. Two solutions
The simplest, and probably optimal, solution of this kind is given by choosing piecewise constant functions f(t) and 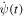 , with f(t) discontinuous. It is given by,
, with f(t) discontinuous. It is given by,
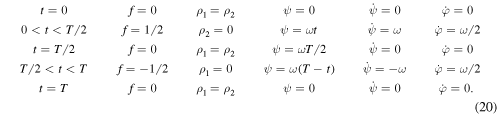
The total rotation angle 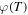 will be π if ω = 2π/T. The maximum relative (twist) angle is then ψ(T/2) = π. The solution is illustrated to the left in figure 3 and in figure 4. There are, obviously, some problems with this solution, also apart from requiring infinite accelerations and neglecting the time taken to extend and retract the rods (legs). It is a bit dubious to put one of the lengths ρk equal to zero since then the relative angle becomes undefined. This, however, can be fixed rather easily by putting the shorter length to 1/10 times the longer, instead of putting it to zero. The values of f(t) will then only change by one per cent, from those given in (20).
will be π if ω = 2π/T. The maximum relative (twist) angle is then ψ(T/2) = π. The solution is illustrated to the left in figure 3 and in figure 4. There are, obviously, some problems with this solution, also apart from requiring infinite accelerations and neglecting the time taken to extend and retract the rods (legs). It is a bit dubious to put one of the lengths ρk equal to zero since then the relative angle becomes undefined. This, however, can be fixed rather easily by putting the shorter length to 1/10 times the longer, instead of putting it to zero. The values of f(t) will then only change by one per cent, from those given in (20).
Figure 3. The piecewise constant solution of equation (20) to the left. The differentiable solution of equations (21)–(26) to the right. Here the duration T = 2 and the peaked (green) curves show the relative angle ψ(t), while the increasing (red) curves show the mean (rotation) angle φ(t). The function f(t) is 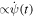 .
.
Download figure:
Standard image High-resolution imageFigure 4. The piecewise constant solution of equation (20) is illustrated here as a sequence of five states corresponding to the five lines of equation (20). Time increases from left to right. The rotating zero length rods are shown as short but non-zero for clarity.
Download figure:
Standard image High-resolution imageA smooth and differentiable solution can be achieved, e.g. by choosing
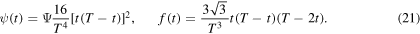
Physically one must have 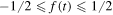 and this choice for f(t) obeys this. Here Ψ = ψ(T/2) is the maximum relative angle, a so far unknown parameter. The angular velocity is then
and this choice for f(t) obeys this. Here Ψ = ψ(T/2) is the maximum relative angle, a so far unknown parameter. The angular velocity is then

and the mean angular velocity (17) is

The rotation angle is then
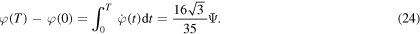
This will be the desired angle π if the maximum relative angle is

We note that this value, approximately 227°, is substantially larger than for the solution in (20). The explicit solution is thus
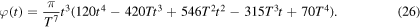
The two solutions are compared in figure 3. There are of course an infinite set of solutions to the differential equation (17) depending on the choice of control functions ψ(t) and f(t). Those presented here are chosen to resemble the observed behaviour of falling cats.
3. Conclusions
Our simple model leads to an illuminating and simple differential equation describing its zero angular momentum rotation. It is a model for the falling cat problem that achieves the turn by means of pulling legs in and out while twisting the front and hind relative to each other. Real cats of course have many more degrees-of-freedom and probably optimise a combination of the 'legs in—legs out' and 'tuck and turn' methods. In this paper we hope that we have shown that the simple text book 'legs in—legs out' mechanism should not be discarded in favour of the kinematically much more complicated tilted cylinders model. In practice our findings agree with Kaufman's [7] in the sense that the turn does not quite reach 180° unless the cat can twist itself more than 180°, which seems unlikely.