Abstract
The classic problem of determining the force on a current-carrying wire in a magnetic field is critically analysed. A common explanation found in many introductory textbooks is to represent the force on the wire as the sum of the forces on charge carriers. In this approach neither the nature of the forces involved nor their application points are fully discussed. In this paper we provide an alternative microscopic explanation that is suitable for introductory electromagnetism courses at university level. By considering the wire as a superposition of a positive and a negative cylindrical charge distributions, we show that the electrons are subject to both magnetic and electric forces, whereas the ionic lattice of the metal is dragged by an electric force. Furthermore, an analysis of the orders of magnitude involved in the problem gives counterintuitive results with valuable educational potential. We argue that this approach allows one to discuss different aspects of the physical knowledge, which are relevant in physics education.
Export citation and abstract BibTeX RIS
1. Introduction
1.1. Force on a current-carrying wire
A classical experiment in introductory physics consists in suspending a current-carrying wire in the magnetic field of a horseshoe magnet (see figure 1). One can vary the intensity of the current as well as the wire's length and obtain different forces on the wire, for instance by measuring the deflection angle θ with respect to the vertical when equilibrium is obtained.
Figure 1. Experiment to measure the force on a current-carrying wire.
Download figure:
Standard image High-resolution imageNeglecting the weights of the vertical wire segments, the equilibrium of forces applied to the horizontal wire segment (figure 1(b)) is expressed by

where  is the wire segment's weight,
is the wire segment's weight,  the resultant tension applied by the vertical/inclined wire segments and
the resultant tension applied by the vertical/inclined wire segments and  the force applied to the horizontal segment when there is current flowing in the wire. Globally everything seems straightforward, but what are the actual application points of these forces? This question will guide our subsequent discussion, but without worrying about it for the moment, simple decomposition of
the force applied to the horizontal segment when there is current flowing in the wire. Globally everything seems straightforward, but what are the actual application points of these forces? This question will guide our subsequent discussion, but without worrying about it for the moment, simple decomposition of  yields
yields

Thus, F can be determined indirectly from W and θ. A pure inductive approach—which could be pedagogically questionable—would aim at showing experimentally that F (meaning  ) is both proportional to the electric current I and the length of the wire's horizontal segment L; the latter obtained by a series of experiments with horizontal wire segments of different lengths. In other words, the goal is to show that the ratio
) is both proportional to the electric current I and the length of the wire's horizontal segment L; the latter obtained by a series of experiments with horizontal wire segments of different lengths. In other words, the goal is to show that the ratio
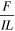
remains constant. This setting is constructed to motivate the creation of a new magnitude to express this proportionality—the magnetic field strength B-which enables one to write (in scalar form)

The goal of this paper is to conduct a critical discussion about the connection between this macroscopic approach and its microscopic interpretation in terms of forces acting on charged particles inside the wire. As we will see, there are many inconsistencies and/or hidden assumptions in the way this topic is usually taught.
1.2. Charge carriers
Without considering the details of the metallic structure of the conducting wire, one can employ the notion of charge carriers and assume that each of them bears a positive charge q. If a carrier moves with velocity  , the force of magnetic origin acting on it is
, the force of magnetic origin acting on it is

In the situation described in figure 2, one has  ,
,  , and
, and
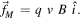
This result is then related with the current density  by means of the expression
by means of the expression
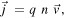
where n is the number of carriers per unit of volume. For a wire with cross-sectional area A, j is related to the current I by j = I/A, the expression for the force acting on a single carrier becomes

As the total number N of carriers within a wire of length L is  , the total magnetic force acting on this wire is
, the total magnetic force acting on this wire is
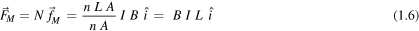
which agrees with equation (1.3) obtained inductively from the experiment described in figure 1.
Figure 2. Conductor wire immersed in a magnetic field  .
.
Download figure:
Standard image High-resolution image
 The critical passage. Although formally correct, the passage from equations (1.5) to (1.6), which implements the transition from a schematic 'microscopic' description to the macroscopic result, has problems. While the force (1.5) is applied to an individual charge carrier, the point of application of (1.6) is not evident. In the spirit of equation (1.1), can we say that the net force
The critical passage. Although formally correct, the passage from equations (1.5) to (1.6), which implements the transition from a schematic 'microscopic' description to the macroscopic result, has problems. While the force (1.5) is applied to an individual charge carrier, the point of application of (1.6) is not evident. In the spirit of equation (1.1), can we say that the net force  is applied also to the parts of the wire which do not move, such as its rigid components? The forces acting on moving carriers can be ascribed to the magnetic field, but those acting on still structures of the wire cannot be.
is applied also to the parts of the wire which do not move, such as its rigid components? The forces acting on moving carriers can be ascribed to the magnetic field, but those acting on still structures of the wire cannot be.
Another reason why the force on the wire cannot be of magnetic nature is that magnetic forces do no work and the wire is moved until it reaches equilibrium. Such conceptual discussions are often omitted in classical textbooks, as we will show in section 2. In section 3 we present a microscopic approach that eliminates the critical passage and allows us to penetrate into the structure of the wire. We believe this approach should be appropriate for physics courses at introductory level.
2. Literature review
2.1. Textbooks
We analysed how the macro–micro connection—i.e. the forces acting on the wire and on the moving charges—is presented in 11 introductory physics textbooks [1–11]. Although we do not claim to have exhausted all the possible references, we are confident that this sample is fairly representative for how the topic is introduced in physics courses worldwide. We identified three different ways to present this connection and divided them into the following categories:
(1) Force on the wire = Sum of forces on individual charge carriers
This category represents the critical passage described above and is by far the most common approach, found in 8 of the textbooks analysed [1, 3–8] and [11]. All the presentations are quite similar and can be exemplified by Tipler's [11, p 890] citation: 'When a current-carrying wire is in a region that has a magnetic field, there is a force on the wire that is equal to the sum of the magnetic forces on the individual charge carriers in the wire'.
It is worth noticing that almost all of them present the Lorentz force first and then use it to obtain the force on the wire. An interesting exception is Demtröder [4], which starts with the description of the experiment of a current-carrying wire suspended in a magnetic field (figure 1) and uses it to introduce the Lorentz force. This approach appears to be more faithful to the historical order and somehow more aligned with a modelling perspective.
Common to the textbooks of this category is the lack of considerations about the internal constitution of the wire. Among the eight textbooks in this category, a small reservation could be made for Halliday et al [6], where the following remark is found: 'We have already seen that a magnetic field exerts a sideways force on electrons moving in a wire. This force must then be transmitted to the wire itself, because the conduction electrons cannot escape sideways out of the wire' (ibid, p 750, our emphasis). Nevertheless, no further explanation about the nature of the interaction between the moving electrons and the ions is given. Furthermore, although [4, 6], and [8] mention electrons and represent the velocity and current density in opposite directions, the remaining textbooks in this category consider current as the movement of (positive) charge carriers in their pictorial representations.
(2) Force on the wire is due to electrons colliding with the atoms that constitute the wire
Although only one textbook fits in this category, the image that it conceives deserves a category of its own. The initial presentation found in Serway and Jewett Jr [10] is very similar to the ones from category 1, but then a consideration about the interaction between the moving electrons and the wire is given. We reproduce the full passage where it appears:
'If a magnetic force is exerted on a single charged particle when the particle moves through a magnetic field, it should not surprise you that a current-carrying wire also experiences a force when placed in a magnetic field. The current is a collection of many charged particles in motion; hence, the resultant force exerted by the field on the wire is the vector sum of the individual forces exerted on all the charged particles making up the current. The force exerted on the particles is transmitted to the wire when the particles collide with the atoms making up the wire' (ibid, p 819, our emphasis).
What is the intended goal behind this mechanical image? Should we use some kind of kinetic gas theory approach and apply Newton's laws to calculate the total pressure generated by the collisions of the electrons with the atoms of the wire? Would that lead us to the experimental result F = BIL? How do the atoms form the structure of the wire's walls? Although these seem reasonable questions, they are left unanswered, since this textbook does not consider any quantitative description of the collisions. The collision model appears to function as a mere qualitative image of the interactions inside the wire.
(3) Force on the wire is related to the Hall effect
A more careful and detailed consideration about the wire's structure is found in only two of the analysed textbooks [2, 9]. When considering the macro–micro passage, both are explicit about the different nature of the forces on the moving charges and on the wire, as exemplified below:
'There is a subtle point about the magnetic force that a magnetic field exerts on a current-carrying wire. The magnetic force only acts on moving particles, which in the case of copper are the drifting electrons. The stationary positive atomic cores do not experience a magnetic force. So why does the entire wire move?' [2, p 727, our emphasis].
'When a current flows in a conductor in the presence of a magnetic field, the force  acts directly on the moving charge carriers. Yet we observe a force on the conductor as a whole. Let's see how this comes about.' [9, p 241, our emphasis].
acts directly on the moving charge carriers. Yet we observe a force on the conductor as a whole. Let's see how this comes about.' [9, p 241, our emphasis].
The main argument of these textbooks is related to the Hall effect. When a magnetic field is applied it causes a deflection of the moving electrons, which creates an asymmetric charge distribution inside the wire; i.e. an excess of positive and of negative charges in opposite sides of the wire. The altered charge distribution inside the wire generates a transverse electric field. In the steady state, the magnetic force on each of the electrons is balanced by the electric force of the (electric) field, but the positive/stationary atom cores experience no magnetic force. Hence, this net electric force on the positive ions is the one responsible for moving the wire. It is worth stressing that now the force moving the wire has an electric nature, eliminating the problematic issue of magnetic forces doing work.
This certainly provides a better understanding of the wire's structure and a qualitative explanation for why it moves. However, both presentations lack a quantitative way to establish the macro–micro connection by considering the forces on electrons and ions separately. This is the main goal of our approach described in section 3.
2.2. Research articles
Although introductory level electromagnetism textbooks usually do not highlight the problem of associating the magnetic force acting on the moving electrons with the resultant force on the wire5 , there are several papers in the physics education literature dealing with this issue. In the following we shall give a brief overview of some works that have a direct relation to ours.
Using the Bloch–Sommerfeld theory of conductivity, Rostoker [15] calculates the momentum lost by conduction electrons due to collisions with the crystal lattice. It is shown that for metals that conduct in a single band, the ponderomotive force  is entirely due to the action of a Hall effect, but for other cases it is a combination of a Hall field and collisions of electrons with the lattice. English [16] considers the case of semiconductors where no Hall field exists, but still a force is applied on the wire. Diffusion effects and transverse variations in the carrier density are the two different explanations given for the existence of the force. Similarly, McKinnon et al [17] point to flaws in the explanation via Hall effect when R (Hall coefficient) is zero or positive. According to these authors, the electrons must feel an additional force
is entirely due to the action of a Hall effect, but for other cases it is a combination of a Hall field and collisions of electrons with the lattice. English [16] considers the case of semiconductors where no Hall field exists, but still a force is applied on the wire. Diffusion effects and transverse variations in the carrier density are the two different explanations given for the existence of the force. Similarly, McKinnon et al [17] point to flaws in the explanation via Hall effect when R (Hall coefficient) is zero or positive. According to these authors, the electrons must feel an additional force  caused by the positive ions which is responsible for deviations from the free electron behaviour.
caused by the positive ions which is responsible for deviations from the free electron behaviour.
The problematic issue of magnetic forces doing work is discussed by Mosca [18] with the classical situation of a conducting rod moving through a magnetic field. By decomposing the movement of electrons in vertical (current) and horizontal (rod) components, it is argued that the magnetic component Fm does no work because it is perpendicular to the (inclined) resultant motion of the electron. Instead, Fr, which is the (electric) force done by the rod on the electron, is the one responsible for the work. Redinz [19] deals with the same issue by considering a rectangular current-carrying loop of wire hanging vertically in a uniform magnetic field. Separating the loop of wire into of a loop of conducting electrons and another one of positive ions, the forces acting on each are carefully analysed and the problematic conclusion of magnetic forces doing work is eliminated.
In the paper 'How can magnetic forces do work? Investigating the problem with students', Onorato and De Ambrosis [20] report a teaching and learning sequence designed with the goal of identifying the main parameters that influence the force acting on a current-carrying wire in a magnetic field. Afterwards, students were questioned about the nature of this force and exposed to the contradiction that magnetic forces can do no work. Faced with this dilemma, students came up with four different models (1. collision, 2. macroscopic constraint, 3. Hall effect and 4. rigid loops) which are similar to some of the ones found in the literature. Goedecke and Kanim [21] conduct a thorough study of the Hall effect explanation by comparing the results obtained in three models (1. single-particle, 2. rigid charge distributions and 3. charged fluids) for both accelerating and stationary situations. The authors conclude that the charged fluids model is the most realistic one because it allows for compression and predicts a unique modified Hall field. Our microscopic approach, described in the next section, uses similar assumptions as the rigid charge distributions, but has some important differences/additions and is thought to be applicable for physics courses at introductory level.
3. Microscopic approach
The microscopic approach relies on a schematic description of metal properties in terms of free electrons and positive ions. The classical picture of a solid metal, such as copper, is that of a lattice of positive ions, full of free space, pervaded by a gas of free electrons [22]. Owing to temperature, the ions vibrate around more or less well-defined positions, whereas the free electrons drift at random inside the space available in the lattice. In general, ion lattices are remarkably stable and account for the stiffness of metal blades or rods, and one may say that when one holds a metallic object, one is holding its lattice. As the mass of a positive ion is many thousands times larger than the mass of an electron, the weight of a metallic object is, to a good approximation, the weight of its ionic lattice. In the present instance, the forces  and
and  , of equation (1.1), are, in fact, applied to the positive lattice.
, of equation (1.1), are, in fact, applied to the positive lattice.
In normal conditions, metallic wires are globally neutral, even when run by currents, since the total amount of positive charge in the lattice is, to a very good precision, equal to the total negative charge amassed in the free electrons. Besides, the metal is also locally neutral.
This local neutrality is part of the strategy of nature to lower the potential energy of a stable piece of metal. As the ionic lattice is rather regular, its charge density  is also rather uniform. Therefore, local electrical neutrality implies that the number n of free electrons per unit volume is uniform too. As a consequence, free electrons within the metal behave as an incompressible gas. Denoting the electron charge by
is also rather uniform. Therefore, local electrical neutrality implies that the number n of free electrons per unit volume is uniform too. As a consequence, free electrons within the metal behave as an incompressible gas. Denoting the electron charge by  , the densities of positive and negative charges are written as
, the densities of positive and negative charges are written as


In this model, in the absence of both currents and external magnetic fields, the horizontal wire of figure 1 may be represented as a superposition of a positive and a negative cylindrical charge distributions, with a common central axis. As the densities are given by equations (3.1) and (3.2), the wire is neutral. This situation is represented in figure 3.
Figure 3. Superposition of charge distributions; please note that the continuous lines representing the cylinders were drawn just to guide the eye and do not exist in nature.
Download figure:
Standard image High-resolution imageIf an electric current I runs though a metal wire, the ion lattice remains still and an orderly drift is added to the thermal motion of the free electrons. When the same current considered in the macroscopic approach is present, but with no external magnetic fields, the two charge distributions of figure 3 still remain coaxial, but the negative distribution moves steadily to the left, with an average constant velocity  .
.
However, when the external magnetic field  of figure 1 is introduced, a magnetic force acts on each moving electron, given by equation (1.4), with
of figure 1 is introduced, a magnetic force acts on each moving electron, given by equation (1.4), with  , whereas no forces act on the ions. The global force on the electron gas is the same as equation (1.6), namely
, whereas no forces act on the ions. The global force on the electron gas is the same as equation (1.6), namely

The net result of this magnetic force is that the axes of the positive and negative charge distributions no longer coincide. The negative distribution is collectively shifted along the positive x-axis, by an amount  , as shown in figure 4. As we discuss in the sequence, in actual situations, this displacement is very small, indeed smaller than a tiny fraction of the radius of a proton. This allows one to assume that the electron density n remains both uniform and unchanged in this process and, even after their relative displacement, the positive and negative charge densities as still given by equations (3.1) and (3.2). This situation is shown in figure 4, where the displacement Δ is largely exaggerated. The superposition between
, as shown in figure 4. As we discuss in the sequence, in actual situations, this displacement is very small, indeed smaller than a tiny fraction of the radius of a proton. This allows one to assume that the electron density n remains both uniform and unchanged in this process and, even after their relative displacement, the positive and negative charge densities as still given by equations (3.1) and (3.2). This situation is shown in figure 4, where the displacement Δ is largely exaggerated. The superposition between  and
and  over the bulk of the wire is very large and, there, the net charge density vanishes. So, the global effect of the displacement of the negative distribution is the appearance of two thin charge distributions with opposite signs, over the sides of the wire.
over the bulk of the wire is very large and, there, the net charge density vanishes. So, the global effect of the displacement of the negative distribution is the appearance of two thin charge distributions with opposite signs, over the sides of the wire.
Figure 4. Displacement of the electron gas along the x axis.
Download figure:
Standard image High-resolution imageThis gives rise to electric forces, which prevent the displacement to increase indefinitely and stabilises the system. In this case, the net force must vanish along the x-axis, for each electron. Correspondingly, there is an electric force on the positive lattice, which pulls it along the positive x-axis.
3.1. Electric field
The horizontal segment of the wire considered in this specific instance has a finite length  . Nevertheless, for the sake of simplifying the discussion, we assume its radius to be much smaller than this length and evaluate the relevant electric fields by means Gauss' law, applied to an infinite cylindrical uniform charge distribution. We begin with the positive distribution and assume, as in figure 3, that its axis lies over the y-axis. Gauss' law in integral form reads
. Nevertheless, for the sake of simplifying the discussion, we assume its radius to be much smaller than this length and evaluate the relevant electric fields by means Gauss' law, applied to an infinite cylindrical uniform charge distribution. We begin with the positive distribution and assume, as in figure 3, that its axis lies over the y-axis. Gauss' law in integral form reads

and we are interested in evaluating the field at a point P described by the vector

with θ on the  plane, measured from the x-axis. To this purpose, one uses a cylindrical Gaussian surface of radius
plane, measured from the x-axis. To this purpose, one uses a cylindrical Gaussian surface of radius  , height h and coaxial with the charge distribution (note that due to the symmetry of the problem its physics does not depend on y).
, height h and coaxial with the charge distribution (note that due to the symmetry of the problem its physics does not depend on y).
Applying Gauss' law for regions inside and outside the wire—where R is its radius—the electric field produced by the ionic lattice can be written as
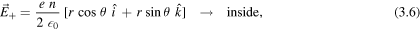
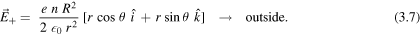
As the axis of the negative charge distribution is displaced by  , the electric field it produces can be found by making
, the electric field it produces can be found by making  and
and

into equations (3.6) and (3.7). This yields

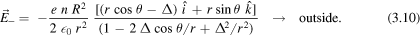
Since  , equation (3.10) can be simplified by keeping terms linear in Δ only. Using
, equation (3.10) can be simplified by keeping terms linear in Δ only. Using
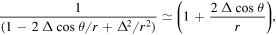
for  , one has
, one has
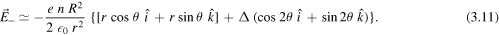
Thus, the total electric field  produced by the wire is
produced by the wire is

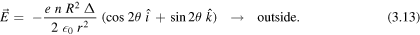
This resultant field is uniform inside the wire and, as expected, depends on both r and θ outside it. The corresponding field lines (green) are sketched in figure 5.
Figure 5. Induced electric field along the wire.
Download figure:
Standard image High-resolution imageWith the later goal of discussing orders of magnitude, we determine the net charge density  on the surface of the wire, at a generic point, located at
on the surface of the wire, at a generic point, located at  . Since the expressions for the electric field are known, we apply Gauss' law with a Gaussian surface in the form of a cylinder with axis along the θ direction and very small height, half inside and half outside the wire. After algebraic manipulations using trigonometric identities we obtain
. Since the expressions for the electric field are known, we apply Gauss' law with a Gaussian surface in the form of a cylinder with axis along the θ direction and very small height, half inside and half outside the wire. After algebraic manipulations using trigonometric identities we obtain

and the total negative charge contained on the surface of the wire is then
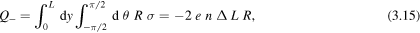
whereas the total positive charge is  . The total number of electrons on the negative charge distribution is therefore
. The total number of electrons on the negative charge distribution is therefore

Figure 6. Electromagnetic forces on the wire. The blue circle represents the ion lattice and the red, free electrons gas.  is equation (3.21),
is equation (3.21),  is equation (3.22) and
is equation (3.22) and  is equation (3.23).
is equation (3.23).
Download figure:
Standard image High-resolution imageFurthermore, there is a potential difference between the sides of the wire along the x-axis, at its diameter, is given by

3.2. Electric forces
The electric fields produced by the charge distributions give rise to forces, which tend to undo the Δ splitting. One now considers the forces  , which the ion distribution causes on the negative free electrons, and
, which the ion distribution causes on the negative free electrons, and  , which the electrons cause in the ions (figure 6). Previous results make the evaluation of the latter somewhat simpler, since the axis of ion charge distribution is the same as the y-axis.
, which the electrons cause in the ions (figure 6). Previous results make the evaluation of the latter somewhat simpler, since the axis of ion charge distribution is the same as the y-axis.
The force acting over an element dq of positive charge is given by

where  is given by equation (3.9) and varies over space. The positive charge contained in a volume dV is
is given by equation (3.9) and varies over space. The positive charge contained in a volume dV is

and

where the integration is to be performed over the volume of the wire. Owing to axial symmetry, the integration of θ vanishes and one has

So, the total electric force acting on the ion lattice is linear on Δ, parallel to the total field  , given by equation (3.12) and orthogonal to both the wire and the magnetic field in figure 1. The electric force acting on the free electrons is
, given by equation (3.12) and orthogonal to both the wire and the magnetic field in figure 1. The electric force acting on the free electrons is

In the instance considered here, the free electron gas is in a dynamic equilibrium: it moves steadily along the y-axis, but remains still along the other two directions. As electrons are subject to electromagnetic forces only, this means that the net force  orthogonal to the current must vanish. Thus
orthogonal to the current must vanish. Thus

and, using equations (3.3) and (3.22), one has an expression which allows Δ to be obtained in terms of measurable quantities

3.3. Forces on the wire
In terms of a microscopic description, equation (1.1) discussed in the introduction becomes a system of three equations, namely

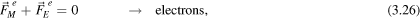
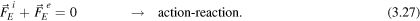
It indicates that the ionic lattice is dragged, in fact, by an electric force, whereas the free electron gas is in equilibrium in the transverse directions to the wire, owing to the joint action of magnetic and electric forces. If ions and electrons are taken as being a single system, equations (3.25) and (3.26) can be added to yield

which is mathematically equivalent to equation (1.1). However, the issues associated with the points of application of the forces now become explicit, as indicated by the upper indices, and therefore both equations are not ontologically equivalent.
3.4. Hall effect and orders of magnitude
The situation discussed here is just an instance of the Hall effect, as already stressed in [21]. Indeed, it involves a conductor which carries a current in the presence of an external transverse magnetic field, and we have shown that, in this case, charge densities appear on its surface, which give rise to a potential difference orthogonal both to the current and to the external magnetic field. For pedagogical reasons, we estimate the order of magnitude of this potential difference, which is an observable, as well as other quantities involved in the calculations. We start by estimating values compatible with reality, thus we assume that the conducting wire is made of copper, with a diameter of 2 mm, and that its horizontal rod in figure 1 is 10 cm long. As the density of copper is 8.960 × 103 kg m−3 , the mass of this rod is 1.126 × 10−2 kg and its weight, taking the acceleration of gravity to be g = 9.82 m s−2 is W = 1.106 × 10−1 N. Assuming the inclination angle in figure 1 to be 30◦, equation (1.2) yields F = 6.384 × 10−2 N for the magnetic force. This force is related to the charge displacement Δ by equation (3.21). Using  C and n = 8.490 × 1028 m−3, one finds
C and n = 8.490 × 1028 m−3, one finds
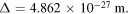
This displacement is rather small, about 10 orders of magnitude smaller than the proton radius  m. This result is compatible with those given in [21] and, as discussed there, depends on the assumption that the electron charge distribution is rigid.
m. This result is compatible with those given in [21] and, as discussed there, depends on the assumption that the electron charge distribution is rigid.
By substituting this value of Δ into equation (3.14), the maximum value of the charge density is
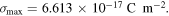
This is also a tiny quantity. In order to have a feeling for its size, we divide it by e and find the maximum electron density ne, given by

Comparing this figure with the total number of free electrons in the surface of copper, which is roughly  electrons m−2, one finds
electrons m−2, one finds
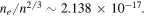
From equation (3.16), we find the number of excess electrons on the negative side of the wire to be Ne = 0.17 i.e., less than 'one fifth' of an electron!
The maximum potential difference along the wire diameter is given by equation (3.17), which yields

This value is way too small to be measured by ordinary means.
4. Conclusions
The derivation of the force acting on a current-carrying wire in a magnetic field is a standard topic in introductory courses on electromagnetism. A common approach is to identify the force on the wire as the sum of the forces on charge carriers. The main purpose of this paper is to raise some problematic issues in the usual approach and provide an alternative derivation that takes a closer look at the structure of the wire. Although the forces on ions and electrons are equivalent, as shown in equation (3.27), a jump from equation (3.25) directly to equation (3.28) would omit a coherent picture of the physical situation.
In the traditional approach, an inherent difficulty appears if one reasons about the application locus of the magnetic force, which is epitomised by equation (3.28). In the alternative microscopic approach proposed here, one faces this problem frontally and reasons in terms of the set of relationships displayed in equations (3.25)–(3.27). This discloses the existence of an internal electric interaction, which gives rise to electric fields both inside and outside the wire. The usual problem of magnetic forces doing work when the wire is being moved is also eliminated.
We have argued that the force on the wire is due to the Hall effect, i.e., an asymmetric distribution of charges along the cross section of the wire. This image may give an impression of several electrons moving transversely inside the wire and accumulating in one region. However, our numerical example in section 3.4 shows that the Hall tension is so negligible that it is simply impossible to measure it. Moreover, the displacement of the negative charge distribution Δ is about 10 orders of magnitude smaller than the radius of a proton. Considering that this insignificant displacement is responsible for the force that lifts the wire, this example provides a sense of how much stronger the electric force is when compared to the gravitational. A similarly shocking comparative statement has been given by Feynman [5, vol 2, p 1–1]:
'If you were standing at arm's length from someone and each of you had one percent more electrons than protons, the repelling force would be incredible. How great? Enough to lift the Empire State Building? No! To lift Mount Everest? No! The repulsion would be enough to lift a 'weight' equal to that of the entire earth!'
The critical passage expressed by equation (1.7) is an instance of a common phenomenon in physics lessons. The argumentation is mathematically correct, although physically inconsistent. When physics instructors focus too much on the certainties of mathematics, students tend to loose sight of the physical reasoning. We consider the kind of epistemological discussion presented here to be of high educational value, specially if one intends to bring to students other elements of the nature of physical knowledge, besides mathematical calculations.
Footnotes
- 5
More advanced condensed-matter physics textbooks do provide careful quantitative descriptions of the microscopic interaction inside the wire based, for instance, on the free electron Fermi gas model or on the nearly free electron model (Bloch functions). We thank one of the anonymous referees for this stressing this point and refer the interested reader to [12, 13, 14]. However, the deep theoretical justifications of these models demand a sound understanding of quantum mechanics, which is beyond the level we are dealing with and our approach described in section 3 is intentionally centred only on classical electromagnetism.








