Abstract
The qualitative change of the type of particle trajectory homotopy in close vicinity of general-relativistic gravitational singularity affects quantum statistics in systems of identical indistinguishable particles at passing the photon sphere rim of a Schwarzschild black hole. This causes a local departure from the Pauli exclusion principle, which results in some high energy effects manifesting themselves when the matter is falling into a black hole. The release of the energy can take place at the rim of the photon sphere of a black hole due to the decay of Fermi spheres in highly compressed fermion systems entering this region. The effect is observable at activity of quasars or at collapses of neutron star mergers. The related supplementation to conventional models of the accretion disc luminosity by additional radiation from close vicinity of the event horizon of a massive black hole powering super-luminous quasar is proposed and compared with observations. The source of short-lasting gamma-ray bursts has been also identified at collapses of unstable neutron star mergers due to the decay of Fermi sphere of neutrons. The duration and spectrum of the related e-m radiation bursts estimated by the Fermi golden rule for the Fermi sphere decay agree with observations. The quantum statistics effect contributes also to the radiation of transients of micro-quasars and short lasting brightening episodes in closer active galactic nuclei. The proposed quantum effect changes the premises for the current discussion of the information paradox and hypothesis of the black hole firewall.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Black holes power quasars and are likely responsible for some kind of giant gamma-ray bursts, both of which are among the most powerful phenomena observed in the Universe. Super-luminous quasars with the luminosity of 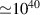 W [1–3], or short giant gamma-ray bursts with energy of
W [1–3], or short giant gamma-ray bursts with energy of  J [4–6] supposed to accompany collapses of neutron star mergers, suggest an enormously effective processes with up to 30% mass to radiation energy conversion rate. Nuclear fusion in stars has a mere 0.7% mass-to-energy conversion efficiency, and matter-antimatter annihilation with 100% efficiency would require a large amount of antimatter, which is unlikely to occur in these phenomena. This raises the question of what mechanism can achieve 30% mass-to-energy conversion rate.
J [4–6] supposed to accompany collapses of neutron star mergers, suggest an enormously effective processes with up to 30% mass to radiation energy conversion rate. Nuclear fusion in stars has a mere 0.7% mass-to-energy conversion efficiency, and matter-antimatter annihilation with 100% efficiency would require a large amount of antimatter, which is unlikely to occur in these phenomena. This raises the question of what mechanism can achieve 30% mass-to-energy conversion rate.
The luminosity of quasars (over a million quasars is known, with a peak of population at a cosmological distance of order of 10 billion light years, referred as Cosmic Noon with 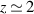 ) is conventionally explained via the accretion of matter [7–9] from gaseous surroundings of a central black hole on the cost of its gravitational energy eventually converted into thermal radiation from the hot accretion disc [10–12] and additionally strengthened by inverse Compton effect. The latter needs, however, a high temperature in plasma to assure sufficient kinetic energy of electrons and ions for Comptonization of soft thermal photons to obtain the highest-energy part of the observed radiation. In the model assessment addressed to 15 Sun mass black hole of the micro-quasar Cygnus X-1, Shapiro et al [13] proposed an increase of the temperature in the accretion disc in a toroidal bulb located at the distance of ca.
) is conventionally explained via the accretion of matter [7–9] from gaseous surroundings of a central black hole on the cost of its gravitational energy eventually converted into thermal radiation from the hot accretion disc [10–12] and additionally strengthened by inverse Compton effect. The latter needs, however, a high temperature in plasma to assure sufficient kinetic energy of electrons and ions for Comptonization of soft thermal photons to obtain the highest-energy part of the observed radiation. In the model assessment addressed to 15 Sun mass black hole of the micro-quasar Cygnus X-1, Shapiro et al [13] proposed an increase of the temperature in the accretion disc in a toroidal bulb located at the distance of ca. 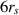 from the central singularity (rs
is the radius of Schwarzschild event horizon) to the level of 109 (1011) K for electrons (ions). However, it is difficult to scale this model to super-luminous quasars powered by black holes of
from the central singularity (rs
is the radius of Schwarzschild event horizon) to the level of 109 (1011) K for electrons (ions). However, it is difficult to scale this model to super-luminous quasars powered by black holes of 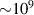 solar masses with a vast accretion discs [14–17]. It is unlikely that a similar toroidal bulb with radius
solar masses with a vast accretion discs [14–17]. It is unlikely that a similar toroidal bulb with radius  , 108 times larger than that for Cygnus X-1 would have so high temperature. Hence, the luminosity of order of 1040 W and its spectrum for super-luminous quasars apparently requires an additional mechanism that has not yet been accounted for.
, 108 times larger than that for Cygnus X-1 would have so high temperature. Hence, the luminosity of order of 1040 W and its spectrum for super-luminous quasars apparently requires an additional mechanism that has not yet been accounted for.
For giant gamma-ray bursts supposed to accompany collapses of neutron star mergers as they cross the Tolman–Oppenheimer–Volkoff (TOV) stability limit [18, 19], no known mechanism can explain the emission of a short impulse of observed burst of gamma-radiation energy 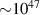 J (assuming isotropic emission from a source) and equivalent to about 0.5 Sun mass fully converted into radiation in sub-second time.
J (assuming isotropic emission from a source) and equivalent to about 0.5 Sun mass fully converted into radiation in sub-second time.
We propose a supplementary mechanism of the gravitation energy conversion into radiation via a quantum channel, which is active in close vicinity of the event horizon of a black hole at passing by a falling matter the photon sphere rim of the black hole, and which, at certain conditions, can achieve the efficiency up to 30% mass to radiation energy conversion rate. This channel can contribute to conventional models of accretion disc [10, 11, 13] with large non-thermal radiation from the vicinity of black hole event horizon inaccessible to classical hydrodynamic models of the matter accretion [14–17]. The applicability of these conventional models of the accretion discs [10, 11, 13] terminates not closer than ca.  from the central singularity [13], thus they do not conflict with quantum effects at the rim of the photon sphere distanced by
from the central singularity [13], thus they do not conflict with quantum effects at the rim of the photon sphere distanced by  from the singularity (for Schwarzschild black hole). The non-thermal radiation can be sourced here by a rapid decay of the Fermi spheres of fermionic multiparticle collective systems (of electrons, protons or neutrons) compressed to a limiting density by the attraction of central gravitational singularity. The energy accumulated in Fermi spheres of collective systems can be released when the Pauli exclusion principle is locally waived off at passing the photon sphere rim. The proposed mechanism is rooted in the topology of the curved space-time close to the gravitational singularity and is associated with a change of the trajectory homotopy class for multiparticle systems at passing the innermost unstable circular orbit (the photon sphere rim) of a Schwarzschild black hole, eventually modifying locally quantum statistics in multiparticle systems. It is an universal property of each black hole and manifests itself at episodes of the matter consumption by black holes and in dependence on the temporal pace of this consumption can achieve up to 30% efficiency for mass to radiation energy conversion. Remarkably, the released energy at the Fermi sphere collapse agrees with 1040 J per second for a giant black hole of a super-luminous quasar consuming ca. 10 Sun masses per year [14, 16], and with 1047 J gamma-ray burst for a collapsing neutron star merger with the mass of ca. 2.3 Sun masses (crossing the TOV limit [18, 19]), when the compressed hadron-electron matter at photon sphere rim reaches its highest possible stable density. Such a situation corresponds to the supply of matter to a black hole limited only by the stability of compressed matter and in cases of lower matter supply the effect of Fermi sphere decay is less powerful, but still can contribute to the luminosity of micro-quasars and transients in closer active galactic nuclei (AGN) also in agreement with observations (as at the recent observation of temporal 100-fold luminosity increase of AGN 1ES 1927+654 [20] and transient AT 2021lwx [21] or even of flare AT 2020neh [22] classified as TDE—in all these cases the quantum statistics effect contributes to x-ray components of the observed radiation, allowing for a clarifying of their noticed properties unexplained by conventional models [20–22]).
from the singularity (for Schwarzschild black hole). The non-thermal radiation can be sourced here by a rapid decay of the Fermi spheres of fermionic multiparticle collective systems (of electrons, protons or neutrons) compressed to a limiting density by the attraction of central gravitational singularity. The energy accumulated in Fermi spheres of collective systems can be released when the Pauli exclusion principle is locally waived off at passing the photon sphere rim. The proposed mechanism is rooted in the topology of the curved space-time close to the gravitational singularity and is associated with a change of the trajectory homotopy class for multiparticle systems at passing the innermost unstable circular orbit (the photon sphere rim) of a Schwarzschild black hole, eventually modifying locally quantum statistics in multiparticle systems. It is an universal property of each black hole and manifests itself at episodes of the matter consumption by black holes and in dependence on the temporal pace of this consumption can achieve up to 30% efficiency for mass to radiation energy conversion. Remarkably, the released energy at the Fermi sphere collapse agrees with 1040 J per second for a giant black hole of a super-luminous quasar consuming ca. 10 Sun masses per year [14, 16], and with 1047 J gamma-ray burst for a collapsing neutron star merger with the mass of ca. 2.3 Sun masses (crossing the TOV limit [18, 19]), when the compressed hadron-electron matter at photon sphere rim reaches its highest possible stable density. Such a situation corresponds to the supply of matter to a black hole limited only by the stability of compressed matter and in cases of lower matter supply the effect of Fermi sphere decay is less powerful, but still can contribute to the luminosity of micro-quasars and transients in closer active galactic nuclei (AGN) also in agreement with observations (as at the recent observation of temporal 100-fold luminosity increase of AGN 1ES 1927+654 [20] and transient AT 2021lwx [21] or even of flare AT 2020neh [22] classified as TDE—in all these cases the quantum statistics effect contributes to x-ray components of the observed radiation, allowing for a clarifying of their noticed properties unexplained by conventional models [20–22]).
2. Change of the particle trajectory homotopy close to a black hole
2.1. Trajectories of free particles in Shwarzschild metric
Let us consider a folded space-time described by Schwarzschild metric [23] being the solution of Einstein general relativity equations for a spherical non-rotating and uncharged body with the mass M and radius R, for r > R,
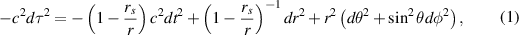
the coordinates 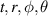 are time-space rigid coordinates (in spherical variables) the same as for a remote observer, whereas τ denotes the proper time,
are time-space rigid coordinates (in spherical variables) the same as for a remote observer, whereas τ denotes the proper time,  is the Schwarzschild radius, which defines the event horizon (G is the gravitational constant, c is the light velocity in the vacuum). The metric (1) in the limit
is the Schwarzschild radius, which defines the event horizon (G is the gravitational constant, c is the light velocity in the vacuum). The metric (1) in the limit  can be addressed to a black hole with gravitational singularity at r = 0, which is surrounded by the event horizon sphere with the radius rs
, from which neither matter nor light can escape. Besides the singularity in r = 0, another one occurs in (1) on the event horizon at
can be addressed to a black hole with gravitational singularity at r = 0, which is surrounded by the event horizon sphere with the radius rs
, from which neither matter nor light can escape. Besides the singularity in r = 0, another one occurs in (1) on the event horizon at  . This singularity is apparent (called as coordinate singularity) and disappears if one changes to other coordinates [11, 24, 25]. A choice of a distinct coordinate system displays a different slicing of the same folded space-time onto its spatial and temporal parts, which can be done in a variety manners allowing various representations of particle motion without changing, however, the trajectory homotopy governed by invariant space-time curvature. In particular, in the metric (1) a remote observer can notice matter falling onto the event horizon of the black hole infinitely long, never crossing the event horizon. Changing, however, to the proper time instead of t, the matter smoothly passes the event horizon within a finite period of the proper time and next after of also finite period of the proper time any motion terminates in the central singularity [11, 24]. The metric (1) expressed in stationary (time independent spatial coordinates) is convenient to analyze the topology (homotopy) of trajectories of particles when they approach the event horizon. Impossibility to cross the event horizon in finite time t follows from the simple property of general relativity singularity, that it does not exist a rigid metric describing simultaneously inner and outer region with respect to the event horizon [26], though it can be done in other coordinates, e.g. in metrics by Novikov, Peinlevé–Gullstrand, Eddington–Finkelstein or Kruskal–Szekeres [11, 24–28].
. This singularity is apparent (called as coordinate singularity) and disappears if one changes to other coordinates [11, 24, 25]. A choice of a distinct coordinate system displays a different slicing of the same folded space-time onto its spatial and temporal parts, which can be done in a variety manners allowing various representations of particle motion without changing, however, the trajectory homotopy governed by invariant space-time curvature. In particular, in the metric (1) a remote observer can notice matter falling onto the event horizon of the black hole infinitely long, never crossing the event horizon. Changing, however, to the proper time instead of t, the matter smoothly passes the event horizon within a finite period of the proper time and next after of also finite period of the proper time any motion terminates in the central singularity [11, 24]. The metric (1) expressed in stationary (time independent spatial coordinates) is convenient to analyze the topology (homotopy) of trajectories of particles when they approach the event horizon. Impossibility to cross the event horizon in finite time t follows from the simple property of general relativity singularity, that it does not exist a rigid metric describing simultaneously inner and outer region with respect to the event horizon [26], though it can be done in other coordinates, e.g. in metrics by Novikov, Peinlevé–Gullstrand, Eddington–Finkelstein or Kruskal–Szekeres [11, 24–28].
The homotopy of trajectories of noninteracting identical indistinguishable particles (with mass m vanishing small in comparison to central mass M) in the upper neighborhood of the Schwarzschild event horizon is displayed by geodesics in the metric (1). These geodesics must lie in planes (because of spherical symmetry) and it is enough to consider the motion in a plane  . The Hamilton–Jacobi equation for geodesics,
. The Hamilton–Jacobi equation for geodesics,

attains for Schwarzschild black hole the following form (with gik metric tensor components corresponding to metric (1) [26])
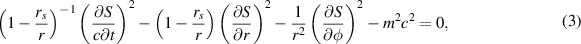
with the function S in the form,

where 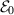 and
and  are the particle energy and its angular momentum, respectively (
are the particle energy and its angular momentum, respectively ( and
and  are constants of motion). Substituting equation (4) into equation (3) one can find,
are constants of motion). Substituting equation (4) into equation (3) one can find,

The radial dependence for a trajectory  is given by the condition
is given by the condition  , whereas the angular dependence
, whereas the angular dependence  by the condition
by the condition  , which have an explicit form, for radius,
, which have an explicit form, for radius,
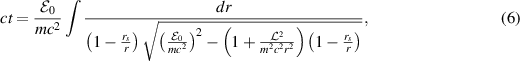
and for azimuth angle,

respectively
If one rewrites equation (6) in a differential form,

the effective potential can be introduced, dependent on angular momentum 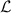 of the particle.
of the particle.

An accessible region for the motion is given by  . Additionally, the condition
. Additionally, the condition  defines circular orbits. The standard analysis [26] of extreme properties of U(r) allows determination of stable circular orbits (corresponding to minima of U(r)) and unstable ones (related to maxima of U(r)). The conditions
defines circular orbits. The standard analysis [26] of extreme properties of U(r) allows determination of stable circular orbits (corresponding to minima of U(r)) and unstable ones (related to maxima of U(r)). The conditions  and
and 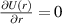 (for extreme) have the explicit form,
(for extreme) have the explicit form,

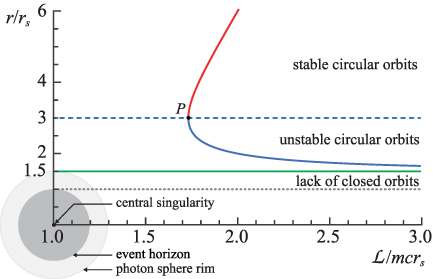
with + and − in the second equation corresponding to stable and unstable orbits, respectively. The solution of equation (10) can be illustrated in figure 1, where the circular orbit radius r versus angular momentum  of the particle is plotted. The upper curve (red one in this figure) gives positions of stable circular orbits and the lower curve (blue one) gives positions of unstable circular orbits. The stable circular orbits terminate at
of the particle is plotted. The upper curve (red one in this figure) gives positions of stable circular orbits and the lower curve (blue one) gives positions of unstable circular orbits. The stable circular orbits terminate at 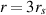 (point P in figure 1 corresponding to particle angular momentum
(point P in figure 1 corresponding to particle angular momentum 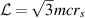 and particle energy
and particle energy  ). Below the innermost stable circular orbit there are possible unstable ones, but they also terminate at
). Below the innermost stable circular orbit there are possible unstable ones, but they also terminate at  (for infinite
(for infinite 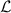 ). Below the innermost unstable circular orbit
). Below the innermost unstable circular orbit 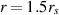 particle trajectories defined by equations (6) and (7) for
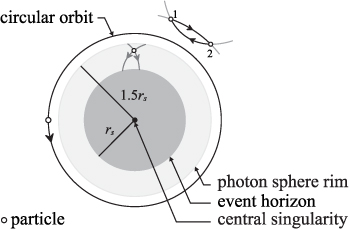
particle trajectories defined by equations (6) and (7) for  have the form of unidirectional short spirals exemplified in figure 2. This is different in comparison to Newton gravitation center, for which conic section trajectories including circular orbits are available arbitrarily close to the center. The specific and transparently noticeable behavior of trajectories in metric (1) close to the event horizon of a black hole has pronounced consequences, because the homotopy class of classical trajectories of particles decides on quantum statistics in multiparticle systems.
have the form of unidirectional short spirals exemplified in figure 2. This is different in comparison to Newton gravitation center, for which conic section trajectories including circular orbits are available arbitrarily close to the center. The specific and transparently noticeable behavior of trajectories in metric (1) close to the event horizon of a black hole has pronounced consequences, because the homotopy class of classical trajectories of particles decides on quantum statistics in multiparticle systems.
Figure 1. Radii of stable (red) and unstable (blue) circular orbits in Schwarzschild geometry. The innermost circular stable orbit occurs at  —point P on the level of dashed line in blue color (the coordinates of point P are, angular momentum
—point P on the level of dashed line in blue color (the coordinates of point P are, angular momentum 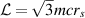 and energy
and energy 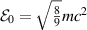 , m is the mass of a particle), whereas the innermost unstable circular orbit occurs at
, m is the mass of a particle), whereas the innermost unstable circular orbit occurs at  (asymptotic green line,
(asymptotic green line, 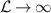 and
and  ). Below
). Below 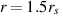 neither circular nor other closed orbits exist.
neither circular nor other closed orbits exist.
Download figure:
Standard image High-resolution imageFigure 2. Simplified pictorial illustration of the change of trajectory homotopy at passing the innermost unstable circular orbit of a black hole. Conic section-like trajectories are available beyond the photon sphere rim, and the particle position interchanges are possible there. Conic section-type oppositely directed trajectories can intersect in two points and local arbitrarily small closed loops can be constructed from pieces of such trajectories. If in cross-points two particles are located, then their mutual interchanging is possible. When for particles passing through the photon sphere inward only short, one-way spiral trajectories are admitted, it is impossible to build local small closed loops made of pieces of these spirals, which precludes mutual exchange of particles.
Download figure:
Standard image High-resolution imageQuantum statistics of identical indistinguishable particles is not a general their property, but can change in response to topological properties of trajectories for particles in some local manifold on which all particles are placed (as commented in appendices
2.2. Qualitative change of trajectory homotopy for indistinguishable particles at passing the innermost unstable circular orbit in Schwarzschild geometry
The qualitative change of the trajectory homotopy takes place at the innermost unstable circular orbit for any massive particle at 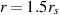 . This orbit is also an unstable smaller orbit for photons [26] and the region ranged by the radius
. This orbit is also an unstable smaller orbit for photons [26] and the region ranged by the radius 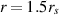 is called as photon sphere. Below the photon sphere upper rim no circular orbits for photons exist.
is called as photon sphere. Below the photon sphere upper rim no circular orbits for photons exist.
Any massive particle unavoidable spirals onto the event horizon if it passes the photon sphere rim in inward direction. This concerns a macroscopic body as well as particles of the microscopic its structure. In particular, if a multiparticle system passes the photon sphere rim inward all particles must fall toward the event horizon along one-way spirals. For free particles these spirals are given by equations (6) and (7) for 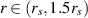 . Considering free particle systems is sufficient to define local quantum statistics in systems of indistinguishable identical particles. The photon sphere rim separates two regions with distinct types of available particle trajectories. Beyond this rim any direction of particle movement is admitted along conic section-like trajectories, whereas for particles passing inward the photon sphere rim, trajectories are only of spiral form irrevocably directed toward the event horizon regardless of initial conditions. This is a qualitative homotopy change of trajectories for free particles, which can be addressed to local multiparticle systems of identical indistinguishable particles considered to define quantum statistics.
. Considering free particle systems is sufficient to define local quantum statistics in systems of indistinguishable identical particles. The photon sphere rim separates two regions with distinct types of available particle trajectories. Beyond this rim any direction of particle movement is admitted along conic section-like trajectories, whereas for particles passing inward the photon sphere rim, trajectories are only of spiral form irrevocably directed toward the event horizon regardless of initial conditions. This is a qualitative homotopy change of trajectories for free particles, which can be addressed to local multiparticle systems of identical indistinguishable particles considered to define quantum statistics.
Below the innermost unstable circular orbit (photon sphere rim in Schwarzschild geometry) no closed small local loops are admissible including also small loops built of pieces of one-way spiral-type particle trajectories. This is different in comparison to Newton gravitation center, for which all conic section trajectories are accessible for particles arbitrarily close to the center. Despite that for large distances from the gravitation center the Schwarzschild trajectories are similar to conic sections-type orbits (modified by some additional precession of elliptical orbits, like that observed for Mercury in Sun gravitation), conic section-like particle trajectories completely disappear below the photon sphere rim. Conic section-type trajectories can form closed arbitrarily small local loops from their pieces, what is easy to be noticed, as conic sections can cross in two arbitrarily close points (like circle with ellipse, hyperbole or parabola), as illustrated schematically in figure 2. For example, two inversely oriented trajectory pieces of conic sections can create together local arbitrarily small loops for mutual particle exchanges (particles can be located in crossing points). This is impossible below the innermost unstable circular orbit (the photon sphere rim), where unidirectional spirals cannot form local closed loops using even an arbitrary large number of small fragments of these spirals. It is impossible to built here local loops for particle exchanges—local loops built of pieces of spirals given by equations (6) and (7) and 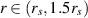 cannot be closed because of one-way their directions for particles passing the photon sphere inward. Hence, the innermost unstable circular orbit separates two space regions with different classes of homotopy of trajectories for massive particles in multiparticle systems passing these limiting sphere inward.
cannot be closed because of one-way their directions for particles passing the photon sphere inward. Hence, the innermost unstable circular orbit separates two space regions with different classes of homotopy of trajectories for massive particles in multiparticle systems passing these limiting sphere inward.
The existence of real classical trajectories for particle exchanges is essential for the definition of quantum statistics for these particles. When N identical indistinguishable particles are located on some spatial manifold  , then to these particles can be assigned a quantum statistics in compliance with one dimensional unitary representation of the braid group [31, 32], which describes all possible exchanges of particles on
, then to these particles can be assigned a quantum statistics in compliance with one dimensional unitary representation of the braid group [31, 32], which describes all possible exchanges of particles on 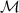 . The braid group is the first homotopy group
. The braid group is the first homotopy group  , where
, where  is the multiparticle configuration classical space of N identical indistinguishable particles with dynamics confined to the manifold
is the multiparticle configuration classical space of N identical indistinguishable particles with dynamics confined to the manifold 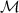 . In this definition
. In this definition  is N-fold product of the manifold
is N-fold product of the manifold 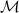 to equally account for all particles. Δ is the diagonal subset of
to equally account for all particles. Δ is the diagonal subset of  (collecting points with coinciding coordinates of at least two particles) and subtracted from the coordination space to assure particle number conservation. Division by the permutation group SN
(the quotient structure of space FN
) introduces indistinguishability of particles, i.e. all distributions of particles, which differ only in their numbering, are unified into a single point in FN
. Hence, braids from the first homotopy group
(collecting points with coinciding coordinates of at least two particles) and subtracted from the coordination space to assure particle number conservation. Division by the permutation group SN
(the quotient structure of space FN
) introduces indistinguishability of particles, i.e. all distributions of particles, which differ only in their numbering, are unified into a single point in FN
. Hence, braids from the first homotopy group  , which are closed loops in FN
, display mutual exchanges of particles positions (braid loops link in FN
differently numbered particle distributions) and their scalar unitary representations defines quantum statistics of these N particles.
, which are closed loops in FN
, display mutual exchanges of particles positions (braid loops link in FN
differently numbered particle distributions) and their scalar unitary representations defines quantum statistics of these N particles.
Quantum statistics is of fundamental significance and imposes severe restrictions on general quantum collective properties. In Schrödinger picture any multiparticle wave function must transform according to scalar unitary representation of a particular braid, which describes interchanges of arguments of this function (arguments are classical positions of particles on 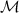 ). The same concerns quantum fields of second quantization with restrictions imposed on their commutation algebra. For 3D manifolds (in unfolded space) the braid groups are always permutation groups SN
[31, 33], which have only two different scalar unitary representations, defined on generators of SN
as
). The same concerns quantum fields of second quantization with restrictions imposed on their commutation algebra. For 3D manifolds (in unfolded space) the braid groups are always permutation groups SN
[31, 33], which have only two different scalar unitary representations, defined on generators of SN
as  or
or  (where σi
,
(where σi
, 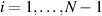 , are elementary braids—exchanges of ith particle with
, are elementary braids—exchanges of ith particle with 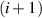 th one, when other particles stay a rest; numeration of particles is arbitrary but fixed; σi
are generators of any braid group [33], in particular of SN
). Two different scalar unitary representations of SN
give rise to statistics of fermions and bosons, respectively. In 3D
th one, when other particles stay a rest; numeration of particles is arbitrary but fixed; σi
are generators of any braid group [33], in particular of SN
). Two different scalar unitary representations of SN
give rise to statistics of fermions and bosons, respectively. In 3D 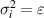 (neutral element in the braid group), but in 2D
(neutral element in the braid group), but in 2D  and braid groups in planar systems of the same classical particles are different than SN
(instead of finite permutation group, the braid group for N particles on a plane, i.e. for
and braid groups in planar systems of the same classical particles are different than SN
(instead of finite permutation group, the braid group for N particles on a plane, i.e. for  , is infinite Artin group BN
[33, 34], with infinite number of different scalar unitary representations, related to so-called anyons with fractional quantum statistics [30]).
, is infinite Artin group BN
[33, 34], with infinite number of different scalar unitary representations, related to so-called anyons with fractional quantum statistics [30]).
The definition of fermionic or bosonic quantum statistics in 3D requires, however, the existence of classical trajectories in 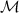 for particle exchanges σi
. Otherwise the braid group generators (here the permutation group) cannot be defined and quantum statistics cannot be assigned (a precise mathematical formulation of the linkage of trajectory homotopy class and quantum statistics can be demonstrated in the framework of path integration quantization for systems of identical indistinguishable particlesis, as summarized in appendix
for particle exchanges σi
. Otherwise the braid group generators (here the permutation group) cannot be defined and quantum statistics cannot be assigned (a precise mathematical formulation of the linkage of trajectory homotopy class and quantum statistics can be demonstrated in the framework of path integration quantization for systems of identical indistinguishable particlesis, as summarized in appendix
For the existence of σi
generators of the braid group for a particular system, the mutual exchanges for particle pairs on the manifold  must be admitted, i.e. there must exist closed loops in
must be admitted, i.e. there must exist closed loops in  built of pieces of individual particle trajectories in
built of pieces of individual particle trajectories in  . It is unreachable to form such closed loops in local
. It is unreachable to form such closed loops in local 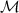 from pieces of one-way spirals defined by equations (6) and (7) for
from pieces of one-way spirals defined by equations (6) and (7) for 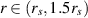 , in contrast to conic-section-like trajectories beyond the photon sphere. This precludes the definition of the braid group generated by σi
in the local multiparticle configuration space beneath the photon sphere rim and related to
, in contrast to conic-section-like trajectories beyond the photon sphere. This precludes the definition of the braid group generated by σi
in the local multiparticle configuration space beneath the photon sphere rim and related to  defined by a macroscopic system passing this rim. Hence, for
defined by a macroscopic system passing this rim. Hence, for  the fermionic or bosonic quantum statistics can be assigned [31, 33] to particles in local manifolds in contrary to the region
the fermionic or bosonic quantum statistics can be assigned [31, 33] to particles in local manifolds in contrary to the region 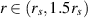 , where none such quantum statistics is defined.
, where none such quantum statistics is defined.
Below the innermost unstable circular orbit the dominating term in the effective potential (equations (8) and (9)) is  , which causes an unavoidable one-way spiral movement toward the event horizon of any particle passing this orbit inward despite its energy and angular momentum and local mutual interaction between particles. The phase shift for such spirals is all the more limited the larger
, which causes an unavoidable one-way spiral movement toward the event horizon of any particle passing this orbit inward despite its energy and angular momentum and local mutual interaction between particles. The phase shift for such spirals is all the more limited the larger  for given
for given  (as illustrated in figure 3). From pieces of these short unidirectional spirals it is impossible to form any closed local loop required for interchanges of particles and braid group implementation. This is in contrary to conic section-like trajectories admissible beyond the photon sphere rim, which can form arbitrary small closed loops.
(as illustrated in figure 3). From pieces of these short unidirectional spirals it is impossible to form any closed local loop required for interchanges of particles and braid group implementation. This is in contrary to conic section-like trajectories admissible beyond the photon sphere rim, which can form arbitrary small closed loops.
Figure 3. Spiral trajectories for particles passing the photon sphere rim of a black hole, shown in spherical variables, phase shift φ versus radius r—the solutions of equation (7) for selected motion constants 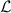 and
and 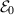 (in the figure legend,
(in the figure legend,  ,
, 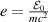 ).
).
Download figure:
Standard image High-resolution image3. Quantum collective transition at the photon sphere rim
3.1. Change of the quantum statistics at passing the photon sphere rim of a black hole
Any local multiparticle system which passes the photon sphere rim inward loses its quantum statistics defined on braid group generators σi
because these generators cannot be constructed in related FN
space beneath this rim. The space FN
is thus simply-connected here and its first homotopy group is trivial 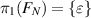 (scalar unitary representation of neutral group element ε is 1, as
(scalar unitary representation of neutral group element ε is 1, as  , which does not display any statistics because ε is not particle exchange).
, which does not display any statistics because ε is not particle exchange).
The foremost quantum property of fermions is expressed as the so-called exclusion principle by Pauli, which asserts that fermionic quantum particles cannot share any common single-particle quantum state. Localized quantum states preclude thus approaching by fermions a space region already occupied by another identical fermion, which results in fermion repulsion, beyond fundamental interactions. This so-called quantum degeneracy repulsion can exert a giant pressure in a dense system and actually stops the collapse of white dwarfs [35] or neutron stars [18, 19, 36]. In white dwarfs electrons halt a collapse, whereas in neutron stars neutrons are of significance.
In sufficiently dense fermionic systems and at temperatures T lower than the chemical potential, i.e. when  (kB
is the Boltzmann constant, µ is the chemical potential—the energy increase caused by the addition of a single particle to the system), fermions form the so-called Fermi sphere, corresponding to one by one filled single-particle stationary states by all fermions respecting Pauli exclusion principle. Even though the Fermi sphere structure is transparent for noninteracting particles, inclusion of inter-particle interaction does not change the notion of the Fermi sphere [37] and its radius (in momentum space) is invariant with respect to interaction according to Luttinger theorem [38]. This radius equals to [39, 40],
(kB
is the Boltzmann constant, µ is the chemical potential—the energy increase caused by the addition of a single particle to the system), fermions form the so-called Fermi sphere, corresponding to one by one filled single-particle stationary states by all fermions respecting Pauli exclusion principle. Even though the Fermi sphere structure is transparent for noninteracting particles, inclusion of inter-particle interaction does not change the notion of the Fermi sphere [37] and its radius (in momentum space) is invariant with respect to interaction according to Luttinger theorem [38]. This radius equals to [39, 40],

and is the function of fermion concentration only, 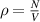 , where N is the total number of particles, V is the spatial volume of the system,
, where N is the total number of particles, V is the spatial volume of the system,  is reduced Planck constant. The proof of Luttinger theorem resolves itself to the observation that in the phase space
is reduced Planck constant. The proof of Luttinger theorem resolves itself to the observation that in the phase space 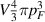 , there exist
, there exist 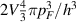 different single-particle quantum states (due to Bohr–Sommerfeld rule for quantization, factor 2 is caused by double spin degeneracy for
different single-particle quantum states (due to Bohr–Sommerfeld rule for quantization, factor 2 is caused by double spin degeneracy for 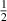 spin of fermions), and if they are filled by N particles, the relation (11) is obtained. Quasiclassical Bohr–Sommerfeld rule [41] is immune to interaction, thus pF
defined by equation (11) is universal for any interacting fermionic system. The energy of fermions on a Fermi surface is called as Fermi energy,
spin of fermions), and if they are filled by N particles, the relation (11) is obtained. Quasiclassical Bohr–Sommerfeld rule [41] is immune to interaction, thus pF
defined by equation (11) is universal for any interacting fermionic system. The energy of fermions on a Fermi surface is called as Fermi energy,  (in relativistic case), which equals to the chemical potential at zero temperature T = 0 K, which is familiar from the Fermi–Dirac distribution function for noninteracting fermions,
(in relativistic case), which equals to the chemical potential at zero temperature T = 0 K, which is familiar from the Fermi–Dirac distribution function for noninteracting fermions,
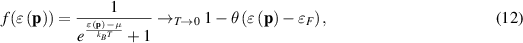
where θ is the Heaviside step function, µ is the chemical potential, which at T = 0 K equals to Fermi energy εF and weakly changes with the temperature increase [37].
The whole Fermi sphere can store a high energy, which can be assessed per spatial volume V (neglecting interaction) as follows [39, 40],

the sum runs over occupied states p in momentum space, which form an isotropic Fermi sphere  with radius pF
;
with radius pF
; 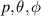 are spherical variables in momentum space and
are spherical variables in momentum space and  (the kinetical energy of a single particle in relativistic case),
(the kinetical energy of a single particle in relativistic case), 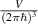 is a number of single-particle quantum states in the element of the phase space
is a number of single-particle quantum states in the element of the phase space  (the density of states according to Bohr–Sommerfeld rule). The energy estimation (13) concerns T = 0 K case, but it very well approximates energy of fermions in Fermi sphere also for nonzero temperatures, provided that
(the density of states according to Bohr–Sommerfeld rule). The energy estimation (13) concerns T = 0 K case, but it very well approximates energy of fermions in Fermi sphere also for nonzero temperatures, provided that  .
.
To demonstrate how large is the energy accumulated in a Fermi sphere one can estimate it via equations (11) and (13) in exemplary systems. In a metal (like Fe) in normal conditions free electrons (with concentration of order of Avogadro number per cm3) form the Fermi sphere accumulating 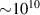 J m−3. In a neutron star merger at TOV stability limit (of ca. 2.3 Sun masses compressed to the sphere with radius lower than 10 km) the Fermi sphere of neutrons has energy
J m−3. In a neutron star merger at TOV stability limit (of ca. 2.3 Sun masses compressed to the sphere with radius lower than 10 km) the Fermi sphere of neutrons has energy 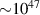 J. The energy collected in Fermi spheres is blocked by Pauli exclusion principle, but can be released when this principle is locally waived off, as at passing the photon sphere rim of a black hole. In both mentioned above examples we deal with quantumly degenerated systems, as the Fermi energy in metal is of order of 8 eV (i.e.
J. The energy collected in Fermi spheres is blocked by Pauli exclusion principle, but can be released when this principle is locally waived off, as at passing the photon sphere rim of a black hole. In both mentioned above examples we deal with quantumly degenerated systems, as the Fermi energy in metal is of order of 8 eV (i.e.  K in temperature units, when
K in temperature units, when 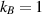 ) and highly exceeds even the melting temperature of a metal, and for a neutron star merger
) and highly exceeds even the melting temperature of a metal, and for a neutron star merger  GeV (i.e.
GeV (i.e.  K in temperature units, cf table 1 for detail) and also highly exceeds the supposed temperature of a merger (106 K), so the formula (13) holds with high accuracy.
K in temperature units, cf table 1 for detail) and also highly exceeds the supposed temperature of a merger (106 K), so the formula (13) holds with high accuracy.
Table 1. Fermi momentum pF
(acc. to equation (11)), Fermi energy 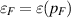 and total energy of the Fermi sphere E released at the collapse of the Fermi sphere, for neutron star (acc. to equation (13)), for quasar luminosity—the energy per second; ξ—density of compressed electron-hadron matter, n—total number of neutrons (ne) in a neutron star; for a quasar of electrons (el) or protons (pr) per second.
and total energy of the Fermi sphere E released at the collapse of the Fermi sphere, for neutron star (acc. to equation (13)), for quasar luminosity—the energy per second; ξ—density of compressed electron-hadron matter, n—total number of neutrons (ne) in a neutron star; for a quasar of electrons (el) or protons (pr) per second.
| pF (kg m s−1) |
ξ (kg m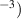
| n |
εF
(GeV) ((K) if 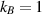 ) ) |
 (J)/luminosity (W) (J)/luminosity (W) |
|---|---|---|---|---|
Unstable neutron star merger of 2.3  with radius ca. 6 km with radius ca. 6 km | ||||
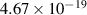
|

|

| ne 0.34 (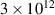 ) ) |
 J J |
Quasar with BH of 109
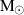 consuming 0.06 Earth mass per second ( consuming 0.06 Earth mass per second ( per year) per year) | ||||

|

|
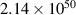
| el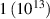 , pr , pr 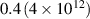
| 1040 W |
4. Astrophysical phenomena related to quantum statistic transition at photon sphere rim
4.1. Gamma-ray burst at collapse of neutron star merger
At collapse of neutron star merger into a black hole the photon radiation is supposed to be released, though the mechanism of the photon burst with energy equivalent to half of Sun mass converted into e-m radiation within subsecond time has not yet been provided. Neutron star attains the density stability limit when its mass crosses ca. 2.3 Sun masses (the TOV limit [18, 19]), what happens if smaller neutron stars merge together and due to the gravitational compression, the merger attains the radius lower than 10 km (for M = 2.3 Sun masses  km). When all the mass is contained inside its own photon sphere, then the local waiving off of Pauli principle takes place and due to the relief in quantum pressure of neutrons the star collapses. Simultaneously, the Fermi sphere of neutrons decays and its energy is released [42]. Neutrons are stabilized in a neutron star by Pauli exclusion principle and at the quantum statistics transition they decay into protons and electrons, which are charged particles interacting with e-m field, thus able to radiate photons according to Fermi golden rule. The energy of neutrons in their Fermi sphere in a neutron star merger at TOV limit, being of order of 1047 J, is thus emitted at suddenly admitted quantum jumps of protons and electrons from their positions in momentum space onto ground state. A neutron with momentum p decays into a proton and electron and antineutrino (along β− transition scheme with time rate strongly accelerated by forced emission of avalanche type in the system of ca. 1057 neutrons in a star merger). Liberated charged particles lose their kinetic energy at suddenly admitted quantum transitions to lower states. The spectrum and timing of these transitions for electrons and protons can be assessed by the Fermi golden rule. Assuming the same concentration of electrons and protons, their initial Fermi spheres have the same Fermi momentum (11).
km). When all the mass is contained inside its own photon sphere, then the local waiving off of Pauli principle takes place and due to the relief in quantum pressure of neutrons the star collapses. Simultaneously, the Fermi sphere of neutrons decays and its energy is released [42]. Neutrons are stabilized in a neutron star by Pauli exclusion principle and at the quantum statistics transition they decay into protons and electrons, which are charged particles interacting with e-m field, thus able to radiate photons according to Fermi golden rule. The energy of neutrons in their Fermi sphere in a neutron star merger at TOV limit, being of order of 1047 J, is thus emitted at suddenly admitted quantum jumps of protons and electrons from their positions in momentum space onto ground state. A neutron with momentum p decays into a proton and electron and antineutrino (along β− transition scheme with time rate strongly accelerated by forced emission of avalanche type in the system of ca. 1057 neutrons in a star merger). Liberated charged particles lose their kinetic energy at suddenly admitted quantum transitions to lower states. The spectrum and timing of these transitions for electrons and protons can be assessed by the Fermi golden rule. Assuming the same concentration of electrons and protons, their initial Fermi spheres have the same Fermi momentum (11).
According to Fermi golden rule, the probability of a quantum transition per time unit due to interaction of a charged quantum particle with e-m field is as follows [41],
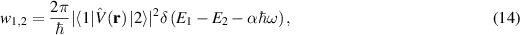
where  is a matrix element of an operator
is a matrix element of an operator  describing coupling of a charged particle to e-m field taken between an initial
describing coupling of a charged particle to e-m field taken between an initial  quantum stationary state of a particle with energy E1, and a final one
quantum stationary state of a particle with energy E1, and a final one 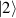 with energy E2.
with energy E2. 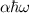 is the energy of emitted photon at the particle transition
is the energy of emitted photon at the particle transition 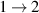 , including gravitational redshift close to the black hole horizon,
, including gravitational redshift close to the black hole horizon, 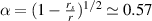 for
for  . For relativistic electrons or protons the kinetic energy single-particle Hamiltonian has the form,
. For relativistic electrons or protons the kinetic energy single-particle Hamiltonian has the form,
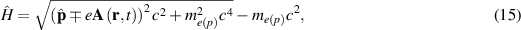
where  is the vector potential of the e-m field for a plane wave (at gauge
is the vector potential of the e-m field for a plane wave (at gauge  ),
), 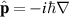 . As the Fermi golden rule is of first order perturbation accuracy [41], thus, the form of operator
. As the Fermi golden rule is of first order perturbation accuracy [41], thus, the form of operator  is defined by the term in single-particle Hamiltonian linear with respect to A,
is defined by the term in single-particle Hamiltonian linear with respect to A,

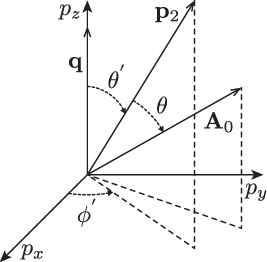
Initial and final states  can be assumed in the form
can be assumed in the form 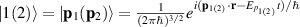 representing states in the isotropic Fermi sphere for
representing states in the isotropic Fermi sphere for 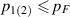 ,
,  . One can calculate the matrix element in equation (14) for
. One can calculate the matrix element in equation (14) for 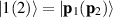 , which gives,
, which gives,
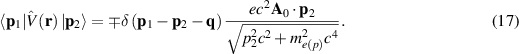
Substituting it into equation (14), we obtain,

where 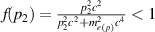 and for
and for  with
with  (because
(because 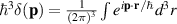 and
and 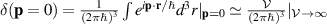 ,
,  ),
),  ,
,  (
( is the volume of a local multi-particle system). The probability
is the volume of a local multi-particle system). The probability  tends to zero for
tends to zero for  , but for
, but for 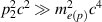 the function
the function 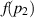 practically does not depend on p2 and in this limit
practically does not depend on p2 and in this limit 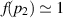 . For electrons (protons) this inequality is satisfied for
. For electrons (protons) this inequality is satisfied for  (
(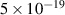 ) kg m s−1. Higher energies of photons dominate as the density of states in isotropic Fermi sphere grows as p2.
) kg m s−1. Higher energies of photons dominate as the density of states in isotropic Fermi sphere grows as p2.
Integration of equation (18) over all occupied states in the Fermi sphere allows the estimation of time-span for entire Fermi sphere collapse. The integration over p1 and p2 gives from equation (18),
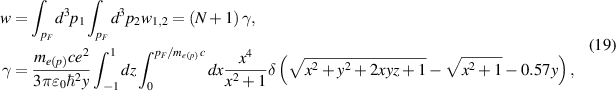
where  ,
,  , ε0 is the dielectric constant and
, ε0 is the dielectric constant and  is the number of photons
is the number of photons  in the volume
in the volume  ,
,  (where E0 and A0 are amplitudes of electric field and of vector potential of e-m radiation, respectively) and the density of energy of e-m field is
(where E0 and A0 are amplitudes of electric field and of vector potential of e-m radiation, respectively) and the density of energy of e-m field is  . Non-zero value of w for N = 0 reveals the spontaneous emission (as in optical transitions the only non-zero matrix element of the creation operator for photons is out of diagonal and equals to
. Non-zero value of w for N = 0 reveals the spontaneous emission (as in optical transitions the only non-zero matrix element of the creation operator for photons is out of diagonal and equals to  for the quantized vector potential in equation (16)). (A technical note: in (19) the integrals over p1 and p2 should be accompanied with the density of states,
for the quantized vector potential in equation (16)). (A technical note: in (19) the integrals over p1 and p2 should be accompanied with the density of states,  , but the states
, but the states  are normalized on the Dirac delta and to restore their probability sense, the matrix element (17) must be divided by
are normalized on the Dirac delta and to restore their probability sense, the matrix element (17) must be divided by  to change the normalization to volume
to change the normalization to volume  ; since the matrix element (17) enters into (14) in the square, then the state density coefficients in (19) cancel. Moreover, the integration over arbitrary orientation of the vector A0 with respect to the vector p2 (assumed along z-axis) has been performed in (19), resulting in
; since the matrix element (17) enters into (14) in the square, then the state density coefficients in (19) cancel. Moreover, the integration over arbitrary orientation of the vector A0 with respect to the vector p2 (assumed along z-axis) has been performed in (19), resulting in  ,
,  .) The above derivation of equation (19) has been performed for wave functions
.) The above derivation of equation (19) has been performed for wave functions  normalized on the Dirac delta. One can repeat calculations also for wave functions normalized on the finite volume
normalized on the Dirac delta. One can repeat calculations also for wave functions normalized on the finite volume 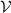 , as shown in detail in
, as shown in detail in
The number of photons satisfies the dynamic equation,

hence, the solution of (20) attains the form  , or
, or  , where
, where  is the time of total Fermi sphere decay for N0 of order of particle number in the system.
is the time of total Fermi sphere decay for N0 of order of particle number in the system.  depends on photon frequency
depends on photon frequency  via function
via function 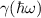 given by equation (19).
given by equation (19).
For a neutron star merger with 2.3 Sun masses, one can estimate the time-span  of the decay of Fermi spheres of electrons (assuming in (19)
of the decay of Fermi spheres of electrons (assuming in (19) 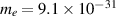 kg) and protons (ca. 1837 times more massive) for particular energy of emitted photons—as shown in table 2, which displays the rapid process of photon emission. In this assessment we did not take into account the time of the decay of neutrons into electrons and protons (and antineutrinos), which slows down the photon burst. The β− decay of an isolated neutron takes ca. 880 s mostly due to quark transitions, the conversion of the negatively charged
kg) and protons (ca. 1837 times more massive) for particular energy of emitted photons—as shown in table 2, which displays the rapid process of photon emission. In this assessment we did not take into account the time of the decay of neutrons into electrons and protons (and antineutrinos), which slows down the photon burst. The β− decay of an isolated neutron takes ca. 880 s mostly due to quark transitions, the conversion of the negatively charged 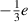 down quark to the positively charged
down quark to the positively charged  up quark by emission of a W− boson (the W− boson subsequently decays, almost instantly, into an electron and an electron antineutrino). In a neutron star neutrons are stabilized by Pauli exclusion principle. If the latter is locally waived off, then neutrons decay in a collective manner also according to Fermi golden rule (similar as in equation (20) with specific
up quark by emission of a W− boson (the W− boson subsequently decays, almost instantly, into an electron and an electron antineutrino). In a neutron star neutrons are stabilized by Pauli exclusion principle. If the latter is locally waived off, then neutrons decay in a collective manner also according to Fermi golden rule (similar as in equation (20) with specific  for spontaneous decay of a neutron). If for
for spontaneous decay of a neutron). If for  one assumes
one assumes 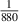 1/s, the decay of all neutrons would take ca 30 hours. Nevertheless, fermionic quarks also lose their quantum statistics at passing the photon sphere rim of a black hole, and the decay of unstable isolated neutron would be here much faster (neutron has larger rest mass than proton, which causes the decay not limited by fermionic nature of quarks and conversion
1/s, the decay of all neutrons would take ca 30 hours. Nevertheless, fermionic quarks also lose their quantum statistics at passing the photon sphere rim of a black hole, and the decay of unstable isolated neutron would be here much faster (neutron has larger rest mass than proton, which causes the decay not limited by fermionic nature of quarks and conversion 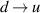 quarks will not be hampered by the presence of second u quark in a proton). This would accelerate the decay by few orders—to be consistent with time span of short giant gamma-ray burst associated with the neutron star collapse, to the order of
quarks will not be hampered by the presence of second u quark in a proton). This would accelerate the decay by few orders—to be consistent with time span of short giant gamma-ray burst associated with the neutron star collapse, to the order of  1/s, which gives the liberation of electrons and protons in the whole merger of mass 2.3 Sun masses within ca.
1/s, which gives the liberation of electrons and protons in the whole merger of mass 2.3 Sun masses within ca. 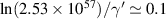 s. The following release of both antineutrinos (with time scale 10−27 s for decay of bosons W−) and photons (cf table 2) is almost instant. Such timing agrees with observations of some kind of short gamma-ray bursts (on the other hand, assuming such a scenario, one can infer about coupling for β− transition, which should be the same regardless of the change in quantum statistics).
s. The following release of both antineutrinos (with time scale 10−27 s for decay of bosons W−) and photons (cf table 2) is almost instant. Such timing agrees with observations of some kind of short gamma-ray bursts (on the other hand, assuming such a scenario, one can infer about coupling for β− transition, which should be the same regardless of the change in quantum statistics).
Table 2. The Fermi golden rule estimation of the time  of complete decay of the Fermi sphere for neutron star merger with the mass 2.3 M
of complete decay of the Fermi sphere for neutron star merger with the mass 2.3 M , as in table 1, for different photon energies
, as in table 1, for different photon energies  and for electron and proton contributions.
and for electron and proton contributions.
| Electrons | Protons | |||
|---|---|---|---|---|
 (eV) (eV) |
 (1/s) (1/s) |
 (s) (s) |
 (1/s) (1/s) |
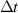 (s) (s) |
| 0.1 GeV |
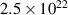
|

|

|

|
| 1 MeV |
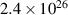
|

|

|

|
| 1 keV |

|

|

|
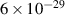
|
Protons give a bit longer burst in the range of high photon energy (though also almost instant, cf table 2), but their Fermi sphere total energy is only 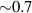 of the Fermi sphere energy of electrons (at the same Fermi momentum of both and due to larger rest mass, cf estimation in next section 4.2).
of the Fermi sphere energy of electrons (at the same Fermi momentum of both and due to larger rest mass, cf estimation in next section 4.2).
According to the presented above scheme of decay of Fermi sphere of neutrons at collapse of unstable neutron star merger, the emission of e-m radiation should be associated by preceding burst of electron-antineutrinos emitted at collective β− decomposition of neutrons. These antineutrino bursts have not been observed as of yet, what can be linked to large distances of potential candidates for collapsing neutron star mergers and almost infinitesimal interaction of antineutrinos with matter in counters.
4.2. Collapse of Fermi spheres of electrons and protons in the accretion disc of a quasar
Conventional models of quasar luminosity consider accretion disc of plasma upon classical hydrodynamic approach [10, 11, 13, 15–17]. Though such an approach reproduces many observed features of quasar radiation, especially well for micro-quasars [13], the super-luminous quasars are still not fully described [14–17]. Thermal radiation from the accretion disc [12] does not cover the observed spectrum and intensity of quasar radiation and the source of x-ray part of this radiation is conventionally assumed [13] due to Comptonization of soft photons in small region of accretion disc with extremely hot plasma. In Shapiro at al. model of microquasar Cygnus X-1 [13] the inverse Compton effect needs 109 K for electrons and 1011 K for ions in the hot bulb in accretion disc at the distance of ca.  from the center of black hole (of 15 Sun masses in this case) to match observed x-ray component of this microquasar radiation. Additionally, the sufficiently large supply of soft photons to such a small region is unclear. In the case of super-luminous quasars powered by
from the center of black hole (of 15 Sun masses in this case) to match observed x-ray component of this microquasar radiation. Additionally, the sufficiently large supply of soft photons to such a small region is unclear. In the case of super-luminous quasars powered by 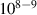 Sun mass black holes the extension of the Shapiro model is problematic, as an extremely hot region in this case would have to be 108 times larger, what is unlikely to be so hot.
Sun mass black holes the extension of the Shapiro model is problematic, as an extremely hot region in this case would have to be 108 times larger, what is unlikely to be so hot.
The decay of Fermi spheres of electrons and protons in the accretion disc of quasars at passing the photon sphere rim supplies, however, a very effective channel for conversion of gravitational energy into e-m radiation, which can solve above mentioned problems of quasar luminosity. Matter falling onto the black hole event horizon is compressed to high density, which can achieve the uppermost its stable value when the supply of the surrounding gas to the accretion disc is unlimited. Assuming an accretion disc formation from the neutral hydrogen surrounding a black hole, a plasma is electrically balanced, thus the Fermi momentum (11) for electrons and protons is the same. Using equation (13) we estimate the energy accumulated in Fermi spheres of electrons and protons at the photon sphere rim for an uppermost fermion concentration (similar as in neutron star at TOW limit) for quasar with the black hole of 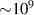 Sun mass consuming in a steady way 5.6 Sun mass per year, i.e. ca. 0.06 Earth mass per second [43]. Because of the steadiness of the process the continuous in time decay of Fermi spheres of electrons and protons can be accounted for per single second resulting in additional contribution to quasar luminosity expressed in W = J s−1. Total energy released from Fermi sphere of electrons and protons at passing the photon sphere rim (acc. to equation (13)) is just 1040 J per second with prevailing contribution of x-ray radiation, which agrees with observable luminosity of such quasars. This energy had been accumulated in Fermi spheres of electrons and protons on the cost of gravitation energy of a black hole, which compressed the matter falling onto the event horizon. At approaching the event horizon the spatial volume in proper coordinates diverse, however. Thus, for calculation of the Fermi momentum (11) the local proper concentration should be taken,
Sun mass consuming in a steady way 5.6 Sun mass per year, i.e. ca. 0.06 Earth mass per second [43]. Because of the steadiness of the process the continuous in time decay of Fermi spheres of electrons and protons can be accounted for per single second resulting in additional contribution to quasar luminosity expressed in W = J s−1. Total energy released from Fermi sphere of electrons and protons at passing the photon sphere rim (acc. to equation (13)) is just 1040 J per second with prevailing contribution of x-ray radiation, which agrees with observable luminosity of such quasars. This energy had been accumulated in Fermi spheres of electrons and protons on the cost of gravitation energy of a black hole, which compressed the matter falling onto the event horizon. At approaching the event horizon the spatial volume in proper coordinates diverse, however. Thus, for calculation of the Fermi momentum (11) the local proper concentration should be taken,  , instead of
, instead of  with
with  (
(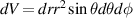 in rigid coordinates of a remote observer). For
in rigid coordinates of a remote observer). For  the renormalization factor in fermion concentration is
the renormalization factor in fermion concentration is  , which causes the reduction of pF
via equation (11) by factor
, which causes the reduction of pF
via equation (11) by factor  . This factor is still of order of unity, thus, general relativistic corrections do not change the order of energy estimation via equation (13).
. This factor is still of order of unity, thus, general relativistic corrections do not change the order of energy estimation via equation (13).
The conversion of gravitational energy at passing the photon sphere rim due to decay of Fermi spheres of electrons and protons achieves, in the exemplary considered here case, the efficiency of 30% mass to radiation energy conversion rate. It means that the compressed plasma at photon sphere rim is by 30% more massive than initial distanced hydrogen captured to the accretion disc, where this increase of the mass is the energy accumulated in Fermi spheres of electrons and protons approaching the photon sphere rim of a black hole (divided by c2), just before their release due to the decay of both Fermi spheres. The release of high energy radiation at the photon sphere rim does not interfere with radiation from more distant regions of an accretion disc and conveniently contributes to the total quasar luminosity filling a loophole in understanding of high energy radiation of super-luminous quasars [14–17].
Comparing the total Fermi sphere energies of electrons and protons with the same Fermi momentum (for the same concentration as in electrically balanced plasma in accretion disc) one can find via equation (13) that  (for
(for 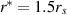 ), due to the difference in rest mass between these particles. The Fermi energy of electrons with Fermi momentum
), due to the difference in rest mass between these particles. The Fermi energy of electrons with Fermi momentum  kg m s−1 (cf table 1) equals to
kg m s−1 (cf table 1) equals to 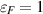 GeV (this gives the limit for uppermost possible energy of emitted photons). In the thermal scale (in units at
GeV (this gives the limit for uppermost possible energy of emitted photons). In the thermal scale (in units at 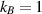 ) this energy is of order of 1013 K, which indicates that the electron liquid in compressed plasma at photon sphere rim of super-luminous quasar is quantumly degenerated at lower temperatures (quasars are not source of thermal gamma radiation, thus their actual temperatures are much lower). Similarly for protons with Fermi momentum
) this energy is of order of 1013 K, which indicates that the electron liquid in compressed plasma at photon sphere rim of super-luminous quasar is quantumly degenerated at lower temperatures (quasars are not source of thermal gamma radiation, thus their actual temperatures are much lower). Similarly for protons with Fermi momentum  kg m s−1, for which Fermi energy equals to
kg m s−1, for which Fermi energy equals to 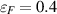 GeV (in thermal scale is of order of
GeV (in thermal scale is of order of  K)—for lower temperatures of plasma, protons also form the quantum degenerate Fermi liquid at photon sphere rim of a quasar.
K)—for lower temperatures of plasma, protons also form the quantum degenerate Fermi liquid at photon sphere rim of a quasar.
4.3. Other probable evidences for the decay of Fermi spheres at photon sphere rim
In many observable events of photon radiation from close vicinity of black holes, the rate of matter consumption is much lower than for super-luminous quasars because of limited matter supply from the black hole surroundings. To such effects belong transients of closer AGN, microquasars, and flares associated to tidal disruption events (TDEs). When the concentration of electrons and protons at the photon sphere rim does not reach its uppermost stable value, then local Fermi momentum (11) is smaller and the energy accumulated in Fermi spheres (13) is also lower. Nevertheless, the local waving off of Pauli exclusion principle still causes the Fermi sphere decay, though the efficiency of mass to radiation energy conversion is lower than 30%. In each such episode, large part of photons released according to Fermi golden rule exceeds in individual energies the thermal radiation in conventional classical models of AGN or TDEs. We refer below to the following examples of recent observations, which could be treated as a confirmation of the proposed model of Fermi sphere decay.
4.3.1. Transient AGN 1ES 1927+654.
The one year lasting 100-fold brightening of AGN 1ES 1927+654 (at z = 0.017) has been observed [20] beginning at December 2017 with optical and UV spectral components increased but gamma-ray flux decreased (by July 2018, the x-ray coronal emission had vanished, only to reappear a few months later). The source has returned to the pre-changing-look state after ca. one year in optic, UV and x-ray range. It has been conjectured [20] that the puzzling behavior of gamma-radiation has been originated by temporal quenching of jets of a spinning black hole by consumption of oppositely magnetized gas cloud in due of changing-look episode. The quantum statistics transition offers, however, an alternative explanation of the observed behavior, without speculation on jet quenching. The source of gamma radiation in the case of AGN 1ES 1927+654 is considered to be linked with electrons and positrons accelerated by magnetic field in jets of the spinning black hole according to Blandford–Znajek model of jet formation [44]. This model explains the jet formation for spinning Kerr-like black holes, where due to dragging of reference frame in Kerr metric, the magnetic field frozen into the accretion matter rotates and an outgoing flux of angular momentum results in extraction of energy to outer space. The rotating magnetic field beams in the form of jets, and electrons and positrons diffuse through nodes of the ergosphere and next are highly accelerated in a magnetic field in jets producing gamma-ray radiation. The source of electron–positron pairs in Blandford–Znajek model is a strong electrical field created by the rotating magnetic field frozen in the ergosphere.
In the case of AGN 1ES 1927+654 transient, the decay of Fermi spheres of electrons and protons from the occasionally captured gas cloud produced sub-MHz radiation (at most 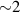 keV, in consistence with x-ray observations [20]) due to not extreme plasma compression at the photon sphere rim. These photons cannot excite additional electron–positron pairs inside the ergosphere, but can push toward the event horizon those pairs created according to Blandford–Znajek mechanism, eventually reducing their supply to jets. The resulting temporal reduction of population of electrons and positrons in jets explains transitional quenching of gamma radiation from jets without need to speculate on demagnetization of the AGN by oppositely magnetized gas cloud during this episode [20].
keV, in consistence with x-ray observations [20]) due to not extreme plasma compression at the photon sphere rim. These photons cannot excite additional electron–positron pairs inside the ergosphere, but can push toward the event horizon those pairs created according to Blandford–Znajek mechanism, eventually reducing their supply to jets. The resulting temporal reduction of population of electrons and positrons in jets explains transitional quenching of gamma radiation from jets without need to speculate on demagnetization of the AGN by oppositely magnetized gas cloud during this episode [20].
4.3.2. TDE flare AT 2020neh.
In [22] it has been reported an observation of a flare AT 2020neh, a fast rising TDE candidate, hosted by a dwarf galaxy SDSSJ152120.07+140410.5 at redshift of z = 0.06 with central black hole mass assessed to be of  Sun masses. The transient AT 2020neh has been observed since June 2020 for next 400 days, and the maximum brightness has been noticed at 1 July (lasting ca. 20 days). Both optical and UV spectra have been registered with x-ray component of
Sun masses. The transient AT 2020neh has been observed since June 2020 for next 400 days, and the maximum brightness has been noticed at 1 July (lasting ca. 20 days). Both optical and UV spectra have been registered with x-ray component of 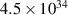 W (in maximum) (similar to other TDEs [45]) with peak of overall luminosity
W (in maximum) (similar to other TDEs [45]) with peak of overall luminosity  W. The rate of fallback of the stellar debris from the disrupted star (assuming disruption of a main sequence star, supposed of 1.3 Sun mass) has been assessed in conventional hydrodynamic model [46] and the registered optical and UV spectra allowed to fit black body temperature and cooling rate
W. The rate of fallback of the stellar debris from the disrupted star (assuming disruption of a main sequence star, supposed of 1.3 Sun mass) has been assessed in conventional hydrodynamic model [46] and the registered optical and UV spectra allowed to fit black body temperature and cooling rate 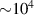 K per 20 days. No mechanism for x-ray components has been identified (no gaseous accretion disc of host galaxy black hole has been confirmed by post-flare observations and earlier survey data). However, using equation (13) for debris of disrupted star in duration of peak luminosity and upper energy of observed (by Swift) x-ray photons (10 keV) one obtains the contribution to the luminosity mostly in x-ray range of order of just
K per 20 days. No mechanism for x-ray components has been identified (no gaseous accretion disc of host galaxy black hole has been confirmed by post-flare observations and earlier survey data). However, using equation (13) for debris of disrupted star in duration of peak luminosity and upper energy of observed (by Swift) x-ray photons (10 keV) one obtains the contribution to the luminosity mostly in x-ray range of order of just 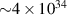 W due to the decay of Fermi spheres in ionized debris consumed by a black hole, congruent with observed spectra of TDEs [22, 45].
W due to the decay of Fermi spheres in ionized debris consumed by a black hole, congruent with observed spectra of TDEs [22, 45].
4.3.3. Transient AT 2021lwx.
It has been reported [21] an observation of the most energetic non-quasar transient ever observed, AT2021lwx (at z = 0.995) with temporal radiation luminosity increase to  W (beginning at April 2021 and lasting over one year), with lack of emission for the previous several years. The optical and UV spectral energy distribution resembled a black-body with a temperature of
W (beginning at April 2021 and lasting over one year), with lack of emission for the previous several years. The optical and UV spectral energy distribution resembled a black-body with a temperature of 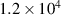 K. The large luminosity and relatively long time-scale of the transient disfavor the disruption of a single solar-mass star. AT2021lwx is supposed to represent by black hole (
K. The large luminosity and relatively long time-scale of the transient disfavor the disruption of a single solar-mass star. AT2021lwx is supposed to represent by black hole ( Sun masses) accretion of large gaseous cloud rather than TDE. The mechanism of observed x-ray component (0.3–10 keV) with the luminosity of
Sun masses) accretion of large gaseous cloud rather than TDE. The mechanism of observed x-ray component (0.3–10 keV) with the luminosity of 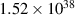 W did not find any explanation upon conventional models at such low temperature. However, including the emission due to the decay of Fermi spheres in compressed fermion systems passing the photon sphere rim of central black hole, one can accommodate the Fermi momentum (related to the compression level via equation (11) and linked to maximal observed energy of photons) and realistic supply of matter at the accretion to get the luminosity of order of
W did not find any explanation upon conventional models at such low temperature. However, including the emission due to the decay of Fermi spheres in compressed fermion systems passing the photon sphere rim of central black hole, one can accommodate the Fermi momentum (related to the compression level via equation (11) and linked to maximal observed energy of photons) and realistic supply of matter at the accretion to get the luminosity of order of 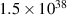 W, supplementing the total luminosity of AT2021lwx and fully explaining the x-ray part of the observed radiation.
W, supplementing the total luminosity of AT2021lwx and fully explaining the x-ray part of the observed radiation.
The described quantum transition terminates quickly after passing the rim of the photon sphere (along the Fermi golden rule, as is estimated in section 4.1)) which can improve conventional models of radiation decline at AGN transients and TDEs.
4.4. Upgrade of premises for information paradox
The problem of the fate of information (related to entropy) encoded in a matter falling to a black hole, in view of the second law of thermodynamics, leads to so-called information paradox [47–49]. It is still unsolved, because the Hawking radiation of black holes is fully stochastic [50, 51] and cannot take away entropy/information in a unitary manner. The concept of creation of particle-antiparticle pairs on the event horizon and escape of a particle associated with capturing by a black hole of its antimatter partner did not solve the problem, because of quantum entanglement property called monogamy. Particles and antiparticles are entangled and Hawking radiation must be also entangled in time, which forces the instant breaking of the entanglement at event horizon leading to the concept of a firewall [49] (immediately broken entanglement between the infalling particle and the outgoing particle would release large energy, creating in this way a searing firewall at the event horizon). Neither Hawking radiation nor firewall have been observed as of yet (some evidences of fuzzy black hole horizon in gravitational wave signature [52] have been eventually excluded [53]).
According to theoretical field models of gravitation singularity, including holographic formulation [54], the unitarity at matter consumption by black holes should be maintained, which challenges, however, Einstein's equivalence principle or existing quantum field theory [49].
The quantum statistics transition at passing the photon sphere rim, presented in this paper, seems to contribute to the debate on information paradox and related concept of a black hole firewall, updating the related premises, to some extent. The decay of quantum statics in multiparticle systems at passing the photon sphere rim removes the quantum statistics origin entanglement, as antisymmetrized wave functions for fermions or symmetrized ones for bosons were entangled nonseparable functions in tensor productive Hilbert space of all particles. The related release of energy (including that released due to local waiving off of Pauli exclusion principle) forms some kind of firewall, shifted to the photon sphere rim and visible to any distant observers, substituting a hypothetical firewall on the event horizon [49] unobservable for distant observers. Although the entropy behavior at passing the photon sphere rim needs a more thorough analysis, it is seen that energy along with entropy escapes into outer space from the the photon sphere rim in a unitary manner at quantum statistics transition, and quantum fields lose their statistics assignment beneath this rim (which should affect local quantum field theory formulation).
5. Conclusions
We have demonstrated a universal quantum property of black holes rooted in topology of gravitation singularity neighborhood. For Schwarzschild black hole the qualitative change of trajectory homotopy class takes place in vicinity of the event horizon, which modifies quantum statistics in any multiparticle system of indistinguishable identical particles when they are passing the photon sphere rim (coinciding with the innermost unstable circular orbit in Schwarzschild geometry). From trajectories of particles passing the photon sphere rim inward it is impossible to form braid loops for particle mutual interchanges using pieces of unidirectional local trajectories in form of short spirals available here. This is in contrast to outer space where conic section-like trajectories are admitted, which can form arbitrary small closed loops for particle interchanges there. This change of homotopy class of trajectories precludes assigning of quantum statistics to indistinguishable particles on local manifolds beneath the photon sphere rim. In particular, Pauli exclusion principle is waived off locally, which leads to the release of energy accumulated in Fermi spheres of dense systems of fermions entering the photon sphere.
We utilized this property to describe a burst of photon radiation associated with a collapse of unstable neutron star merger into a black hole. This radiation has been characterized via Fermi golden rule and it occurs to comply with some kind of short giant gamma-ray bursts equivalent with mass conversion into radiation with ca. 30% efficiency at neutron star merger collapse. The timing of the Fermi sphere decomposition has been assessed within Fermi golden rule scheme in the present paper developing former estimations [42, 43]. The similar mass to radiation conversion rate we demonstrated for super-luminous quasars via non-thermal radiation from the photon sphere rim of a black hole at passing it by accretion disc of plasma approaching the event horizon. The effect of decay of Fermi spheres of electrons and protons in matter falling onto black hole offers also a mechanism for generation of x-ray components of observed radiation at lower intense transients of AGN and even of flares related to TDEs, which can supplement an understanding of these observations. In particular, the presented mechanism offers an independent way for the estimation of the mass consumed by a black hole using the highest observed x-ray frequency of a particular radiation event to identify Fermi energy for electrons being a function of matter density at the photon sphere rim. Next, combining it with the overall radiation intensity we can conclude about the mass consumption rate. The proposed quantum statistics effect considerably changes also premises for information paradox of black holes, shifting a hypothetical firewall from event horizon to photon sphere rim.
In this paper we considered a multiparticle system of indistinguishable particles, which together with local manifold enters the photon sphere crossing its edge inward. For these particles the homotopy change of trajectories causes a disappearance of braid loops at passing the photon sphere rim. We did not consider other systems, like out-falling matter, which, due to some additional factors, may redirect a movement, gain sufficient energy to overcome gravitational attraction and escape from the photon sphere to outer space. It is not a mirrored case to a free in-falling at passing the photon sphere edge, as the reversion of the Fermi sphere decay needs energy and various scenarios might be possible, decrease of density to reduce quantum degeneracy or again falling down toward the event horizon. Such restrictions do not concern photons as their collective systems do not experience energy changes at passing the photon sphere rim. In addition one can also ask about blending of in-falling particles with potentially encountered out-falling systems within a photon sphere. This needs, however, the essential redefinition of the system and proper identification of indistinguishable particles. Consideration of such other systems and hypothetical situations needs independent studies exceeding the framework of the present paper.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix A: Classical trajectories and quantum statistics
Quantum statistics is assigned to identical indistinguishable particles via choice of one dimensional unitary representation of the braid group describing all possible mutual exchanges of particles on manifold  , to which the dynamics of particles is confined. The braid group is the first homotopy group π1 [55] of the multiparticle configuration space, i.e.
, to which the dynamics of particles is confined. The braid group is the first homotopy group π1 [55] of the multiparticle configuration space, i.e.  , where
, where  is the configuration space of N identical indistinguishable particles located on
is the configuration space of N identical indistinguishable particles located on 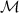 (as defined in section 2.2). The linkage of scalar unitary representations of a braid group with quantum statistics is visible from quantization by path integrals. Feynman path integral written for a system of N identical indistinguishable particles has the form [29, 32, 56–59],
(as defined in section 2.2). The linkage of scalar unitary representations of a braid group with quantum statistics is visible from quantization by path integrals. Feynman path integral written for a system of N identical indistinguishable particles has the form [29, 32, 56–59],
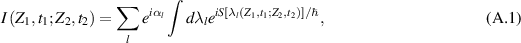
and it defines the propagator (matrix element of the quantum evolution operator in position representation [60, 61]) between points  and
and  in the space FN
at time t1 and t2, respectively.
in the space FN
at time t1 and t2, respectively. ![$S[\lambda_l(Z_1,t_1;Z_2,t_2)]$](https://content.cld.iop.org/journals/0264-9381/41/3/035006/revision2/cqgad1a53ieqn240.gif) is the action functional on the domain of trajectories linking Z1 and Z2. The trajectory
is the action functional on the domain of trajectories linking Z1 and Z2. The trajectory  is assigned with the discrete index l numbering braids from the braid group for considered system and it means that to the open trajectory is attached a certain braid loop, which displays possibility of exchanges of indistinguishable particles on the way between start and final points in FN
. Braid groups are countable as multicyclic groups with finite number of generators, thus l is discrete. Braids are nonhomotopic (cannot be deformed one into another in a continuous way without cutting), hence, the domain of trajectories splits into disjoint sectors numbered by l, and due to the requirement of continuity for the measure in path space, the measure must be independently defined on each sector, which results in countable family of measures
is assigned with the discrete index l numbering braids from the braid group for considered system and it means that to the open trajectory is attached a certain braid loop, which displays possibility of exchanges of indistinguishable particles on the way between start and final points in FN
. Braid groups are countable as multicyclic groups with finite number of generators, thus l is discrete. Braids are nonhomotopic (cannot be deformed one into another in a continuous way without cutting), hence, the domain of trajectories splits into disjoint sectors numbered by l, and due to the requirement of continuity for the measure in path space, the measure must be independently defined on each sector, which results in countable family of measures 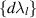 . All sectors must be taken into account, thus, separate path integrals form each sector must be added together with arbitrary scalar unitary weight factors
. All sectors must be taken into account, thus, separate path integrals form each sector must be added together with arbitrary scalar unitary weight factors  ,
, 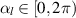 (due to causality of quantum mechanics). These unitary factors form a one dimensional unitary representation of the braid group [32]. The choice of this representation of the braid group defines quantum statistics in a multiparticle system.
(due to causality of quantum mechanics). These unitary factors form a one dimensional unitary representation of the braid group [32]. The choice of this representation of the braid group defines quantum statistics in a multiparticle system.
For the problem of the existence of braids, the key question is which trajectories (including braids) contribute to path integrals. This is defined by the domain of the measure in path space. This measure is a generalization of the Wiener measure [62] in stochastic processes applied earlier to Brownian motion study [61], next extended for complex integrand by Feynman [60]. The resulted restrictions for trajectories specify what does a popular, but not a precise term, 'summation over all trajectories', mean. As pointed out in [60] chapters 2–4, not arbitrary trajectories contribute to path integral but only those, which can be obtained via a time discretization and built of classically attainable trajectory pieces on consecutive time discretization sectors (infinitesimal in limit), matched together into a piece-wise continuous but not smooth paths. When real trajectories do not exist on some time-discretization sectors, then related paths cannot be constructed and do not contribute to the measure domain in path space. This has been noticed first by Pauli [61] and can be applied to equation (A.1). Therefore, if closed braid loops cannot be constructed from pieces of real trajectories in FN , as it happens beneath the photon sphere rim of a black hole, then the sum over l disappears from (A.1), which means that quantum particles are locally devoid of statistics.
Appendix B: Pauli theorem on connection between statistics and spin
According to Pauli theorem on spin-statistics connection [63], quantum statistics of particles with half spin must be of fermionic type, whereas of particles with integer spin of bosonic type. A proof of this theorem is provided only for noninteracting particles [64, 65], taking advantage from the fact that within the Dirac electrodynamics for 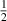 spin particles, the Hamiltonian formulation is admitted for simultaneously particles and antiparticles and positively defined kinetic energy of free particles requires anticommutation of field operators of particles and antiparticles, causing their fermionic statistics. Pauli theorem holds, however, also for interacting particles, which is noticeable in terms of topology, basing on topological ground for quantum statistics definition [32, 57, 66]. Pauli theorem is the consequence of the coincidence of unitary irreducible representations of the rotation group and of the braid group, which overlap on some elements. The representation of the rotation group defines quantized spin [67], whereas the braid group determines quantum statistics [31, 32]. The representations agree on group generators, thus are the same for whole groups. For 3D manifolds the rotation group O(3) is covered by SU(2) group, which has only two classes of irreducible unitary representations assigning integer and half-integer angular momenta. These classes agree with two admissible scalar unitary representations of the braid group (SN
in 3D). Half-integer spin must coincide thus with fermionic statistics, while integer one with bosonic statistics. The topological approach allows for the extension of Pauli theorem also on anyons, which, in general, are neither fermions nor bosons. For 2D manifolds the rotation symmetry is governed by Abelian O(2) group isomorphic with U(1) group. The latter group does not cause quantization of spin in 2D space, as U(1) has the continuous unitary representations
spin particles, the Hamiltonian formulation is admitted for simultaneously particles and antiparticles and positively defined kinetic energy of free particles requires anticommutation of field operators of particles and antiparticles, causing their fermionic statistics. Pauli theorem holds, however, also for interacting particles, which is noticeable in terms of topology, basing on topological ground for quantum statistics definition [32, 57, 66]. Pauli theorem is the consequence of the coincidence of unitary irreducible representations of the rotation group and of the braid group, which overlap on some elements. The representation of the rotation group defines quantized spin [67], whereas the braid group determines quantum statistics [31, 32]. The representations agree on group generators, thus are the same for whole groups. For 3D manifolds the rotation group O(3) is covered by SU(2) group, which has only two classes of irreducible unitary representations assigning integer and half-integer angular momenta. These classes agree with two admissible scalar unitary representations of the braid group (SN
in 3D). Half-integer spin must coincide thus with fermionic statistics, while integer one with bosonic statistics. The topological approach allows for the extension of Pauli theorem also on anyons, which, in general, are neither fermions nor bosons. For 2D manifolds the rotation symmetry is governed by Abelian O(2) group isomorphic with U(1) group. The latter group does not cause quantization of spin in 2D space, as U(1) has the continuous unitary representations 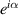 ,
,  . The same scalar unitary representations posses also the Artin group [31, 33, 34], which is the braid group for
. The same scalar unitary representations posses also the Artin group [31, 33, 34], which is the braid group for  . Due to required representation coincidence, in 2D spaces Pauli theorem also holds though for not quantized spin
. Due to required representation coincidence, in 2D spaces Pauli theorem also holds though for not quantized spin  ,
,  , where α defines simultaneously specific for s fractional statistics of related anyons [30].
, where α defines simultaneously specific for s fractional statistics of related anyons [30].
Quantum statistics and spin are in fact independent to some extent. The coincidence of representations of rotation and braid groups requires the existence of both groups. In the case when the nontrivial braid group does not exist, as for 3D local manifolds beneath the photon sphere rim of a black hole, the quantum statistics of indistinguishable particles is not assigned to particles with local dynamics confined to such manifolds, regardless of spin quantization.
Appendix C: Derivation of formula (19)
For initial and final states in Fermi golden rule (14) one can assume states
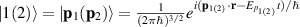 normalized on the Dirac delta and representing states in the isotropic Fermi sphere for
normalized on the Dirac delta and representing states in the isotropic Fermi sphere for  , or equivalent states
, or equivalent states
 normalized on the finite volume
normalized on the finite volume  . The advantage of such a change is the discretization of quantum numbers p and substitution of momentum Dirac delta in equation (17) by Kronecker delta, for which its square in equation (14) is equal to itself. To be specific, the matrix element (17) for wave functions normalized on the finite volume
. The advantage of such a change is the discretization of quantum numbers p and substitution of momentum Dirac delta in equation (17) by Kronecker delta, for which its square in equation (14) is equal to itself. To be specific, the matrix element (17) for wave functions normalized on the finite volume  has the form,
has the form,
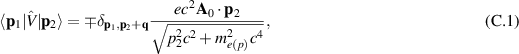
where  is the Kronecker delta. Thus, the probability
is the Kronecker delta. Thus, the probability  attains the form (according to equation (14)),
attains the form (according to equation (14)),
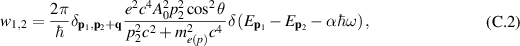
where  .
.
To obtain the probability (per time unit) of the decay of all states in the Fermi sphere, the sum over occupied states  must be performed. The sum over p1 cancels the Kronecker delta and causes substitution of p1 by
must be performed. The sum over p1 cancels the Kronecker delta and causes substitution of p1 by  . The next sum over p2 is as follows,
. The next sum over p2 is as follows,
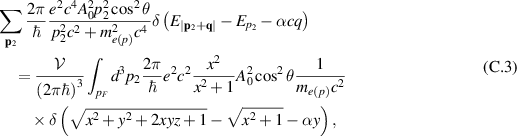
as 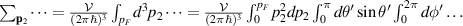 (mutual orientation of vectors is shown in figure C1). In above equation the Dirac delta of energy
(mutual orientation of vectors is shown in figure C1). In above equation the Dirac delta of energy  is rewritten in dimensionless variables
is rewritten in dimensionless variables  ,
,  and
and 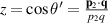 .
.
Figure C1. Mutual orientation of vectors A0, p2 and  .
.
Download figure:
Standard image High-resolution imageHence, we obtain,

which leads to the expression,
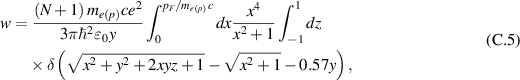
which is the same as equation (19) obtained at normalization of wave functions on the Dirac delta. We have taken into account that averaging over polarization, i.e. the integer  (where
(where  and
and  is the solid angle in spherical angular coordinates when p2 is oriented along z direction).
is the solid angle in spherical angular coordinates when p2 is oriented along z direction).