Abstract
We present fitting formulae for the dynamical ejecta properties and remnant disk masses from the largest to date sample of numerical relativity simulations. The considered data include some of the latest simulations with microphysical nuclear equations of state (EOS) and neutrino transport as well as other results with polytropic EOS available in the literature. Our analysis indicates that the broad features of the dynamical ejecta and disk properties can be captured by fitting expressions, that depend on mass ratio and reduced tidal parameter. The comparative analysis of literature data shows that microphysics and neutrino absorption have a significant impact on the dynamical ejecta properties. Microphysical nuclear EOS lead to average velocities smaller than polytropic EOS, while including neutrino absorption results in larger average ejecta masses and electron fractions. Hence, microphysics and neutrino transport are necessary to obtain quantitative models of the ejecta in terms of the binary parameters.
Export citation and abstract BibTeX RIS
1. Introduction
The UV/optical/NIR transient AT2017gfo [1–14], counterpart of the gravitational-wave signal GW170817 [15–18], is explained as the kilonova signal from the radioactive decay of r-process elements synthesized in the mass ejected during binary neutron star mergers [10, 19–32]. Minimal models of the kilonova AT2017gfo require at least two ejecta components to account for the observed light curves: a lanthanide-poor (for the blue signal) and a lanthanide-rich (for the red signal) one [10, 28–32]. These components are often identified as the dynamical ejecta and the wind ejecta from the remnant disk, although simulations clearly indicate that this interpretation is not complete e.g. [33, 34].
Mass ejection in mergers can be triggered by different mechanisms acting on different timescales (see [35–38] for reviews on various aspects of the problem). Simulations robustly identify dynamical ejecta, of mass  launched during merger at average velocities ⟨v∞⟩ ∼ 0.1–0.3c, e.g. [23, 24, 39–45], and (for many fiducial postmerger configurations) more massive but slower winds launched on secular timescales from the remnant disk [33, 46–58]. The most accurate approach to compute the dynamical ejecta and the remnant evolution is to employ ab initio 3 + 1 simulations in numerical relativity (NR), e.g. [39, 41–45, 59–68]. The increasing amount of data (both in terms of simulated binaries, physics input and numerical resolutions) allows us to explore the dependencies of ejecta and remnant properties on the binary parameters. Fitting formulae of NR data for the dynamical ejecta and remnant disk properties from binary neutron star mergers have been previously presented in [64, 69, 70]. The interest in these formulae is at least twofold. On the one hand, they can be used to identify the main parametric dependencies of the ejecta mechanisms; on the other hand, they can be employed to constrain the source parameters from kilonova observations, e.g. [31, 71–73]. Additionally, they are key to predict the amount and the properties of the ejecta that enter chemical evolution models, e.g. [74].
launched during merger at average velocities ⟨v∞⟩ ∼ 0.1–0.3c, e.g. [23, 24, 39–45], and (for many fiducial postmerger configurations) more massive but slower winds launched on secular timescales from the remnant disk [33, 46–58]. The most accurate approach to compute the dynamical ejecta and the remnant evolution is to employ ab initio 3 + 1 simulations in numerical relativity (NR), e.g. [39, 41–45, 59–68]. The increasing amount of data (both in terms of simulated binaries, physics input and numerical resolutions) allows us to explore the dependencies of ejecta and remnant properties on the binary parameters. Fitting formulae of NR data for the dynamical ejecta and remnant disk properties from binary neutron star mergers have been previously presented in [64, 69, 70]. The interest in these formulae is at least twofold. On the one hand, they can be used to identify the main parametric dependencies of the ejecta mechanisms; on the other hand, they can be employed to constrain the source parameters from kilonova observations, e.g. [31, 71–73]. Additionally, they are key to predict the amount and the properties of the ejecta that enter chemical evolution models, e.g. [74].
Here we employ an extended set of data presented in previous works that includes also recent simulations with approximate neutrino transport and large mass ratios [34, 65, 68, 75].
We re-calibrate the fit models proposed in the literature with this extended dataset. Additionally we test simple polynomials as fitting models for the ejecta mass, velocity, and electron fraction.
Throughout the paper we label the two NSs with subscripts A, B. The individual gravitational masses are indicated as MA , MB , the baryonic masses as Mb A , Mb B , the total mass as M = MA + MB , and the mass ratio q = MA /MB ⩾ 1.
We define the quadrupolar tidal parameters as  where
where  is the dimensionless gravitoelectric Love number [78], Ci
≡ GMA
/(c2
RA
) the compactness parameter, and i = A, B. The reduced tidal parameter [79] is:
is the dimensionless gravitoelectric Love number [78], Ci
≡ GMA
/(c2
RA
) the compactness parameter, and i = A, B. The reduced tidal parameter [79] is:
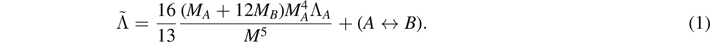
We use CGS units except for masses and velocities, given in units of M⊙ and c, respectively.
2. Data and method
The datasets used in this paper are summarized in table 1. We group them with respect to the employed neutrino treatment:
-
M0/M1Set comprises a set of models with neutrino emission and absorption and microphysical EOS. It includes 8 models with leakage + M0 of [64] and models of [42, 44, 45] in which a leakage + M1 scheme or an M1 gray scheme are employed for the neutrino transport. Models reported in these works span q ∈ [1, 1.30],
![$\tilde{{\Lambda}}\in [340,1437]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , Mtot ∈ [2.52, 2.88], and Mchirp ∈ [1.10, 1.25].
, Mtot ∈ [2.52, 2.88], and Mchirp ∈ [1.10, 1.25]. -
M0RefSet harbors models with similar physical setup as those of M0/M1Set (specifically, they were computed with the same setup as models with leakage + M0 neutrino scheme of [64]). Presented in [34, 65, 68, 75] these models are uniform in terms of the numerical setup, code and physics and have fixed chirp mass. For that reason we group them into a separate, reference dataset. The models of this set span q ∈ [1, 1.82],
![$\tilde{{\Lambda}}\in [400,850]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , Mtot ∈ [2.73, 2.88] with the chirp mass Mchirp = 1.19.
, Mtot ∈ [2.73, 2.88] with the chirp mass Mchirp = 1.19. -
LeakSet comprises models with leakage scheme as neutrino treatment and microphysical EOS. The dataset includes a subset of models from [64] (35 runs denoted as LK), and the set of models from [63]. The models in this dataset span q ∈ [1, 1.31],
![$\tilde{{\Lambda}}\in [116,1688]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , Mtot ∈ [2.40, 3.42], and Mchirp ∈ [1.04, 1.49].
, Mtot ∈ [2.40, 3.42], and Mchirp ∈ [1.04, 1.49]. -
NoNusSet is composed of models with piecewise-polytropic EOSs [40, 59, 60, 66, 77], in which temperature effects are approximated by a gamma-law pressure contribution, while composition and weak effects are neglected. The models in this dataset span q ∈ [1, 2.06],
![$\tilde{{\Lambda}}\in [50,3196]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , Mtot ∈ [2.4, 4.0], and Mchirp ∈ [1.04, 1.74].
, Mtot ∈ [2.4, 4.0], and Mchirp ∈ [1.04, 1.74].
Table 1. Datasets with the dynamical ejecta data and disk masses employed in this work. The available data is shown in the columns starting from the fourth, that contain: gravitational mass of the binary, baryonic mass of the binary, reduced tidal parameter, ejecta mass, ejecta velocity, ejecta electron fraction, disk/torus mass. EOS are either microphysical or piecewise polytropic (PWP). Neutrino schemes are: leakage, leakage + M0 or M1 for free streaming neutrinos, or M1. The compiled data are available online at [76].
| Reference | EOS | Neutrinos | M | Mb |
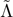
| Mej | υej | Ye | Mdisk | Dataset |
|---|---|---|---|---|---|---|---|---|---|---|
| [65] | Micro | Leak + M0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | M0RefSet & M0/M1Set |
| [75] | Micro | Leak + M0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | M0RefSet & M0/M1Set |
| [68] | Micro | Leak + M0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | M0RefSet & M0/M1Set |
| [34] | Micro | Leak + M0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | M0RefSet & M0/M1Set |
| [45] | Micro | M1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | M0/M1Set |
| [42] | Micro | Leak + M1 | ✓ | ✗ | ✗ | ✓ | ✗ | ✓ | ✗ | M0/M1Set |
| [44] | Micro | Leak + M1 | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | M0/M1Set |
| [64] (M0) | Micro | Leak + M0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | M0/M1Set |
| [63] | Micro | Leak | ✓ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | LeakSet |
| [64] (LK) | Micro | Leak | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | LeakSet |
| [66] | PWP | — | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | NoNusSet |
| [77] | PWP | — | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | NoNusSet |
| [77] | PWP | — | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | NoNusSet |
| [59] | PWP | — | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | NoNusSet |
| [40] | Micro | — | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | NoNusSet |
In total we collect 324 models. For 271 of them we have/compute the binary parameters required for the analysis. For all of them the ejecta mass, Mej, is available. For the models in [66] the ejecta velocity is not reported, thus only for 246 models the mass-averaged ejecta velocity, ⟨v∞⟩, is given. In addition to NoNusSet models, the average electron fraction of the ejecta is not provided also in [63]. Hence, there are 99 models for which the mass-averaged electron fraction of the dynamical ejecta, ⟨Ye⟩, is available. Finally, for 76 models the root mean square (RMS) half opening angle of the outflow about the equatorial plane, ⟨θRMS⟩, is available. The disk mass, Mdisk, is provided for 119 models.
Since uncertainties estimates are not available for all datasets, we assign errors following reference [64], that were motivated by the observed resolution dependency of ejecta properties. Different error measures, if adopted consistently, do not change results qualitatively, as we show in the case of M0RefSet in appendix

For the ejecta velocity and for the electron fraction we consider Δυej = 0.02c and ΔYe = 0.01 as fiducial uncertainties, respectively. The latter value is justified by the robust behavior of the average electron fraction in simulations where multiple resolutions are available 8 .
For the disk mass we assume [64]
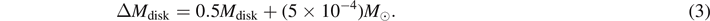
In this paper we aim to asses (i) the quality of the various fitting formulae to the ejecta properties and the disk mass. Because of the limited number of simulations in datasets, and having in mind multimessenger applications, instead of analyzing each dataset individually, in the main text we employ the following strategy. We study the progressively larger sample of simulations by iteratively adding datasets, starting from M0RefSet. The order in which we add the datasets is governed by the complexity of the physical setup, i.e. M0/M1Set, LeakSet and finally NoNusSet. By progressively including datasets into the analysis we provide a suite of possible calibrations that can either contain the simulations with the most advanced physics input but relatively small number of them (i.e. M0RefSet and M0/M1Set), or all the simulations available. Using the standard statistical methods we rank the fitting formulae and discuss their application. Additionally, we assess (ii) how the progressive inclusion changes the statistical properties of the enlarged set of simulations, aiming to assess the impact that simulating microphysics and neutrino transport has on the ejecta properties. Finally, we elaborate on which fitting formula and what calibration are favorable based on our analysis in the discussion and directly apply it to modeling the key kilonova properties.
For (i) we consider the fitting formulae that exist in the literature as well as new fitting formulae based on simple polynomials in the key BNS parameters i.e. reduced tidal deformability,  , and mass ratio, q. Then we perform a standard fitting procedure with least square method, minimizing the residuals and display the fit performance on the residual plots for every quantity. To quantitatively gauge the fit performance (for each ejecta property) we employ the sum of squared residuals (SSR) defined as
, and mass ratio, q. Then we perform a standard fitting procedure with least square method, minimizing the residuals and display the fit performance on the residual plots for every quantity. To quantitatively gauge the fit performance (for each ejecta property) we employ the sum of squared residuals (SSR) defined as  and the reduced χ2 statistics:
and the reduced χ2 statistics:
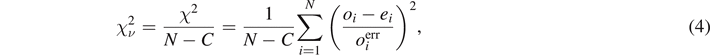
where N is the number of points in the dataset, C is the number of coefficients in the fitting model (thus N − C defines the number of degrees of freedom), oi
are the dataset values and  their errors, ei
are the values predicted by the fitting model, and oi
− ei
are the residuals. The model comparison thus states that the lower SSR is and the closer to
their errors, ei
are the values predicted by the fitting model, and oi
− ei
are the residuals. The model comparison thus states that the lower SSR is and the closer to  is, the better the model performs. Note: a fit with the lowest
is, the better the model performs. Note: a fit with the lowest  may not necessarily be the fit with the lowest residuals if the error measure is not constant, e.g. for Mej and Mdisk. This allows us to further asses the influence of the error measure.
may not necessarily be the fit with the lowest residuals if the error measure is not constant, e.g. for Mej and Mdisk. This allows us to further asses the influence of the error measure.
This procedure is repeated for every dataset added. We provide the calibration for all fitting formulae and for all sets of datasets. We also perform the analysis for all datasets individually. Results, reported in appendix
For (ii) we employ the following procedure. We start with the set that is uniform in physics and code, the M0RefSet that covers a narrow range in parameter space and allows to establish the base line. Then we add the rest of the models with neutrino heating and cooling effects, the M0/M1Set, and asses how the basic statistical properties have changed, employing the simplest quantitative measure that characterizes a statistical ensemble, and standard deviation. To investigate the effects of the absence of neutrino reabsorption, we add the dataset that does not include this effect, the LeakSet and repeat the analysis. Finally, to asses the effect of the absence of neutrino cooling and differences in the EOS treatment we repeat the analysis with all datasets, including the NoNusSet. This iterative procedure allows to gauge the qualitative effect that different physical treatments have of the statistical behavior of the ejecta parameters and disk mass. We leave a more rigorous quantitative analysis to future works, when larger sample of data with physically motivated error measures and that cover a broader range in parameter space becomes available.
3. Dynamical ejecta
The mechanism behind the production of dynamical ejecta as well as the details on the NR simulations of M0RefSet are discussed in e.g. [34, 37, 38]. Here, we focus on overall properties of the mass ejecta in relation to other results in the literature, and provide approximate fitting formulae for the total ejecta mass, the mass-averaged velocity, the electron fraction and the RMS half opening angle. Importantly, the are several criteria for a fluid element to become gravitationally unbound—to become ejecta. Due to the 'burst-like' nature of dynamical ejecta, the geodesic criterion, that considers fluid elements moving on ballistic trajectories, neglecting the fluid pressure [83], is commonly employed [43, 64, 68]. Another broadly used criterion is the Bernoulli criterion, that takes into account the internal energy of the fluid. With respect to the dynamical ejecta, these two criteria was found to lead to the ejecta mass estimations different by a factor of 2 [84]. Additionally, depending on the length of the postmerger evolution of a simulation, different methods are employed to compute the ejecta properties. For instance, in [64], the ejecta was computed following the matter passing an extraction sphere until the matter flux subsided. Simulations were sufficiently long to allow the mass flux to saturate. Meanwhile in [45], a combination ejecta that was able to leave the simulation domain and that was still within the domain of the simulation at the end was considered. These differences in ejecta criteria and method of calculation present an additional source of systematics in data.
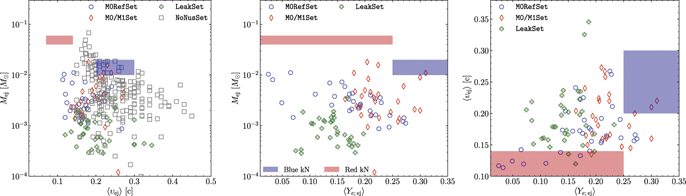
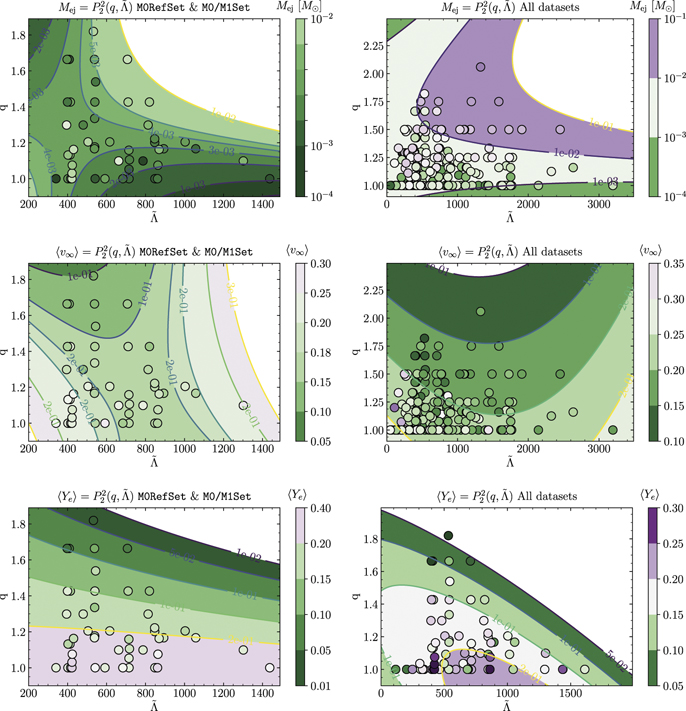
Figure 1 summarizes the total mass, the mass-averaged velocity and mass-averaged electron fraction (where available) for the used datasets. Overall we note that the ejecta properties of the models of M0RefSet are compatible with those of M0/M1Set, as they include the same physics with respect to the EOS treatment and also include the effect of neutrino absorption. Notably, the very high mass-ratio, q, models of M0RefSet, discussed in [68], show slightly different properties, as their ejecta is of tidal origin only. Comparing the properties of M0/M1Set and LeakSet we observe that neutrino absorption leads, on average, to a larger ejecta mass, which is especially noticeable for the leakage subset of [64] (LK). Additionally, neutrino absorption leads to a higher ⟨Ye⟩ of the ejecta, while the average velocity, ⟨v∞⟩, appears to be independent of it.
Figure 1. Summary of dynamical ejecta properties used in this work. Blue circles represent models of M0RefSet, red diamonds stands for models from M0/M1Set, green crosses are models from LeakSet and gray squares stand for models from NoNusSet, we show for comparison the two-component fit to AT2017gfo as colored patches from [29, 80].
Download figure:
Standard image High-resolution imageIn the following we discuss the fitting formulae for the different quantities.
3.1. Mass
In order to asses the systematic changes in ejecta masses between different datasets with different physics input, we restrict the binary parameter space to q ∈ (1, 1.2) and  , common for all datasets that we compare. In doing so we reduce the number of simulations significantly. Thus, we aim to assess the changes on the qualitative level only. A more rigorous analysis would require significantly larger sample of simulations, homogeneously distributed in the parameter space. The dynamical ejecta mass, averaged over 8 simulations of M0RefSet is
, common for all datasets that we compare. In doing so we reduce the number of simulations significantly. Thus, we aim to assess the changes on the qualitative level only. A more rigorous analysis would require significantly larger sample of simulations, homogeneously distributed in the parameter space. The dynamical ejecta mass, averaged over 8 simulations of M0RefSet is  where hereafter we report also the standard deviation computed over the relevant simulation sample
9
.
where hereafter we report also the standard deviation computed over the relevant simulation sample
9
.
Adding the rest of M0/M1Set (7 models) we obtain (5.1 ± 3.9) × 10−3
M⊙. The increase is given largely by datasets that include the M1 neutrino scheme [44, 45]. However, adding models of LeakSet, (another 8 models) we observe that the mean value decreases to 3.8 × 10−3
M⊙, as models without neutrino absorption predict, on average, lower ejecta masses. Finally, adding models without neutrinos at all, some of which have polytropic EOS (7 models in the restricted parameter space), we do not observe change in the  .
.
Lifting the restrictions on the parameter space, we fit all the available data using second-order polynomials in one parameter  , and in two parameters,
, and in two parameters,  , namely:
, namely:

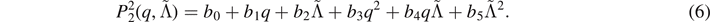
Additionally, we consider the fitting model presented references [64, 69, 85]

and the model presented in [70]:
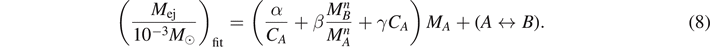
As in some cases the values of Mej change by orders of magnitude for very close values of q and  , we calibrate the fitting models to log10(Mej) instead of the Mej.
, we calibrate the fitting models to log10(Mej) instead of the Mej.
Regarding equations (7) and (8), we also note that these formulae deliver ill-conditioned fits, with coefficients that change up to a factor of two for the same data, depending on the guesses or on the nonlinear fitting algorithm employed. While such formulae may allow to account for a non-smooth behavior in data, their calibration presents an additional challenge.
Fitting coefficients as well as values of  are reported in appendix
are reported in appendix
Different fits for the dynamical ejecta properties are compared in terms of the SSR, in table 2. We find that fitting the data from only M0RefSet as well as all the data from all datasets combined, the lowest SSR is given by  . The equation (8) gives similar, albeit slightly larger values for these sets of simulations, while performing slightly better for the other two combinations of datasets. Invoking the error measure and the
. The equation (8) gives similar, albeit slightly larger values for these sets of simulations, while performing slightly better for the other two combinations of datasets. Invoking the error measure and the  statistic we observe a very similar picture with
statistic we observe a very similar picture with  giving the lowest
giving the lowest  when all datasets are considered and equation (8) performing better when only M0/M1Set and M0RefSet are considered. The small difference in performance between these two fitting formulae can be attributed to the fact that both include the mass ratio explicitly, which allows to capture the leading trend in the data.
when all datasets are considered and equation (8) performing better when only M0/M1Set and M0RefSet are considered. The small difference in performance between these two fitting formulae can be attributed to the fact that both include the mass ratio explicitly, which allows to capture the leading trend in the data.
Table 2. Values of SSR for different fitting models for the dynamical ejecta properties. Mean is the simulation average, Pn (x, y) is a polynomial of order n in the variables x, y. Fits are performed for the data of this work and for an increasingly larger combined dataset from the literature. See text for discussion. The best fitting model for a given dataset is characterized by the lowest value of SSR.
| log10(Mej) | Datasets | Mean | Equation (7) | Equation (8) |
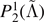
|
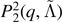
|
|---|---|---|---|---|---|---|
| M0RefSet | 2.57 | 1.65 | 1.40 | 2.43 | 0.97 | |
| & M0/M1Set | 8.19 | 7.51 | 6.35 | 7.84 | 6.55 | |
| & LeakSet | 33.13 | 26.37 | 21.57 | 29.62 | 24.40 | |
| & NoNusSet | 86.93 | 80.08 | 63.38 | 86.85 | 55.09 |
| ⟨vej⟩ | Datasets | Mean | Equation (9) |

|
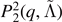
|
|---|---|---|---|---|---|
| M0RefSet | 0.04 | 0.02 | 0.04 | 0.01 | |
| & M0/M1Set | 0.09 | 0.05 | 0.07 | 0.04 | |
| & LeakSet | 0.29 | 0.24 | 0.25 | 0.21 | |
| & NoNusSet | 0.78 | 0.66 | 0.74 | 0.67 |
| ⟨Ye⟩ | Datasets | Mean |
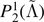
|
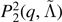
|
|---|---|---|---|---|
| M0RefSet | 0.14 | 0.13 | 0.02 | |
| & M0/M1Set | 0.24 | 0.23 | 0.06 | |
| & LeakSet | 0.35 | 0.35 | 0.23 |
| ⟨θRMS⟩ | Datasets | Mean |
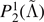
|
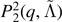
|
|---|---|---|---|---|
| M0RefSet | 2775 | 2631 | 498 | |
| & M0/M1Set | 2949 | 2788 | 574 | |
| & LeakSet | 4681 | 4116 | 2382 |
The equation (7) cannot sufficiently well reproduce the low ejecta masses of models with microphysic EOS and leakage neutrino transport scheme and high ejecta masses of models with polytropic EOS and no neutrino transport. This results in the truncated Mej;fit (see figure 2) and larger SSR and  . In addition, it was previously found in [64], that this fit model does not accurately reproduce the data and misses systematic trends. The simplest model, a polynomial of only
. In addition, it was previously found in [64], that this fit model does not accurately reproduce the data and misses systematic trends. The simplest model, a polynomial of only  , cannot capture leading trends in the data, resulting in considerably larger SSR and
, cannot capture leading trends in the data, resulting in considerably larger SSR and  once all datasets are considered. Similarly, taking the simple mean value as a fitting model results in an even larger SSR and
once all datasets are considered. Similarly, taking the simple mean value as a fitting model results in an even larger SSR and  . Thus, the inclusion of the dependency on mass-ratio is of crucial importance for modeling dynamical ejecta mass.
. Thus, the inclusion of the dependency on mass-ratio is of crucial importance for modeling dynamical ejecta mass.
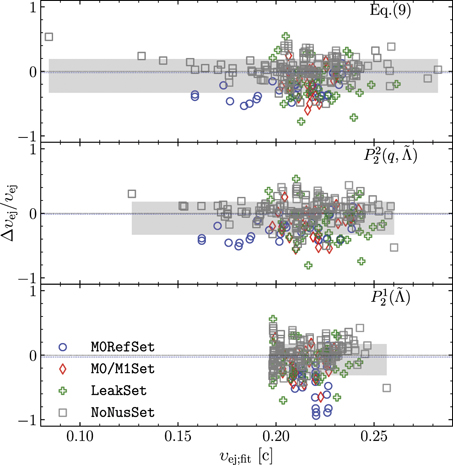
Figure 2. Relative differences between data and fits for the dynamical ejecta mass,  . We show polynomial fits and fitting formulae equations (7) and (8) calibrated with all datasets available. From top to bottom the models arrange based on their SSR: from lowest to highest see table 2. The gray region represents the fit's 68% confidence level. Note that fitting was performed minimizing log10(Mej). See text for details.
. We show polynomial fits and fitting formulae equations (7) and (8) calibrated with all datasets available. From top to bottom the models arrange based on their SSR: from lowest to highest see table 2. The gray region represents the fit's 68% confidence level. Note that fitting was performed minimizing log10(Mej). See text for details.
Download figure:
Standard image High-resolution imageIn figure 2 we show the relative differences between all datasets values and values from the fitting models. We observe that none of the fitting models can adequately capture the subset of LeakSet with a leakage scheme only as neutrino treatment, (cf [63, 64]). While the lowest SSR and  are found for
are found for  , the plot shows that the equation (8) can also capture the large ejecta mass of NoNusSet and M0RefSet with however higher residuals. Notably equation (7) cannot capture that tail, truncating the distribution at ∼10−2
M⊙. The polynomial in
, the plot shows that the equation (8) can also capture the large ejecta mass of NoNusSet and M0RefSet with however higher residuals. Notably equation (7) cannot capture that tail, truncating the distribution at ∼10−2
M⊙. The polynomial in  fits the data very poorly, showing an almost flat distribution around the mean value of the ejecta mass.
fits the data very poorly, showing an almost flat distribution around the mean value of the ejecta mass.
3.2. Mass-averaged velocity
The mass-averaged terminal velocity of the dynamical ejecta, ⟨v∞⟩, from M0RefSet ranges from 0.11c to 0.27c, in agreement with the leakage simulations performed with the same code in [64]. However, differently from the analysis of [64], the correlation of the ⟨υ∞⟩ with the tidal parameter  was found in the models of M0RefSet with the fixed chirp mass [34]. Models with lower
was found in the models of M0RefSet with the fixed chirp mass [34]. Models with lower  , showed higher velocities. This is a consequence of the fact that the dynamical ejecta in comparable-mass mergers are dominated by the shocked component and that the shock velocity is larger the more compact the binary is. On the contrary, for high mass ratios q ≳ 1.5, the ejecta are dominated by the tidal component and a larger q leads to a smaller ⟨v∞⟩ in M0RefSet.
, showed higher velocities. This is a consequence of the fact that the dynamical ejecta in comparable-mass mergers are dominated by the shocked component and that the shock velocity is larger the more compact the binary is. On the contrary, for high mass ratios q ≳ 1.5, the ejecta are dominated by the tidal component and a larger q leads to a smaller ⟨v∞⟩ in M0RefSet.
Restricting the parameter space again, we asses the change in mean value of ejecta velocity,  . For the models of M0RefSet we find
. For the models of M0RefSet we find  . When we iteratively add models of M0/M1Set, LeakSet and NoNusSet, the
. When we iteratively add models of M0/M1Set, LeakSet and NoNusSet, the  remains largely unchanged, taking values of 0.20c, 0.20c and 0.21c. Notably, figure 1, shows that some models of NoNusSet (models of cf [40])
10
have an overall larger velocity. However, they lie outside of the restricted parameter space.
remains largely unchanged, taking values of 0.20c, 0.20c and 0.21c. Notably, figure 1, shows that some models of NoNusSet (models of cf [40])
10
have an overall larger velocity. However, they lie outside of the restricted parameter space.
Lifting the restrictions on the parameter space we fit the data with a second-order polynomials, as in equation (5), and also with the fit formula reported in [64, 77]:
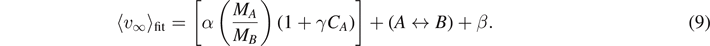
We note, that similarly to the equations (7) and (8), the outcome of the calibration of the equation (9) depends on the initial guesses of the minimization algorithm.
The coefficients of the polynomial regressions for ⟨v∞⟩ are reported in table 4; fits coefficients for equation (9) are reported in table 5. The fit models' performance is summarized in table 2 in terms of SSR.
We find that unless models of NoNusSet are included, the  displays the lowest SSR and
displays the lowest SSR and  among other fitting formulae. When models of NoNusSet are also included, the
among other fitting formulae. When models of NoNusSet are also included, the  and equation (9) perform rather similar.
and equation (9) perform rather similar.
In figure 3 we show the differences between the data and the fits for the considered fitting models. We find that equation (9) and the second order polynomial in ( ) reproduce most of the data within an error of ∼50% and overall perform very similarly. In both cases, the largest deviations are obtained for models of the LeakSet, with the neutrino leakage scheme. The one parameter polynomial of
) reproduce most of the data within an error of ∼50% and overall perform very similarly. In both cases, the largest deviations are obtained for models of the LeakSet, with the neutrino leakage scheme. The one parameter polynomial of  fails to capture the low velocity tail of the distribution and overall gives considerably higher differences between the dataset and the model predicted values of ⟨v∞⟩.
fails to capture the low velocity tail of the distribution and overall gives considerably higher differences between the dataset and the model predicted values of ⟨v∞⟩.
Figure 3. Relative differences between data and fits for the mass-averaged velocity of the dynamical ejecta,  . Calibration is done for all datasets available. We show the fitting formula equation (9) and the polynomial fits. From top to bottom the models are arranged based on their
. Calibration is done for all datasets available. We show the fitting formula equation (9) and the polynomial fits. From top to bottom the models are arranged based on their  : from lowest to highest.
: from lowest to highest.
Download figure:
Standard image High-resolution image3.3. Electron fraction
The mass-averaged electron fraction, ⟨Ye⟩, in M0RefSet varies from 0.03 to 0.27.
Restricting the parameter space to the common region, we obtain the mean value of electron fraction for M0RefSet
 . Adding models of M0/M1Set increases the mean to 0.20 ± 0.04 which is largely due to models of [42, 44] with leakage + M1 scheme (see figure 1). When models of the LeakSet are added, the mean values decreases back, which is as expected as models with leakage scheme only have lower ejecta electron fraction e.g. [64]. Notably, the number of simulations added is rather small
11
.
. Adding models of M0/M1Set increases the mean to 0.20 ± 0.04 which is largely due to models of [42, 44] with leakage + M1 scheme (see figure 1). When models of the LeakSet are added, the mean values decreases back, which is as expected as models with leakage scheme only have lower ejecta electron fraction e.g. [64]. Notably, the number of simulations added is rather small
11
.
Regarding the fitting functions, we explore the low-order polynomials in  and in
and in  only. The coefficients of polynomial regressions are reported in table 4. We observe that for all datasets, the
only. The coefficients of polynomial regressions are reported in table 4. We observe that for all datasets, the  displays consistently lower SSR and
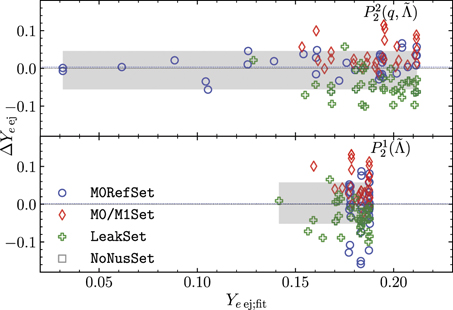
displays consistently lower SSR and  . Notably, the addition of LeakSet models leads to a jump in these measures, as the data in this set is statistically different (different physics setup). In figure 4 we show the performance of the different fitting models for the mass-averaged electron fraction of the ejecta. When all datasets are considered, the second order polynomial manages to reproduce both the low-Ye tail and high Ye values for models with advanced neutrino treatment. The accurate computation of the electron fraction naturally requires neutrino absorption to be included into simulation setups. The availability of a larger number of simulations with advanced neutrino transport will undoubtedly improve fitting models.
. Notably, the addition of LeakSet models leads to a jump in these measures, as the data in this set is statistically different (different physics setup). In figure 4 we show the performance of the different fitting models for the mass-averaged electron fraction of the ejecta. When all datasets are considered, the second order polynomial manages to reproduce both the low-Ye tail and high Ye values for models with advanced neutrino treatment. The accurate computation of the electron fraction naturally requires neutrino absorption to be included into simulation setups. The availability of a larger number of simulations with advanced neutrino transport will undoubtedly improve fitting models.
Figure 4. Relative differences between data and fits for the mass-averaged electron fraction of the dynamical ejecta. We show the polynomial fits, and equations (5) and (6). Calibration is done for all datasets available. Here  . From top to bottom the models are arranged based on their
. From top to bottom the models are arranged based on their  : from lowest to highest.
: from lowest to highest.
Download figure:
Standard image High-resolution image3.4. Root mean square half opening angle
Ejecta geometry was found to have a strong imprint on the properties of the electromagnetic counterparts to mergers e.g. [31]. NR simulations show that the form of the angular distribution of ejecta properties is quite complex e.g. [64], and presents challenges for a statistical analysis. Here we employ the mass-averaged RMS half opening angle (under the assumption of axial symmetry), a quantity that can be used to separate the massive, low-latitude outflow and less massive, polar one. In the discussion we show an example of how this quantity can be used in kilonova modeling. Following [64], we define the mass-averaged RMS half opening angle as by assuming axial symmetry and computing:

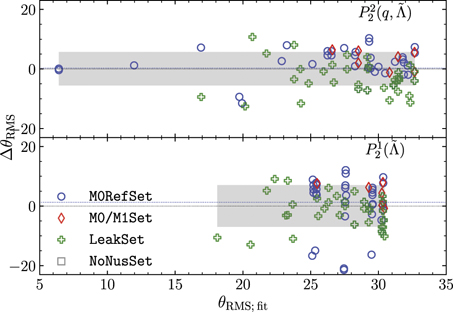
where θi and mi are the angle (from the binary plane) and mass of the ejecta element. This quantity is available only for M0RefSet and for the models of [64]. In figure 5 we show the dependency of θRMS on the previously discussed ejecta parameters. Comparing the data from M0RefSet and the leakage dataset of reference [64], we find that the inclusion of neutrino absorption leads to larger θRMS on average with the exception of highly asymmetric models of M0RefSet. Notably we observe a clear linear relation between the θRMS and ⟨Ye⟩ (see figure 5). The origin of this relation lies in the dependency of the ejecta properties on the binary mass-ratio. Asymmetric binaries produce low-Ye, tidal ejecta confined largely to the lane of the binary, while for more symmetric models with prominent shocked ejecta component there is a trend to have higher Ye and more spread-out ejecta. This further suggests that θRMS can help capturing the transition between the low- and high-opacity ejecta in kilonova modeling.
Figure 5. Relations between the ejecta θRMS and other parameters of the dynamical ejecta: mass, Mej, velocity, ⟨v∞⟩, and electron fraction ⟨Ye⟩ for models from M0RefSet and [64] from LeakSet and M0/M1Set. Plots show that models with neutrino absorption have higher Mej and larger θRMS as well as a clear correlation between θRMS and ⟨Ye⟩.
Download figure:
Standard image High-resolution imageThe number of models within the restricted parameter space for which we have the θRMS is very limited. Thus we only report the average value for M0RefSet,  .
.
In light of the considerably smaller sample of models for which we have θRMS, we simplify the statistical analysis, considering as fitting models only polynomials:  and
and  . The coefficients of the polynomial regressions are reported in table 4. Following [64] we adopt a uniform error for all models of 2 degrees. We find that similarly to the case of ejecta electron fraction, the
. The coefficients of the polynomial regressions are reported in table 4. Following [64] we adopt a uniform error for all models of 2 degrees. We find that similarly to the case of ejecta electron fraction, the  performs consistently better here than other options for all datasets in terms of both SSR and
performs consistently better here than other options for all datasets in terms of both SSR and  .
.
In figure 6 we show the performance of polynomial fitting models to the ejecta θRMS. The second order polynomial provides a better fit to the low-θRMS tail of the distribution than  and reproduces the data within
and reproduces the data within  deg. Overall, we observe that the inclusion of both q and
deg. Overall, we observe that the inclusion of both q and  in a fitting formula is important for capturing the trends in data. However, the small sample of models does not allow us to conduct a more thorough investigation, in particular, to study the effects of various physics included in simulations.
in a fitting formula is important for capturing the trends in data. However, the small sample of models does not allow us to conduct a more thorough investigation, in particular, to study the effects of various physics included in simulations.
Figure 6. Relative differences between data and fits of dynamical ejecta mass-averaged electron fraction. We show polynomial fits only. Here  . From top to bottom the models are arranged based on their
. From top to bottom the models are arranged based on their  : from lowest to highest.
: from lowest to highest.
Download figure:
Standard image High-resolution image3.5. Application of the polynomial fit
Overall, comparing the performance of different fitting formulae to the ejecta properties, we find that the  gives a comparatively better fit when all simulation data from all datasets are considered. When only the M0RefSet and M0/M1Set are considered, however, the ejecta mass is slightly better fitted by non-polynomial fitting formula, equation (8). The implicit inclusion of mass-ratio allows the
gives a comparatively better fit when all simulation data from all datasets are considered. When only the M0RefSet and M0/M1Set are considered, however, the ejecta mass is slightly better fitted by non-polynomial fitting formula, equation (8). The implicit inclusion of mass-ratio allows the  to capture leading trends in the behaviour of ⟨v∞⟩, ⟨Ye⟩ and θRMS. For its calibration we suggest datasets with the most advanced physics i.e. M0/M1Set and M0RefSet. A caution must be exercised when using datasets computed with different physics input and at various resolutions, as in certain cases (e.g. Mej), the systematics introduced by these differences might obscure the leading trends in data. This conclusion is supported by the analysis of the statistical behaviour of data from different datasets and further corroborated by the analysis of the individual datasets (see appendix
to capture leading trends in the behaviour of ⟨v∞⟩, ⟨Ye⟩ and θRMS. For its calibration we suggest datasets with the most advanced physics i.e. M0/M1Set and M0RefSet. A caution must be exercised when using datasets computed with different physics input and at various resolutions, as in certain cases (e.g. Mej), the systematics introduced by these differences might obscure the leading trends in data. This conclusion is supported by the analysis of the statistical behaviour of data from different datasets and further corroborated by the analysis of the individual datasets (see appendix  -statistics and residual plots, we consider a direct application of the,
-statistics and residual plots, we consider a direct application of the,  and compare it to the data used for calibration in figure 7. The plot shows that the behaviour of the fitting formula depends sensibly on the choice of datasets used for calibration, and the predictive power of the fit reduces when datasets with different physics (the difference in contour shapes between left and right column of subplots) and numerical setups are employed. The ejecta properties, especially, mass, velocity and electron fraction depend strongly on the neutrino treatment scheme and larger number of high resolution NR simulations with advanced treatment of neutrino emission and absorption is required to further constrain the statistics of ejecta properties.
and compare it to the data used for calibration in figure 7. The plot shows that the behaviour of the fitting formula depends sensibly on the choice of datasets used for calibration, and the predictive power of the fit reduces when datasets with different physics (the difference in contour shapes between left and right column of subplots) and numerical setups are employed. The ejecta properties, especially, mass, velocity and electron fraction depend strongly on the neutrino treatment scheme and larger number of high resolution NR simulations with advanced treatment of neutrino emission and absorption is required to further constrain the statistics of ejecta properties.
Figure 7. Comparsion between ejecta parameters informed by the fit (colored contours), and the simulation ejecta data (colored markers) for  fitting model calibrated with advanced-physics datasets, M0RefSet and M0/M1Set, (left column of panels) and with all available datasets (right column of panels). The plot shows that for some physical quantities, such as ejecta electron fraction and velocity, the leading trends in data appear to be captured by the
fitting model calibrated with advanced-physics datasets, M0RefSet and M0/M1Set, (left column of panels) and with all available datasets (right column of panels). The plot shows that for some physical quantities, such as ejecta electron fraction and velocity, the leading trends in data appear to be captured by the  calibrated with datasets with advanced physics. When all datasets are considered, however, the limitations of the smooth polynomial fitting function becomes apparent as it is not able to fit the non-smooth data well.
calibrated with datasets with advanced physics. When all datasets are considered, however, the limitations of the smooth polynomial fitting function becomes apparent as it is not able to fit the non-smooth data well.
Download figure:
Standard image High-resolution image4. Remnant disk
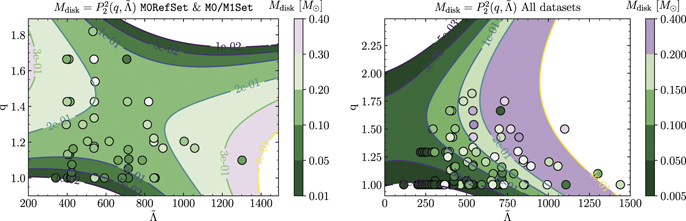
The disk mass at the end of the simulation of models of M0RefSet varies from 0.01M⊙ to 0.3M⊙. Within the restricted parameter space the mean value of the disk mass,  , for models of the M0RefSet is (0.12 ± 0.05)M⊙ and it decreases only slightly when models from M0/M1Set, LeakSet are added, to (0.11 ± 0.04)M⊙. Notably, large variations in the mean value are observed when the parameter space is enlarged to include very asymmetric and promptly collapsing models. However, there is not enough models for the comparison. While this might suggest that the disk mass depends weakly on the physical setup of simulations, the large uncertainties in data and the fundamental difference between the disk around a neutron star and a black hole must be taken into consideration. In particular, we stress that the disk mass is estimated in different ways in the different datasets. In [60, 77] the disk is estimated only for BNS forming BH, at approximately ≈1 ms after collapse and computing the rest mass outside the apparent horizon (AH). In [44], the disk mass is extracted at ≈30 ms outside the AH. In [64], the disk mass is computed as the baryonic mass outside the AH at BH formation, while for NS remnants the criterion ρ < 1013 g cm−3 is used. In [66] for both BH and NS outcome the ρ < 1013 g cm−3 criterion is used and time of the extraction is not specified. In [45] the density criterion is the same, however the simulations are significantly shorter (∼7.5 ms) than in other works. Overall, we estimate that these differences can amount to a systematic factor of a few.
, for models of the M0RefSet is (0.12 ± 0.05)M⊙ and it decreases only slightly when models from M0/M1Set, LeakSet are added, to (0.11 ± 0.04)M⊙. Notably, large variations in the mean value are observed when the parameter space is enlarged to include very asymmetric and promptly collapsing models. However, there is not enough models for the comparison. While this might suggest that the disk mass depends weakly on the physical setup of simulations, the large uncertainties in data and the fundamental difference between the disk around a neutron star and a black hole must be taken into consideration. In particular, we stress that the disk mass is estimated in different ways in the different datasets. In [60, 77] the disk is estimated only for BNS forming BH, at approximately ≈1 ms after collapse and computing the rest mass outside the apparent horizon (AH). In [44], the disk mass is extracted at ≈30 ms outside the AH. In [64], the disk mass is computed as the baryonic mass outside the AH at BH formation, while for NS remnants the criterion ρ < 1013 g cm−3 is used. In [66] for both BH and NS outcome the ρ < 1013 g cm−3 criterion is used and time of the extraction is not specified. In [45] the density criterion is the same, however the simulations are significantly shorter (∼7.5 ms) than in other works. Overall, we estimate that these differences can amount to a systematic factor of a few.
As fitting formulae we consider the polynomials equations (5) and (6), and the formula provided in [64].
Similarly to the mass of dynamical ejecta, the disk mass varies by up to an order of magnitude for, in some cases, very similar values of q and  . In order to simplify the fitting procedure and reproduce both, high and low mass tails, we consider the log10(Mdisk). Notably, the equations (11) and (12) are segmented, and include constant parts. For clarity we write the equations in the form used for fitting, that read
. In order to simplify the fitting procedure and reproduce both, high and low mass tails, we consider the log10(Mdisk). Notably, the equations (11) and (12) are segmented, and include constant parts. For clarity we write the equations in the form used for fitting, that read
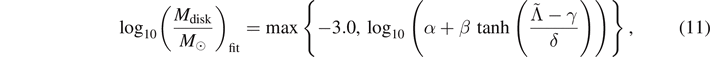
and the fitting formula provided in [70]:
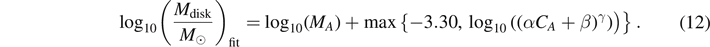
The exact from of polynomials,  and
and  , used in this section than reads,
, used in this section than reads,
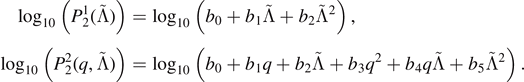
As before we opt here for the minimization of residuals in the fitting procedure. We rank the fitting formulae performance based on the SSR, augmenting the discussion with  , computed using the error measure (3).
, computed using the error measure (3).
The coefficients of the polynomial regressions are reported in table 6; the fit coefficients for equations (11) and (12) are reported in table 7. The SSR for these fits are reported in table 4. As for those for the dynamical ejecta, the formulae in equations (11) and (12) give ill-conditioned fits. Notably, we find that depending on the initial guess for coefficients the equation (12) may develop singularities when data from all datasets is fitted and no limitations are imposed upon the coefficients. However, such non-smooth fitting functions may allow to capture the complex behavior in data, not reproduced by  and
and  (table 3).
(table 3).
Table 3. SSR for different fit models for the final disk mass, log10(Mdisk).
| Datasets | Mean | Equation (11) | Equation (12) |
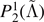
|
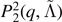
|
|---|---|---|---|---|---|
| M0RefSet | 15.11 | 13.28 | 9.96 | 13.95 | 8.81 |
| & M0/M1Set | 17.03 | 14.42 | 11.58 | 15.24 | 10.70 |
| & LeakSet | 54.02 | 32.56 | 17.65 | 29.72 | 19.56 |
| & NoNusSet | 80.47 | 45.71 | 30.06 | 44.04 | 26.73 |
Fitting the data of M0RefSet and combined M0RefSet dataset and M0/M1Set we observe that the  consistently shows the lowest SSR and
consistently shows the lowest SSR and  . Notably, the equation (12) gives only slightly higher values in both cases. When all models from all datasets are considered, we again observe that the
. Notably, the equation (12) gives only slightly higher values in both cases. When all models from all datasets are considered, we again observe that the  is statistically preferred with equation (12) being the close second. The observed similarity in fitting formulae performance further suggests that indeed mass-ratio and
is statistically preferred with equation (12) being the close second. The observed similarity in fitting formulae performance further suggests that indeed mass-ratio and  allow to capture the main trends in the disk mass data.
allow to capture the main trends in the disk mass data.
When performing the calibration of equations (12) and (11) with standard least-square method we observed that the result of the calibration depends strongly on the initial guesses for the coefficients. This behavior makes the use of these fitting formulae difficult from the point of view of the reproducible of result. We also note that equations (11) and (12) include constant 'floor values'. The physical motivation behind these constants is not very clear and while they might help to constrain the fit behaviour at known limits of the parameter space, e.g. at Λ → 0, their applicability for all datasets may not be optimal. The  fitting formula is free from aforementioned issues and allows for stable and reproducible fits.
fitting formula is free from aforementioned issues and allows for stable and reproducible fits.
In figure 8 we show the relative differences between the data and the values given by the fitting models. Here the relative performance of the fits can be inferred from the 67% confidence level bar. We observe that the equation (11) cannot reproduce the high disk masses found in asymmetric binaries of M0RefSet. Meanwhile other fitting formulae can reproduce both the low and the large disk masses with varying degree of success. Notably, the fit with equation (12) displays the smallest residuals, i.e. with the narrowest 67% confidence level bar. The second best fit here is  . The reason why the
. The reason why the  for the equation (12) is larger than that for
for the equation (12) is larger than that for  (see table 4) lies in the error measure, equation (3), that is used only in
(see table 4) lies in the error measure, equation (3), that is used only in  calculation. Thus, while the fit with lowest
calculation. Thus, while the fit with lowest  provides a better fit for lower disk masses (with tighter errors), the equation (12) gives a fit with overall smaller residuals.
provides a better fit for lower disk masses (with tighter errors), the equation (12) gives a fit with overall smaller residuals.
Figure 8. Relative differences between data and the fits of the disk mass. The calibration was performed for log10(Mdisk) using simulations from all datasets. Different panels show polynomial fits in  and
and  , fitting formulae equations (7) and (8). The best fitting model is characterized by the lowest value of
, fitting formulae equations (7) and (8). The best fitting model is characterized by the lowest value of  . Best fitting coefficients are given in the tables in appendix
. Best fitting coefficients are given in the tables in appendix  . The fitting procedure here was based in minimizing residuals instead of
. The fitting procedure here was based in minimizing residuals instead of  as otherwise, the error measure adapted, equation (3), would lead to the fit underestimating most of datasets used.
as otherwise, the error measure adapted, equation (3), would lead to the fit underestimating most of datasets used.
Download figure:
Standard image High-resolution imageWe show the performance of the  fitting formula in the q-
fitting formula in the q- space in figure 9. The plot shows that certain main trends in data, e.g. higher disk mass in low-q, low-
space in figure 9. The plot shows that certain main trends in data, e.g. higher disk mass in low-q, low- simulations, are reproduced by the fit calibrated with either combined M0RefSet and M0/M1Set or all datasets. However, being a smooth function, the
simulations, are reproduced by the fit calibrated with either combined M0RefSet and M0/M1Set or all datasets. However, being a smooth function, the  , cannot capture the rapid oscillations in data.
, cannot capture the rapid oscillations in data.
Figure 9. Same as figure 7 but for the disk mass. The plot shows that at low values of q and  the fit is able to capture the leading trends in data. However, in the region where there are fewer data preset, at high q and
the fit is able to capture the leading trends in data. However, in the region where there are fewer data preset, at high q and  , the fit becomes increasingly less accurate (see text).
, the fit becomes increasingly less accurate (see text).
Download figure:
Standard image High-resolution imageOverall, the statistical analysis shows that the value of the disk mass is subjected to large uncertainties, that include systematic and method-of-computation uncertainties. The leading trends in the data appears to be captured by the fitting formulae that include mass-ratio and reduced tidal deformability. This result is generally supported by the datasets separate statistical analysis (see appendix  , compared to other fitting formulae available in the literate literature and formulated in terms of other binary parameters, we conclude that the former two quantities describe the leading trends in data. The analysis of all datasets individually generally confirms this conclusion, further suggesting that both
, compared to other fitting formulae available in the literate literature and formulated in terms of other binary parameters, we conclude that the former two quantities describe the leading trends in data. The analysis of all datasets individually generally confirms this conclusion, further suggesting that both  and equation (12) perform similarly well (see appendix
and equation (12) perform similarly well (see appendix
5. Discussion
In this paper we considered NR datasets available in the literature for the dynamical ejecta properties and the remnant disk mass from binary neutron star mergers. We performed a simple statistical analysis of the ejecta parameters that highlighted that the ejecta parameters are subjected to large systematic uncertainties, partially due to different treatment of neutrinos, in addition to the EOS formulations. We also compared different fitting formulae for the ejecta properties and disk mass and found that fitting formulae that include the reduced tidal parameter and mass ratio can relatively well reproduce the leading trends in certain datasets with more uniform physics input. In particular, low order polynomials in these quantities provide a simple description of the data available and also favorably compare to the other options in terms of SSR when only models of M0RefSet are considered as well or models from all datasets. Large values of SSR and  as well as wild oscillations of fitting coefficients for a given quantity between calibrations (see appendix
as well as wild oscillations of fitting coefficients for a given quantity between calibrations (see appendix  perform comparatively well, higher-order formulae might be necessary to capture the true physics of mergers. We leave their exploration to future works when more simulation data becomes available.
perform comparatively well, higher-order formulae might be necessary to capture the true physics of mergers. We leave their exploration to future works when more simulation data becomes available.
When all data from all available datasets are considered, the fitting formulae with the best statistical performance among those considered are able to reproduce the dynamical ejecta velocity typically to ∼50%, with the 68% significance range being Δv∞/v∞ ∈ (−0.4, 0.2). The electron fraction is reproduced with an accuracy of ∼0.1. The ejecta RMS half opening angle about the orbital plane is reproduced with an accuracy of ∼10 deg. The ejecta and disk masses, however, are rather uncertain having (−0.8, 0.2) and (−0.4, 0.2) 68% significance ranges respectively. The smooth fitting formulae can reproduce these quantities to a factor of ∼2.
The main conclusion of this work is that the currently available data on the ejecta properties and disk masses from binary neutron star mergers contains large systematic uncertainties. Different treatments of EOS and neutrino transport, as well as different resolutions, and methods of calculation of ejecta and disk properties lead to large systematic differences between various datasets. As neutrino re-absorption is a crucial component for reliable estimates of the dynamical ejecta mass, e.g. [31, 41, 42, 82], it is of paramount importance to enlarge the M0/M1Set and refine the statistics of ejecta properties. Additionally, different methodologies used to extract and compute these quantities contribute to the uncertainties. Simulations of sequences of binaries at different chirp masses could also be useful to identify new trends in the data that cannot be currently explored. The statistical analysis that we have performed is further subjected to biases as the data in different datasets span different ranges in parameter space of the binary. Considerably larger sets of simulations that cover the parameter space more uniformly are need to alleviate these biases.
Fitting formulae to the ejecta properties and disk mass are commonly used to study sources of the gravitational waves and electromagnetic counterparts. However, caution ought to be exercised when applying the fitting formulae presented here to infer the source parameters from observations.
As an example, we discuss the impact of using our recommended,  , fitting formula for the computation of synthetic kilonova light curves as opposed to the direct NR input
12
. We use the semi-analytic model of reference [31] with one or two kilonova components, i.e. the dynamical ejecta and the disk wind. We consider a set of selected BNS models from the M0RefSet with 5 different EOS and several mass rations between q = 1.00 and q = 1.82. From the
, fitting formula for the computation of synthetic kilonova light curves as opposed to the direct NR input
12
. We use the semi-analytic model of reference [31] with one or two kilonova components, i.e. the dynamical ejecta and the disk wind. We consider a set of selected BNS models from the M0RefSet with 5 different EOS and several mass rations between q = 1.00 and q = 1.82. From the  we estimate the dynamical ejecta mass and velocity and angle separating the low opacity polar part and high opacity part about the plane of the binary, using the θRMS as a separation angle. We invoke the ejecta mass-averaged RMS half opening angle to separate the low-altitude high opacity part and the low-opacity polar part. This allows us to include the change in ejecta geometry with binary parameters. For the secular ejecta mass we assume it to be 40% of the disk mass, evaluated from the best fitting formula. The opacities, heating rates and extrinsic parameters are kept fixed in the comparison.
we estimate the dynamical ejecta mass and velocity and angle separating the low opacity polar part and high opacity part about the plane of the binary, using the θRMS as a separation angle. We invoke the ejecta mass-averaged RMS half opening angle to separate the low-altitude high opacity part and the low-opacity polar part. This allows us to include the change in ejecta geometry with binary parameters. For the secular ejecta mass we assume it to be 40% of the disk mass, evaluated from the best fitting formula. The opacities, heating rates and extrinsic parameters are kept fixed in the comparison.
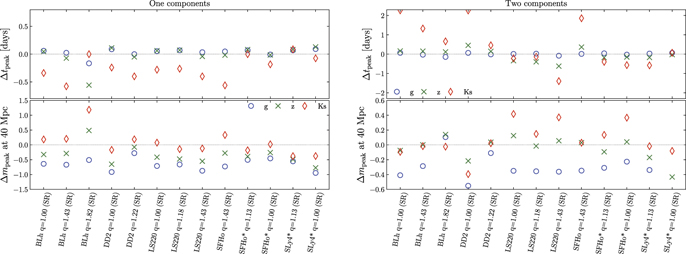
The results are collected in figure 10, where we show peak times and peak magnitudes for the g, z, and Ks filters. In the one component case (left panels), we find that the peak times are reproduced on average within ∼0.2 days in the g an z bands, and within ∼0.5 days in Ks band. The latter is systematically underestimated. The highly asymmetric binary q = 1.8 and BLh EOS shows overall the largest deviations. Peak magnitudes in the three bands computed with the fitting formulae differ by ∼0.5 mag from the NR informed ones, reaching ∼1 mag in the g band. In the two component case (right panels) the peak times in the Ks band based on the best fitting formulae are more uncertain and amount to ∼2 days. The peak magnitude show deviations of ∼±0.5 mag in z and Ks bands. The reason why the peak magnitudes are more uncertain in the one component case lies in the complex geometry that are inherited in kilonova models from the NR data, but is not sufficiency well captured by the single parameter, mass-averaged RMS half opening angle, considered here. While the precise details and origin of these differences can be related to the specific light curve model employed here, this example indicates the minimum systematic variation is to be expected in the light curve predictions when using our recommended fitting formula.
Figure 10. Comparison between one component light curves (left panel) and two components light curves (right panel) in g, z and Ks bands using direct NR input or the fitting formulae for the dynamical ejecta and disk mass. The y-axis displays the difference between the peak time (top panel), Δtpeak = tpeak; NR − tpeak; fit, and peak magnitude, Δmpeak = mpeak; NR − mpeak; fit, (bottom panel); the x-axis shows selected BNS models of M0RefSet. The fits employed here are the polynomials in  used with the best fitting coefficients, calibrated to M0/M1Set (that includes M0RefSet). The plot shows that the light curves generated with the dynamical ejecta fits (one component) tend to underestimate the peak times and magnitudes of NR-informed light curves, especially in the Ks band. In case of dynamical ejecta and disk wind (two components) light curves, the peak time is less constrained (±2 days) in the Ks band, but the peak magnitudes is predicted more accurately ±0.5 mag.
used with the best fitting coefficients, calibrated to M0/M1Set (that includes M0RefSet). The plot shows that the light curves generated with the dynamical ejecta fits (one component) tend to underestimate the peak times and magnitudes of NR-informed light curves, especially in the Ks band. In case of dynamical ejecta and disk wind (two components) light curves, the peak time is less constrained (±2 days) in the Ks band, but the peak magnitudes is predicted more accurately ±0.5 mag.
Download figure:
Standard image High-resolution imageAcknowledgments
We thank the anonymous referees for their comments that helped us improve the manuscript. We thank Erika Holmbeck for useful discussions. SB, BD and FZ acknowledge support by the EU H2020 under ERC Starting Grant No. BinGraSp-714626. DR acknowledges support from the US Department of Energy, Office of Science, Division of Nuclear Physics under Award Number(s) DE-SC0021177 and from the National Science Foundation under Grant No. PHY-2011725. Data postprocessing was performed on the Virgo 'Tullio' server at Torino supported by INFN.
Data availability statement
The data that support the findings of this study are openly available at the following URL/DOI: 10.5281/zenodo.4283516.
Appendix A.: Tables with fitting coefficients
This appendix summarizes all fit coefficients. Dynamical ejecta coefficients can be found in tables 4 and 5 for the polynomials and fitting formulae respectively. Disk coefficients can be found in tables 6 and 7 for the polynomials and fitting formulae respectively. The coefficients of the recommended fitting formulae, as discussed in the conclusion, are highlighted in the tables. Importantly, the range of the binary parameters of the datasets used for calibration ought to be taken into account when the fitting formulae are used. The corresponding ranges are discussed in section 2.
Table 4. Dynamical ejecta properties: coefficients for polynomial regression of various quantities. Results for both first order and second order polynomials are reported  and
and  . The recommended calibration for
. The recommended calibration for  is highlighted.
is highlighted.
| Quantity | Datasets | b0 | b1 | b2 | b3 | b4 | b5 |
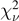
|
|---|---|---|---|---|---|---|---|---|
| log10(Mej) | M0RefSet | −3.49 | 3.51 × 10−3 | −3.01 × 10−6 | 1.9 | |||
| & M0/M1Set | −2.40 | −7.11 × 10−5 | −1.60 × 10−7 | 18.8 | ||||
| & LeakSet | −3.37 | 1.85 × 10−3 | −1.21 × 10−6 | 14.3 | ||||
| & NoNusSet | −2.53 | −2.03 × 10−5 | −6.74 × 10−9 | 46.0 | ||||
| v∞ [c] | M0RefSet | 4.28 × 10−1 | −8.46 × 10−4 | 6.42 × 10−7 | 2.9 | |||
| & M0/M1Set | 3.37 × 10−1 | −4.70 × 10−4 | 3.16 × 10−7 | 3.2 | ||||
| & LeakSet | 2.75 × 10−1 | −2.36 × 10−4 | 1.39 × 10−7 | 6.2 | ||||
| & NoNusSet | 2.50 × 10−1 | −6.66 × 10−5 | 2.15 × 10−8 | 7.6 | ||||
| Ye | M0RefSet | 3.26 × 10−1 | −6.16 × 10−4 | 5.70 × 10−7 | 42.7 | |||
| & M0/M1Set | 1.98 × 10−1 | −3.05 × 10−5 | 4.64 × 10−8 | 38.3 | ||||
| & LeakSet | 1.45 × 10−1 | 1.09 × 10−4 | −6.89 × 10−8 | 36.0 | ||||
| ⟨θRMS⟩ (deg) | M0RefSet | 3.95 × 10+1 | −4.96 × 10−2 | 5.00 × 10−5 | 21.2 | |||
| & M0/M1Set | 2.41 × 101 | 7.21 × 10−3 | 2.28 × 10−6 | 18.3 | ||||
| & LeakSet | 1.44 × 101 | 3.42 × 10−2 | −1.81 × 10−5 | 14.1 |
| Quantity | Datasets | b0 | b1 | b2 | b3 | b4 | b5 |
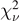
|
|---|---|---|---|---|---|---|---|---|
| log10(Mej) | M0RefSet | 0.436 | −2.75 | −6.18 × 10−3 | 2.75 × 10−1 | 4.78 × 10−3 | 3.96 × 10−7 | 1.2 |
| & M0/M1Set | −1.32 | −3.82 × 10−1 | −4.47 × 10−3 | −3.39 × 10−1 | 3.21 × 10−3 | 4.31 × 10−7 | 20.8 | |
| & LeakSet | −6.96 | 5.26 | 7.84 × 10−4 | −1.71 | 5.69 × 10−4 | −9.09 × 10−7 | 7.9 | |
| & NoNusSet | −6.01 | 4.91 | −1.24 × 10−3 | −1.57 | 1.00 × 10−3 | 2.77 × 10−8 | 17.9 | |
| v∞ [c] | M0RefSet | 6.10 × 10−1 | −1.12 × 10−1 | −1.04 × 10−3 | −6.56 × 10−2 | 3.56 × 10−4 | 4.25 × 10−7 | 0.9 |
| & M0/M1Set | 5.94 × 10−1 | −1.48 × 10−1 | −8.62 × 10−4 | −5.02 × 10−2 | 3.25 × 10−4 | 3.16 × 10−7 | 1.6 | |
| & LeakSet | 2.55 × 10−1 | 1.88 × 10−1 | −4.44 × 10−4 | −1.46 × 10−1 | 1.87 × 10−4 | 1.38 × 10−7 | 5.3 | |
| & NoNusSet | 3.46 × 10−1 | −8.11 × 10−2 | −8.11 × 10−5 | −3.67 × 10−3 | 8.89 × 10−6 | 1.99 × 10−8 | 7.0 | |
| Ye | M0RefSet | −3.49 × 10−2 | 3.01 × 10−1 | 5.55 × 10−4 | −1.52 × 10−1 | −2.06 × 10−4 | −2.44 × 10−7 | 8.7 |
| & M0/M1Set | 2.55 × 10−1 | 3.83 × 10−2 | 2.36 × 10−4 | −6.66 × 10−2 | −1.92 × 10−4 | −1.86 × 10−8 | 9.6 | |
| & LeakSet | −2.58 × 10−1 | 6.33 × 10−1 | 5.02 × 10−4 | −2.41 × 10−1 | −3.04 × 10−4 | −1.25 × 10−7 | 24.8 | |
| ⟨θRMS⟩ (deg) | M0RefSet | −7.79 × 101 | 1.38 × 102 | 1.30 × 10−1 | −5.50 × 101 | −3.33 × 10−2 | −7.25 × 10−5 | 4.4 |
| & M0/M1Set | −5.61 × 101 | 1.29 × 102 | 6.88 × 10−2 | −5.27 × 101 | −2.72 × 10−2 | −2.78 × 10−5 | 4.1 | |
| & LeakSet | −1.06 × 102 | 1.79 × 102 | 1.11 × 10−1 | −6.10 × 10+1 | −6.59 × 10−2 | −2.48 × 10−5 | 8.5 |
Table 5. Dynamical ejecta properties: coefficients for the fitting formulae discussed in the text for various datasets.
| Quantity | Fit | Datasets | α | β | γ | δ | n |
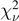
|
|---|---|---|---|---|---|---|---|---|
| log10(Mej) | Equation (7) | M0RefSet | 9.662 × 10−2 | 1.037 | 5.034 | −8.316 | 2.432 × 10−1 | 1.6 |
| & M0/M1Set | −1.004 × 10−1 | −4.403 × 10−1 | −6.452 × 10−1 | 2.696 × 10−1 | 3.222 × 10−1 | 6.0 | ||
| & LeakSet | −1.067 × 10−1 | −1.651 | 2.806 | 2.784 | 3.013 × 10−1 | 13.6 | ||
| & NoNusSet | 9.429 × 10−2 | −7.036 × 10−1 | 2.121 | −1.026 | 5.328 × 10−1 | 29.9 | ||
| log10(Mej) | Equation (8) | M0RefSet | −2.361 × 10−3 | 2.750 × 10−2 | −8.573 × 10−2 | 1.279 | 1.4 | |
| & M0/M1Set | −1.261 × 10−3 | 1.449 × 10−2 | −4.715 × 10−2 | 1.306 | 5.1 | |||
| & LeakSet | −1.153 × 10−3 | 1.285 × 10−2 | −4.164 × 10−2 | 1.339 | 6.1 | |||
| & NoNusSet | −3.351 × 10−4 | 2.697 × 10−3 | −9.738 × 10−3 | 1.729 | 20.0 | |||
| v∞ [c] | Equation (9) | M0RefSet | −7.242 × 10−1 | 1.279 | −1.537 | 1.2 | ||
| & M0/M1Set | −5.631 × 10−01 | 1.109 | −1.186 | 2.3 | ||||
| & LeakSet | −4.007 × 10−1 | 9.164 × 10−1 | −6.881 × 10−1 | 6.0 | ||||
| & NoNusSet | −3.627 × 10−1 | 8.191 × 10−1 | −1.128 | 6.8 |
Table 6. Disk mass: coefficients for polynomial regression of various quantities. Results for both first order and second order polynomials are reported  and
and  . The recommended calibration for
. The recommended calibration for  is highlighted. Note, that here the log10 of the rhs of respective polynomials is considered.
is highlighted. Note, that here the log10 of the rhs of respective polynomials is considered.
| Datasets | b0 | b1 | b2 | b3 | b4 | b5 |
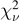
|
|---|---|---|---|---|---|---|---|
| M0RefSet | −3.62 × 10−1 | 1.42 × 10−3 | −9.60 × 10−7 | 477.8 | |||
| & M0/M1Set | −1.76 × 10−1 | 7.50 × 10−4 | −4.01 × 10−7 | 323.6 | |||
| & LeakSet | 3.53 × 10−2 | −3.12 × 10−4 | 6.88 × 10−7 | 37.3 | |||
| & NoNusSet | 1.05 × 10−2 | −1.44 × 10−4 | 4.99 × 10−7 | 61.0 | |||
| M0RefSet | −1.80 | 2.44 | 7.87 × 10−4 | −6.78 × 10−1 | −8.08 × 10−4 | 2.80 × 10−7 | 8.8 |
| & M0/M1Set | −1.85 | 2.59 | 7.07 × 10−4 | −7.33 × 10−1 | −8.08 × 10−4 | 2.75 × 10−7 | 26.6 |
| & LeakSet | −1.26 | 1.76 | 3.51 × 10−4 | −4.82 × 10−1 | −5.20 × 10−4 | 3.68 × 10−7 | 18.9 |
| & NoNusSet | −5.10 × 10−1 | 7.78 × 10−1 | −3.29 × 10−4 | −2.60 × 10−1 | 2.33 × 10−4 | 2.92 × 10−7 | 18.1 |
Table 7. Disk mass: coefficients for the fitting formulae discussed in the text for various datasets.
| Fit | Datasets | α | β | γ | δ |
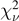
|
|---|---|---|---|---|---|---|
| Equation (11) | M0RefSet | 9.958 × 10−2 | 5.346 × 10−2 | 4.793 × 102 | 6.106 | 298.4 |
| & M0/M1Set | 1.026 × 10−1 | 5.095 × 10−2 | 4.710 × 102 | 5.351 × 10−1 | 203.0 | |
| & LeakSet | 7.677 × 10−2 | 8.752 × 10−2 | 5.835 × 102 | 3.429 × 102 | 105.1 | |
| & NoNusSet | 7.656 × 10−2 | 8.765 × 10−2 | 5.840 × 102 | 3.474 × 102 | 75.0 | |
| Equation (12) | M0RefSet | −6.852 | 1.191 | 1.346 | 25.5 | |
| & M0/M1Set | −7.184 | 1.303 | 1.613 | 55.4 | ||
| & LeakSet | −5.217 | 0.902 | 1.090 | 18.8 | ||
| & NoNusSet | −8.963 | 1.769 | 2.841 | 39.3 |
Appendix B.: Statistics for individual datasets
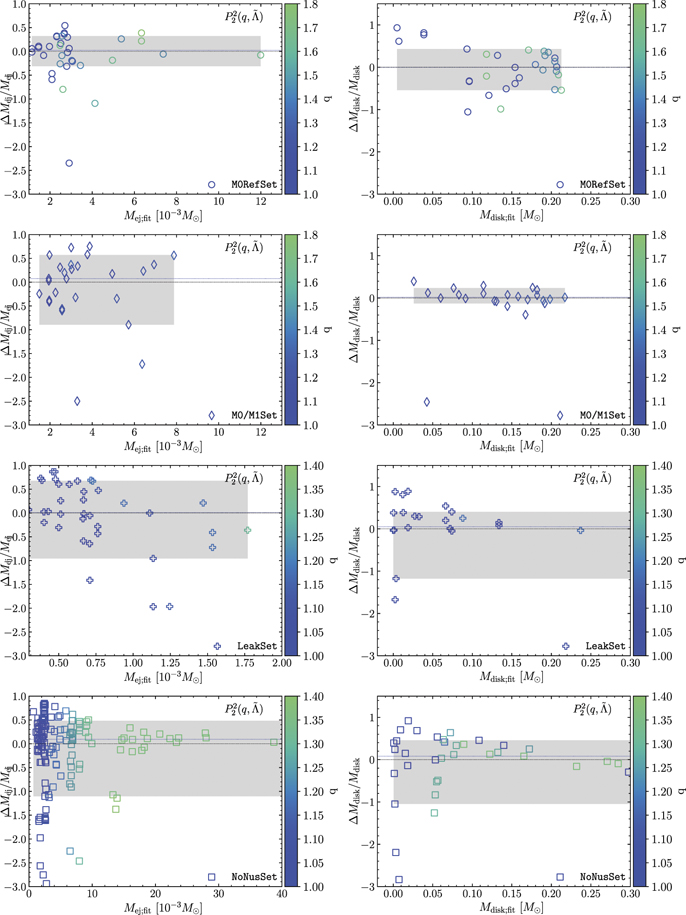
In this appendix we discuss the SSR and  statistics of all fitting formulae dataset-vise instead of adding them up, as was done in the main text. In table 8 we compare the different fits for the dynamical ejecta properties and disk mass in terms of the SSR, and in the figure 11 we show the residuals of the
statistics of all fitting formulae dataset-vise instead of adding them up, as was done in the main text. In table 8 we compare the different fits for the dynamical ejecta properties and disk mass in terms of the SSR, and in the figure 11 we show the residuals of the  , with different calibrations for ejecta mass and disk mass.
, with different calibrations for ejecta mass and disk mass.
Table 8. SSR, for different fitting models for the dynamical ejecta properties and disk mass (see descriptions of the tables 2 and 3). Here datasets are not added, but considered individually.
| log10(Mej) | Datasets | N | Mean | Equation (7) | Equation (8) |
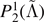
|
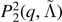
|
|---|---|---|---|---|---|---|---|
| M0RefSet | 34 | 2.57 | 1.65 | 1.40 | 2.43 | 0.97 | |
| M0/M1Set | 30 | 5.56 | 3.32 | 4.35 | 5.04 | 4.49 | |
| LeakSet | 42 | 12.70 | 10.24 | 9.73 | 11.36 | 10.64 | |
| NoNusSet | 165 | 43.74 | 25.78 | 25.57 | 43.35 | 20.40 |
| ⟨vej⟩ | Datasets | N | Mean | Equation (9) |
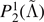
|
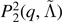
|
|---|---|---|---|---|---|---|
| M0RefSet | 34 | 0.04 | 0.02 | 0.04 | 0.01 | |
| M0/M1Set | 27 | 0.04 | 0.03 | 0.03 | 0.02 | |
| LeakSet | 42 | 0.17 | 0.17 | 0.16 | 0.14 | |
| NoNusSet | 143 | 0.40 | 0.30 | 0.33 | 0.29 |
| ⟨Ye⟩ | Datasets | N | Mean |
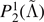
|
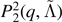
|
|---|---|---|---|---|---|
| M0RefSet | 34 | 0.14 | 0.13 | 0.02 | |
| M0/M1Set | 30 | 0.05 | 0.05 | 0.02 | |
| LeakSet | 35 | 0.04 | 0.04 | 0.04 |
| ⟨θRMS⟩ | Datasets | N | Mean |
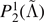
|
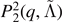
|
|---|---|---|---|---|---|
| M0RefSet | 34 | 2775 | 2631 | 498 | |
| M0/M1Set | 7 | 54 | 49 | 30 | |
| LeakSet | 35 | 1355 | 1048 | 843 |
| Mdisk | Dataset | N | Mean | Equation (11) | Equation (12) |
|
|
|---|---|---|---|---|---|---|---|
| M0RefSet | 31 | 15.11 | 13.28 | 9.96 | 13.95 | 8.81 | |
| M0/M1Set | 23 | 1.88 | 0.93 | 0.59 | 1.18 | 0.44 | |
| LeakSet | 26 | 28.33 | 14.42 | 6.85 | 6.73 | 6.36 | |
| NoNusSet | 39 | 25.66 | 12.08 | 4.24 | 10.37 | 5.14 |
Figure 11. Comparison between the data and values obtained from the fitting formula  for the ejecta mass (left column of plots) and disk mass (right column of plots). The plot is similar to the 2 and 8, but instead of showing the result for the combined dataset with all models, in each panel only one dataset is used to calibrate the
for the ejecta mass (left column of plots) and disk mass (right column of plots). The plot is similar to the 2 and 8, but instead of showing the result for the combined dataset with all models, in each panel only one dataset is used to calibrate the  fitting formula.
fitting formula.
Download figure:
Standard image High-resolution imageRegarding the ejecta mass we find that  and equation (8) display the lowest SSR. While for M0RefSet and NoNusSet the
and equation (8) display the lowest SSR. While for M0RefSet and NoNusSet the  is preferred, for the other two datasets, the equation (8) gives slightly lower SSR. Additionally we note that the datasets that are more uniform in their physics and method, e.g. M0RefSet and LeakSet display the lowest
is preferred, for the other two datasets, the equation (8) gives slightly lower SSR. Additionally we note that the datasets that are more uniform in their physics and method, e.g. M0RefSet and LeakSet display the lowest  . The largest
. The largest  is found for the M0/M1Set, that incorporates both, models with M1 and leakage + M0 neutrino schemes. Notably, (7) shows similar values of
is found for the M0/M1Set, that incorporates both, models with M1 and leakage + M0 neutrino schemes. Notably, (7) shows similar values of  for M0/M1Set, M0RefSet and LeakSet. Figure 11 also shows that the
for M0/M1Set, M0RefSet and LeakSet. Figure 11 also shows that the  reproduces the models of M0/M1Set, LeakSet and NoNusSet less robustly than those of M0RefSet. In part this is due to the limited
reproduces the models of M0/M1Set, LeakSet and NoNusSet less robustly than those of M0RefSet. In part this is due to the limited  range of models of M0RefSet and fixed chirp mass, and in part it hints at the systematic uncertainties due to different physics setup of simulations.
range of models of M0RefSet and fixed chirp mass, and in part it hints at the systematic uncertainties due to different physics setup of simulations.
For the ejecta velocity, the  gives the lowest SSR for all datasets. Meanwhile, the largest
gives the lowest SSR for all datasets. Meanwhile, the largest  is found for the LeakSet across all fitting formulae. This might be attributed to the systematic uncertainties that pure leakage neutrino scheme introduces for models with different outcomes, e.g. prompt collapse and stable remnants.
is found for the LeakSet across all fitting formulae. This might be attributed to the systematic uncertainties that pure leakage neutrino scheme introduces for models with different outcomes, e.g. prompt collapse and stable remnants.
With respect to ejecta electron fraction and RMS half opening angle,  gives significantly lower SSR than
gives significantly lower SSR than  and the difference in
and the difference in  are small. Notably, for the ⟨Ye⟩, the
are small. Notably, for the ⟨Ye⟩, the  is similar between the M0RefSet and M0/M1Set. This indicates the consistency in neutrino reabsorption effects on the ejecta composition in these datasets.
is similar between the M0RefSet and M0/M1Set. This indicates the consistency in neutrino reabsorption effects on the ejecta composition in these datasets.
For the disk mass we find that the lowest SSR is given  for all datasets. The largest
for all datasets. The largest  is found for M0RefSet and the smallest for M0/M1Set. The reason for that is largely due to the error measure that we use to compute the
is found for M0RefSet and the smallest for M0/M1Set. The reason for that is largely due to the error measure that we use to compute the  . For instance, if we employ the error bars for the M0RefSet individually for each model (see table 1 in [34]), we obtain
. For instance, if we employ the error bars for the M0RefSet individually for each model (see table 1 in [34]), we obtain  . However, this information is not available for other datasets and the uniform error measure, equation (3) was chosen for consistency. The figure 11 shows that indeed, the
. However, this information is not available for other datasets and the uniform error measure, equation (3) was chosen for consistency. The figure 11 shows that indeed, the  reproduces the data of M0/M1Set much better than of any other dataset, with lower residuals. This can be attributed to the fact that models of M0/M1Set span a more narrow range in mass ratios and does not include prompt collapse models that can lead to either massive disks in very asymmetric binaries [68] or a negligible disks in equal mass but massive ones [64].
reproduces the data of M0/M1Set much better than of any other dataset, with lower residuals. This can be attributed to the fact that models of M0/M1Set span a more narrow range in mass ratios and does not include prompt collapse models that can lead to either massive disks in very asymmetric binaries [68] or a negligible disks in equal mass but massive ones [64].
Overall, the datasets-wise statistical analysis of ejecta properties and disk mass shows the same qualitative picture reported in the main text.
Appendix C.: Effect of the error measure on the fitting procedure results
In the main text, the comparison between different fitting formulae and their respective calibration is performed using residuals SSR. Additionally we discuss the  using the error measures found in the literature.
using the error measures found in the literature.
In this appendix we investigate how different error measures and different criteria for fitting procedure affect the result. We focus on the models of M0RefSet only, for which we have errors estimated directly from the NR simulations performed at different resolutions (see table 1 in [34]). We also limit the analysis to the  fitting formula. We consider three approaches: (i) minimizing the residuals, (ii) minimizing the
fitting formula. We consider three approaches: (i) minimizing the residuals, (ii) minimizing the  with the default errors, discussed in the main text and (iii) minimizing
with the default errors, discussed in the main text and (iii) minimizing  with the NR-informed errors. For the (i) we compute two
with the NR-informed errors. For the (i) we compute two  , computed for both error measures.
, computed for both error measures.
For the Mej we observe that for (i) the  increases by almost 3 orders of magnitude when employing the NR-informed errors from 1.17 to 563.92. Meanwhile, the difference in the quality of the fit computed with minimization of
increases by almost 3 orders of magnitude when employing the NR-informed errors from 1.17 to 563.92. Meanwhile, the difference in the quality of the fit computed with minimization of  using these two error measures, i.e. (ii) and (iii), changes only slightly, as figure 12 shows. As expected, the extrema of ΔMej/Mej are the lowest, (−2.34, 0.54) when the residuals are minimize. However, even when
using these two error measures, i.e. (ii) and (iii), changes only slightly, as figure 12 shows. As expected, the extrema of ΔMej/Mej are the lowest, (−2.34, 0.54) when the residuals are minimize. However, even when  is minimized, the increase in extrema is not significant (with respect to the overall fit performance): (−2.73, 0.50) for default error measure and (−2.60, 0.51) for NR-informed errors.
is minimized, the increase in extrema is not significant (with respect to the overall fit performance): (−2.73, 0.50) for default error measure and (−2.60, 0.51) for NR-informed errors.
Figure 12. Effects of different calibration methods for  fit for models of M0RefSet for the ejecta mass (left panel) and disk mass (right panel). We consider the minimization of residuals,
fit for models of M0RefSet for the ejecta mass (left panel) and disk mass (right panel). We consider the minimization of residuals,  with default error measures (equations (2) and (3)), and the errors estimated from multi-resolution analysis in [34]. Gray/pastel shaded regions mark the 1σ (68%)/2σ (95.4%) confidence intervals.
with default error measures (equations (2) and (3)), and the errors estimated from multi-resolution analysis in [34]. Gray/pastel shaded regions mark the 1σ (68%)/2σ (95.4%) confidence intervals.
Download figure:
Standard image High-resolution imageFor the ⟨v∞⟩, we observe no difference between the fit calibrated minimizing residuals (i) or minimizing  with default error (ii), as the error measure is a constant value. However, the increase in
with default error (ii), as the error measure is a constant value. However, the increase in  amounts to an order of a magnitude from 0.9 to 9.3. When the NR-informed error is used the fit changes slightly at the lower tail of the velocity with the decrease in
amounts to an order of a magnitude from 0.9 to 9.3. When the NR-informed error is used the fit changes slightly at the lower tail of the velocity with the decrease in  to 3.3.
to 3.3.
Similar behaviour is observed for the ⟨Ye⟩ and ⟨θRMS⟩ as the error measure for these quantities are also constants.
For the Mdisk we observe the similar picture as for the Mej. For (i) the  increases by ≳3 orders of magnitude from 1.5 to 192. However, the difference in the fit quantitative performance with minimization of
increases by ≳3 orders of magnitude from 1.5 to 192. However, the difference in the fit quantitative performance with minimization of  using the two error measures, i.e. (ii) and (iii), remains within data points' error bars (see figure 12, left panel).
using the two error measures, i.e. (ii) and (iii), remains within data points' error bars (see figure 12, left panel).
For a fixed q = 1 the performance of the  is shown in figure 13. We observe that the largest difference in both cases amounts to 0.25 in log10 of the respective quantity. The fit computed minimizing the
is shown in figure 13. We observe that the largest difference in both cases amounts to 0.25 in log10 of the respective quantity. The fit computed minimizing the  gives higher values across the considered range of
gives higher values across the considered range of  .
.
Figure 13. Visual representation of the  fit for ejecta mass (left panel) and disk mass (right panel). The fits are calibrated with M0/M1Set and M0RefSet, however, only models with q = 1 are plotted. The fit calibration is done either minimizing residuals or
fit for ejecta mass (left panel) and disk mass (right panel). The fits are calibrated with M0/M1Set and M0RefSet, however, only models with q = 1 are plotted. The fit calibration is done either minimizing residuals or  . In the latter case, the default errors are used (and also plotted) namely, equations (2) and (3).
. In the latter case, the default errors are used (and also plotted) namely, equations (2) and (3).
Download figure:
Standard image High-resolution imageThe qualitative behavior of the fits remain, however, unchanged.
That the outcome of the fit calibration depends on the choice of the error measure only when this measure is biased. Otherwise, it is equivalent to minimizing residuals, as is the case for all quantities considered except masses. Regarding the latter, while the qualitative behavior of the fit appears to be independent of the minimization technique, the quantitative difference is present. The error measures considered in the main text are motivated by the finite-resolution errors found in numerical simulations [64]. However, their use for the statistical analysis of different datasets performed with different physics and numerical setups might not be optimal. This was our motivation to minimize residuals in the fitting formulae analysis in the main text. Employing a more physically and statistically motivated error measure in future analysis, when larger sample of data is available, would lead to better constrained fits.
Footnotes
- 8
- 9
We report here the mean value as it is the simplest quantitative measure to characterizes the differences between the different datasets.
- 10
In [40] the different treatment of gravity was employed. Specifically, the evolution was performed under the assumption of conformal flatness.
- 11
Note that [63] does not provide electron fraction.
- 12
The ejecta mass, velocity and electron fraction distributions are used to compute the light curve as in reference [75].


![$\tilde{{\Lambda}}\in [340,1437]$](https://content.cld.iop.org/journals/0264-9381/39/1/015008/revision2/cqgac35a8ieqn4.gif)
![$\tilde{{\Lambda}}\in [400,850]$](https://content.cld.iop.org/journals/0264-9381/39/1/015008/revision2/cqgac35a8ieqn5.gif)
![$\tilde{{\Lambda}}\in [116,1688]$](https://content.cld.iop.org/journals/0264-9381/39/1/015008/revision2/cqgac35a8ieqn6.gif)
![$\tilde{{\Lambda}}\in [50,3196]$](https://content.cld.iop.org/journals/0264-9381/39/1/015008/revision2/cqgac35a8ieqn7.gif)