Abstract
Gauge invariant, Hamiltonian formulation of field dynamics within a compact region Σ with boundary ∂Σ is given for the gravitational field linearized over a Kottler metric. The boundary conditions which make the system autonomous are discussed. The corresponding Hamiltonian functional  uniquely describes the energy carried by the (linearized) gravitational field. It is shown that, under specific boundary conditions, the quasi-local Hawking mass
uniquely describes the energy carried by the (linearized) gravitational field. It is shown that, under specific boundary conditions, the quasi-local Hawking mass  reduces to
reduces to  in the weak field approximation. This observation is a quasi-local version of the classical Brill–Deser result (Brill and Deser 1968 Ann.Phys.(N.Y.) 50 3) and enables us to declare Hawking mass as the correct expression (at least up to quadratic terms in the Taylor expansion) for the quasi-local mass, which correctly describes energy carried by the gravitational field.
in the weak field approximation. This observation is a quasi-local version of the classical Brill–Deser result (Brill and Deser 1968 Ann.Phys.(N.Y.) 50 3) and enables us to declare Hawking mass as the correct expression (at least up to quadratic terms in the Taylor expansion) for the quasi-local mass, which correctly describes energy carried by the gravitational field.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Dynamics of the linear theory of gravity can be formulated in terms of two gauge-invariant, non-constrained degrees of freedom. For this purpose one can use e.g. selected components of the (linearized) Weyl tensor [2–5]. The two degrees of freedom contain the entire information about dynamics: knowing them, the complete field configuration can be uniquely (up to gauge transformations) reconstructed in a quasi-local way. The phase space of (complete) initial data on a given Cauchy surface  carries a canonical ADM-symplectic structure. The value of its Hamiltonian functional is uniquely determined by this structure and the field dynamics: it is a positive, quadratic form of gauge invariants [3, 5]. In case of a flat background, this quantity satisfies an important consistency test: it is equal to the second variation (the leading term in the Taylor expansion) of the total ADM energy, commonly accepted as the global Hamiltonian function (i.e. the total field energy) in the complete, nonlinear theory [1].
carries a canonical ADM-symplectic structure. The value of its Hamiltonian functional is uniquely determined by this structure and the field dynamics: it is a positive, quadratic form of gauge invariants [3, 5]. In case of a flat background, this quantity satisfies an important consistency test: it is equal to the second variation (the leading term in the Taylor expansion) of the total ADM energy, commonly accepted as the global Hamiltonian function (i.e. the total field energy) in the complete, nonlinear theory [1].
Any reasonable definition of a quasi-local mass should also satisfy a quasi-local version of the above test in the following sense. Given a compact region  with boundary ∂Σ on a Cauchy surface, the field dynamics within Σ of the linearized gravitational field is not an autonomous system because of the influence of the exterior ∁Σ on the interior of Σ. But, there is a unique way to impose boundary conditions on ∂Σ which act like an adiabatic insulation, i.e. the dynamics becomes an autonomous Hamiltonian system and the corresponding Hamiltonian functional
with boundary ∂Σ on a Cauchy surface, the field dynamics within Σ of the linearized gravitational field is not an autonomous system because of the influence of the exterior ∁Σ on the interior of Σ. But, there is a unique way to impose boundary conditions on ∂Σ which act like an adiabatic insulation, i.e. the dynamics becomes an autonomous Hamiltonian system and the corresponding Hamiltonian functional  is positive (cf e.g. [6, 7]). This way, the field energy acquires a quasi-local
3
(and not only global) meaning.
is positive (cf e.g. [6, 7]). This way, the field energy acquires a quasi-local
3
(and not only global) meaning.
In the present paper we check the consistency of the (quasi)-local Hawking mass with the local energy content of the linear theory for a general spherically-symmetric background: an arbitrary Kottler metric. Our main result is that the second variation of the Hawking mass assigned to topological two-dimensional (2D) spheres constituting a boundary ∂Σ of a compact region Σ agrees with the amount of (gauge-independent) field energy of the linearized gravity contained within, modulo a certain gauge-dependent boundary term. The complete agreement can be obtained if we impose an appropriate gauge condition at the boundary ∂Σ which annihilates the undesirable term in the Taylor expansion.
The gauge-dependence of the field energy is not a paradox. We stress that the imposed gauge condition plays a role which is much more fundamental than merely a 'convenient gauge' used to annihilate unwanted terms in the expansion. Indeed, the 2D surface ∂Σ plays a double role in the definition of quasi-local mass E∂Σ. The first, obvious one, is to demarcate the region Σ whose energy content we want to measure
4
. But the second role, that of a 'reference frame', is related to the very notion of field energy, which is not a scalar quantity: it is always measured with respect to a reference frame. In special relativity theory, reference frame can be identified with a vector field, say T, which must be a symmetry field of the spacetime geometry. Field evolution consisting in shifting the field configuration along this field becomes an autonomous Hamiltonian system, with the Hamiltonian function provided by the Noether theorem. The same procedure works not only for the total energy, but also for local energy contained in a bounded 3D region Σ, provided appropriate boundary conditions at the boundary of the world tube  are satisfied, which assure the adiabatic insulation of its interior from the exterior
5
.
are satisfied, which assure the adiabatic insulation of its interior from the exterior
5
.
In principle, nothing prevents us from using the same construction for an arbitrary vector field T. But the resulting Hamiltonian system is no longer autonomous if T is not a symmetry field. The value of the corresponding Hamiltonian is no longer conserved and cannot be interpreted as the field energy. If T is a combination of time translation, space translation, rotation, boost etc, the resulting Hamiltonian function is a strange combination of energy, momentum, angular momentum, static moment etc, but for a generic T it is difficult to find any reasonable interpretation of such a quantity (see [8]).
In general relativity, Noether theorem does not provide any valuable 'energy density' and Penrose introduced the notion of a 'quasi-local mass', cf [9], to stress the fact that energy contained in Σ must depend only upon geometric properties of its boundary ∂Σ
6
. Nevertheless, the field evolution can still be interpreted as a Hamiltonian system, provided the interior of the tube  is adiabatically insulated by appropriate boundary conditions [6, 8, 12]. Again, it is hard to call 'energy' a Hamiltonian functional obtained via such a procedure, unless we choose the field T in a way that eliminates all those unwanted ingredients (like rotation, boost, space translation etc). To do that, the only 'reference frame' being at our disposal when defining the quasi-local energy E∂Σ is the surface itself: whenever the extrinsic curvature vector Hμ
of the boundary is spacelike there is a geometrically preferred timelike vector field Tμ
which is orthogonal to ∂Σ and to Hμ
, i.e. satisfying gμν
Tμ
Hν
= 0.
is adiabatically insulated by appropriate boundary conditions [6, 8, 12]. Again, it is hard to call 'energy' a Hamiltonian functional obtained via such a procedure, unless we choose the field T in a way that eliminates all those unwanted ingredients (like rotation, boost, space translation etc). To do that, the only 'reference frame' being at our disposal when defining the quasi-local energy E∂Σ is the surface itself: whenever the extrinsic curvature vector Hμ
of the boundary is spacelike there is a geometrically preferred timelike vector field Tμ
which is orthogonal to ∂Σ and to Hμ
, i.e. satisfying gμν
Tμ
Hν
= 0.
In the flat Minkowski spacetime this procedure produces a useful, self-parallel vector field T only when the surface ∂Σ is sufficiently 'rigid', i.e. contained in a flat 3D hyperplane. Otherwise, the value of the Hamiltonian function obtained this way cannot be interpreted as a field energy. In particular, one cannot expect any reasonable properties (like positivity, convexity etc) that usually characterize the energy functional and enable us to prove important properties of the field evolution (e.g. stability).
It turns out that the above rigidity condition can be generalized to a generic, curved spacetime (see [13, 14], where the existence of the eight-parameter family of rigid spheres has been proved). A natural hypothesis arises that the quasi-local Hamiltonian function, defined by imposing appropriate boundary conditions, can be interpreted as the field energy only for such 'rigid spheres'. The main result of our paper supports this hypothesis. Indeed, the curious gauge condition, which is necessary to obtain equality between the quadratic term in the expansion of the Hawking mass and the field energy of the linear gravity, is just the linearized version of the rigidity condition of the surface ∂Σ.
In our opinion, this result shows that the Hawking mass is a viable candidate for the correct expression for the quasi-local gravitational field energy. It also becomes a sort of 'reference gauge'—any other proposed expression should not differ from the Hawking mass up to second order approximation to be a sensible option.
1. Technical setup
We will work within the framework of the Cauchy problem for the Einstein equation in vacuum, in the ADM formulation thereof. The background for linearization of the theory will be a Kottler metric:

This is a general spherically symmetric solution, which encompasses Minkowski, (anti)de Sitter and Schwarzschild solutions as special cases. The function f has the form:  . Our choice of coordinates: (x0, x1, x2, x3) = (t, ϑ, φ, r) is fixed by this form of the background metric.
. Our choice of coordinates: (x0, x1, x2, x3) = (t, ϑ, φ, r) is fixed by this form of the background metric.
We consider a compact region on a Cauchy surface, foliated by a family of 2D spheres:

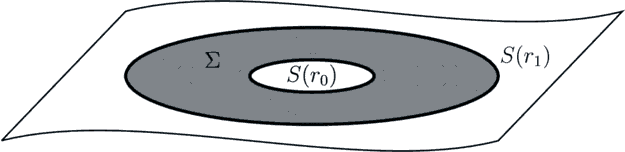
We assume that Σ lies within the domain of positive f—outside of the black hole horizon and within the cosmological horizon (if it exists 7 ). One should note that apart from its impact on the location and existence of horizons, the value of the cosmological constant Λ does not influence our derivations. Our formalism and reasoning remain valid whether Λ is positive, negative or zero, and since we are dealing with a compact region—the changes in asymptotic behaviour of the metric due to the presence and sign of the cosmological constant Λ do not come into play. We are therefore able to consider all three cases simultaneously.
A following indexing convention will be used to denote dimensionality of geometric objects: lowercase Greek, lowercase Latin and uppercase Latin indices will denote full spacetime (μ, ν = 0, 1, 2, 3), Cauchy surface (k, l = 1, 2, 3) and 2D sphere (A, B = 1, 2) coordinates repectively. The coordinate derivative and the 2D covariant derivative on S(r) will be denoted by a comma and the symbol '||'. The volume form on the spheres defined by the Kottler metric is Π := r2 sin θ and λ denotes the counterpart volume form for gAB
. The symbol  is the Laplace–Beltrami operator on a unit sphere (which is a negative-definite operator). We use a geometric set of units, in which both the speed of light and the gravitational constant are equal to one, c = 1 = G.
is the Laplace–Beltrami operator on a unit sphere (which is a negative-definite operator). We use a geometric set of units, in which both the speed of light and the gravitational constant are equal to one, c = 1 = G.
1.1. Reduced variables. Hamiltonian formulation of linearized theory
The complete description of the canonical structure of linear gravity on the Kottler background has been given in paper [5] (a generalization of earlier results [3] to the case with cosmological constant). We summarize crucial results below. Initial (Cauchy) data for Einstein equation can be represented in the form of two symmetric tensors—the induced metric and the ADM momentum (trace-corrected extrinsic curvature of Σ):

In linearized theory, we consider vacuum solutions of the form gμν = ημν + hμν and obtain corresponding Cauchy data as perturbations of the point (ηkl , Pkl (ημν ) = 0).
The linearized data set (hkl , Pkl ) is constrained by four Gauss–Codazzi constraint equations and partially redundant due to a four-parameter family of gauge transformations. This redundancy can be removed by condensing the data into a set of two pairs of mutually conjugate (like positions and momenta) observables. As a preliminary step, we perform a (2 + 1) decomposition of the ADM data with respect to the geometry of the spherical foliation. The tensors are therefore split into components that behave like scalar, vector-like and tensor objects with respect to the 2D sphere geometry (e.g. h33, h3A and hAB ). We then extract traces from the 2D tensors:
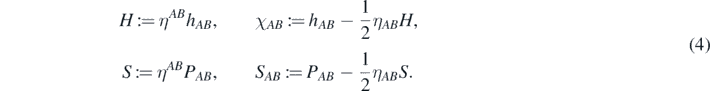
Finally, by acting upon tensor and vector-like components with 2D divergence and rotation operators we obtain a set of 12 scalar (and pseudo-scalar) functions, from which we compose our reduced variables:
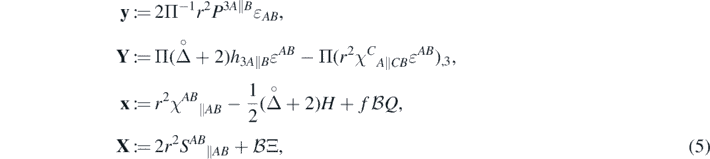
where ɛAB
:= Π AB
is the Levi–Civita tensor on the 2D leaves (
AB
is the Levi–Civita tensor on the 2D leaves ( AB
is the Levi–Civita symbol,
AB
is the Levi–Civita symbol,  12 = 1) and Ξ and Q denote the following expressions:
12 = 1) and Ξ and Q denote the following expressions:


and we have introduced a following quasi-local (non-local on individual spheres S(r)) operator:
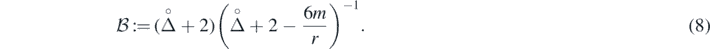
The set of four scalar functions (x, X, y, Y):
- (a)is gauge invariant,
- (b)is no longer restricted by any constraint,
- (c)diagonalizes the ADM symplectic structure of the phase space of Cauchy data (i.e. is a set of canonical variables),
- (d)carries the entire physical information about the gravitational field, i.e. (hkl , Pkl ) can be uniquely reconstructed up to gauge transformations from this set,
- (e)reduces field dynamics to a set of four equations of motion:
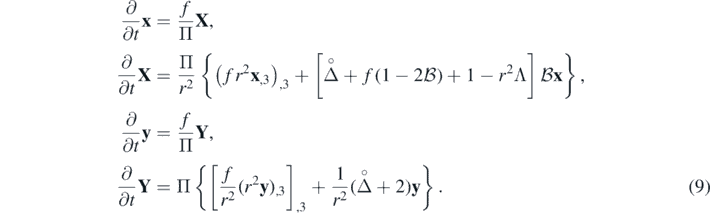
One subtle point needs to be discussed here: when decomposed into spherical harmonics on S(r), the monopole and dipole parts of (x, X, y, Y) are not dynamical—they encode conserved charges. There are up to ten charges in the perturbation, depending on the symmetry of the background metric. The monopole part of x is the mass (energy) of the perturbation. For m = 0 (pure de Sitter or Minkowski background) the dipole parts of X and x describe the linear momentum and the static moment (i.e. information about center of mass) respectively, producing six charges altogether. When m ≠ 0 we lose the translational symmetry of the background and these charges vanish. Finally, the dipole part of y (denoted dip y) describes the angular momentum, providing the last three charges. The remaining mono-dipole parts of the canonical variables vanish identically.
In the regime of weak fields, the first seven charges can be easily eliminated, as the splitting of gμν into background and perturbation is not unique. By changing the background to a Kottler metric with a different mass parameter and/or acting upon it with a small boost or translation we can modify the value of the charges and shift them from the dynamical field h to the background η. To eliminate the angular momentum, however, one would need to use a background with a non-vanishing angular momentum (Kerr–de Sitter). For the sake of simplicity we keep the spherical symmetry of the background and describe angular momentum on the level of perturbation.
The space of Cauchy data of the complete (non-linear) theory is endowed with the canonical symplectic form Ω, known as the ADM structure. In case of a bounded region Σ with boundary ∂Σ, the symplectic form Ω contains not only the ADM bulk term ∫Σ
δPkl
∧ δgkl
, but also an extra boundary term, which makes it gauge invariant (see [6, 8]). It turns out that for linearized theory only the dynamical, 'mono-dipole-free' part, denoted by underscored symbols  8
of the initial data remains in the bulk integral. The ADM symplectic structure assumes a canonical form:
8
of the initial data remains in the bulk integral. The ADM symplectic structure assumes a canonical form:
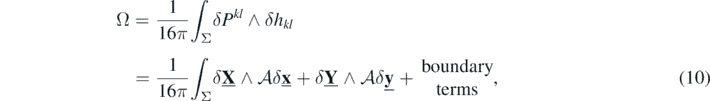
where  and the boundary terms can be killed by appropriate gauge conditions.
and the boundary terms can be killed by appropriate gauge conditions.
Field dynamics (9), symbolically represented as  , uniquely defines the gauge-invariant Hamiltonian functional through formula:
, uniquely defines the gauge-invariant Hamiltonian functional through formula:
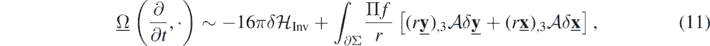
where the symbol ∼ indicates the fact that we omit the gauge-dependent boundary terms. If the values of x and y are controlled on the boundary (δ
x|∂Σ = 0 = δ
y|∂Σ) then the system becomes autonomous and is governed by the Hamiltonian  , whose explicit form is:
, whose explicit form is:

V(+) and V(−) are quasi-local, positive-definite potential operators (cf [5]):

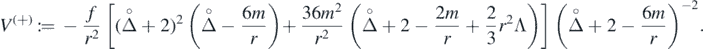
1.2. Extrinsic curvature and torsion of a 2D manifold. Rigid sphere condition
For a metric manifold  with a submanifold
with a submanifold  , the extrinsic curvature
, the extrinsic curvature
 of
of  in
in  is defined by:
is defined by:

where  , ∇ is the metric connection on
, ∇ is the metric connection on  and
and  denotes the orthogonal projection onto the space of vectors orthogonal to
denotes the orthogonal projection onto the space of vectors orthogonal to  (the normal bundle
(the normal bundle  ). The trace of
). The trace of  with respect to the intrinsic metric of
with respect to the intrinsic metric of  is called the mean extrinsic curvature Hμ
and is a vector in
is called the mean extrinsic curvature Hμ
and is a vector in  .
.
If  , we identify elements of
, we identify elements of  with scalar functions on
with scalar functions on  by choosing a unit normal vector field as a basis in
by choosing a unit normal vector field as a basis in  .
.
For  of codimension two and a spacelike Hμ
we can find
of codimension two and a spacelike Hμ
we can find  complementing Hμ
/||H|| to an orthonormal basis and define the extrinsic torsion
complementing Hμ
/||H|| to an orthonormal basis and define the extrinsic torsion
 :
:

The symbol ||H|| denotes the length of the vector Hμ .
If  is a 2D topological sphere, then it is conformally equivalent to a standard unit sphere
is a 2D topological sphere, then it is conformally equivalent to a standard unit sphere  . This conformal equivalence can be used to define a notion of spherical harmonics on
. This conformal equivalence can be used to define a notion of spherical harmonics on  . Consider a sufficiently smooth isomorphism
. Consider a sufficiently smooth isomorphism  , such that
, such that  , where
, where  is the standard metric on a unit sphere and p is a strictly positive conformal factor. The decomposition of functions on
is the standard metric on a unit sphere and p is a strictly positive conformal factor. The decomposition of functions on  into a series of spherical multipoles (i.e. eigenfunctions of the operator
into a series of spherical multipoles (i.e. eigenfunctions of the operator  ) is now defined by their pullback with respect to ϕ. Imposing a condition dip(p) = 0 on ϕ makes this decomposition unique (whereas the representation of these multipole components in terms of spherical harmonic functions is not unique: it is unique up to rotations).
) is now defined by their pullback with respect to ϕ. Imposing a condition dip(p) = 0 on ϕ makes this decomposition unique (whereas the representation of these multipole components in terms of spherical harmonic functions is not unique: it is unique up to rotations).
Using this apparatus, we may now formulate the rigid sphere conditions [13, 14]. A topological sphere  is called a rigid sphere if:
is called a rigid sphere if:
- (a)Its mean curvature Hμ is everywhere spacelike,
- (b)The mono-dipole-free parts of the length of Hμ and of the divergence of extrinsic torsion vanish:

This conditions were created to distinguish, in a generic spacetime, a set of spheres which in some way resemble the standard round spheres in Minkowski spacetime and could therefore provide some kind of analogue to the group of Poincaré symmetries. In the Minkowski metric, the solution to the above equations is exactly the eight-parameter family of round spheres. Likewise, an eight-parameter family of solutions exists in a generic spacetime, if it is sufficiently close to the Minkowski metric [14].
2. Relation of the Hawking mass to a volume integral
The Hawking mass [10, 15] of a region surrounded by a topological 2D sphere  is defined by:
is defined by:
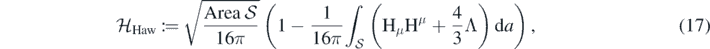
where Hμ
is the mean extrinsic curvature of the boundary  in the enveloping four-dimensional spacetime. Formula (17) includes a correction term
in the enveloping four-dimensional spacetime. Formula (17) includes a correction term  , which accounts for presence of the cosmological constant.
, which accounts for presence of the cosmological constant.
We wish to compare the Hawking mass, defined in terms of a boundary integral, to the Hamiltonian function of the linearized theory, which is a volume integral of linearized ADM data over the whole region Σ. We will therefore begin by finding a way to express the Hawking boundary integral in terms of a volume integral of ADM data in the full theory. Such relation can be obtained from the scalar Gauss–Codazzi constraint:

where g := det gkl . We also remind the reader that we are working in vacuum, hence no matter density term. The Gauss–Codazzi geometric identities allow one to express the three-dimensional Ricci scalar by objects related to the 2D spherical foliation:
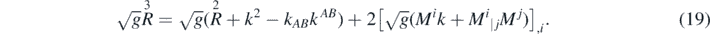
Here Mi
is the unit normal vector to the leaves of the 2D spherical foliation, kAB
is the extrinsic curvature of these spheres in Σ,  is the mean curvature, and
is the mean curvature, and  is the inverse of gAB
.
is the inverse of gAB
.  and
and  are the Ricci scalars of the Cauchy surface and of the leaves of the 2D foliation within. The symbol | denotes the covariant derivative with respect to the three-dimensional geometry of Σ.
are the Ricci scalars of the Cauchy surface and of the leaves of the 2D foliation within. The symbol | denotes the covariant derivative with respect to the three-dimensional geometry of Σ.
Substituting (19) into (18) and taking into account that  , we can obtain the following equation:
, we can obtain the following equation:
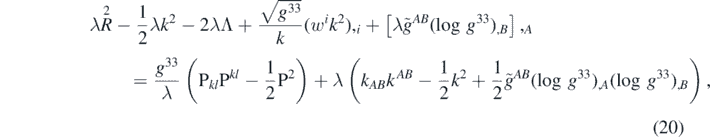
where  . We will now integrate both sides of this equation over the region Σ. The last term in the first line will then vanish, since it is a total divergence on each of the 2D spheres of the foliation of Σ. A similar argument proves that
. We will now integrate both sides of this equation over the region Σ. The last term in the first line will then vanish, since it is a total divergence on each of the 2D spheres of the foliation of Σ. A similar argument proves that  . Using this identity, the Gauss–Bonnet theorem, and the relation
. Using this identity, the Gauss–Bonnet theorem, and the relation  , one can show that:
, one can show that:

With this identity, we can replace the volume integral of the first three terms in (20) with a boundary integral. After transferring the remaining volume integrals to the right-hand side, we arrive at the desired relation between a boundary data integral and a volume integral of ADM data:
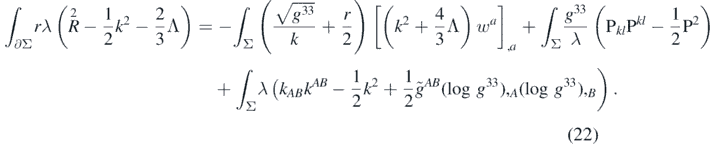
The boundary integral on the left-hand side of (22) resembles the definition of the Hawking mass (17), since due to Gauss–Bonnet theorem the expression  integrates to a constant, 8π, on both spheres constituting the boundary, and the coefficient r can be thought to roughly correspond to the square root of area of the sphere. However, we must make note of one serious discrepancy—instead of Hμ
Hμ
, the square of mean curvature of the 2D spheres with respect to the four-dimensional spacetime, in formula (22) we have k2, a square of mean curvature with respect to the 3D Cauchy hypersurface. In fact, the left-hand side of (22) is an expression for the Geroch energy [10], a modified version of the Hawking mass. We could, in principle, further manipulate the above expression to explicitly obtain the Hawking mass integral on the left-hand side. It turns out, however, that it is much simpler to introduce the adjustment to the left-hand side later, after performing the approximation of the right-hand side, since a suitable correction term will then appear by itself.
integrates to a constant, 8π, on both spheres constituting the boundary, and the coefficient r can be thought to roughly correspond to the square root of area of the sphere. However, we must make note of one serious discrepancy—instead of Hμ
Hμ
, the square of mean curvature of the 2D spheres with respect to the four-dimensional spacetime, in formula (22) we have k2, a square of mean curvature with respect to the 3D Cauchy hypersurface. In fact, the left-hand side of (22) is an expression for the Geroch energy [10], a modified version of the Hawking mass. We could, in principle, further manipulate the above expression to explicitly obtain the Hawking mass integral on the left-hand side. It turns out, however, that it is much simpler to introduce the adjustment to the left-hand side later, after performing the approximation of the right-hand side, since a suitable correction term will then appear by itself.
3. The second order approximation
We now perform a second order approximation of the right-hand side of equation (22). After grouping appropriate terms together, the result turns out to be the volume integral for the Hamiltonian function of the linearized theory (12) with a correction from the angular momentum charge and several boundary terms:
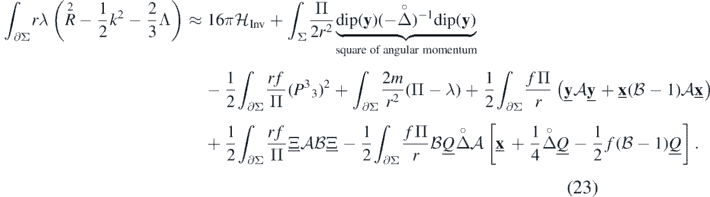
The calculation is rather straightforward, but tedious in its length. The discussion of techniques used in the derivation of (23) was therefore moved to appendix
3.1. Correcting the mean curvature
We will begin by looking at the first term in the second line of (23):  . Note that due to vanishing of the ADM momentum of the background metric, the term
. Note that due to vanishing of the ADM momentum of the background metric, the term  is by itself of second order in the perturbation. Using this and the ADM momentum definition (3), we see that up to second order corrections:
is by itself of second order in the perturbation. Using this and the ADM momentum definition (3), we see that up to second order corrections:
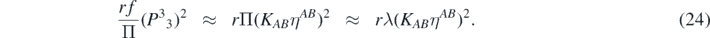
We can now transfer this term to the left-hand side of (23), which results in the following expression:
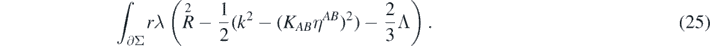
Note that we have not yet performed an approximation of the left-hand side of (23). All objects in the expression above, except for  , are fully non-linear. We should remember, however, that we are ultimately interested only in the value of this integral up to second order corrections in
hμν
. Within this level of precision, a following identity holds:
, are fully non-linear. We should remember, however, that we are ultimately interested only in the value of this integral up to second order corrections in
hμν
. Within this level of precision, a following identity holds:

which allows us to rewrite (25) as:
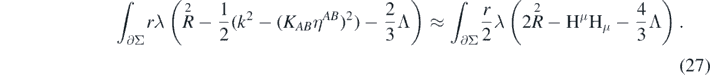
3.2. The radial coordinate
Next, we would like to address the second term in the second line of (23):  . It is a difference between boundary integrals of volume densities defined by the full and the background metric. Since the volume density λ is approximated by:
. It is a difference between boundary integrals of volume densities defined by the full and the background metric. Since the volume density λ is approximated by:
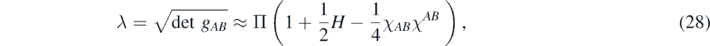
this term is actually a combination of first and second order corrections.
To obtain an equality between the Hawking mass and  we need for this term to vanish. This could be achieved simply by treating it as a boundary condition on the perturbation. However, one may also look at it from a different perspective. Let us return for a moment to the basic conceptual construction of the linearized theory. We may either start from the background metric and introduce some perturbation field on it, or go the other way around—begin with a 'perturbed' metric and try to compare it with a 'background' spacetime by means of an appropriate diffeomorphism. The second approach, although a bit more convoluted, strongly highlights the amount of freedom we posses when aligning the two metrics. Being given the perturbed Cauchy surface Σ with its intrinsic topologically spherical foliation, we are not only able to choose the mass and cosmological constant parameters of the background, but also the precise way in which we identify the points of Σ with the points in the 'reference' spacetime. Although some of this freedom is already fixed, since we wish to identify the leafs of the spherical foliation of Σ with the natural spherical foliation in the Kottler metric, we still have some leeway left in the way we pair the leafs of the foliations. This pairing is naturally represented by the labelling of the 2D spheres in Σ by the radial coordinate. Different choices of pairings will in turn result in monotonous rescaling of this coordinate. We may use this freedom to demand that on the two boundary spheres r is equal to the areal radius. Since the radial coordinate we use in Kottler is the areal radius, by choosing the identification of boundary spheres in this way we obtain the desired equality:
we need for this term to vanish. This could be achieved simply by treating it as a boundary condition on the perturbation. However, one may also look at it from a different perspective. Let us return for a moment to the basic conceptual construction of the linearized theory. We may either start from the background metric and introduce some perturbation field on it, or go the other way around—begin with a 'perturbed' metric and try to compare it with a 'background' spacetime by means of an appropriate diffeomorphism. The second approach, although a bit more convoluted, strongly highlights the amount of freedom we posses when aligning the two metrics. Being given the perturbed Cauchy surface Σ with its intrinsic topologically spherical foliation, we are not only able to choose the mass and cosmological constant parameters of the background, but also the precise way in which we identify the points of Σ with the points in the 'reference' spacetime. Although some of this freedom is already fixed, since we wish to identify the leafs of the spherical foliation of Σ with the natural spherical foliation in the Kottler metric, we still have some leeway left in the way we pair the leafs of the foliations. This pairing is naturally represented by the labelling of the 2D spheres in Σ by the radial coordinate. Different choices of pairings will in turn result in monotonous rescaling of this coordinate. We may use this freedom to demand that on the two boundary spheres r is equal to the areal radius. Since the radial coordinate we use in Kottler is the areal radius, by choosing the identification of boundary spheres in this way we obtain the desired equality:
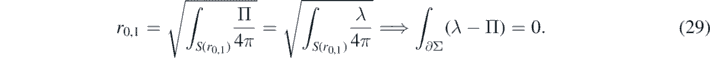
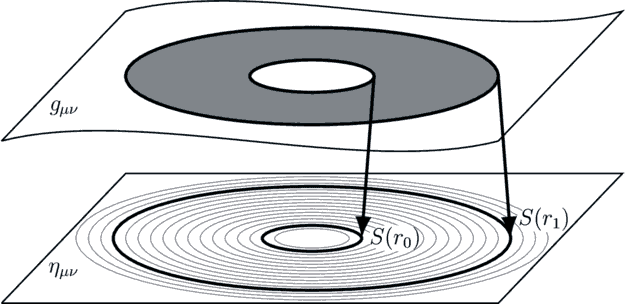
We note that both approaches to the construction of the linearization lead to the same final result. They just differ in the way in which we interpret equation (29)—we may either view it as a constraint on the perturbation, or as a recipe for the identification of the region boundaries between the two spacetimes, as shown in the graphic.
Finally, we need to observe that fulfilling (29) has another important consequence. If we multiply this equation by a factor of 1/2, we obtain:
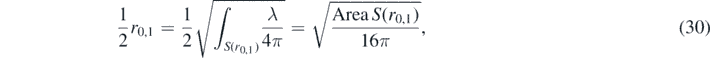
which is exactly the relation required to turn the left-hand side of (23), in its corrected form (27) into the Hawking mass expression (17). In fact, we could also start from the demand that expression (27) becomes the Hawking mass integral, deduce condition (29) from this and obtain the vanishing of the right-hand side correction term as a consequence.
3.3. Final result
With these observations and assumption (29), we may rewrite (23) in a cleaned up, final form:
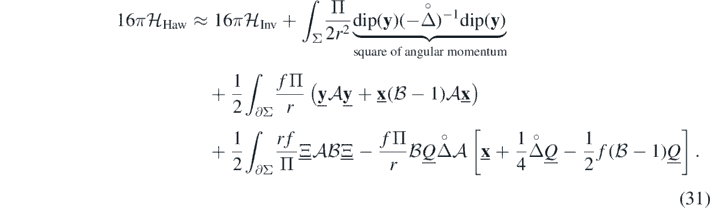
We would now like to interpret the remaining boundary integrals on the right-hand side. The quadratic expressions in  and
and  are constant if we control the value of these 'true degrees of freedom' at the boundary and can then be neglected: once we calculate the variation of (31), these expressions will turn into terms of the form
are constant if we control the value of these 'true degrees of freedom' at the boundary and can then be neglected: once we calculate the variation of (31), these expressions will turn into terms of the form  and
and  , which vanish if
, which vanish if  . This is, in fact, the same boundary condition that appeared during the derivation of
. This is, in fact, the same boundary condition that appeared during the derivation of  , cf (11). Mathematically, controlling the Dirichlet data on ∂Σ for the 'true degrees of freedom' is necessary whenever we want to describe field evolution within the domain Σ as a Hamiltonian system (see [6, 8, 12, 16]). Physically, such control defines an adiabatic insulation of the physical system we want to describe (i.e. the field contained in the interior of Σ) from the 'rest of the World'. This belongs to the standard repertoire of the Hamiltonian field theory.
, cf (11). Mathematically, controlling the Dirichlet data on ∂Σ for the 'true degrees of freedom' is necessary whenever we want to describe field evolution within the domain Σ as a Hamiltonian system (see [6, 8, 12, 16]). Physically, such control defines an adiabatic insulation of the physical system we want to describe (i.e. the field contained in the interior of Σ) from the 'rest of the World'. This belongs to the standard repertoire of the Hamiltonian field theory.
The meaning of the last line in (31) is a bit more puzzling. The quantities  and
and  are gauge dependent and the whole integral could be just brushed off as some artefact of the gauge freedom of linearized theory. However, they might actually posses a deeper meaning. If we look at the first order approximations of the mean curvature vector length and the divergence of extrinsic torsion:
are gauge dependent and the whole integral could be just brushed off as some artefact of the gauge freedom of linearized theory. However, they might actually posses a deeper meaning. If we look at the first order approximations of the mean curvature vector length and the divergence of extrinsic torsion:
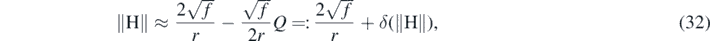

we observe that the last line of (31) could actually be rewritten in terms of perturbations of these functions:

We remind the reader that these are the same functions that are used to define the rigid sphere conditions (16). The spheres S(r) in the Kottler metric satisfy these conditions. Therefore, the gauge choice forced upon us by the last line in (31) can be interpreted as a linearized Rigid sphere condition. We stress that it arises spontaneously in our calculation, as a result of demanding that the approximation of the Hawking mass and the linear gravity Hamiltonian coincide.
The gauge choice can also be interpreted as a condition imposed on the vector field  , i.e. on the reference frame. As noted in the introduction, a Hamiltonian functional generating evolution with respect to a generic reference frame does not have the properties which we expect from a true energy, namely positivity, convexity etc. But the quadratic expression
, i.e. on the reference frame. As noted in the introduction, a Hamiltonian functional generating evolution with respect to a generic reference frame does not have the properties which we expect from a true energy, namely positivity, convexity etc. But the quadratic expression  does fulfill these properties! Thus, the Hawking mass measured on a rigid sphere is positive and convex, at least in the regime of weak fields, when its quadratic approximation prevails. It represents the field energy measured with respect to a reference frame T satisfying the condition: gμν
Tμ
Hν
= 0. If the boundary of Σ does not satisfy the rigidity condition
does fulfill these properties! Thus, the Hawking mass measured on a rigid sphere is positive and convex, at least in the regime of weak fields, when its quadratic approximation prevails. It represents the field energy measured with respect to a reference frame T satisfying the condition: gμν
Tμ
Hν
= 0. If the boundary of Σ does not satisfy the rigidity condition  , the corresponding quantity
, the corresponding quantity  is not necessarily positive even in the weak field regime and cannot be identified with the field energy contained in Σ because the corresponding field T cannot be treated as a 'time translation' in any reasonable sense.
is not necessarily positive even in the weak field regime and cannot be identified with the field energy contained in Σ because the corresponding field T cannot be treated as a 'time translation' in any reasonable sense.
4. Conclusions
We used our formalism of reduced variables to investigate the behaviour of Hawking mass for weak gravitational perturbations of the Kottler metric. It turns out that quadratic approximation of the quasi-local mass is related to the gauge-invariant Hamiltonian (the generator of dynamics of linear theory) provided that the boundary of the considered region is composed of spheres satisfying a certain gauge condition. This condition is a linearization of the 'rigid sphere condition' from the complete, non-linear theory. The rigid sphere condition, in turn, characterizes spheres which provide a physically reasonable 'reference frame' for defining time translations of a region in spacetime—which is necessary to talk about energy. This observation supports our hypothesis that the quasi-local energy can be reasonably defined only for 2D surfaces ∂Σ which satisfy extra conditions—those for which such time translations are well defined.
The relation (31) contains an extra bulk term: the 'square of angular momentum'. But, due to the vector constraint, this term can be rewritten as a boundary term, see [17].
Acknowledgments
This work was supported in part by Narodowe Centrum Nauki (Poland) under Grant No. 2016/21/B/ST1/00940. One of the authors (PW) was also supported by a special internal Grant for young researchers, provided by Center for Theoretical Physics, PAS, Warsaw, Poland.
Data availability statement
No new data were created or analysed in this study.
Appendix A.: Performing the second order approximation
Deriving the approximation of the right-hand side of equation (22) is a lengthy calculation, consisting mostly of simple algebraic manipulations. Therefore, we do not present it in detail. Instead, we will just outline the crucial points of the procedure.
To briefly summarize the calculation: we begin by replacing the objects under the integral on the right-hand side of (22) with their expansions in terms of the perturbation, then trim the results so only corrections up to second order remain, and finally express as much of the outcome as possible in terms of our reduced variables (x, X, y, Y) and auxiliary objects Ξ and Q (as can be seen in the second row of (23), some leftover terms will remain). We also use the emergent radial derivatives to change volume integrals into boundary ones.
The first two parts of the task are greatly simplified by the way in which the terms of equation (22) are already arranged. Observe that the second and third row is comprised of squares of objects which vanish for the unperturbed background metric: Pkl
, P, ∂A
( log g33), and finally  . This means that the first terms in the perturbative expansion of these rows will already be of second order and all we need to do is just replace the above expressions with their first order approximations. Unfortunately, the product of brackets in the first row of (22) does not posses this useful property and to calculate its approximation we need to compute second order corrections of its factors. Still, even in this case some effort can be saved by performing the calculations in an appropriate order and noticing that the left bracket in the product is again an object which vanishes for the unperturbed background.
. This means that the first terms in the perturbative expansion of these rows will already be of second order and all we need to do is just replace the above expressions with their first order approximations. Unfortunately, the product of brackets in the first row of (22) does not posses this useful property and to calculate its approximation we need to compute second order corrections of its factors. Still, even in this case some effort can be saved by performing the calculations in an appropriate order and noticing that the left bracket in the product is again an object which vanishes for the unperturbed background.
The next step is to rewrite the result in terms of the gauge-invariant variables. For this, we must perform a (2 + 1) decomposition in a manner similar to the original construction of the reduced variables in section 1.1. The less obvious part is perhaps generating the 2D rotations and divergences of the tensors. This can be done by employing the following integral identities: for two vector fields vA and wA , tangent to a 2D sphere S(r), the following holds:
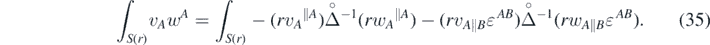
Similarly, for a pair of traceless, symmetric tensor fields pAB , tAB on a 2D sphere:

Once the decomposition has been performed, we may use the system of linear equations consisting of definitions of gauge-invariant variables, definitions of auxiliary variables Q and Ξ, and the set of linearized Gauss–Codazzi constraints (cf [5]):

to replace the ADM data components by the gauge-invariant variables through algebraic substitution. Applying the linearized Gauss–Codazzi constraints will produce some radial derivatives in the approximated formula. As mentioned earlier, these should be combined into total divergences in the radial direction and turned into boundary integrals, until the remaining terms in the volume integral contain either no radial derivatives or squares of them (which become part of the Hamiltonian of the linearized theory (12)). This concludes the derivation.
Footnotes
- 3
The term 'quasi-local' refers to the fact that the obtained notion of gravitational field energy, although no longer dependent on the whole global field configuration, is not a local object. It can be defined for a finite, but extended region of spacetime, and to compute it for a given bounded region Σ one requires not only the knowledge of the whole field configuration on Σ, but also of the boundary conditions on ∂Σ.
- 4
In General relativity theory, two 3D regions Σ1 and Σ2 having the same boundary ∂Σ1 = ∂Σ2 contain the same amount of energy due to the diffeomorphism invariance of the dynamics.
- 5
Here, again, two 3D regions Σ1 and Σ2 having the same boundary contain the same amount of energy due to: (1) 'conservation laws' satisfied by the Noether energy–momentum tensor and (2) boundary conditions. The latter assure the uniqueness of the evolution.
- 6
Although we pursue the way of defining quasi-local mass as a boundary object, one should note that competitive approaches exist, in which the quasi-local mass is being assigned to a three-dimensional region or even to whole four-dimensional domains of dependence [10]. Various approaches naturally coincide in certain special cases, eg. the Tolman mass, originally defined as an integral of the stress-energy tensor over a three-dimensional volume can be rewritten as a boundary integral of generalized surface gravity in stationary spacetimes [11].
- 7
Existence and location of horizons is determined by positive roots of the cubic polynomial r f(r). For Λ < 0 only one positive root, the black hole radius rS , exists and we assume rS ⩽ r0 < r1. For Λ > 0 there are two positive roots, interpreted as the black hole and cosmological horizon radii rS < rC . In this case, we take rS ⩽ r0 < r1 ⩽ rC .
- 8
By the 'mono-dipole-free' part of a function q we mean the function with its projections onto monopole and dipole harmonics removed,
 .
.

