Abstract
In this paper we present geometry which has been designed to fit a layperson's description of a 'time machine'. It is a box which allows those within it to travel backwards and forwards through time and space, as interpreted by an external observer. Timelike observers travel within the interior of a 'bubble' of geometry which moves along a circular, acausal trajectory through spacetime. If certain timelike observers inside the bubble maintain a persistent acceleration, their worldlines will close.
Our analysis includes a description of the causal structure of our spacetime, as well as a discussion of its physicality. The inclusion of such a bubble in a spacetime will render the background spacetime non-orientable, generating additional consistency constraints for formulations of the initial value problem. The spacetime geometry is geodesically incomplete, contains naked singularities, and requires exotic matter.
Export citation and abstract BibTeX RIS
1. Introduction
The possibility that some spacetime geometries permit retrograde time travel has long been a preoccupation of both general relativists and popular fiction [24]. Among physicists, General Relativity's allowance for closed timelike curves (CTCs) resulting from exotic spacetime geometry is a subject of heated debate. While CTCs are—strictly speaking—a mathematical possibility; they are philosophically undesirable. In a fashion similar to the debate over the physicality of curvature singularities, we burn to know whether the physical laws of our universe would actually permit CTCs to form.
Most of this discussion has taken place in the context of the derivation and analysis of geometries where CTCs exist. Thus, the bulk of the debate involves arguments concerning physical plausibility of these specific examples.
We can classify most of the CTC spacetimes into one of three types.
In the first class: CTCs naturally appear in very symmetric geometries characterized as having strong angular momentum. Gödel derived the first geometry to contain CTCs: a homogeneous universe filled with rotating dust [14]. The Kerr spacetime and the Tomimatsu–Sato spacetimes [35] are rotating vacuum geometries, and all contain CTCs near their centre. CTCs can be generated by infinitely long cylinders of rotating matter, known as Tipler cylinders [34, 36]. Two moving cosmic strings can generate CTCs as they pass near enough to one another [6, 16].
The second class geometries are those which have been deliberately designed to contain CTCs for the purpose of studying the physical consequences. Famously, two mouths of a traversable wormhole can be accelerated with respect to one-another, harnessing the effect of the 'twin paradox' to generate CTCs in a region where none were previously present [8, 11]. The Ori [32] and Ori-Soen [31] spacetimes generate CTCs through an escalating frame dragging effect in a toroidal domain.
The third class of geometries are the exotic geometries which have been engineered to permit superluminal travel; where although generating CTCs were not the direct intention, they occur as a natural consequence. The Alcubierre warp drive [1] can be used to generate CTCs [9, 15]; as can the Krasnikov tube [10, 23]. Note, however, that due to the details of their construction it is not possible to generate CTCs within a single warp bubble or tube. A timelike observer would need to travel through a succession of tubes or bubbles, undergoing acceleration between each, for their worldline to close.
Although CTCs are generally held to be unphysical, we have not yet discovered a universal mechanism or argument which would preempt the formation or existence of CTCs in our universe. Rather, the bulk of the counterargument is piecemeal, identifying the specific unphysical idiosyncrasies or impracticalities of each individual geometry where CTCs are present [20, 28]:
- The CTCs in the Kerr geometry lie behind the black hole's event horizon, and since a physical Kerr black hole cannot be spun up beyond its extremal limit [38], the CTCs remain inaccessible to the outside universe.
- Tomimatsu–Sato geometries are vacuum spacetimes possessing naked singularities, and are not recognized as the endstate of gravitational collapse.
- The remaining mentioned models of the first class require infinite distributions of matter.
- Traversable wormholes are forbidden by the topological censorship theorem, requiring matter which violates the classical energy conditions [12].
- Spacetimes geometries which permit superluminal travel require matter source which must violate the classical energy conditions [24, 29, 30].
General arguments against the formation of CTCs have also been proposed. The ambition is that these arguments would forbid the construction of a physical time machine in our universe.
Hawking's chronology protection conjecture [17, 22] attempts to curtail the formation of CTCs, and is concerned with a CTC whose presence in the spacetime is preceded by a compactly generated Cauchy horizon. The argument follows that null matter, in following the coiling null geodesic which approaches the Cauchy horizon compact closed null curve as a limiting curve, will cause the energy density in the volume of spacetime near the Cauchy horizon to diverge. Thus, these spacetimes are not stable, and are more likely to generate a black hole than a time machine [37].
The conjecture's reliance on compactly generated Cauchy horizons limits the scope of the counterargument. Closed timelike curves can form in a spacetime without being preceded by a closed null curve. However, a theorem by Maeda et al concerning these geometries argues that if such a spacetime obeys the classical energy conditions, it cannot also be geodesically complete (it must contain singularities) [27].
Finally, Gibbons and Hawking have argued that our physical requirement for spinor structure in our spacetime should impose a constraint on which spacetimes are permissible and which ones are not. They find, for instance, that wormholes must exist in pairs, in order to retain the appropriate spinor structure through the rest of the spacetime [13].
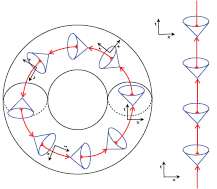
In spite of this rich history of study, the menagerie of CTC geometries is by no means complete. The purpose of this paper is to add a simple model of the second class to the list: a spacetime which means to fit the popular conception of a 'time machine'. It is a box which travels 'forwards' and then 'backwards' in time along a circular path through spacetime (figure 1). Delighted external observers would be able to watch the time travellers within the box evolving backwards in time: un-breaking eggs and separating cream from their coffee.
Figure 1. A schematic of the timelike observers confined to the interior and exterior of the bubble. Observers A (inside the bubble) and B (outside the bubble) experience the events in dramatically different ways. Arrows indicate the local arrow of time. Within the bubble, A will see the B's events periodically evolve, and then reverse. Outside the bubble, observer B will see two versions of A emerge from the same location: one's clock hands will turn clockwise, the other counterclockwise. The two versions of A will then accelerate towards one another and annihilate.
Download figure:
Standard image High-resolution image2. TARDIS geometry
The Traversable Acausal Retrograde Domain in Spacetime (TARDIS) is a bubble geometry, derived in a similar way to the Alcubierre warp drive, which uses a shell of exotic matter to transport timelike observers along a trajectory which, to external observers, appears acausal. Unlike the Alcubierre drive, the TARDIS bubble follows a closed trajectory in spacetime, and observers must maintain a persistent, constant acceleration to have a closed worldline.
2.1. Metric
Our geometry has the following metric:

Similar to the Alcubierre bubble, this metric relies on a top-hat function h(x, y, z, t) to partition the interior of the bubble h(x, y, z, t) = 1 from the exterior spacetime h(x, y, z, t) = 0.
The exterior of the bubble and the interior of the bubble are both flat Minkowski vacuums. To illustrate, consider that under the coordinate transformation:

the interior metric (when h(x, y, z, t) = 1) explicitly takes the form of the metric of Rindler spac etime:

In this context the Rindler geometry has a modified topology, amounting to identifying the surfaces  with
with 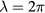 in the maximal extension Rindler geometry. Thus, within our bubble, trajectories described with constant spatial coordinates:
in the maximal extension Rindler geometry. Thus, within our bubble, trajectories described with constant spatial coordinates: 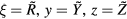 will be CTCs. Such curves are not geodesics. If
will be CTCs. Such curves are not geodesics. If ![${{L}^{a}}=[\frac{1}{{\tilde{R}}},0,0,0]$](https://content.cld.iop.org/journals/0264-9381/34/9/095006/revision2/cqgaa6549ieqn004.gif) denotes a normalized vector tangent to one of these CTC, and Ka = [0, 1, 0, 0] is an orthogonal spacelike vector:
denotes a normalized vector tangent to one of these CTC, and Ka = [0, 1, 0, 0] is an orthogonal spacelike vector:
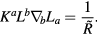
An observer moving along one of these curves will feel an acceleration equal to 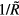 : the wider the 'radius' of the circular CTC, the weaker the acceleration required to travel along it.
: the wider the 'radius' of the circular CTC, the weaker the acceleration required to travel along it.
For the purpose of this paper, we shall define the boundary of the bubble to have rounded boxy shape (whose size is given in terms of radial parameter R) moving along a circle of 'radius' A in the x − t plane (see figure 2):
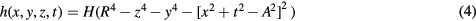
where H(x) denotes the Heaviside function.
Figure 2. Evolution of the boundaries of the bubble, as defined in section 2.1, as seen by an external observer. At T = −100 the bubble will suddenly appear, and split in to two pieces which will move away from one another (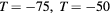 ). At T = 0, the two bubbles will come to rest, and then begin accelerating towards one-another (
). At T = 0, the two bubbles will come to rest, and then begin accelerating towards one-another (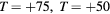 ). Whereupon, at T = +100 the two bubbles will merge and disappear. (a) TARDIS boundaries at T = 0. (b) TARDIS boundaries at
). Whereupon, at T = +100 the two bubbles will merge and disappear. (a) TARDIS boundaries at T = 0. (b) TARDIS boundaries at  . (c) TARDIS boundaries at
. (c) TARDIS boundaries at 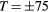 . (d) TARDIS boundaries at
. (d) TARDIS boundaries at 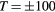 .
.
Download figure:
Standard image High-resolution imageWe smoothly approximate the Heaviside function using a hyperbolic tangent function:

The α parameter is used to define the thickness of the bubble wall: the larger it is, the more abrupt the transition between the interior and exterior geometries.
All of the numerical models plotted in this paper share the parameters A = 100, R = 70 and  .
.
2.2. Causal structure
2.2.1. Null geodesics.
By design, the light cones of this spacetime are meant to tip in a way which allows observers inside the bubble to travel along circular CTCs (see figure 3). To illustrate the details of the causal structure of our geometry we have numerically integrated and plotted null geodesics crossing the slice y = 0, z = 0 in figure 4. Since the intersection of null geodesics dictates the orientation of the lightcones, it is clear that they tip in the desired fashion. Observers inside the bubble will clearly be able to see and interact with their past and future selves, as null geodesics move through and across the geometry. Also, for an arrow of time to be consistent inside the bubble, an external observer would see two versions of the objects inside of it: one version evolving forwards in time, the other backwards.
Figure 3. The light cones inside the bubble are meant to tip in a circular path relative to the exterior light cones. For illustrative purposes we have chosen to make counter-clockwise and upwards the 'future' directions in our diagram. This orientation is confirmed in the null curve diagram in figure 4.
Download figure:
Standard image High-resolution imageFigure 4. Null geodesics travelling through a cross section  . The intersection of null curves can indicate the orientation of the light cone. The curves are colour coded according to the conformal infinities they extend towards. The red and green curves have both endpoints at the same respective conformal null infinity, while the blue ones stretch from one null infinity to the other.
. The intersection of null curves can indicate the orientation of the light cone. The curves are colour coded according to the conformal infinities they extend towards. The red and green curves have both endpoints at the same respective conformal null infinity, while the blue ones stretch from one null infinity to the other.
Download figure:
Standard image High-resolution imageSome of the null curves in figure 4 may undergo dramatic lensing when they intersect with the walls of the bubble: appearing to 'kink'. These kinks in the trajectory occur at the boundary of the bubble in places where the orientation of timelike vectors differs dramatically on the inside (sideways) from the outside (vertically). These locations are illustrated with a dashed line in figure 4.
It should be noted that our software could not illustrate some of these geodesics beyond where many of these 'kinks' occur due to underlying issues involving their parametrization. Thus, some of the null curves in figure 4 deceptively appear to end in the vicinity of the dashed line. In terms of an affine parametrization μ, and the interior coordinates given in the metric from equation (2), the null vectors at a point ![${{r}^{a}}=\left[\lambda,\,\xi,\,y,\,z\right]$](https://content.cld.iop.org/journals/0264-9381/34/9/095006/revision2/cqgaa6549ieqn013.gif) on this plane satisfy:
on this plane satisfy:

The kinks in the null geodesic all occur along the surface 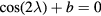 : where one of the two null vectors must satisfy
: where one of the two null vectors must satisfy  , while the other satisfies
, while the other satisfies 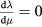 . Thus, when a null geodesics encounters this surface, it will either move in a purely 'radial' direction, or move tangentially to a 'circle' centred at
. Thus, when a null geodesics encounters this surface, it will either move in a purely 'radial' direction, or move tangentially to a 'circle' centred at 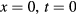 . And thus, depending on the affine parametrization
. And thus, depending on the affine parametrization 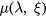 we are using, either
we are using, either 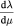 or
or 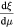 will diverge. The numerical errors generated by these divergences halt the execution of our Maple plot, even though the metric is smooth and continuous at and near these points.
will diverge. The numerical errors generated by these divergences halt the execution of our Maple plot, even though the metric is smooth and continuous at and near these points.
2.2.2. Global causal structure.
The embedding of the TARDIS bubble in the exterior spacetime dramatically modifies the spacetime's causal structure. To illustrate these effects, it is helpful to put ourselves in the shoes of an astrophysicist (named 'Tim') who has concerned himself with the problem of determining what effect the bubble geometry would have on the future time evolution of some test matter, positioned on a constant time hypersurface in the coordinate past of the bubble's formation. Tim, in his confusion, would surely describe the issues he encounters by using the terminology ordinarily used to describe the causal structure of Minkowski space.
Begin by considering the null geodesics which are destined kink across the dashed line in figure 4 twice. Suppose that the affine parameter we choose to describe the given null curves' position initially increases with time coordinate t. Since some of these geodesics will refract across the bubble walls in a way which ultimately turns them in the direction of decreasing coordinate t; the spacetime manifold is not time orientable [18]. Tim poetically describes the effect of the bubble as having 'reflected' these null geodesics in time.
Tim will therefore make a note that, while most of the null geodesics begin at past null infinity and end at future null infinity; there will be a family of 'reflected' null geodesics which have both endpoints at past null infinity, and another family which have both endpoints at future null infinity. Tim's friends might helpfully point out that in a non-time orientable spacetime, the concepts of 'future null infinity' and 'past null infinity' are meaningless as descriptors, and that the global causal structure of this spacetime is dramatically different from that of Minkowski spacetime, but Tim marches on.
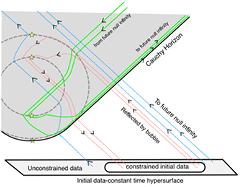
In describing the setup of the initial value problem on a constant time hypersurface in the coordinate past of the bubble, Tim will note that any such hypersurface (no matter how far in the 'past') will be intersected twice by these 'reflected' null geodesics, and thus any initial conditions posed on such a surface would be subject to additional consistency conditions. A specific photon, deposited on the hypersurface in one location, may need to reappear in a second place on the same hypersurface as it crosses the surface after being reflected by the bubble (figure 5). Tim's helpful friends will remind him that this specific property disqualifies these constant time hypersurfaces from being Cauchy surfaces [18], but Tim stops for no one.
Figure 5. Tim has drawn a diagram, explaining his difficulties in setting up an initial value hypersurface and simulation. Two families of null curves in this diagram are 'reflected' by the bubble geometry. The red curves start and end at 'past' null infinity, causing them to intersect spacelike hypersurfaces in more than one place and forcing initial conditions placed on these surfaces will also need to satisfy additional consistency conditions. The green curves start and end at 'future' null infinity, bringing in new information which was not present on the initial hypersurface, and making predictions past the 'Cauchy horizon' impossible.
Download figure:
Standard image High-resolution imageTim goes on, and manages to come up with some initial data which satisfies these additional constraints, and now seeks to evolve the system forward in time. In doing so, Tim discovers that there are limits to how far a numerical evolution of initial data posed on such a hypersurface would progress into the future. Among the null geodesics which have an endpoint at one of the singularities located where 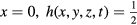 are lines which act as a boundary for the family of null curves which have both endpoints at future null infinity (figure 5). Tim would describe this collection of geodesics as forming a 'Cauchy horizon'; where new information which was not present on his hypersurface (originating from the singularity, or from future null infinity) might skew his system's evolution in unforseeable ways. His friends might disagree that this surface is a true Cauchy horizon, arguing that the 'reflected' null geodesics pass beyond this surface, and thus, potentially interact with the information originating from 'future null infinity' or the singularity. The events occurring in the far far future will influence the constraints applied to the data on Tim's initial surface as a form of a global consistency condition [11].
are lines which act as a boundary for the family of null curves which have both endpoints at future null infinity (figure 5). Tim would describe this collection of geodesics as forming a 'Cauchy horizon'; where new information which was not present on his hypersurface (originating from the singularity, or from future null infinity) might skew his system's evolution in unforseeable ways. His friends might disagree that this surface is a true Cauchy horizon, arguing that the 'reflected' null geodesics pass beyond this surface, and thus, potentially interact with the information originating from 'future null infinity' or the singularity. The events occurring in the far far future will influence the constraints applied to the data on Tim's initial surface as a form of a global consistency condition [11].
Additionally, since the null curves generating the 'Cauchy Horizon' are not compactly generated (instead, they have an endpoint), Hawking's chronology protection conjecture will not apply to this spacetime [17, 19]. This is not the first CTC spacetime to have this attribute [5, 7, 21, 26, 33].
2.3. Geometry and matter
The stress energy tensor required to generate this spacetime is nonzero only at the boundary of the bubble (points satisfying 0 < h(x, y, z, t) < 1). Since we have taken a 'metric-first' approach to deriving this geometry, the source matter can be readily found using the Einstein equation. However, there is no expectation that it would behave like any familiar type of matter, since this constraint was not factored into the derivation of this geometry. Graphs of the components of the stress energy tensor in this region of the spacetime are not very informative.
A more interesting set of questions to ask is whether this geometry is physically reasonable? Is the matter everywhere finite, or are there singularities? Does the spacetime curve in a way consistent with familiar matter: are the the classical energy conditions satisfied [18]?
There are naked curvature singularities in the Kretschmann scalar (figure 6(a)) and in the first principal invariant of they Weyl tensor at points where the top hat function has values  and the shell intersects the plane x = 0. Along these 2-surfaces,
and the shell intersects the plane x = 0. Along these 2-surfaces, 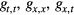 are all equal to zero, meaning that these locations are not part of the spacetime manifold and that the spacetime is geodesically incomplete. Geodesic incompleteness is an expected property for a spacetime which does not satisfy the chronology protection conjecture [21, 27].
are all equal to zero, meaning that these locations are not part of the spacetime manifold and that the spacetime is geodesically incomplete. Geodesic incompleteness is an expected property for a spacetime which does not satisfy the chronology protection conjecture [21, 27].
Figure 6. (a) The Kretschmann scalar along z = 0, y = 0. (b) The value  along
along  , where Na is a null vector field along the surface.
, where Na is a null vector field along the surface.
Download figure:
Standard image High-resolution imageFurthermore, the geometry in the nonsingular parts of the bubble is also unphysical. In figure 6(b) we plot the 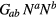 (where Na are null vectors) for a
(where Na are null vectors) for a  slice. In Einstein gravity, this quantity corresponds to the energy density as seen along null geodesics. That it has a negative value in some places implies that this matter will not satisfy the null energy condition.
slice. In Einstein gravity, this quantity corresponds to the energy density as seen along null geodesics. That it has a negative value in some places implies that this matter will not satisfy the null energy condition.
Note, however, that interpreting these aspects of the geometry in terms of the matter required to create it depends upon the relationship between the two as it is specified by the Einstein Equation. In generalized theories of gravity, the Einstein equation is only a first order approximation to a more sophisticated relationship between the geometry and the matter in the spacetime [3, 4]. Introducing extra degrees of freedom between these two allow for the possibility that classically forbidden curvature can be generated without requiring matter which violates the classical energy conditions. F(R) theories of gravity have been used to derive traversable wormholes, and accelerating cosmological expansion using physically plausible matter [2, 25].
3. Discussion
This spacetime is both fascinating and problematic.
On one hand, it explicitly possesses many attributes of a 'time machine' from popular fiction: embedding a compact region with circular closed timelike curves in a simple, asymptotically flat background. There are places where an observer inside the bubble will travel 'sideways' in time relative to external observers; and other places where the the arrow of time inside the bubble must be retrograde to direction of time just outside the bubble wall. As such, it works as a playground for examining the consequences such a time machine would have on the global causal structure. The presence of such a bubble would impose strong consistency constraints on the information imposed on any spacelike hypersurface to the 'past' or 'future' of the bubble. Furthermore, since timelike observers can exit the bubble after completing only a half-tour, the inclusion of a TARDIS bubble to the spacetime can render the entire manifold non time-orientable.
On the other hand, the spacetime possesses naked singularities and requires manifestly unphysical matter to generate it. The violation of the classical energy conditions is unsurprising, since the derivation of this metric mirrors that of the Alcubierre warp drive, and both bubbles are seen by outside observers to be travelling superluminally.
One question which has dogged us as we constructed this geometry is whether the multiple unphysical aspects are necessary consequences of the desired causal structure, or merely artifacts arising from its derivation or symmetry. Specifically, it is expected that the energy conditions should be violated, or that the spacetime be singular [21, 27]; but it is it necessary for our spacetime to be both?
For example, it may be possible to use Israel junction conditions to connect the CTC Rindler interior with the Minkowski exterior by identifying a pair of 3-surfaces in a way which satisfies the classical energy conditions.
Or, on the other hand, considering the way in which Alcubierre warp drives can be used to generate CTCs without singularities might provide a clue to removing the singularities from the TARDIS bubble.
Regardless, we are sure that the coming years will provide ample motivation for further study in this field.