Abstract
We present a comprehensive study of the relationship between the ferromagnetism and the structural properties of Fe systems from three-dimensional ones to isolated atoms based on the spin-density functional theory. We have found a relation between the magnetic moment and the volume of the Voronoi polyhedron, determining, in most cases, the value of the total magnetic moment as a function of this volume with an average accuracy of ±0.28 μB and of the 3d magnetic moment with an average accuracy of ±0.07 μB when the atomic volume is larger than 22 Å3. It is demonstrated that this approach is applicable for many three-dimensional systems, including high-symmetry structures of perfect body-centered cubic (bcc), face-centered cubic (fcc), hexagonal close-packed (hcp), double hexagonal close-packed (dhcp), and simple cubic (sc) crystals, as well as for lower-symmetry ones, for example atoms near a grain boundary (GB) or a surface, around a vacancy or in a linear chain (for low-dimensional cases, we provide a generalized definition of the Voronoi polyhedron). Also, we extend the validity of the Stoner model to low-dimensional structures, such as atomic chains, free-standing monolayers and surfaces, determining the Stoner parameter for these systems. The ratio of the 3d-exchange splitting to the magnetic moment, corresponding to the Stoner parameter, is found to be I3d = (0.998 ± 0.006) eV /μB for magnetic moments up to 3.0 μB. Further, the 3d exchange splitting changes nearly linearly in the region of higher magnetic moments (3.0–4.0 μB) and the corresponding Stoner exchange parameter equals  . The existence of these two regions reflects the fact that, with increasing Voronoi volume, the 3d bands separate first and, consequently, the 3d magnetic moment increases. When the Voronoi volume is sufficiently large (≥22 Å3), the separation of the 3d bands is complete and the magnetic moment reaches a value of 3.0 μB. Then, when the volume further increases, the 4s bands start to separate, increasing thus the 4s magnetic moment. Surprisingly, in the region of higher magnetic moments (≥3.0 μB), there is also a linear relationship between the 4s exchange splitting and the total magnetic moment with a slope of
. The existence of these two regions reflects the fact that, with increasing Voronoi volume, the 3d bands separate first and, consequently, the 3d magnetic moment increases. When the Voronoi volume is sufficiently large (≥22 Å3), the separation of the 3d bands is complete and the magnetic moment reaches a value of 3.0 μB. Then, when the volume further increases, the 4s bands start to separate, increasing thus the 4s magnetic moment. Surprisingly, in the region of higher magnetic moments (≥3.0 μB), there is also a linear relationship between the 4s exchange splitting and the total magnetic moment with a slope of  eV /μB, which is nearly identical to I3d for magnetic moments up to 3.0 μB. These linear relations can be considered as an extension of the Stoner model for low-dimensional systems.
eV /μB, which is nearly identical to I3d for magnetic moments up to 3.0 μB. These linear relations can be considered as an extension of the Stoner model for low-dimensional systems.
Export citation and abstract BibTeX RIS
1. Introduction
Magnetic ordering is known to directly correlate with the structure and dimensionality of materials. For example, the atomic configuration at surfaces [1, 2], in nanowires [3] and clusters [4, 5], of ferromagnetic materials may exhibit higher local atomic magnetic moments than in a perfect bulk. Some of these configurations, such as clusters, can turn non-magnetic Rh, V, and Ag into ferromagnetic states [6, 7]. With increasing cluster size, the magnetic moment of Fe, Co, and Ni clusters gradually transfers from atomic-like to bulk-like magnetism, as observed in experiments [4]. The magnetic frustration of the FeCr system depends strongly on the Cr concentration and the distribution of Cr atoms (dispersed or clustered) [8]. All these phenomena may be explained on the basis of the magnetovolume effect [9, 10], which manifests itself in increasing local magnetic moment with increasing atomic volume [9, 11–14]. The physical basis of the magnetovolume effect is the interplay between the kinetic and exchange energies (which are enhanced and decreased, respectively, by increasing the magnetic coupling), leading to a higher magnetic moment at larger volumes.
An isolated atom exhibits the maximum spin according to Hund's rules, resulting in a maximum magnetic moment of 4.0 μB for an isolated Fe atom. When Fe atoms form a bulk, each atom is confined to a reduced volume. The interactions among the atoms in the bulk cause overlapping of majority and minority states. Therefore there is a concomitant promotion of electrons from the majority-spin band to minority spins, leading to a reduced local magnetic moment. Not only in perfect bulk Fe systems, but also in those with defects or strains, magnetic moments are enhanced when atomic volumes are expanded.
The relation between the magnetic properties and the atomic configuration of a solid has been a subject of considerable interest for the scientific community. Liu et al [15–17] have studied the local magnetic moments of Fe and Ni in the bulk, clusters, surfaces, thin films, and voids, and found that they increase as the coordination number (CN) decreases or the lattice expands. Kim et al [18] have developed an empirical model to characterize the local magnetic moment with the help of the CN and interatomic bond length in high-index Fe surfaces. Although, qualitatively, the coupling of the CN and the bond length can reflect the magnetovolume effect, they are limited to perfect (high-symmetry) configurations. We face a difficulty when estimating the atomic magnetic moment in low-symmetry defected systems, for example, in a grain boundary (GB), near a surface, or in the neighborhood of a dislocation core. Firstly, the CN is not uniquely defined in terms of the number of first nearest neighbors (1NN) [17]. Particularly in defected systems, 2NN or more distant neighbors should also be included into the CN because of the contribution of the low-symmetry configurations. Secondly, even with the same CN and bond length, configurations with different angle distributions can also lead to different magnetic moments, as we show in the GB part in this work.
Liot et al [19] and Li et al [20] recently studied a correlation between the magnetic moment and the local atomic volume in binary Fe alloys. The local atomic volume was defined by a sphere [19] or by an average volume obtained by the supercell volume over the number of atoms in the supercell [20]. For the spherical local atomic volume, the radius was equal to half of the mean distance between the Fe site and its 1NNs [19]. In all the perfect systems considered, the sphere volumes and average volumes are related to local magnetic volumes and may be employed, to some degree, as geometrical characteristics. However, in comparison with the methods of Liu et al [15–17] and Kim et al [18], the sphere volume only reflects the average bond length with the 1NN atoms, ignoring partly the effect of the CN on the magnetic moment. The average volume, on the other hand, is only determined by the relaxed lattice dimensions and does not reflect the local atomic geometry. Therefore, relating the sphere and/or average volume to magnetic effects in low-dimensional and defected systems is obviously limited.
Here we consider the local atomic volume as the volume of a corresponding Voronoi polyhedron. This approach is widely applied in physics, chemistry, statistical geography and biology. We have found here that the volume of the Voronoi polyhedron is closely connected with the local magnetic moment in Fe. Further, we have analyzed the validity of the Stoner theory of itinerant magnetism in low-dimensional systems. Our research provides a basic understanding of the relationship between the local magnetic moment and the structural properties of Fe and extends the Stoner model to low-dimensional systems.
Let us note that most theoretical papers studying the stability of Fe (and other solids) are dealing only with stability under pressure. That is understandable as pressure experiments, even to hundreds of GPa, are routinely performed these days in many laboratories. However, to the best of our knowledge, there are very few papers analyzing the stability of solids under negative pressures or higher atomic volumes (see e.g. [21] for an exception). In this sense, our paper is a pioneering study exploring the structural and magnetic behavior of various Fe systems up to an atomic volume of 135 Å3, from three-dimensional bulk structures over surfaces and two-dimensional embedded and free-standing systems to one-dimensional atomic chains and free atoms. For this purpose, we also extend the definition of the Voronoi volume for low-dimensional systems and analyze the validity of the Stoner model in this region.
This paper is organized as follows. After the introduction, we summarize the computational details in section 2. Subsequently, section 3 deals with perfect bulk systems, whereas section 4 is devoted to vacancies and grain boundaries and section 5 to surfaces. In section 6 we analyze the magnetic moments for three-dimensional, surface and two-dimensional embedded systems. In section 7 we study free-standing low-dimensional systems and extend the definition of the Voronoi volume for low-dimensional cases. In section 8 we explore the validity of the Stoner model for low-dimensional systems and demonstrate that it can be extended also to these cases. Section 9 summarizes the results and concludes the whole paper.
2. Computational details
Our first-principles calculations are performed in the framework of the density functional theory (DFT), as implemented in the SIESTA code [22], which has already been successfully applied to the description of the magnetic properties of Fe [23]. The generalized gradient approximation (GGA) is used for the exchange–correlation functional in the Perdew–Burke–Ernzerhof (PBE) form [24]. Core electrons are treated with the help of nonlocal norm-conserving pseudopotentials [25], including the relativistic effects and nonlinear partial-core corrections [26]. The valence electrons are described by linear combinations of numerical pseudoatomic orbitals. We define ten localized functions for Fe with a cutoff radius of 2.95 Å. More details of the pseudopotentials and basis sets are given in our previous studies [27–30]. The Fermi–Dirac occupation function is smeared by a function with a width equal to 25 meV. The valence charge density is represented on an equidistant (0.074 Å) three-dimensional real-space grid. When performing structural optimizations, the structures are considered as relaxed when the residual forces and the stress components are smaller than 0.04 eV Å−1 and 1.0 GPa, respectively.
Local magnetic moments are obtained from a Mulliken population analysis, as implemented in the SIESTA code. In some other DFT codes, such as VASP, the magnetic moment is calculated by integrating the spin density on each orbital inside a muffin-tin spherical region [12, 19, 20]. Our test calculations reveal that the differences in the magnetic moments calculated by the two methods are quite small for the same configurations (typically less than 0.01 μB/atom) and, therefore, they may be ignored.
In three-dimensional (3D) systems, the Voronoi polyhedron is constructed with the help of the faces perpendicular to vectors connecting an atom to its nearest neighbors [31]. The volume of the Voronoi polyhedron is then calculated by the Voro++ code [32]. The construction of the Voronoi polyhedra for low-dimensional systems is discussed in detail in section 7.2.
3. Perfect bulk
We first concentrate on the most common crystal structures of perfect Fe, including body-centered cubic (bcc), face-centered cubic (fcc), hexagonal close-packed (hcp), double hexagonal close-packed (dhcp), and simple cubic (sc) structures. The hcp and dhcp configurations have been observed experimentally under high pressure [33–35]. The sc structure occurs, at ambient conditions, only in polonium [36, 37], and may be reached from the bcc structure by continuous trigonal deformation [38, 39]. As it is not a close-packed structure, it may be quite instructive to include it here as well. We have one Fe atom in the sc, bcc, and fcc supercells, two Fe atoms in the hcp supercell, and four Fe atoms in the dhcp supercell, respectively.
Figure 1 presents the dependences of the total energy and magnetic moment of the Fe atom in these five systems on the Voronoi volume. The total energy in figure 1(a) clearly indicates the equilibrium volume of 11.94 Å3 for the bcc crystal, corresponding to an equilibrium lattice constant of 2.88 Å, which is nearly the same as the experimental value of 2.87 Å [40]. Here, the atomic magnetic moment at equilibrium amounts to 2.32 μB, which is quite close to the experimental value of 2.22 μB [40]. For comparison, our VASP calculations deliver an equilibrium lattice constant of 2.83 Å and atomic magnetic moment of 2.19 μB.
Figure 1. Total energies and magnetic moments of (a) bcc, (b) fcc, (c) hcp, (d) dhcp, and (e) sc bulk structures as functions of the Voronoi volume.
Download figure:
Standard image High-resolution imageFigure 1(b) shows two equilibrium states of the fcc crystal, namely the low- and high-spin states. At the low-spin state where the local magnetic moment is 1.55 μB, the lattice constant amounts to 3.52 Å, corresponding to an equilibrium Voronoi volume of 10.90 Å3. At the high-spin state the magnetic moment amounts to 2.65 μB and the lattice constant is 3.68 Å, corresponding to an equilibrium volume of 12.46 Å3. The behavior of the total energies and magnetic moments with increasing lattice constants of the fcc crystal shows a similarity with previous work [41, 42], but their equilibrium lattice constants and the corresponding magnetic moments are generally lower than the present results: the local magnetic moment is 0.62 μB [41] (0.95 μB [42]) at a lattice constant of 3.45 Å [41] (3.47 Å [42]) (low-spin state) and 2.54 μB [41] (2.62 μB [42]) at a lattice constant of 3.63 Å [41] (3.64 Å [42]) (high-spin state).
For both hcp and dhcp, the FM and NM states were determined by minimizing the total energy as a function of the lattice constant a and of the ratio c/a. For the FM hcp structure, we obtained a = 2.55 Å, c/a = 1.74, an equilibrium volume of V = 12.49 Å3 and a magnetic moment of 2.60 μB. The equilibrium NM hcp structure was determined with the same c/a, providing a = 2.42 Å and V = 10.66 Å3. The NM hcp structure has an energy 0.16 eV /atom higher than that of the FM hcp structure. Our calculated structural parameters are slightly higher than c/a = 1.585 and V = 9.8 Å3 (presumably for the NM hcp structure [43]) as well as 10.08 Å3 (NM hcp structure) and 11.17 Å3 (FM hcp structure) reported in [44] or, as found by Moroni et al [45], 10.4 Å3 (figure 10, NM hcp structure), 9.63 Å3 (table VIII, NM hcp structure) and 12.5 Å3 (figure 10, FM hcp structure). For the dhcp structure we have revealed the low-spin and high-spin FM arrangements, similarly to the fcc structure, the energy of the low-spin state being 0.43 eV /atom higher than that of the high-spin state. The parameters of the high-spin dhcp structure are a = 2.56 Å, c/2a = 1.73, the equilibrium volume equals 12.57 Å3 and the magnetic moment 2.60 μB. For the low-spin dhcp structure we get (with the same c/2a) a = 2.42 Å, V = 10.62 Å3 and the magnetic moment equals 0.90 μB. This may be compared with the values of c/2a = 1.62, V = 9.8 Å3 in [43] (presumably for the NM dhcp structure).
The sc structure (figure 1(e)) exhibits just one energy minimum in the energy–volume curve and a steep jump to the NM structure when the volume is decreased. At equilibrium, the atomic volume V = 13.82 Å3 and the magnetic moment amounts to 2.49 μB, which compares favorably with V = 13.33 Å3 [39] and a magnetic moment of 2.44 μB [46].
Let us note that the equilibrium lattice dimensions and magnetic moments for the bcc structure obtained by the SIESTA code are slightly higher than those by the VASP [12, 41] and WIEN [47] codes. However, the experimental lattice constant is reproduced much better by the present SIESTA calculation (the difference is about 0.3%) than by VASP (the typical difference is 1.2–1.4%). A similar conclusion was reported by Guo and Barnard [48] (see their table III). On the other hand, VASP delivers a more favorable value of the magnetic moment (the difference in comparison with experiment is of the order of 1%) than SIESTA (4.5%). These differences are acceptable in electronic structure calculations.
For the fcc, hcp, dhcp and sc structures, SIESTA also delivers somewhat larger equilibrium atomic volumes and magnetic moments than most other calculations. The root-mean-square deviation in atomic volumes amounts to 0.71 Å3, which is about 6%. For magnetic moments, the most serious deviation is obtained for the fcc low-spin state, where we have obtained a value of 1.55 μB compared with the values of 0.62 and 0.95 μB; this may be connected with a larger calculated value of the equilibrium atomic volume, as the dependence of the magnetic moment on the volume is very steep in this region. In all other cases, the differences in magnetic moments are at most 0.11 μB for values in the range of 2.44−2.65 μB, i.e. cca 4.5%. The reason for these differences may consist in the fact that SIESTA employs an LCAO-type basis and the other approaches a plane-wave-type basis. Similarly to [48], we find that the results obtained with the help of the plane-wave and LCAO basis sets are comparable for most structures studied.
From figure 1 we may observe that the magnetic moment of Fe atoms increases with increasing Voronoi volume. We note that in these high-symmetry cases, the magnetic moment is also a monotonic function of the CN and bond length [15–18] as well as of the sphere volume with the radius equal to the mean distance between the Fe site and its 1NNs [19], and of the average volume equal to the volume of the supercell over the number of atoms in the supercell [20].
4. Vacancies and grain boundaries
We next consider a vacancy in the bcc crystal and the Σ5 (310)/[001] GB (without and with a vacancy).
For a vacancy in a bcc crystal, we use a supercell with 53 Fe atoms and the dimensions 8.65 × 8.65 × 8.65 Å3. Table 1 shows the effect of a vacancy on the local magnetic moments and Voronoi volumes of its neighboring Fe atoms. The vacancy increases the Voronoi volume by 1.17Å3 around the 1NN Fe atoms, decreases it by 0.06 Å3 around the 2NN atoms, and increases it again by 0.10 Å3 around the 3NN atoms. Corresponding to these volume changes, the local magnetic moment of the 1NN Fe atom increases by 0.23 μB, that of the 2NN atom decreases by 0.06 μB, and that of the 3NN atom increases by 0.06 μB. There is an obvious positive correlation between the change in the Voronoi volume and the local magnetic moment. Similar conclusions are also obtained in a previous work [49] investigating the moment variation around a vacancy and a self-interstitial atom. The magnetic moments of the Fe atoms in the 1NN position of a vacancy are increased, as would be expected from the larger volume, while the 1NN atoms of a self-interstitial atom show reduction of the moments due to the decrease of the volume.
Table 1. Change in magnetic moments (μB) and Voronoi volumes (Å3) of the Fe atoms neighboring a vacancy both in bcc crystal and at the Σ5 (310)/[001] GB, from the 1NN to 3NN. The magnetic moment and Voronoi volume of an Fe atom in the bcc structure are taken as references.
| Magnetic moment change | Voronoi volume change | |||||
|---|---|---|---|---|---|---|
| 1NN Fe | 2NN Fe | 3NN Fe | 1NN Fe | 2NN Fe | 3NN Fe | |
| Bulk | +0.23 | −0.06 | +0.07 | +1.17 | −0.06 | +0.10 |
| GB | +0.26 | +0.14 | +0.14 | +3.36 | +1.16 | +1.20 |
Now, let us discuss the local magnetic moments of atoms at the Σ5 (310)/[001] symmetrical tilt GB. The GB structure is modeled by a supercell containing 60 Fe atoms with two equivalent and oppositely oriented GBs and the distance between the two GBs is 14.32 Å. From the GB interface to the layer in the middle of two GBs, there are eight non-equivalent (310) layers denoted as L0 to L7 (and symmetrically L0'−−L7'), respectively. After a full structural relaxation, the interlayer distance exhibits a drastic oscillation near the GB interface L0 and it gradually converges to the value of a bcc crystal (0.91 Å) when going from L0 to L7, as shown in figure 2(d). From figure 2(a), the local magnetic moment in L0 is 2.66 μB, and it gradually decreases (with one jump) to the value of a bcc crystal (2.32 μB). These results are in a good agreement with the findings of [12]. It is interesting to note that the Voronoi volume (figure 2(b)) displays very similar variations to the local magnetic moment (figure 2(a)). The behavior of the CN and bond length obviously does not correlate with the changes in the magnetic moment at the GB. For example, for atoms in the GB plane L0 (before structural relaxation), the CN (8) and the bond lengths (2.50 Å) to 1NN atoms are exactly the same as those in the bcc bulk. However, the local magnetic moment of atoms in the GB plane (2.61 μB) is quite different from that in a bcc crystal (2.32 μB). We also studied the sphere volumes from L0 to L7, as shown in figure 2(c). Here we define, in the spirit of [19], the sphere radii as a half of the distance between the atom studied and the nearest neighbor (we do not employ the mean NN distance as in [19]). The sphere volumes display little relation to the local magnetic moment. Therefore, the local magnetic moment of atoms at the GB follows the Voronoi volume, whereas none of the other variables like the CN, bond length, and sphere volume do.
Figure 2. (a) Magnetic moment, (b) Voronoi volume, and (c) sphere volume for the Fe atoms in the Σ5 (310)/[001] supercell in different (310) layers; (d) interlayer distance with increasing distance from the GB interface.
Download figure:
Standard image High-resolution imageFor a detailed analysis of the local magnetic moments in different layers surrounding the GB plane, we determined the density of states (DOS) of atoms from L0 to L7 (figure 3). The shapes of the DOS in L0−L2 (figures 3(a)–(c)) show large differences from the DOS in the middle of our supercell (i.e. in the L7 plane (figure 3(h))), which is the interior of the grain and corresponds to unperturbed bulk. In the L0 plane (figure 3(a)), the majority-spin states are more and the minority-spin states are less occupied in comparison with an atom in a bcc Fe crystal, leading to an enhanced local magnetic moment. From L0 to L7 in the GB (figures 3(a)–(h)), the majority-spin states are gradually less occupied and there is a concomitant shift of electrons from the majority- to the minority-spin band, so that the DOS gradually approaches the shape of the DOS of a bcc crystal (figures 3(d)–(h)).
Figure 3. 3d-, 4p- and 4s-projected DOS for different (310) layers of the GB.
Download figure:
Standard image High-resolution imageTo investigate the effect of a vacancy on the magnetic moments and Voronoi volumes at the GB, we used a larger supercell with 120 atoms. More details may be found in our previous study [28]. The most energetically favorable vacancy site at the GB was found to be in the L1 layer [28]. As shown in table 1, the presence of the vacancy at the GB increases the Voronoi volumes by + 0.25 Å3, + 0.14 Å3, and + 0.14 Å3 for the 1NN, 2NN, and 3NN Fe atoms, respectively. Corresponding to the volume changes, the local magnetic moments also show enhancements by + 3.36 μB, + 1.16 μB, and + 1.20 μB, respectively. Consequently, a strong correlation between the local magnetic moment and the Voronoi volume occurs also at the Fe atoms surrounding a vacancy at the GB.
5. Surfaces
In order to investigate magnetism and its dependence on the structure, we also studied the (001), (110), (111), and (310) surfaces. To avoid the surface–surface interaction due to the periodic boundary condition, we used large supercells: the dimensions normal to the surfaces were 76.43 Å, 58.69 Å, 52.42 Å, and 47.02 Å for (001), (110), (111), and (310) surfaces, each with a corresponding vacuum region of height 21.46 Å, 20.24 Å, 21.76 Å, and 20.39 Å, respectively. Then there are 40, 20, 40, and 60 Fe atoms in the (001), (110), (111), and (310) surface supercells, respectively. Similarly to the GB case, the layers from the top to the middle between the two surfaces are labeled from L0 to L9. The local magnetic moment, Voronoi volume, sphere volume, and the interlayer distance for the four surfaces studied are shown in figure 4. From figure 4(d) we may see that the interlayer distances generally exhibit oscillations around the top layer L0 for all four surfaces. When going from L0 to L9, the interlayer distances gradually converge to the values corresponding to a bcc crystal, which are 1.44 Å, 2.04 Å, 0.83 Å, and 0.91 Å for the (001), (110), (111), and (310) surfaces, respectively. In figure 4(a) we may see that the local magnetic moments are strongly enhanced at the surfaces with respect to the bcc bulk; they amount to 3.05 μB, 2.75 μB, 3.02 μB and 3.01 μB for the (001), (110), (111), and (310) surfaces, respectively. These values are very similar to those obtained in previous studies (3.05 μB and 2.74 μB for the (001) and (110) surfaces, respectively) [12, 50], whereas the atoms at the (110) surface of a nanowire display a smaller magnetic moment of 2.53 μB [51]. From L0 to L9, the magnetic moments gradually converge to the value corresponding to a bcc crystal (2.32 μB). The behavior of the magnetic moments in different layers near the (001), (110), and (310) surfaces is very similar to the results found in previous studies using a first-principles approach and a parameterized tight-binding model [12, 52]. We also studied the sphere volumes of atoms in different layers, as exhibited in figure 4(c). We may see that there is no obvious relationship between the magnetic moment and the sphere volume. For the atoms surrounding L0 in different layers, the CN = 8 is the same and the bond length exhibits a very similar trend to the interlayer distance (figure 4(d)). We may see, also, that the correlation between the magnetic moment and the interlayer distance is vague. Again, there is no reasonable correlation between the local magnetic moment on one hand and the CN, bond length and sphere volume on the other.
Figure 4. (a) Magnetic moment, (b) Voronoi volume, (c) sphere volume, and (d) interlayer distance near the (001), (110), (111), and (310) surfaces.
Download figure:
Standard image High-resolution imageFinally, let us analyze the behavior of the Voronoi volumes. The Voronoi polyhedra cannot be defined in the usual way for surface atoms and, in some cases, for atoms in subsurface layers. Here we introduce auxiliary walls parallel to the surfaces at the distances of 1.7 Å, 1.8 Å, 1.5 Å and 1.7 Å for the (001), (110), (111) and (310) surfaces. This construction is described in detail in section 7.2. We may see that the Voronoi volumes in different layers of the four surfaces (figure 4(b)) generally show similar trends to the local magnetic moments (figure 4(a)), except for the layer L2 in the (111) surface.
Figure 5 presents the d-projected DOS of the Fe atoms in different layers near the (001), (110), (111), and (310) surfaces. From L0 to L7, the DOS gradually converge to the shape of the DOS of a bcc Fe crystal, whereas the DOS near the top layer (L0−L3) show a large difference from that in L7. Let us take the atoms in layers L0 and L2 as examples for explanation of the relationship between the local magnetic moment and the corresponding Voronoi volume. The atoms in L0 have larger Voronoi volumes than the atoms in L2 in all the four surfaces. Correspondingly, there is an apparent expansion of the bands in L2 (figure 5(c)) in comparison to L0 (figure 5(b)), leading to electron transfer from the majority- to the minority-spin states. Therefore, the local magnetic moment in L2 displays a drastic decrease with respect to the magnetic moment in L0.
Figure 5. 3d-projected DOS for different layers of the (001), (110), (111), and (310) surfaces.
Download figure:
Standard image High-resolution image6. Magnetic moments for three-dimensional, surface and two-dimensional embedded systems
Until now, we have considered the local magnetic moments in various configurations of bcc, fcc, hcp, dhcp and sc bulk structures, surfaces, GBs as well as vacancies in the bulk and at the GBs. It may be interesting to see the dependence of the local magnetic moments on the corresponding Voronoi volumes considering all the three-dimensional (3D), surface and embedded two-dimensional (2D) systems, such as GBs and subsurface layers.
Let us note that for the three-dimensional bcc, fcc, hcp, dhcp and sc crystals, the Voronoi volumes are obtained by a standard procedure for each lattice dimension. For the GBs and surfaces, different Voronoi volumes correspond to atoms in different layers normal to the interfaces. The 2D systems studied here exhibit the minimum energy (equilibrium) configuration.
In the entire region, the 4s- and 4p-magnetic moments change very little with increasing Voronoi volume and the total magnetic moments are dominated by the 3d-component. We may see from figures 6(a) and (b) that in the region of Voronoi volumes from ∼3 Å3 up to ∼11−12 Å3, the atomic moments are strongly scattered. Some crystalline structures (hcp, sc) are non-magnetic up to ∼10 Å3, whereas the bcc structure exhibits considerable magnetic moments for atomic volumes larger than ∼7 Å3. Therefore, in the region of atomic volumes lower than ∼11 Å3, the crystal structure and, in general, local atomic configuration has a more pronounced effect on the magnetic moment than the atomic volume. Only for volumes larger than ∼15 Å3 is the scatter of magnetic moments distinctly smaller, and here we may see that they obey a roughly linear dependence.
Figure 6. (a) Total magnetic moment, (b) 3d magnetic moment, (c) 4s-magnetic moment, and (d) 4p-magnetic moment as a function of Voronoi volume for bulk Fe, GBs and surfaces.
Download figure:
Standard image High-resolution imageTo summarize this part, the magnetic moments of Fe for lower atomic volumes (including equilibrium volumes of bcc, fcc, hcp, dhcp, and sc structures) are determined predominantly by the atomic configuration and the local atomic environment, whereas for higher atomic volumes (larger than ∼15 Å3) the effect of the atomic volume on the magnetic moment becomes predominant. This is because for relatively high Voronoi volumes, the electrons belonging to individual atoms do not influence each other so much and, therefore, the neighborhood is not so important.
7. Free-standing low-dimensional systems
7.1. Crystallographic description and magnetic moments
For the free-standing low-dimensional cases, we have studied the magnetic moment of an isolated Fe atom, a linear Fe chain and (001), (110), (111), and (310) monolayers, and one Fe atom is included in the supercells of these systems. For comparison, we also included the results for the Σ5 (310)/[001] GB and for the (001), (110), (111), and (310) surfaces.
After full structural relaxation, the magnetic moments, CN and bond lengths for each system studied, including also the surfaces and grain boundaries from the previous sections, are listed in table 2, and the DOS of these systems are shown in figure 7.
Table 2. Local magnetic moment (μB), coordination number (CN), bond length (Å), wall distance (Å), and Voronoi volume (Å3) of the low-dimensional systems studied after full structural relaxation. The numbers in parentheses characterize the number and bond length between a particular atom and its next nearest neighbors.
| System | Magnetic moment | CN | Bond length | Wall distance | Voronoi volume |
|---|---|---|---|---|---|
| Isolated atom | 4 | 0 | — | 2.15 | 79.5 |
| Chain | 3.26 | 2 | 2.26 | 1.8 | 29.3 |
| (310) monolayer | 3.16 | 2 (+4) | 2.15 (3.57) | 1.7 | 24.9 |
| (001) surface | 3.05 | 4 (+4) | 2.47 (2.88) | 1.7 | 19.6 |
| (111) surface | 3.02 | 4 (+3) | 2.41 (2.47) | 1.5 | 22.6 |
| (310) surface | 3.01 | 2 (+2) | 2.42 (2.53) | 1.7 | 21.3 |
| (110) monolayer | 2.77 | 4 (+2) | 2.36 (2.73) | 1.8 | 18.9 |
| (001) monolayer | 2.77 | 4 (+4) | 2.34 (3.31) | 1.7 | 18.6 |
| (110) surface | 2.75 | 6 (+4) | 2.50 (2.88) | 1.8 | 16.5 |
| (111) monolayer | 2.74 | 6 (+6) | 2.45 (4.24) | 1.5 | 15.6 |
| (310) grain boundary | 2.66 | 8 (+2) | 2.58 (2.65) | — | 13.8 |
Figure 7. 3d-, 4p- and 4s-DOS of an isolated Fe atom, a chain, (001), (110), (111), and (310) monolayers and surfaces. Fermi energy is set to zero.
Download figure:
Standard image High-resolution imageTheoretically, for an isolated Fe atom, there are five electrons in the 3d spin-up states and one electron in the 3d spin-down state. In this way, we obtain the maximum spin according to Hund's rules. The difference of electron numbers in the majority and minority states gives the magnetic moment of an isolated Fe atom, i.e. 4.0 μB. To treat an isolated Fe atom here, we consider an sc structure with a lattice parameter of 20 Å, which guarantees that the atoms do not interact. The corresponding DOS (figure 7(a)) clearly shows the total and partial occupation of the majority- and minority-spin states, respectively.
In the linear chain, the equilibrium interatomic distance is 2.26 Å and the local magnetic moment is 3.26 μB. These results are comparable with the interatomic distances of 2.27 and 2.26 Å and the magnetic moments of 3.13 and 3.40 μB reported in previous studies [53, 54]. The monolayers are modeled by distributing the atoms in the xy plane, with a distance of 20 Å between the monolayers along the z axis. For the (001) monolayer, the magnetic moment is calculated to be 2.77 μB and the equilibrium NN distance is 2.34 Å, with the lattice vectors perpendicular to each other. For the (110) monolayer, the magnetic moment is 2.77 μB and the NN distance is 2.36 Å. The angle between the lattice vectors in the xy plane is 68.67° and the coordination number (CN) is four. For the (111) monolayer, the angle between the lattice vectors is 60° and the CN is six due to a higher symmetry. The magnetic moment is 2.74 μB and the NN distance is 2.45 Å. This configuration is comparable with the hexagonal stripe discussed in a previous work [53], in which the magnetic moment was found to be 2.84 μB and the NN distance was 2.37 Å. Let us note that the (310) monolayer could not be obtained with the help of full structural relaxation because of the unsymmetrical stress distribution which causes a variation of the angle between the lattice vectors. In order to get the ground state of the (310) monolayer, the angle between lattice vectors and the ratio of their lengths had to be fixed to 72.45° and  , respectively. The equilibrium structure is obtained by the total energy minimization with respect to the NN interatomic distance, keeping the constraints mentioned above. The equilibrium interatomic distances are found to be 2.15 Å and 3.57 Å along the
, respectively. The equilibrium structure is obtained by the total energy minimization with respect to the NN interatomic distance, keeping the constraints mentioned above. The equilibrium interatomic distances are found to be 2.15 Å and 3.57 Å along the ![$[00\bar {1}]$](https://content.cld.iop.org/journals/0953-8984/26/8/086002/revision1/cm489809ieqn4.gif) and
and ![$[1\bar {3}0]$](https://content.cld.iop.org/journals/0953-8984/26/8/086002/revision1/cm489809ieqn5.gif) directions, respectively, and the magnetic moment is 3.16 μB.
directions, respectively, and the magnetic moment is 3.16 μB.
Similarly, we obtained the values of the magnetic moments and NN interatomic distances also for the (001), (110), (111), and (310) surfaces as well as for the Σ5 (310) GB. They are also given in table 2.
We can observe from table 2 that increasing CN and shortening bond lengths generally reduce the local magnetic moment, which is in accordance with previous studies (see e.g. [16–18]). However, in the low-symmetry configurations, such as surfaces and GBs, it is difficult to define the CNs and the representative bond lengths due to their variations in the relaxed structures. The bond lengths of the surfaces and GBs given in table 2 are the average quantities of several close values. It turns out, however, that we can reasonably introduce the Voronoi polyhedra in these cases.
7.2. Definition of the Voronoi polyhedron for low-dimensional systems
Basically speaking, the true Voronoi polyhedron cannot be obtained in many low-dimensional systems because of a lack of neighboring atoms in some directions. Nevertheless, as we show below, we can introduce reasonably positioned walls which allow us to construct a Voronoi polyhedron and calculate its volume.
Let us start with an isolated Fe atom which we described with the help of the sc lattice with a lattice parameter of 20 Å; the atomic magnetic moment was 4.0 μB. Now, let us decrease the lattice parameter (i.e. supercell size) until the Fe atoms in neighboring supercells can feel each other and the local magnetic moments start to decrease. The corresponding lattice parameter and, simultaneously, the NN interatomic distance, is 4.30 Å, as shown in figure 8(a). Let us now construct the corresponding Voronoi polyhedron—it is a cube with a volume of 79.5 Å3. In this way, we can introduce the walls for constructing Voronoi polyhedra also for other low-dimensional cases, such as an Fe chain and (001), (110), (111), and (310) monolayers and surfaces.
Figure 8. Voronoi polyhedra for (a) an isolated atom, (b) a chain, (c) the (111) monolayer, and (d) the (310) surface.
Download figure:
Standard image High-resolution imageThe magnetic moment of Fe atoms in an isolated chain (simulated in our case by a periodic array of chains separated by 20 Å) is 3.26 μB. In analogy with the case of an isolated atom, we decrease the distance between the chains until the local magnetic moment starts to decrease. The corresponding chain distance is 3.60 Å and the Voronoi polyhedron is constructed with the help of four walls parallel to the chain, as shown in figure 8(b). Here the volume of the Voronoi polyhedron depends linearly on the interatomic distance within the chain; for the equilibrium NN distance, it amounts to 29.3 Å3. Similarly, the wall distance can be determined by the minimum distance between the monolayers where the magnetic moment keeps its size for the isolated monolayers. The calculated wall distances are 1.7 Å, 1.8 Å, 1.5 Å, and 1.7 Å for the (001), (110), (111), and (310) monolayers, respectively. Both walls are set parallel to the monolayers, as shown in figure 8(c). Here the volume of the Voronoi polyhedron depends quadratically on the NN distance and, at each equilibrium configuration of the (001), (110), (111), and (310) monolayers, the corresponding Voronoi volumes are 18.6 Å3, 18.9 Å3, 15.6 Å3, and 24.9 Å3, respectively. For the surfaces, we introduce one wall that is placed parallel to the surface in the same distance as found for the corresponding monolayers. Taking the (310) surface as an example, the distance of the wall is 1.7 Å from the top layer (L0) and 2.5 Å from the second layer (L1) (figure 8(d)). (Let us note that the interlayer distance between L0 and L1 is 0.76 Å.) Again, the Voronoi polyhedron for an atom at the surface is obtained by a standard procedure for a configuration including the walls introduced in the way described above.
7.3. Dependence of magnetic moments on Voronoi volume
The corresponding wall distances and Voronoi volumes are listed in table 2. Here we can observe that local magnetic moments generally increase with increasing Voronoi volume and that the dependence of the magnetic moment on the Voronoi volume is much more pronounced than the dependence on CNs and bond lengths.
The underlying mechanism for the increase of the magnetic moment with the volume of the Voronoi polyhedron can be interpreted as a magnetovolume effect. According to the Stoner model, the physical basis of this effect is the interplay between the single-particle (kinetic) and exchange energies which leads to higher magnetic moments at larger volumes. The larger the volume is, the smaller the width of the 3d band is(it decreases with increasing atomic spacing d as d−5) [55, 56] and the larger the density of states is. A mutual shift of bands creating the spin polarization (i.e. a non-zero magnetic moment) induces a decrease in exchange energy (due to an increased spin alignment) and an increase in the single-particle (kinetic) energy; a non-zero magnetic moment arises when the sum of these energy contributions is negative. This moment amounts to 2.2 μB in equilibrium bcc iron. As shown by equation (3.9) in [57] and by [58], at a larger volume (inducing a larger density of states) the increase of the single-particle term is smaller and, therefore, a larger magnetic moment may be created. Finally, a free iron atom exhibits a magnetic moment of 4 μB. Let us note, however, that this relationship is not strictly monotonic. For example, the Voronoi volume of an atom at the (001) surface is 19.6 Å3 and the magnetic moment is 3.05 μB, whereas atoms at the (111) surface exhibit a larger volume of 22.6 Å3 but a smaller magnetic moment of 3.02 μB. Such deviation implies certain limitations of the relation between the local magnetic moment and the Voronoi volume.
In the following, we analyze the properties of each low-dimensional (2D and 1D) system as a function of homogeneous expansion or contraction. When calculating the corresponding Voronoi volume, we keep the position of the introduced walls constant. Then the Voronoi volume is a quadratic (in 2D systems) or linear (in 1D systems) function of proportionally increasing interatomic distances. We also determine the local magnetic moments for these configurations. Let us note that the ground state of the (110) monolayer exhibits a collinear ferromagnetic ordering in equilibrium and under tension while it undergoes a transition from collinear ferromagnetic to noncollinear spin-spiral ordering under in-plane compression [59]. As the energy gain and change in the size of the magnetic moment due to this transition are quite small [59], we keep the collinear ferromagnetic ordering in the (110) monolayer in the present study. It turns out that there is a close relationship between the Voronoi volume and the total and 3d magnetic moments; it is exhibited in figures 9(a) and (b) together with the results for 3D systems. We may see that in the region I with Voronoi volumes from ∼6 Å3 up to ∼15 Å3 the magnetic moments are strongly scattered and are determined primarily by the local atomic configuration. Then there is a sharp bend between 15−22 Å3 and, after that we can see roughly linear behavior in region II (22−75 Å3) with a slope of 0.02 μB Å−3. Finally, for Voronoi volumes higher than ∼75 Å3 (region III), the magnetic moment is nearly constant and approaches 4.0 μB, which corresponds to a free atom.
Figure 9. (a) Total magnetic moment, (b) 3d magnetic moment, (c) 4s-magnetic moment, and (d) 4p-magnetic moment in Fe as a function of Voronoi volume for all the systems studied. The insets show the detailed behavior of the magnetic moments in the region of 9−15 Å3, which includes the equilibrium volumes of three-dimensional systems.
Download figure:
Standard image High-resolution imageA comparison of the behavior of magnetic moments between figures 9(a) and (b), and 10(a) and (b), which include, respectively, all the studied systems and the selected 3D bulk structures, can help in estimating the reliability of our method of construction of the Voronoi polyhedra for low-dimensional systems. Namely, for all structures included in figures 10(a) and (b), the Voronoi volume may be constructed by a standard geometric procedure evoking no objections. All atoms are, from the point of view of atomic volume, equivalent; there is the same volume belonging to each atom.
Figure 10. (a) Total magnetic moment, (b) 3d magnetic moment, (c) 4s-magnetic moment, and (d) 4p-magnetic moment in Fe as a function of Voronoi volume for bcc, fcc, hcp, dhcp and sc bulk structures.
Download figure:
Standard image High-resolution imageOn inspecting figures 10(a) and (b), we may see that the values of the magnetic moments in region I are strongly scattered, similarly to figures 6(a) and (b), where some other structures were also added. Here we must state that, in region I, the crystal structure and/or local atomic configuration has a stronger influence on the magnetic moment than the atomic volume. In regions II and III, the scatter of values of the magnetic moments is much smaller and, in a good approximation, the behavior of the total and 3d magnetic moments versus the atomic volume is roughly linear. In region II, the maximum width of the 'band' of total magnetic moments (measured vertically, i.e. at a particular value of the Voronoi volume) amounts to 0.29 μB and that of the 3d magnetic moments to 0.09 μB, the average 'band-widths' being 0.13 μB and 0.05 μB, respectively. Consequently, we may state that in region II the total (3d) magnetic moment of 3D crystal structures is determined by the standard Voronoi volume with an average accuracy of ± 0.07 μB (±0.03 μB). In region III, we observe a practically constant value equal to the magnetic moment of a free atom, 4.0 μB. For the sake of completeness, we show also the behavior of the 4s- and 4p-magnetic moments in figures 10(c) and (d). These moments are relatively small and do not affect the overall course of the total magnetic moment shown in figure 10(a).
Now, comparing these findings with figures 9(a) and (b), which contain the results for all systems with various dimensionalities studied here, we may see that the trends in behavior of the total and 3d magnetic moments are very similar, the main difference being a larger scatter (the 'band-width') of magnetic moments at each value of the Voronoi volume. Let us discuss region II again. Here the maximum width of the 'band' of total magnetic moments (again measured vertically) is 0.88 μB and that of the 3d magnetic moments is 0.43 μB. The average 'band-widths' then amount to 0.56 μB and 0.13 μB, which means that, on average, the total and 3d magnetic moments are determined by the Voronoi volume (including our extension for low-dimensional systems) with accuracies of ± 0.28 μB and ± 0.07 μB, respectively. From figure 9(c) we may see that the larger scatter of the total magnetic moments is due to the behavior of the 4s-magnetic moments, which exhibit quite a large dispersion; the scatter of the 3d magnetic moments is, therefore, much smaller than that of the total magnetic moments.
Given the variety of the systems considered, with different geometries and dimensionalities, from 3D bulk configurations to isolated atoms, we may conclude that our extension of the definition of Voronoi volumes with the help of appropriate walls perpendicular to the directions lacking neighboring atoms may be justified.
It may be expected that a similar relation between the magnetic moment and the Voronoi volume for larger Voronoi volumes would hold also for the other 3d ferromagnetic metals, Co and Ni, but, again, probably not at ambient atomic volumes. For example, the previous study [39] has found that the magnetic moment of Ni varies quite wildly along a trigonal deformation path at a constant experimental volume. However, a relative independence of the magnetic moment on the type of the atomic configuration and/or local neighborhood, in favor of a determining role of the Voronoi volume, seems to be a general tendency.
8. Validity of the Stoner model for low-dimensional systems
It is well known that there is a universal relation between the 3d-exchange splitting and the local magnetic moment for a wide class of systems [60, 61]. This has also been studied with the help of first-principles calculations in the highly distorted region around the Fe GB [12], in amorphous Fe [62], and in amorphous transition-metal alloys [63]. The calculations suggest that the Stoner model of itinerant magnetism, which introduces this relation, is valid for the local magnetic moments in these systems. However, the systems studied up to now were limited to three-dimensional systems [62, 63] and GBs [12]. Here we may test the validity of the proportionality between the magnetic moment and the 3d-exchange splitting for both three- and low-dimensional systems with local magnetic moments in the interval from 0.0 to 4.0 μB.
In most cases, the Stoner parameter (or Stoner exchange integral) I is introduced by
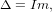
where Δ is the exchange splitting (mostly of d bands) and m is the magnetic moment [64, 65]. Some other papers define the exchange energy contribution due to the existence of the magnetic moment as Eexch = −Im2/4 [57, 66]. Both approaches are equivalent. Here we use the first formula and treat the Stoner parameter as the slope of the dependence between the exchange splitting and the total magnetic moment [12, 60–63]. The exchange splitting is calculated as the difference between the centers of gravity of the corresponding majority- and minority-spin bands.
We have determined this parameter for Fe atoms in all the systems studied, as shown in figure 11. For the systems in region I in figure 11, it was obtained by linear fitting of the dependence of the 3d-exchange splitting on the total magnetic moment and it equals I3d = (0.998 ± 0.006) eV /μB. This demonstrates the validity of the Stoner model for magnetic moments of Fe up to 3.0 μB (region I in figure 11), even in highly distorted regions like GBs and surfaces. This finding is in perfect agreement with the results of previous papers [12, 62, 63].
Figure 11. The dependence of the 3d-exchange splitting on the total magnetic moment for all the systems.
Download figure:
Standard image High-resolution imageFor higher magnetic moments of 3.0−4.0 μB (regions II and III in figure 11), we see an abrupt change. The 3d-exchange splitting also behaves roughly linearly but the corresponding Stoner exchange parameter equals  .
.
Considering the case of an isolated atom, we obtain the electron distribution as 1.000 s↑, 0.305 s↑, 5.000 d↑, 1.695 d↓, 0 p↑, and 0 p↓, so that the effective atomic configuration is 3d6.6954s1.305. The magnetic moment is 4.0 μB, where 3.305 μB is contributed by the 3d electrons and 0.695 μB is contributed by the 4s electrons. The 3d-splitting is 3.13 eV, which is the maximum exchange splitting we have obtained in Fe. These results are consistent with the previous work [56].
It is important to understand what is going on in the region of higher magnetic moments (regions II and III in figure 11) and to find out the reason why the total magnetic moment can increase, although the 3d-exchange splitting keeps almost constant. In figures 9(b)–(d), we plot the dependence of the magnetic moment on the Voronoi volume for 3d, 4s, and 4p electrons, respectively. In region I (up to Voronoi volumes of 22 Å3), the 3d magnetic moment increases with increasing Voronoi volume whereas the 4s-magnetic moment is very small and almost constant. For Voronoi volumes of 22−75 Å3, however, the 4s-magnetic moment strongly increases with increasing Voronoi volume whereas the 3d magnetic moment remains nearly unchanged. The contribution of 4p electrons is quite small and, therefore, it may be neglected in this consideration. We can therefore draw a conclusion that with increasing Voronoi volume, the 3d bands separate first and, consequently, the 3d magnetic moment increases. At a Voronoi volume of ∼22 Å3, the separation of 3d bands reaches an upper limit, and then the 4s bands start to separate and increase the 4s-magnetic moment.
On the basis of this, it seems logical to look for a correlation between the 4s-exchange splitting and the total magnetic moment in regions II and III, i.e. for magnetic moments greater than 3.0 μB. By analogy, we define the Stoner parameter I4s for the 4s electrons as the slope of the dependence of the 4s-exchange splitting on the total magnetic moment. The 4s-exchange splitting is obtained as the difference between the centers of gravity of 4s majority- and minority-spin bands. We distinguish the s-, p- and d-components in relation to DOS.
Figure 12 shows the correlation between the 4s-exchange splitting and the total magnetic moment for all the systems studied. The values in region I (for magnetic moments less than 3.0 μB) are quite scattered, but they are irrelevant, as in region I the 3d-exchange splitting determines the magnetic moment, as shown in figure 11; here we show these values only for the sake of completeness. Much more important is the fact that for magnetic moments greater than 3.0 μB we observe again a linear correlation with the slope  , which is nearly the same as the slope I3d = (0.998 ± 0.006) eV /μB of the linear dependence between the 3d-exchange splitting and the total magnetic moment for magnetic moments up to 3.0 μB. At present, we are not able to say whether this is just a coincidence or whether the equality
, which is nearly the same as the slope I3d = (0.998 ± 0.006) eV /μB of the linear dependence between the 3d-exchange splitting and the total magnetic moment for magnetic moments up to 3.0 μB. At present, we are not able to say whether this is just a coincidence or whether the equality  could have been expected. In our opinion, all this can be considered as a certain variation of the Stoner model.
could have been expected. In our opinion, all this can be considered as a certain variation of the Stoner model.
Figure 12. The correlation between the 4s-exchange splitting and the total magnetic moment for all the systems.
Download figure:
Standard image High-resolution imageFinally, let us note that the kink at 3.0 μB in figure 11 and the linear relation for moments higher than 3.0 μB in figure 12 may be associated with a gradual filling of some bands when the magnetic moment is increased. We illustrate this in figure 13, which shows the behavior of the electron population for the bcc structure as a function of the total magnetic moment, but, as we discussed above, for magnetic moments larger than 3.0 μB, this behavior is not influenced by a particular structure. It may be seen that at 3.0 μB the 3d majority band is full (containing five electrons). The separation of the 3d bands is nearly complete at this point and, with increasing volume, the magnetic moment increases mostly due to the change of population of the 4s states. Figure 13 shows that in the region of magnetic moments of 3.0−4.0 μB electron transfer occurs from 3d↓ and 4p states to 4s states, where 4s↑ states gain most. In this way, we approach the isolated atom, obtaining the above-mentioned atomic configuration 3d6.6954s1.305.
Figure 13. Population of 3d, 4s, and 4p electrons as a function of the total magnetic moment in the bcc structure.
Download figure:
Standard image High-resolution image9. Conclusions
In conclusion, we have studied the relationship between the ferromagnetism and the structural properties of Fe systems from three-dimensional ones to isolated atoms. We find that the volume of the Voronoi polyhedron is closely connected with the local magnetic moments of iron atoms when the volume is larger than ∼22 Å3. It is demonstrated that this relation is valid for many three-dimensional systems, including high-symmetry structures of a perfect bcc, fcc, hcp, dhcp or sc bulk, as well as for low-symmetry ones, for example a GB or atoms near a surface or around a vacancy. However, the local magnetic moments of systems with atomic volumes smaller than ∼15 Å3 are determined predominantly by the crystal structure and/or by the type of local atomic configuration.
To be able to treat low-dimensional systems, we have extended the standard definition of Voronoi polyhedra by introducing walls in the directions lacking atoms, including an isolated atom, a linear chain, a monolayer, or a surface. Taking free-standing low-dimensional systems into account, the volume of the Voronoi polyhedron determines in most cases the value of the total magnetic moment with an average accuracy of ± 0.28 μB and of the 3d magnetic moment with an average accuracy of ± 0.07 μB.
Let us note that the Voronoi volume is not the only, but the most important, factor that influences the magnetic moment at high Voronoi volumes. As follows from figures 9(b) and 10(b), the magnetic moment due to 3d electrons in regions II and III, i.e. for Voronoi volumes larger than 22 Å3, does not practically depend on the structure. This is due to the fact that 3d electrons are more localized and do not feel their neighborhood for these large Voronoi volumes. There are some variations in the total magnetic moment in region II (figures 9(a) and 10(a)), but they are due to the behavior of the magnetic moments of the 4s electrons (figures 9(c) and 10(c)), which are not so localized and reflect their local neighborhood up to Voronoi volumes equal to 75 Å3. In region III (for Voronoi volumes >75 Å3), the total magnetic moment acquires the value for a free atom, namely 4.0 μB.
The validity of the Stoner model is also extended to low-dimensional systems, such as surfaces and free-standing low-dimensional systems, by fitting the Stoner parameter in the region of lower atomic moments (up to 3.0 μB). The ratio of the 3d-exchange splitting to the magnetic moment, corresponding to the Stoner parameter, was found to be I3d = (0.998 ± 0.006) eV /μB for these lower magnetic moments. Further, the 3d-exchange splitting changes roughly linearly in the region of higher magnetic moments (3.0−4.0 μB) and the corresponding Stoner exchange parameter equals  . This is because, with increasing Voronoi volume, the 3d bands separate first and, consequently, the 3d magnetic moment increases. When the Voronoi volume is sufficiently large (∼22 Å3), the separation of 3d bands is complete and the 4s bands start to separate, increasing thus the 4s-magnetic moment. Surprisingly, here we then observe a linear relation between the 4s-exchange splitting and the total magnetic moment with a slope of
. This is because, with increasing Voronoi volume, the 3d bands separate first and, consequently, the 3d magnetic moment increases. When the Voronoi volume is sufficiently large (∼22 Å3), the separation of 3d bands is complete and the 4s bands start to separate, increasing thus the 4s-magnetic moment. Surprisingly, here we then observe a linear relation between the 4s-exchange splitting and the total magnetic moment with a slope of  . These linear relations can be considered as a variation of the Stoner model for low-dimensional systems.
. These linear relations can be considered as a variation of the Stoner model for low-dimensional systems.
Acknowledgments
This research was supported by the National Magnetic Confinement Fusion Program, Grant No. 2009GB106003, and the National Natural Science Foundation of China (NSFC), Grant No. 51061130558 (LZ, ZW, YZ, GHL), as well as by the Grant Agency of the Czech Republic, Project No. GAP108/12/0311, by the Grant Agency of the Academy of Sciences of the Czech Republic, Project No. IAA100100920, and by the Project CEITEC—Central European Institute of Technology (CZ.1.05/1.1.00/02.0068) from the European Regional Development Fund (MŠ). We thank Professor I Turek for fruitful discussions.













