Abstract
Density functional theory calculations (DFT) are used to investigate the strain-induced changes to the electronic structure of biaxially strained (parallel to the (001), (110) and (111) planes) and uniaxially strained (along the [001], [110] and [111] directions) germanium (Ge). It is calculated that a moderate uniaxial strain parallel to the [111] direction can efficiently transform Ge to a direct bandgap material with a bandgap energy useful for technological applications.
Export citation and abstract BibTeX RIS
Ge is a material with advantageous properties such as high mobility of holes and electrons, which has attracted the interest of the microelectronics community due to the advent of high-k dielectrics [1]. Interestingly, recent studies reported the possibility of laser emission of Ge on a silicon (Si) wafer [2]. The optical recombination properties can be enhanced by n-type doping and by strain [3].
Ge is an indirect bandgap material so an electron transits from an energy level in the conduction band to a level in the valence band mainly via phonon-assisted non-radiative recombinations. Direct optical recombinations are therefore slow and inefficient. It is desirable to obtain a direct bandgap for Ge; some results have been achieved by growing SnxGe1−x alloys on Si where a direct bandgap of 0.41 eV was obtained with a Sn content of 14% [4]. The correlation between the structure and the electronic properties of semiconductors means that these properties can be engineered by applying deformations to the material. Uniaxial and biaxial strains have been studied and applied extensively in Si to increase the carrier mobilities for integrated circuit applications [5]. Typically, biaxial strain in Si enhances the carrier mobility: however, the gains diminish at high vertical electric fields [6]. The enhancement of mobility is maintained for uniaxially strained Si [7]. The deformation potential theory has been widely and successfully used to study the electronic properties of semiconductors [8]. Niquet et al [9] used a model for the on-site matrix elements of the sp3d5s* tight binding Hamiltonian to study the effect of strain on Si, Ge and their alloys. They complemented their results with a post-DFT (local density approximation (LDA)) GW-corrected approximation. This model was used to calculate the band energies for the (001), (110) and (111) biaxial strain as well as the deformation potentials for Si and Ge. For the latter, their model showed an agreement between the LDA and experimental results in the case of Si but deviated to a larger extent in the case of Ge. Lim et al [3] studied the emission characteristics of Ge micromechanical structures under tensile biaxial stain. According to their simulations they found out that while at 1.5% strain Ge was still an indirect bandgap material a net optical gain could be achieved with an electron–hole injection of 9 × 108 cm−3. Kurdi et al [3], employing the k ⋅p formalism, concluded that for biaxial (001) tensile strained Ge the cross-over from indirect to direct occurs at 1.9%. An optical gain of 3000 cm−1 for a carrier density of 1 × 1018 cm−3 and a strain of 3% is also predicted, which is higher than what has been calculated for GaAs.
Recently, Murphy-Armando and Fahy [10] used electronic structure calculations and calculated that electron mobilities can be enhanced several hundred times for thin Ge films (strained biaxially parallel to (001)) and 5–20 times (strained uniaxially along [111]) in Ge nanowires. In this paper, we investigate using DFT biaxial and uniaxial strain-induced changes to the indirect to direct bandgap transition as a function of strain in bulk Ge.
The band structure calculations were performed using DFT as implemented in the Vienna ab initio simulation package (VASP) code [11]. Electron exchange and correlation were described using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional [12]. The electrons occupying the 4s24p2 states were treated as valence, whereas the [Ar]3d10 were approximated by a pseudopotential generated according to the projector augmented wave (PAW) method [13]. We use a primitive cell with two Ge atoms as basis located at (0, 0, 0) and (1/4,1/4,1/4). For such a small cell we used a 10 × 10 × 10 k-point grid generated according to the Monkhorst–Pack scheme to sample the Brillouin zone [14]. The kinetic energy cutoff was set to 400 eV. The total energy was iterated until changes in energy were lower than 1 × 10−5 eV. To simulate the strain in the cells the deformed lattice parameters were not allowed to relax and only the internal parameters of the atoms were allowed to vary such that the forces on them were below 0.001 eV Å−1. To correct the underestimation of the bandgap (typical for GGA) we used a GGA + U approach by setting the on-site Coulomb parameter, U, to 0 eV and the on-site exchange parameter, J, to 3.33 eV [15]. This results in a bandgap of 0.74 eV for the unstrained Ge structures, which is in agreement with the experimental bandgap. This method employed to correct for the bandgap has been tested before and yielded accurate results in agreement with available experimental data. Its computational efficiency in comparison with hybrid functionals of post-DFT calculations (HSE06 or GW) and its ability to reproduce similar electronic structures in relaxed unstrained Ge makes it a desirable choice.
For the unstrained Ge it is calculated that the difference in energy between the indirect and direct bandgap is 0.18 eV (close to the experimental value of 0.14 eV) [16]. The bandgaps are measured from the top of the valence band at the Γ-point to the minimum of the different minima along the conduction band at the high symmetry points in the reciprocal lattice, namely the L, Γ and X, with the bandgaps denoted by  ,
,  and
and  , respectively. Notably,
, respectively. Notably, 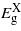 does not occur exactly at the X-point but somewhere along the Δ path connecting the Γ and the X high symmetry points in the Brillouin zone. This description of the electronic structure led to accurate lattice and elastic properties of the material as shown in table 1 where the DFT results are compared to previous experimental evidence [17–20].
does not occur exactly at the X-point but somewhere along the Δ path connecting the Γ and the X high symmetry points in the Brillouin zone. This description of the electronic structure led to accurate lattice and elastic properties of the material as shown in table 1 where the DFT results are compared to previous experimental evidence [17–20].
Table 1. The calculated and experimental lattice parameter and elastic constants C11, C12 and C44 along with the indirect and direct conduction and valence band transitions.
| This work | Experimental | |
|---|---|---|
| Lattice parameter (Å) | 5.5987 | 5.6569a |
| C11 (GPa) | 128.1 | 128.5b |
| C12 (GPa) | 46.1 | 48.3b |
| C44 (GPa) | 69.7 | 68.0b |
| Indirect bandgap, Γv → Lc (eV) | 0.74 | 0.74c |
| Indirect bandgap, Γv → Xc (eV) | 0.89 | — |
| Direct bandgap, Γv → Γc (eV) | 0.92 | 0.89d |
aReference [17]. bReference [18]. cReference [19]. dReference [20].
Figures 1 and 2 report the change in bandgaps with respect to the biaxial strain (parallel to (001), (110) and (111)) and the uniaxial strain (along [001], [110] and [111]), respectively. As the strain is applied biaxially parallel to the (001) plane all three bandgaps drop for positive (tensile) strain and the 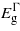 and
and 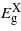 for negative (compressive) strain. For the compressive strain
for negative (compressive) strain. For the compressive strain 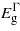 , and to a lesser extent
, and to a lesser extent 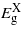 , exhibits a quadratic dependence on strain.
, exhibits a quadratic dependence on strain. 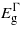 increases initially with compression before starting to fall beyond − 1% strain. The three bandgaps fall but no cross-over between
increases initially with compression before starting to fall beyond − 1% strain. The three bandgaps fall but no cross-over between 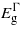 and
and 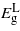 occurs within the limits considered. At around
occurs within the limits considered. At around 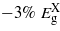 attains the minimum among the bandgaps but Ge maintains an indirect bandgap. Between 0 and 3.5% strain, the bandgaps depend linearly on strain. Beyond this, however, the band edges show a remarkable deviation from the nearly linear dependence on strain, which is a behavior not normally accounted for using deformation potential theories and results from the shear strain component [9]. The rate at which
attains the minimum among the bandgaps but Ge maintains an indirect bandgap. Between 0 and 3.5% strain, the bandgaps depend linearly on strain. Beyond this, however, the band edges show a remarkable deviation from the nearly linear dependence on strain, which is a behavior not normally accounted for using deformation potential theories and results from the shear strain component [9]. The rate at which  decreases is greater than the other two bandgaps, and it becomes the lowest energy bandgap at ∼1.7%, at which point Ge changes from an indirect to a direct bandgap material. At this strain the direct bandgap is about 0.47 eV, which is 36% lower than the unstrained indirect bandgap.
decreases is greater than the other two bandgaps, and it becomes the lowest energy bandgap at ∼1.7%, at which point Ge changes from an indirect to a direct bandgap material. At this strain the direct bandgap is about 0.47 eV, which is 36% lower than the unstrained indirect bandgap.
Figure 1. Change in the bandgaps with biaxial strain parallel to (a) the (001) plane, (b) the (110) plane and (c) the (111) plane.
Download figure:
Standard imageFigure 2. Change in the bandgaps with uniaxial strain parallel to (a) the [001] direction, (b) the [110] direction and (c) the [111] direction.
Download figure:
Standard imageFor compression parallel to the (110) plane 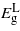 behaves differently from that calculated for the (001) case, that is it increases instead of decreasing with strain.
behaves differently from that calculated for the (001) case, that is it increases instead of decreasing with strain.  depends quadratically on strain increasing before it gradually starts falling again; only
depends quadratically on strain increasing before it gradually starts falling again; only 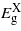 drops linearly with compression until a minimum bandgap at about −1.14%. Overall there is no transition to a direct bandgap. For tensile strain,
drops linearly with compression until a minimum bandgap at about −1.14%. Overall there is no transition to a direct bandgap. For tensile strain,  and
and 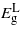 decrease linearly: however, the decrease is not enough to change the material as only at ∼3.5% the two bandgaps become nearly equal, beyond which they diverge once more and
decrease linearly: however, the decrease is not enough to change the material as only at ∼3.5% the two bandgaps become nearly equal, beyond which they diverge once more and 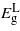 remains the minimum energy valley. Even if Ge is converted into a direct bandgap material, the bandgap would be about 0.1 eV, which is too small for solar or telecommunications applications.
remains the minimum energy valley. Even if Ge is converted into a direct bandgap material, the bandgap would be about 0.1 eV, which is too small for solar or telecommunications applications.
For the (111) plane, compression leads to similar effects as with the (110) case: however, 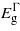 exhibits a greater increase with strain but as before no transition in the bandgap nature will occur. Under tensile strain
exhibits a greater increase with strain but as before no transition in the bandgap nature will occur. Under tensile strain 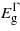 and
and 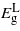 drop at nearly the same rate maintaining an energy difference of about 0.18 eV for any given strain level.
drop at nearly the same rate maintaining an energy difference of about 0.18 eV for any given strain level.
For uniaxial strain parallel to the three directions [001], [110] and [111] the bandgaps exhibit a more linear dependence on strain. For [001] 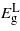 ,
, 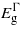 and
and 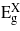 drop with both compression and tension. The rate at which
drop with both compression and tension. The rate at which  decreases is greater than the other two bandgaps, giving rise to a transition from indirect to direct at −2.41% and 3.05% where the direct bandgaps are about 0.41 eV and 0.59 eV, respectively. The [110] and [111] cases show similar trend for the bandgaps, and only tensile uniaxial strains cause a transition to a direct bandgap. The transitions for these two directions occur at 1.71% and 1.05% with direct bandgaps of 0.78 eV and 0.82 eV, respectively. These two direct bandgaps are higher than the indirect bandgap for unstrained Ge. This is because
decreases is greater than the other two bandgaps, giving rise to a transition from indirect to direct at −2.41% and 3.05% where the direct bandgaps are about 0.41 eV and 0.59 eV, respectively. The [110] and [111] cases show similar trend for the bandgaps, and only tensile uniaxial strains cause a transition to a direct bandgap. The transitions for these two directions occur at 1.71% and 1.05% with direct bandgaps of 0.78 eV and 0.82 eV, respectively. These two direct bandgaps are higher than the indirect bandgap for unstrained Ge. This is because 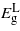 increases with tensile strain and, at the same time,
increases with tensile strain and, at the same time, 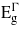 does not fall as rapidly as it does under biaxial strain. The uniaxial strain offers two interesting features: firstly, compressive strain in the [001] direction allows a transition to a direct bandgap. This is advantageous as it is more feasible to grow Ge on materials with smaller lattice constants (e.g. Si1−xGex). Secondly, the [111] tensile strain allows this transition to occur at relatively small strains (compared with the other strain conditions considered), while at the same time maintaining a bandgap that is large enough for practical use. This agrees qualitatively with recent work performed by Zhang et al [21]. Their finding was that 4.2% uniaxial stress along [111] is needed to convert Ge to a 0.34 eV direct bandgap material. While this level of strain might be achievable in nanowires, it has not been reported experimentally for bulk materials [22] and is beyond the limit of Si/Ge lattice mismatch. Another complication in real materials arises due to the formation of cracks and the fact that the linearity of stress/strain relations breaks beyond certain stress [22]. Our results for [111] strain, are within the realm of what could be achieved experimentally.
does not fall as rapidly as it does under biaxial strain. The uniaxial strain offers two interesting features: firstly, compressive strain in the [001] direction allows a transition to a direct bandgap. This is advantageous as it is more feasible to grow Ge on materials with smaller lattice constants (e.g. Si1−xGex). Secondly, the [111] tensile strain allows this transition to occur at relatively small strains (compared with the other strain conditions considered), while at the same time maintaining a bandgap that is large enough for practical use. This agrees qualitatively with recent work performed by Zhang et al [21]. Their finding was that 4.2% uniaxial stress along [111] is needed to convert Ge to a 0.34 eV direct bandgap material. While this level of strain might be achievable in nanowires, it has not been reported experimentally for bulk materials [22] and is beyond the limit of Si/Ge lattice mismatch. Another complication in real materials arises due to the formation of cracks and the fact that the linearity of stress/strain relations breaks beyond certain stress [22]. Our results for [111] strain, are within the realm of what could be achieved experimentally.
The valence band electrons of each Ge atom are composed of spherical s orbitals and directional px, py and pz orbitals, with each atom forming tetrahedral bonds with its neighbors. These in-plane orbitals form the heavy holes, whereas out-of-plane orbitals form light holes [23]. Tensile or compressive strain causes elongations of bonds along one direction, shrinking in another and a change in the bonds' orientation. The result of this is a change in the orbitals' weights and interactions, which changes the energies of the heavy and light holes. The orbitals' rehybridization also affects the energies of the conduction band that is mainly composed of p electrons. Depending on the plane or direction and whether it is in compressive or tensile strain, these lead to a variation in the edges of the valence and conduction band minima and hence the width of the bandgap.
Figure 3 shows how the conduction and valence band minima vary with uniaxial [111] strain. Other directions and planes show a similar variation, but we have considered this case as it provides a complete transition to a direct bandgap. The figure shows how the energy of the top of the conduction band at the Γ-point drops with tensile strain accompanied by an increase in the energy of the valence band maximum, leading to a shrinkage in the bandgap.
Figure 3. Change in the conduction and valence band minima with respect to uniaxial strain along the [111] direction.
Download figure:
Standard imageThe effective mass was calculated using the relation 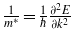 . The required data are obtained from the band structure by approximating the curvature of the energy eigenvalues by fitting the E − k points around the high symmetry points into a parabola of the form E(k) = ak2 + bk + c. The high symmetry points of interest are L(0.5, 0.5, 0.5) and Γ(0.0, 0.0, 0.0) from which we can calculate the electron effective masses
. The required data are obtained from the band structure by approximating the curvature of the energy eigenvalues by fitting the E − k points around the high symmetry points into a parabola of the form E(k) = ak2 + bk + c. The high symmetry points of interest are L(0.5, 0.5, 0.5) and Γ(0.0, 0.0, 0.0) from which we can calculate the electron effective masses 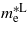 and
and 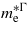 and the hole's effective mass,
and the hole's effective mass,  . For unstrained Ge we calculated
. For unstrained Ge we calculated 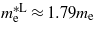 ,
,  and
and 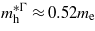 , which are consistent with the experimental values of
, which are consistent with the experimental values of  [24],
[24],  [25] and
[25] and 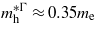 [26]. At the point where Ge makes the transition to a direct bandgap material the excited electrons in the conduction band, formed either thermally or by n-doping, start occupying the Γ valley and scatter back to the valence band via this channel. The calculations are consistent with experimental [20, 21] results, indicating that the electrons occupying the Γ valley have a much smaller effective mass than those occupying the L valley. Consequently an enhancement in the carrier mobility is expected when the transition occurs since it is inversely proportional to the effective mass of the carrier.
[26]. At the point where Ge makes the transition to a direct bandgap material the excited electrons in the conduction band, formed either thermally or by n-doping, start occupying the Γ valley and scatter back to the valence band via this channel. The calculations are consistent with experimental [20, 21] results, indicating that the electrons occupying the Γ valley have a much smaller effective mass than those occupying the L valley. Consequently an enhancement in the carrier mobility is expected when the transition occurs since it is inversely proportional to the effective mass of the carrier.
In summary, we used DFT to investigate the impact of biaxial and uniaxial strain on the electronic structure of Ge. For tensile strains the bandgap undergoes a transition from indirect to direct for biaxial strain parallel to the (001) plane and for uniaxial strains parallel to the [001], [110] and [111] directions. For compressive strain this transition occurs for the only uniaxial [001] direction. Uniaxial tensile strain parallel to the [111] direction most readily transform Ge to a direct bandgap material, that is at a relatively low strain.
Acknowledgments
This publication was based on research supported by King Abdullah University for Science and Technology (KAUST). HT is grateful to Samuel Murphy (ICL) for useful discussions. Computing resources were provided by the HPC facility at ICL ( www3.imperial.ac.uk/ict/services/highperformancecomputing). AC and AD acknowledge financial support from the EU FP7-PEOPLE-2010-IEF project REACT-273631.



