Abstract
A transition state for a Hamiltonian system is a closed, invariant, oriented, codimension-2 submanifold of an energy level that can be spanned by two compact codimension-1 surfaces of unidirectional flux whose union, called a dividing surface, locally separates the energy level into two components and has no local recrossings. For this to happen robustly to all smooth perturbations, the transition state must be normally hyperbolic. The dividing surface then has locally minimal geometric flux through it, giving an upper bound on the rate of transport in either direction.
Transition states diffeomorphic to
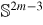are known to exist for energies just above any index-1 critical point of a Hamiltonian of m degrees of freedom, with dividing surfaces
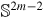. The question addressed here is what qualitative changes in the transition state, and consequently the dividing surface, may occur as the energy or other parameters are varied? We find that there is a class of systems for which the transition state becomes singular and then regains normal hyperbolicity with a change in diffeomorphism class. These are Morse bifurcations.
Various examples are considered. Firstly, some simple examples in which transition states connect or disconnect, and the dividing surface may become a torus or other. Then, we show how sequences of Morse bifurcations producing various interesting forms of transition state and dividing surface are present in reacting systems, by considering a hypothetical class of bimolecular reactions in gas phase.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Y G Kevrekidis
Footnotes
- 4
The state space of Hamiltonian systems is often referred to as phase space.
- 5
Nb: 'surface' means an (embedded) submanifold of codimension-1.
- 6
We say that a manifold S spans N if the latter is its boundary, N = ∂S.
- 7
An invariant submanifold whose linearized normal dynamics are hyperbolic and dominate those tangent to it, see appendix B.
- 8
This possibility was pointed out by MacKay in the course of a workshop in Bristol in 2009. Some examples have been reported in Mauguière et al [35], a paper that appeared in preprint form at about the same time as ours.
- 9
A closed, non-degenerate 2-form.
- 10
By 'positive' we mean 'non-negative', and by 'negative' we mean 'non-positive' but the terminology is too cumbersome.
- 11
Systems for which the Hamiltonian function is the sum of kinetic and potential energy.
- 12
Actually N is not (necessarily) compact, but the level sets NE are invariant, so the sub-level sets N⩽E are compact submanifolds with (invariant) boundary NE and normally hyperbolic.
- 13
The literature nowadays often also refers to it as the McGehee representation.
- 14
J-P Marco instead has results showing that normally hyperbolic submanifolds of Hamiltonian systems, which also satisfy some extra conditions, are symplectic.
- 15
In the chemistry literature, which until now has focused on the basic scenario, these are referred to as the 'activated' complexes, states or surfaces, see e.g. Henriksen and Hansen [20, p 140].
- 16
This is not necessarily the case. An example of an orientable, codimension-2 normally hyperbolic submanifold with non-orientable stable and unstable manifolds is the orbit cylinder formed by a family of inversion hyperbolic periodic orbits (with negative characteristic multipliers) parametrized by the energy in a two degree of freedom system. This has local stable and unstable manifolds diffeomorphic to a Möbius strip cross an interval, and emerges, for example, out of a period doubling bifurcation of an elliptic periodic orbit, see e.g. [1, p 599].
- 17
Assumed non-degenerate and hence a smooth energy function, else it can have conical singularities, see e.g. [11].